Taking the right course navigating the ERC universe

Abstract

We study the equal risk contribution (ERC) investment strategies exploring how these portfolios perform relative to traditional risk-only (minimum variance portfolio), risk–return (Markowitz portfolio) and naïve (1/n) investment schemes when expanding the asset class universe. We propose a combinatorial mechanism to expand the investment universe of all feasible ERC portfolios and then combine them, thus realizing an ERC efficient frontier consistent with the mutual fund separation theorem (Merton in J Financ Quant Anal 7:1851–1872, 1972). In doing this, we mitigate the out-of-sample estimation error in portfolio weights and better diversify asset allocation against unpredictable extreme events. Simulation, bootstrapping and empirical experiments indicate that the corresponding tangency portfolio, computed through the regression-based approach introduced in Britten-Jones (J Finance 54:655–671, 1999), offers better risk-adjusted performance relative to risk-only, risk–return-based competitors as well as the 1/n strategy.

Introduction

Wealth allocation across risky assets can be more efficient when limiting the informational set to a risk-only parameter instead of solving the portfolio selection problem using the two-moment distribution as in Markowitz (1952). This is, in a nutshell, the main message of the risk parity (RP) approach, which has been gaining popularity among practitioners (Asness et al. 2012), especially during (and after) the global financial crisis of 2008–2011, when the risk–return informational set led to huge estimation errors. A number of papers devoted considerable effort to the issue of estimation error in the portfolio optimization problem. Green and Hollifield (1992) observe that when using sample moments, the resulting portfolios are often highly non-diversified. Merton (1980) proves that the influence of the estimation error in the mean is more critical than the error in the variance. And again, Jobson and Korkie (1980) write “naïve formation rules such as the equal weight rule can outperform the Markowitz rule.”

The reason why the risk-only paradigm should be better than the risk–return approach is technically linked to parameter estimation and portfolio diversification issues. As Michaud (1989) discussed in his Markowitz optimization enigma, mean–variance (MV) optimizers act as estimation error maximizers, producing extreme weights over time with poor performance and lack of diversification. Estimation error maximization is also exacerbated by jumps in correlations and volatilities in equity markets, next reflecting on asset class risk contributions that greatly exceed their corresponding wealth allocations: A typical 60/40 (equity/bond) portfolio may indeed show 90/10, or even more, risk contributions during times of stress. Moreover, DeMiguel et al. (2009) prove that the $1/n$ naïve portfolio outperformed traditional MV optimal portfolios and other various asset allocation models, thus reopening the question of better portfolio diversification.

RP offers a simple rule, based on risk instead of wealth diversification. The beauty of this approach is that by equalizing the risk allocation/contribution across asset classes, thus overweighting safer assets relative to their weight in the market portfolio, we obtain better performance out-of-sample and better portfolio diversification. As noted by de Jong (2018), risk parity is the solution to the Markowitz optimization problem if portfolios are presumed vulnerable to unforeseen price shocks.

The literature on RP is extensive¹ and focuses on the inner technicalities of risk-only portfolios (Lindberg 2009; Maillard et al. 2010), as well as on a possible theoretical foundation of the approach, such as the leverage aversion theory introduced in Asness et al. (2012).

Being part of the risk-based portfolio strategies, RP is conceptually linked to the minimum portfolio variance. On this issue, Jurczenko et al. (2013) have shown that risk-based portfolios can be conceived as special cases of a generic function defined by a first parameter that controls the intensity of regularization and a second one that determines the tolerance for individual total risk. However, as argued in Clarke et al. (2013), minimum variance portfolios “… equalize the marginal contributions of each asset to portfolio risk, in contrast to the risk parity portfolio, which equalizes each asset’s total risk contribution. Thus, risk parity portfolios generally lie within the efficient frontier, rather than on it.”

The question on risk-based portfolio strategies has been recently addressed in Lee (2014), who notes that the superiority of the risk-based approaches is not deriving from a novel asset-pricing theory but rather is built upon the ability to further push the resulting portfolio toward the efficient frontier.

One distinct subclass of the risk parity approach that has attracted great interest among practitioners is the equal risk contribution (ERC), where the objective is to equalize risk contributions from each asset to the portfolio (Roncalli 2013). Empirical evidence proves that ERC portfolios perform better than other portfolio optimization schemes based on Sharpe ratios and average returns. Nevertheless, such a performance superiority seems exploitable under some specific circumstances, namely when using diversified asset classes (Maillard et al. 2010) and when asset classes have similar Sharpe ratios and constant correlation structures (Kaya and Lee 2012).

On the other hand, possible lack of portfolio diversification due to its “genetic” propensity to overweight low-volatility assets (Qian 2011) and potential biases in risk assessment (volatility), especially during extreme events (Inker 2011), can lead toward sub-optimal ERC portfolios. These two criticisms are of course strictly intertwined and connected to the asset class universe that portfolio managers use in forming their expectations on parameter estimates, which translate into specific asset allocation decisions.

In this paper, we first explore how ERC portfolios perform relative to traditional risk-only (minimum variance portfolio), risk–return (Markowitz portfolio) and 1/n schemes when changing and expanding the asset classes. Secondly, we introduce a novel approach in forming ERC portfolios in which: (1) we expand the investment universe based on subset ERC portfolios, each computing optimal weights over all possible subsets of m to n, with $n > m$, assets; (2) we realize the corresponding ERC efficient frontier, using the full set of ERC portfolios and select the corresponding tangency portfolio using the regression-based approach introduced in Britten-Jones (1999). We prove that such a tangency portfolio, we call Dynamic-ERC portfolio, mitigates the out-of-sample estimation error in portfolio weights and better diversify asset allocation against unpredictable extreme events.

The approach is theoretically consistent with the mutual fund separation theorem (Merton 1972), implying an investment in the tangency portfolio which should contain, first, the original securities only and, second, all assets (old and new). It is also computationally complimentary to Gillen (2016), who recently proposed the “subset optimization algorithm” in which many “subset portfolios” are first computed by optimizing weights over a subset of only randomly selected securities from the full set, next naively weighting these subset portfolios.

As in Gillen (2016), we create a large number of subset portfolios in order to diversify the impact of estimation error across subsets, next computing the Dynamic ERC as the tangency portfolio using the subset portfolio clusters as meta-assets. In doing this, we realize a Markowitz–ERC mixing strategy, which reduces extreme negative and unpredictable events through diversification and allows to benefit from momentum.

In our experimental exercises, we prove that our Dynamic-ERC portfolio offers better risk-adjusted performance relative to portfolio competitors.

In more depth, using data over the period from January 2001 to August 2013, we implement a rolling backtest by running a comparative analysis between ERC portfolios and corresponding Markowitz, minimum variance and 1/n portfolios, finding significant overperformance against the MV and 1/n approaches, but no clear statistical evidence relative to minimum variance. On the other hand, the tangency portfolio strongly overperforms the minimum variance competitor as well as single ERC, Markowitz and 1/n portfolios, also offering higher diversification and low portfolio weight concentration (Herfindahl index).

To understand whether the empirical results are robust or purely incidental, we conduct both Monte Carlo simulation and bootstrapping analysis, thus taking into account, in one case (Monte Carlo simulation), only the first two moments of the return distribution, and in the other (bootstrap analysis), the entire return distribution, and then include extreme negative returns (e.g., Lehman collapse). Interestingly, bootstrap analysis confirms significant overperformance of our approach versus all competing strategies, while Monte Carlo simulation does not confirm the overperformance versus MV portfolio. The reason is because the approach is well suited for mitigating the impacts from extreme negative and unpredictable events, and these are replicated when bootstrapping the original dataset, while they are not with Monte Carlo simulation.

The rest of the paper is organized as follows. In “The equal risk contribution problem” section, we briefly introduce the equal risk contribution approach and then propose our algorithmic method to realize the ERC universe and compute the tangency portfolio through Britten-Jones (1999). The theoretical framework is presented and discussed in “Theoretical motivations” section, while empirical experiments and computational results are in “Empirical experiments” section. This paper ends with “Conclusion” section.

The equal risk contribution problem

Setting the scene

As discussed in Maillard et al. (2010), the idea of the ERC strategy is to find a risk-balanced portfolio such that the risk contribution is the same for all assets of the portfolio. Specifically, let us start by defining w the vector of portfolio weights, ${\varvec{\Sigma}}$ is the covariance matrix, and $k = 1, \ldots , N$ the number of asset classes used in forming the optimal portfolio. Mathematically, the problem of finding the ERC portfolio can be expressed as the following optimization problem:

$${\mathbf{w}}^{\varvec{*}} = {\text{argmin}}\;f\left( {{\mathbf{w}};\,{\mathbf{a}}} \right)$$

(1)

s.t.:

$${\mathbf{1^{\prime}w}} = 1 \wedge 0 \le w_{k} \le 1$$

(2)

where

$$f\left( {{\mathbf{w}};\,{\mathbf{a}}} \right) = \mathop \sum \limits_{k = 1}^{N} \left( {w_{k} \partial_{{w_{k} }} \sigma \left( w \right) - a_{k} \sigma \left( w \right)} \right)^{2}$$

(3)

s.t.:

$${\mathbf{1^{\prime}}}{\mathbf{a}} = 1 \wedge 0 \le a_{k} \le 1$$

(4)

The function $f\left( {{\mathbf{w}};\,{\mathbf{a}}} \right)$ is the objective function to be minimized under the additional constraints ${\mathbf{1^{\prime}}}{\mathbf{a}} = 1$ and $0 \le a_{k} \le 1$ in which $\left[ {w_{k} \partial_{{w_{k} }} \sigma \left( w \right)} \right] = RC_{k}$ is the risk contribution of asset k to the total portfolio risk $\sigma \left( w \right)$, also expressed in matrix form as $RC_{k} = w_{k} \frac{{\left( {{\mathbf{\varSigma w}}} \right)_{k} }}{{\left( {{\mathbf{w^{\prime}\varSigma w}}} \right)^{1/2} }}$. The ERC portfolio is obtained by setting $a_{k} = a\; \forall k$ in $a_{k} \sigma \left( w \right)$, which represents the risk budget allocated to asset k. Note the no short-sale restriction and weights summing to unity (Eq. (2)), as commonly imposed by many institutional investors.

As pointed out by Lee (2011), while in the MV optimization global optimal solution is achieved thanks to the convex objective function,²$f\left( {{\mathbf{w}};\,{\mathbf{a}}} \right)$ has multiple local optima and hence a numerical method may easily be trapped in sub-optimal solutions. To overcome this problem, we can optimize a convex function and then modify the vector w by nonlinear constraints, in order to achieve the equally weighted risk contributions for all assets. More formally:³

$${\mathbf{w}}^{\varvec{*}} = {\text{argmin}}\frac{1}{2}{\mathbf{w^{\prime}\varSigma }}\varvec{w}$$

(5)

s.t.:

$$RC_{k} = RC_{j} \forall k,\forall j \wedge {\mathbf{1^{\prime}}}{\mathbf{w}} = 1\varvec{ } \wedge \varvec{ }0 \le w_{k} \le 1 \wedge {\mathbf{1^{\prime}}}{\mathbf{a}} = 1 \wedge 0 \le a_{k} \le 1$$

(6)

in which w is the vector of weights assigned to each asset, ${\varvec{\Sigma}}$ is the covariance matrix and $a_{k}$ is the risk budget for the asset k.

Maillard et al. (2010) observe that ERC portfolio is an intermediary between the minimum variance and the equal weight portfolios, also proving that ERC portfolio is optimal when assuming a constant correlation matrix and supposing that the assets have all the same Sharpe ratio: Under these conditions, portfolio’s weights are the Sharpe ratio maximizing portfolio’s weights. However, when correlation differs or when assets have different Sharpe ratios, the ERC portfolio will be different from the maximum Sharpe ratio portfolio.

Another issue is about the risk preferences implied in the ERC approach. Indeed, as the ERC portfolios tend to favor low-beta and low idiosyncratic risk assets by construction (Maillard et al. 2010; Kaya and Lee 2012), investors may be perceived as risk seeking rather than risk averse in their search for return target. In our framework, this is not the case, since the objective function we use in the portfolio optimization problem assumes a strictly concave utility function, which, in turns, implies that investors are risk averse. This is true for ERC approach as well as for other portfolio competitors we consider in our study (MV and minimum variance portfolios), as the corresponding objective functions assume in all cases the same standard quadratic utility function.

Expanding the investment universe

As discussed in “Introduction,” ERC portfolios are expected to perform better than other portfolio optimization schemes when using diversified asset classes with: (1) similar Sharpe ratios, (2) constant correlation structures. As a result, one fundamental issue concerns the investable asset universe used in forming the equally weighted risk contribution portfolios.

To handle this issue, we start characterizing a generic set of n asset classes by using a combinatorial expansion mechanism through which we generate all possible portfolios consisting of a series of asset class subsets.

Mathematically, having n asset classes we impose a minimum of m asset classes to be included in the portfolio. Therefore, the combinations available to the investor, upon which she/he next proceeds with the optimization process, lie within the space $\left[ {m;\,n} \right]$ and can be determined through the binomial coefficient $\left( {\begin{array}{*{20}c} n \\ k \\ \end{array} } \right) = \frac{n!}{{k!\left( {n - k} \right)!}}$ where $k = n - m$.

Based on this argument, we then expand the investment universe by realizing piecemeal portfolio combinations with $\left[ {k + 1, k + 2, \ldots , k + \left( {n - k} \right)} \right]$ asset classes and then obtain a total of

$$Q = \mathop \sum \limits_{k = m}^{n} \left( {\frac{n!}{{k!\left( {n - k} \right)!}}} \right)$$

(7)

portfolios with $m < n$. Suppose, as we arbitrarily put in our empirical experiment, that $m = 4$ and $n = 8$, the resulting number of possible portfolios forming the investment universe is 163.

In such a doing, we can next proceed by solving the portfolio optimization problem taking into account all feasible combinations.

ERC tangency portfolio

The combinatorial mechanism through which we expand the investable universe allows us to look at ERC portfolios as risky asset classes to be combined in forming the optimal ERC portfolio. To do this, we follow the regression-based approach introduced in Britten-Jones (1999) running an ordinary least squares (OLS) regression of a constant vector of 1s onto a set of risky asset excess returns without an intercept term. As proven in Theorem 1 (Britten-Jones 1999, p 658), the corresponding estimated scaled (so that weights sum to one) coefficient vector is the tangency portfolio whose returns are located in terms of least squares distance as closely as possible in mean–standard deviation space to the arbitrage return vector 1, which is highly desirable as the portfolio has positive return with zero sample standard deviation, and then it is sample efficient.

The procedure executed within the ERC universe needs, of course, a parsimonious number of “covariates” to use in the artificial OLS regression. We then realize equally weighted beta-sorted ERC portfolios using the CAPM-based beta estimated through the following equation,

$$r_{it} = \alpha_{i} + \beta_{i} r_{Bt} + \varepsilon_{t}$$

(8)

where $r_{it}$ is the return of the ith ERC with $\mathop \sum \nolimits_{i} = Q$ at time t and $r_{Bt}$ is the return on the portfolio-specific benchmark B at time t, while $\varepsilon_{it}$ is the error term at time t for portfolio i.

Computationally, we first proceed by estimating the rolling CAPM-based betas according to Algorithm 1.

Based on this routine, we then obtain a $Q \times \left( {T - v} \right)$ matrix of rolling betas B:

$${\mathbf{B}} = \left[ \begin{aligned} {\mathbf{b^{\prime}}}_{1} \hfill \\ \vdots \hfill \\ {\mathbf{b^{\prime}}}_{{\left( {T - v} \right)}} \hfill \\ \end{aligned} \right]$$

(9)

with

$${\mathbf{b^{\prime}}}_{t} = \left[ {\beta_{1t} , \ldots ,\;\beta_{it} , \ldots ,\;\beta_{Qt} } \right]$$

(10)

the CAPM-based betas on the i portfolios in period t with $t = \left( {v + 1} \right),\; \ldots ,\;T$.

Next, we construct beta-sorted portfolio deciles on each element of the matrix B deciles as

$$\overline{ERC}_{dt} = \frac{1}{{N_{d} }}\sum\limits_{f = 1}^{{N_{d} }} {ERC_{ft} }$$

(11)

which denotes the dth equally beta-sorted portfolio of N_d single f ERC pertaining to the same decile at time t with $t = \left( {v + 1} \right),\; \ldots ,\;T$ and $d = 1,\; \ldots ,\;D \equiv 10$.

The returns on the D portfolio deciles at time t in $t = \left( {v + 1} \right),\; \ldots ,\;T$ are denoted by the D elements of the vector ${\mathbf{erc}}_{t}$:

$${\mathbf{erc^{\prime}}}_{t} = \left[ {erc_{1t} , \ldots ,\;erc_{it} , \ldots ,\;erc_{Dt} } \right]$$

(12)

The $\left( {T - v} \right)$ observations of the returns of the erc portfolio deciles are next combined in the following $D \times \left( {T - v} \right)$ matrix:

$${\mathbf{ERC}}_{t} = \left[ \begin{aligned} {\mathbf{erc^{\prime}}}_{1} \hfill \\ \vdots \hfill \\ {\mathbf{erc^{\prime}}}_{t} \hfill \\ \vdots \hfill \\ {\mathbf{erc^{\prime}}}_{{\left( {T - v} \right)}} \hfill \\ \end{aligned} \right]$$

(13)

At this point, the tangency portfolio is computed on a monthly basis by running the Britten-Jones (1999) auxiliary OLS regression, while constraining the coefficients to be nonnegative and to sum to 1, based on Algorithm 2.

where 1 is the vector of 1 s and ${\mathbf{g}}_{t}$ is the vector of portfolio loadings at time t.

Theoretical motivations

In this section, we provide theoretical motivations of the proposed approach and discuss on the connections with recent portfolio theory literature. Firstly, the model we propose is consistent with Ukhov (2006), who studies the mean–variance optimization problem when adding a new risky asset to the existing investment universe deriving the analytical relation between the original and the new minimum variance frontiers. Secondly, the approach is also contextualized within the issue on portfolio weights’ estimation error, as the subset portfolio generation mechanism reduces the individual subset portfolio weights’ variance, thereby increasing portfolio diversification.

Expanding the investment universe

The first theoretical reason why the proposed approach is expected to be outperforming relative to competing portfolio strategies relates to the impact on covariances and tangency portfolio when expanding the asset set. As proven by Ukhov (2006), when adding a new asset to the original investment universe, the novel efficient frontier can be related to the original one through covariance matrix partitioning. Analytically, having m risky assets and adding another a risky asset with m-vector of covariances with the original risky assets $\varvec{\sigma}_{{ma}} = \left( {\sigma_{1a} ,\sigma_{2a} , \ldots ,\sigma_{ma} } \right)^{'}$, and $\sigma_{a}^{2}$ denoting the variance of the a-asset, the novel covariance matrix is

$$\mathop \sum \limits_{{\left( {m + 1} \right)}} = \left( {\begin{array}{*{20}c} {\varSigma_{\left( m \right)} } & {\varvec{\sigma}_{ma} } \\ {\varvec{\sigma}_{{ma}}^{\varvec{'}} } & {\sigma_{a}^{2} } \\ \end{array} } \right) ,$$

(14)

where $\varSigma_{\left( m \right)}$ is the covariance matrix of the original m assets. The analytical relation between $\varSigma_{\left( m \right)}$ and $\varSigma_{{\left( {m + 1} \right)}}$, which involves matrix manipulation in order to compute the inverse of the covariance matrix,⁴ leads to identify the point of tangency of the two frontiers where no wealth is invested in the new asset. Commenting the properties of this point of tangency, Ukhov (2006) extends the two mutual fund theorem of Merton (1972),⁵ proving that given m original assets and adding a new one, to span the frontier the investor cannot simply sell some shares in each of the two mutual funds and use the proceeds to buy the new asset, but she/he needs a third mutual fund investing in all assets in the economy. With such a third fund, the investor re-allocates between the two original funds and the new fund.

The characterization of the effect of increasing the asset space leads the tangency portfolio (TP) of the expanded asset space to dominate the global minimum variance portfolio (GMV), as the variance of the complete subset portfolio that minimizes portfolio variance declines monotonically in subset portfolio size. To put this point into perspective, let us consider the following numerical example with two securities in two scenarios and next add a third security to finally explore the location in the risk–return space of the TP and GMV.⁶

Input parameters are reported in Table 1, and efficient frontiers in both scenarios with two and three securities are reported in Fig. 1. Note that TP dominates GMV in terms of expected reward-to-volatility ratio in both scenarios with 2 and 3 assets.

Table 1 Numerical example—input parameters

Fig. 1

GMV and TP on the expanded efficient frontier. The figure reports efficient frontiers generated with 2 and 3 assets using data in Table 1 corresponding to Scenario 1 and Scenario 2. For both scenarios, we report the tangency portfolio with 2 (OPT2) and 3 (OPT3) assets with corresponding reward-to-volatility ratio (RTV), as well as for global minimum variance portfolios with 2 (GMV2) and 3 (GMV3) assets

As is clear, the expanded efficient frontier depends on the expected return on the new assets as well as on the modified covariance structure. Certainly, the implication of this result is extremely relevant for our problem, since we theoretically explain why mean–variance maximizer should invest in the tangency portfolio of the expanded frontier, as it is expected to outperform GMV through better diversification effects also taking into account expected returns of the new assets. According to the mutual fund separation theorem (Merton 1972), such a portfolio will reflect the need to, first, invest in the original securities only and, second, hold additional funds for investing in all assets (old and new).

Out-of-sample estimation error

A second reason why our methodology is expected to be ex ante efficient is because of the effect on the out-of-sample estimation error of portfolio’s weights. To make the point clear, let us consider first Kan and Zhou (2007), who show that portfolio weights can be thought as function of the observed data and, as such, they suffer from estimation error. More formally, if we denote by $\varvec{w}^{\varvec{*}}$ the vector of optimal weights, namely the weights computed based on the true parameters, and by $\widehat{\varvec{w}}$ the vector of the estimated weights, those computed based on the observed data, then a strictly positive expected loss function can be obtained by comparing expected utility from $\varvec{w}^{\varvec{*}}$ and $\widehat{\varvec{w}}$:

$$E\left[ {L\left( {\varvec{w}^{\varvec{*}} \varvec{ },\widehat{\varvec{w}}} \right)} \right] = U\left( {\varvec{w}^{\varvec{*}} } \right) - E\left[ {U\left( {\widehat{\varvec{w}}} \right)} \right] .$$

(15)

Moreover, the authors show that when $T > N + 2$, $\left| {\widehat{w}_{i} } \right| > \left| {w_{i}^{*} } \right|$; therefore, investors who do not know the true parameters and estimate from the data tend to take bigger positions in the risky assets than those who know the true parameters.

The results of Kan and Zhou (2007) are generalized in Gillen (2016), who shows that averaging the weights from many subset portfolios reduces the total sampling error in the complete subset portfolio. In fact, by averaging across subset portfolios, each subset portfolio’s weight is scaled by $m/n$, where $m \ll n$ is the subset security size and n the complete set of securities.

Following the same reasoning, our procedure generates a large number of subset portfolios in order to diversify the impact of estimation error across subsets. However, we improve the estimation error minimization by clustering the full set of subset portfolios based on their systematic risk exposure toward a specific benchmark (beta deciles as clusters), next averaging the weights across subsets in the same cluster. In such a doing, we then reduce the individual subset portfolio weights’ variance, thereby reducing the sampling error in portfolio weights. Once reduced the estimation error, the tangency portfolio we compute using the subset portfolio clusters as meta-assets is therefore expected to be ex post the optimal portfolio in the mean–variance space. Through our Dynamic-ERC portfolio, we realize a Markowitz–ERC mixing strategy, providing a way to reduce extreme negative and unpredictable events through diversification (ERC-component), while benefiting from buying winners and selling losers (Markowitz-component).

To explore this intuition in more depth, in the next section we run an empirical experiment with ERC portfolios compared with GMV, Markowitz and 1/n competitors.

Empirical experiments

Data

As in Kohler and Wittig (2014), we focus on the risk contribution of asset classes, rather than individual assets within an asset class. The investable universe we use in forming ERC, MV, global minimum variance and 1/n portfolios consists of 8 asset classes selected to proxy the global investable universe available to RP-based portfolio managers operating, in particular, in Europe. At the same time, we also run preliminary analyses on their correlation structures to avoid severe multicollinearity. The data were collected over the period from January 1996 to August 2013.

The list of the 8 asset classes (and their proxies) includes: (1) Euro Bond Market (JPMorgan Government Bond Index EMU); (2) Euro Equity Market (STOXX Europe 600 Index); (3) US Equity Market (S&P 500); (4) Equity Emerging Markets (MSCI Emerging Markets Index); (5) Commodity (Dow Jones-UBS Commodity Index Total Return); (6) Bond Emerging Markets (JPMorgan Government Bond Index-Emerging Markets Global); (7) High-Yield Bond Market (Barclays Global High-Yield Index); (8) US Corporate Bond Market (Barclays US Corporate Investment Grade Total Return Index). Summary statistics and correlations of the 8 asset classes are given in “Appendix”.⁷

ERC and portfolio competitors

Based on the listed 8 asset classes, we first expand the investable universe according to Eq. (7) setting $m = 4$ and $n = 8$. Then, the resulting feasible portfolios are $Q = \sum\nolimits_{k = 4}^{8} {\left( {\frac{8!}{{4!\left( {8 - 4} \right)!}}} \right)} = 163$. We next realize the corresponding 163 ERC portfolios following the procedure outlined in “Setting the scene” section over 60-month rolling window estimation in an out-of-sample exercise $\left[ {t_{\tau - 60} ;t_{\tau - 1} } \right]$. Within each of the fixed monthly rolling time windows, we estimate covariance matrix and mean returns, to be then used to compute portfolio weights for the month τ, thus obtaining a pure out-of-sample back-testing. The first estimation of w is for January 2001, using the monthly returns over the period from December 1995 to December 2000. Next, the matrix $\varSigma$ is recalculated on a monthly basis by using a rolling time window of 60 observations following an exponential weighting mechanism to assign greater weight to more recent observations.⁸ We use the same computational scheme to estimate global minimum variance (GMV), mean variance (MV) and 1/n portfolios.

In doing this, we follow the common practice of estimating monthly rolling window covariance matrix (e.g., DeMiguel et al. 2009) as a forward-looking estimate of the future covariance matrix, while controlling for heteroskedasticity and volatility clustering. In fact, as also recently proven in Zakamulin (2015), exponentially weighted covariance matrix, popularized by the RiskMetrics™ group, proves to be an efficient method to provide robust covariance matrix estimates, thereby reducing forecasting error and portfolio tracking error. While Zakamulin (2015) finds that GARCH seems to perform slightly better than exponentially weighted covariance matrix, we are also aware that in medium-/long-time horizons GARCH tends to perform poorly (Laurent et al. 2012). For this reason, we implemented an exponentially weighted covariance matrix estimation.

Moreover, to estimate expected returns in forming MV portfolios, we used an equally weighted moving average approach, since there is a common consensus that expected returns are notoriously difficult to predict, and sophisticated forecasting techniques are usually prone to higher estimation errors. On this point, Goyal and Welch (2008) observe that “the evidence suggests that most models are unstable or even spurious. Most models are no longer significant even in-sample,” and then suggest that models do not help investors seeking to use the predictability when forming portfolios.⁹

The global minimum variance portfolio

GMV is computed by solving the following constrained optimization problem:

$${\mathbf{w}}^{*} = \arg \hbox{min} \frac{1}{2}{\mathbf{w^{\prime}\varSigma w}}$$

(16)

s.t.:

$${\mathbf{1^{\prime}w}} = 1\quad \wedge \quad 0 \le w_{k} \le 1$$

(17)

where w is the vector of portfolio weights, $\varSigma$ is the covariance matrix and $k = 1,\; \ldots ,\;N$ the number of asset classes used in forming the optimal portfolio. The constraints in (17) are because we impose no short-sale restriction and weights sum to unity as for ERC portfolios.

The mean variance portfolio

MV portfolio is computed by maximizing the return to volatility ratio of the portfolio using the same constraints as in the GMV (no short-sale and weights sum to 1), with a risk target equal to the ERC standard deviation:

$${\mathbf{w}}^{*} = \arg \hbox{max} \frac{{{\mathbf{w^{\prime}\mu }}}}{{\sqrt {{\mathbf{w^{\prime}\varSigma w}}} }}$$

(18)

s.t.:

$$\sqrt {{\mathbf{w^{\prime}\varSigma w}}} \equiv \sigma_{\text{ERC}} \quad \wedge \quad {\mathbf{1^{\prime}w}} = 1\quad \wedge \quad 0 \le w_{k} \le 1$$

(19)

where w is the vector of portfolio weights, $\varSigma$ is the covariance matrix, $\mu$ is the vector of mean returns and $\sigma_{\text{ERC}}$ is the volatility of the corresponding ERC portfolio in terms of both size (number of assets) and investable universe (asset class typologies). The constraint $\sqrt {{\mathbf{w^{\prime}\varSigma w}}} \equiv \sigma_{\text{ERC}}$ is introduced to make ERC comparable with Markowitz in a homogeneous risk–return setting and corresponds to the standard deviation of the homolog ERC.¹⁰

The 1/n portfolio

The 1/n strategy involves holding a portfolio weight $w = \frac{1}{n}$ each of the n risky assets. This strategy completely ignores the moments’ estimation (then it ignores the data), only relating to the old wisdom for which in a world that is uncertain, where prediction power lacks, the best strategy is to hold assets in equal amounts (de Jong 2018). DeMiguel et al. (2009) explore almost all sophisticated extensions of the Markowitz rule and find that none is consistently better than the 1/n rule in terms of Sharpe ratio. This is because 1/n rule is less prone to estimation error than more sophisticated approaches. The 1/n strategy is a natural candidate to compare with ERC portfolios, since the equal risk contribution approach mimics the diversification effect of equally weighted portfolios, as commented before.

Comparative analysis of ERC, GMV, Markowitz and 1/n Portfolios

We first inspect and contrast the ERC universe with the corresponding minimum variance, Markowitz and 1/n universes, exploring each of all possible asset combinations inside the space of feasible portfolios. Specifically, we compare one-to-one the 163 ERC portfolios with corresponding GMVs, MV and 1/n portfolios. In so doing, we measure the extra performance of each ERC portfolio against the corresponding competitor, which act as ERC-specific benchmark in a CAPM framework.

Over the entire period January 2001–August 2013, we compute the Jensen’s alpha by regressing each ERC onto the corresponding GMV, MV and 1/n, namely

$$r_{i} = \alpha_{i}^{b} + \beta_{i} r_{i}^{b} + \varepsilon_{i}^{b}$$

(20)

with $i = 1, \ldots , 163$ and $b = {\text{GMV}},\;{\text{MV}},1/n$ where $r_{i}$ denotes the ith ERC return, $r_{i}^{b}$ the return of the ERC-specific benchmark and α and β the Jensen’s alpha and the CAPM. This signifies that we run $163 \times 3 = 489$ regressions obtaining: (a) 163 alphas for the ERC versus GMV; (b) 163 alphas for ERC versus MV universe; (c) 163 alphas for the ERC versus 1/n. The results of the comparative analyses are reported in Table 2.

Table 2 ERCs versus MVs, GMVs, (1/n)s

ERC versus Markowitz

Consider first the ERC versus MV portfolio analysis. Table 2 shows statistics about alphas and corresponding t statistics. On average, the annualized Jensen’s alpha is 1.86%, ranging from − 2.72% (min) to 3.89% (max). The overall mean is statistically significant, and the proportion of positive alphas over the 163 portfolio combinations (${\text{Prob}} > 0$) is 87.73%. Inspecting in more depth the statistical significance of these results, individual t-stats of alphas confirm the strong outperformance of ERC relative to MV. On average, the t-stat is 2.09 and the number of significant positive alphas at least at the 0.1 level is 104, while only one negative alpha is statistically significant. Hence, we confirm the strong dominance of the ERC frontier over the Markowitz portfolios.

ERC versus GMV

Consider now the ERC versus GMV comparison and look at alphas and t statistics in Table 2. Although ${\text{Prob}} > 0$ is 80.98% with significant overall annualized mean alpha of 0.30%, statistics on individual t-stat lead us to conclude that on a risk-adjusted basis ERC and GMV performances are not statistically different. In fact, only two positive alphas are statistically significant, thus indicating that while the ERC frontier is slightly over the GMV one, we cannot conclude for ERC dominance over the GMV portfolios. These findings confirm Leote de Carvalho et al. (2012), who analyze different risk-only-based strategies over the period from 1997 to 2010, finding that minimum variance shows the highest Sharpe ratio and behaves as one of the most efficient portfolios in terms of maximized returns per unit of risk over the last few decades.¹¹

ERC versus 1/n

Finally, let us observe how ERC performs relative to the 1/n rule. Alphas and t statistics in Table 2 document the strong performance superiority of ERC: Jensen’s alpha is positive for all 163 cases, of which 138 (approximately the 85%) exhibit statistical significance at least at 0.1 level. We therefore confirm the findings of Maillard et al. (2010), who empirically prove that equally weighted portfolios are inferior in terms of performance compared to ERC.

The ERC tangency portfolio

As discussed in “Theoretical motivations” section, tangency portfolio is expected to outperform GMV on the expanded efficient frontier in force of the mutual fund separation theorem (Merton 1972), which leads to better diversification effect while taking into account expected returns of the new assets, and in force of portfolio weights’ estimation error minimization through the subset portfolio generation mechanism which translates into a better portfolio diversification. To compute tangency portfolios using the entire ERC universe of 163 portfolios, we implement Algorithm 1 and Algorithm 2. As specified in “ERC tangency portfolio” section, the benchmark in Eq. (8) is fund specific, as the tangency portfolio is conceived with the objective to outperform specific portfolio competitors. Based on our empirical findings, which prove that ERCs significantly outperform MV and 1/n competitors, while comparing with GMV the extra performance is not statistically significant for all but 1 ERC, we then choose the GMV as fund-specific benchmark in running Eq. (8). In more depth, we use the equally weighted average of the GMV portfolios generated through the combinatorial mechanism of universe expansion (Eq. (7)):

$$r_{Bt} = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} r_{i,t}^{\text{GMV}}$$

(21)

with $N = 163$ as for ERC portfolios.

In running the procedure, we recompute weights one step ahead, thereby estimating the time-varying sequence of optimal ten beta-sorted ERC portfolios to be next used to project the estimated weights onto the asset classes within each of the ten equally weighted portfolios of ERC portfolios. The portfolio of ERC portfolios we propose is thus dynamic by construction and this explains why we call Dynamic-ERC (D-ERC).

Performance

In Fig. 2, we report the portfolio value of D-ERC over the period from September 2003 to August 2013 and the values for single ERC, GMV, MV and 1/n based on all the 8 asset classes together with the plain 60/40 benchmark computed as 60% equity (MSCI World) and 40% bonds (JPM Global Aggregate) with a monthly rebalancing. This comparative analysis gives us the first answer to the question involving the overperforming ability taking into account the complete 8-asset-class universe. Note that over the inspected period, our D-ERC exhibits a rising path until May 2008, next exhibiting a negative performance during the Lehman crash, while just from February 2009 the performance turns positive with a new growing cycle until the period August 2011–June 2012, when contagion in Europe from the Greek crisis, and reinforced by the Ireland, Portugal, Spain and Italy debt and bank problems, spreads across markets. However, from the “whatever it takes” speech by the ECB president Mario Draghi of July 2012, the D-ERC again shows high positive performance until the end of the period. The portfolio value moved from 100 in August 2003 to 225.37 in August 2013, against end-of-period portfolio values of 174.54 for ERC, 170.12 for 60/40, 158.36 for GMV, 152.72 for MV and 209.09 for 1/n. These data clearly prove the strong overperformance of D-ERC in a “buy-and-hold ‘till the end” perspective, while 1/n exhibits a final value approaching that of our D-ERC. To explore in more depth the risk-adjusted performance and better understand the behavior of all the investment schemes, in Table 3 we report performance statistics for D-ERC and the other portfolio alternatives, which confirm the overall performance superiority on a risk-adjusted basis. The Sharpe ratio is the highest (0.267 vs. 0.217 for ERC, 0.201 for GMV, 0.140 for MV, 0.116 for 60/40 and 0.180 for 1/n), and the number of positive returns over the period (${\text{Prob}} > 0$) is 72.50% of the total observations, which is greater than those shown by portfolio competitors (ERC: 67.50%; GMV: 64.17%; MV: 65.83%; 60/40: 61.67%; 1/n: 70%). Interestingly, risk-only portfolios (D-ERC, ERC, GMV) exhibit moderate worst scenarios (Min) compared to risk–return (MV, 60/40) portfolios that show high excess kurtosis with low Sharpe ratios; 1/n exhibits the highest worst scenario (Min) with very high volatility. Finally, by regressing the D-ERC returns against all competitors, we obtain significant positive Jensen’s alphas except for ERC, thus confirming the strong outperformance against almost all competitors.

Fig. 2

D-ERC and portfolio competitors. The figure shows the portfolio values of D-ERC, and the ERC, GMV, MV, 60/40 and 1/n portfolios computed using the 8 asset classes over the period September 2003–August 2013. The starting value for all portfolios is set at 100

Table 3 D-ERC performance metrics

Even looking at monthly statistics, we then confirm the D-ERC overperformance, albeit the comparative analysis was carried out by only considering one out of the 163 possible portfolio combinations.

To better scrutinize the D-ERC performance inside single ERC, GMV, MV and 1/n universes, we run the CAPM-based equation, using as benchmark each of the 163 GMV, MV and 1/n portfolios, and then inspect alphas and t statistics. The results in Table 4 confirm the strong and significant outperformance of D-ERC: On average, the annualized alpha is 4.60, 3.61 and 3.91% relative to GMV, MV and 1/n portfolios, respectively. All alphas are positive, ranging from (min–max) 3.62 to 6.14% (vs. GMV), 1.38 to 6.49% (vs. MV) and 2.65 to 5.38% (vs. 1/n) with all single t-stats significant at least at the 0.1 level when comparing against GMV and 1/n, while 149 out of 163 against MV.

Table 4 D-ERC versus ERCs, GMVs, MVs, (1/n)s

The overall average of annualized alphas exhibited by D-ERC against single ERCs is positive (2.95%) with a range from 1.83% (min) to 5.38% (max). However, by exploring single t-stat values, 90 out of 163 appear to be statistically significant, that is, slightly more than 50% of all ERCs. This result is indicative of how the dynamic linear combination of single ERCs made through the Britten-Jones technology does not dominate the overall ERC universe, which is in a sense consistent with the inner philosophical rationale of the D-ERC, conceivable as the “coarse-grained” ERC universe, thus removing extremes in the multidimensional behavior of the ERC portfolios while catching up their main dynamics.

The important findings we obtain in this comparative analysis are related to the strong statistical significance of the D-ERC outperformance relative to the GMV and 1/n universe. Indeed, having found beforehand a not significant overperformance of the ERCs relative to the GMVs, we next moved on to questioning the real value offered by complex risk-only portfolios compared to simple risk-only solutions, finally proposing a Britten-Jones-based combination of beta-sorted ERC portfolios as the best way to navigate through the ERC universe. And this is indeed the case, since our D-ERC portfolio is at the top of the possible portfolio allocation strategies in terms of risk-adjusted performance.

Robustness checks: bootstrap analysis and Monte Carlo simulation

To check the robustness of our approach, we run bootstrap analysis and Monte Carlo simulation. In fact, the results obtained and commented in the previous section could be incidental and reflecting the data used to run our experiments. Bootstrap analysis allows us to take into account the entire return distributions of portfolios, then include extreme events (e.g., Lehman collapse) and therefore mimic the same dependence structure as the original data, while Monte Carlo simulation gives us insights on the robustness of the model using only the first two moments of the distributions. Both robustness checks are therefore interesting, as differences from the results of the two analyses are informative on the impacts of higher moment distributions.

More specifically, for bootstrap analysis we randomly resampled 1553 daily returns of the 8 asset classes (about 6-year horizon) from the entire data sample 1996–2013, next using 48-month rolling windows to realize, on a monthly basis, all the 163 subset ERC, GMV, MV, 1/n portfolios. Based on the ERC portfolios, we assembled the D-ERC using Algorithms 1¹² and 2, finally computing the risk-adjusted performance against all the portfolio competitors by estimating the CAPM-based equation using as benchmark each of the 163 GMV, MV and 1/n portfolios. We run this procedure 1000 times, thereby obtaining 1000 Jensen’s alphas for each competitor. Monte Carlo simulation was run following the same procedure, but instead of randomly resampling from the original data sample, we simulated returns for the 8 original asset classes through a Brownian motion process using their covariance structure and their return averages computed over the entire time horizon 1996–2013. Table 5 presents the results showing annualized mean of Jensen’s alphas and corresponding t test. Bootstrap analysis confirms significant overperformance of D-ERC versus all competing strategies, with mean alphas ranging from 0.69 to 1.60% and all p-values close to zero. Differently, Monte Carlo simulation does not confirm the overperformance versus MV portfolio, and ERC shows a lesser robustness relative to bootstrap analysis with mean alpha 0.30% and p-value around 0.04; GMV and 1/n show results similar to those obtained through bootstrap analysis. The higher robustness of bootstrap analysis, which mimics the same structure of the original sample, indicates that D-ERC is particularly appropriate to mitigate impacts from extreme negative and unpredictable events, such as the Lehman collapse. We then conclude that the results obtained from our empirical experiments are not a consequence of the data used but reflect the robustness of our approach, and then confirm the intuitions discussed in “Theoretical motivations” section.

Table 5 D-ERC robustness checks

Portfolio diversification

The final feature we inspect relates to portfolio diversification of the D-ERC. As we discussed before, the expected outperformance of the tangency portfolio is massively based on better diversification effect according to the mutual fund separation theorem (Merton 1972) and reduced portfolio weights’ out-of-sample estimation error.

As a portfolio of ten beta-sorted portfolios of the 163 ERCs, the regression-based coefficients obtained through the constrained Britten-Jones auxiliary OLS are used to spread out over the 8 asset classes the implied asset allocation of D-ERC. As commented before $R_{{{\text{D - ERC}},t}} = \sum\nolimits_{d = 1}^{D} {b_{dt} \overline{\text{ERC}}_{dt} }$ where b are the Britten-Jones constrained regression coefficients and $\overline{\text{ERC}}_{dt} = \frac{1}{{N_{d} }}\sum\nolimits_{f = 1}^{{N_{d} }} {{\text{ERC}}_{ft} }$ denotes the dth equally beta-sorted portfolio of N_d single fth ERC pertaining to the same decile at time t with $t = \left( {v + 1} \right),\; \ldots ,\;T$ and $d = 1,\; \ldots ,\;D \equiv 10$. The return of a single fth ERC is the weighted average of the $N_{d}$ asset returns ${\text{ERC}}_{ft} = \sum\nolimits_{k = 1}^{{N_{k} }} {w_{k,t} R_{k,t} }$ where $N_{k}$ denotes the number of assets used in running the ERC algorithm and $R_{k,t}$ the corresponding return of the kth asset class at month t. Based on this mathematical characterization, we can then reformulate the equation for the D-ERC return at time t as:

$$R_{{{\text{D - ERC}},t}} = \sum\nolimits_{d = 1}^{D} {b_{dt} \frac{1}{{N_{d} }}\sum\limits_{f = 1}^{{N_{d} }} {\sum\limits_{k = 1}^{{N_{k} }} {w_{k,t} R_{k,t} } } } ,$$

(22)

and focus on $b_{dt} \frac{1}{{N_{d} }}\sum\nolimits_{f = 1}^{{N_{d} }} {\sum\nolimits_{k = 1}^{{N_{k} }} {w_{k,t} } }$ for each k asset class, which gives the implied D-ERC portfolio loadings at time t.

Using Eq. (22), we inspect the implied diversification of D-ERC compared to that offered by the 8 assets ERC, GMV, MV and 1/n competitors. The portfolio diversification is explored based on different indicators over the estimation period. The first measure is the diversification ratio (Choueifaty and Coignard 2008) computed as the ratio of the portfolio’s weighted average volatility to its overall volatility:

$$D_{p} = \frac{{{\mathbf{w^{\prime}}}_{p} {\varvec{\upsigma}}}}{{\sigma_{p} }} ,$$

(23)

where ${\mathbf{w^{\prime}}}_{p}$ is the transposed vector of weights of portfolio p, σ is the $1 \times 8$ vector of standard deviations of the 8 asset classes, and $\sigma_{p}$ is the standard deviation of the portfolio p. To compute this ratio, we use the averages of asset weights over the inspected period. The diversification ratio is at the core of the concept of diversification as it compares the risk without the covariance term (numerator) to the portfolio risk including the covariance terms. This reflects in ratios greater than or equal to one (for long-only portfolios) and equals unity for a single asset portfolio.

The diversification level can also be assessed focusing on portfolio concentration through the Herfindahl index. We use the normalized version proposed in Maillard et al. (2010) by computing

$$HI_{p,t} = \frac{{h_{p,t} - 1/n}}{1 - 1/n} ,$$

(24)

where $h_{p,t} = \sum\nolimits_{i = 1}^{n} {\left( {w_{i,t}^{p} } \right)^{2} }$ is the Herfindahl index for portfolio p at time t and $w_{i,t}^{p}$ are the weights of asset i at time t for portfolio p with n the number of assets in the portfolio. $HI_{p,t}$ ranges from 0 (maximum diversification) to 1 (no diversification).

Our third measure derives from Blume and Friend (1975), who measure the diversification as the deviation from the market portfolio weights. In our study, instead of measuring the sum of squared portfolio weights from those of the market portfolio, we focus on the risk contribution of each asset by computing the deviation of each asset risk contribution from 1/n. Computationally, we calculate the root sum of squared asset risk contribution from ERC as follows:

$$\varPsi_{p} = \left[ {\sum\limits_{i = 1}^{n} {\left( {RC\left( {\mathbf{w}} \right)_{p\left( i \right)} - 1/n} \right)^{2} } } \right]^{1/2} ,$$

(25)

with

$$RC_{p\left( i \right)} = \frac{{{\mathbf{w^{\prime}}}_{p\left( i \right)} {\mathbf{\varvec{\sigma} w}}_{p} }}{{\sigma_{p} }},$$

(26)

with ${\mathbf{w^{\prime}}}_{p\left( i \right)}$ denoting the transposed vector of portfolio weights with all zeros except for ith asset class, σ the $1 \times 8$ vector of standard deviations of the 8 asset classes and $\sigma_{p}$ the standard deviation of portfolio p. RC is measured by using the averages of asset weights over the inspected period.

In Table 6, we report results on the three measures used to assess the portfolio diversification. D-ERC is the portfolio with the highest diversification ratio, followed by ERC, GMV, 1/n and MV. The same conclusion is confirmed by the HI index, except for 1/n which is by construction the portfolio with the lowest value, thus indicating low concentration in portfolio weights for D-ERC. All statistics of the index in terms of mean, median, standard deviation, min and max are less than portfolio competitors, again with the exception of 1/n, and also for ERC when considering standard deviation and max. The main message from these features is in favor of the dynamic combination realized through the Britten-Jones regression using the beta-sorted ERCs. As expected, the proposed procedure enhances portfolio diversification, thereby reflecting on better risk-adjusted performance.

Table 6 Portfolio diversification

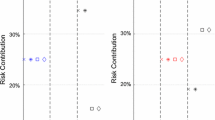
The $\varPsi_{p}$ measure tells us a quite expected story about risk asset contribution, with the single ERC showing the highest diversification and D-ERC exhibiting asset risk contributions ranging from 11.72 to 17.60% excluding Bond Euro, which contributes 0.27% to total portfolio risk. This is the main difference relative to GMV and MV, which have risk contributions of 78.66% (GMV) and 19.85% (MV) for the same bond asset class. Finally, when contrasting D-ERC with 1/n the highest difference in terms of asset class risk contribution is for Equity Emerging Markets, the contribution is 17.60% for D-ERC while for 1/n the contribution is 27.70%.

Conclusion

In this study, we explore the RP paradigm focusing on the ERC approach, shedding light on how these portfolios perform relative to global minimum variance, mean–variance and 1/n portfolios, also proposing a novel approach based on an expansion mechanism of all feasible ERC, to be next assembled within a tangency portfolio consistent with the mutual fund separation theorem (Merton 1972) and conceived with the end to minimize the out-of-sample portfolio weights’ estimation error. By generating a large number of subset ERC portfolios, thus diversifying the impact of estimation error across subsets, we improve the estimation error minimization by clustering the full set of subset portfolios based on their systematic risk exposure toward a specific benchmark (beta deciles as clusters). Finally, we compute the tangency portfolio using the subset portfolio clusters as meta-assets, thus generating our D-ERC model which is therefore expected to be ex post the optimal portfolio in the mean–variance space through better portfolio diversification also taking into account expected returns of assets.

In our experimental exercise, we first generate the space of all possible portfolios using subsets of 4-to-8 asset classes and look inside the resulting ERC universe by running the relative performance analysis contrasting the ERC portfolios with GMV, MV and 1/n competitors. In doing this, we prove that ERCs significantly outperform against Markowitz and 1/n alternatives. However, the tangency portfolio realized through a regression-based approach (Britten-Jones 1999) dominates alternative asset allocation schemes in terms of risk-adjusted performance and portfolio diversification. The robustness of our results was checked through bootstrap analysis and Monte Carlo simulation, both confirming that the results are not a consequence of the data used. We attribute the significant outperformance of D-ERC versus the portfolio alternatives to the Markowitz–ERC nature of the strategy, which provides a way to reduce unpredictable negative events through diversification (ERC-component), while benefiting from buying winners and selling losers (Markowitz-component).

Appendix: Asset class benchmarks

In this Appendix, we report summary statistics and correlations computed for the 8 indices we used as benchmarks for the asset class universe used to realize ERC, GMV, MV and 1/n portfolios. Statistics and correlations are computed over different time intervals.

Tables 7 and 8 report, respectively, summary statistics and correlation structures computed for different time intervals over the entire period from January 1996 to August 2013 of the 8 asset classes used in forming portfolios in our empirical analysis. We first note, as expected, high correlations between equity-based indices especially during stress scenarios (2007–2008 and 2009–2011). Despite the increasing integration of equity markets as shown by correlation structures computed for different time periods reported in the table, European and US equity indices have been notwithstanding included in the dataset, since they are representative of the two main equity markets taken into account by portfolio managers.

Table 7 Asset class benchmarks summary statistics

Table 8 Asset class benchmarks correlations

The Euro government bonds market index plays an important role in portfolio construction, as it tends to act as “portfolio stabilizer” for two reasons. First, as given in Table 7, the index exhibits low volatility also across time with a range of 1.1–1.4%. Second, the index contributes substantially to the portfolio diversification, as proven by looking at correlations with equity markets (except for the periods 1996–2000 and 2012–2013). Similarly, the US Corporate Bond Market index contributes to better diversifying portfolios, as it shows stable returns (Table 7) and sometimes negative correlations (Table 8). However, the index differs from government bond dynamics, especially during periods of corporate default clustering as in 2007–2011, when returns dynamics were mostly driven by credit spreads.

High-Yield and Emerging Market bond indices are two important asset classes, especially in the short run. While descriptive statistics and correlations show that the two indices seem to deliver the same risk-adjusted profile with high correlations, in the short run they may differ significantly in terms of risk and returns (see, e.g., Table 7, 1996–2000 and 2012–2013). Another interesting feature of the High-Yield bond index concerns the high correlation with equity markets with spikes during extreme negative returns of equities, as was the case during the period from 2007 to 2008. This pattern is contrasting with correlations between Investment Grade bonds and equity markets that remained low during times of negative equity returns (see correlations with the Euro, the US and Emerging Markets equity indices during the period 2007–2008).

The emerging market bond index shows higher correlations relative to equity than relative to fixed income, and the Emerging Markets equity index has shown increasing correlations with the Euro and US equity markets as capital market integration became substantial across countries.

Finally, data in tables confirm that commodity acts as an important asset class portfolio diversifier due to its low or negative correlation with traditional asset classes over the long term. However, during periods of economic downturn, such as in the late 2000s, commodities’ correlation with other asset classes, especially equity, tended to sharply increase. Note that commodity delivered equity-like performance over the long run, albeit with significant variations in recent decades. Specifically, such an asset class experienced the best performance relative to equity and fixed income during times of high inflation (2001–2007), thus helping in mitigating the negative effects of inflation risk.