Introduction

“Don’t put all your eggs in one basket”; that is, through portfolio diversification one achieves the best risk-return tradeoff. This is the guiding principle of asset allocation. This principle has led to a growing literature of performance metrics. For example, the Sharpe ratio (Sharpe, 1966) trades off expected excess return for risk measured by volatility. The Sortino ratio (Sortino and Price, 1994) is similar to the Sharpe ratio where the risk depends on the downside deviation. Omega ratio (Keating and Shadwick, 2002) and Kappa ratio (Kaplan and Knowles, 2004) measure risk by the lower partial moments of excess returns. The implication of the metrics is simple: the higher the better. That is, investors should allocate assets in portfolios with the highest Sharpe, Sortino, Omega and Kappa ratios. Another such metric is the Treynor ratio (TR). In this article, we analyze the Treynor ratio’s implications for asset allocation.

Jack Treynor was one of the first to derive a performance metric that depended on the risk-return profile of a portfolio (Treynor, 1965). He posed a simple question: how to evaluate portfolio performance with the market effect subtracted? The result is the TR:

$${\text{TR}}\left( h \right) = \frac{{\varvec{E}\left[ {R\left( h \right)} \right] - R_{f} \left( h \right)}}{\beta \left( h \right)}.$$
(1)

The term \(\varvec{E}\left[ {R\left( h \right)} \right]\) is the expected portfolio return; the term \(R_{f} \left( h \right)\) is the risk-free rate, and the term \(\beta \left( h \right)\) is the portfolio beta. We write the three terms as a function of the investment horizon \(h\) to emphasize that each term is horizon dependent. For example, \(E\left[ {R\left( 5 \right)} \right]\) is the 5-year expected return for an investment horizon of 5 years. The horizon dependence of the numerator \(E\left[ {R\left( h \right)} \right] - R_{f} \left( h \right)\) is natural – we anticipate the expected returns to increase with the investment horizon. Although understudied, the market risk, as measured by \(\beta\), is also horizon dependent (Levhari and Levy, 1977).

As a result, the TR is horizon dependent as well (Levhari and Levy, 1977; Hodges et al, 2002).

To understand the impact of the investment horizon, consider the following example. Jane, a 50-year-old investor, is looking to invest in two funds: VTSMX (Vanguard Total Stock Market Index Fund) and NAESX (Vanguard Small Capitalization Index Fund). She is 15 years from retirement. Figure 1 shows the \(\beta\) (calculated by Morningstar) for the two funds across different horizons. For all horizons, NAESX has a higher \(\beta\) than VTSMX. This result is expected. After all, NAESX is weighted heavily by small cap stocks, and VTSMX is weighted heavily by large cap stocks. Additionally, since VTSMX represents the overall market, it has a \(\beta\) of one across all horizons.

Figure 1
figure 1

Morningstar \(\varvec{\beta }\) across different horizons for two funds: VTSMX (Vanguard Total Stock Market Index Fund) and NAESX (Vanguard Small Capitalization Index Fund) as of August 19, 2015.

Full size image

Figure 2 shows the TR across different horizons. Due to the 15-year investment horizon, Jane finds it optimal to invest in NAESX. Her choice is different from another investor John who is 5 years from retirement. Since the TR of VTSMX is higher than NAESX at a 5-year horizon, John would optimally choose VTSMX. That is, both Jane and John choose differently. The difference in choice is not because the inherent risky of the two funds. The difference is simply due to horizon. Hodges et al (2002) lucidly capture the problematic implications:

Figure 2
figure 2

Treynor ratio across different horizons for two funds: VTSMX (Vanguard Total Stock Market Index Fund) and NAESX (Vanguard Small Capitalization Index Fund) as of August 19, 2015.

Full size image

Betas and Treynor ratios computed from annual returns will not be valid for long-run investors.

In this paper, we theoretically explain the different choices by Jane and John. After the explanation, we offer a solution that resolves the undesirable effect of horizon on the TR. Our solution is deceivingly simple. We suggest to compute the TR using log-returns – not simple returns.

Log-returns provide a solution by addressing the problem at its mathematical root. On the one hand, when one uses simple returns, the h-year multi-period return, \(R\left( h \right),\) aggregates multiplicatively. The multiplicative feature causes the expected excess return, the beta and the TR in turn to depend on the horizon in a nonlinear fashion. On the other hand, if one uses log-returns, the multi-period return aggregates additively. The additive feature causes the expected excess return to increase linearly with the horizon and the beta to be independent of the horizon. Thus, the TR increases linearly with the horizon, which eliminates the ranking reversal.

This study makes three main contributions. First, it provides a theoretical model showing the effect of horizon on both the beta and the TR. Levhari and Levy (1977) were the first to show the adverse effect of horizon on the TR. Hodges et al (2003) empirically corroborate their theory. Both of these studies measure TR using simple returns. As far as we know, we are the first to both theoretically and empirically document the effect of horizon on the TR calculated using log-returns. Specifically, we show that the undesirable effect of TR is overcome when the TR is calculated using log-returns. That is, if both Jane and John were to look at TR calculated using log-returns, then they both would make the same choice.

The second contribution concerns our empirical analysis. Using bootstrapping with replacement, we empirically test the theory using large cap, small cap and corporate bond returns. The data set is the same as the one used by Hodges et al (2002). We are the first to provide TR of several popular test assets over a long horizon (up to 30 years). Taken together, these two contributions show how log-returns eliminate the undesirable effect of horizon on the TR. The third contribution concerns the cross section of TR. Consistent with Hodges et al (2002), we show that corporate bonds have the highest TR across all horizons.

The implications of our study are particularly useful for long horizon investors like Jane. Particularly, we explicitly indicate how the TR (calculated using simple returns) leads to a wrong choice by Jane. The implications of our study also concern the portfolio composition of target-date retirement funds (TRF). Typically, the TRF portfolio becomes more conservative with age. To be more specific, consider the Vanguard Target Retirement 2045 Fund (VTIVX). Even though corporate bonds have the highest TR, the allocation to bonds is less than 10% and the allocation to equity is 90%. In fact, all long-term TRFs overwhelmingly overweigh equities relative to bonds. Based on the TR performance metric, this result is puzzling.

The paper proceeds as follows. In Section “Theoretical model”, we theoretically clarify the effect of horizon on the TR using both simple and log-returns. In Section “Empirical test of the model”, we empirically corroborate our theory. Finally, in Section “Conclusion”, we provide concluding remarks.

Theoretical model

There are three traded assets at time t: a stock with price P S (t), a market index with price P M (t), and a money market account with price P B (t). The h-period log changes in both the stock price and the market are composed of independent and normally distributed increments:

$${\text{Ln}}P_{i} \left( {t + h} \right) - {\text{Ln}}P_{i} \left( t \right) = \left( {\mu_{i} - \frac{1}{2} \sigma_{i}^{2} } \right)h + \sigma_{i} \mathop \sum \limits_{n = 1}^{n = h} \varepsilon_{i} \left( {t + n} \right) for i \in \left\{ {S,M} \right\}$$
(2)

The random variables \(\varepsilon_{S} \left( t \right)\) and \(\varepsilon_{M} \left( t \right)\) are standard normal with mean zero, variance one and correlation ρ.1 The parameters \(\mu_{S}\) and \(\mu_{M}\) are the instantaneous drift rates of the stock and the market index, while parameters \(\sigma_{S}\) and \(\sigma_{M}\) are the instantaneous volatilities. Additionally, we assume that the risk-free rate is constant:

$${\text{Ln}}P_{B} \left( {t + h} \right) - {\text{Ln}}P_{B} \left( t \right) = r_{f} h .$$
(3)

Then h-period simple return \(R_{i}^{S} \left( h \right)\) and the log-return \(r_{i}^{L} \left( h \right)\) are

$$R_{i}^{S} \left( h \right) \equiv P_{i} \left( h \right)/P_{i} \left( 0 \right) - 1\,{\text{and}}\, r_{i}^{L} \left( h \right) \equiv {\text{Ln}}P_{i} \left( h \right) - {\text{Ln}}P_{i} \left( 0 \right) for i \in \left\{ {S,M,B} \right\}.$$
(4)

When the horizon \(h\) is small, slight algebra shows that \(R_{i}^{S} \left( h \right) \approx r_{i}^{L} \left( h \right)\). However, the approximation gets worse with horizon. The worsening of the approximation can be better understood by analyzing the first two moments of the simple and log-returns.2 The expectation, the variance and the covariance of the simple return depend nonlinearly on the horizon \(h\). That is, the statistical properties of the simple returns, ironically, are not so simple. The statistical properties of the log-returns, on the other hand, are considerably simpler. The first two moments of the log-returns are linear functions of the horizon \(h.\)

With the expression for the moments at bay, we define the TR using simple return as

$${\text{TR}}^{S} \left( h \right) \equiv \frac{{\varvec{E}\left[ {R_{S} \left( h \right)} \right] - R_{B} \left( h \right)}}{{\beta^{S} \left( h \right)}} ,$$
(5)

and the TR using log-return as

$${\text{TR}}^{L} \left( h \right) \equiv \frac{{\varvec{E}\left[ {r_{S} \left( h \right)} \right] - r_{B} \left( h \right) + \frac{{\varvec{V}\left[ {r_{S} \left( h \right)} \right]}}{2}}}{{\beta^{L} \left( h \right)}} ,$$
(6)

where the betas are defined as

$$\beta^{S} \left( h \right) = \frac{{\varvec{COV}\left[ {R_{S} \left( h \right),R_{M} \left( h \right)} \right]}}{{\varvec{V}\left[ {R_{M} \left( h \right)} \right]}}\quad {\text{and}}\quad \beta^{L} \left( h \right) = \frac{{\varvec{COV}\left[ {r_{S} \left( h \right),r_{M} \left( h \right)} \right]}}{{\varvec{V}\left[ {r_{M} \left( h \right)} \right]}} .$$
(7)

The variance term in the numerator of Eq. 6 is non-traditional. The term is effectively a convexity adjustment that adjusts for the differences in compounding between simple and log-returns.3

After substituting the germane moments in Eqs. 5 and 6, the \({\text{TR}}^{S} \left( h \right)\) becomes

$${\text{TR}}^{S} \left( h \right) = \frac{{ \exp \left\{ {\left( {\mu_{M} - \mu_{S} } \right)h} \right\}\left( {\exp \left\{ {\mu_{S} h} \right\} - \exp \left\{ {r_{f} h} \right\}} \right)\left( {\exp \left\{ {\sigma_{M}^{2} h} \right\} - 1} \right)}}{{\left( {\exp \left\{ {\rho \sigma_{S} \sigma_{M} h} \right\} - 1} \right)}} ;$$
(8)

and the \({\text{TR}}^{L} \left( h \right)\) becomes

$${\text{TR}}^{L} \left( h \right) = h \times \frac{{\left( {\mu_{S} - r_{f} } \right)\sigma_{M} }}{{\rho \sigma_{S} }} = h \times {\text{TR}}^{L} \left( 1 \right) .$$
(9)

Equation 8 shows that \({\text{TR}}^{S} \left( h \right)\) depends nonlinearly on the horizon \(h.\) The nonlinearity causes non-monotonicity in the TR as evinced in the introductory example.4 Much simpler, Eq. 9 avoids the nonlinearity. \({\text{TR}}^{L} \left( h \right)\) changes linearly with the horizon: \({\text{TR}}^{L} \left( h \right)\) is a mono-tonic function of the horizon, and no ranking reversal occurs.

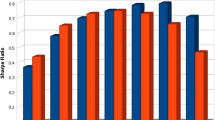
To understand the effect of horizon, consider the TR of large and small cap stocks in Figure 3. We use the large and small cap stocks to be consistent with Hodges et al (2002).5 First, take the case of TR calculated using simple returns (dark filled columns). Upon inspection, the ranking reversal is clear. Large stocks underperform small stocks for a horizon up to 4 years. In fact, the magnitude of underperformance decreases with horizon, so much so that it eventually turns into overperformance. Now consider the case of TR calculated using log-returns (gray filled columns). There is no ranking reversal. Large stocks underperform small stocks for any horizon – there is no ranking ambiguity. The magnitude of the underperformance changes linearly with horizon.

Figure 3
figure 3

This figure shows the difference in the TR between large and small stocks.

Full size image

We conclude this section by highlighting the theoretical implications of the model. In the next section, we empirically test the following hypotheses:

  1. 1.

    The beta calculated using simple returns, \(\beta^{S} \left( h \right)\), changes nonlinearly with horizon. The beta calculated using log-returns, \(\beta^{L} \left( h \right)\), does not change with horizon.

  2. 2.

    The TR calculated using simple returns, \({\text{TR}}^{S} \left( h \right)\), changes nonlinearly with horizon. The TR calculated using log-returns, \({\text{TR}}^{L} \left( h \right)\), changes linearly with horizon.

  3. 3.

    There is no ranking reversal with \(TR^{L} \left( h \right).\)

Empirical test of the model

We test our theory using the same dataset used by Hodges et al (2002). Specifically, we use Ibbotson annual return data from 1928 to 2000 for portfolios of US Treasury bills, long-term corporate bonds, (large) common stocks and small stocks. Additionally, we also test our theory against the Fama–French value, size and industry portfolios across different sample periods. To ensure that sampling frequency does not change our results, we also test our theory using daily, weekly and quarterly data. The change in the sampling frequency does not affect the results qualitatively. To summarize, the empirical predictions of the theory are robust.

Table 2 shows the summary statistics of simple returns, while Table 3 shows the summary statistics using log-returns. The first two moments using both the simple and log-returns for bonds and T-bills are similar in magnitude. This is expected. Neither bonds nor T-bills are volatile, and hence the difference between the simple return and the log-return is negligible over a “small” horizon. However, as we will show later, the first two moments are quite different as the horizon increases. The mean of small stock returns is the most different when one uses simple returns relative to log-returns. With simple returns, the mean is approximately 17% and with log-returns, the mean is around 11%. The difference in magnitude is due to the variance – small stocks are the most volatile.

In Table 4, we show the multi-period beta using both simple and log-returns. We follow the bootstrapping with replacement procedure of Hodges et al (1997) to calculate beta over different horizons, \(\beta \left( h \right)\). Suppose that the horizon is 20 years. Using sampling with replacement, we generate 250, 20-year excess returns (both log and simple). While calculating the 20-year return, we compound appropriately. The number 250 is consistent with Hodges et al (1997). From the set of 250, 20-year returns, we calculate a point estimate of both \(\beta^{S} \left( h \right)\) and \(\beta^{L} \left( h \right)\).

We repeat the procedure 100,000 times and get 100,000 estimates of \(\beta^{S} \left( h \right)\) and \(\beta^{L} \left( h \right)\). Since this portion is computationally intensive, we run the program on a graphics card. Also, we use parallel computing. The number 100,000 is a lot higher than the one used by Hodges et al (1997); this number ensures high degree of accuracy. We report the average value of \(\beta^{S} \left( h \right)\) and \(\beta^{L} \left( h \right)\) from the 100,000 estimates.

Two observations are in order. First, consider the beta calculated using simple returns. The multi-period beta for large and small stocks increases with horizon and the beta of bonds decreases. The 30-year \(\beta^{S}\) for corporate bonds is approximately zero, while the 30-year \(\beta^{S}\) for large stocks increases gradually from approximately one to about 1.09. The \(\beta^{S}\) for small stocks experiences a steeper rise: it increases from 1.34 to 5.34 in 30 years. The dramatic evolution of the beta for the three assets expectedly leads to complex TR behavior. Now, consider the beta calculated using log-returns. Consistent with the theory, the multi-period beta for the three assets does not change with horizon.

Table 5 shows the multi-period TR using simple and log-returns. Again, we use bootstrapping with replacement to calculate the TR. Here, several observations can be made. First, there is a ranking reversal. Small stocks outperform large when the investment horizon is small, and the relative ranking changes as the horizon increases. The ranking reversal takes place when the TR is calculated using simple returns. Second, there is no ranking reversal when the TR is calculated using log-returns. Third, corporate bonds have the highest TR, consistent with Hodges et al (2002). That is, at least from a TR perspective, corporate bonds are the best investment. That being said, their outperformance does not seem to be well known. In fact, their outperformance is often ignored. For example, the allocation to bonds is less than 15% for most TRFs.

Conclusion

Hodges et al (2002) empirically highlight a problematic feature of the TR. They show that the horizon affects the TR in a complex manner. The TR, for example, may decrease with the horizon. More importantly, there may be a ranking reversal. Namely, it may appear that one stock outperforms the other at an annual horizon, but that the opposite holds true at a 5-year horizon. These problematic features are due to compounding. The TR performance metric, which is traditionally calculated using simple returns, is biased because both the expected return and the beta change nonlinearly with horizon. The bias casts doubt on the use of TR for asset allocation.

In this paper, we offer a simple solution. We recommend that investors calculate the TR using log-returns. By using log-returns, we eliminate the negative effect of compounding. With our change, we show that the betas and Treynor ratios computed from annual returns will indeed be valid for long-run investors.

Notes

  1. 1.

    Equation 2 implies that both the stock and the market index dynamics follow a correlated geometric Brownian motion process. Additionally, without loss of generality, we ignore dividends. We can consider dividends by assuming that they are reinvestment back in the asset.

  2. 2.

    The derivation is standard and is available upon request. The expectation and the variance of the simple returns are calculated using a simple application of the moment generating function of a normally distributed random variable. The covariance term is slightly more complicated. It involves application of the moment generating function of a bi-variate normal random variable.

  3. 3.

    The convexity adjustment term is necessary to calculate the risk premia [see equation 12 in Campbell (2003)].

  4. 4.

    Equation 8 is also isomorphic to the multi-period TR as defined in Eq. 4 of Hodges et al (2002). Our formula implicitly assumes that the stock increments take place in continuous time while their formula assumes that time is discrete. When both the independent and dependent variables in a regression are additive, the correlaton coefficient is independent of the horizon [see Eq. 6 in Jea et al (2005)]. Our expression for \(\beta^{L} \left( h \right)\) is an elaboration of their result.

  5. 5.

    We calibrate the model to match the moments in Table 1 of Hodges et al (2002). Specifically, r f  = 3.78%; μ small = 15.93%; μ Large = 12.18%; μ M  = 11.60%; σ M  = 17.02%, ρ small × σ small = 22.95% and ρ Large × σ Large = 17.60%.

    Table 1 This Table calculates the first and the second moments of the simple and log-returns
    Full size table
    Table 2 This Table shows the first four moments and market covariance of different asset classes using Ibbotson annual return data from 1928 to 2000. The moments are calculated using simple returns
    Full size table
    Table 3 This Table shows the first four moments and market covariance of different asset classes using Ibbotson annual return data from 1928 to 2000
    Full size table
    Table 4 This Table calculates the portfolio beta using both simple and log-returns for corporate bonds, large stocks and small stocks
    Full size table
    Table 5 This Table calculates the TR using both simple and log-returns for corporate bonds, large stocks and small stocks
    Full size table