Introduction

Computational tools have become indispensable in high-frequency electronics, among others, microwave design. These include both equivalent network simulators1,2, and full-wave electromagnetic (EM) analysis3,4. Versatility and reliability of the latter has been unquestionable, especially when it comes to quantifying phenomena difficult to be accounted for otherwise (EM cross-coupling, substrate anisotropy, the effects of surrounding components such as connectors, feed radiation, etc.). In particular, EM simulation is imperative for accurate evaluation of numerous modern circuits, e.g., compact structures obtained using line meandering5, the employment of slow-wave phenomenon6,7, multi-layer implementations8, or defected ground structures9.

The downside of EM analysis is it high computational cost, which is usually acceptable for one-time design verification or limited-scope parametric studies, but becomes a bottleneck for procedures requiring massive analyses (parameter tuning10,11, uncertainty quantification12,13,14, global optimization15,16, multi-criterial design17,18). Globalized search is the most troublesome as it is often performed using nature-inspired algorithms19,20,21,22,23,24, operating at the budgets corresponding to many thousands of system evaluations. Not surprisingly, considerable research has been focused on development of accelerated algorithms. Some of available techniques include the employment of adjoint sensitivities25, sparse Jacobian updating schemes26,27,28, parallelization29, mesh deformation methods30 (all of the above used to lower the expenses pertinent to sensitivity estimation in gradient-based algorithms), feature-based technology31, cognition-driven design32, multi-resolution techniques (e.g., space mapping33, response correction34,35,36), dimensionality reduction approaches37, including model-order reduction38,39. A growing number of approaches incorporates surrogate modelling methods33,40,41, often in the form of iterative design procedures42,43 (also referred to as machine learning44,45,46). Some of popular modelling methods include polynomial regression47, radial basis functions48, kriging49, support vector machines50, Gaussian process regression (GPR)51, neural networks52,53,54, ensemble learning55, or polynomial chaos expansion56.

As mentioned earlier, surrogate modelling (especially behavioral, or data-driven) is a potentially attractive way to mitigate the challenges associated with high cost of multiple EM analyses. Replacing expensive simulations with a low-cost metamodel altogether would be a desirable solution to expedite procedures such as design optimization. Nevertheless, constructing models of microwave components is a challenging task for several reasons: nonlinearity of circuit outputs, curse of dimensionality57, and utility requirements (which entails coverage of wide geometry and material parameter ranges but also frequencies). Addressing these issues is a daunting task. Some of the methods attempt to make a better use of available data (e.g., adjust the very structure of the model to the distribution and nature of the input information, e.g., ensemble learning58,59), efficiently handle large datasets (e.g., deep neural networks60,61), or target a specific structure of the modeled responses (e.g., high-dimensional model representation (HDMR)62, orthogonal matching pursuit63). On the other hand, the improvement of computational efficiency can be achieved using multi-resolution methods, for example, co-kriging64, Bayesian model fusion65, or two-stage GPR66. Yet another option is performance-driven modelling67,68,69,70. The techniques of this class capitalize on defining the surrogate’s domain so that it covers the region encapsulating high-quality designs67, and can be generalized to multi-resolution regime71, and employ deep learning methods72. The limitation is that the model setup is specific to a given set of performance specifications68, and domain definition itself requires reference designs that need to be acquired beforehand69. The latter increases the cost of the process. Recently, reference-design-free variations have been suggested73 to mitigate this particular issue.

This research proposes a procedure for improved-efficiency generation of design-ready behavioral models of microwave passive circuits. An inherent part of our methodology is a procedure for fast global sensitivity analysis (FGSA), which has been developed to determine correlations between design parameters (both geometry and material), and establish their effects on the circuit responses. The results of FGSA allow for defining a reduced-dimensionality model domain, which is constructed using a set of directions responsible for the largest variability of the circuit responses. A rendition of a reliable data-driven model in restricted regions necessitates a limited amount of training points compared to traditional approaches. Nonetheless, the model accounts for the majority of the circuit response changes, which makes it suitable for design purposes. Comprehensive numerical studies conducted using three microstrip circuits demonstrate excellent dependability and accuracy of the proposed surrogate, and its superiority over modeling in conventional domains. The model design utility is corroborated through application case studies, in particular, circuit optimization under different scenarios concerning a variety of performance specifications.

Behavioral modeling by fast global sensitivity evaluation and dimensionality reduction

In this part of the manuscript, we elaborate on the algorithmic components of the modeling approach introduced in the study. The surrogate modeling task is stated in Section "Modelling problem statement". Section "Low-cost global sensitivity analysis" discusses a fast global sensitivity analysis (FGSA) procedure introduced to determine the relationships between design variables and frequency characteristics of the system. The latter is expressed in terms of an orthonormal set of directions, which influences the circuit responses most significantly. In Section "Domain Definition", these directions are employed to define a reduced-dimensionality domain of the behavioral model. The operation of the entire modeling framework is elucidated in Section "Complete modelling procedure".

Modelling problem statement

In the following, we mark as Rf(x) a response of the high-fidelity circuit model, evaluated through EM analysis. Here, x stands for a vector of designable parameters (cf. Table 1 for modelling-related terminology). Typically, we are interested in scattering parameters Skj(x,f), where k and j stand for the respective circuit ports; frequency is marked as f. The goal of behavioral modeling is to render a fast replacement model (surrogate) Rs(x) of Rf(x), valid over the region of interest (parameter space) X. The latter is normally an interval determined by the lower and upper parameter bounds (cf. Table 1). The surrogate is supposed to represent the system responses as well as possible in a given sense. The performance metric utilized here is the relative RMS error, defined as ||Rs(x)–Rf(x)||/||Rf(x)||. The model accuracy will be estimated using the average error Eaver, evaluated using an independent set of testing points {xt(k)}k = 1, …, Nt, and defined as

$$ E_{aver} = \frac{1}{{N_{t} }}\sum\limits_{k = 1}^{{N_{t} }} {\frac{{||{\mathbf{R}}_{s} ({\mathbf{x}}_{t}^{(k)} ) - {\mathbf{R}}_{f} ({\mathbf{x}}_{t}^{(k)} )||}}{{||{\mathbf{R}}_{f} ({\mathbf{x}}_{t}^{(k)} )||}}} $$
(1)
Table 1 Surrogate modeling of microwave components. Notation and terminology.
Full size table

The relative error is typically more intuitive than absolute metrics because it is independent of the actual value (and the unit) of the model output. In engineering applications, the error level of a few (e.g., five) percent, typically makes the model sufficient for design purposes. A discussion of alternative error measures can be found, e.g., in74,75.

Low-cost global sensitivity analysis

In Section "Introduction", we discussed some fundamental challenges encountered in the behavioral modeling of microwave components. These challenges include the curse of dimensionality, the nonlinearity of frequency characteristics, and the necessity for the model to remain valid across wide ranges of geometry and material parameters. This latter requirement is particularly crucial for practical applications, such as design optimization. Among these challenges, those associated with the number of design variables are particularly critical, as they often underpin other difficulties. Consider a scenario where the parameter space X is assumed to be uniform, meaning that typical response nonlinearity remains consistent across all regions within X. Whatever technique is employed for constructing a surrogate model (radial basis function48, kriging49, neural networks52, etc.), the modelling error is primarily a function of the mean distance between the data samples used for model training. More specifically, the smaller the distance, the better accuracy of the surrogate. The average distance, in turn, depends on the cardinality N of the dataset, and dimensionality of the space n: it is proportional to (1/N)1/n. Note that dimensionality n plays a major role here, e.g., to reduce the average distance by a factor of two for n = 3, the training dataset has to be enlarged by a factor of eight, whereas for n = 10, the corresponding factor exceeds 1,000.

Thus, dimensionality reduction is critical to facilitate a reliable behavioural modelling of microwave components. One of possible approaches is variable screening, where the system variables having the least significance are identified and eliminated from the problem. Some of available techniques include the Morris method76, Pearson correlation coefficients77, partial or correlation coefficients78. Another approach is global sensitivity analysis (GSA) (Sobol indices79, Jansen method80, regression-based methods81), the goal of which is similar, i.e., to determine the relative importance of the system parameters, and to potentially exclude those that are of minor importance. Notwithstanding, the mentioned techniques are computationally expensive: estimation of the sensitivity indicators is based on large numbers of data samples. Another issue is that for most microwave components, dropping out individual variables is not possible without impairing the system capability to reach any particular set of target operating conditions. Most parameters (including the material ones, e.g., substrate permittivity) act in synergy and affect the system characteristics through their interactions.

In this research, an alternative technique for global sensitivity analysis is developed, which is to satisfy the following requirements:

  • It is cheap to execute, i.e., involves less than a hundred EM analyses of the system being modelled;

  • It allows for identifying important parameter space directions rather than to determine important variables; the ‘importance’ is understood in terms of the effects on the circuit response variability.

The operating flow of the proposed fast GSA technique (further referred to as FGSA) has been shown in Fig. 1. The eigenvectors ej of the relocation matrix S form represent the parameter space directions that have a decreasing impact on the response variability. The latter is quantified by the corresponding eigenvalues λj. By definition, the eigenvectors form an orthonormal basis in X. It should be mentioned that FGSA has a certain resemblance to the active subspace (AS) approaches (cf.82,83). Therein, the objective is also to identify a lower-dimensionality parameter subspace corresponding to the largest response variations. However, the spectral analysis is carried out on the matrix composed of gradient vectors of the (scalar) function of interest obtained for a set of random observables. This makes AS computationally more expensive than FGSA, especially for higher-dimensional problems. On the other hand, similarly to GSA methods mentioned earlier, AS is likely to provide higher accuracy.

Figure 1
figure 1

Pseudocode of the proposed fast global sensitivity analysis (FGSA). The eigenvectors ej represent the parameter space directions having major effects on the circuit characteristics; the importance is quantified using the eigenvalues λj.

Full size image

FGSA is employed as a tool for defining a reduced-dimensionality region for surrogate model establishment. For that purpose, we use a few most important eigenvectors, the number of which is determined as the smallest integer Nd ∈ {1, 2, …, n} that satisfies

$$ \frac{{\sqrt {\sum\nolimits_{j = 1}^{{N_{d} }} {\lambda_{j}^{2} } } }}{{\sqrt {\sum\nolimits_{j = 1}^{n} {\lambda_{j}^{2} } } }} \ge C_{\min } $$
(5)

In other words, Nd is the smallest number of vectors for which the corresponding (joint) relative least-square variability exceeds the user-defined threshold Cmin. In Section "Verification results", we use Cmin = 0.9; accordingly, the selected directions should account for at least ninety percent of the overall circuit response variability.

The operation of FGSA is illustrated using several examples. The first instance is a linear function f(x) = f([x1 x2]T) = 3x1 – 2x2, shown in Fig. 2. This function has been chosen because due to linearity, the direction of the maximum function variability can be readily identified as the gradient vector g = [3–2]T. This has been confirmed by FGSA, here based on twenty random points, cf. Figure 2b. Figure 3 shows two more examples involving nonlinear functions defined so that the directions of maximum function variability can be easily assessed visually (specifically, as the vectors perpendicular to the directions of the f(x) ‘ripples’). Also in these cases, FGSA involving twenty random points correctly identified the relevant directions.

Figure 2
figure 2

FGSA illustration using a linear function f(x) = f([x1 x2]T) = 3x1–2x2: (a) surface plot of the function (gray), twenty random observables xs(k) (circles), and relocation vectors xc(k)–xs(k) (line segments); (b) relocation matrix vectors rs(k)vs(k) (thin lines), the largest principal component e1 (thick solid line), and the normalized gradient g = [3–2]T/131/2 (thick dotted line). In this example, all function variability occurs along the gradient g (the function is constant in the direction orthogonal to g), which is well aligned with the vector e1, obtained using the proposed FGSA.

Full size image
Figure 3
figure 3

FGSA illustration using nonlinear functions of two variables: (a) surface plot of the first function f1(x) = f1([x1 x2]T) = 2sin(2.5x1)–1.5x2–2exp(x2/5) + x1x2 (gray), twenty random observables xs(k) (circles), and relocation vectors xc(k)–xs(k) (line segments), as well as the principal component e1 (thick arrow); (b) relocation matrix vectors rs(k)vs(k) (thin lines), and the largest principal component e1 (thick solid line); (c) and (d) surface plot and relocation matrix vectors for the second function f2(x) = f2([x1 x2]T) = 1.5sin(3x1 + 2x2)–1.1x12–0.3x22. It can be noticed that the vector e1 obtained using FGSA visually corresponds to the direction associated with the highest variability of f(x).

Full size image

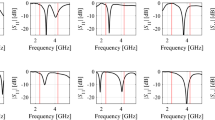
Our final example is a miniaturized microstrip coupling structure shown in Fig. 4a. The circuit features six design variables, x = [l1 l2 l3 d w w1]T. Here, FGSA is carried out based on fifty random points uniformly allocated in the design space X. The latter is determined by the lower and upper bounds l = [2.0 7.0 12.5 0.2 0.7 0.2]T, and u = [4.5 12.5 22.0 0.65 1.5 0.9]T. Figure 4b illustrates the EM-evaluated scattering parameters at a random parameter vector x and designs perturbed along the eigenvectors identified by FGSA, x + hek, k = 1, …, n. As it can be observed, the response variability is the largest for k = 1, and gradually diminishes for increasing k.

Figure 4
figure 4

FGSA applied to a miniaturized rat-race coupler: (a) circuit topology, (b) scattering characteristics at a random vector x and designs perturbed along the principal components, x + hek (here, h = 0.1) for the first four vectors (from top left to bottom right) obtained using FGSA, solid lines denote S-parameters at design x (|S11| through |S41|), whereas dashed lines denote corresponding S-parameters at the perturbed design; (c) normalized eigenvalues of the relocation matrix S obtained using FSGA based on twenty random samples, as well as average EM-simulated variability indicators dRj computed as in (6). It can be observed that response variability is gradually reduced for increasing k, which demonstrates that subsequent eigenvectors correspond to directions having less and less effect on circuit characteristics.

Full size image

To estimate the actual response variability, Nr = 20 random designs have been allocated in the parameter space, xr(k), k = 1, …., Nr, along with the perturbations xr(k.j) = xr(k) + hej, j = 1, …, n. Having acquired the EM simulation data Rf(xr(k)), k = 1, …, Nr, and Rf(xr(k.j)), k ∈ {1, …, Nr}, j ∈ {1, …, n}, the variability indicators have been computed as

$$ dR_{j} = \frac{1}{{N_{r} }}\sum\limits_{k = 1}^{{N_{r} }} {\left\| {{\mathbf{R}}_{f} ({\mathbf{x}}_{r}^{(k)} ) - {\mathbf{R}}_{f} ({\mathbf{x}}_{r}^{(k.j)} )} \right\|} $$
(6)

for j = 1, …, n. In (6), the norm \(\left\| {{\mathbf{R}}_{f} ({\mathbf{x}}) - {\mathbf{R}}_{f} ({\mathbf{y}})} \right\|\) is computed for all circuit responses, here, the scattering parameters Sj1(x,f), j = 1, 2, 3, 4, and takes the form

$$ \left\| {{\mathbf{R}}_{f} ({\mathbf{x}}) - {\mathbf{R}}_{f} ({\mathbf{y}})} \right\| = \sqrt {\sum\limits_{j = 1}^{4} {\int\limits_{F} {\left[ {S_{j1} ({\mathbf{x}},f) - S_{j1} ({\mathbf{y}},f)} \right]^{2} df} } } $$
(7)

where F is the simulation frequency range. The number dRj represents an average response variability in the direction ej. Upon normalization, dRj agree well with the normalized eigenvalues λj, as shown in Fig. 4(c), which demonstrates relevance of the presented sensitivity analysis approach.

Note that FGSA is computationally efficient. Many of the global sensitivity analysis techniques mentioned earlier (e.g., Sobol indices79, regression-based methods81) require from a few hundred to a few thousands of data samples to yield accurate sensitivity assessment, depending on the problem size. FGSA is carried out based on a few dozen points. More specifically, in Section "Verification results", only fifty samples are utilized. The sensitivity estimation accuracy is somehow compromised as compared to the expensive methods, but it is sufficient of our needs. It should also be reiterated that FGSA generates a set of principal directions that generally do not coincide with the coordinate system axes. Thus, instead of eliminating individual parameters, our method enables exploration of variable interactions and their joint effects on the circuit responses.

Domain Definition

The eigenvectors ej generated by FGSA are employed to establish the model domain Xd, which is determined by Nd most significant vectors ej, j = 1, …, Nd. Recall that Nd has been determined using (5). This arrangement allows for the domain to account for the majority of the circuit response variability within X (more specifically, the fraction equal or higher than Cmin, cf. Section "Low-cost global sensitivity analysis"). The formal definition of the domain is

$$ X_{d} = \left\{ {{\mathbf{x}} \in X:{\mathbf{x}} = {\mathbf{x}}_{c} + \sum\limits_{j = 1}^{{N_{d} }} {a_{j} {\mathbf{e}}_{j} } } \right\} $$
(8)

i.e., the set encapsulating parameter vectors xc + a1e1 + … + aNdeNd, where xc = [l + u]/2 is the centre of the original domain X (cf. Table 1), and aj, j = 1, …, Nd, are real numbers. Figure 5 provides a graphical illustration of generating Xd.

Figure 5
figure 5

Constructing reduced-dimensionality domain Xd. In the example shown, the original parameter space is three dimensional, whereas Xd is determined by two principal vectors e1 and e2. Note that Xd is a set theory intersection of X and the affine subspace xc + Σj=1,2 ajej.

Full size image

Again, while dim(Xd) < n, the domain accounts for the parameter space directions that are significant for the circuit response variability. This is necessary to secure design utility of the behavioural model to be established in Xd. In this work, the underlying modelling technique is kriging84. However, a particular choice of the modelling method unimportant: our main goal is to investigate the benefits of dimensionality reduction by means of FGSA.

Complete modelling procedure

Figure 6 showcases the modelling process pseudocode. Meanwhile, Fig. 7 illustrates the flow diagram. The procedures consists of the three major stages: (i) fast global sensitivity analysis, FGSA (Stage I), (ii) domain definition (Stage II), and acquisition of the training data as well as surrogate model identification (Stage III). It should be emphasized that there is only one control parameter, which is the variability threshold Cmin. It is set to 0.9 in the verification studies considered in Section "Verification results".

Figure 6
figure 6

Surrogate modelling of microwave circuits using FGSA and reduced-dimensionality surrogates.

Full size image
Figure 7
figure 7

Flow diagram of the behavioral modeling procedure using FGSA and reduced-dimensionality domain.

Full size image

Verification results

The modeling methodology outlined in Section "Behavioral modeling by fast global sensitivity evaluation and dimensionality reduction" is validated in this section through three examples of microwave components. The modeling captures the scattering parameters of these structures across broad ranges of geometry dimensions and frequencies. Reduced-dimensionality surrogates are compared to traditional metamodels concerning both accuracy and computational cost during model setup. Additionally, we explore how the predictive power of the model scales with the size of the training dataset. The practical applicability of the proposed approach will be further discussed in Section "Application case studies".

Test cases

Validation of the modeling framework introduced in Section "Behavioral modeling by fast global sensitivity evaluation and dimensionality reduction" is realized with the help of three microwave circuits. These are:

  • A miniaturized rat-race coupler (Circuit I)85;

  • A branch-line coupler using compact microstrip resonant cells (CMRCs) (Circuit II)86;

  • A dual-band equal-split power divider (Circuit III87.

The architectures of the circuits have been shown in Figs. 8a, 9a, and 10a, respectively. Information about material parameters (substrate permittivity and height), design variables, parameter spaces, as well as modeled characteristics have been included in Figs. 8b, 9b, and 10b for Circuit I, II, and III. One can note that the considered modeling problems are intricate. The parameter spaces are of relatively high dimensionality (when juxtaposing them with what is typically available in the literature), whereas the parameter ranges are wide. In particular, the mean values of the ratio between upper and lower bounds is close to three for Circuit I and II, and about nine for Circuit II. Furthermore, the modeling is conducted over broad ranges of frequency (0.5 GHz to 2.5 GHz for Circuit I, 0.1 GHz to 2.5 GHz for Circuit II, and 0.5 GHz to 7.0 GHz for Circuit III). Finally, the surrogates are to represent several complex responses of each structure.

Figure 8
figure 8

Test Circuit I: (a) parameterized geometry, (b) important data.

Full size image
Figure 9
figure 9

Test Circuit II: (a) parameterized geometry, (b) important data.

Full size image
Figure 10
figure 10

Test Circuit III: (a) parameterized geometry, (b) important data.

Full size image

Experimental setup

The validation studies have been carried out to verify the two hypotheses concerning the properties of our modelling methodology:

  • Dimensionality reduction by means of the fast GSA of Section "Low-cost global sensitivity analysis" enables a considerable enhancement of the model accuracy and scalability, i.e., more favourable relation between the training set size and the model’s predictive power;

  • Dimensionality reduction and the computational benefits associated with it are not detrimental to design suitability of the surrogate.

The second hypothesis will be discussed in Section "Application case studies". Its meaning is whether operating in a reduced space leaves sufficient flexibility for surrogate to be used for design purposes. The first hypothesis will be addressed in the remaining part of this section. To investigate the features of the presented modelling approach, we compare surrogate models rendered in the full-dimensional space X with those obtained within the reduced set. The FGSA procedure is conducted based on fifty random samples allocated in X by means of modified Latin Hypercube Sampling 88. The dimensionality Nd of the model domain is computed for the threshold Cmin = 0.9 in (5), cf. Section "Low-cost global sensitivity analysis", i.e., the domain is to account for ninety percent of the system response variability or more. Furthermore, the surrogate models are established using sample sets of several sizes NB = 50, 100, 200, 400, and 800. This will allow us to determine the scalability of the model predictive power as a function of NB.

In this study, the modelling routine of choice is kriging (setup: 2nd-order polynomial as a regression function, Gaussian correlation function). However, this is of secondary importance as our goal is mainly to determine potential benefits of using FGSA and dimensionality-reduced domains. As mentioned earlier, the model accuracy is estimated using the relative root-mean square (RMS) error, ||Rs(x)–Rf(x)||/||Rf(x)||, where Rs and Rf stand for the model-predicted and EM-evaluated circuit responses. To compute the error we utilize one hundred independent test samples randomly distributed within the model domain.

Results

The first point for discussion is the sensitivity analysis of Section "Behavioral modeling by fast global sensitivity evaluation and dimensionality reduction". Table 2 includes the data on the eigenvalues λk generated by FGSA, and the dimensionality Nd of the model domain determined according to (5) with Cmin = 0.9. Note that in practice, Nd corresponding to variability factor slightly lower than Cmin was approved in order to keep the domain dimensionality as small as possible. One can observe that Nd is considerably smaller than the number n of the circuit design variables. The (multiplicative) dimensionality reduction factor is 2.0 (Circuit I), 2.8 (Circuit II), and 1.8 (Circuit III). It is the smallest for Circuit III, which is the most difficult case for two reasons: (i) the modelled characteristics are defined over broad range of frequencies, and (ii) the circuit responses are highly nonlinear over the entire frequency spectrum. Furthermore, it should be emphasized that for this structure, the eigenvalues are much less reduced between λ1 and λn (here, from 1.00 to 0.45), which indicates low parameter redundancy. This is in contrast to Circuits I and especially Circuit II, where the eigenvalues drop down much faster. This behaviour is typical for miniaturized components, both CMRC-based and those employing line meandering, and enables a more efficient dimensionality reduction.

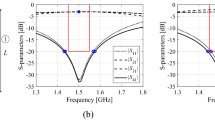
Table 2 Fast global sensitivity analysis: eigenvalues λk and domain dimensionality for Cmin = 0.9
Full size table

The reliability of the conventional and the proposed surrogates constructed using training datasets of sizes 50 through 800 samples have been shown in Table 3. Only for Circuit III, the models were also constructed using 1,600 samples, which is because it is the most challenging case, for which it was not possible to reduce the modelling error below ten percent with the 800-sample training set. The plots of the metamodel-predicted and EM-evaluated scattering parameters of Circuit I through III for chosen test points can be found in Figs. 11, 12, and 13, respectively.

Table 3 Modeling results for Circuit I through III.
Full size table
Figure 11
figure 11

Circuit I: scattering parameters at the chosen testing points: EM analysis (—), and the introduced FGSA-based model (o). The training set size NB = 400.

Full size image
Figure 12
figure 12

Circuit II: scattering parameters at the chosen testing points: EM analysis (—), and the introduced FGSA-based model (o). The training set size NB = 800.

Full size image
Figure 13
figure 13

Circuit III: scattering parameters at the chosen testing points: EM analysis (—), and the introduced FGSA-based model (o). The training set size NB = 1,600.

Full size image

The data encapsulated in Table 3 corroborates that dimensionality reduction greatly affects the surrogate model accuracy. Circuit I is the only case where modeling in the original parameter space is capable of rendering surrogates that feature relative error below ten percent. For this structure, modeling in a reduced-dimensionality domain allows for keeping the error below five percent already for training sample sets as small as 100 samples. Circuit II is considerably more challenging. Here, the conventional model is clearly unusable (RMS error over twenty percent) even for the largest dataset. At the same time, dimensionality reduction using fast GSA enables a dramatic accuracy improvement to about six percent. Finally, for Circuit III, the most difficult case, conventional modeling is exceptionally poor, also when the training dataset cardinality is enlarged to 1,600 samples. Dimensionality reduction enables error level reduction to only eight percent, which allows us to expect that the surrogate might be usable as a design aid.

Application case studies

The numerical results presented in Section "Results" unanimously demonstrate the benefits of reducing domain dimensionality through the proposed fast global sensitivity analysis. In particular, it makes it possible to render accurate surrogate models using reasonably small numbers of training points, as shown in Figs. 11, 12, 13. Nevertheless, a more important question is whether domain restriction is not detrimental for design utility of the model. Although a dimensionality-reduced domain is smaller than the original one, recall that it is spanned along the directions that correspond to the maximum response variability (i.e., those associated with the largest eigenvalues of the variability matrix S of (4)). Consequently, limiting the number of dimensions should not affect the ability of the surrogate to accommodate the optimum designs to a large extent. In order to verify this property, the GSA-based models are employed in this section to optimize Circuits I through III under different design scenarios. As the modeling process has been carried out over broad frequency spectra, the surrogate are utilized to optimize the respective circuit for a variety of operating frequencies, but—in the case of Circuit II—also different substrate materials (note that substrate permittivity εr is one of the design parameters for Circuit II, with the range from 2.0 to 5.0).

Table 4 delineates performance requirements for the considered devices. It should be noted that for Circuit III, equal power division is ensured by the structure’s symmetry. The parameters of each circuit were tuned for four distinct target values of the operating parameters, which are f0 and KP for Circuit I, f0 and εr for Circuit II, as well as f1 and f2 for Circuit III. The findings have been compiled in Tables 5, 6, and 7, while Figs. 14, 15, and 16 illustrate the optimized circuit responses for Circuit I, II, and III. Notably, optimization of the proposed surrogate model produces satisfactory designs across all cases. Moreover, there is excellent alignment between the model-predicted characteristics and those simulated through electromagnetic (EM) methods. These results collectively support the practical applicability of the modeling methodology discussed in this study, especially its effectiveness in designing circuits across wide ranges of operating conditions, such as center frequencies and power split ratios.

Table 4 Design optimization scenarios for Circuits I, II, and III.
Full size table
Table 5 Circuit I: optimization results.
Full size table
Table 6 Circuit II: optimization results.
Full size table
Table 7 Circuit III: optimization results.
Full size table
Figure 14
figure 14

Optimization results for Circuit I: surrogate- (gray) and EM-simulation (black) at designs found by optimizing the proposed surrogate (NB = 400). Operating frequency marked using the vertical line: (a) Case 1, (b) Case 2, (c) Case 3, (d) Case 4.

Full size image
Figure 15
figure 15

Optimization results for Circuit II: surrogate- (gray) and EM-simulation (black) at designs found by optimizing the proposed surrogate (NB = 800). Operating frequency marked using the vertical line: (a) Case 1, (b) Case 2, (c) Case 3, (d) Case 4.

Full size image
Figure 16
figure 16

Optimization results for Circuit I: surrogate- (gray) and EM-simulation (black) at designs found by optimizing the proposed surrogate (NB = 1600). Operating frequencies marked using the vertical lines: (a) Case 1, (b) Case 2, (c) Case 3, (d) Case 4.

Full size image

Conclusion

This study presents a method for enhancing the accuracy of surrogate modeling for passive microwave components. The approach introduced is grounded in fast global sensitivity analysis (FGSA), which has been developed to identify, at a low cost, the parameter space directions that exert the most significant influence on circuit responses. By employing a small subset of these critical directions, determined through eigenvalue analysis, the surrogate model domain is effectively spanned. This setup facilitates the creation of reliable metamodels across wide frequency ranges, as well as varying geometry and material parameters, using relatively modest training datasets. Importantly, this approach preserves the design versatility of the surrogates, as the directions defining the domain capture the majority of circuit response variability.

The proposed technique has undergone comprehensive validation using three microstrip components, including two compact couplers and a dual-band power divider. The results demonstrate a significant improvement in predictive power compared to conventional methods, with relative RMS errors reaching only a few percent even with just a few hundred training samples. This improvement is notable despite considering wide frequency ranges (0.5 GHz to 2.5 GHz, 0.1 GHz to 2.5 GHz, and 0.5 GHz to 7.0 GHz for the first, second, and third circuits, respectively) and material parameter variations (substrate permittivity ranging from 2.0 to 5.0 for the second circuit). At the same time, modeling in the original domains results in remarkably poor performance and unusable models featuring relative errors of over twenty percent (except the simplest case of a rat-race coupler).

The aforementioned investigations have been supplemented by the application case studies. In these experiments, the proposed surrogate models were employed to optimize the test circuits under a variety of scenarios (different center frequencies, power division ratios, substrate permittivity values). The obtained results allowed us to establish that dimensionality reduction as described in the paper is not detrimental to design utility of the models. The findings of this work suggest that the presented methodology may be viewed an attractive alternative to state-of-the-art modeling techniques. Although demonstrated using kriging interpolation, it can be coupled with any specific approximation method. Furthermore, it is generic as opposed to some of the recent methods, which are also domain-oriented (e.g., performance-driven techniques). Finally, it is easy to implement, which is of a practical value for researchers with less experience in the fields of numerical modeling and optimization.

It should also be emphasized that due to its data-driven nature, the proposed modelling methodology can be applied to a broader class of microwave structures. In particular, the constructed surrogate models and the dimensionality reduction process are entirely based on acquired EM simulation data. The microstrip circuits employed in Section "Application case studies" were merely illustration examples. Some of worth mentioning areas include components for 5G/6G applications (e.g., antennas operating within frequency bands beyond 24 GHz), as well as broadband systems implemented on fiberglass substrates (challenging due to geometrical complexity, position-based permittivity variations, and multi-resonance outputs).