Two-stage variable-fidelity modeling of antennas with domain confinement

Abstract

Surrogate modeling has become the method of choice in solving an increasing number of antenna design tasks, especially those involving expensive full-wave electromagnetic (EM) simulations. Notwithstanding, the curse of dimensionality considerably affects conventional metamodeling methods, and their capability to efficiently handle nonlinear antenna characteristics over broad ranges of the system parameters is limited. Performance-driven (or constrained) modeling frameworks may be employed to mitigate these issues by considering a construction of surrogates from the standpoint of the antenna performance figures rather than directly geometry parameters. This permits a significant reduction of the model setup cost without restricting its design utility. This paper proposes a novel modeling framework, which capitalizes on the domain confinement concepts and also incorporates variable-fidelity EM simulations, both at the surrogate domain definition stage, and when rendering the final surrogate. The latter employs co-kriging as a method of blending simulation data of different fidelities. The presented approach has been validated using three microstrip antennas, and demonstrated to yield reliable models at remarkably low CPU costs, as compared to both conventional and performance-driven modeling procedures.

Introduction

Design of contemporary antenna structures is to a large degree based on full-wave electromagnetic (EM) simulation models^1,2,3,4, which are used for the development of antenna topology⁵, parametric studies⁶, as well as geometry adjustment^7,8. The need for EM analysis arises from the fact that alternative representations (e.g. parameterized equivalent networks) are either non-reliable or non-existent. Moreover, EM simulations reliably account for mutual coupling, the effects of housing, connectors, etc. Furthermore, antenna structures become increasingly sophisticated to realize the assumed functionalities (multi-band and MIMO operation, circular polarization, etc.)^{9,10,11,12,13}. To enable these, a variety of topological alterations are incorporated (stubs, defected grounds structures and so on)^14,15,16,17, all of which have to be properly dimensioned. EM analysis is CPU intensive, which impedes execution of EM-driven procedures that entail repetitive simulations, such as optimization¹⁸, statistical analysis^19,20, design centering^21,22, let alone global²³ or multi-objective search²⁴, especially for complex devices^25,26,27.

Accelerating EM-based procedures is a matter of practical necessity. Numerous techniques have been developed for that purpose. In the realm of local optimization, we have adjoint sensitivities²⁸, mesh deformation²⁹, selective gradient updates^30,31, or the employment of customized EM solvers³². In a broader context, surrogate-assisted approaches has been growing in popularity, both concerning physics-based models (space³³ or manifold mapping³⁴, shape-preserving response prediction³⁵, or adaptive response scaling³⁶), and data-driven ones, e.g. kriging³⁷, artificial neural networks (ANN)³⁸, radial-basis functions (RBF)³⁹, support vector regression (SVR)⁴⁰, Gaussian process regression (GPR)⁴¹, or polynomial chaos expansion⁴². The latter are frequently used in global and multi-criterial optimization^43,44,45. Among other noteworthy methods feature-based optimization (FBO)^46,47,48 and cognition-based design⁴⁹, in which the design task is re-mapped into the space of adequately pinpointed attributes (points) of the system outputs, the latter being in weakly nonlinear relationship with the geometry parameters.

Needless to say, replacing EM analysis by fast surrogates is invaluable as an acceleration tool. Approximation models (kriging⁵⁰, RBF⁵¹, PCE⁵², SVR⁵³, ANNs and numerable variants thereof, e.g. convolutional neural networks (CNN)⁵⁴ or deep neural networks (DNN)⁵⁵) are particularly popular due to their accessibility^56,57. However, data-driven modeling methodologies are largely influenced by the curse of dimensionality and at the same time, have limited capability to represent highly nonlinear antenna characteristics. Available mitigation tools, e.g. least-angle regression (LAR)⁵⁸, high-dimensional model representation (HDMR)⁵⁹, are not suitable for general-purpose antenna modeling. Meanwhile, variable-resolution methods have been demonstrated to be beneficial in this context (co-kriging⁶⁰, two-level GPR⁶¹), also in combination with sequential sampling^62,63,64,65.

Recent performance-driven (or constrained) modeling⁶⁶ proposes a different manner of alleviating the problems of standard techniques by limiting the metamodel domain to a small district that contains increased-quality designs (w.r.t. the assumed figures of interest, e.g. operating frequencies). Domain confinement remarkably lowers computational expenditures of acquiring the training data without restricting the design utility of the model⁶⁷. Constrained modeling comes in several variations that incorporate, among others, dimensionality reduction and variable-fidelity EM models^68,69,70,71. The fundamental problem of the aforementioned techniques is an inflated initial cost associated with identification of the database designs, otherwise necessary to set up the domain of the surrogate⁶⁸. To some extent, this issue can be mitigated by involving sensitivity information⁷². In⁷³, an alternate way to performance-driven modeling has been introduced, which abandons the use of reference designs in favor of random trial points. Information extracted therefrom is used to define the domain with the use of an auxiliary inverse regression model. The method of⁷³ has been shown to retain the benefits of constrained modeling which reduces the initial cost by almost seventy percent in some cases.

In this paper, we propose a novel antenna modeling approach, which employs the performance-driven paradigm, and advances over the reference-design-free approach presented in⁷³ by exploiting variable-resolution EM simulations. More specifically, generation of the trial points, necessary to identify the inverse regression model, is executed at the level of a coarse-discretization EM simulations. Furthermore, the majority of the training data points acquired to build the final metamodel are obtained at the same level, and supplemented by a small amount of high-fidelity samples. The data of both resolution levels is then blended using co-kriging⁷⁴. Numerical validation performed using three antenna structures demonstrates that our framework allows to achieve additional computational savings of up to 64 percent over the technique of⁷³, and as high as 82 percent over the nested kriging framework⁶⁸ with regard to the model setup costs. This speedup is obtained without degrading the predictive power of the surrogate. Moreover, it ensures a remarkable accuracy improvement over conventional modeling methods.

Two-level variable-fidelity modeling within restricted domain

This section formulates the modeling methodology proposed in the paper. First, the concept of performance-driven modeling is recalled, along with an outline of the trial point acquisition (section “Performance-driven modeling basics”). In sections two-stage modeling: trial points and inverse regression model and surrogate domain definition, inverse regression model and surrogate domain definition are delineated, respectively. Section final surrogate. variable-resolution models and co-kriging discusses a construction of the final model using co-kriging, whereas section modeling procedure summary summarizes the complete procedure.

Performance-driven modeling basics

Here, we recall the basics of constrained (or performance-driven) modeling. The main concept is to construct the surrogate in a small portion of the parameter space, which encloses the designs being nearly optimum with regard to the target objective vectors. The computational benefits are due to a small volume of such a subset and a smaller sizes of training data sets that are needed to construct model of a satisfactory predictive power⁷⁵.

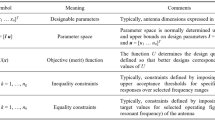
Table 1 outlines the notation used by constrained modeling frameworks⁶⁸. The figures of interest may include antenna operating frequencies (but also the bandwidths or permittivity of a dielectric substrate). The central idea here pertains to the objective space F that determines the validity zone of the metamodel. Another important entity is the model domain. Its establishment involves the concept of design optimality, that is measured using a merit function U(x, f)⁶⁹. The solution x^*, which is optimal with respect to a performance vector f ∈ F, is given as

$${\mathbf{x}}^{*} = U_{F} ({\mathbf{f}}) = \arg \mathop {\min }\limits_{{\mathbf{x}}} U({\mathbf{x}},{\mathbf{f}}).$$

(1)

Table 1 Notation used in performance-driven modeling.

The optimum design manifold, consisting of designs (1) obtained for all f ∈ F, constitutes an N-dimensional object in X, given as

$$U_{F} (F) = \left\{ {U_{F} ({\mathbf{f}}):{\mathbf{f}} \in F} \right\}.$$

(2)

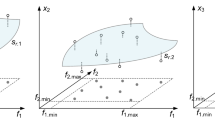
The domain of the surrogate model is determined as a neighborhood of U_F(F)⁶⁹. In a majority of performance-driven frameworks, its definition exploits database designs x^(j) = [x₁^(j) … x_n^(j)]^T, j = 1, …, p, optimal with respect to (1) for objective vectors f^(j) = [f₁^(j) … f_N^(j)], distributed in F. More specifically, the couples {f^(j),x^(j)}, j = 1, …, p, serve as a training points to build the first-layer model s_I(f) : F → X ⁶⁸ that approximates U_F(F), see Fig. 1. The metamodel domain itself constitutes an orthogonal extension of the first-level surrogate⁶⁹.

Figure 1

Basics of confined modeling⁶⁸: (a) the objectives’ space F, (b) design space X (black circles mark the trial points, grey surface indicates the manifold of optimum designs U_F(F)). The image of the first-layer metamodel s_I(F) yields a rough assessment of the manifold, so it needs to be outstretched to encompass entire U_F(F).

Acquisition of the database designs is a bottleneck of performance-driven modeling procedures because it requires a large number (a few hundreds to over a thousand) of antenna simulations⁷³. These extra expenses contribute to the overall model setup cost. As mentioned earlier, the number of trial points can be reduced by exploiting the sensitivity information⁷², whereas their identification costs may be diminished by warm-start optimization algorithms (e.g.⁷⁶).

The recent constrained modeling framework⁷³ introduced an alternative method for defining the model domain, which utilizes random trial points in place of the reference designs. The details of this method will be recalled in section two-stage modeling: trial points and inverse regression model, as it is one of the constituent parts of the introduced modeling procedure proposed.

Two-stage modeling: trial points and inverse regression model

First, we will define the surrogate model domain. Toward this end, we need to roughly assess the optimum design manifold U_F(F) of Eq. (2). We follow the methodology of⁷³, where the required information is extracted from a set of random trial points, allocated in the design space X.

We denote by x_r^(j) = [x_r.1^(k) … x_r.n^(k)]^T, j = 1, 2, … a series of random trial points yielded according to a uniform probability distribution and by f_r^(j) = [f_r.1^(j) … f_r.N^(j)]^T the performance figure vectors derived from the antenna response rendered by the full-wave model at x_r^(j). The performance figures are the same as the elements of the objective space F, e.g. the antenna resonant frequencies. The trial point is accepted if the extracted f_r^(j) resides in F and rejected otherwise (i.e. if the entries of f_r^(j) are located outside the lower and upper limits f_k.min and f_k.max, cf. Table 1, or if f_r^(j) cannot be identified due to distorted antenna responses). Figure 2 gives a graphical illustration of the trial point selection for an exemplary dual-band antenna. The process of generating the trial points continues until the assumed number N_r (e.g. 50) has been identified. For each accepted point x_r^(j), an additional vector p_r^(j) = [p_r.1^(j) … p_r.M^(j)]^T is extracted from antenna responses. The said vector p_r^(j) contains the information pertaining to antenna performance. In our example, these may refer to the reflection coefficient levels at the resonant frequencies, in which case M = N.

Figure 2

Procedure of the random trial point rendition for an exemplary dual-band antenna (the objective and parameter space are two- and three-dimensional, respectively). The random designs whose resonant frequencies reside within the required confines of the objective space are retained, the remaining ones are discarded. The inverse regression model s_r(⋅) is built using the ultimate trial point set {x_r^(j)}_{j = 1,…,Nr}.

Using the set {x_r^(j),f_r^(j),p_r^(j)}_{j = 1,…,Nr}, an inverse regression metamodel s_r: F → X is constructed, serving as a rough assessment of the manifold U_F(F). The analytical form of the model is taken as (cf.⁷³)

$$s_{r} ({\mathbf{f}}) = {\mathbf{s}}_{r} \left( {[f_{1} \;...\;f_{N} ]^{{\text{T}}} } \right) = \left[ \begin{gathered} s_{r.1} ({\mathbf{f}}) \\ \cdots \\ s_{r.n} ({\mathbf{f}}) \\ \end{gathered} \right] = \left[ \begin{gathered} a_{1.0} + a_{1.1} \exp \left( {\sum\nolimits_{k = 1}^{N} {a_{1.k + 1} f_{k} } } \right) \\ \cdots \\ a_{n.0} + a_{n.1} \exp \left( {\sum\nolimits_{k = 1}^{N} {a_{n.k + 1} f_{k} } } \right) \\ \end{gathered} \right].$$

(3)

The rationale for adopting the specific analytical form of the inverse surrogate as in Eq. (3) is that it is sufficient to adequately reflect typically weakly-nonlinear relationships between the antenna geometry and operating parameters. Moreover, exponential terms feature only few parameters, and are flexible in the sense that they allow for modeling various curvatures, e.g. inverse proportionality occurring for certain parameters.

The coefficients of the inverse surrogate are found as the solutions of the following tasks.

$$\left[ {a_{j.0} \;a_{j.1} \;...\;a_{j.N + 1} } \right] = \arg \mathop {\min }\limits_{{[b_{0} \;b_{1} \;...\;b_{K + 1} ]}} \sum\limits_{k = 1}^{{N_{r} }} {w_{k} \left[ {s_{r.j} \left( {{\mathbf{f}}_{r}^{(k)} } \right) - x_{r.j}^{(k)} } \right]^{2} } ,\,{\text{j}}\,{ = }\,{1,} \ldots {\text{,n}}{.}$$

(4)

The weigh factors w_k are computed as

$$w_{k} = \left[ {W - \max \{ p_{1} ({\mathbf{x}}^{(j)} ),...,p_{N} ({\mathbf{x}}^{(j)} )\} } \right]^{2} ,\,{\text{k}}\,{ = }\,{1,} \ldots {\text{,N}}_{r} ,$$

(5)

where W = max{k = 1,…,N_r, j = 1,…,N: p_j^(k)}. Here, we assume that p_j^(k) > 0, and better designs are associated with lower values of p_j^(k). The factors w_k are introduced to promote high-quality trial points so as to increase their contribution to the inverse model, which is because these vectors are located in a closer proximity of U_F(F). Figure 3 shows graphically the concepts of the model s_r in accordance with the example of Fig. 2. Observe that the design space needs to be selected with a proper consideration with respect to the anticipated design quality therein, i.e. the ranges of the antenna geometry parameters have to be established reasonably. Otherwise, the number of trial points necessary to gather the assumed number of the observables of decent quality may be too excessive and thus, the computational benefits of the introduced technique may be compromised. In this work, we assume that the design space has been selected using at least a rudimentary problem-specific knowledge.

Figure 3

Inverse regression model s_r constructed based on the pre-selected trial points x_r^(j) along with their respective objectives f_r^(j). The model elements s_r.j are are shown as grey surfaces for the parameters x₁ (left), x₂ (middle), and x₃ (right), respectively.

Surrogate domain definition

As discussed earlier, the set s_r(F) approximates the manifold U_F(F). The metamodel domain should contain a possibly large part of U_F(F) so as to account for the designs being optimum (or close to optimum) with respect to all f ∈ F. In⁷³, this is achieved by orthogonally extending s_r(F) in all directions orthogonal to this set. Let us define a orthonormal basis of vectors normal to s_r(F) at f as {v_n^(k)(f)}, k = 1,…,n–N. Let also T = [T₁ … T_n]^T denote a vector of non-negative extension factors. Further, let us compute the coefficients of the extension

$${{\varvec{\upalpha}}}({\mathbf{f}}) = [\alpha_{1} ({\mathbf{f}})\;...\;\alpha_{n - N} ({\mathbf{f}})]^{{\text{T}}} = \left[ {|{\mathbf{Tv}}_{n}^{(1)} ({\mathbf{f}})|\;\;...\;\;|{\mathbf{Tv}}_{n}^{(n - N)} ({\mathbf{f}})|} \right]^{{\text{T}}} .$$

(6)

Using (6), the metamodel domain X_S is given as

$$X_{S} = \left\{ \begin{gathered} {\mathbf{x}} = s_{r} ({\mathbf{f}}) + \sum\limits_{k = 1}^{n - N} {\lambda_{k} \alpha_{k} ({\mathbf{f}}){\mathbf{v}}_{n}^{(k)} ({\mathbf{f}})} :{\mathbf{f}} \in F,\; \hfill \\ \;\;\;\;\; - 1 \le \lambda_{k} \le 1,\;k = 1,...,n - N \hfill \\ \end{gathered} \right\}.$$

(7)

The meaning of this definition is that X_S comprises of all designs given by (7), generated for every possible combination of the objective vectors from the space F and λ_k ∈ [−1, 1], k = 1,…,n–N. Observe that the domain lateral bounds are the manifolds $S_{ + } = \left\{ {{\mathbf{x}} \in X:{\mathbf{x}} = s_{r} \left( {\mathbf{f}} \right) + \sum\nolimits_{k = 1}^{n - N} {\alpha_{k} ({\mathbf{f}}){\mathbf{v}}_{n}^{(k)} ({\mathbf{f}})} } \right\}$ and $S_{ - } = \left\{ {{\mathbf{x}} \in X:{\mathbf{x}} = s_{r} \left( {\mathbf{f}} \right) - \sum\nolimits_{k = 1}^{n - N} {\alpha_{k} ({\mathbf{f}}){\mathbf{v}}_{n}^{(k)} ({\mathbf{f}})} } \right\}$.

The extension factors T_j are established individually for all parameters using the trial points {x_r^(j)} and the following procedure. We denote the kth parameter’s lower and upper bounds as l_k and u_k, respectively. Given the pair {x_r^(j), f_r^(j)}, we define P_k(x_r^(j)) ∈ [l_k u_k] × F as the vector for which the distance between [x_r.k^(j) (f_r^(j))^T]^T and [s_r.k(f) f^T]^T, f ∈ F, i.e.

$$P_{k} ({\mathbf{x}}_{r}^{(j)} ) = \arg \mathop {\min }\limits_{{{\mathbf{f}} \in F}} ||[x_{r.k}^{(j)} \;({\mathbf{f}}_{r}^{(j)} )^{{\text{T}}} ]^{{\text{T}}} - [s_{r} ({\mathbf{f}})\;{\mathbf{f}}^{{\text{T}}} ]^{{\text{T}}} ||,$$

(8)

is minimal; with the orthogonal projection of [x_r.k^(j) (f_r^(j))^T]^T onto the representation of s_r.k in [l_k u_k] × F denoted as P_k(x_r^(j)). Consequently

$$d_{r.k} ({\mathbf{x}}_{r}^{(j)} ) = ||[x_{r.k}^{(j)} \;({\mathbf{f}}_{r}^{(j)} )^{{\text{T}}} ]^{{\text{T}}} - [s_{r} (P({\mathbf{x}}_{r}^{(j)} ))\;P({\mathbf{x}}_{r}^{(j)} )^{{\text{T}}} ]^{{\text{T}}} ||,$$

(9)

refers to the minimal distance between the said image and [x_r.k^(j) (f_r^(j))^T]^T (note that d_r.k may be viewed as the distance between the entries of the trial vector and the gray surfaces of Fig. 3). Based on these considerations, we define the extension factors T_k as

$$T_{k} = \frac{1}{{2N_{r} }}\sum\limits_{j = 1}^{{N_{r} }} {d_{r.k} ({\mathbf{x}}_{r}^{(j)} )} .$$

(10)

Thus, T_k constitutes a half of the averaged distance from the trial point entry to the corresponding image of s_r.k. The value of the factor 0.5 is chosen because many trial points are of poor quality and using (full) average distance would lead to excessively large domain containing too many designs that are far from the optimum ones⁷³.

Final surrogate. variable-resolution models and co-kriging

One of the important mechanisms employed in this work to lower the cost of surrogate model construction are variable-resolution EM models. In most cases, the modeling process is executed at a single level of fidelity, except situations where the lower-resolution model is corrected with the use of a handful of high-fidelity samples (e.g. space mapping⁷⁷, co-kriging⁷⁴). In this work, we employ low-fidelity models to accelerate the process of defining the surrogate model domain, as well as to downsize the training data acquisition cost.

Variable-resolution EM models

The fundamental benefit of using low-fidelity models, which typically means coarse-discretization EM simulations in the case of antennas⁷⁸, is that the associated simulation time may be considerably shortened, as compared to the high-fidelity version. The latter is normally established to ensure sufficiently accurate rendition of antenna characteristics. The speedup obtained due to low-fidelity analysis is obtained at the expense of the accuracy loss (cf. Fig. 4), which may or may not be problematic, depending on the particular context. For example, in space mapping optimization, the low-fidelity model should to be corrected to make it a reliable prediction tool, at least in the vicinity of the current iteration point⁷⁹. When the low-fidelity model is used to, e.g. parameter space pre-screening, it can usually be used uncorrected⁸⁰.

Figure 4

Variable-fidelity models: (a) an exemplary dual-band antenna, (b) antenna reflection responses evaluated with the low-fidelity EM model (- - -) and the high-fidelity one (—). Here, the high-fidelity model simulation time is about 80 s, whereas the time of the coarse model is only 25 s.

In this work, the low-fidelity or coarse model, denoted as R_c(x), will be used for two purposes: (i) generation of the trial points and metamodel definition as delineated in section two-stage modeling: trial points and inverse regression model, and (ii) accelerating the acquisition of the training data by complementing sparsely-sampled high-fidelity model responses (denoted as R_f(x)) with densely-sampled low-fidelity ones. In the case of (ii), co-kriging⁷⁴ is used to combine simulation data of different fidelities. As for (i), because the trial points are only employed to provide an inaccurate approximation of the manifold comprising optimum designs, there is no need to correct a low-fidelity model at this phase of the modeling process, which is advantageous from the standpoint of simplicity of implementation.

Final surrogate construction using co-kriging

The final surrogate s_CO(x) is generated in the domain X_S using co-kriging⁶⁰. The training data set contains N_Bf high-fidelity pairs {x_Bf^(k),R_f(x_Bf^(k))}_{k = 1, …, NBf}, where x_Bf^(k) ∈ X_S, and N_Bc low-fidelity pairs {x_Bc^(k),R_c(x_Bc^(k))}_{k = 1, …, NBc}, x_Bc^(k) ∈ X_S. We also use notation X_Bf = {x_Bf^(k)}_{k = 1,…,NBf}, and X_Bc = {x_Bc^(k)}_{k = 1,…,NBc}.

Let us begin by a recollection of the kriging interpolation, followed by formulation of co-kriging. The kriging surrogate s_KR(x) is given as

$${\mathbf{s}}_{KR} ({\mathbf{x}}) = {\mathbf{M}}\gamma + r({\mathbf{x}}) \cdot {{\varvec{\Psi}}}^{ - 1} \cdot ({\mathbf{R}}_{f} (X_{Bf} ) - {\mathbf{F}}\gamma ),$$

(11)

with M being a N_Bf × t model matrix of X_Bf, whereas F denotes a row vector of the design x comprising t elements (t denotes the number of regression function factors⁶⁰); and γ refer to coefficients of the regression function

$$\gamma = (X_{Bf}^{T} {{\varvec{\Psi}}}^{ - 1} X_{Bf} )^{ - 1} X_{Bf} {{\varvec{\Psi}}}^{ - 1} {\mathbf{R}}_{f} (X_{Bf} ).$$

(12)

We also have $r({\mathbf{x}}) = (\psi ({\mathbf{x}},{\mathbf{x}}_{Bf}^{(1)} ),...,\psi ({\mathbf{x}},{\mathbf{x}}_{Bf}^{{(N_{Bf} )}} ))$, constitutes an N_Bf—element row vector whose entries are the correlations between X_Bf and x, whereas Ψ = [Ψ_i,j] denotes a correlation matrix, where Ψ_i,j = ψ(x_Bf⁽ⁱ⁾,x_Bf^(j)). An exemplary widely used correlation function may be

$$\psi ({\mathbf{x}},{\mathbf{x}}^{^{\prime}} ) = \exp \left( {\sum\nolimits_{k = 1}^{n} { - \theta_{k} |x^{k} - x^{^{\prime}k} |^{P} } } \right),$$

(13)

where θ_k, k = 1, …, n, are the hyperparameters to be found during model identification, which is achieved through Maximum Likelihood Estimation (MLE)⁶⁰ as

$$(\theta_{1} ,...,\theta_{n} ) = \arg \min - (N_{Bf} /2)\ln (\hat{\sigma }^{2} ) - 0.5\ln (|\Psi |),$$

(14)

where $\hat{\sigma }^{2} = ({\mathbf{R}}_{f} (X_{Bf} ) - F\alpha )^{T} {{\varvec{\Psi}}}^{ - 1} ({\mathbf{R}}_{f} (X_{Bf} ) - F\alpha )/N_{Bf} ,$ with |Ψ| being the determinant of Ψ. In practice, a correlation function of Gaussian type (P equal to 2) is often employed, as well as M = 1 and F = [1 … 1]^T.

Co-kriging blends together two models: (i) a kriging surrogate s_KRc set up with the low-fidelity samples (X_Bc, R_c(X_Bc)) and (ii) the model s_KRf built using the residuals (X_Bf, r), with r = R_f(X_Bf) − ρ⋅R_c(X_Bf). In the latter, ρ is a portion of the maximum likelihood estimate of the s_KRf surrogate. R_c(X_Bf) is roughly equal to s_KRc(X_Bf). The correlation function of the two models is described by Eq. (13).

The co-kriging model s_CO(x) is given by

$${\mathbf{s}}_{CO} ({\mathbf{x}}) = {\mathbf{M}}\gamma + r({\mathbf{x}}) \cdot {{\varvec{\Psi}}}^{ - 1} \cdot ({\mathbf{r}} - {\mathbf{F}}\gamma ),$$

(15)

where

$$r({\mathbf{x}}) = [\rho \cdot \sigma_{c}^{2} \cdot r_{c} ({\mathbf{x}}),\rho^{2} \cdot \sigma_{c}^{2} \cdot r_{c} ({\mathbf{x}},X_{{B_{f} }} ) + \sigma_{d}^{2} \cdot r_{d} ({\mathbf{x}})]$$

(16)

$${{\varvec{\Psi}}} = \left[ {\begin{array}{*{20}c} {\sigma_{c}^{2} {{\varvec{\Psi}}}_{c} (X_{Bc} ,X_{Bc} )} & {\rho \,\sigma_{c}^{2} {{\varvec{\Psi}}}_{c} (X_{Bc} ,X_{Bf} )\,} \\ {\rho \,\sigma_{c}^{2} {{\varvec{\Psi}}}_{c} (X_{Bf} ,X_{Bc} )} & {\rho^{2} \sigma_{c}^{2} {{\varvec{\Psi}}}_{c} (X_{Bf} ,X_{Bf} ) + \sigma_{d}^{2} {{\varvec{\Psi}}}_{d} } \\ \end{array} } \right],$$

(17)

with M = [ρM_c M_d], moreover matrices (F_c, σ_c, Ψ_c, M_c) and (F_d, σ_d, Ψ_d, M_d) are derived, in turn, from s_KRc and s_KRf⁶⁰.

Design of experiments

A separate note should be made about the domain sampling procedure. Performing the design of experiments in a direct manner is inconvenient, as a geometry of the set X_S is relatively complex. Instead, we use the procedure explained in Fig. 5, which involves a surjective transformation between the unit cube [0, 1]ⁿ and the constrained domain. According to this procedure, the samples x_B^(k) = h₂(h₁(z^(k))) ∈ X_S are uniformly distributed w.r.t. the objective space F, but not w.r.t. X_S. The normalized samples {z^(k)}, k = 1, …, N_B, are distributed using Latin Hypercube Sampling, LHS⁸¹). Observe that the proposed modeling technique belong to a wider class of performance-driven (or constrained) modeling techniques, in which the surrogate is constructed within a region of the design space confined from the point of view of the design objectives. In contrast to the conventional modeling techniques, in performance-driven modeling, the surrogate domain constitutes a thin set within the classical deign space delimited by the lower and upper bounds on the design variables. As demonstrated in⁸², performing sequential sampling in a constrained domain does not bring any advantages over one-shot data sampling in terms of improving the model predictive power. This can be explained by a particular geometry of the constrained domain of the performance-driven surrogate, which encompasses nearly-optimum designs, the latter forming a manifold of a lower dimension than that of the original parameters space.

Figure 5

Conceptual illustration of the training data sampling process: (i) samples distributed according to Latin Hypercube Sampling (LHS)⁸¹ (top), (ii) mapping onto the Cartesian product of the performance figure space F and [−1,1]^n–N using function h₁ (middle), (iii) black circles mark data samples projected onto the confined domain X_S using function h₂ (bottom); gray circles indicate the samples distributed over the image of design space F prior to orthogonal extension.

The function h₂(h₁()) also facilitates solving design tasks that involve the surrogate model, such as optimization. More specifically, the optimization process may be carried out over the unity cube [0, 1]ⁿ, where the design variables (i.e. geometry parameters of the antenna at hand) are transformed into the model domain for metamodel evaluation. Additionally, s_r(f) can be used as an initial design of a high quality for any assumed performance figure vector f ∈ F.

It is expected that the incorporation of variable-fidelity models into the domain-confined surrogate, as described in this section, will lead to an additional computational savings over the method of⁷³ with regard to the total costs of the model setup. This is because majority of the costs (related to the acquisition of both the trial and training points) will be reduced by the factor equal to the EM simulation time ratio between the models of low- and high-fidelity.

Modeling procedure summary

Here, we summarize the proposed modeling procedure, the components of which were described in sections performance-driven modeling basics through final surrogate. variable-resolution models and co-kriging. It should be noted that there is only one control parameter, the number of trial points N_r, which is normally set to 50. The number of training data points (N_Bf of high-fidelity, and N_Bc of low-fidelity) depends on the required model accuracy. The modeling workflow has been provided in Fig. 6. Furthermore, Fig. 7 shows the flowchart of the process.

Figure 6

The workflow of the proposed antenna modeling procedure with variable-resolution EM simulations.

Figure 7

Operational flow of the presented two-layer modeling technique with domain confinement and variable-resolution EM simulations.

Results

The modeling procedure introduced in section two-level variable-fidelity modeling within restricted domain has been validated in this section with the use of three exemplary microstrip antennas. The results obtained for various training data set sizes are compared to a number of benchmark methods including traditional (i.e. unconstrained) metamodels (kriging and RBF), along with the performance-driven frameworks (nested kriging⁶⁸, and the reference-design-free approach⁷³). The major figures of interest include the surrogates’ predictive power, its dependence on the cardinality of the training dataset, as well as the computational cost of the model setup.

Verification antennas

The antenna structures used for verification have been shown in Figs. 8, 9 and 10. These include a ring-slot antenna⁸³, a dual-band dipole⁸⁴, and a quasi-Yagi antenna with a parabolic reflector⁸⁵, which henceforth are referred to as Antenna I, II and III, respectively. Figures 8, 9 and 10 also contain the relevant data, among others, designable parameters, operating parameters, and the details on the parameter and objective spaces. Furthermore, Fig. 11 shows the families of reflection responses corresponding to various model fidelities for all the benchmark antenna structures. Observe that all the benchmark antennas have been already validated, first, in their respective source papers^83,84,85, and also in our previous work, e.g.^68,86). Therefore, the experimental validation has not been provided, as being immaterial to the scope of the paper.

Figure 8

Antenna I: ring-slot microstrip antenna: (a) antenna geometry, (b) antenna parameters.

Figure 9

Antenna II: dual-band uniplanar dipole antenna: (a) antenna geometry, (b) antenna parameters.

Figure 10

Antenna III: qasi-Yagi antenna with parabolic reflector: (a) antenna geometry, (b) antenna parameters.

Figure 11

Grid convergence plots for: (a) Antenna I, (b) Antenna II, and (c) Antenna III for different numbers of mesh cells corresponding to various model fidelities from the lowest employed fidelity up to the highest one.

Validation experiments setup

Antennas I, II and III have been modelled utilizing the technique proposed in this paper, as well as a number of benchmark methods, as listed in Table 2. The benchmark surrogates have been built using the training sets comprising 50, 100, 200, 400 and 800 data samples. The proposed models were obtained using several combinations of the coarse and fine datasets, in particular, N_Bf = 50 and N_Bc ∈ {50, 100, 200, 400, 800}, as well as N_Bf = 100 and N_Bc ∈ {50, 100, 200, 400, 800}. The cost of model construction is calculated in terms of the equivalent number of high-fidelity simulations, which considers the simulation time ratio of R_f versus R_c. Also, the cost includes all additional expenses, e.g. those associated with the reference database designs acquisition for the nested kriging framework⁶⁸, or generating the trial points for the method of⁷³, and the introduced technique.

Table 2 Benchmark modeling methods.

A relative RMS error has been used as a measure of the model accuracy. It has been computed as ||R_s(x)–R_f(x)||/||R_f(x)||, where R_s and R_f are the surrogate and EM-simulated antenna characteristics, respectively. The average errors are reported, which are obtained for one hundred independent testing points.

Discussion

The results can be found in Tables 3, 4 and 5, for Antenna I, II and III, respectively. Furthermore, Figs. 12, 13 and 14 illustrate the antenna responses at selected test locations, evaluated using the proposed model and EM simulation. The analysis of the data in the tables leads to the following observations:

• The accuracy of the presented model outperforms that of the conventional (i.e. unconstrained) models. In particular, for Antennas I and III, the unconstrained surrogates are unable to yield the surrogates of usable accuracy: the modeling error is still beyond 25% even for the training sets of the largest sizes.

• The predictive power of the introduced surrogate is also better than for the nested kriging metamodel⁶⁸ set up using smaller training data sets, which is due to the inclusion of the random trial points into the training dataset. For larger values of N_B, the models exhibit similar accuracy. This is also the case for the reference-design-free method, the accuracy of which is comparable to the proposed model due to sharing the rules for model domain definition. Yet, for the smaller training sets, the proposed model is more accurate, which is because the overall number of samples (low- and high-fidelity together) is larger than for the method of⁷³. Perhaps the most important advantage of the proposed methodology is an excellent computational efficiency. Executing majority of the operations with the use of low-fidelity model leads to considerable savings, as reported in Tables 3, 4 and 5. For example, the cost reduction over conventional surrogates is as high as 55, 54 and 60 percent for Antennas I, II and III, respectively, assuming N_B = 800 and N_Bf = 50.

• The savings over the nested kriging model are even higher due to the extra expenses entailed by the reference design acquisition in⁶⁸. We have 78, 79 and 88 percent savings for Antennas I through III, respectively, also for N_B = 800 and N_Bf = 50. The savings over the reference-design-free methods⁷³ are 61, 64 and 68 percent, for Antenna I, II and III, respectively, again assuming N_B = 800 and N_Bf = 50. It should be reiterated that the cost reduction with respect to the benchmark performance-driven methods does not deteriorate the modeling accuracy.

Table 3 Antenna I: modeling results and benchmarking.

Table 4 Antenna II: modeling results and benchmarking.

Table 5 Antenna III: modeling results and benchmarking.

Figure 12

Antenna I: reflection responses at the representative test designs: full-wave model (—), and the presented two-level variable-fidelity surrogate (o) with N_Bf = 50 and N_Bc = 800.

Figure 13

Antenna II: reflection responses at the representative test designs: full-wave model (—), and the presented two-level variable-fidelity surrogate (o) with N_Bf = 50 and N_Bc = 800.

Figure 14

Antenna III: reflection responses at the representative test designs: full-wave model (—), and the presented two-level variable-fidelity surrogate (o) with N_Bf = 50 and N_Bc = 800.

Conclusion

This work presented a novel framework for surrogate modeling of antenna structures. Our approach exploits a constrained modeling paradigm with the surrogate model domain established using random trial points and the operating parameter data extracted therefrom. Furthermore, variable-resolution EM models are used at the domain definition stage and the surrogate construction phase. The latter combines sparsely acquired data samples of high-fidelity with densely collected low-fidelity training points. The final surrogate is rendered using co-kriging. Extensive numerical experiments confirm that the proposed method outperforms conventional methods. Furthermore, the predictive power of the presented surrogate is comparable or slightly better than for the benchmark performance-driven models. In terms of the computational efficiency, our modeling framework by far outperforms all the techniques employed in the numerical studies, both the conventional and the performance-driven ones. The computational savings over the traditional models are as high as 56 percent on the average, whereas they are 82 and 64 percent over the nested kriging modeling technique and the database-design-free method, respectively. The procedure presented in this work can be considered a viable alternative to state-of-the-art modeling routines, especially for more demanding conditions that include multi-dimensional spaces with broad geometry and material parameters’ ranges, the same pertains to the operating conditions.