Main

A comprehensive understanding of conventional superconductors, in which lattice vibrations bind electrons in Cooper pairs, is provided by the Bardeen–Cooper–Schrieffer (BCS)–Eliashberg theory. Several families of unconventional superconductors, however, defy explanation within this paradigm, presenting a series of intellectual challenges. For many years, attention was split between cuprate superconductors1, with critical temperatures (Tc) up to 165 K, and the heavy-fermion and organic superconductors, with lower Tc values2. In 2008, a family of superconductors based on iron (Fe) was discovered3. The discovery was noteworthy given that Fe is generally seen as a strongly magnetic ion, and magnetism is typically antithetical to superconductivity. It rapidly became more remarkable as more members of the family were discovered with progressively higher Tc values—high enough that the materials were soon referred to as ‘high Tc’.

A large body of evidence now indicates that these Fe-based superconductors (FeSCs) are unconventional, that is, the pairing is not driven by lattice vibrations (phonons)4,5,6,7,8. They have provided a fascinating array of insights into the conditions of occurrence and nature of unconventional superconductivity, particularly in systems where the electrons can occupy multiple orbitals. Before their discovery, unconventional pairing was synonymous with Cooper pairs with non-zero angular momentum and gap nodes, exemplified, for instance, by the d-wave superconducting state realized in cuprates1. In Fe-based materials, however, the Cooper pairs are widely believed to have zero angular momentum, with their unconventional nature arising from the different phases they take on different bands4,5. A variety of pairing structures have been observed, but attributed to the same dominant pairing mechanism.

In addition, the normal state of the FeSCs is unusual. Similar to many other quantum materials, electron–electron interactions have an important role in shaping their phase diagrams. However, owing to the multi-orbital character of these compounds, it is the Hund’s interaction that is believed to have the most prominent role9. The resulting ‘Hund metal’10 interpolates between a description of incoherent atomic states at high temperatures and one of coherent states at low temperatures. At intermediate temperatures, charge and orbital degrees of freedom seem itinerant, whereas spin degrees of freedom appear localized11. In contrast, in the cuprates, the on-site Hubbard repulsion is the dominant interaction, whereas in heavy-fermion materials, it is the Kondo coupling between localized and itinerant electrons. Another distinguishing feature of FeSCs is that although the distinct Fe orbitals are subjected to the same interactions, they experience different degrees of correlation—a phenomenon dubbed orbital differentiation10,12,13,14,15,16.

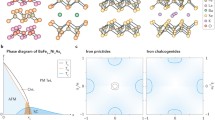
It is from this correlated normal state that not only superconductivity emerges but also other electronic ordered states. The majority of FeSCs order magnetically17; for example, BaFe2As2 exhibits magnetic order with a stripe pattern below a critical temperature of 134 K, although more unusual spin configurations are found under hole doping (Fig. 1a). Other compounds, such as FeSe, exhibit no magnetic order at ambient pressure (Fig. 1b). More ubiquitously, magnetic fluctuations at the stripe-order wavevectors are commonly observed for superconducting compositions. The observation, by neutron scattering, of an associated resonance in the magnetic spectrum at this specific wavevector18,19 has been widely interpreted as evidence for a sign-changing superconducting gap and for magnetic fluctuations playing a key role in the pairing interaction2.

Fig. 1: General structural and electronic properties.
figure 1

a, b, Phase diagrams of two families of FeSCs: BaFe2As2 (ref. 80; a) and FeSe (refs. 32,51,104; b). The different electronic phases are schematically shown: nematic, spin density wave (SDW, where nematic order remains present), double-stripe, C4 magnetic phase and superconductivity (SC). The tuning parameter can be electron doping or hole doping, isoelectronic substitution (As/P or Se/S, Se/Te) or applied pressure. c, The common structure of the FeSCs consists of Fe planes and pnictogens (As) or chalcogens (Se) outside the plane. A simplified representation considering a single Fe per unit cell is shown in beige and the crystallographic unit cell containing two Fe atoms is shown in blue. d, A schematic representation of the crystal field levels of an isolated Fe2+ ion (d6) inside a distorted FeAs4 tetrahedron9. The spins’ alignment corresponds to the high-spin state, but other configurations are possible. e, f, Schematic Fermi surface in the tetragonal phase. It consists of hole pockets at the centre and of electron pockets at the corner of the 1-Fe (e) and 2-Fe (f) Brillouin zone. In f, the two electron pockets fold along the diagonal wavevector in e. The colours indicate the dominant orbital character of each band6. An additional dxy-dominated hole pocket (dashed) is shown centred at M = (π, π) in the 1-Fe zone ((0, 0) in the 2-Fe zone). The size of this pocket, which is absent in some materials, varies widely across compounds. The momenta k in e are in units of the inverse lattice constant 1/a.

Full size image

Another common feature in the FeSC phase diagrams is a tetragonal-to-orthorhombic phase transition. It often occurs either concurrently or at a higher temperature than the magnetic transition (Fig. 1a), although in FeSe it occurs in the absence of magnetic order at ambient pressure (Fig. 1b). A variety of experiments have revealed that lattice strain is not the primary order parameter for this phase transition20. Borrowing language from liquid crystals, the state is referred to as an electronic nematic phase21, in which interactions among electronic degrees of freedom drive the breaking of (discrete) rotational symmetry, while translational symmetry is unaffected. Experiments have indicated that nematic fluctuations extend far across the phase diagram22,23,24, motivating the question of what role nematicity has in these materials.

The most recent surprise is the realization that several representative FeSC compounds can show topologically non-trivial band structures25. They have been proposed to promote various topological phenomena, such as spin-momentum-locked surface states and semi-metallic Dirac bulk states. Owing to their intrinsic fully gapped unconventional superconductivity, they have become prime candidates in the search for robust topological superconducting states and their associated Majorana excitations.

The above brief overview showcases an important feature of the FeSCs. After 14 years of research, there is a wide consensus as to the nature of the various states found in the phase diagrams. In the Landau paradigm, these phases are characterized by the symmetries that they break, and there has been little, if any, disagreement about them. Yet, knowing what these states are is different from understanding how they arise and inter-relate with each other. This enables a series of well posed questions that are, in some sense, better defined than what can currently be asked for the other family of unconventional high-Tc superconductors, the cuprates1. In this review, we outline what is well understood about FeSCs and pose a series of open challenges that we believe are central to understanding the origins of their superconductivity.

Electronic structure and correlations

All FeSCs are characterized by a common structural motif comprising tetrahedrally coordinated Fe atoms arranged on a square lattice (Fig. 1c). The coordinating ligands are typically from group V (the pnictogens phosphorus (P) and arsenic (As)) or group VI (the chalcogens sulfur (S), selenium (Se) and tellurium (Te)). Parent compounds have a formal valence of Fe2+, corresponding to a 3d6 electronic configuration for an isolated atom. Bond angles vary somewhat between compounds, differing from the perfect tetrahedral angle of 109.5°, thus leading to additional orbital splittings (Fig. 1d).

From a band theory perspective, the FeSCs are compensated semimetals with the same number of electron-like and hole-like carriers26. A widely used, simplified model features a Brillouin zone corresponding to the unit cell of the square Fe lattice (shaded beige area in Fig. 1c). The low-lying bands form the electron and hole Fermi-surface pockets shown in Fig. 1e and coloured according to the orbitals that contribute the largest spectral weight6. More realistic models include the puckering of the As/Se atoms above and below the Fe plane, which introduces a glide plane symmetry and implies a crystallographic unit cell (and corresponding Brillouin zone) containing two Fe atoms (blue shaded areas in Fig. 1c, f)27,28. Additional effects include the spin–orbit coupling29, which splits the intersecting electron pockets in Fig. 1f, the three-dimensional dispersion of the bands27 and the hybridization between the As/Se p band and Fe d band30, which is the root of several topological phenomena.

In the FeSCs, the charge and orbital degrees of freedom appear to be itinerant, as most compounds are metallic at all temperatures. Moreover, the X-ray absorption spectrum of the unoccupied Fe d states is in good agreement with density functional theory (DFT) calculations31. At low temperatures, in most cases, the normal state of the FeSCs is well described by the Fermi liquid theory. This does not imply the absence of electronic correlations, which can strongly renormalize the Fermi liquid parameters, making them deviate from DFT-based expectations. Indeed, the qualitative features of the quasiparticles dispersion, predicted by DFT and sketched in Fig. 1e, are often similar to those detected experimentally using angle-resolved photoemission spectroscopy (ARPES)32,33,34 and quantum oscillation measurements32,35,36. However, the bandwidth of the quasiparticles dispersions is generally reduced relative to the DFT results. Such mass enhancements, also observed in optical conductivity measurements37, are attributed to electronic correlations, and were anticipated by DFT + dynamical mean-field theory (DMFT) calculations38,39,40,41,42. Moreover, the sizes of the Fermi pockets are smaller in experiments36,43,44 compared with the DFT predictions. Whether the correlations causing this effect are promoted by low-energy spin fluctuations44,45,46 or can be captured by first-principles calculations going beyond DFT47 remains under debate.

Correlations arise from the screened Coulomb repulsion between electrons, resulting in an on-site Hubbard repulsion U, which penalizes the system when two electrons occupy the same site and suppresses spin fluctuations. However, as multiple orbitals are available in the FeSCs, other on-site terms are also generated by the Coulomb repulsion. Among them is the Hund’s interaction JH, which favours the alignment of the spins of electrons in different orbitals. In contrast to the Hubbard U, JH is barely screened from its atomic value48. The resulting Hund metal state differs from a Mott insulator, in that charge/orbital degrees of freedom are itinerant, whereas spins remain nearly localized down to low temperatures. This is illustrated schematically in Fig. 2c, which depicts the histogram of all possible 3d Fe atomic states in a Hund metal. Although the histogram extends over a wide range of electronic occupations, showcasing the itinerant nature of the charge carriers, it also shows sharp peaks at high-spin configurations, illustrating the local nature of the spins.

Fig. 2: Electronic correlations and orbital differentiation.
figure 2

a, b, The schematic energy dispersions of the three hole bands along a high-symmetry direction of the 2-Fe Brillouin zone (Fig. 1f) at high temperatures (a) and low temperatures (b). The topmost hole band, which has dxy character, becomes incoherent at high temperatures, as represented by the faint line. At low temperatures, this band can re-establish its coherence, but its effective mass can remain sizeable, as indicated by its flatness. The two other hole bands have dxz and dyz character. Note that the dxy band crosses the Fermi level only in some compounds (Fig. 1e, f). c, Histogram of the Fe atomic states in a parent FeSC, as obtained from DMFT calculations9. There are 210 possible states involving the 3d Fe orbitals. The atomic states are distributed in different colours in the histogram according to their electronic occupation n. Within a given sector n of the histogram, the states are ordered by decreasing probability; in all cases, the higher probability corresponds to the high-spin configuration for that occupation. d, The typical schematic momentum-resolved spin-excitation spectrum, shown here in the 1-Fe Brillouin zone, is peaked at different wavevectors at low energies (in this case, the stripe state (π, 0)) and high energies ((π, π)).

Full size image

A prime feature of the Hund metal phase is the coherence–incoherence crossover9. In very clean FeSCs, this manifests in the resistivity behaviour, which crosses over from the characteristic Fermi-liquid T2 dependence at low temperatures to values of the order of several hundred µΩ cm at high temperatures49. In a semiclassical treatment, these values imply a mean free path comparable to the inverse Fermi momentum, which is inconsistent with a picture of propagating Bloch waves.

Another manifestation of the coherence–incoherence crossover is illustrated in Fig. 2a, b. At high temperatures, the dxy hole band is much fainter and flatter than the two dxz/dyz hole bands, reflecting the small coherence factor and large effective mass of the former. On decreasing the temperature, this dxy band becomes much sharper and thus more coherent. Such an effect, predicted theoretically14,15,50, has been observed in FeSe1−xTex, LiFeAs and KxFe2−ySe2, among others34. In extreme cases, the dxy orbital could remain completely localized down to zero temperature, whereas the dxz/dyz orbitals remain coherent, giving rise to an orbital-selective Mott state12,14 that behaves differently from a renormalized Fermi liquid. The fact that the dxy orbital is less coherent than the others is an example of a broader phenomenon called orbital differentiation10,13,51, by which different orbitals are affected by correlations in distinct ways in both the normal15 and superconducting states52,53. Orbital differentiation has been invoked to explain the strong anisotropy of the superconducting gap observed in FeSe (ref. 54). However, the origin of this anisotropy and its relationship to orbital order remain unsettled51,53,55,56.

Correlations also affect the spin-excitation spectrum probed by neutron scattering, which is rather different at low and high energies17. In momentum space, as sketched in Fig. 2d, the magnetic spectral weight at low energies is strongly peaked near the wavevector of the magnetic ground state—usually, the in-plane stripe vectors (π, 0) and (0, π). As the energy increases, the magnetic spectral weight generally moves towards (π, π)57.

This dichotomy between low and high energies is clearly seen in the local magnetic susceptibility extracted from neutron-scattering experiments17, the imaginary part of which is schematically plotted in Fig. 3a. At energies E0 of about 100 meV, it shows a broad peak indicative of a large local fluctuating magnetic moment. Evidence for local moments are also observed in the X-ray emission spectrum, whose changes with temperature and doping have also been interpreted in terms of a spin-freezing crossover58. Experimental estimates give a fluctuating moment of about 2–3 Bohr magneton (µB) across different parent compounds (inset of Fig. 3a). In contrast, at energy scales of about 10 meV, the imaginary part of the local susceptibility in the paramagnetic state increases with energy59, which is indicative of Landau damping caused by the decay of spin fluctuations into particle–hole excitations—a hallmark of itinerant magnets. Indeed, the system remains metallic inside the magnetically ordered state.

Fig. 3: Dual local–itinerant nature of magnetism.
figure 3

a, Schematics of the imaginary part of the local susceptibility versus energy in a typical FeSC17. All FeSCs show very similar high-energy behaviour, but differ at low energies depending on the occurrence of magnetic order (red curve and red arrow, denoting the magnetic Bragg peak) or superconductivity (green). The inset shows the variation of the static ordered moment \(\left\langle m\right\rangle \) across materials, and of the fluctuating local moment, given by the energy-integrated susceptibility \(\sqrt{\left\langle {m}^{2}\right\rangle }\). b, c, Single-stripe (b) and double-stripe (c) configurations of the Fe spins. The single-stripe configuration is realized in most FeSCs, whereas the double-stripe configuration is realized in FeTe. In momentum space, they correspond respectively to Bragg peaks at (π, 0) (or (0, π)) and (π/2, π/2) in the 1-Fe Brillouin zone. d, e, C4-symmetric spin configurations observed in electron-doped CaKFe4As4 (ref. 70; d) and hole-doped SrFe2As2 (ref. 67; e). They correspond to a superposition of (π, 0) and (0, π) wavevectors resulting in either a non-collinear spin-vortex phase (d), characterized by a staggered spin-vorticity across the Fe square plaquettes, or a charge–spin density wave phase (e), a non-uniform state with out-of-plane moments in which half of the Fe atoms have vanishing magnetization and a smaller charge density than the average (smaller yellow spheres). Panels b–e were created using VESTA151.

Full size image

Thus, although charge and orbital degrees of freedom are itinerant, the spin degrees of freedom show properties that are typical of local-spin systems at high energies and of itinerant-spin systems at low energies. This ‘orbital–spin’ separation11 is the most striking feature of the Hund metal. As the temperature is lowered, this correlated metallic state shows Fermi liquid behaviour and an ordered phase emerges—magnetic, nematic or superconducting. Understanding them requires considering both the Fermi surface details (Fig. 1e) and the magnetic spectrum (Fig. 3a).

Magnetism: between itinerancy and localization

The vast majority of FeSC parent compounds, such as BaFe2As2 in Fig. 1a, undergo a magnetic transition to a stripe-like configuration17, which consists of parallel spins along one in-plane Fe–Fe direction and antiparallel along the other (Fig. 3b). There are two energetically equivalent stripe states, related by an in-plane 90° rotation in real and spin spaces. The spin–orbit coupling generates magnetic anisotropies that force the spins to point parallel to the selected ordering vector60, opening a spin gap in the local magnetic susceptibility at low energies (Fig. 3a). In contrast to the fluctuating moment, the ordered moment can be rather small, and changes considerably across different compounds (inset of Fig. 3a)18. Parent compounds such as LiFeAs and FeSe, which do not undergo a magnetic transition, still show low-energy fluctuations associated with the stripe state61,62. Even in FeTe, which shows a different magnetic configuration—the double-stripe state of Fig. 3c—magnetic fluctuations at the single-stripe wavevectors emerge on modest substitution of Se for Te (refs. 63,64).

Perturbations such as doping, isovalent chemical substitutions and pressure tend to reduce the magnetic transition temperature of the pristine compositions (Fig. 1a) and can also give rise to previously unknown magnetic ground states. Locally, impurities can promote puddles of Néel and other orders65. Globally, doping BaFe2As2 with electrons stabilizes an incommensurate stripe order66, whereas hole-doping promotes the so-called C4 magnetic phases67. The C4 magnetic phases are combinations of the magnetic configurations with different stripe wavevectors that preserve the tetragonal (that is, C4) symmetry of the lattice68,69. They can be either the non-collinear spin-vortex crystal (Fig. 3d), as observed in electron-doped CaKFe4As4 (ref. 70), or the non-uniform charge–spin density wave (Fig. 3e), as observed in hole-doped SrFe2As2 (ref. 67; Fig. 1a).

The simultaneous presence of features commonly associated with localized and itinerant magnetism has motivated theoretical models adopting both a strong-coupling perspective71,72,73, usually based on substantial exchange interactions beyond nearest-neighbour spins, and a weak-coupling approach13,74,75, often associated with Fermi-surface nesting. Nesting refers to the situation when the hole and electron pockets in Fig. 1e have comparable shapes and sizes. Deterioration of the nesting conditions was invoked to explain and anticipate the onset of C4 magnetic phases and of incommensurability with doping75. DFT has also been widely employed to investigate magnetism in FeSCs. Although DFT successfully captures the magnetic ground-state configuration of most compounds4,76, it has problems in explaining the size of the ordered moment or the absence of magnetism in FeSe (ref. 77). Advanced, beyond-DFT ab initio methods have been able to address some of these problems10,78.

Magnetism in FeSCs also provides an arena in which to explore quantum criticality79. A quantum critical point (QCP) is a zero-temperature second-order phase transition, in this case tuned by pressure, composition or strain. The fact that the stripe magnetic transition temperature extrapolates to zero near the point where the superconducting dome is peaked (Fig. 1a) is reminiscent of certain heavy-fermion materials2. Quantum criticality in those compounds is empirically associated with non-Fermi-liquid behaviour, such as a resistivity whose temperature dependence deviates from the standard metallic T2 behaviour at low temperatures. It is noted, however, that this behaviour can also arise due to other mechanisms besides a QCP. Among the FeSCs, BaFe2(As1−xPx)2 (Fig. 1a) shows the clearest evidence for the strange metal behaviour associated with a putative QCP. There, a linear-in-T resistivity accompanied by a mass enhancement and an unusual scaling of the magnetoresistance are observed above Tc near optimal doping80,81. Below Tc, a sharp peak of the T = 0 superconducting penetration depth is observed near the extrapolated QCP80, the origin of which remains unsettled82,83.

Electronic nematicity and vestigial orders

Although on symmetry grounds the nematic transition seen in most FeSCs is no different than a tetragonal-to-orthorhombic transition, the driving force can arise from various mechanisms. In general, one can define order parameters that break the tetragonal symmetry of the system in different channels—spin, orbital and lattice (Fig. 4a–c)20. Symmetry requires that all of these are simultaneously non-zero or zero, but cannot determine which is the primary one. Indeed, direct experimental manifestations of nematic order have been reported in orbital34, magnetic84 and elastic23 degrees of freedom, with associated anisotropies in transport85, optical86 and local electronic87 properties. A crucial insight came from the realization that strain is either the primary order parameter—in which case the nematic transition would be a simple structural instability—or a conjugate field to it, in which case the instability would be electronically driven. Elasto-resistivity22, Raman24 and elastic stiffness23 measurements settled this issue, establishing the dominant low-energy electronic character of the nematic state. Nevertheless, coupling to the lattice raises the critical temperature by a small amount from \({T}_{{\rm{nem}}}^{0}\) to Tnem (Fig. 4d).

Fig. 4: Electronic nematic order and its coupling to the lattice.
figure 4

The nature of the electronic nematic transition remains a matter of investigation, and might involve one or a combination of the following mechanisms20. a, In the case of spin-driven nematic order, partial melting of the stripe magnetic phase results in a state for which <Si> = 0, where Si denotes the spin of a specific site i, but for which <Si · Si+x> = − <Si · Si+y>. b, In the case of orbitally driven nematic order, interactions lead to a finite difference in the on-site occupancy of orbitals dxz and dyz (denoted by red and green in the left panel) and/or in the dxy orbital hopping (blue, right panel). Symmetry ensures that all these order parameters take on a finite value in the nematic state. In all cases, an associated bare (unrenormalized) nematic susceptibility \({\chi }_{{\rm{n}}{\rm{e}}{\rm{m}}}^{0}\) can be measured via a number of experimental techniques 22,23,24. c, Coupling to the lattice results in a spontaneous strain with the same symmetry (that is, a concomitant ferroelastic structural phase transition) at Ts = Tnem, occurring at a slightly higher temperature than the bare nematic transition temperature \({T}_{{\rm{n}}{\rm{e}}{\rm{m}}}^{0}\). d, The nemato-elastic coupling also leads to a renormalization of the nematic susceptibility χnem for temperatures above Ts, and a softening of the elastic modulus Cs in the same symmetry channel from its bare value. The grey shading indicates the magnitude of the nematic order parameter, with darker (lighter) denoting larger (smaller) magnitude.

Full size image

Two general electronic mechanisms for the nematic transition have been proposed, attributing it primarily to either spin or orbital degrees of freedom. This distinction, however, can become subtle, as they can work in tandem44,88. In the simplest realization of the orbital scenario, interactions spontaneously lift the degeneracy between the dxz and dyz orbitals89,90, distorting the Fermi surfaces in Fig. 1e. In contrast, the spin scenario relies on the proximity to the stripe magnetic instability, which breaks both the (discrete) rotational and translational symmetries of the lattice20,91,92. The idea is that the stripe magnetic phase melts in two stages, first restoring the broken translational symmetry and then the four-fold rotational symmetry. The intermediate paramagnetic orthorhombic phase that onsets between the magnetic orthorhombic and paramagnetic tetragonal phases is the electronic nematic. Since it is a partially melted magnetic phase, it has been identified as a ‘vestigial’ phase of the stripe magnetic state93. Theoretically, because it is stabilized by magnetic fluctuations, vestigial nematicity can be captured by phenomenological, beyond mean-field Ginzburg–Landau analyses. Microscopically, it has been found in both localized spin91,92,94 and itinerant magnetic44,95 models.

The spin-driven mechanism naturally accounts for the close proximity between the stripe-magnetic and nematic phase boundaries observed in most FeSCs. Whether these two transitions are split or simultaneous, second-order or first-order, depends on doping and pressure96. Direct experimental evidence for this scenario is the scaling between the shear modulus Cs and the nuclear magnetic resonance (NMR) spin-lattice relaxation rate 1/T1, which suggests that the lattice softening is caused by magnetic fluctuations97. Application of this mechanism to FeSe is problematic98, however, as stripe-magnetic order is absent at ambient pressure99 or upon S substitution (Fig. 1b). The orbital-order scenario also faces challenges, at least in its simplest form, as ARPES measurements indicate the inadequacy of simple on-site ferro-orbital order100.

The existence of a doping-dependent nematic transition also opens the possibility of a nematic QCP. Several theoretical studies point to possible exotic non-Fermi-liquid behaviour near such a QCP, with implications for the description of the normal state from which the superconductor emerges101,102. Probing this, however, is challenging because of its proximity to a putative magnetic QCP in most FeSCs. The very nature of the coupled nematic–magnetic quantum phase transitions remains unsettled both experimentally and theoretically. Nevertheless, recent data unveiling the power-law scaling of the nematic critical temperature as it is suppressed by doping and strain provide strong evidence for a nematic QCP in BaFe2As2, with an associated quantum critical regime that spans a large part of the phase diagram103. Another promising arena to study nematic quantum criticality is FeSe1−xSx (refs. 51,104; Fig. 1b), where magnetic order is absent. Experimental evidence for possible non-Fermi-liquid behaviour near the nematic QCP remains controversial, however104,105.

Unconventional superconducting states

The FeSCs show a wide range of superconducting transition temperatures, as illustrated in Fig. 5a. The largest Tc ≈ 65 K is observed in monolayer FeSe grown on SrTiO3, but the precise temperature where phase-coherent superconductivity sets in remains under dispute106. Several unsubstituted compounds show superconductivity, such as bulk FeSe, LiFeAs and CaKFe4As4. In others, such as BaFe2As2 and LaFeAsO, the competing magnetic and nematic orders need to be suppressed, for example, via doping, chemical substitution or pressure, to obtain superconductivity (Fig. 1a, b). In some compounds, a second superconducting dome can be accessed by pressure or doping107. In all cases, NMR measurements support a singlet pairing state.

Fig. 5: Superconducting gap structures and gap symmetries.
figure 5

a, Superconducting critical temperatures, Tc, of six canonical Fe-based superconductors. b, Schematic gap structures for these materials in the 1-Fe Brillouin zone (borders coloured according to a) based on weak-coupling calculations, ARPES and STM experiments (see refs. 6,7,118 and references therein). The line thickness represents the magnitude of the gap, and the green and orange colours denote different signs. c, The ratio between twice the maximum gap (2Δmax, based on ARPES data) and kBTc of FeSCs, compared with that of conventional superconductors (see also ref. 119). The coloured symbols correspond to some of the materials labelled in a. The open square symbols correspond to conventional BCS superconductors. d, Possible superconducting ground states realized in a three-band toy model with repulsive interband interactions (see refs. 120,122 for the analogous case of an s + is state). The red (blue) arrows are associated with the complex value of the gap averaged around the electron (hole) pockets (see inset). TRSB denotes time-reversal symmetry breaking. The electron-pocket gaps have distinct averaged values in the nematic case.

Full size image

As the DFT-calculated electron–phonon coupling cannot account for the Tc of the FeSCs38,108, an electronic mechanism has been proposed 4,5,6,7,8. However, this does not preclude phonons, which can be enhanced by correlations109, from having a role in superconductivity, as it has been proposed in monolayer FeSe (ref. 110). Quite generally, electronic repulsion forces the gap function to change sign in real or momentum space. For a large Fermi surface, such as the cuprates, this can be accomplished by an anisotropic gap (for example, with d-wave symmetry). For multiple small Fermi pockets, such as the FeSCs, the gap can remain nearly isotropic around each Fermi surface, as long as it acquires different signs (that is, phases) on different pockets. We refer to any gap structure that satisfies this criterion as s+− wave. In the FeSCs, a strong repulsive pairing interaction is believed to be promoted by magnetic correlations associated with the nearby stripe magnetic state (Fig. 1a)4.

In a weak-coupling approach, which can be implemented via random phase approximation (RPA) or (functional) renormalization group ((f)RG) calculations, the inter-pocket interaction is boosted by spin fluctuations peaked at the stripe wavevectors (π, 0) and (0, π), which connect the hole and electron pockets, thus overcoming the intra-pocket repulsion6,7,111. In a strong-coupling approach, real-space pairing is promoted by the dominant next-nearest-neighbour antiferromagnetic exchange interaction33,71,72. Despite their differences, both approaches generally give an s+− gap with opposite signs on the electron and the hole pockets.

Besides stripe magnetism, nematic order is also strongly suppressed in the region of the phase diagram where Tc is the largest (Fig. 1a, b). This has led to an important question that remains unresolved, namely, what role nematic fluctuations have in the pairing state of the FeSCs20. Theoretically, nematic fluctuations generate an attractive pairing interaction peaked at zero momentum. Hence, they can boost the Tc of any pairing state promoted by a more dominant pairing interaction (for example, due to spin fluctuations). Nematic fluctuations can plausibly promote superconducting order on their own, particularly near a QCP101,102. However, in the clearest case of FeSe1−xSx (Fig. 1b), no strong change in Tc is observed at the putative nematic QCP104, an issue that remains under investigation105,112.

Traditional phase-sensitive experiments face difficulties in distinguishing the s+− state from the more conventional s++ state, which has also been proposed to be mediated by orbital fluctuations113, because the Cooper pairs have zero angular momentum in both cases. Nevertheless, phase-sensitive setups using composite loops of polycrystalline FeSCs114 or scanning tunnelling microscopy (STM) quasiparticle interference51,115 strongly support the s+−-wave state. The strongest evidence for an s+− gap is the observation of a resonance mode in the magnetic susceptibility below Tc (refs. 18,19), manifested as a sharp peak at the stripe wavevectors and at an energy Eresonance below twice the gap value, 2Δ (schematically illustrated in Fig. 3a). Such a feature is naturally explained if the gaps at momenta separated by the stripe wavevectors have opposite signs2. Additional indirect evidence comes from experiments that introduce controlled disorder via irradiation. Specifically, the lifting of accidental nodes by disorder and the observed rate of suppression of Tc with impurity scattering are consistent with an s+− state116. Moreover, the observation of in-gap bound states at non-magnetic impurities is also a hallmark of a sign-changing gap117.

Various gap structures can be realized under the s+−-wave umbrella, depending on details of the Fermi surface and on the orbital degrees of freedom6,7,111. Although the gap generally has opposite signs on electron and hole pockets, additional sign changes between same-character pockets may occur57. Moreover, although ARPES observes nearly isotropic gaps in many compounds33, accidental nodes may occur as well118, which are well described by weak-coupling models5,6. Some of these gap structures are illustrated in Fig. 5b in the 1-Fe Brillouin zone. They represent the leading gap-structure candidates of the materials in Fig. 5a, partly motivated by theoretical considerations, but consistent with ARPES, STM and/or neutron-scattering measurements. The variety of gap structures in Fig. 5b and the wide range of Tc values in Fig. 5a raise the question of whether there is really a common, dominant pairing mechanism in the FeSCs. Evidence in favour of this comes from the dimensionless ratio 2Δmax/(kBTc), where Δmax is the zero-temperature value of the largest gap and kB is the Boltzmann constant. As shown schematically in Fig. 5c, this ratio falls between 6.0 and 8.5 for many FeSCs (blue shaded region)119, in contrast to the 3.5–4.5 range observed in canonical electron–phonon superconductors (red shaded region).

The multiband nature of the FeSCs also provides opportunities for more exotic pairing states besides s+−. This is illustrated by a toy model with one hole and two electron pockets subjected to repulsive pairing interactions (see ref. 120 for a related toy model). Figure 5d schematically shows the pairing states obtained on tuning the ratio between the interband electron–pocket/electron–pocket and electron–pocket/hole–pocket interactions, which can be different, for example, if the orbital compositions of the pockets are distinct. When the ratio is small, an s+− state is obtained: the gaps on the electron pockets are identical and have a π phase shift with respect to the hole–pocket gap. When the ratio is large, a d-wave state emerges: the gaps on the two electron pockets have equal magnitude but a relative π phase, whereas the anisotropic gap on the hole pocket averages to zero. When the ratio is of order one, it is possible to realize a nematic s + d superconducting state75, in which the electron–pocket gaps have the same phase but distinct magnitudes. This is different from the case where nematicity onsets separately above Tc, as in FeSe. Another option is a time-reversal symmetry-breaking (TRSB) s + id state121, in which the electron–pocket gaps have equal magnitude but their relative phase is neither 0 (as in an s+− state) nor π (as in a d wave). A different type of TRSB pairing state, called s + is (ref. 120), has been proposed in heavily K-doped BaFe2As2, based on muon-spin-rotation measurements122.

More broadly, the variation of orbital spectral weight along the Fermi pockets (Fig. 1e) endows the projected pairing interaction with an angular dependence, which can favour non-s-wave pairing. Microscopic calculations have in fact suggested that the s+−- and d-wave interactions can be comparable in strength6,7,111. Experimentally, peculiar peaks observed in the Raman spectrum have been interpreted as collective d-wave excitations inside the s+− state123,124 or as a collective nematic excitation125. The non-monotonic evolution of Tc with pressure in KFe2As2 has also been interpreted as evidence for nearly degenerate superconducting states126. Finally, the fact that the small Fermi energy of some FeSCs is comparable to the gap value has motivated the search for strong-coupling superconductivity described by the Bose–Einstein condensate (BEC) prescription of tightly bound pre-formed Cooper pairs. Although certain properties of FeSe and FeTe1−xSex have been described in terms of a BEC–BCS crossover104,127, direct evidence for pre-formed pairs remains to be seen.

Topological phenomena

One of the most recent developments in the field is the discovery of topological properties in some FeSCs. As schematically shown in Fig. 6a, this arises from p–d band inversions along the Γ–Z direction involving an odd-parity anionic pz band and an even-parity Fe d-band (t2g)25. Bulk band inversion was observed by ARPES30,128, but in a renormalized electronic dispersion compared with DFT predictions30. The crossings of the pz band with the dxy band and the spin–orbit-coupling mixed dxz,↑ + idyz,↑ band are protected, resulting in bulk topological Dirac semimetal states (purple shaded region in Fig. 6a, left panel)129, 130. However, the crossing with the dxz,↑ − idyz,↑ band is gapped, resulting in a topological insulating state (green shaded region in Fig. 6a, left panel)30. Both the bulk Dirac semimetal states and the helical surface Dirac cones emerging when the chemical potential crosses the topological gap were observed by ARPES in a few FeSCs, most notably FeTe1−xSex (refs. 25,129.)

Fig. 6: Band inversion and topological phenomena.
figure 6

a, The topological p–d band inversion in the FeSCs is illustrated in the left panel25. The downward shift of the pz-orbital band along the Γ–Z direction causes different topological phenomena such as bulk Dirac semimetal states (purple shaded region) and helical Dirac surface states (green shaded region), depending on whether it crosses the dxy and (dxz,↑ + idyz,↑) bands or the (dxz,↑ − idyz,↑) band, respectively. The bands (dxz,↑ ± idyz,↑) arise from the spin–orbit coupling between the degenerate dxz and dyz Fe orbitals in Fig. 1d, and have total angular momentum of 3/2 (plus sign) and 1/2 (minus sign)130; thus, only the former can hybridize with the pz band, as the latter has angular momentum of 1/2. The right panel illustrates the topological superconductivity (TSC) induced on the surface Dirac states by the bulk superconducting (SC) state. b, In the quantum limit, which is achievable in some FeSCs, discrete levels can be observed inside a vortex by probing the local density of states (LDOS) via STM. In an ordinary vortex (upper panels), these bound states are all at finite energies, whereas in a topological vortex (lower panels), a sharp zero-energy mode, called an MZM, appears well separated from the other bound states. Panels reproduced with permission from: a, right, ref. 25, AAAS; b, left, ref. 131, Springer Nature Ltd; lower right, ref. 152, Chinese Physical Society.

Full size image

Upon emergence of the s+−-wave state in the bulk, superconductivity can be induced on these Dirac surface states (right panel of Fig. 6a). Similar to topological insulator/superconductor heterostructures, the surface Dirac states of the FeSCs can also support Majorana zero modes (MZMs) in the vortex cores of the superconducting state. Importantly, the topological superconductivity on the FeSC surface is intrinsic, shows high Tc values and avoids the interfacial complexities of the heterostructures.

Inside the vortex of any superconductor, there are discrete energy levels of νΔ2/EF, where EF is the Fermi energy and ν is related to the planar angular momentum of the vortex. They can only be resolved in the quantum limit, where thermal broadening is smaller than the level spacing. As discussed above, FeSCs usually have small EF owing to correlations. In FeTe1−xSex, EF can become comparable to Δ, making the quantum limit achievable. In an ordinary vortex, ν is expected to be half-integer, and the discrete levels never have zero energy (upper panels of Fig. 6b). However, in a topological vortex, ν is shifted to integer values due to the spin texture of the Dirac states131. As a result, a MZM emerges as the vortex bound state with zero energy (lower panels of Fig. 6b). Experimentally, both zero-energy bound states and higher-energy discrete levels have been observed in FeTe1−xSex via STM measurements131,132,133, providing strong support for the existence of MZMs.

Notwithstanding its simplicity, the FeSC Majorana platform is subjected to issues such as spatial inhomogeneity and the interlayer coupling in bulk crystals. Some of these issues may be the reason why zero modes are observed in only a fraction of the vortices131. Besides in the interior of vortices, signatures consistent with Majorana fermions have also been observed in different types of lattice defect, such as interstitials134, line defects135 and crystalline domain boundaries136, where a one-dimensional dispersing Majorana mode was reported. On the theory front, several ideas have been put forward for realizing other exotic topological effects, such as dispersing Majorana fermions130 and higher-order Majorana modes in corners and hinges of samples137.

Outlook

After 14 years, FeSCs continue to provide a rich and unmatched framework to assess the interplay between correlations, unconventional superconductivity, magnetism, nematicity, quantum criticality and topology. Although substantial advances have occurred, deep questions linger and continue to emerge.

The correlation effects in FeSCs, which are primarily driven by the Hund’s interaction, appear to be enhanced on hole doping49. Although several factors affect the strength of correlations10, this observation has also been interpreted in terms of a proximate Mott insulator71 that would exist for d5 compositions15,138, analogous to the Mott state of half-filled parent cuprates. Effects typically associated with Mott physics, such as Hubbard bands, have been proposed even in d6 compounds139. However, experimental observation of such a Mott state has remained elusive, leaving the interplay between Mott insulating and Hund metallic states an open question.

Understanding how and why the different ordered states—superconducting, nematic and magnetic—emerge also remains a challenge. Although different approaches are possible, in the Hund-metal description this generally happens in the regime where charge degrees of freedom are itinerant but spins are localized. Explaining the phase-transition mechanisms in this regime will require the development of ideas that can seamlessly combine long-wavelength, low-energy physics with local, intermediate-energy physics. The former is captured by perturbative methods such as (f)RG and RPA, which focus on the momentum dependence of the interactions and on the resulting instabilities of the system. The latter is well described by DMFT approaches that focus on the frequency dependence of the interactions.

The discovery of the FeSCs provided an arena to test and develop ab initio methods for correlated electron materials10,40,41,78,138,140. They proved to be of immense value for suggesting new concepts and aiding the interpretation of experiments. This line of research will continue to have an important role in the future, potentially assisting in the discovery of compounds with desirable properties.

Another problem that will benefit from these first-principles correlated approaches is the elucidation of the topological properties of FeSCs, as most of the existing analyses rely on DFT. More broadly, it will be invaluable to better understand how correlations and other electronic states, such as nematicity and magnetism, impact and are impacted by topological states141. Experimental progress will benefit from controllable tuning of MZMs in the vortex state of homogeneous compounds and from designing a feasible pathway for braiding them142.

For antiferromagnetism and nematicity, although their symmetry-breaking properties are well understood, key issues remain unresolved, such as the origin of nematicity in Fe chalcogenides or the role of the C4 magnetism in Fe pnictides. Moreover, it is still unclear whether quantum criticality is a central ingredient to the FeSCs. Experimentally disentangling signatures from putative nematic and magnetic QCPs will be an important step towards elucidating this issue. Theoretically, a full description of the nematic QCP, and of its impact on the superconducting instability, will require incorporating two often neglected lattice effects. The first comes from lattice vibrations, which mediate long-range nematic interactions capable of suppressing critical fluctuations112,143. The second arises from random local strains caused by dopants and other defects ubiquitously present in the samples144,145. Promoting effects typical of the random-field Ising model, random strains have been argued to cause a deviation from Curie–Weiss behaviour of the nematic susceptibility146. The related issue of electronic inhomogeneity and phase separation is not covered in this review.

Important questions about superconductivity also remain open, despite substantial theoretical progress, particularly in multi-orbital weak-coupling approaches. They include establishing how the gap structure and the Tc depend on materials parameters, such as the FeAs4 tetrahedral angle or the correlation-driven mass enhancement, and explaining the seemingly universal 2Δmax/(kBTc) ratio. Another challenge is posed by compounds with only hole pockets (such as KFe2As2) or only electron pockets (such as monolayer FeSe), which do not fall within the standard weak-coupling s+− paradigm, and for which the relevance of magnetic fluctuations is not well established. Yet, both display superconductivity, with some of the electron-pocket-only compounds showing the highest Tc’s among all FeSCs. This requires new approaches that can elucidate the pairing mechanism in these compounds (see, for example, ref. 147) and its relationship with other FeSCs.

Opportunities to address some of these unanswered questions and venture into unexplored directions are provided by other Fe-based compounds, which continue to be regularly discovered. Some of them have unusual structural properties owing to their spacing layers, such as CaKFe4As4 with centres of inversion away from the FeAs layer, the monoclinic Ca1−xLaxFeAs2 (refs. 148) with a metallic spacer layer, and the insulating ladder compound BaFe2Se3 (refs. 149,150). Conversely, many of the theoretical and experimental advances spurred by FeSC studies have found fertile ground in other quantum materials. For instance, Hund-metal concepts have been used to explain the normal-state properties of various quantum materials, most notably Sr2RuO4 (ref. 16). Multi-orbital pairing models have been extensively employed to elucidate multi-band superconductors such as ruthenates and nickelates. The concept of vestigial orders and the associated phenomenological models have led to important insights into antiferromagnetic and topological superconducting materials93. Experimentally, symmetry-breaking strain has been recognized as a uniquely appropriate tool to probe electronic nematic order. Strain-based techniques applied to transport, thermodynamic, scattering, spectroscopic and local probe measurements are now considered mainstream. They have enabled the identification and manipulation of electronic nematicity and a variety of other electronic states in disparate materials such as cuprates and f-electron systems. Overall, the constantly evolving toolbox developed and refined in FeSC studies has equipped the community with powerful methods to both revisit old problems and search for new quantum electronic phenomena.