Mastering Atari, Go, chess and shogi by planning with a learned model

Abstract

Constructing agents with planning capabilities has long been one of the main challenges in the pursuit of artificial intelligence. Tree-based planning methods have enjoyed huge success in challenging domains, such as chess¹ and Go², where a perfect simulator is available. However, in real-world problems, the dynamics governing the environment are often complex and unknown. Here we present the MuZero algorithm, which, by combining a tree-based search with a learned model, achieves superhuman performance in a range of challenging and visually complex domains, without any knowledge of their underlying dynamics. The MuZero algorithm learns an iterable model that produces predictions relevant to planning: the action-selection policy, the value function and the reward. When evaluated on 57 different Atari games³—the canonical video game environment for testing artificial intelligence techniques, in which model-based planning approaches have historically struggled⁴—the MuZero algorithm achieved state-of-the-art performance. When evaluated on Go, chess and shogi—canonical environments for high-performance planning—the MuZero algorithm matched, without any knowledge of the game dynamics, the superhuman performance of the AlphaZero algorithm⁵ that was supplied with the rules of the game.

Main

Planning algorithms based on lookahead search have achieved remarkable successes in artificial intelligence. Human world champions have been defeated in classic games such as checkers⁶, chess¹, Go² and poker^7,8, and planning algorithms have had real-world impact in applications from logistics⁹ to chemical synthesis¹⁰. However, these planning algorithms all rely on knowledge of the environment’s dynamics, such as the rules of the game or an accurate simulator, preventing their direct application to real-world domains such as robotics, industrial control or intelligent assistants, where the dynamics are normally unknown.

Model-based reinforcement learning (RL)¹¹ aims to address this issue by first learning a model of the environment’s dynamics and then planning with respect to the learned model. Typically, these models have either focused on reconstructing the true environmental state^12,13,14 or the sequence of full observations^15,16. However, previous work^15,16,17 remains far from the state of the art in visually rich domains, such as Atari 2600 games³. Instead, the most successful methods are based on model-free RL^18,19,20—that is, they estimate the optimal policy and/or value function directly from interactions with the environment. However, model-free algorithms are in turn far from the state of the art in domains that require precise and sophisticated lookahead, such as chess and Go.

Here we introduce MuZero, a new approach to model-based RL that achieves both state-of-the-art performance in Atari 2600 games—a visually complex set of domains—and superhuman performance in precision planning tasks such as chess, shogi and Go, without prior knowledge of the game dynamics. MuZero builds on AlphaZero’s⁵ powerful search and policy iteration algorithms, but incorporates a learned model into the training procedure. MuZero also extends AlphaZero to a broader set of environments, including single agent domains and non-zero rewards at intermediate time steps.

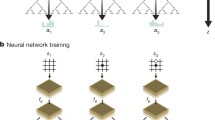
The main idea of the algorithm (summarized in Fig. 1) is to predict those aspects of the future that are directly relevant for planning. The model receives the observation (for example, an image of the Go board or the Atari screen) as an input and transforms it into a hidden state. The hidden state is then updated iteratively by a recurrent process that receives the previous hidden state and a hypothetical next action. At every one of these steps, the model produces a policy (predicting the move to play), value function (predicting the cumulative reward, for example, the eventual winner) and immediate reward prediction (for example, the points scored by playing a move). The model is trained end to end, with the sole objective of accurately estimating these three important quantities, to match the improved policy and value function generated by search, as well as the observed reward. There is no direct requirement or constraint on the hidden state to capture all information necessary to reconstruct the original observation, drastically reducing the amount of information the model has to maintain and predict. Neither is there any requirement for the hidden state to match the unknown, true state of the environment; nor any other constraints on the semantics of state. Instead, the hidden states are free to represent any state that correctly estimates the policy, value function and reward. Intuitively, the agent can invent, internally, any dynamics that lead to accurate planning.

Fig. 1: Planning, acting and training with a learned model.

a, How MuZero uses its model to plan. The model consists of three connected components for representation, dynamics and prediction. Given a previous hidden state s^k−1 and a candidate action a^k, the dynamics function g produces an immediate reward r^k and a new hidden state s^k. The policy p^k and value function v^k are computed from the hidden state s^k by a prediction function f. The initial hidden state s⁰ is obtained by passing the past observations (for example, the Go board or Atari screen) into a representation function h. b, How MuZero acts in the environment. An MCTS is performed at each timestep t, as described in a. An action a_t+1 is sampled from the search policy π_t, which is proportional to the visit count for each action from the root node. The environment receives the action and generates a new observation o_t+1 and reward u_t+1. At the end of the episode, the trajectory data are stored into a replay buffer. c, How MuZero trains its model. A trajectory is sampled from the replay buffer. For the initial step, the representation function h receives as input the past observations o₁, ..., o_t from the selected trajectory. The model is subsequently unrolled recurrently for K steps. At each step k, the dynamics function g receives as input the hidden state s^k−1 from the previous step and the real action a_t+k. The parameters of the representation, dynamics and prediction functions are jointly trained, end to end, by backpropagation through time, to predict three quantities: the policy p^k ≈ π_t+k, value function v^k ≈ z_t+k and reward r^k ≈ u_t+k, where z_t+k is a sample return: either the final reward (board games) or n-step return (Atari). Schematic Go boards at the top of the figure represent the sequence of observations.

Previous work

RL can be subdivided into two principal categories: model based and model free¹¹. Model-based RL constructs, as an intermediate step, a model of the environment. Classically, this model is represented by a Markov decision process (MDP)²¹ consisting of two components: a state transition model, predicting the next state given the selected action, and a reward model, predicting the expected reward during that transition. Once a model has been constructed, it is straightforward to apply MDP planning algorithms, such as value iteration²¹ or Monte Carlo tree search (MCTS)²², to compute the optimal value function or optimal policy for the MDP. In large or partially observed environments, the algorithm must first construct the state representation that the model should predict. This tripartite separation between representation learning, model learning and planning is potentially problematic, as the agent is not able to optimize its representation or model for the purpose of effective planning, so, for example, modelling errors may compound during planning.

A common approach to model-based RL focuses on directly modelling the observation stream at the pixel level. It has been hypothesized that deep, stochastic models may mitigate the problems of compounding error^15,16. However, planning at pixel-level granularity is not computationally tractable in large-scale problems. Other methods build a latent state-space model that is sufficient to reconstruct the observation stream at the pixel level^23,24 or to predict its future latent states^25,26, which facilitates more efficient planning but still focuses the majority of the model capacity on potentially irrelevant detail. None of these previous methods have constructed a model that facilitates effective planning in visually complex domains such as Atari; results lag behind well tuned, model-free methods, even in terms of data efficiency²⁷.

A quite different approach to model-based RL has recently been developed, focused end to end on predicting the value function^{28,29,30,31,32,33}. The main idea of these methods is to construct an abstract MDP model such that planning in the abstract MDP is equivalent to planning in the real environment. This is achieved by ensuring value equivalence, that is, that, starting from the same real state, the cumulative reward of a trajectory through the abstract MDP matches the cumulative reward of a trajectory in the real environment.

The predictron²⁹ introduced value equivalent models for predicting value functions (without actions). Although the underlying model still takes the form of an MDP, there is no requirement for its transition model to match real states in the environment. Instead the MDP model is viewed as a hidden layer of a deep neural network. The unrolled MDP is trained such that the expected cumulative sum of rewards matches the expected value with respect to the real environment, for example, by temporal-difference learning.

Value equivalent models have also been applied to optimizing value (with actions). Value-aware model learning^30,31 constructs an MDP model, such that a step of value iteration using the model produces the same outcome as the real environment. TreeQN³² learns an abstract MDP model, such that a tree search over that model (represented by a tree-structured neural network) approximates the optimal value function. Value iteration networks²⁸ learn a local MDP model, such that many steps of value iteration over that model (represented by a convolutional neural network) approximates the optimal value function.

Value prediction networks³³ are perhaps the closest precursor to MuZero: they learn an MDP model grounded in real actions; the unrolled MDP is trained such that the cumulative sum of rewards, conditioned on the actual sequence of actions generated by a simple lookahead search, matches the real environment. Unlike MuZero there is no policy prediction, and the search utilizes only value prediction.

MuZero algorithm

We now describe the MuZero algorithm in more detail. Predictions are made at each time step t, for each of k = 0, …, K steps, by a model μ_θ, with parameters θ, conditioned on past observations o₁, ..., o_t and for k > 0 on future actions a_t+1, ..., a_t+k. The model predicts three future quantities: the policy ${p}_{t}^{k}\approx \pi ({a}_{t+k+1}|{o}_{1}\,,\ldots ,\,{o}_{t},\,{a}_{t+1},\ldots ,\,{a}_{t+k})$, the value function ${v}_{t}^{k}\approx {\mathbb{E}}[{u}_{t+k+1}+\gamma {u}_{t+k+2}+\ldots |{o}_{1},\,\ldots ,{o}_{t},\,{a}_{t+1},\ldots ,\,{a}_{t+k}]$ and, for k > 0, also the immediate reward ${r}_{t}^{k}\approx {u}_{t+k}$, where u_. is the true, observed reward, π is the policy used to select real actions and γ is the discount function of the environment.

Internally, at each time step t (subscripts t are suppressed for simplicity), the model is represented by the combination of a representation function, a dynamics function and a prediction function. The dynamics function g_θ, is a recurrent process, r^k, s^k = g_θ(s^k−1, a^k), that computes, at each hypothetical step k, an immediate reward r^k and an internal state s^k. It mirrors the structure of an MDP model that computes the expected reward and state transition for a given state and action²¹. However, unlike traditional approaches to model-based RL¹¹, this internal state s^k has no semantics of environment state attached to it—it is simply the hidden state of the overall model and its sole purpose is to accurately predict relevant, future quantities: policies, values and rewards. In this paper, the dynamics function is represented deterministically; the extension to stochastic transitions is left for future work. A prediction function f_θ computes the policy and value functions from the internal state s^k, p^k, v^k = f_θ(s^k), akin to the joint policy and value network of AlphaZero. A representation function h_θ initializes the ‘root’ state s⁰ by encoding past observations, s⁰ = h_θ(o₁, ..., o_t); again, this has no special semantics beyond its support for future predictions.

Given such a model, it is possible to search over hypothetical future trajectories a¹, ..., a^k given past observations o₁, ..., o_t. For example, a naive search could simply select the k-step action sequence that maximizes the value function. More generally, we may apply any MDP planning algorithm to the internal rewards and state space induced by the dynamics function. Specifically, we use an MCTS algorithm similar to AlphaZero’s search, generalized to allow for single-agent domains and intermediate rewards (Methods). The MCTS algorithm may be viewed as a search policy π_t = ℙ[a_t+1|o₁, ..., o_t] and search value function ν_t ≈ ${\mathbb{E}}$[u_t+1 + γu_t+2 +...|o₁, ..., o_t] that both selects an action and predicts cumulative reward given past observations o₁, ..., o_t. At each internal node, it makes use of the policy, value function and reward estimate produced by the current model parameters θ, and combines these values together using lookahead search to produce an improved policy π_t and improved value function ν_t at the root of the search tree. The next action a_t+1 ≈ π_t is then chosen by the search policy.

All parameters of the model are trained jointly to accurately match the policy, value function and reward prediction, for every hypothetical step k, to three corresponding targets observed after k actual time steps have elapsed. Similarly to AlphaZero, the first objective is to minimize the error between the actions predicted by the policy ${p}_{t}^{k}$ and by the search policy π_t+k. Also like AlphaZero, value targets are generated by playing out the game or MDP using the search policy. However, unlike AlphaZero, we allow for long episodes with discounting and intermediate rewards by computing an n-step return z_t that bootstraps n steps into the future from the search value, z_t = u_t+1 + γu_t+2 + ... + γⁿ⁻¹u_t+n + γⁿν_t+n. Final outcomes {lose, draw, win} in board games are treated as rewards u_t ∈ {−1, 0, +1} occurring at the final step of the episode. Specifically, the second objective is to minimize the error between the value function ${v}_{t}^{k}$ and the value target, z_t+k. The third objective is to minimize the error between the predicted immediate reward ${r}_{t}^{k}$ and the observed immediate reward u_t+k. Finally, an L2 regularization term is also added, scaled by a constant c, leading to the overall loss

$${l}_{t}(\theta )=\mathop{\sum }\limits_{k=0}^{K}{l}^{{\rm{p}}}({\pi }_{t+k},{p}_{t}^{k})+\mathop{\sum }\limits_{k=0}^{K}{l}^{{\rm{v}}}({z}_{t+k},{v}_{t}^{k})+\mathop{\sum }\limits_{k=1}^{K}{l}^{{\rm{r}}}({u}_{t+k},{r}_{t}^{k})+c||\theta |{|}^{2},$$

(1)

where l^p, l^v and l^r are loss functions for policy, value and reward, respectively. Supplementary Fig. 2 summarizes the equations governing how the MuZero algorithm plans, acts and learns. We note that for chess, Go and shogi, the same squared error loss as AlphaZero is used for rewards and values. A cross-entropy loss was found to be more stable than a squared error when encountering rewards and values of variable scale in Atari. Cross-entropy was used for the policy loss in both cases.

Results

We applied the MuZero algorithm to the classic board games Go, chess and shogi, as benchmarks for challenging planning problems, and to all 57 games in the Atari learning environment³, as benchmarks for visually complex RL domains.

In each case, we trained MuZero for K = 5 hypothetical steps. Training proceeded for one million mini-batches of size 2,048 in board games and of size 1,024 in Atari. During both training and evaluation, MuZero used 800 simulations for each search in board games and 50 simulations for each search in Atari. The representation function uses the same convolutional³⁴ and residual³⁵ architecture as AlphaZero, but with 16 residual blocks instead of 20. The dynamics function uses the same architecture as the representation function and the prediction function uses the same architecture as AlphaZero. All networks use 256 hidden planes (see Methods for further details).

Figure 2 shows the performance throughout training in each game. In Go, MuZero slightly exceeded the performance of AlphaZero, despite using less computation per node in the search tree (16 residual blocks per evaluation in MuZero compared with 20 blocks in AlphaZero). This suggests that MuZero may be caching its computation in the search tree and using each additional application of the dynamics model to gain a deeper understanding of the position.

Fig. 2: Evaluation of MuZero throughout training in chess, shogi, Go and Atari.

The x axis shows millions of training steps. For chess, shogi and Go, the y axis shows Elo rating, established by playing games against AlphaZero using 800 simulations per move for both players. MuZero’s Elo is indicated by the blue line and AlphaZero’s Elo is indicated by the horizontal orange line. For Atari, mean (full line) and median (dashed line) human normalized scores across all 57 games are shown on the y axis. The scores for R2D2¹⁹ (the previous state of the art in this domain, based on model-free RL) are indicated by the horizontal orange lines. Performance in Atari was evaluated using 50 simulations every fourth time step, and then repeating the chosen action four times, as in previous work³⁹. Supplementary Fig. 1 studies the repeatability of training in Atari.

In Atari, MuZero achieved state-of-the-art performance for both mean and median normalized score across the 57 games of the arcade learning environment, outperforming the previous state-of-the-art method R2D2¹⁹ (a model-free approach) in 42 out of 57 games, and outperforming the previous best model-based approach SimPLe¹⁶ in all games (Table 1 and Supplementary Table 1).

Table 1 Comparison of MuZero against previous agents in Atari

We also evaluated a second version of MuZero that was optimized for greater sample efficiency. Specifically, it reanalyses old trajectories by re-running the MCTS using the latest network parameters to provide fresh targets (see ‘MuZero Reanalyze’ in Methods). When applied to 57 Atari games, using 200 million frames of experience per game, MuZero Reanalyze achieved 731% median normalized score, compared with 192%, 231% and 431% for previous state-of-the-art model-free approaches IMPALA¹⁸, Rainbow³⁶ and LASER³⁷, respectively.

To understand the role of the model in MuZero, we also ran several experiments, focusing on the board game of Go and the Atari game of Ms. Pac-Man.

First, we tested the scalability of planning (Fig. 3a), in the canonical planning problem of Go. We compared the performance of search in AlphaZero, using a perfect model, to the performance of search in MuZero, using a learned model. Specifically, the fully trained AlphaZero or MuZero was evaluated by comparing MCTS with different thinking times. MuZero matched the performance of a perfect model, even when doing much larger searches (thinking time of up to 10 s) than those from which the model was trained (thinking time of around 0.1 s; see also Supplementary Fig. 3a).

Fig. 3: Evaluations of MuZero on Go, all 57 Atari games and Ms. Pac-Man.

a, Scaling with search time per move in Go, comparing the learned model with the ground truth simulator. Both networks were trained at 800 simulations per search, equivalent to 0.1 s per search. Remarkably, the learned model is able to scale well to up to two orders of magnitude longer searches than seen during training. b, Scaling of final human normalized mean score in Atari with the number of simulations per search. The network was trained at 50 simulations per search. Dark line indicates mean score and the shaded regions indicate the 25th to 75th and 5th to 95th percentiles. The learned model’s performance increases up to 100 simulations per search. Beyond, even when scaling to much longer searches than during training, the learned model’s performance remains stable and decreases only slightly. This contrasts with the much better scaling in Go (a), presumably due to greater model inaccuracy in Atari than Go. c, Comparison of MCTS-based training with Q-learning in the MuZero framework on Ms. Pac-Man, keeping network size and amount of training constant. The state-of-the-art Q-learning algorithm R2D2 is shown as a baseline. Our Q-learning implementation reaches the same final score as R2D2, but improves slower and results in much lower final performance compared with MCTS-based training. d, Different networks trained at different numbers of simulations (sims) per move, but all evaluated at 50 simulations per move. Networks trained with more simulations per move improve faster, consistent with ablation (b), where the policy improvement is larger when using more simulations per move. Surprisingly, MuZero can learn effectively even when training with less simulations per move than are enough to cover all eight possible actions in Ms. Pac-Man.

We also investigated the scalability of planning across all Atari games (Fig. 3b). We compared MCTS with different numbers of simulations, using the fully trained MuZero. The improvements due to planning are much less marked than in Go, perhaps because of greater model inaccuracy; performance improved slightly with search time, but plateaued at around 100 simulations. Even with a single simulation—that is, when selecting moves solely according to the policy network—MuZero performed well, suggesting that, by the end of training, the raw policy has learned to internalize the benefits of search (see also Supplementary Fig. 3b).

Next, we tested our model-based learning algorithm against a comparable model-free learning algorithm (Fig. 3c). We replaced the training objective of MuZero (equation (1)) with a model-free Q-learning objective (as used by R2D2), and the dual policy and value heads with a single head representing the action-value function Q(⋅|s_t). Subsequently, we trained and evaluated the new model without using any search. When evaluated on Ms. Pac-Man, our model-free algorithm achieved identical results to R2D2, but learned much slower than MuZero and converged to a much lower final score. We conjecture that the search-based policy improvement step of MuZero provides a stronger learning signal than the high-bias, high-variance targets used by Q-learning.

To better understand the nature of MuZero’s learning algorithm, we measured how MuZero’s training scales with respect to the amount of search it uses during training. Figure 3d shows the performance in Ms. Pac-Man, using an MCTS of different simulation counts per move throughout training. Surprisingly, and in contrast to previous work³⁸, even with only six simulations per move—fewer than the number of actions—MuZero learned an effective policy and improved rapidly. With more simulations, the performance jumped much higher. For analysis of the policy improvement during each individual iteration, see also Supplementary Fig. 3c, d.

Conclusions

Many of the breakthroughs in artificial intelligence have been based on either high-performance planning^1,2,5 or model-free RL methods^39,40,41. Here we have introduced a method that combines the benefits of both approaches. Our algorithm, MuZero, has both matched the superhuman performance of high-performance planning algorithms in their favoured domains (logically complex board games such as chess and Go) and outperformed state-of-the-art model-free RL algorithms in their favoured domains (visually complex Atari games). Crucially, our method does not require any knowledge of the environment dynamics, potentially paving the way towards the application of powerful learning and planning methods to a host of real-world domains for which there exists no perfect simulator.

Methods

Comparison to AlphaZero

MuZero is designed for a more general setting than AlphaGo Zero⁴³ and AlphaZero⁵.

In AlphaGo Zero and AlphaZero, the planning process makes use of a simulator that samples the next state and reward (for example, according to the environment’s dynamics, or the rules of the game). The simulator updates the state of the game while traversing the search tree (Fig. 1a). The simulator is used to provide three important pieces of knowledge: (1) state transitions in the search tree, (2) actions available at each node of the search tree and (3) episode termination within the search tree. In MuZero, all of these have been replaced with the use of a single implicit model learned by a neural network (Fig. 1b).

(1) State transitions. AlphaZero had access to a perfect simulator of the environment’s dynamics. In contrast, MuZero employs a learned dynamics model within its search. Under this model, each node in the tree is represented by a corresponding hidden state; by providing a hidden state s_k−1 and an action a_k to the model, the search algorithm can transition to a new node s_k = g(s_k−1, a_k).

(2) Actions available. We consider a standard problem formulation where the set of available actions is provided at each time step alongside the observation. During search, however, it could be helpful to specify the available actions at each interior node—which would require knowledge of how the available actions change over time. AlphaZero used the set of legal actions obtained from the simulator to mask the policy network at interior nodes. MuZero does not perform any masking within the search tree, but only masks legal actions at the root of the search tree where the set of available actions is directly observed. The policy network rapidly learns to exclude actions that are unavailable, simply because they are never selected.

(3) Terminal states. AlphaZero stopped the search at tree nodes representing terminal states and used the terminal value provided by the simulator instead of the value produced by the network. MuZero does not give special treatment to terminal states and always uses the value predicted by the network. Inside the tree, the search can proceed past a state that would terminate the simulator. In this case, the network is expected to always predict the same value, which may be achieved by modelling terminal states as absorbing states during training.

In addition, MuZero is designed to operate in the general RL setting: single-agent domains with discounted intermediate rewards of arbitrary magnitude. In contrast, AlphaGo Zero and AlphaZero were designed to operate in two-player games with undiscounted terminal rewards of ±1.

Many other generalizations of MuZero may be possible, for example, to stochastic, continuous, non-stationary or temporally extended environments, or to imperfect information or general sum games. These generalizations are left for future work.

Search

We now describe the search algorithm used by MuZero. Our approach is based on MCTS with upper confidence bounds, an approach to planning that converges asymptotically to the optimal policy in single agent domains and to the minimax value function in zero sum games⁴⁴.

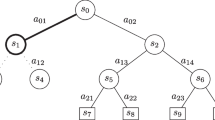
Every node of the search tree is associated with an internal state s. For each action a from s there is an edge (s, a) that stores a set of statistics {N(s, a), P(s, a), Q(s, a), R(s, a), S(s, a)}, respectively representing visit counts N, policy P, mean value Q, reward R and state transition S.

Similar to AlphaZero, the search is divided into three stages, repeated for a number of simulations.

Selection

Each simulation starts from the internal root state s⁰, and finishes when the simulation reaches a leaf node s^l. For each hypothetical time step k = 1 ... l of the simulation, an action a^k is selected according to the stored statistics for internal state s^k−1, by maximizing over a probabilistic upper confidence tree (PUCT) bound^5,45

$$\begin{array}{c}\,{a}^{k}=\arg \,\mathop{max}\limits_{a}\{Q(s,a)\phantom{\frac{\sqrt{{\sum }_{b}N(s,b)}}{1+N(s,a)}}\\ \,+P(s,a)\frac{\sqrt{{\sum }_{b}N(s,b)}}{1+N(s,a)}[{c}_{1}+\,\log \,(\frac{{\sum }_{b}N(s,b)+{c}_{2}+1}{{c}_{2}})]\},\end{array}$$

(2)

where a and b are possible actions. The constants c₁ and c₂ are used to control the influence of the policy P(s, a) relative to the value Q(s, a) as nodes are visited more often. In our experiments, c₁ = 1.25 and c₂ = 19,652.

For k < l, the next state and reward are looked up in the state transition and reward table s^k = S(s^k−1, a^k), r^k = R(s^k−1, a^k).

Expansion

At the final time step l of the simulation, the reward and state are computed by the dynamics function, r^l, s^l = g_θ(s^l−1, a^l), and stored in the corresponding tables, R(s^l−1, a^l) = r^l, S(s^l−1, a^l) = s^l. The policy and value function are computed by the prediction function, p^l, v^l = f_θ (s^l). A new node, corresponding to state s^l is added to the search tree. Each edge (s^l, a) from the newly expanded node is initialized to {N(s^l, a) = 0, Q(s^l, a) = 0, P(s^l, a) = p^l}. Note that the search algorithm makes at most one call to the dynamics function and prediction function respectively per simulation; the computational cost is of the same order as in AlphaZero.

Backup

At the end of the simulation, the statistics along the trajectory are updated. The backup is generalized to the case where the environment can emit intermediate rewards, have a discount γ different from 1 and the value estimates are unbounded. (We note that in board games, the discount is assumed to be 1 and there are no intermediate rewards.) For k = l ... 0, we form an l − k-step estimate of the cumulative discounted reward, bootstrapping from the value function v^l

$${G}^{k}=\mathop{\sum }\limits_{\tau =0}^{l-1-k}{\gamma }^{\tau }{r}_{k+1+\tau }+{\gamma }^{l-k}{v}^{l}.$$

(3)

For k = l ... 1, we update the statistics for each edge (s^k−1, a^k) in the simulation path as follows

$$\begin{array}{c}Q({s}^{k-1},{a}^{k}):=\frac{N({s}^{k-1},{a}^{k})\times Q({s}^{k-1},{a}^{k})+{G}^{k}}{N({s}^{k-1},{a}^{k})+1},\\ N({s}^{k-1},{a}^{k}):=N({s}^{k-1},{a}^{k})+1.\end{array}$$

(4)

In two-player zero sum games, the value functions are assumed to be bounded within the [0, 1] interval. This choice allows us to combine value estimates with probabilities using a variant of the PUCT rule⁴⁵ (equation (2)). However, as in many environments the value is unbounded, it is necessary to adjust the PUCT rule. A simple solution would be to use the maximum score that can be observed in the environment to either rescale the value or set the PUCT constants appropriately⁴⁶. However, both solutions are game specific and require adding prior knowledge to the MuZero algorithm. To avoid this, MuZero computes normalized Q-value estimates $\bar{Q}\in [0,1]$ by using the minimum–maximum values observed in the search tree up to that point. When a node is reached during the selection stage, the algorithm computes the normalized $\bar{Q}$ values of its edges to be used in place of the Q values in the PUCT rule using the equation

$$\bar{Q}({s}^{k-1},{a}^{k})=\frac{Q({s}^{k-1},{a}^{k})-\,\mathop{min}\limits_{s,a\in {\rm{T}}{\rm{r}}{\rm{e}}{\rm{e}}}\,Q(s,a)}{\mathop{max}\limits_{s,a\in {\rm{T}}{\rm{r}}{\rm{e}}{\rm{e}}}\,Q(s,a)-\,\mathop{min}\limits_{s,a\in {\rm{T}}{\rm{r}}{\rm{e}}{\rm{e}}}\,Q(s,a)}.$$

(5)

Hyperparameters

For simplicity we preferentially use the same architectural choices and hyperparameters as in previous work. Specifically, we started with the network architecture and search choices of AlphaZero⁵. For board games, we use the same PUCT constants, Dirichlet exploration noise and the same 800 simulations per search as in AlphaZero.

Owing to the much smaller branching factor and simpler policies in Atari, we used only 50 simulations per search to speed up experiments. As shown in Fig. 3b, the algorithm is not very sensitive to this choice. We also use the same discount (0.997) and value transformation (see ‘Network architecture’) as R2D2¹⁹.

For parameter values not mentioned in the text, please refer to the pseudocode (see ‘Code availability’).

Data generation

To generate training data, the latest checkpoint of the network (updated every 1,000 training steps) is used to play games with MCTS. In the board games Go, chess and shogi, the search is run for 800 simulations per move to pick an action; in Atari, due to the much smaller action space 50 simulations per move are sufficient.

For board games, games are sent to the training job as soon as they finish. Owing to the much larger length of Atari games (up to 30 min or 108,000 frames), intermediate sequences are sent every 200 moves. In board games, the training job keeps an in-memory replay buffer of the most recent one million games received; in Atari, where the visual observations are larger, the most recent 125,000 sequences of length 200 are kept.

During the generation of experience in the board game domains, the same exploration scheme as the one described in AlphaZero⁵ is used. Using a variation of this scheme, in the Atari domain, actions are sampled from the visit count distribution throughout the duration of each game, instead of just the first k moves. Moreover, the visit count distribution is parametrized using a temperature parameter T

$$\pi (a|s)=\frac{N{(s,a)}^{1/T}}{{{\sum }_{b}N(s,b)}^{1/T}}.$$

(6)

T is decayed as a function of the number of training steps of the network. Specifically, for the first 500,000 training steps a temperature of 1.0 is used, for the next 250,000 steps a temperature of 0.5 and for the remaining 250,000 a temperature of 0.25. This ensures that the action selection becomes greedier as training progresses.

Observation and action encoding

Representation function

The history over board states used as input to the representation function for Go, chess and shogi is represented similarly to AlphaZero⁵. In Go and shogi, we encode the last eight board states as in AlphaZero; in chess, we increased the history to the last 100 board states to allow correct prediction of draws.

For Atari, the input of the representation function includes the last 32 RGB frames at resolution 96 × 96 along with the last 32 actions that led to each of those frames. We encode the historical actions because unlike board games, an action in Atari does not necessarily have a visible effect on the observation. RGB frames are encoded as one plane per colour, rescaled to the range [0, 1], for red, green and blue, respectively. We perform no other normalization, whitening or other preprocessing of the RGB input. Historical actions are encoded as simple bias planes, scaled as a/18 (there are 18 total actions in Atari).

Dynamics function

The input to the dynamics function is the hidden state produced by the representation function or previous application of the dynamics function, concatenated with a representation of the action for the transition. Actions are encoded spatially in planes of the same resolution as the hidden state. In Atari, this resolution is 6 × 6 (see description of downsampling in ‘Network architecture’), in board games, this is the same as the board size (19 × 19 for Go, 8 × 8 for chess, 9 × 9 for shogi).

In Go, a normal action (playing a stone on the board) is encoded as an all-zero plane, with a single one in the position of the played stone. A pass is encoded as an all-zero plane.

In chess, eight planes are used to encode the action. The first one-hot plane encodes which position the piece was moved from. The next two planes encode which position the piece was moved to: a one-hot plane to encode the target position, if on the board, and a second binary plane to indicate whether the target was valid (on the board) or not. This is necessary because for simplicity, our policy action space enumerates a superset of all possible actions, not all of which are legal, and we use the same action space for policy prediction and to encode the dynamics function input. The remaining five binary planes are used to indicate the type of promotion, if any (queen, knight, bishop, rook, none).

The encoding for shogi is similar, with a total of 11 planes. We use the first eight planes to indicate where the piece moved from—either a board position (first one-hot plane) or the drop of one of the seven types of prisoner (remaining seven binary planes). The next two planes are used to encode the target as in chess. The remaining binary plane indicates whether the move was a promotion or not.

In Atari, an action is encoded as a one-hot vector that is tiled appropriately into planes.

Network architecture

The prediction function p^k, v^k = f_θ(s^k) uses the same architecture as AlphaZero: one or two convolutional layers that preserve the resolution but reduce the number of planes, followed by a fully connected layer to the size of the output.

For value and reward prediction in Atari, we follow ref. ⁴⁷ in scaling targets using an invertible transform $h(x)={\rm{sign}}(x)(\sqrt{|x|+1}-1)+\varepsilon x$, where ε = 0.001 in all our experiments. We then apply a transformation ϕ to the scalar reward and value targets to obtain equivalent categorical representations. We use a discrete support set of size 601 with one support for every integer between −300 and 300. Under this transformation, each scalar is represented as the linear combination of its two adjacent supports, such that the original value can be recovered by x = x_low × p_low + x_high × p_high. As an example, a target of 3.7 would be represented as a weight of 0.3 on the support for 3 and a weight of 0.7 on the support for 4. The value and reward outputs of the network are also modelled using a softmax output of size 601. During inference, the actual value and rewards are obtained by first computing their expected value under their respective softmax distribution and subsequently by inverting the scaling transformation. Scaling and transformation of the value and reward happens transparently on the network side and is not visible to the rest of the algorithm.

Both the representation and dynamics function use the same architecture as AlphaZero, but with 16 instead of 20 residual blocks³⁵. We use 3 × 3 kernels and 256 hidden planes for each convolution.

For Atari, where observations have large spatial resolution, the representation function starts with a sequence of convolutions with stride 2 to reduce the spatial resolution. Specifically, starting with an input observation of resolution 96 × 96 and 128 planes (32 history frames of 3 colour channels each, concatenated with the corresponding 32 actions broadcast to planes), we downsample as follows: 1 convolution with stride 2 and 128 output planes, output resolution 48 × 48; 2 residual blocks with 128 planes; 1 convolution with stride 2 and 256 output planes, output resolution 24 × 24; 3 residual blocks with 256 planes; average pooling with stride 2, output resolution 12 × 12; 3 residual blocks with 256 planes; average pooling with stride 2, output resolution 6 × 6. The kernel size is 3 × 3 for all operations.

For the dynamics function (which always operates at the downsampled resolution of 6 × 6), the action is first encoded as an image, then stacked with the hidden state of the previous step along the plane dimension.

Training

During training, the MuZero network is unrolled for K hypothetical steps and aligned to sequences sampled from the trajectories generated by the MCTS actors. Sequences are selected by sampling a state from any game in the replay buffer, then unrolling for K steps from that state. In Atari, samples are drawn according to prioritized replay⁴⁸, with priority $P(i)=\frac{{p}_{i}^{\alpha }}{{\sum }_{k}{p}_{k}^{\alpha }}$, where p_i = |ν_i − z_i|, ν is the search value and z the observed n-step return. To correct for sampling bias introduced by the prioritized sampling, we scale the loss using the importance sampling ratio ${w}_{i}={\left(\frac{1}{N},\times ,\frac{1}{P(i)}\right)}^{\beta }$. In all our experiments, we set α = β = 1. For board games, states are sampled uniformly.

Each observation o_t along the sequence also has a corresponding search policy π_t, search value function ν_t and environment reward u_t. At each unrolled step k, the network has a loss to the policy, value and reward target for that step, summed to produce the total loss for the MuZero network (see equation (1)). Note that, in board games without intermediate rewards, we omit the reward prediction loss. For board games, we bootstrap directly to the end of the game, equivalent to predicting the final outcome; for Atari we bootstrap for n = 10 steps into the future.

To maintain roughly similar magnitude of gradient across different unroll steps, we scale the gradient in two separate locations. (1) We scale the loss of each head by 1/K, where K is the number of unroll steps. This ensures that the total gradient has similar magnitude irrespective of how many steps we unroll for. (2) We also scale the gradient at the start of the dynamics function by 1/2. This ensures that the total gradient applied to the dynamics function stays constant.

In the experiments reported in this paper, we always unroll for K = 5 steps. For a detailed illustration, see Fig. 1.

To improve the learning process and bound the activations, we also scale the hidden state to the same range as the action input ([0,1]): ${s}_{{\rm{scaled}}}=\frac{s-\,\min (s)}{\max (s)-\,\min (s)}$.

All experiments were run using third-generation Google Cloud tensor processing units (TPUs)⁴⁹. For each board game, we used 16 TPUs for training and 1,000 TPUs for self-play. For each game in Atari, in the 20 billion frame setting we used 8 TPUs for training and 32 TPUs for self-play. In the smaller 200 million frame setting, we used only four TPUs for training and two TPUs for self-play, equivalent to two weeks of training on 1 GPU. The much smaller proportion of TPUs used for acting in Atari is due to the smaller number of simulations per move (50 instead of 800) and the smaller size of the dynamics function compared with the representation function.

Note that the network is trained separately for each environment (that is, one model for each different Atari game or board game). However, in principle, the same model could be shared between different environments during training, or could be tested in new environments (that is, zero-shot generalization); this approach is left to future work.

MuZero Reanalyze

To improve the sample efficiency of MuZero, we introduced a second variant of the algorithm, MuZero Reanalyze. MuZero Reanalyze revisits its past time steps and re-executes its search using the latest model parameters, potentially resulting in a better-quality policy than the original search. This fresh policy is used as the policy target for 80% of updates during MuZero training. Furthermore, a target network³⁹ $\,\cdot ,{v}^{-}={f}_{{\theta }^{-}}({s}^{0})$, based on recent parameters θ⁻, is used to provide a fresher, stable n-step bootstrapped target for the value function, ${z}_{t}={u}_{t+1}+\gamma {u}_{t+2}+\ldots +{\gamma }^{n-1}{u}_{t+n}+{\gamma }^{n}{v}_{t+n}^{-}\,$. In addition, several other hyperparameters were adjusted— primarily to increase sample reuse and avoid overfitting of the value function. Specifically, 2.0 samples were drawn per state, instead of 0.1; the value target was weighted down to 0.25 compared with weights of 1.0 for policy and reward targets; and the n-step return was reduced to n = 5 steps instead of n = 10 steps.

Evaluation

We evaluated the relative strength of MuZero (Fig. 2) in board games by measuring the Elo rating of each player. We estimate the probability that player a will defeat player b by a logistic function $p(a\,{\rm{d}}{\rm{e}}{\rm{f}}{\rm{e}}{\rm{a}}{\rm{t}}{\rm{s}}\,b)={(1+{10}^{{c}_{{\rm{e}}{\rm{l}}{\rm{o}}}[e(b)-e(a)]})}^{-1}$, and estimate the ratings e(⋅) by Bayesian logistic regression, computed by the BayesElo program⁵⁰ using the standard constant c_elo = 1/400.

Elo ratings were computed from the results of an 800-simulations-per-move tournament between iterations of MuZero during training, and also a baseline player: either Stockfish, Elmo or AlphaZero, respectively. Baseline players used an equivalent search time of 100 ms per move. The Elo rating of the baseline players was anchored to publicly available values⁵.

In Atari, we computed mean reward over 1,000 episodes per game, limited to the standard 30 min or 108,000 frames per episode⁵¹, using 50 simulations per move unless indicated otherwise. To mitigate the effects of the deterministic nature of the Atari simulator, we employed two different evaluation strategies: 30 noop random starts and human starts. For the former, at the beginning of each episode, a random number of between 0 and 30 noop actions are applied to the simulator before handing control to the agent. For the latter, start positions are sampled from human expert play to initialize the Atari simulator before handing the control to the agent⁵¹.