Universal prethermal dynamics of Bose gases quenched to unitarity

Abstract

Understanding strongly correlated phases of matter, such as the quark–gluon plasma and neutron stars, and in particular the dynamics of such systems, for example, following a Hamiltonian quench (a sudden change in some Hamiltonian parameter, such as the strength of interparticle interactions) is a fundamental challenge in modern physics. Ultracold atomic gases are excellent quantum simulators for these problems, owing to their tunable interparticle interactions and experimentally resolvable intrinsic timescales. In particular, they provide access to the unitary regime, in which the interactions are as strong as allowed by quantum mechanics. This regime has been extensively studied in Fermi gases^1,2. The less-explored unitary Bose gases^{3,4,5,6,7,8,9,10,11} offer possibilities¹² such as universal physics controlled solely by the gas density^13,14 and new forms of superfluidity^15,16,17. Here, through momentum- and time-resolved studies, we explore degenerate and thermal homogeneous Bose gases quenched to unitarity. In degenerate samples, we observe universal post-quench dynamics in agreement with the emergence of a prethermal state^{18,19,20,21,22,23,24} with a universal non-zero condensed fraction^22,24. In thermal gases, the dynamic and thermodynamic properties generally depend on the gas density and the temperature, but we find that they can still be expressed in terms of universal dimensionless functions. Surprisingly, we find that the total quench-induced correlation energy is independent of the gas temperature. These measurements provide quantitative benchmarks and challenges for the theory of unitary Bose gases.

Main

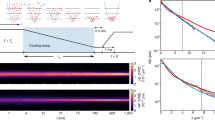
In ultracold atomic gases, two-body contact interactions are characterized by the s-wave scattering length a, and the unitary regime is realized in the limit a → ∞, with a tuned using magnetic Feshbach resonances²⁵. In Bose gases, tuning a to infinity also enhances three-body recombination, which leads to particle loss and heating, making unitary Bose gases inherently dynamic, non-equilibrium systems. Experimentally, these systems are studied by rapidly quenching a to infinity (Fig. 1a), which initiates the non-equilibrium dynamics. If starting with a Bose–Einstein condensate (BEC) in the k ≈ 0 momentum state, after the quench the momentum distribution broadens (the kinetic energy increases) owing to lossless correlation dynamics and to recombination heating (Fig. 1b). The interplay between these two processes raises many questions, such as whether the gas attains a strongly correlated quasi-equilibrium steady state before degeneracy is lost.

Fig. 1: Dynamics of a degenerate Bose gas quenched to unitarity.

a, Quench protocol. The red circles depict atoms, and their sizes the interaction strength, which is limited at unitarity by the interparticle spacing; a is the s-wave scattering length and t_hold is the hold time at unitarity. b, Momentum distribution n_k(k) for different t_hold values; the initial gas density is n = 5.1 μm⁻³, corresponding to a Fermi momentum of k_n = 6.7 μm⁻¹ and a Fermi time of t_n = 27 μs. c, Populations of individual k states show rapid initial growth, saturation at (quasi-)steady-state values of ${\bar{n}}_{k}(k)$ (dashed lines) and long-time heating. The error bars reflect 1 s.e.m. (not visible when smaller than the symbol size). The solid lines are sigmoid fits used to extract the initial-growth half-way times τ(k).

The timescales of the different processes are set by the natural length scales of the system. Within the universality hypothesis¹⁴, in a homogeneous degenerate unitary gas the only relevant length scale is the interparticle spacing n^−1/3, where n is the particle density, which (in analogy with Fermi gases) sets the Fermi momentum ħk_n = ħ(6π²n)^1/3, energy ${E}_{n}={\hbar }^{2}{k}_{n}^{2}{\rm{/}}(2m)$ and time t_n = ħ/E_n, where m is the particle mass and ħ is the reduced Planck constant. Additional, potentially relevant length scales are the sizes of the Efimov trimer states that exist as a result of resonant two-body interactions^{17,26,27,28,29,30,31}. Three-body correlations⁸ and Efimov trimers⁹ have been observed experimentally, but all degenerate-gas dynamics have been consistent with t_n being the only characteristic timescale^6,9,10. This universality has so far made it impossible to disentangle the lossless from the recombination-induced dynamics. Experimental evidence has suggested that the lossless processes are faster, sufficiently so that the gas attains a degenerate steady state^6,10; however, almost nothing could be established about the nature of this state. Here we isolate the effects of the lossless post-quench dynamics through momentum- and time-resolved studies of degenerate and thermal Bose gases.

We prepare a homogeneous ³⁹K Bose gas in an optical-box trap¹⁰ with a volume of around 3 × 10⁴ μm³ and use a Feshbach resonance centred at⁸ 402.70(3) G. Initially, we prepare either a quasi-pure BEC or a thermal gas. In both cases, we start with a weakly interacting system, with na³ < 10⁻⁴, then quench the gas to unitarity (within 2 μs) and let it evolve for a time t_hold; in our box trap, t_n is a global variable and after the quench all parts of the system evolve in the same way. After the time t_hold, we quench the gas back to low a, release it from the trap and measure its momentum distribution n_k(k); we normalize n_k so that

$$\int 4{\rm{\pi }}{k}^{2}{n}_{k}{\rm{d}}k=1$$

See Methods for further experimental details.

We first present our study of degenerate gases. In Fig. 1b we show n_k(k) for an initial BEC density of n = 5.1 μm⁻³ and various t_hold. In Fig. 1c we illustrate our key experimental observation. By looking at n_k values for individual k states, we discern separate stages in the evolution of n_k: after a rapid initial growth, n_k reaches a (quasi-)steady-state plateau, before the long-time heating takes over. All timescales are of order t_n, but distinguishable. We discern such time separation for k/k_n ≳ 0.8. For each k in this range, we identify the plateau occupation ${\bar{n}}_{k}$ (dashed lines in Fig. 1c) and use sigmoid fits (solid lines) to extract the characteristic time τ(k) for the initial rapid growth of n_k, defined such that ${n}_{k}(k,\tau (k))={\bar{n}}_{k}(k)/2$ . We note that t_n and k_n correspond to the initial n; for our longest τ we observe particle loss of approximately 20%.

In Fig. 1c we also see that the curves for different k values are not aligned in time; n_k(2k_n) shows signs of heating before n_k(k_n) reaches its steady-state value. This finding illustrates why lossless and recombination dynamics could not be separated quantitatively by considering all k at the same evolution time^6,10, such as by looking at the kinetic energy per particle E(t_hold)¹⁰. Instead, we separately obtain ${\bar{n}}_{k}$ for different k values and piece together the function ${\bar{n}}_{k}(k)$. Doing so does not give the momentum distribution at any specific time, but allows us to infer what the steady-state n_k(k) would be if the gas did not suffer from losses and heating. We assume that at early times $\left({t}_{{\rm{hold}}}={\mathscr{O}}({t}_{n})\right)$, all non-zero-k states are primarily fed from the macroscopically occupied BEC (Fig. 1b).

In Fig. 2 we plot the dimensionless τ/t_n and ${\bar{n}}_{k}{k}_{n}^{3}$ versus the dimensionless k/k_n, for three BEC densities. By expressing all quantities in dimensionless form, all of our data fall onto universal curves (within experimental errors).

Fig. 2: Universal post-quench dynamics and the steady-state momentum distribution in the degenerate Bose gas.

a, b, The momentum-dependent half-way time τ(k) for reaching the steady state (a) and the steady-state momentum distribution ${\bar{n}}_{k}(k)$ (b), for three different BEC densities n. Expressing all quantities in dimensionless form, using the Fermi time t_n and momentum k_n as the natural scales, collapses all of our data onto universal curves. The error bars show fitting errors (not visible when smaller than the symbol size). The solid line in b is an exponential fit, ${\bar{n}}_{k}{k}_{n}^{3}=1.53{\rm{e}}{\rm{x}}{\rm{p}}(-3.62k/{k}_{n})$.

In the experimentally accessible range of momenta, our data are consistent with the scaling τ/t_n ∝ k_n/k at low k and τ/t_n ∝ (k_n/k)² at high k. These scalings were predicted for the emergence of a prethermal steady state^{20,21,22,23,24}. According to this prediction, at short times after the quench, the excitations are similar to the Bogoliubov modes in a weakly interacting BEC—which are phonons at low k and particles at high k—but with the usual mean-field energy replaced by an energy of order E_n. The speed of sound is then of order ħk_n/m and the crossover between the two regimes is at $k={\mathscr{O}}({k}_{n})$. Finally, τ(k) is set by the dephasing time, which is given approximately by the inverse of the excitation energy.

The form of the universal ${\bar{n}}_{k}{k}_{n}^{3}$ curve was not anticipated and poses a new theoretical challenge. Empirically, over three orders of magnitude of ${\bar{n}}_{k}{k}_{n}^{3}$, our data are well captured by a simple exponential, Aexp(−Bk/k_n), with A = 1.53(5) and B = 3.62(2) (where the errors are 1σ fitting errors). This function implies a condensed fraction of

$$\eta =1-\int 4\pi {k}^{2}{\bar{n}}_{k}{\rm{d}}k=19(4){\rm{ \% }}$$

Up to k ≈ 3k_n we do not observe the asymptotic form n_k ~ 1/k⁴ that is expected³² at very high k; however, even if n_k changed to this more slowly decaying form immediately outside of our experimental range, η would change by less than 3%. Previous theoretical work^22,24 has predicted values of η in the prethermal state that are close to our estimate, but the exponential form of ${\bar{n}}_{k}{k}_{n}^{3}$ has not previously been predicted. Explaining this experimental observation may require explicit consideration of the quench back to low a.

We now turn to thermal gases, which reveal some simplifications, but also more surprises. A simplification is that, while in a thermal gas the three-body recombination and the lossless dynamics are both slowed down compared to the degenerate-gas case, the three-body recombination is slowed down more^4,5,33. As shown in Fig. 3a, now E(t_hold) exhibits two separate stages in the post-quench dynamics: a rapid initial growth (here for t_hold ≲ 100 μs) and long-time heating (for t_hold ≫ 100 μs). The shape of the curve is similar to those for individual k states in Fig. 1c and the long-time energy growth matches the theory of recombination heating^4,10. These results reinforce our interpretation of the two-step dynamics, both for degenerate and for thermal gases. We now focus on the early-time dynamics. As we show in Fig. 3b, n_k(k) is essentially identical at 60 μs and 126 μs, meaning that on this timescale a steady state is established for all k.

Fig. 3: Thermal Bose gas quenched to unitarity.

a, The kinetic energy per particle E shows rapid growth for t_hold ≲ 100 μs and substantial heating only for t_hold ≫ 100 μs; the black line is the prediction for recombination heating. Here, and in b–d, the initial gas density and temperature are n = 5.6 μm⁻³ and T = 150 nK, respectively. b, Momentum distribution n_k(k) for different hold times at unitarity. The initial redistribution of particles from low k to high k (indicated by the dotted arrow) is essentially complete within 60 μs, and n_k is almost identical at 126 μs and 60 μs. c, Population changes in different k-space shells, 4πk²δn_k(k); the population in k₀ = 6.0 μm⁻¹ (dotted line) remains essentially unchanged. d, Vertical cuts through the plot in c. Solid lines are sigmoid fits used to extract the half-way time τ(k). e, f, τ(k) and the change in the spectral energy density (between the initial, pre-quench state and the post-quench steady state), $\bar{{\rm{\delta }}\varepsilon }(k)\propto {k}^{4}\bar{{\rm{\delta }}{n}_{k}}(k)$. Here we show data for n = 5.6 μm⁻³ and T = 150 nK (blue) and for n = 1.3 μm⁻³ and T = 70 nK (red). For the data in a and d, 1 s.e.m. error bars are smaller than the symbol size. In e and f, the error bars (in most cases smaller than the symbol size) show fitting errors.

In a thermal gas, even before the quench to unitarity, n_k is substantial for all k ≲ 1/λ, where $\lambda =h/\sqrt{2{\rm{\pi }}m{k}_{{\rm{B}}}T}$ is the thermal wavelength, T is the initial temperature (before the quench to unitarity), k_B is the Boltzmann constant and h = 2πħ. We therefore look at the redistribution of particles in k space, in particular, the change δn_k(k) with respect to t_hold = 0 and the corresponding change δε in the spectral energy density ε = ħ²/(2m) × 4πk⁴n_k. An additional challenge in understanding the thermal-gas case is that we have two relevant length scales, n^−1/3 and λ, and it is not a priori clear whether the dynamic and thermodynamic properties can be expressed in terms of dimensionless universal functions.

In Fig. 3c we show time-resolved population changes in different spherical shells in k space, 4πk²δn_k. For some special k₀ (dotted line), the population remains essentially constant. In Fig. 3d we show vertical cuts through Fig. 3c for k < k₀, k = k₀ and k > k₀. Away from k₀, we use sigmoid fits (solid lines) to extract τ(k), both for diminishing and for growing populations. Near k₀ we see only a small wiggle in δn_k, to which we cannot assign a single timescale.

In Fig. 3e, f we show τ(k) and the steady state $\bar{{\rm{\delta }}\varepsilon }(k)$ for two different combinations of n and T. The $\bar{{\rm{\delta }}\varepsilon }(k)$ curve conveys the redistribution of particles from k < k₀ to k > k₀ and the resulting energy growth

$$\bar{{\rm{\Delta }}E}=\int \bar{{\rm{\delta }}\varepsilon }{\rm{d}}k$$

The dispersive shape of τ(k) was not anticipated and invites further theoretical work. Here, we empirically investigate whether these curves can be scaled into universal dimensionless functions.

For the horizontal scaling we find that the natural scale for k is 1/λ, independent of n. In Fig. 4a we plot τ(k) versus kλ, for 15 combinations of n and T (corresponding to phase-space densities nλ³ between 0.2 and 2). Similarly, in Fig. 4d we plot $\overline{{\rm{\delta }}\varepsilon }(k){\rm{/}}\lambda$ versus kλ, so that the area under each curve is still $\overline{{\rm{\Delta }}E}(n,T)$. In both cases, we see horizontal alignment of all of the curves, with k₀ = 4.4/λ.

Fig. 4: Universal dynamic and thermodynamic functions for the thermal Bose gas quenched to unitarity.

a, d, Plotting the half-way time τ for reaching the post-quench steady state (a) and the change in the spectral energy density $\overline{{\rm{\delta }}\varepsilon }\,{\rm{/}}\,\lambda$ (where λ is the thermal wavelength; d) versus kλ horizontally aligns all of our curves for 15 different combinations of the initial gas density n and temperature T (see key). The vertical grey line corresponds to k₀. b, Supposing that the characteristic timescale for the dynamics is ${t}_{{\rm{s}}}\propto {t}_{n}^{{\alpha }_{t}}{t}_{\lambda }^{{\beta }_{t}}$, where t_λ = ħ/(k_BT), we obtain the best data collapse, corresponding to the minimum of σ/σ₀ (see text for details), for α_t ≈ β_t ≈ 1/2 (dashed cross indicates α_t = β_t = 1/2). This suggests that ${t}_{{\rm{s}}}=\sqrt{{t}_{n}{t}_{\lambda }}$. e, Similarly, for the energy scale ${E}_{{\rm{s}}}\propto {E}_{n}^{{\alpha }_{E}}{({k}_{{\rm{B}}}T)}^{{\beta }_{E}}$, we find α_E ≈ 1 and β_E ≈ 0, which suggests that E_s = E_n. c, f, The dimensionless $\tau \,{\rm{/}}\,\sqrt{{t}_{n}{t}_{\lambda }}$ (c) and $\overline{{\rm{\delta }}\varepsilon }/(\lambda {E}_{n})$ (f) are, to within experimental errors, universal functions of the dimensionless kλ. All error bars (not visible when smaller than the symbol size) show fitting errors.

A more challenging question is whether these n- and T-dependent curves may be collapsed vertically, by scaling them by some time t_s(n, T) and energy E_s(n, T). We conjecture that ${t}_{{\rm{s}}}\propto {t}_{n}^{{\alpha }_{t}}{t}_{\lambda }^{{\beta }_{t}}$, where t_λ = ħ/(k_BT), and similarly ${E}_{{\rm{s}}}\propto {E}_{n}^{{\alpha }_{E}}{({k}_{{\rm{B}}}T)}^{{\beta }_{E}}$, and determine for which α_t,E and β_t,E we get the best collapse. We treat α_t,E and β_t,E as independent, but physically (if there are no other relevant scales) we expect α_t + β_t = α_E + β_E = 1.

We quantify the degree of the data collapse by a single number σ, which is obtained by calculating the standard deviation of the data for all n and T at a fixed kλ and then summing over kλ. In Fig. 4b, e, we show plots of σ/σ₀ for τ and $\overline{{\rm{\delta }}\varepsilon }\,{\rm{/}}\,\lambda$; here, σ₀ corresponds to no scaling.

For the temporal scaling, in Fig. 4b we find the lowest σ near α_t = β_t = 1/2, which suggests that ${t}_{{\rm{s}}}=\sqrt{{t}_{n}{t}_{\lambda }}$. In Fig. 4c we plot $\tau \,{\rm{/}}\,\sqrt{{t}_{n}{t}_{\lambda }}$ and see that all of our data collapse onto a universal curve (within experimental scatter). For this scaling we have an intuitive interpretation. In a thermal gas, particles do not overlap, so to feel the unitary interactions after the quench they must first meet. The t_s that we find, $\sqrt{{t}_{n}{t}_{\lambda }}\propto {n}^{-1/3}\lambda m/\hbar$, matches the expected scaling for the characteristic time until meeting, which is given by the ratio of the interparticle spacing n^−1/3 and the characteristic thermal velocity ħ/(mλ).

In Fig. 4e we find that the optimal values of α_E and β_E are α_E ≈ 1 and β_E ≈ 0, suggesting that E_s = E_n. This scaling implies that, surprisingly, whereas $\overline{{\rm{\delta }}\varepsilon }(k)$ naturally depends on n and T, its integral $\overline{{\rm{\Delta }}E}$ is independent of T; in Fig. 4f we see that this scaling collapses all of our data onto a universal curve.

This lack of T dependence suggests that $\overline{{\rm{\Delta }}E}\,{\rm{/}}\,{E}_{n}$ in a thermal gas should also be equal to $\bar{E}\,{\rm{/}}\,{E}_{n}$ in a degenerate gas (where $\overline{{\rm{\Delta }}E}=\bar{E}$). Bearing in mind the caveat that we do not observe very high-k tails experimentally, from the data in Fig. 4f we estimate that $\overline{{\rm{\Delta }}E}\,{\rm{/}}\,{E}_{n}=0.7(1)$ for a thermal gas; from the exponential ${\bar{n}}_{k}{k}_{n}^{3}$ in Fig. 2b, we obtain a consistent value of $\bar{E}\,{\rm{/}}\,{E}_{n}=0.74(4)$ for a degenerate gas.

Our experiments establish a comprehensive view of the prethermal dynamics and thermodynamics of homogeneous Bose gases quenched to unitarity, at low and high temperatures. They provide quantitative benchmarks and new questions for the theory of unitary Bose gases. Open problems include explaining the forms of our experimentally observed universal dynamic and thermodynamic functions, and elucidating the connections between these universal features and previously observed signatures^8,9 of non-universal Efimov physics. Experimentally, an important future challenge is to probe the coherence and the potential superfluid properties of the prethermal state of a degenerate unitary Bose gas.

While this paper was under review, we learned of two other experiments that observe universality in the many-body dynamics of out-of-equilibrium quantum systems^34,35.

Methods

Optical-box trap and sample preparation

As described previously^36,37, our box trap is formed by blue-detuned, 532-nm laser beams. It is cylindrical in shape, with a diameter of about 30 μm and a length of about 45 μm. We deduce n from the measured atom number, and take into account the fact that the trap walls are not infinitely steep³⁶, owing to the diffraction limit on the sharpness of the laser beams, so the effective trap volume depends slightly on the energy per particle in the initially prepared sample.

Our clouds are in the lowest hyperfine ground state and we initially prepare them at a field of approximately 399.1 G. At this field, the scattering length is a_i ≈ 400a₀, where a₀ is the Bohr radius.

Quench protocol and measurement details

At the end of t_hold we quench a back to a_i using an exponential field ramp with a time constant of 1 μs. We use the fastest ramp that is technically possible to minimize the conversion of atoms into molecules^9,10. We then release the gas from the trap and simultaneously (within about 3 ms) completely turn off interactions (a → 0). After letting the cloud expand for 6–12 ms of time of fight, we take an absorption image of it. We typically repeat each measurement about 20 times. To reconstruct n_k(k) from the two-dimensional absorption images, which give the momentum distribution integrated along the line of sight, we average each image azimuthally, then average over the experimental repetitions, and finally perform the inverse Abel transform. Owing to the initial cloud size and non-infinite time of flight, our measurements of n_k(k) are not quantitatively reliable for k < 2 μm⁻¹.

Extrapolation of ${\bar{{\boldsymbol{n}}}}_{{\boldsymbol{k}}}{{\boldsymbol{k}}}_{{\boldsymbol{n}}}^{{\bf{3}}}$ in a degenerate gas

We also use our experimental data to estimate how the function ${\bar{n}}_{k}{k}_{n}^{3}$ extrapolates to lower k/k_n, without presuming its functional form. For k/k_n < 0.8, we do not see clear steady-state plateaux in n_k(t_hold), such as indicated by the dashed lines in Fig. 1c. However, we can extrapolate τ ∝ t_nk_n/k according to the dashed line in Fig. 2a; then, assuming that heating effects are not yet substantial at t_hold = τ(k) and following our definition of τ, we estimate ${\bar{n}}_{k}=2{n}_{k}(\tau )$, where n_k(τ) is the n_k measured at the extrapolated τ. These extrapolated values of ${\bar{n}}_{k}{k}_{n}^{3}$ are shown by open symbols in Extended Data Fig. 1. They fall on the same exponential curve that fits our directly measured values of ${\bar{n}}_{k}{k}_{n}^{3}$ (solid symbols), lending further support for this unexpected functional form.

Extended data figures and tables

Extended Data Fig. 1 Extrapolation of ${\bar{{\boldsymbol{n}}}}_{{\boldsymbol{k}}}{{\boldsymbol{k}}}_{{\boldsymbol{n}}}^{{\bf{3}}}$ in a degenerate gas to lower k/k_n.

Solid symbols show directly measured values (also shown in Fig. 2b), here combining the data for all three BEC densities. Open symbols show experimentally extrapolated values, for all three densities, as described in Methods. The solid line is the same as in Fig. 2b.