Main

Isolated quantum many-body systems offer particularly clean settings for studying fundamental properties of the underlying unitary time evolution19. For systems initialized far from equilibrium, different scenarios have been identified, including the occurrence of many-body oscillations20 and revivals21, the manifestation of many-body localization22, and quasi-stationary behaviour in a prethermalized stage of the evolution23.

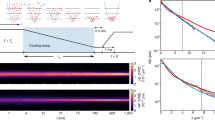
Here we observe a new scenario associated with the notion of non-thermal fixed points. This is illustrated schematically in Fig. 1a: starting from a class of far-from-equilibrium initial conditions, the system develops a universal scaling behaviour in time and space. This is a consequence of the effective loss of details about initial conditions and system parameters long before a quasi-stationary or equilibrium situation may be reached. The transient scaling behaviour is found to be governed by the transport of an emergent collective conserved quantity towards low momentum scales.

Fig. 1: Universal dynamics and experimental procedure.
figure 1

a, Starting from a class of far-from-equilibrium initial conditions, universal dynamical evolution indicates the emergence of a non-thermal fixed point. Experimentally, we probe the system at different evolution times during the stages indicated by numbers 1 to 4. b, A condensate is prepared in the mF = 0 state of the F = 1 hyperfine manifold, that is, with a vanishing mean spin length (left spin sphere). With microwave dressing (see Methods) we initiate spin-exchange dynamics, which leads to a growth of spin orthogonal to the magnetic field B in the Fx–Fy plane (right spin sphere). Subsequently, spatial structures of the spin orientation θ are found along the cloud. c, Exemplary absorption images of the three hyperfine levels taken after a π/2 spin rotation and Stern–Gerlach separation together with the inferred local spin Fx(y) (green lines). Furthermore, histograms for around 160 experimental realizations are shown. In the universal regime (see step 3 in panel a) we extract the spin length and its fluctuation by a fit to the double-peaked structure of the histogram, as indicated in the corresponding plot (see Methods).

Full size image

For our experimental study we employ an elongated Bose–Einstein condensate of about 70,000 87Rb atoms. We use the F = 1 hyperfine manifold with its three magnetic sublevels mF = 0, ±1 as a spin-1 system with ferromagnetic interactions24. Initially, all atoms are prepared in the mF = 0 sublevel, forming a spinor condensate with zero spin length. The dynamics is initiated by instantaneously changing the energy splitting of the F = 1 magnetic sublevels by means of microwave dressing (see Methods). Consequently, spin excitations develop in the Fx–Fy plane12 as sketched in Fig. 1b. Our experimental setup allows the extraction of the spin distribution in terms of the spin component \({\hat{F}}_{x}\left(y\right)=\left[{\hat{\psi }}_{0}^{\dagger }\left(y\right)\left({\hat{\psi }}_{+1}^{}\left(y\right)+{\hat{\psi }}_{-1}^{}\left(y\right)\right){\rm{+h}}{\rm{.c}}{\rm{.}}\right]/\sqrt{2}\)  where \({\hat{\psi }}_{m}^{\dagger }\left(y\right)\) is the creation operator of an atom in the magnetic sublevel m at position y and h.c. denotes the Hermitian conjugate. At a given time t this is achieved by a spin rotation from the Fx–Fy plane to the Fz-direction and subsequently detecting the atomic density difference Fz(y) = n+1(y)− n−1(y) (see Methods for details). Representative absorption images are shown in Fig. 1c together with the extracted spin profiles (green lines). The histograms in Fig. 1c show the probability distribution of Fx for all positions y and experimental realizations for the corresponding evolution time (see Extended Data Fig. 1 for all evolution times). Results are presented for characteristic stages associated with the initial condition (1), the nonequilibrium instability regime (2), the universal scaling regime (3) and the departure from the non-thermal fixed point (4), as also indicated in Fig. 1a.

We find that during the time evolution the angular orientation θ of the transverse spin (see Fig. 1b) becomes the relevant dynamical degree of freedom. For short evolution times unstable longitudinal spin modes grow exponentially25, well described by Bogoliubov theory, but nonlinear evolution quickly takes over (after about 100 ms). This leads to a double-peaked structure of the histograms (see Fig. 1c) indicating that the spin has a mean length and a random orientation in the Fx–Fy plane. On the basis of this observation we extract the mean spin length \(\langle |{F}_{\perp }(t)|\rangle \), where F⊥ = Fx + iFy, and its fluctuations using a fit. Building on that knowledge, we extract the local angle from the profiles as \(\theta (y,t)={\rm{a}}{\rm{r}}{\rm{c}}{\rm{s}}{\rm{i}}{\rm{n}}({F}_{x}(y,t)/\langle |{F}_{\perp }(t)|\rangle )\) (see Methods for details).

The time evolution of the fluctuations of the spin orientation is described in terms of correlation functions of the scalar field θ(y,t). The fluctuations are analysed by evaluating the two-point correlation function C(y,y ′;t) = 〈θ(y,t)θ(y ′,t)〉. To distinguish the role of different length scales we consider a momentum-resolved picture of the dynamics. Hence we evaluate the structure factor, which is the Fourier transform of C(y,y ′;t) with respect to the relative coordinate \(\bar{y}={y}^{^{\prime} }-y\), averaged over y:

$${f}_{\theta }(k,t)=\int \int {\rm{d}}y{\rm{d}}\bar{y}C(y+\bar{y},y;t){\rm{e}}{\rm{x}}{\rm{p}}(-i2{\rm{\pi }}k\bar{y})$$
(1)

In general, the structure factor fθ is a function of momentum k which evolves in time t in a way determined by the system parameters and initial conditions. In Fig. 2a, we plot fθ(k,t) as a function of k on a double-logarithmic scale for times between 4 s and 9 s. A characteristic shift of the structure factor towards smaller momenta as well as an increase of the low-momentum amplitude with time is observed.

Fig. 2: Scaling in space and time at a non-thermal fixed point.
figure 2

a, Structure factor fθ(k,t) as a function of the spatial momentum k = 1/λ in the scaling regime between 4 s and 9 s. The colour indicates the evolution time t. The statistical error is of the order of the size of the plot markers. In the infrared the structure factor shifts in time to smaller k (bigger wavelengths), which is connected to transport of excitations towards lower momenta. Characteristic for the non-thermal fixed point dynamics is the rescaling of the amplitude with universal exponent α and rescaling of the length scale with β (see inset). b, By rescaling the data with tref = 4.5 s, α = 0.33 and β = 0.54 the data collapses to a single curve. We parameterize the universal scaling function with fs ∝ 1/[1 + (k/ks)ζ]. Using a fit (grey solid line) we find ζ ≈ 2.6 and ks ≈ 1/133 µm−1. The quality of the rescaling is revealed by the small and symmetric scatter of the rescaled data divided by the fit (see inset).

Source data

Full size image

In fact, instead of separately depending on k and t we find that in this regime the datasets collapse to a single curve if the rescaled distribution t−αfθ is plotted as a function of the single variable tβk. This implies that the data satisfy the scaling form

$${f}_{\theta }(k,t)={t}^{\alpha }{f}_{{\rm{s}}}({t}^{\beta }k)$$
(2)

with universal scaling exponents α, β and scaling function fs. Figure 2b shows this collapse, where the same data points as in Fig. 2a are plotted with times normalized to the reference time tref = 4.5 s. The ability to reduce the full nonequilibrium time evolution of the correlation function in the scaling regime to a time-independent, so-called fixed-point distribution fs(k) and associated scaling exponents is a striking manifestation of universality.

We find the amplitude scaling exponent to be α = 0.33 ± 0.08 and the momentum scaling exponent to be β = 0.54 ± 0.06. The errors correspond to one standard deviation obtained from a resampling technique (see Methods). However, the actual uncertainty for α is expected to be larger since the rescaling analysis is much less constraining on α than on β. We find that fθ(k,t) develops a plateau at the lowest momenta and an approximate power-law fall-off above a characteristic length scale in the scaling regime. To parameterize the universal scaling function, we fitted the rescaled data with a function of the form26: fs(k) ∝1/[1 + (k/ks)ζ] and find ζ ≈ 2.6, with ks ≈ 1/133 µm−1 for our system. The value of ζ becomes constant after about 4 s (see Fig. 3a). Analysing fθ(k = 0, t) as shown in Fig. 3b reveals that the occupation of k = 0, which cannot be seen on the logarithmic scale employed in Fig. 2, builds up in the scaling regime. This growth is consistent with the power law proportional to tα with α obtained from the rescaling analysis, as indicated by the solid line. After 9 s the system departs from the scaling behaviour.

Fig. 3: Characterization of the scaling regime.
figure 3

a, For each evolution time (see Fig. 2) we extract the power-law exponent ζ from a fit. After 4 s it settles to about 2.6 (red solid line), revealing the build-up of the universal scaling function. The grey-shaded region indicates the scaling regime. b, The transport to the infrared in the scaling regime is connected to a monotonic increase of the occupation of k = 0. The solid line depicts the expected scaling fθ(k = 0,t) ∝ tα with α = 0.33. After 9 s a rapid decay signals the departure from the scaling regime. c, The emergence of a conserved quantity is signalled by the sum over all k-modes of fθ(k,t). After a fast initial growth this observable is approximately constant in the scaling regime and starts to decay after 9 s.

Source data

Full size image

The nature of the observed scaling phenomenon is explained by the emergence of an approximately conserved quantity and its transport. In terms of our dynamical degree of freedom θ(y,t) we identify ∫dk〈|θ(k,t)|2〉 ≡ ∫dk fθ(k,t) as the conserved quantity. In fact, Fig. 3c shows that the sum over all modes k for different evolution times—after a fast initial rise due to the instability—settles around a constant within the scaling regime (see also Extended Data Fig. 2). According to the scaling (2), ∫dk fθ(k,t) = tα−β∫dk fs(k) ≈ const. corresponds to α ≈ β so that in our case only one independent dynamical scaling exponent remains. A distinct feature is the transport of the conserved quantity directed towards the infrared, corresponding to a positive sign of β. Theoretically it is expected to find the scaling only for momenta smaller than some scale10 (in our case about 0.04 µm−1; see Extended Data Fig. 3). The transport towards the infrared is in contrast to the turbulent transport into the ultraviolet observed in direct cascades27.

These experimental findings of scaling behaviour, implying universality, allow comparison with predictions in a variety of models in the non-thermal universality class, which is defined by the scaling function fs and α = dβ for given spatial dimension d. N interacting Bose gases with equal intra- and interspecies Gross–Pitaevskii couplings are described by an O(N) symmetric model. This is closely related to O(N) symmetric scalar models28, such as the relativistic Higgs sector of the Standard Model with N = 4 for d = 3. For these types of models, both Gross–Pitaevskii and relativistic, a universal value of β ≈ 0.5 has been predicted and found to be insensitive to the spatial dimension10 for d ≥ 2. This describes the self-similar transport of excitations of the relative phases between the components to lower wavenumbers. The scaling function fs is known to depend on dimensionality29 and has not yet been theoretically estimated for d = 1. Our setup is, to our knowledge, the first realization of an effective N = 3 model for the transport of conserved quantities associated with non-thermal fixed points in a quasi-one-dimensional situation. Finding scaling behaviour in one dimension was not expected and sheds new light on the concept of universality classes far from equilibrium.

We emphasize that the non-thermal scaling phenomenon studied here involves no fine-tuning of parameters. This is in contrast to equilibrium critical phenomena, which require a careful adjustment of system variables, such as the temperature, to a critical value30. To illustrate this insensitivity we employ the high level of control of the atomic spin system and prepare three qualitatively different initial conditions (for details see Methods). The corresponding absorption images of single realizations are shown in Fig. 4a along with the Fourier transform of the spatial correlation function of Fx(y).

Fig. 4: Robustness of universal dynamics at a non-thermal fixed point.
figure 4

a, Absorption images of all three mF components after spin rotation with the extracted transversal spin (solid lines) of three different initial conditions. The preparations show different initial amplitudes in the Fourier transform of the transversal spin. b, All initial conditions lead to scaling dynamics. The data shown were obtained in a time window between 4 s and 9 s after preparation of the initial state. In the inset the scaling exponents of all four initial conditions, including the preparation in mF = 0 (see Fig. 1), are shown; the error bars are 1 s.d., obtained from a resampling method (see Methods). The mean values (red and blue solid lines) of α and β are used to rescale the data. We allow for overall scaling factors in k and amplitude for each initial condition.

Source data

Full size image

We find universal dynamics for all initial conditions with comparable inferred scaling exponents (see inset of Fig. 4b). We rescale the data with the same exponents obtained from the mean of all four measurements and take into account overall scaling factors and reference momentum scales. This procedure leads to a collapse of all data, manifesting the robustness of non-thermal fixed point scaling.

The level of control demonstrated here and the accessible observables on our platform open the door to the discovery of further non-thermal universality classes. This represents a crucial step towards a comprehensive understanding of out-of-equilibrium dynamics with potential impact in various fields of science.

(We note that similar phenomena have recently been observed by the Schmiedmayer group31 in Vienna in a single-component Bose gas, where a scaling exponent β ≈ 0.1 was extracted.)

Methods

Microscopic parameters

The dynamics of the spinor Bose gas is described by the Hamiltonian

$$\hat{H}={\hat{H}}_{0}+\,\int {\rm{d}}V\left[:\frac{{c}_{0}}{2}{\hat{n}}^{2}+\frac{{c}_{1}}{2}\left({\hat{F}}_{x}^{2}+{\hat{F}}_{y}^{2}+{\hat{F}}_{z}^{2}\right):+q\left({\hat{n}}_{+1}+{\hat{n}}_{-1}\right)+p{\hat{F}}_{z}\right]$$
(3)

where \({\hat{n}}_{m}={\hat{\psi }}_{m}^{\dagger }{\hat{\psi }}_{m}\), with \({\hat{\psi }}_{m}^{\dagger }\) the bosonic field creation operator of the magnetic substate m ∈ {0,±1}, and : : denotes normal ordering. \({\hat{H}}_{0}\) contains the spin-independent kinetic energy and trapping potential. The spin operators are given by \({\hat{F}}_{x}=\left[{\hat{\psi }}_{0}^{\dagger }\left({\hat{\psi }}_{+1}^{}+{\hat{\psi }}_{-1}^{}\right){\rm{+h}}{\rm{.c}}{\rm{.}}\right]/\sqrt{2}\) and \({\hat{F}}_{y}=[i{\hat{\psi }}_{0}^{\dagger }({\hat{\psi }}_{+1}^{}-{\hat{\psi }}_{-1}^{})+{\rm{h}}.{\rm{c}}.]/\sqrt{2}\) and \({\hat{F}}_{z}={\hat{n}}_{+1}-{\hat{n}}_{-1}\). The parameter p describes the linear Zeeman shift in a magnetic field. For the hyperfine spin F = 1 of 87Rb the spin interaction is ferromagnetic, that is, c1 <  0.

For the experimental control parameter q > 2n|c1|, with n being the total density, the mean-field ground state is the polar state, which corresponds to all atoms occupying the mF = 0 state. In the range 0 < q < 2n|c1| a spin with non-vanishing length in the x–y plane is energetically favoured (easy-plane ferromagnet)32. This is the parameter regime employed in the experiment.

Experimental system

We prepare a Bose–Einstein condensate of about 70,000 atoms in the state (F,mF) = (1, 0) in an optical dipole trap of 1,030 nm light with trapping frequencies ωǁ ≈ 2π × 2.2 Hz and ω⊥ ≈ 2π × 250 Hz.

The control parameter q is given by q = qB − qMW, where qB ≈ 2π × 56 Hz is the second-order Zeeman splitting in a magnetic field of B ≈ 0.884 G and qMW = Ω2/4δ is the energy shift due to the microwave dressing. For dressing33 we use a power-stabilized microwave generator with resonant Rabi frequency Ω ≈ 2π × 5.3 kHz and δ ≈ 2π × 137 kHz blue detuned with respect to the (1, 0) ↔ (2, 0) transition. For the spin dynamics we adjust Ω and δ so that q ≈ n|c1| (with nc1 ≈ −2π × 2 Hz). To monitor the long-term stability of q we do a reference measurement every 4 h (corresponding to about 250 experimental realizations). For this we observe spin dynamics for a fixed evolution time of 4 s as a function of the control parameter q (changing the detuning δ). Analysing the integrated side mode population we infer that the drifts of q are well below 0.5 Hz.

Preparation of different initial conditions

We prepare three initial conditions (see Fig. 4) that differ from the polar state. For initial condition 1 the control parameter is first set to q ≈ n|c1|+1 Hz. After 500 ms of spin dynamics at this value we quench to the final value q ≈ n|c1|. For the preparation of initial condition 2 we apply a resonant π/5 radio-frequency pulse to populate the (1, ±1) states. After a hold time of 100 ms at a magnetic field gradient of around 0.2 µG µm−1 in the longitudinal trap direction we apply a second π/5 radio-frequency pulse. The combination of q and an inhomogeneous p during the hold time leads to a spatially modulated transversal spin on a length scale of λ ≈ 80 µm. For initial condition 3 we populate homogeneously the (1, ±1) states with a short radio-frequency pulse such that (n+1 + n−1)/n ≈ 0.1.

Spin read-out

The spin dynamics is initiated by quenching the control parameter. After a fixed evolution time t we apply a short magnetic field gradient pulse (Stern–Gerlach) in the z-direction and switch off the waveguide potential. Following a short time of flight (about 1 ms) we perform high-intensity absorption imaging with a resonant light pulse of duration 15 µs. The resolution of the imaging system is about 1.2 µm, corresponding to three pixels on the charge-coupled-device camera34; we accordingly bin the spin profiles by three pixels. As our Stern–Gerlach analysis is oriented in the z-direction, for the read-out of the spin in the x–y plane we apply, before the magnetic field gradient, a radio-frequency pulse resonant with the transitions (1, 0) ↔ (1, ±1).

The radio-frequency pulse can be modelled as a spin rotation described by the Hamiltonian \({\hat{H}}_{{\rm{r}}{\rm{f}}}={\Omega }_{{\rm{r}}{\rm{f}}}{\hat{F}}_{y}\) with resonant Rabi frequency Ωrf ≈ 2π × 17.5 kHz. Applying a π/2-pulse of duration 14.3 µs, the observable \({\hat{F}}_{x}\) is mapped to the measurable density difference n+1 − n−1.

Inferring the spin orientation

The double-peaked spin distributions in the scaling regime (see Extended Data Fig. 1) resemble a distribution of a transversal spin with random orientation. To extract the corresponding ensemble average length \(\left\langle \left|{F}_{\perp }\right|\right\rangle \) of the transversal spin and its fluctuation σ we fit a probability density of the form \(p({F}_{x})\propto 1/\sqrt{1-{({F}_{x}/\langle |{F}_{\perp }|\rangle )}^{2}}\) convolved with a Gaussian distribution with root-mean-square σ. Under the assumption of a homogeneous spin length the spatial profile of the angular orientation is given by \(\theta (y)={\rm{a}}{\rm{r}}{\rm{c}}{\rm{s}}{\rm{i}}{\rm{n}}({F}_{x}(y)/\langle |{F}_{\perp }|\rangle )\). If the maximal amplitude is larger than \(\langle |{F}_{\perp }|\rangle -\sigma \) we use the maximal amplitude of the single realization instead of \(\left\langle \left|{F}_{\perp }\right|\right\rangle \).

Extraction of scaling exponents

After rescaling the results of the discrete Fourier transform according to equation (2) we interpolate with cubic splines to obtain a common k-grid for all evolution times. We vary the scaling exponents α and β to minimize the sum of the squared relative differences of all structure factors fθ. To estimate the statistical error on the exponents we employ a jackknife resampling analysis35.