1 Introduction

It is eminent that the viruses of the infection of HIV attacks the immune system and target CD4\({ }^{+}\) T-cells, which play a significant role in the body’s cover against infections. HIV weakens the immune system over time, making individuals vulnerable to several infections and diseases. HIV is a global health concern, with millions of people affected worldwide. It has significant social, economic, and healthcare impacts, both at the individual and societal levels. HIV can result in decreased productivity and increased healthcare costs, as well as a reduced life expectancy in some cases. Antiretroviral therapy (ART) is the standard treatment for HIV which can effectively suppress the virus, slow down the infection and improve the quality of life of infected individuals [1]. Prevention measures, such as practicing safe sex, using clean needles, and accessing early testing and treatment, are essential in controlling the spread of HIV. Education, awareness, and access to healthcare services are vital in addressing the complex challenges associated with HIV and supporting those living with the virus [2]. Additionally, ongoing research and understanding of the dynamics of HIV infection and its interaction with the immune system are important for developing effective control strategies, treatment and management of HIV/AIDS.

HIV infection can decrease the number of CD4\({ }^{+}\) T-cells over time, leading to immunodeficiency, which weakens the immune system and makes the body more vulnerable to other infections. HIV invades and replicates inside T-cells, leading to their destruction and a gradual decline in their numbers [3]. This depletion of T-cells hinders the immune system’s ability to mount a strong immune response against other diseases and infections. If HIV is not treated properly, then it leads to AIDs and the immune system is not able to fight against other infections. AIDs is reported when T-cell falls below a specific level, or when they develop certain infections or cancers. Nevertheless, proper medical care and treatment can enable people with HIV to manage the virus and prevent it from causing immunodeficiency and AIDS. Antiretroviral therapy (ART) is a permutation of medications that can overturn HIV replication and control further damage to the immune system. When taken consistently and correctly, ART can help people with HIV live long, healthy lives. In vivo study of HIV play a critical role in advancing our understanding of the virus, guiding the development of effective interventions, and addressing the multifaceted challenges associated with HIV infection. They provide a realistic and dynamic platform for research that ultimately contributes to improved prevention, treatment, and care strategies for individuals living with or at risk of HIV.

It has been recognized that mathematical models are useful tools for forecasting, understanding, optimising and making choices in a wide range of domains [4, 5]. They enhance our ability to evaluate ideas, analyse complex systems and offer direction for practical applications, ultimately leading to advancements in various fields like, engineering, economics, medicine and science [6, 7]. Recent advancements have allowed mathematical tools to formulate, investigate and analyze the intricate nature of biological processes [8]. In view of this, experts in epidemiological modeling [9,10,11,12] have been created novel models to examine HIV infection from different perspectives. These mathematical models afford intuitions into the dynamics of the immune response and viruses and are used to provide strategies for the management of the infection. These mathematical models described the intricate phenomena of immune system and virus with the effect of treatment and preventive measures [13]. Mostly of these models consists of three state-variables such as HIV virions, uninfected and infected T-cells, to provide basic understanding of the regulation of viral propagation. In [14], the authors studied the interaction of HIV viruses, healthy and infected T-cells. It is eminent that the infection of HIV can effectively suppressed through antiretroviral therapy, however, therapeutic approaches may not fully restore the immune system [15]. In order to acquire more exact and accurate findings that can contribute to the prevention and control of HIV infection, further research is required to thoroughly study the complex dynamics of the immune system and HIV infection.

This research is organized as: In the second section, we constructed the dynamics of HIV infection to highlight the intricate phenomena of immune system and HIV viruses with the effect of antiretroviral therapy. In section three, we illustrate the rudimentary concepts of the fractional theory for examination of our model. In section four, the dynamics is represented through fractional framework. Section five investigates the solution pathways and oscillatory nature of the system using numerical techniques. Finally, we conclude our work by summarizing our findings in the last section.

2 Evaluation of HIV Dynamics

Here, we will construct the dynamics of HIV that represents the interface between viruses and immune cells with the effect of antiretroviral therapy. There are numerous mathematical models for this viral infection in the literature [16,17,18]. In accordance with the findings of the researcher in [19], the phenomenon of HIV transmission can be described as

$$\left\{\begin{array}{lll}\frac{d\text{T}}{dt}& =& s-k\text{V}\text{T}+r\text{T}\Bigg(1-\frac{\text{T}+\text{I}}{{\text{T}}_{\text{m}\text{a}\text{x}}}\Bigg)-{\mu }_{T}\text{T},\\ \frac{d\text{I}}{dt}& =& k\text{V}\text{T}-{\mu }_{I}\text{I},\\ \frac{d\text{V}}{dt}& =& {\mu }_{I}N\text{I}-\text{V}{\mu }_{V},\end{array}\right.$$
(1)

in which \(r\) is the growth rate of healthy T-cells and \(s\) indicating the recruitment rate of healthy T-cells. The death rates for viruses, vigorous and diseased T-cells are denoted by \({\mu }_{V}\), \({\mu }_{T}\), and \({\mu }_{I}\), respectively. The number at which viruses are reproduced by infected T-cells denoted by \(N\) while \(\eta\) denotes the rate of infection of healthy T-cells. The HIV model proposed by Perelson & Nelson in [20] can be represented as follows

$$\left\{\begin{array}{lll}\frac{dT}{dt}& =& rT\Bigg(1-\frac{T}{{T}_{\text{m}\text{a}\text{x}}}\Bigg)-\frac{VT\eta }{1+\alpha V},\\ \frac{dI}{dt}& =& \frac{VT\eta }{1+\alpha V}-{\mu }_{I}I,\\ \frac{dV}{dt}& =& NI{\mu }_{I}-{\mu }_{V}V.\end{array}\right.$$
(2)

In [21], the concept of saturated incidence rate has been presented in the dynamics of HIV infection. It is well-known that including the concept of saturated incidence, can help improve our understanding of in what way the virus interrelates with the host’s immune system, and how this may impact the clinical course of the infection, treatment strategies, and prevention efforts. Then, we have

$$\left\{\begin{array}{lll}\frac{d\text{T}}{dt}& =& s-{\mu }_{T}\text{T}+r\text{T}\Bigg(1-\frac{\text{T}}{{\text{T}}_{\text{m}\text{a}\text{x}}}\Bigg)-\frac{k\text{V}\text{T}}{1+{\alpha }_{1}\text{V}}-\frac{\alpha \text{I}\text{T}}{1+{\alpha }_{2}\text{I}},\\ \frac{d\text{I}}{dt}& =& \frac{k\text{V}\text{T}}{1+{\alpha }_{1}\text{V}}+\frac{\alpha \text{I}\text{T}}{1+{\alpha }_{2}\text{I}}-{\mu }_{I}\text{I},\\ \frac{d\text{V}}{dt}& =& {\mu }_{I}N\text{I}-{\mu }_{V}\text{V}-\frac{k\text{V}\text{T}}{1+{\alpha }_{1}\text{V}}.\end{array}\right.$$
(3)

In this context, we are examining the levels of CD\({8}^{+}\) T-cells and triggered CD\({8}^{+}\) T-cells represented as \(C\) and \(A,\) respectively. We epitomize the reproduction of CD\({8}^{+}\) T-cells from thymus by \({\hslash }_{C}\) while these cells are naturally removed at a rate of \({\mu }_{C}\). The activation of CD\({8}^{+}\) T-cells happens in the existence of HIV and eliminated at \({\mu }_{A}\). Therefore, assuming the above conditions, the dynamics of HIV can be described as

$$\left\{\begin{array}{ccc}\frac{dT}{dt}& =& s-{\mu }_{T}T+rT(1-\frac{T}{{T}_{\text{m}\text{a}\text{x}}})-\frac{kVT}{1+{\alpha }_{1}V}-\frac{\alpha IT}{1+{\alpha }_{2}I},\\ \frac{dI}{dt}& =& \frac{kVT}{1+{\alpha }_{1}V}+\frac{\alpha IT}{1+{\alpha }_{2}I}-{\mu }_{I}I,\\ \frac{dV}{dt}& =& N{\mu }_{I}I-{\mu }_{V}V-\frac{kVT}{1+{\alpha }_{1}V}-\beta V,\\ \frac{dC}{dt}& =& {\hslash }_{C}-\frac{\eta IC}{1+{\alpha }_{2}I}-{\mu }_{C}C,\\ \frac{dA}{dt}& =& \frac{\eta IC}{1+{\alpha }_{2}I}-{\mu }_{A}A,\end{array}\right.$$
(4)

where \(\beta\) is the rate at which antiretroviral therapy reduce the load of viruses. Moreover, we have the following

$$T\left( 0 \right) = T_{0} ,I\left( 0 \right) = I_{0} ,V\left( 0 \right) = V_{0} ,C\left( 0 \right) = C_{0} \,and\,A\left( 0 \right) = A_{0} .$$

It’s important to note that HIV treatment plans are highly individualized and may vary depending on factors such as the stage of HIV infection, overall health of the person living with HIV, potential drug interactions, and adherence to medication regimens. The development of an effective treatment strategy for controlling HIV requires close collaboration with an experienced health-care official.

3 Fractional-calculus Analysis

Fractional calculus provides a powerful mathematical tool for studying and analyzing complex biological processes that exhibit non-local and memory-dependent behavior. It allows for a more accurate and comprehensive description compared to classical integer-order models [22,23,24] and it has found applications in various areas of biology, ranging from cancer growth to neuronal dynamics.

Fractional calculus has been used in some studies to represent the dynamics of this viral infection, particularly in understanding the memory-dependent behavior and complex dynamics associated with the virus. The use of fractional derivatives in modeling HIV infection provides a way to account for the long-term memory effects and anomalous diffusion that can occur in the progression of the disease. It’s worth noting that while fractional calculus has been used in some studies to model HIV infection dynamics, it is not the only mathematical approach used in this field, and more research is required to completly understand the intricate process of HIV infection. HIV infection is a complex and dynamic process that involves multiple biological, immunological, and epidemiological factors, and mathematical modeling, including fractional calculus, can provide valuable insights into its dynamics and potential treatment strategies. Therefore, we represent our model in framework of CF fractional derivative as

$$\left\{ {\begin{array}{*{20}c} {_{0} ^{{{\text{CF}}}} {\text{D}}_{{\text{t}}}^{\xi } T} & = & {s - \mu _{T} T + rT\left( {1 - \frac{T}{{T_{{{\text{max}}}} }}} \right) - \frac{{kVT}}{{1 + \alpha _{1} V}} - \frac{{\alpha IT}}{{1 + \alpha _{2} I}},} \\ {_{0} ^{{C{\text{F}}}} {\text{D}}_{t}^{\xi } I} & = & {\frac{{kVT}}{{1 + \alpha _{1} V}} + \frac{{\alpha IT}}{{1 + \alpha _{2} I}} - \mu _{I} I,} \\ {_{0} ^{{C{\text{F}}}} {\text{D}}_{t}^{\xi } V} & = & {N\mu _{I} I - \mu _{V} V - \frac{{kVT}}{{1 + \alpha _{1} V}} - \beta V,} \\ {_{0} ^{{C{\text{F}}}} {\text{D}}_{t}^{\xi } C} & = & {\hbar _{C} - \frac{{\eta IC}}{{1 + \alpha _{2} I}} - \mu _{C} C,} \\ {_{0} ^{{C{\text{F}}}} {\text{D}}_{t}^{\xi } A} & = & {\frac{{\eta IC}}{{1 + \alpha _{2} I}} - \mu _{A} A,} \\ \end{array} } \right.$$
(5)

with the initial condition

$$T\left( 0 \right) = T_{0} ,I\left( 0 \right) = I_{0} ,V\left( 0 \right) = V_{0} ,C\left( 0 \right) = C_{0} \,and\,A\left( 0 \right) = A_{0} .$$

There are numerous applications of fractional theory in modeling of infectious diseases. Here, we focussed to model the dynamics of HIV, taking into account the non-local interactions and memory effects that influence the dynamics of the virus in the body. CFD.

3.1 Results of Fractional Operator

In this subsection, we will present fundamental definitions and results that are crucial for analyzing in-vivo dynamics of HIV with the effect of antiretroviral therapy. These analyses will be conducted within the framework of Caputo-Fabrizio (CF) derivative. The rudimentary findings of the Caputo-Fabrizio operator is given below:

Definition 1

Take a function f in, then the CF derivative is given by the following

$$D_{t}^{\xi } (f(t)) = \frac{{{\mathbf{U}}\left( \xi \right)}}{{1 - \xi }}\int_{a}^{t} {f^{\prime } \left( z \right)} {\text{exp}}\left[ { - \xi \frac{{t - z}}{{1 - \xi }}} \right]dz,$$
(6)

where a is smaller than b and the fractional order \(\xi\) belongs to the interval \(\left[\text{0,1}\right]\). In addition to this, the normality in the above is indicated by \(U\left(\xi \right)\) with the condition \(\mathbf{U}\left(0\right)=\mathbf{U}\left(1\right)=1\) [25]. On the other hand, if \(f\) does not belong \({\mathbf{H}}^{1}(a,b)\), then, we have

$$D_{t}^{\xi } (f(t)) = \frac{{\xi {\mathbf{U}}\left( \xi \right)}}{{1 - \xi }}\int_{a}^{t} {(f(t) - f(z))} {\text{exp}}\left[ { - \xi \frac{{t - z}}{{1 - \xi }}} \right]dz.$$
(7)

Remark 1

In the case, if and, then Eq. (6) implies that

$$D_{t}^{\xi } (f(t)) = \frac{{{\mathbf{M}}\left( \alpha \right)}}{\alpha }\int_{a}^{t} {f^{\prime}\left( z \right)} e^{{[ - \frac{{t - z}}{\alpha }]}} dz,{\mathbf{M}}\left( 0 \right) = {\mathbf{M}}\left( \infty \right) = 1.$$
(8)

Furthermore, we have

$$\mathop {{\text{lim}}}\limits_{{\alpha \to 0}} \frac{1}{\alpha }{\text{exp}}\left[ { - \frac{{t - z}}{\alpha }} \right] = \delta (z - t).$$
(9)

Now, we will represent the concept of integral for CF fractional operator introduced in [26].

Definition 2

Take a function, then the integral in CF structure is given by the following

$$I_{t}^{\xi } (f(t)) = \frac{{2(1 - \xi )}}{{(2 - \xi ){\mathbf{U}}\left( \xi \right)}}f\left( t \right) + \frac{{2\xi }}{{(2 - \xi ){\mathbf{U}}\left( \xi \right)}}\int_{0}^{t} {f\left( u \right)du,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} } t \ge 0.$$
(10)

in which the fractional order \(\xi\) obeys the condition \(0<\xi <1\).

Remark 2

The aforementioned Definition 2further leads to

$$\frac{{2(1 - \xi )}}{{(2 - \xi ){\mathbf{U}}\left( \xi \right)}} + \frac{{2\xi }}{{(2 - \xi ){\mathbf{U}}\left( \xi \right)}} = 1,$$
(11)

with \(\mathbf{U}\left(\xi \right)=\frac{2}{2-\xi }\), \(0<\xi <1\). After that, the Eq. (10) is utilized and the following is introduced, given by

$$D_{t}^{\xi } (f(t)) = \frac{1}{{1 - \xi }}\int_{0}^{t} {f^{\prime} \left( z \right)} {\text{exp}}\left[ {\xi \frac{{t - z}}{{1 - \xi }}} \right]dz,\,\,\,\,\,\,0 < \xi < 1.$$
(12)
Fig. 1
figure 1

Representation of the solution paths of HIV infection system with the fractional parameter \(\xi =1.00\)

Full size image
Fig. 2
figure 2

Representation of the solution paths of HIV infection system with the fractional parameter \(\xi =0.856\)

Full size image
Fig. 3
figure 3

Representation of the solution paths of HIV infection system with the fractional parameter \(\xi =0.656\)

Full size image
Fig. 4
figure 4

Plotting the solution paths of HIV infection system with the variation of the input parameter \(\alpha\), i.e., \(\alpha =11{0}^{-5},101{0}^{-5},501{0}^{-5},1001{0}^{-5}\)

Full size image
Fig. 5
figure 5

Plotting the solution paths of HIV infection system with the variation of the input parameter \(\eta\), i.e., \(\eta =\text{0.003,0.005,0.007,0.009}\)

Full size image
Fig. 6
figure 6

Graphical respresentation of the solution pathways of healthy CD\({4}^{+}\) T-cells, infected CD\({4}^{+}\) T-cells and HIV viruses with the variation of \(\beta\), i.e., \(\beta =\text{0.35,0.45,0.55,0.65}\)

Full size image
Fig. 7
figure 7

Graphical analysis of the phase portrait of the system with diverse values of input parameters of HIV model with \(\xi =0.9\), \(s=3.0\) and \(r=3\)

Full size image
Fig. 8
figure 8

Graphical investigation of the phase portrait of the system with dissimilar values of input parameters of HIV model with \(\xi =0.8\), \(s=5\) and \(r=1\)

Full size image

4 Numerical Scheme for HIV Dynamics

Here, our key objective is to demonstrate the solution pathways of the recommended system (4) of HIV with the help of numerical findings. Various numerical methods have been previously employed in the literature to investigate the dynamics of Caputo-Fabrizio fractional systems, such as those discussed in references [27,28,29]. In this study, we will adopt the numerical scheme presented in [29] as it is stable, easily implementable and more reliable for representing the dynamics of fractional system. We will visually depict the trajectory behavior of the system and illustrate the fluctuations that occur with variations in different input factors.

Initially, the recommended dynamics of HIV infection is represented in Volterra type, and then we utilized the basic results of fractional theory. The numerical scheme is obtained by utilizing the first equation of our system as

$${\text{z}}_{1} \left( t \right) - {\text{z}}_{1} \left( 0 \right) = \frac{{1 - \xi }}{{{\mathbf{U}}\left( \xi \right)}}{\mathbf{H}}_{1} (t,{\text{z}}_{1} ) + \frac{\xi }{{{\mathbf{U}}\left( \xi \right)}}\int_{0}^{t} {{\mathbf{H}}_{1} (\omega ,{\text{z}}_{1} )d\omega } .$$
(13)

For \(t={t}_{m+1},m=\text{0,1},\dots ,\), we have the below

$${\text{z}}_{1} \left( {t_{{m + 1}} } \right) - {\text{z}}_{1} \left( 0 \right) = \frac{{1 - \xi }}{{{\mathbf{U}}\left( \xi \right)}}{\mathbf{H}}_{1} (t_{m} ,{\text{z}}_{1} (t_{m} )) + \frac{\xi }{{{\mathbf{U}}\left( \xi \right)}}\int_{0}^{{t_{{m + 1}} }} {{\mathbf{H}}_{1} (t,{\text{z}}_{1} )dt} .$$
(14)

and

$${\text{z}}_{1} \left( {t_{m} } \right) - {\text{z}}_{1} \left( 0 \right) = \frac{{1 - \xi }}{{{\mathbf{U}}\left( \xi \right)}}{\mathbf{H}}_{1} (t_{{m - 1}} ,{\text{z}}_{1} (t_{{m - 1}} )) + \frac{\xi }{{{\mathbf{U}}\left( \xi \right)}}\int_{0}^{{t_{m} }} {{\mathbf{H}}_{1} (t,{\text{z}}_{1} )dt} .$$
(15)

In this step, we calculate the differences between successive terms of the system as

$${\text{z}}_{{1_{{m + 1}} }} - {\text{z}}_{{1_{m} }} = \frac{{1 - \xi }}{{{\mathbf{U}}\left( \xi \right)}}({\mathbf{H}}_{1} (t_{m} ,{\text{z}}_{{1_{m} }} ) - {\mathbf{H}}_{1} (t_{{m - 1}} ,{\text{z}}_{{1_{{m - 1}} }} )) + \frac{\xi }{{{\mathbf{U}}\left( \xi \right)}}\int_{m}^{{t_{{m + 1}} }} {{\mathbf{H}}_{1} (t,{\text{z}}_{1} )dt} .$$
(16)

In addition, we utilize an interpolation polynomial to approximate the function \(\mathbf{H}1(t,{\text{z}}_{1})\) within the time interval \([{t}_{k},tk+1]\), resulting in:

$${\mathbf{P}}_{k}\left(t\right)\cong \frac{{\mathbf{H}}_{1}({t}_{k},{\text{z}}_{k})}{h}(t-{t}_{k-1})-\frac{{\mathbf{H}}_{1}({t}_{k-1},{\text{z}}_{k-1})}{h}(t-{t}_{k}),$$
(17)

where \(h\) represents the time duration and is defined as \(h={t}_{m}-{t}_{m-1}\). The expression of \({\mathbf{P}}_{k}\left(t\right)\) is utilized to compute the value of the subsequent integral:

$$\begin{array}{*{20}l} {\int_{m}^{{t_{{m + 1}} }} {{\mathbf{H}}_{1} (t,{\text{z}}_{1} )dt} } \hfill & {amp; = } \hfill & {amp;\int_{m}^{{t_{{m + 1}} }} {\left( {\frac{{{\mathbf{H}}_{1} \left( {t_{m} ,{\text{z}}_{{1_{m} }} } \right)}}{h}} \right)\left( {t - t_{{m - 1}} } \right) - \frac{{{\mathbf{H}}_{1} \left( {t_{{m - 1}} ,{\text{z}}_{{1_{{m - 1}} }} } \right)}}{h}(t - t_{m} )dt,} } \hfill \\ {} \hfill & {amp; = } \hfill & {amp;\frac{{3h}}{2}{\mathbf{H}}_{1} \left( {t_{m} ,{\text{z}}_{{1_{m} }} } \right) - \frac{h}{2}{\mathbf{H}}_{1} \left( {t_{{m - 1}} ,{\text{z}}_{{1_{{m - 1}} }} } \right).} \hfill \\ \end{array}$$
(18)

Now, putting (17) in (15), we have the following

$$\begin{array}{*{20}c} {{\text{z}}_{{1_{{m + 1}} }} } & {amp; = } & {amp;{\text{z}}_{{1_{m} }} + \left( {\frac{{1 - \xi }}{{{\mathbf{U}}\left( \xi \right)}} + \frac{{3\xi h}}{{2{\mathbf{U}}\left( \xi \right)}}} \right){\mathbf{H}}_{1} (t_{m} ,{\text{z}}_{{1_{m} }} )} \\ {} & {amp;} & {amp; - \left( {\frac{{1 - \xi }}{{{\mathbf{U}}\left( \xi \right)}} + \frac{{\xi h}}{{2{\mathbf{U}}\left( \xi \right)}}} \right){\mathbf{H}}_{1} (t_{{m - 1}} ,{\text{z}}_{{1_{{m - 1}} }} ).} \\ \end{array}$$

The provided numerical scheme corresponds to the first equation in our system (5) that models HIV infection. By applying the same methodology, we can obtain the appropriate scheme for the other equations of the recommended model (5) of HIV as:

$$\begin{array}{*{20}c} {{\text{z}}_{{2_{{m + 1}} }} } & {amp; = } & {amp;{\text{z}}_{{2_{m} }} + \left( {\frac{{1 - \xi }}{{{\mathbf{U}}\left( \xi \right)}} + \frac{{3\xi h}}{{2{\mathbf{U}}\left( \xi \right)}}} \right){\mathbf{H}}_{2} (t_{m} ,{\text{z}}_{{2_{m} }} )} \\ {} & {amp;} & {amp; - \left( {\frac{{1 - \xi }}{{{\mathbf{U}}\left( \xi \right)}} + \frac{{\xi h}}{{2{\mathbf{U}}\left( \xi \right)}}} \right){\mathbf{H}}_{2} (t_{{m - 1}} ,{\mathbf{z}}_{{2_{{m - 1}} }} ),} \\ \end{array}$$
$$\begin{array}{*{20}c} {{\text{z}}_{{3_{{m + 1}} }} } & {amp; = } & {amp;{\text{z}}_{{3_{m} }} + \left( {\frac{{1 - \xi }}{{{\mathbf{U}}\left( \xi \right)}} + \frac{{3\xi h}}{{2{\mathbf{U}}\left( \xi \right)}}} \right){\mathbf{H}}_{3} (t_{m} ,{\text{z}}_{{3_{m} }} )} \\ {} & {amp;} & {amp; - \left( {\frac{{1 - \xi }}{{{\mathbf{U}}\left( \xi \right)}} + \frac{{\xi h}}{{2{\mathbf{U}}\left( \xi \right)}}} \right){\mathbf{H}}_{3} \left( {t_{{m - 1}} ,{\text{z}}_{{3_{{m - 1}} }} } \right),} \\ \end{array}$$
$$\begin{array}{*{20}c} {{\text{z}}_{{4_{{m + 1}} }} } & {amp; = } & {amp;{\text{z}}_{{4_{m} }} + \left( {\frac{{1 - \xi }}{{{\mathbf{U}}\left( \xi \right)}} + \frac{{3\xi h}}{{2{\mathbf{U}}\left( \xi \right)}}} \right){\mathbf{H}}_{4} (t_{m} ,{\text{z}}_{{4_{m} }} )} \\ {} & {amp;} & {amp; - \left( {\frac{{1 - \xi }}{{{\mathbf{U}}\left( \xi \right)}} + \frac{{\xi h}}{{2{\mathbf{U}}\left( \xi \right)}}} \right){\mathbf{H}}_{4} (t_{{m - 1}} ,{\text{z}}_{{4_{{m - 1}} }} ),} \\ \end{array}$$

and

$$\begin{array}{*{20}c} {{\text{z}}_{{5_{{m + 1}} }} } & {amp; = } & {amp;{\text{z}}_{{5_{m} }} + \left( {\frac{{1 - \xi }}{{{\mathbf{U}}\left( \xi \right)}} + \frac{{3\xi h}}{{2{\mathbf{U}}\left( \xi \right)}}} \right){\mathbf{H}}_{5} (t_{m} ,{\text{z}}_{{5_{m} }} )} \\ {} & {amp;} & {amp; - \left( {\frac{{1 - \xi }}{{{\mathbf{U}}\left( \xi \right)}} + \frac{{\xi h}}{{2{\mathbf{U}}\left( \xi \right)}}} \right){\mathbf{H}}_{5} (t_{{m - 1}} ,{\text{z}}_{{5_{{m - 1}} }} ).} \\ \end{array}$$

The method employed involves a two-step Adams-Bashforth scheme to handle the Caputo-Fabrizio operator, which considers the nonlinearity of the kernel. Moreover, it includes an exponential decay law that is specially designed for the Caputo-Fabrizio operator.

5 Numerical Results

The infection of HIV have a high negative impact on households in APR despite massive worldwide efforts to avoid it. A loss of capital needed to address the income-to-expenditure gap, decreased employment income, and increased health care costs are all contributory factors to this burden. In order to avoid these losses, it is crucial to understand and more accurately represent the dynamics of this viral infection. In this section, we will illustrate the dynamical behaviour of the system to show the impact of input parameters on the system. For numerical purposes, the values of state-variables and input parameters are considered.

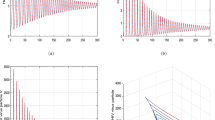
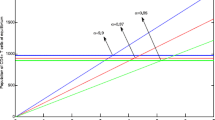
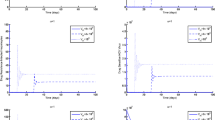
In the first scenario presented in Figs. 1, 2 and 3, we have shown the impact of the fractional parameter on the system and presented a comparative view of integer and non-integer cases. In Fig. 1, we assumed the value of fractional parameter \(\xi =1.0\) to represent the integer case of the system. In Figs. 2 and 3, we assumed the values of \(\xi\) to be \(0.856\) and \(0.656\) to illustrate the non-integer case of the system. It has been observed that the fractional parameter has an attractive impact on the dynamics of the HIV infection. We showed the influence of the input parameter \(\eta\) on the output of the system in Fig. 4. In this simulation, \(\eta\) is assumed to be \(0.003\), \(0.005\), \(0.007\) and \(0.009\) to highlight the dynamics of CD\({8}^{+}\) T-cells. In Fig. 5, the tracking paths of the concentrations of CD\({4}^{+}\) T-cells, HIV viruses and CD\({8}^{+}\) T-cells has been illustrated with the variation of the input parameter \(\alpha\). For this purpose, we take the values of \(\alpha\) to be \(1\times 1{0}^{-5},\) \(10\times 1{0}^{-5},\) \(50\times 1{0}^{-5},\) and \(100\times 1{0}^{-5}\). The solution pathways of the system is highlighted with different values of \(\beta\) in Fig. 6. In this simulation, we take \(\beta =\text{0.35,0.45,0.55,0.65}\) and observed the role of \(\beta\) on the output of the system.

In the last simulation illustrated in Figs. 7 and 8, we plotted the phase portrait of the system with different input factors to conceptualize the phenomena. In Fig. 7, we considered the input parameters \(\xi =0.9\), \(s=3.0\) and \(r=3.0\) while input values are taken to be \(\xi =0.8\), \(s=5.0\) and \(r=1.0\) in Fig. 8. It can be observed that the system possesses oscillatory behaviour which is due to the nonlinear nature of the system. These types of phenomena depend on the initial conditions, system parameters and strong nonlinearity of the system which needs to be controlled. Further developments in in vivo models of HIV will provide critical insights into the mechanisms immune responses, viral persistence and the advancement of targeted strategies. These studies will pave the way for the advancement of more effective treatment interventions and ultimately aid in achieving long-term remission or a functional cure for HIV.

6 Conclusion

The defensive system of humans is weakened by HIV infection against other infections by attacking the immune system and destroying T-cells. The global public health community is currently quite concerned about this issue. Despite recent evidence that the infection is declining, further study is necessary to completely understand how the viruses interact with T-cells. In this study, we formulated the dynamics of HIV, considering the interaction of viruses and immune system with the effect of antiretroviral therapy. The basic concepts of fractional calculus are presented for the analysis of the model and a fractional framework is used for the dynamics of HIV infection. To represent the dynamical behaviour of the system, we introduced a numerical scheme. The tracking paths and the phase portraits of the system are depicted to illustrate the most sensitive parameters of the system. We have illustrated different simulations to show the importance of input parameters on the output of the system and to conceptualize the most crucial circumstances of the system. The impact of input factors has been visualized with the help of numerical findings and most critical parameters are suggested to the policymakers and health officials. In vivo models will remain crucial in assessing cutting-edge therapeutic approaches and HIV treatment plans. Testing of novel antiretroviral medications, immunotherapies, gene treatments, and combination strategies are included in this. Future models will be used to evaluate the effectiveness, safety, and possibility of viral eradication or long-term remission of the therapy.