Darcy’s Law for Porous Media with Multiple Microstructures

Abstract

In this paper we study the homogenization of the Dirichlet problem for the Stokes equations in a perforated domain with multiple microstructures. First, under the assumption that the interface between subdomains is a union of Lipschitz surfaces, we show that the effective velocity and pressure are governed by a Darcy law, where the permeability matrix is piecewise constant. The key step is to prove that the effective pressure is continuous across the interface, using Tartar’s method of test functions. Secondly, we establish the sharp error estimates for the convergence of the velocity and pressure, assuming the interface satisfies certain smoothness and geometric conditions. This is achieved by constructing two correctors. One of them is used to correct the discontinuity of the two-scale approximation on the interface, while the other is used to correct the discrepancy between boundary values of the solution and its approximation.

1 Introduction

In this paper we study the homogenization of the Dirichlet problem for the Stokes equations in a perforated domain $\Omega _\varepsilon$,

$$\begin{aligned} \left\{ \begin{aligned}&-\varepsilon ^2 \mu \Delta u_\varepsilon +\nabla p_\varepsilon = f \quad \text { in } \Omega _\varepsilon ,\\&\textrm{div} (u_\varepsilon ) =0 \quad \text { in } \Omega _\varepsilon ,\\&u_\varepsilon = 0 \quad \text { on } \partial \Omega _\varepsilon , \end{aligned}\right. \end{aligned}$$

(1.1)

where $0< \varepsilon < 1$ and $\mu >0$ is a constant. Let $\Omega$ be a bounded Lipschitz domain in ${\mathbb {R}}^d$, $d\ge 2$. Let $\{ \Omega ^\ell : 1\le \ell \le L\}$ be a finite number of disjoint subdomains of $\Omega$, each with a Lipschitz boundary, such that

$$\begin{aligned} \overline{\Omega } = \bigcup _{\ell =1}^L \overline{\Omega ^\ell }. \end{aligned}$$

(1.2)

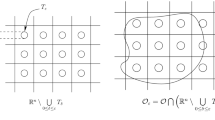
To describe the porous domain $\Omega _\varepsilon$, let $Y=[-1/2, 1/2]^d$ be a closed unit cube and $\{ Y_s^\ell : 1\le \ell \le L \}$ open subsets (solid parts) of Y with Lipschitz boundaries. Assume that for $1\le \ell \le L$, dist$(\partial Y, \partial Y_s^\ell )>0$ and $Y^\ell _f=Y \setminus \overline{Y_s^\ell }$ (the fluid part) is connected. For $0< \varepsilon <1$ and $1\le \ell \le L$, define

$$\begin{aligned} \Omega _\varepsilon ^\ell =\Omega ^\ell \setminus \bigcup _z \varepsilon \left( \overline{Y_s^\ell } +z\right) , \end{aligned}$$

(1.3)

where $z \in {\mathbb {Z}}^d$ and the union is taken over those z’s for which $\varepsilon (Y+z)\subset \Omega ^\ell$. Thus the subdomain $\Omega ^\ell$ is perforated periodically, using the solid obstacle $Y_s^\ell$. Let

$$\begin{aligned} \Omega _\varepsilon = \Sigma \cup \bigcup _{\ell =1}^L \Omega _\varepsilon ^\ell =\Omega \setminus \bigcup _{\ell =1}^L \bigcup _z \varepsilon \left( \overline{Y_s^\ell } +z\right) , \end{aligned}$$

(1.4)

where $\Sigma$ is the interface between subdomains, given by

$$\begin{aligned} \Sigma = \Omega \setminus \bigcup _{\ell =1}^L\Omega ^\ell =\bigcup _{\ell =1}^L \partial \Omega ^\ell \setminus \partial \Omega . \end{aligned}$$

(1.5)

For $f\in L^2(\Omega ; {\mathbb {R}}^d)$, let $(u_\varepsilon , p_\varepsilon ) \in H_0^1(\Omega _\varepsilon ; {\mathbb {R}}^d)\times L^2(\Omega _\varepsilon )$ be the weak solution of (1.1) with $\int _{\Omega _\varepsilon } p_\varepsilon \, \mathrm{{d}}x =0$. We extend $u_\varepsilon$ to the whole domain $\Omega$ by zero. Let $P_\varepsilon$ denote the extension of $p_\varepsilon$ to $\Omega$, defined by (2.21). In the case $L=1$, where $\Omega$ is perforated periodically with small holes of same shape, it is well known that as $\varepsilon \rightarrow 0$, $u_\varepsilon \rightarrow u_0$ weakly in $L^2(\Omega ; {\mathbb {R}}^d)$ and $P_\varepsilon \rightarrow P_0$ strongly in $L^2(\Omega )$, where the effective velocity and pressure $(u_0, P_0)$ are governed by the Darcy law,

$$\begin{aligned} \left\{ \begin{aligned}&u_0 =\mu ^{-1} K (f-\nabla P_0) \quad \text { in } \Omega , \\&\text {div} (u_0) =0 \quad \text { in } \Omega ,\\&u_0\cdot n =0 \quad \text { on } \partial \Omega , \end{aligned}\right. \end{aligned}$$

(1.6)

with $\int _\Omega P_0\, \mathrm{{d}}x=0$. Note that in (1.1) we have normalized the velocity vector by a factor $\varepsilon ^2$, where $\varepsilon$ is the period. For references on the Darcy law, we refer to the reader to [1, 3, 4, 10, 13].

In (1.6) the permeability matrix K is a $d\times d$ positive-definite, constant and symmetric matrix and n denotes the outward unit normal to $\partial \Omega$. It was observed in [3] by G. Allaire that as $\varepsilon \rightarrow 0$,

$$\begin{aligned} u_\varepsilon - \mu ^{-1} W(x/\varepsilon ) (f-\nabla P_0) \rightarrow 0 \quad \text {strongly in } L^2(\Omega ; {\mathbb {R}}^d), \end{aligned}$$

(1.7)

where W(y) is an 1-periodic $d\times d$ matrix defined by a cell problem and . Recently, it was proved in [14] by the present author that

$$\begin{aligned} \Vert u_\varepsilon - \mu ^{-1} W(x/\varepsilon ) (f-\nabla P_0)\Vert _{L^2(\Omega )} + \Vert P_\varepsilon -P_0\Vert _{L^2(\Omega )} \le C\sqrt{\varepsilon } \Vert f\Vert _{C^{1, 1/2}(\Omega )}, \end{aligned}$$

(1.8)

and that

$$\begin{aligned} \Vert \varepsilon \nabla u_\varepsilon -\mu ^{-1} \nabla W(x/\varepsilon ) (f-\nabla P_0) \Vert _{L^2(\Omega )} \le C \sqrt{\varepsilon } \Vert f\Vert _{C^{1, 1/2}(\Omega )}. \end{aligned}$$

(1.9)

We point out that due to the discrepancy between boundary values of $\mu ^{-1} W(x/\varepsilon )(f-\nabla P_0)$ and $u_\varepsilon$ on $\partial \Omega$, the $O(\varepsilon ^{1/2})$ convergence rates in (1.8) and(1.9) are sharp. See [11] for an earlier partial result on solutions with periodic boundary conditions.

The primary purpose of this paper is to study the Darcy law for the case $L\ge 2$, where the domain $\Omega$ is divided into several subdomains and different subdomains are perforated with small holes of different shapes.

Theorem 1.1

Let $\Omega$ be a bounded Lipschitz domain in ${\mathbb {R}}^d$, $d\ge 2$, and $\Omega _\varepsilon$ be given by (1.4). Let $(u_\varepsilon , p_\varepsilon ) \in H_0^1(\Omega _\varepsilon ; {\mathbb {R}}^d) \times L^2(\Omega _\varepsilon )$ be a weak solution of (1.1), where $f\in L^2(\Omega ; {\mathbb {R}}^d)$ and $\int _{\Omega _\varepsilon } p_\varepsilon \, \mathrm{{d}}x =0$. Let $P_\varepsilon$ be the extension of $p_\varepsilon$, defined by (2.21). Then $u_\varepsilon \rightarrow u_0$ weakly in $L^2(\Omega ; {\mathbb {R}}^d)$ and strongly in $L^2(\Omega )$, as $\varepsilon \rightarrow 0$, where $P_0\in H^1(\Omega )$ and $(u_0, P_0)$ is governed by the Darcy law (1.6) with the matrix

$$\begin{aligned} K =\sum _{\ell =1}^L K^\ell \chi _{\Omega ^\ell } \qquad \text { in } \Omega . \end{aligned}$$

(1.10)

The matrix $K^\ell$ in (1.10) is the (constant) permeability matrix associated with the solid obstacle $Y_s^\ell$. Thus, the matrix K is piecewise constant in $\Omega$, taking the value $K^\ell$ in the subdomain $\Omega ^\ell$, and

$$\begin{aligned} u_0= K^\ell (f-\nabla P_0) \quad \text { in } \Omega ^\ell . \end{aligned}$$

(1.11)

Since $\textrm{div}(u_0)=0$ in $\Omega$ and $P_0\in H^1(\Omega )$, both the normal component $u_0\cdot n$ and $P_0$ are continuous across the interface $\Sigma$ (in the sense of trace) between subdomains. However, the tangential components of $u_0$ may not be continuous across $\Sigma$.

The Dirichlet problem for the Stokes equations (1.1) is used to model fluid flows in porous media with different microstructures in different subdomains. The continuity of the effective pressure $P_0$ and the normal component $u_0\cdot n$ of the effective velocity across the interface is generally accepted in engineering [6, 9]. Theorem 1.1 is probably known to experts. However, to the best of the author’s knowledge, the existing literatures on rigorous proofs only treat the case of flat interfaces. In particular, the result was proved in [9] under the assumptions that $d=2$, the interface $\Gamma ={\mathbb {R}}\times \{0 \}$ and the solutions are 1-periodic in the direction $x_1$. Also see related work in [5, 12]. We provide a proof here for the general case, where the interface is a union of Lipschitz surfaces, using Tartar’s method of test functions. We point out that the proof for (1.11) and $P_0\in H^1(\Omega ^\ell )$ for each $\ell$ is the same as in the classical case $L=1$. The challenge is to show that the effective pressure $P_0$ is continuous across the interface and thus $P_0\in H^1(\Omega )$, which is essential for proving the uniqueness of the limits of subsequences of $\{ u_\varepsilon \}$.

Our main contribution in this paper is on the sharp convergence rates and error estimates for $u_\varepsilon$ and $P_\varepsilon$. We are able to extend the results in [14] for the case $L=1$ to the case $L\ge 2$ under some smoothness and geometric conditions on subdomains. More specifically, we assume that each subdomain is a bounded $C^{2, 1/2}$ domain, and that there exists $r_0>0$ such that if $x_0\in \partial \Omega ^k \cap \partial \Omega ^m$ for some $1\le k, m \le L$ and $k \ne m$, there exists a coordinate system, obtained from the standard one by translation and rotation, such that

$$\begin{aligned} \begin{aligned} B(x_0, r_0)\cap \Omega ^k&=B(x_0, r_0) \cap \big \{ (x^\prime , x_d)\in {\mathbb {R}}^d: x_d > \psi (x^\prime ) \big \},\\ B(x_0, r_0)\cap \Omega ^m&=B(x_0, r_0) \cap \big \{ (x^\prime , x_d)\in {\mathbb {R}}^d: x_d < \psi (x^\prime ) \big \}, \end{aligned} \end{aligned}$$

(1.12)

where $\psi : {\mathbb {R}}^{d-1} \rightarrow {\mathbb {R}}$ is a $C^{2, 1/2}$ function. Roughly speaking, this means that inside a small ball centered on the interface $\Sigma$, the domain $\Omega$ is divided by $\Sigma$ into exactly two subdomains. In particular, the condition excludes the cases where the interface intersects with each other or with the boundary of $\Omega$.

The following is the main result of the paper. The matrix $W^\ell (y)$ in (1.13)-(1.14) is the 1-periodic matrix associated with the solid obstacle $Y_s^\ell$.

Theorem 1.2

Let $\Omega$ be a bounded $C^{2, 1/2}$ domain and $\Omega _\varepsilon$ be given by (1.4). Assume that the subdomains $\{ \Omega ^\ell \}$ are bounded $C^{2, 1/2}$ domains satisfying the condition (1.12). Let $(u_\varepsilon , P_\varepsilon )$ and $(u_0, P_0)$ be the same as in Theorem 1.1. Then, for $f\in C^{1, 1/2}(\Omega ; {\mathbb {R}}^d)$,

(1.13)

and

$$\begin{aligned} \sum _{\ell =1}^L \Vert \varepsilon \nabla u_\varepsilon -\mu ^{-1} \nabla W^\ell (x/\varepsilon ) (f-\nabla P_0)\Vert _{L^2(\Omega ^\ell )} \le C \sqrt{\varepsilon } \Vert f\Vert _{C^{1, 1/2} (\Omega )}, \end{aligned}$$

(1.14)

where C depends on d, $\mu$, $\Omega$, $\{\Omega ^\ell \}$ and $\{Y_s^\ell \}$.

As we mentioned earlier, the sharp convergence rates in (1.13) and (1.14) were proved in [14] for the case $L=1$. In the case of two porous media with a flat interface, partial results were obtained in [9] for solutions with periodic boundary conditions. Theorem 1.2 is the first result that treats the general case of smooth interfaces.

As in [9], the basic idea in our approach to Theorem 1.2 is to use

$$\begin{aligned} V_\varepsilon (x)=\sum _{\ell =1}^L W^\ell (x/\varepsilon ) (f-\nabla P_0) \chi _{\Omega _\varepsilon ^\ell } \end{aligned}$$

(1.15)

to approximate the solution $u_\varepsilon$ and obtain the error estimates by the energy method. Observe that $V_\varepsilon =0$ on $\Gamma _\varepsilon =\partial \Omega _\varepsilon {\setminus } \partial \Omega$. There are three main issues with this approach: (1) the divergence of $V_\varepsilon$ is not small in $L^2$; (2) $V_\varepsilon$ does not agree with $u_\varepsilon$ on $\partial \Omega$; and (3) $V_\varepsilon$ is not in $H^1(\Omega _\varepsilon ; {\mathbb {R}}^d)$, as it is not continuous across the interface. To overcome these difficulties, we introduce three corresponding correctors: $\Phi _{\varepsilon }^{(1)}$, $\Phi _{\varepsilon }^{(2)}$, and $\Phi _{\varepsilon }^{(3)}$. To correct the divergence of $V_\varepsilon$, we construct $\Phi _\varepsilon ^{(1)} \in H_0^1(\Omega _\varepsilon ; {\mathbb {R}}^d)$ with the property that

$$\begin{aligned} \varepsilon \left\| \nabla \Phi _\varepsilon ^{(1)} \right\| _{L^2(\Omega _\varepsilon ^\ell )} + \left\| \textrm{div} \left( \Phi _\varepsilon ^{(1)} +V_\varepsilon \right) \right\| _{L^2(\Omega _\varepsilon ^\ell )} \le C \sqrt{\varepsilon } \Vert f\Vert _{C^{1, 1/2}(\Omega )} \end{aligned}$$

(1.16)

for $1\le \ell \le L$. The construction of $\Phi _\varepsilon ^{(1)}$ is similar to that in [9, 11, 14]. Next, we correct the boundary data of $V_\varepsilon$ on $\partial \Omega$ by constructing $\Phi _\varepsilon ^{(2)} \in H^1(\Omega _\varepsilon ; {\mathbb {R}}^d)$ such that $\Phi _\varepsilon ^{(2)} + V_\varepsilon =0$ on $\partial \Omega$, $\Phi _\varepsilon ^{(2)} =0$ on $\Gamma _\varepsilon$, and that

$$\begin{aligned} \varepsilon \left\| \nabla \Phi _\varepsilon ^{(2)} \right\| _{L^2(\Omega _\varepsilon )} + \left\| \textrm{div} \left( \Phi _\varepsilon ^{(2)}\right) \right\| _{L^2(\Omega _\varepsilon )} \le C \sqrt{\varepsilon } \Vert f\Vert _{C^{1, 1/2}(\Omega )}. \end{aligned}$$

(1.17)

The construction of $\Phi _\varepsilon ^{(2)}$ is similar to that in [14] for the case $L=1$. The key observation is that the normal component of $V_\varepsilon$ on $\partial \Omega$ can be written in the form

$$\begin{aligned} \varepsilon \nabla _{\tan } \left( \phi (x/\varepsilon )\right) \cdot g, \end{aligned}$$

(1.18)

where $\nabla _{\tan }$ denotes the tangential gradient on $\partial \Omega$. We remark that a similar observation is also used in the proof of Theorem 1.1. Finally, to correct the discontinuity of $V_\varepsilon$ across the interface, we introduce

$$\begin{aligned} \Phi _\varepsilon ^{(3)} =\sum _{\ell =1}^L I_\varepsilon ^\ell (x) (f-\nabla P_0)\chi _{\Omega _\varepsilon ^\ell }, \end{aligned}$$

(1.19)

with the properties that $V+ \Phi _\varepsilon ^{(3)} \in H^1(\Omega _\varepsilon ; {\mathbb {R}}^d)$, $\Phi _\varepsilon ^{(3)} =0$ on $\partial \Omega _\varepsilon$, and that

$$\begin{aligned} \varepsilon \left\| \nabla \Phi _\varepsilon ^{(3)} \right\| _{L^2(\Omega _\varepsilon ^\ell )} + \left\| \textrm{div} \left( \Phi _\varepsilon ^{(3)}\right) \right\| _{L^2(\Omega _\varepsilon ^\ell )} \le C \sqrt{\varepsilon } \Vert f\Vert _{C^{1, 1/2}(\Omega )}. \end{aligned}$$

(1.20)

More specifically, for each $1\le \ell \le L$, the matrix-valued function $I_\varepsilon ^\ell$ is a solution of the Stokes equations in $\Omega _\varepsilon ^\ell$ with $I_\varepsilon ^\ell =0$ on $\partial \Omega _\varepsilon ^\ell {\setminus } \partial \Omega ^\ell$. On each connected component $\Sigma ^k$ of the interface $\Sigma$, the boundary value of $I_\varepsilon ^\ell$ is either 0 or given by

$$\begin{aligned} W_j^- (x/\varepsilon ) -W_j^+ (x/\varepsilon ) -W_i^- (x/\varepsilon ) \left( K_{mj}^- -K_{mj}^+\right) \frac{n_i n_m}{ \langle n K^-, n \rangle }, \end{aligned}$$

(1.21)

where the repeated indices i and m are summed from 1 to d. Here the subdomains $\Omega ^\pm$ are separated by $\Sigma ^k$, and $(W^\pm , K^\pm )$ denote the corresponding 1-periodic matrices for $\Omega ^\pm$ and their averages over Y, respectively. To show $V+\Phi _\varepsilon ^{(3)}$ is continuous across $\Sigma$, we use the fact that $(\nabla _{\tan } P_0)^+= (\nabla _{\tan } P_0)^-$ and

$$\begin{aligned} n \cdot K^+ (f-\nabla P_0)^+=n \cdot K^- (f-\nabla P_0)^-, \end{aligned}$$

(1.22)

where $(v)^\pm$ denote the trace of v taken from $\Omega ^\pm$, respectively. The proof of the estimate (1.20) again relies on the observation that the normal component of (1.21) is of form (1.18).

Theorem 1.2 is proved under the assumption that $\{Y_s^\ell : 1\le \ell \le L\}$ are subdomains of Y with Lipschitz boundaries. The $C^{2, 1/2}$ condition and the geometric condition (1.12) for $\Omega$ and subdomains $\{ \Omega ^\ell \}$ are dictated by the smoothness requirement in its proof for $P_0$ in each subdomain. Note that $P_0$ is a solution of an elliptic equation with piecewise constant coefficients in $\Omega$. Not much is known about the boundary regularity of $P_0$ if the interface intersects with the boundary $\partial \Omega$ or with each other.

The paper is organized as follows. In Sect. 2 we collect several useful estimates that are more or less known. In Sect. 3 we establish the energy estimates for the Dirichlet problem (1.1). Theorem 1.1 is proved in Sect. 4. In Sect. 5 we give the proof of Theorem 1.2, assuming the existence of suitable correctors. Finally, we construct correctors $\Phi _\varepsilon ^{(1)}$, $\Phi _\varepsilon ^{(2)}$, and $\Phi _\varepsilon ^{(3)}$, described above, in the last three sections of the paper. Throughout the paper we will use C to denote constants that may depend on d, $\mu$, $\Omega$, $\{\Omega ^\ell \}$, and $\{Y_s^\ell \}$. Since the viscosity constant $\mu$ is irrelevant in our study, we will assume $\mu =1$ in the rest of the paper.

2 Preliminaries

Let $Y=[-1/2, 1/2]^d$ and $\{Y_s^\ell : 1\le \ell \le L \}$ be a finite number of open subsets of Y with Lipschitz boundaries. We assume that dist$(\partial Y, \partial Y^\ell _s)>0$ and that $Y_f^\ell =Y \setminus \overline{Y_s^\ell }$ is connected. Let

$$\begin{aligned} \omega ^\ell =\bigcup _{z\in {\mathbb {Z}}^d} \left( Y_f^\ell +z\right) \end{aligned}$$

be the periodic repetition of $Y_f^\ell$. For $1\le j \le d$ and $1\le \ell \le L$, let

$$\begin{aligned} \left( W_j^\ell (y), \pi _j^\ell (y)\right) =\left( W_{1j}^\ell (y), \dots , W_{dj}^\ell (y), \pi _j^\ell (y)\right) \in H^1_{\text {loc}} (\omega ^\ell ; {\mathbb {R}}^d) \times L^2_{\text {loc}}(\omega ^\ell ) \end{aligned}$$

be the 1-periodic solution of

$$\begin{aligned} \left\{ \begin{aligned}&-\Delta W_j^\ell + \nabla \pi _j^\ell = e_j \quad \text { in } \omega ^\ell ,\\&\textrm{div} (W_j^\ell ) =0 \quad \text { in } \omega ^\ell ,\\&W_j^\ell =0 \quad \text { on } \partial \omega ^\ell , \end{aligned}\right. \end{aligned}$$

(2.1)

with $\int _{Y^\ell _f} \pi _j^\ell \, \mathrm{{d}}y =0$, where $e_j =(0, \dots , 1, \dots , 0)$ with 1 in the jth place. We extend the $d\times d$ matrix $W^\ell =(W_{ij}^\ell )$ to ${\mathbb {R}}^d$ by zero and define

$$\begin{aligned} K^\ell _{ij} =\int _{Y} W_{ij}^\ell (y)\, \mathrm{{d}}y. \end{aligned}$$

(2.2)

Since

$$\begin{aligned} K_{ij}^\ell =\int _{Y} \nabla W_{ik}^\ell \cdot \nabla W^\ell _{jk}\, \mathrm{{d}}y \end{aligned}$$

(the repeated index k is summed from 1 to d), it follows that $K^\ell =(K^\ell _{ij})$ is symmetric and positive definite.

The existence and uniqueness of solutions to (2.1) can be proved by applying the Lax-Milgram Theorem on the closure of the set,

$$\begin{aligned} \left\{ u\in C^\infty ({\mathbb {R}}^d; {\mathbb {R}}^d): u \text { is 1-periodic, } u=0 \text { in } Y_s^\ell , \text { and } \textrm{div}(u)=0 \text { in } {\mathbb {R}}^d\right\} , \end{aligned}$$

in $H^1(Y; {\mathbb {R}}^d)$. By energy estimates,

$$\begin{aligned} \int _{Y} \left( |\nabla W^\ell |^2 + |W^\ell |^2+ |\pi ^\ell |^2 \right) \mathrm{{d}}y \le C, \end{aligned}$$

(2.3)

where we have also extended $\pi ^\ell$ to ${\mathbb {R}}^d$ by zero. By periodicity this implies that

$$\begin{aligned} \int _D \left( |\nabla W^\ell (x/\varepsilon )|^2 + |W^\ell (x/\varepsilon )|^2 + |\pi ^\ell (x/\varepsilon )|^2 \right) \mathrm{{d}}x \le C, \end{aligned}$$

(2.4)

where D is a bounded domain and C depends on diam(D).

Lemma 2.1

Let D be a bounded Lipschitz domain in ${\mathbb {R}}^d$. Then

$$\begin{aligned} \int _{\partial D } \left( |\nabla W^\ell (x/\varepsilon )|^2 + |W^\ell (x/\varepsilon )|^2 + |\pi ^\ell (x/\varepsilon )|^2 \right) \mathrm{{d}}\sigma \le C, \end{aligned}$$

(2.5)

where C depends on D.

Proof

If $Y_s^\ell$ is of $C^{1, \alpha }$, the inequality above follows directly from the fact that $\nabla W^\ell$ and $\pi ^\ell$ are bounded in Y. To treat the case where $\partial Y_s^\ell$ is merely Lipschitz, by periodicity, we may assume that $\varepsilon =1$ and D is a subdomain of Y. Note that the bound for the integral of $|W^\ell |^2$ on $\partial D$ follows from (2.3). Indeed, if D is a subdomain of Y with Lipschitz boundary,

$$\begin{aligned} \int _{\partial D} |W^\ell |^2\, \mathrm{{d}}\sigma \le C \int _{D} \left( |\nabla W^\ell |^2 + |W^\ell |^2 \right) \mathrm{{d}}y. \end{aligned}$$

The estimates for $\nabla W^\ell$ and $\pi ^\ell$ are a bit more involved. By using the fundamental solutions for the Stokes equations in ${\mathbb {R}}^d$, we may reduce the problem to the estimate

$$\begin{aligned} \Vert \nabla u \Vert _{L^2(\partial D)} + \Vert p \Vert _{L^2(\partial D)} \le C \left\{ \Vert \nabla u \Vert _{L^2(\widetilde{Y}\setminus Y_s^\ell )} + \Vert p \Vert _{L^2(\widetilde{Y}\setminus Y_s^\ell )} + \Vert h \Vert _{H^1(\partial Y_s^\ell )} \right\} , \end{aligned}$$

for solutions of the Stokes equations,

$$\begin{aligned} \left\{ \begin{aligned}&-\Delta u+\nabla p =0 \quad \text { in } \widetilde{Y} \setminus \overline{Y_s^\ell },\\&\textrm{div}(u) =0 \quad \text { in } \widetilde{Y}\setminus \overline{Y_s^\ell },\\&u = h \quad \text { on } \partial Y_s^\ell , \end{aligned}\right. \end{aligned}$$

where $h \in H^1(\partial Y_s^\ell ; {\mathbb {R}}^d)$ and $\widetilde{Y}=(1+c)Y$. The desired estimates follow from the interior estimates as well as the nontangential-maximal-function estimate,

$$\begin{aligned} \Vert (\nabla u)^*\Vert _{L^2(\partial Y_s^\ell )} + \Vert (p)^* \Vert _{L^2(\partial Y_s^\ell )} \le C \left\{ \Vert h \Vert _{H^1(\partial Y_s^\ell )} + \Vert u\Vert _{L^2(\widetilde{Y}\setminus Y_s^\ell )} + \Vert p\Vert _{L^2(\widetilde{Y}\setminus Y_s^\ell )}\right\} , \end{aligned}$$

(2.6)

where the nontangential maximal function $(v)^*$ is defined by

$$\begin{aligned} (v)^*(x) =\sup \left\{ |v(y)|: \ y\in Y \setminus Y_s^\ell \text { and } |y-x|< C_0\, \textrm{dist} \left( y, \partial Y_s^\ell \right) \right\} \end{aligned}$$

for $x\in \partial Y_s^\ell$. The estimate (2.6) is a consequence of the nontangential-maximal-function estimates, established in [7], for solutions of the Dirichlet problem for the Stokes equations in a bounded Lipschitz domain. $\square$

Lemma 2.2

Fix $1\le j \le d$ and $1\le \ell \le L$. There exist 1-periodic functions $\phi _{kij}^\ell (y)$, $i, k=1, 2, \dots , d$, such that $\phi _{kij}^\ell \in H^1(Y)$, $\int _Y \phi _{kij}^\ell \, \mathrm{{d}}y=0$,

$$\begin{aligned} \frac{\partial }{\partial y_k} \left( \phi _{kij}^\ell \right) = W^\ell _{ij} -K^\ell _{ij} \quad \text { and } \quad \phi _{kij}^\ell = -\phi _{ikj}^\ell , \end{aligned}$$

(2.7)

where the repeated index k is summed from 1 to d. Moreover,

$$\begin{aligned} \int _{\partial D} \left| \phi ^\ell _{kij} (x/\varepsilon )\right| ^2\, \mathrm{{d}}\sigma \le C, \end{aligned}$$

(2.8)

where D is a bounded Lipschitz domain in ${\mathbb {R}}^d$ and C depends on D.

Proof

See [14, Lemma 5.3] for the proof of (2.7). Indeed, $\phi _{kij}^\ell$ is given by

$$\begin{aligned} \phi _{kij}^\ell = \frac{\partial h_{ij}^\ell }{\partial y_k} -\frac{\partial h_{kj}^\ell }{\partial y_i}, \end{aligned}$$

where $h_{ij}^\ell$ satisfies

$$\begin{aligned} \left\{ \begin{aligned}&\Delta h_{ij}^\ell =W_{ij}^\ell -K_{ij}^\ell \quad \text { in } Y,\\&h_{ij}^\ell \text { is 1-periodic.} \end{aligned}\right. \end{aligned}$$

The estimate (2.8) follows from the observation,

$$\begin{aligned} \Vert \nabla \phi _{kij}^\ell \Vert _{L^2(Y)} + \Vert \phi _{kij}^\ell \Vert _{L^2(Y)}&\le C \Vert \nabla ^2 h_{ij}^\ell \Vert _{L^2(Y)} + C \Vert \nabla ^2 h_{kj}^\ell \Vert _{L^2(Y)}\\&\le C \Vert W^\ell \Vert _{L^2(Y)} \le C. \end{aligned}$$

$\square$

Let $\Omega$ be a bounded Lipschitz domain in ${\mathbb {R}}^d$ and $\{\Omega ^\ell : 1\le \ell \le L\}$ be disjoint subdomains of $\Omega$, each with Lipschitz boundary, and satisfying the condition,

$$\begin{aligned} \overline{\Omega } =\cup _{\ell =1}^L \overline{\Omega ^\ell }. \end{aligned}$$

(2.9)

Define

$$\begin{aligned} K =\sum _{\ell =1}^L K^\ell \chi _{\Omega ^\ell }, \end{aligned}$$

(2.10)

where $K^\ell$ is given by (2.2) and $\chi _{\Omega ^\ell }$ denotes the characteristic function of $\Omega ^\ell$.

Lemma 2.3

Let $f\in L^2(\Omega ; {\mathbb {R}}^d)$. Then there exists $P_0 \in H^1(\Omega )$, unique up to constants, such that

$$\begin{aligned} \left\{ \begin{aligned}&\textrm{div} \left( K (f -\nabla P_0)\right) =0 \quad \text { in } \Omega ,\\&n \cdot K (f-\nabla P_0) =0 \quad \text { on } \partial \Omega , \end{aligned}\right. \end{aligned}$$

(2.11)

in the sense that

$$\begin{aligned} \int _\Omega K(f-\nabla P_0) \cdot \nabla \varphi \, \mathrm{{d}}x =0 \end{aligned}$$

(2.12)

for any $\varphi \in H^1(\Omega )$.

Proof

This is standard since the coefficient matrix K is positive-definite in each subdomain $\Omega ^\ell$ and thus in $\Omega$. $\square$

For each $1\le \ell \le L$ and $0< \varepsilon <1$, let $\Omega ^\ell _\varepsilon$ be the perforated domain defined by (1.3), using $Y_s^\ell$. Let $\Omega _\varepsilon$ be given by (1.4). Note that

$$\begin{aligned} \partial \Omega _\varepsilon =\partial \Omega \cup \Gamma _\varepsilon , \end{aligned}$$

(2.13)

where $\Gamma _\varepsilon =\cup _{\ell =1}^L {\Gamma _\varepsilon ^\ell }$ and $\Gamma _\varepsilon ^\ell$ consists of the boundaries of holes $\varepsilon (Y_s^\ell +z)$ that are removed from $\Omega ^\ell$.

Lemma 2.4

Let $u \in H^1(\Omega _\varepsilon )$ with $u=0$ on $\Gamma _\varepsilon$. Assume $\Gamma ^\ell _\varepsilon \ne \emptyset$ for all $1\le \ell \le L$. Then

$$\begin{aligned} \Vert u \Vert _{L^2(\Omega _\varepsilon )} \le C \varepsilon \Vert \nabla u_\varepsilon \Vert _{L^2(\Omega _\varepsilon )}. \end{aligned}$$

(2.14)

Proof

It follows from Lemma 2.2 in [14] that for $1 \le \ell \le L$,

$$\begin{aligned} \Vert u\Vert ^2_{L^2(\Omega _\varepsilon ^\ell )} \le C \varepsilon ^2 \Vert \nabla u \Vert ^2_{L^2(\Omega _\varepsilon ^\ell )}, \end{aligned}$$

which yields (2.14) by summation. Note that we do not assume $u=0$ on $\partial \Omega ^\ell$. $\square$

From now on we will assume that $\varepsilon >0$ is sufficiently small so that $\Gamma _\varepsilon ^\ell \ne \emptyset$ for all $1\le \ell \le L$. The main results in this paper are only relevant for small $\varepsilon$.

Lemma 2.5

Let $\Omega$ be a bounded Lipschitz domain and $\Omega _\varepsilon$ be given by (1.4). There exists a bounded linear operator,

$$\begin{aligned} R_\varepsilon : H^1(\Omega ; {\mathbb {R}}^d) \rightarrow H^1\left( \Omega _\varepsilon ; {\mathbb {R}}^d\right) , \end{aligned}$$

(2.15)

such that

$$\begin{aligned} \left\{ \begin{aligned}&R_\varepsilon (u)=0 \quad \text { on } \Gamma _\varepsilon \quad \text { and } \quad R_\varepsilon (u)= u \quad \text { on } \partial \Omega ,\\&R_\varepsilon (u) \in H_0^1(\Omega _\varepsilon ; {\mathbb {R}}^d) \quad \text { if } \ u\in H_0^1(\Omega ; {\mathbb {R}}^d),\\&R_\varepsilon (u)=u \quad \text { in } \Omega \quad \text { if } \ u=0 \quad \text { on } \Gamma _\varepsilon ,\\&\textrm{div} (R_\varepsilon (u))=\textrm{div}(u) \quad \text { in } \Omega _\varepsilon \ \text { if }\,\, \textrm{div} (u)=0 \quad \text { in } \Omega \setminus \Omega _\varepsilon , \end{aligned}\right. \end{aligned}$$

(2.16)

and

$$\begin{aligned} \varepsilon \Vert \nabla R_\varepsilon (u)\Vert _{L^2(\Omega _\varepsilon )} + \Vert R_\varepsilon (u)\Vert _{L^2(\Omega _\varepsilon )} \le C \left\{ \varepsilon \Vert \nabla u \Vert _{L^2(\Omega )} + \Vert u \Vert _{L^2(\Omega )} \right\} . \end{aligned}$$

(2.17)

Moreover,

$$\begin{aligned} \Vert \textrm{div} (R_\varepsilon (u))\Vert _{L^2(\Omega _\varepsilon )} \le C \Vert \textrm{div}(u)\Vert _{L^2(\Omega )}. \end{aligned}$$

(2.18)

Proof

A proof for the case $L=1$, which is similar to that of a lemma due to Tartar (in an appendix of [13]), may be found in [14, Lemma 2.3]. Also see [1, 10]. The same proof works equally well for the case $L\ge 2$. Indeed, let $u\in H^1(\Omega ; {\mathbb {R}}^d)$. For each $\varepsilon (Y+z)\subset \Omega ^\ell$ with $1\le \ell \le L$ and $z\in {\mathbb {Z}}^d$, we define $R_\varepsilon (u)$ on $\varepsilon (Y_f^\ell +z)$ by the Dirichlet problem,

$$\begin{aligned} \left\{ \begin{aligned}&-\varepsilon ^2 \Delta R_\varepsilon (u) +\nabla q = -\varepsilon ^2 \Delta u \quad \text { in } \varepsilon \left( Y_f^\ell +z\right) ,\\&\textrm{div}(R_\varepsilon (u)) = \textrm{div} (u) +\frac{1}{|\varepsilon (Y_f^\ell +z)|} \int _{\varepsilon (Y_s^\ell +z)} \textrm{div} (u)\, \mathrm{{d}}x \quad \text { in } \varepsilon \left( Y_f^\ell +z\right) ,\\&R_\varepsilon (u) =0 \quad \text { on } \partial \left( \varepsilon (Y_s^\ell +z)\right) ,\\&R_\varepsilon (u) = u \quad \text { on } \partial \left( \varepsilon (Y+z)\right) . \end{aligned}\right. \end{aligned}$$

(2.19)

If $x\in \Omega _\varepsilon$ and $x\notin \varepsilon (Y_f +z)$ for any $\varepsilon (Y+z) \subset \Omega ^\ell$, we let $R_\varepsilon (u)=u$. $\square$

Lemma 2.6

Let $f\in L^2(\Omega _\varepsilon )$ with $\int _{\Omega _\varepsilon } f \, \mathrm{{d}}x =0$. Then there exists $u_\varepsilon \in H_0^1(\Omega _\varepsilon ; {\mathbb {R}}^d)$ such that $\textrm{div} (u_\varepsilon )=f$ in $\Omega _\varepsilon$ and

$$\begin{aligned} \Vert u_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} + \varepsilon \Vert \nabla u_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} \le C \Vert f \Vert _{L^2(\Omega _\varepsilon )}. \end{aligned}$$

(2.20)

Proof

Let F be the zero extension of f to $\Omega$. Since $F\in L^2(\Omega )$ and $\int _\Omega F\, \mathrm{{d}}x =0$, there exists $u\in H_0^1(\Omega ; {\mathbb {R}}^d)$ such that div$(u)=F$ in $\Omega$ and $\Vert u \Vert _{L^2(\Omega )} + \Vert \nabla u \Vert _{L^2(\Omega )} \le C \Vert F \Vert _{L^2(\Omega )}$. Let $u_\varepsilon =R_\varepsilon (u)$. Then $u_\varepsilon \in H_0^1(\Omega _\varepsilon , {\mathbb {R}}^d)$, and by (2.17),

$$\begin{aligned} \varepsilon \Vert \nabla u_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} +\Vert u_\varepsilon \Vert _{L^2(\Omega _\varepsilon )}&\le C \left\{ \varepsilon \Vert \nabla u\Vert _{L^2(\Omega )} + \Vert u \Vert _{L^2(\Omega )} \right\} \\&\le C \Vert f \Vert _{L^2(\Omega _\varepsilon )}. \end{aligned}$$

Since div$(u)=F=0$ in $\Omega {\setminus } \Omega _\varepsilon$, by the last line in (2.16), we obtain div$(u_\varepsilon )=\textrm{div} (u)=f$ in $\Omega _\varepsilon$. $\square$

For $p\in L^2(\Omega _\varepsilon )$, as in [10], we define an extension P of p to $L^2(\Omega )$ by

(2.21)

Lemma 2.7

Let $p\in L^2(\Omega _\varepsilon )$ and P be its extension given by (2.21). Then

$$\begin{aligned} \langle \nabla p, R_\varepsilon (u) \rangle _{H^{-1}(\Omega _\varepsilon ) \times H_0^1(\Omega _\varepsilon )} =\langle \nabla P, u \rangle _{H^{-1}(\Omega ) \times H_0^1(\Omega )}, \end{aligned}$$

(2.22)

where $u\in H_0^1(\Omega ; {\mathbb {R}}^d)$ and $R_\varepsilon (u)$ is given by Lemma 2.5.

Proof

We use an argument found in [1, 2, 10]. Note that if $u \in H_0^1(\Omega ; {\mathbb {R}}^d)$, we have $R_\varepsilon (u) \in H_0^1(\Omega _\varepsilon ; {\mathbb {R}}^d)$ and

$$\begin{aligned} |\langle \nabla p, R_\varepsilon (u) \rangle _{H^{-1} (\Omega _\varepsilon ) \times H^1_0(\Omega _\varepsilon )} |&= |\langle p, \textrm{div} (R_\varepsilon (u) ) \rangle _{L^2(\Omega _\varepsilon )\times L^2(\Omega _\varepsilon )} |\\&\le \Vert p \Vert _{L^2(\Omega _\varepsilon )} \Vert \textrm{div} (R_\varepsilon (u)) \Vert _{L^2(\Omega _\varepsilon )}\\&\le C \Vert p \Vert _{L^2(\Omega _\varepsilon )}\Vert \textrm{div}(u) \Vert _{L^2(\Omega )}, \end{aligned}$$

where we have used the estimate (2.18) for the last inequality. Thus there exists $\Lambda \in H^{-1} (\Omega ; {\mathbb {R}}^d)$ such that

$$\begin{aligned} \langle \nabla p, R_\varepsilon (u) \rangle _{H^{-1}(\Omega _\varepsilon ) \times H_0^1(\Omega _\varepsilon )} =\langle \Lambda , u \rangle _{H^{-1}(\Omega ) \times H_0^1(\Omega )} \end{aligned}$$

for any $u\in H_0^1(\Omega ; {\mathbb {R}}^d)$. Since $\langle \Lambda , u\rangle =0$ if div$(u)=0$ in $\Omega$, it follows that $\Lambda =\nabla Q$ for some $Q\in L^2(\Omega )$.

Next, using the fact that $R_\varepsilon (u)=u$ for $u\in H_0^1(\Omega _\varepsilon ; {\mathbb {R}}^d)$, we obtain

$$\begin{aligned} \langle \nabla p-\nabla Q, u \rangle _{H^{-1}(\Omega _\varepsilon ) \times H_0^1(\Omega _\varepsilon )} =0 \end{aligned}$$

for any $u \in H_0^1(\Omega _\varepsilon ; {\mathbb {R}}^d)$. This implies that $p-Q$ is constant in $\Omega _\varepsilon$. Since Q is only determined up to a constant, we may assume that $Q=p$ in $\Omega _\varepsilon$. Moreover, we note that if $\varepsilon (Y +z)\subset \Omega ^\ell$ for some $1\le \ell \le L$ and $z\in {\mathbb {Z}}^d$, and $u \in C_0^1(\varepsilon (Y_s^\ell +z), {\mathbb {R}}^d)$, then $R_\varepsilon (u)=0$ in $\Omega _\varepsilon$. It follows that $\nabla Q=0$ in $\varepsilon (Y_s^\ell +z)$. Thus Q is constant in each $\varepsilon (Y_s^\ell +z)$.

Finally, for any $u \in C_0^1(\varepsilon (Y+z); {\mathbb {R}}^d)$ with $\varepsilon (Y+z) \subset \Omega ^\ell$, we have

$$\begin{aligned} R_\varepsilon (u) \in H_0^1 \left( \varepsilon (Y_f^\ell +z); {\mathbb {R}}^d\right) , \end{aligned}$$

and by (2.19),

$$\begin{aligned} \textrm{div} (R_\varepsilon (u)) =\textrm{div} (u) +\frac{1}{\left| \varepsilon \left( Y_f^\ell +z\right) \right| } \int _{\varepsilon (Y_s^\ell +z)} \textrm{div} (u) \, \mathrm{{d}}x \end{aligned}$$

in $\varepsilon (Y_f^\ell +z)$. This, together with

$$\begin{aligned} \int _{\varepsilon (Y_f^\ell +z)} p \cdot \textrm{div} (R_\varepsilon (u))\, \mathrm{{d}}x =\int _{\varepsilon (Y+z)} Q \cdot \textrm{div} (u)\, \mathrm{{d}}x \end{aligned}$$

and the fact that $Q=p$ in $\Omega _\varepsilon$, yields

Consequently,

As a result, we have proved that $Q=P$, an extension of p given by (2.21). $\square$

3 Energy Estimates

Let $\Omega _\varepsilon$ be given by (1.4). Recall that $\partial \Omega _\varepsilon =\partial \Omega \cup \Gamma _\varepsilon$, where $\Gamma _\varepsilon$ consists of the boundaries of the holes of size $\varepsilon$ that are removed from $\Omega$. In this section we establish the energy estimates for the Dirichlet problem,

$$\begin{aligned} \left\{ \begin{aligned}&-\varepsilon ^2 \Delta u_\varepsilon +\nabla p_\varepsilon =f +\varepsilon \, \textrm{div} (F) \quad \text { in } \Omega _\varepsilon ,\\&\textrm{div} (u_\varepsilon ) = g \quad \text { in } \Omega _\varepsilon ,\\&u_\varepsilon =0 \quad \text { on } \Gamma _\varepsilon ,\\&u_\varepsilon =h \quad \text { on } \partial \Omega , \end{aligned}\right. \end{aligned}$$

(3.1)

where (g, h) satisfies the compatibility condition,

$$\begin{aligned} \int _{\Omega _\varepsilon }g\, \mathrm{{d}}x =\int _{\partial \Omega } h \cdot n \, \mathrm{{d}}\sigma . \end{aligned}$$

(3.2)

Throughout this section we assume that $\Omega$, $\Omega ^\ell$ and $Y_s^\ell$ for $1\le \ell \le L$ are domains with Lipschitz boundaries. We use $L^2_0(\Omega _\varepsilon )$ to denote the subspace of functions in $L^2(\Omega _\varepsilon )$ with mean value zero.

Theorem 3.1

Let $f\in L^2(\Omega _\varepsilon ; {\mathbb {R}}^d)$ and $F \in L^2(\Omega _\varepsilon ; {\mathbb {R}}^{d\times d})$. Let $g \in L^2(\Omega _\varepsilon )$ and $h\in H^{1/2} (\partial \Omega ; {\mathbb {R}}^d)$ satisfy the condition (3.2). Let $(u_\varepsilon , p_\varepsilon )\in H^1(\Omega _\varepsilon ; {\mathbb {R}}^d) \times L^2_0(\Omega _\varepsilon )$ be a weak solution of (3.1). Then

$$\begin{aligned}&\varepsilon \Vert \nabla u_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} + \Vert u_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} + \Vert p_\varepsilon \Vert _{L^2(\Omega _\varepsilon )}\nonumber \\&\quad \le C \Big \{ \Vert f\Vert _{L^2(\Omega _\varepsilon )} + \Vert F \Vert _{L^2(\Omega _\varepsilon )} +\Vert g \Vert _{L^2(\Omega _\varepsilon )} + \Vert H \Vert _{L^2(\Omega )}\nonumber \\&\qquad +\Vert \textrm{div} (H) \Vert _{L^2(\Omega )} + \varepsilon \Vert \nabla H \Vert _{L^2(\Omega )} \Big \}, \end{aligned}$$

(3.3)

where H is any function in $H^1(\Omega ; {\mathbb {R}}^d)$ with the property $H=h$ on $\partial \Omega$.

Proof

This theorem was proved in [14, Sect. 3] for the case $L=1$. The proof for the case $L\ge 2$ is similar. We provide a proof here for the reader’s convenience.

Step 1. We show that

$$\begin{aligned} \Vert p_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} \le C \left\{ \varepsilon \Vert \nabla u_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} + \Vert f\Vert _{L^2(\Omega _\varepsilon )} + \Vert F \Vert _{L^2(\Omega _\varepsilon )} \right\} . \end{aligned}$$

(3.4)

To this end we use Lemma 2.6 to find $v_\varepsilon \in H_0^1(\Omega _\varepsilon ; {\mathbb {R}}^d)$ such that $\textrm{div} (v_\varepsilon )=p_\varepsilon$ in $\Omega _\varepsilon$ and

$$\begin{aligned} \varepsilon \Vert \nabla v_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} + \Vert v_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} \le C \Vert p_\varepsilon \Vert _{L^2(\Omega _\varepsilon )}. \end{aligned}$$

(3.5)

By using $v_\varepsilon$ as a test function we obtain

$$\begin{aligned} \Vert p_\varepsilon \Vert _{L^2(\Omega _\varepsilon )}^2&\le \varepsilon ^2 \Vert \nabla u_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} \Vert \nabla v_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} + \Vert f\Vert _{L^2(\Omega _\varepsilon )} \Vert v_\varepsilon \Vert _{L^2(\Omega _\varepsilon )}\\&\quad + \varepsilon \Vert F \Vert _{L^2(\Omega _\varepsilon )} \Vert \nabla v_\varepsilon \Vert _{L^2(\Omega _\varepsilon )}\\&\le C \Vert p_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} \left\{ \varepsilon \Vert \nabla u_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} + \Vert f\Vert _{L^2(\Omega _\varepsilon )} + \Vert F \Vert _{L^2(\Omega _\varepsilon )} \right\} , \end{aligned}$$

where we have used (3.5) for the last inequality. This yields (3.4).

Step 2. We prove (3.3) in the case $h=0$. In this case we may use $u_\varepsilon \in H_0^1(\Omega _\varepsilon ; {\mathbb {R}}^d)$ as a test function to obtain

$$\begin{aligned} \varepsilon ^2 \Vert \nabla u_\varepsilon \Vert ^2_{L^2(\Omega _\varepsilon )}&\le \Vert p_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} \Vert g\Vert _{L^2(\Omega _\varepsilon )} + \Vert f\Vert _{L^2(\Omega _\varepsilon )} \Vert u_\varepsilon \Vert _{L^2(\Omega _\varepsilon )}\\&\quad + \varepsilon \Vert F \Vert _{L^2(\Omega _\varepsilon )} \Vert \nabla u_\varepsilon \Vert _{L^2(\Omega _\varepsilon )}. \end{aligned}$$

By using the Cauchy inequality as well as the estimate $\Vert u_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} \le C \varepsilon \Vert \nabla u_\varepsilon \Vert _{L^2(\Omega _\varepsilon )}$, we deduce that

$$\begin{aligned} \Vert u_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} + \varepsilon \Vert \nabla u_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} \le C \left\{ \Vert p_\varepsilon \Vert ^{1/2} _{L^2(\Omega _\varepsilon )} \Vert g\Vert ^{1/2}_{L^2(\Omega _\varepsilon )} + \Vert f\Vert _{L^2(\Omega _\varepsilon )} + \Vert F \Vert _{L^2(\Omega _\varepsilon )} \right\} . \end{aligned}$$

This, together with (3.4), gives (3.3) for the case $h=0$.

Step 3. We consider the general case $h \in H^{1/2}(\partial \Omega ; {\mathbb {R}}^d)$. Let H be a function in $H^1(\Omega ; {\mathbb {R}}^d)$ such that $H=h$ on $\partial \Omega$. Let $w_\varepsilon = u_\varepsilon -R_\varepsilon (H)$, where $R_\varepsilon (H)$ is given by Lemma 2.5. Then $w_\varepsilon \in H_0^1(\Omega _\varepsilon ; {\mathbb {R}}^d)$ and

$$\begin{aligned} \left\{ \begin{aligned}&-\varepsilon ^2 \Delta w_\varepsilon +\nabla p_\varepsilon = f+\varepsilon \, \textrm{div}(F) +\varepsilon ^2 \Delta R_\varepsilon (H),\\&\textrm{div} (w_\varepsilon ) =g-\textrm{div} (R_\varepsilon (H)), \end{aligned}\right. \end{aligned}$$

in $\Omega _\varepsilon$. By Step 2 we obtain

$$\begin{aligned}&\varepsilon \Vert \nabla w_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} + \Vert w_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} + \Vert p_\varepsilon \Vert _{L^2(\Omega _\varepsilon )}\\&\quad \le C\Big \{\Vert f\Vert _{L^2(\Omega _\varepsilon )} + \Vert F \Vert _{L^2(\Omega _\varepsilon )} + \varepsilon \Vert \nabla R_\varepsilon (H)\Vert _{L^2(\Omega _\varepsilon )} + \Vert g \Vert _{L^2(\Omega _\varepsilon )}\\&\qquad + \Vert \textrm{div} (R_\varepsilon (H))\Vert _{L^2(\Omega _\varepsilon )} \Big \}. \end{aligned}$$

It follows that

$$\begin{aligned}&\varepsilon \Vert \nabla u_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} + \Vert u_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} + \Vert p_\varepsilon \Vert _{L^2(\Omega _\varepsilon )}\\&\quad \le C \Big \{\Vert f\Vert _{L^2(\Omega _\varepsilon )} + \Vert F \Vert _{L^2(\Omega _\varepsilon )} + \Vert g \Vert _{L^2(\Omega _\varepsilon )} \\&\qquad + \varepsilon \Vert \nabla R_\varepsilon (H)\Vert _{L^2(\Omega _\varepsilon )} +\Vert R_\varepsilon (H)\Vert _{L^2(\Omega _\varepsilon )} + \Vert \textrm{div} (R_\varepsilon (H))\Vert _{L^2(\Omega _\varepsilon )}\Big \}\\&\quad \le C \Big \{\Vert f\Vert _{L^2(\Omega _\varepsilon )} + \Vert F \Vert _{L^2(\Omega _\varepsilon )} +\Vert g \Vert _{L^2(\Omega _\varepsilon )} + \varepsilon \Vert \nabla H \Vert _{L^2(\Omega )}\\&\qquad +\Vert H \Vert _{L^2(\Omega )} + \Vert \textrm{div} (H)\Vert _{L^2(\Omega )}\Big \}, \end{aligned}$$

where we have used estimates (2.17) and (2.18) for the last inequality. $\square$

Corollary 3.2

Let $(u_\varepsilon , p_\varepsilon )$ be the same as in Theorem 3.1. Then

$$\begin{aligned}&\varepsilon \Vert \nabla u_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} + \Vert u_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} + \Vert p_\varepsilon \Vert _{L^2(\Omega _\varepsilon )}\nonumber \\&\quad \le C \Big \{ \Vert f\Vert _{L^2(\Omega _\varepsilon )} + \Vert F \Vert _{L^2(\Omega _\varepsilon )} + \Vert g \Vert _{L^2(\Omega _\varepsilon )} + \Vert h \Vert _{L^2(\partial \Omega )} + \varepsilon \Vert h \Vert _{H^{1/2} (\partial \Omega )} \Big \}. \end{aligned}$$

(3.6)

Proof

For $h \in H^{1/2} (\partial \Omega ; {\mathbb {R}}^d)$, let H be the weak solution in $H^1(\Omega ; {\mathbb {R}}^d)$ of the Dirichlet problem,

$$\begin{aligned} \left\{ \begin{aligned}&-\Delta H +\nabla q =0 \quad \text { in } \Omega ,\\&\textrm{div} (H) =\gamma \quad \text { in } \Omega ,\\&u =h&\quad \text { on } \partial \Omega , \end{aligned}\right. \end{aligned}$$

where the constant

$$\begin{aligned} \gamma =\frac{1}{|\Omega |} \int _{\partial \Omega } h \cdot n \, \mathrm{{d}}\sigma \end{aligned}$$

is chosen so that the compatibility condition (3.2) is satisfied. Note that

$$\begin{aligned} \Vert \textrm{div}(H)\Vert _{L^2(\Omega )} =C |\gamma |\le C \Vert h\Vert _{L^2(\partial \Omega )}, \end{aligned}$$

and by the standard energy estimates, $\Vert \nabla H \Vert _{L^2(\Omega )} \le C \Vert h \Vert _{H^{1/2}(\partial \Omega )}.$ In view of (3.3) we only need to show that

$$\begin{aligned} \Vert H \Vert _{L^2(\Omega )} \le C \Vert h\Vert _{L^2(\partial \Omega )}. \end{aligned}$$

(3.7)

To this end, let

$$\begin{aligned} H_1=H-\gamma (x-x_0)/d, \end{aligned}$$

where $x_0\in \Omega$. Since $-\Delta H_1 +\nabla q=0$ and div$(H_1)=0$ in $\Omega$, it follows from [7] that

$$\begin{aligned} \Vert H_1\Vert _{L^2(\Omega )}&\le C \Vert (H_1)^* \Vert _{L^2(\partial \Omega )}\\&\le C \Vert H_1\Vert _{L^2(\partial \Omega )} \le C \Vert h\Vert _{L^2(\partial \Omega )}, \end{aligned}$$

where $(H_1)^*$ denotes the nontangential maximal function of $H_1$. As a result, we obtain

$$\begin{aligned} \Vert H\Vert _{L^2(\Omega )}&\le \Vert H_1 \Vert _{L^2(\Omega )} + C |\gamma | \\&\le C \Vert h\Vert _{L^2(\partial \Omega )}, \end{aligned}$$

which completes the proof. $\square$

Corollary 3.3

Let $(u_\varepsilon , p_\varepsilon )$ be the same as in Theorem 3.1. Let $P_\varepsilon$ be the extension of $p_\varepsilon$, defined by (2.21). Then

$$\begin{aligned} \Vert P_\varepsilon \Vert _{L^2(\Omega )} \le C \left\{ \Vert f\Vert _{L^2(\Omega _\varepsilon )} + \Vert F \Vert _{L^2(\Omega _\varepsilon )} + \Vert g\Vert _{L^2(\Omega _\varepsilon )} + \Vert h \Vert _{L^2(\partial \Omega )} + \varepsilon \Vert h\Vert _{H^{1/2} (\partial \Omega )}\right\} . \end{aligned}$$

(3.8)

Proof

By the definition of $P_\varepsilon$, we have

which, together with (3.6), gives (3.8). $\square$

4 Homogenization and Proof of Theorem 1.1

Let $f\in L^2(\Omega ; {\mathbb {R}}^d)$ and $h\in H^{1/2}(\partial \Omega ; {\mathbb {R}}^d)$ with $\int _{\partial \Omega } h\cdot n\, \mathrm{{d}}\sigma =0$, where n denotes the outward unit normal to $\partial \Omega$. Consider the Dirichlet problem,

$$\begin{aligned} \left\{ \begin{aligned}&-\varepsilon ^2 \Delta u_\varepsilon +\nabla p_\varepsilon =f \quad \text { in } \Omega _\varepsilon ,\\&\textrm{div} (u_\varepsilon ) =0 \quad \text { in } \Omega _\varepsilon ,\\&u_\varepsilon =0 \quad \text { on } \Gamma _\varepsilon ,\\&u_\varepsilon =h \quad \text { on } \partial \Omega , \end{aligned}\right. \end{aligned}$$

(4.1)

where $\Omega _\varepsilon$ is given by (1.4) and $\partial \Omega _\varepsilon =\partial \Omega \cup \Gamma _\varepsilon$. Throughout the section we assume that $\Omega$, $\Omega ^\ell$ and $Y_s^\ell$ for $1\le \ell \le L$, are domains with Lipschitz boundaries. As before, we extend $u_\varepsilon$ to $\Omega$ by zero and still denote the extension by $u_\varepsilon$. We use $P_\varepsilon$ to denote the extension of $p_\varepsilon$ to $\Omega$, given by (2.21). The goal of this section is to prove the following theorem, which contains Theorem 1.1 as a special case $h=0$.

Theorem 4.1

Let $f\in L^2(\Omega ; {\mathbb {R}}^d)$ and $h \in H^{1/2}(\partial \Omega ; {\mathbb {R}}^d)$ with $\int _{\partial \Omega } h \cdot n \, \mathrm{{d}}\sigma =0$. Let $(u_\varepsilon , p_\varepsilon )\in H^1(\Omega _\varepsilon ; {\mathbb {R}}^d) \times L_0^2(\Omega _\varepsilon )$ be the weak solution of (4.1). Let $(u_\varepsilon , P_\varepsilon )$ be the extension of $(u_\varepsilon , p_\varepsilon )$. Then $u_\varepsilon \rightarrow u_0$ weakly in $L^2(\Omega ; {\mathbb {R}}^d)$ and strongly in $L^2(\Omega )$, as $\varepsilon \rightarrow 0$, where $P_0 \in H^1(\Omega )$, $\int _\Omega P_0\, \mathrm{{d}}x =0$, $(u_0, P_0)$ is governed by a Darcy law,

$$\begin{aligned} \left\{ \begin{aligned}&u_0 = K (f-\nabla P_0) \quad \text { in } \Omega ,\\&\textrm{div} (u_0) =0 \quad \text { in } \Omega ,\\&u_0\cdot n = h\cdot n \quad \text { on } \partial \Omega , \end{aligned}\right. \end{aligned}$$

(4.2)

with the permeability matrix K given by (1.10).

We begin with the strong convergence of $P_\varepsilon$.

Lemma 4.2

Let $(u_{\varepsilon _k}, p_{\varepsilon _k})$ be a weak solution of (4.1) with $\varepsilon =\varepsilon _k$. Suppose that as $\varepsilon _k \rightarrow 0$, $P_{\varepsilon _k} \rightarrow P$ weakly in $L^2(\Omega )$ for some $P\in L^2(\Omega )$. Then $P_{\varepsilon _k} \rightarrow P$ strongly in $L^2(\Omega )$.

Proof

The proof is similar to that for the classical case $L=1$ (see e.g. [4]). One argues by contradiction. Suppose that $P_{\varepsilon _k}$ does not converge strongly to P in $L^2(\Omega )$. Since

and $\int _\Omega P_{\varepsilon _k} \, \mathrm{{d}}x \rightarrow \int _\Omega P\, \mathrm{{d}}x$, it follows that $\nabla P_{\varepsilon _k}$ does not converge to $\nabla P$ strongly in $H^{-1}(\Omega ; {\mathbb {R}}^d)$. By passing to a subsequence, this implies that there exists a sequence $\{\psi _k \} \subset H_0^1(\Omega ; {\mathbb {R}}^d)$ such that $\Vert \psi _k \Vert _{H^1_0(\Omega )} =1$ and

$$\begin{aligned} |\langle \nabla P_{\varepsilon _k} -\nabla P, \psi _k \rangle _{H^{-1}(\Omega ) \times H^1_0(\Omega )}| \ge c_0>0. \end{aligned}$$

By passing to another subsequence, we may assume that $\psi _k \rightarrow \psi _0$ weakly in $H_0^1(\Omega ; {\mathbb {R}}^d)$. Let $\varphi _k =\psi _k -\psi _0$. Using $P_{\varepsilon _k} \rightarrow P$ weakly in $L^2(\Omega )$, we obtain

$$\begin{aligned} |\langle \nabla P_{\varepsilon _k} -\nabla P, \varphi _k \rangle _{H^{-1}(\Omega ) \times H^1_0(\Omega )}| \ge c_0/2, \end{aligned}$$

(4.3)

if k is sufficiently large. Since $\varphi _k \rightarrow 0$ weakly in $H^1_0(\Omega ; {\mathbb {R}}^d)$, we may conclude further that

$$\begin{aligned} |\langle \nabla P_{\varepsilon _k} , \varphi _k \rangle _{H^{-1}(\Omega ) \times H^1_0(\Omega )}| \ge c_0/4, \end{aligned}$$

(4.4)

if k is sufficiently large. On the other hand, by (2.7), we have

$$\begin{aligned}&\left| \langle \nabla P_{\varepsilon _k}, \varphi _k \rangle _{H^{-1} (\Omega ) \times H_0^1(\Omega )} \right| =\left| \langle \nabla p_{\varepsilon _k}, R_{\varepsilon _k} (\varphi _k) \rangle _{H^{-1}(\Omega _{\varepsilon _k}) \times H_0^1(\Omega _{\varepsilon _k})} \right| \nonumber \\&\quad =\left| \langle \varepsilon _k^2 \Delta u_{\varepsilon _k} + f , R_{\varepsilon _k} (\varphi _k) \rangle _{H^{-1}(\Omega _{\varepsilon _k} ) \times H_0^1(\Omega _{\varepsilon _k} )} \right| \nonumber \\&\quad \le \varepsilon _k^2 \Vert \nabla u_{\varepsilon _k} \Vert _{L^2(\Omega _{\varepsilon _k})} \Vert \nabla R_{\varepsilon _k} (\varphi _k)\Vert _{L^2(\Omega _{\varepsilon _k})} + \Vert f\Vert _{L^2(\Omega )} \Vert R_{\varepsilon _k} (\varphi _k)\Vert _{L^2(\Omega _{\varepsilon _k})}\nonumber \\&\quad \le C \left( \Vert f\Vert _{L^2(\Omega )} + \Vert h \Vert _{H^{1/2}(\partial \Omega )} \right) \left( \varepsilon _k \Vert \nabla R_{\varepsilon _k} (\varphi _k)\Vert _{L^2(\Omega _{\varepsilon _k})} + \Vert R_{\varepsilon _k} (\varphi _k)\Vert _{L^2(\Omega _{\varepsilon _k})} \right) \nonumber \\&\quad \le C \left( \Vert f\Vert _{L^2(\Omega )} + \Vert h \Vert _{H^{1/2}(\partial \Omega )} \right) \left( \varepsilon _k \Vert \nabla \varphi _k\Vert _{L^2(\Omega )} + \Vert \varphi _k\Vert _{L^2(\Omega )} \right) , \end{aligned}$$

(4.5)

where we have used the estimate (3.6) for the second inequality and (2.17) for the last. This contradicts with (4.4) as the right-hand side of (4.5) goes to zero. $\square$

By Corollaries 3.2 and 3.3, the sets $\{ u_\varepsilon : 0< \varepsilon < 1 \}$ and $\{ P_\varepsilon : 0< \varepsilon < 1 \}$ are bounded in $L^2(\Omega ; {\mathbb {R}}^d)$ and $L^2 (\Omega )$, respectively. It follows that for any sequence $\varepsilon _k \rightarrow 0$, there exists a subsequence, still denoted by $\{\varepsilon _k\}$, such that $u_{\varepsilon _k} \rightarrow u$ and $P_{\varepsilon _k} \rightarrow P$ weakly in $L^2(\Omega ; {\mathbb {R}}^d)$ and $L^2(\Omega )$, respectively. By Lemma 4.2, $P_{\varepsilon _k} \rightarrow P$ strongly in $L^2(\Omega )$. Thus, as in the classical case $L=1$, to prove Theorem 4.1, it suffices to show that if $\varepsilon _k \rightarrow 0$, $u_{\varepsilon _k} \rightarrow u$ weakly in $L^2(\Omega ; {\mathbb {R}}^d)$, and $P_{\varepsilon _k} \rightarrow P$ strongly in $L^2(\Omega )$, then $P\in H^1(\Omega )$ and (u, P) is a weak solution of (4.2). Since the solution of (4.2) is unique under the conditions that $P_0\in H^1(\Omega )$ and $\int _\Omega P_0\, \mathrm{{d}}x =0$, one concludes that as $\varepsilon \rightarrow 0$, $u_\varepsilon \rightarrow u_0$ weakly in $L^2(\Omega ; {\mathbb {R}}^d)$ and strongly in $L^2(\Omega )$, where $(u_0, P_0)$ is the unique solution of (4.2) with the property $P_0\in H^1(\Omega )$ and $\int _\Omega P_0\, \mathrm{{d}}x =0$.

Lemma 4.3

Let $\{ \varepsilon _k \}$ be a sequence such that $\varepsilon _k \rightarrow 0$. Suppose that $u_{\varepsilon _k} \rightarrow u$ weakly in $L^2(\Omega ; {\mathbb {R}}^d)$ and $P_{\varepsilon _k} \rightarrow P$ strongly in $L^2(\Omega )$. Then $P\in H^1(\Omega ^\ell )$ for $1\le \ell \le L$ and (u, P) is a solution of (4.2).

Proof

Since

$$\begin{aligned} \int _{\Omega } u_{\varepsilon _k} \cdot \nabla \varphi \, \mathrm{{d}}x =\int _{\partial \Omega } (h\cdot n) \varphi \, \mathrm{{d}}\sigma \end{aligned}$$

for any $\varphi \in C^\infty ({\mathbb {R}}^d)$, by letting $k \rightarrow \infty$, we see that

$$\begin{aligned} \int _{\Omega } u \cdot \nabla \varphi \, \mathrm{{d}}x =\int _{\partial \Omega } (h\cdot n) \varphi \, \mathrm{{d}}\sigma \end{aligned}$$

for any $\varphi \in C^\infty ({\mathbb {R}}^d)$. It follows that div$(u)=0$ in $\Omega$ and $u\cdot n = h\cdot n$ on $\partial \Omega$.

Next, we show that $P\in H^1(\Omega ^\ell )$ for each subdomain $\Omega ^\ell$ and that

$$\begin{aligned} u=K^\ell (f-\nabla P) \quad \text { in } \Omega ^\ell , \end{aligned}$$

(4.6)

where $K^\ell =(K^\ell _{ij})$ is defined by (2.2). The argument is the same as that of Tartar for the case $L=1$ (see [13]). Fix $1\le \ell \le L$, $1\le j\le d$, and $\varphi \in C_0^\infty (\Omega ^\ell )$. We assume $k>1$ is sufficiently large that supp$(\varphi ) \subset \{ x\in \Omega ^\ell : \text {dist}(x, \partial \Omega ^\ell ) \ge C_d \varepsilon _k \}$. Let $( W_j^\ell (y), \pi _j^\ell (y))$ be the 1-periodic functions given by (2.1). By using $W_j^\ell (x/\varepsilon _k) \varphi$ as a test function, we obtain

$$\begin{aligned}&\varepsilon _k\int _{\Omega ^\ell } \nabla u_{\varepsilon _k} \cdot \nabla W_j^\ell (x/\varepsilon _k ) \varphi \, \mathrm{{d}}x + \varepsilon ^2_k \int _{\Omega ^\ell } \nabla u_{\varepsilon _k} \cdot W_j^\ell (x/\varepsilon _k) \nabla \varphi \, \mathrm{{d}}x\nonumber \\&\qquad -\int _{\Omega ^\ell } P_{\varepsilon _k} W_j^\ell (x/\varepsilon _k) \cdot \nabla \varphi \, \mathrm{{d}}x\nonumber \\&\quad =\int _{\Omega ^\ell } f\cdot W_j^\ell (x/\varepsilon _k) \varphi \, \mathrm{{d}}x, \end{aligned}$$

(4.7)

where we have used the facts that $\textrm{div} (W^\ell _j (x/\varepsilon ))=0$ in ${\mathbb {R}}^d$ and $W_j^\ell (x/\varepsilon )=0$ on $\Gamma _{\varepsilon }$. Since $W_{ij}^\ell (x/\varepsilon _k) \rightarrow K^\ell _{ij}$ weakly in $L^2(\Omega ^\ell )$ and $P_{\varepsilon _k} \rightarrow P$ strongly in $L^2(\Omega ^\ell )$, we deduce from (4.7) that

$$\begin{aligned} \lim _{k \rightarrow \infty } \varepsilon _k\int _{\Omega ^\ell } \nabla u_{\varepsilon _k} \cdot \nabla W_j^\ell (x/\varepsilon _k ) \varphi \, \mathrm{{d}}x =\int _{\Omega ^\ell } P K^\ell _{ij} \frac{\partial \varphi }{\partial x_i}\, \mathrm{{d}}x +\int _{\Omega ^\ell } f_iK_{ij}^\ell \varphi \, \mathrm{{d}}x, \end{aligned}$$

(4.8)

where the repeated index i is summed from 1 to d.

Note that

$$\begin{aligned} -\varepsilon ^2 \Delta \left( W_j^\ell (x/\varepsilon ) \right) +\nabla \left( \varepsilon \pi _j^\ell (x/\varepsilon ) \right) =e_j \end{aligned}$$

in the set $\{ x\in \Omega ^\ell _\varepsilon : \textrm{dist}(x, \partial \Omega ^\ell ) \ge c_d \varepsilon \}$. By using $u_{\varepsilon _k} \varphi$ as a test function, we see that

$$\begin{aligned}&\varepsilon _k \int _{\Omega ^\ell } \nabla W_j^\ell (x/\varepsilon _k) \cdot ( \nabla u_{\varepsilon _k} ) \varphi \, \mathrm{{d}}x +\varepsilon _k \int _{\Omega ^\ell } \nabla W_j^\ell (x/\varepsilon _k) \cdot u_{\varepsilon _k} (\nabla \varphi )\, \mathrm{{d}}x\nonumber \\&\quad -\varepsilon _k \int _{\Omega ^\ell } \pi _j^\ell (x/\varepsilon _k) u_{\varepsilon _k} (\nabla \varphi )\, \mathrm{{d}}x =\int _{\Omega ^\ell } e_j \cdot u_{\varepsilon _k} \varphi \, \mathrm{{d}}x, \end{aligned}$$

(4.9)

which leads to

$$\begin{aligned} \lim _{k \rightarrow \infty } \varepsilon _k \int _{\Omega ^\ell } \nabla W_j^\ell (x/\varepsilon _k) \cdot ( \nabla u_{\varepsilon _k} ) \varphi \, \mathrm{{d}}x =\int _{\Omega ^\ell } e_j \cdot u \varphi \, \mathrm{{d}}x. \end{aligned}$$

(4.10)

In view of (4.8) and (4.10) we obtain

$$\begin{aligned} \int _{\Omega ^\ell } e_j \cdot u \varphi \, \mathrm{{d}}x =\int _{\Omega ^\ell } P K^\ell _{ij} \frac{\partial \varphi }{\partial x_i}\, \mathrm{{d}}x +\int _{\Omega ^\ell } f_iK_{ij}^\ell \varphi \, \mathrm{{d}}x. \end{aligned}$$

Since $\varphi \in C_0^\infty (\Omega ^\ell )$ is arbitrary and the constant matrix $K^\ell =(K_{ij}^\ell )$ is invertible, we conclude that $P\in H^1(\Omega ^\ell )$ and

$$\begin{aligned} u_j = K_{ij}^\ell \Big (f_i -\frac{\partial P}{\partial x_i}\Big ) \end{aligned}$$

in $\Omega ^\ell$. Since $K^\ell$ is also symmetric, this gives (4.6). $\square$

To prove the effective pressure in Lemma 4.3$P\in H^1(\Omega )$, it remains to show that P is continuous across the interface $\Sigma =\Omega \setminus \cup _{\ell =1}^L \Omega ^\ell$ between subdomains.

Lemma 4.4

Let $f\in C^m (B(x_0, 2c\varepsilon ); {\mathbb {R}}^d)$ for some $x_0\in {\mathbb {R}}^d$, $m\ge 0$ and $c>0$. Suppose that

$$\begin{aligned} \left\{ \begin{aligned}&-\varepsilon ^{2} \Delta u_\varepsilon +\nabla p_\varepsilon = f \quad \text { in } B(x_0, 2c\varepsilon ),\\&\textrm{div} (u_\varepsilon ) =0 \quad \text { in } B(x_0, 2c\varepsilon ). \end{aligned}\right. \end{aligned}$$

(4.11)

Then

(4.12)

where C depends only on d, m and c.

Proof

The case $\varepsilon =1$ is given by interior estimates for the Stokes equations. The general case follows by a simple rescaling argument. $\square$

Define

$$\begin{aligned} \gamma _\varepsilon = \big \{ x\in \Sigma : \ \textrm{dist} (x, \partial \Omega )\ge \varepsilon \big \}, \end{aligned}$$

(4.13)

where $\Sigma$ is the interface given by (1.5)

Lemma 4.5

Let $(u_\varepsilon , p_\varepsilon )$ be a solution of (4.1) with $f\in C^\infty ({\mathbb {R}}^d; {\mathbb {R}}^d)$ and $h \in H^{1/2}(\partial \Omega ; {\mathbb {R}}^d)$. Then, for $m\ge 0$,

$$\begin{aligned} \Vert \nabla ^m u_\varepsilon \Vert _{L^2 (\gamma _\varepsilon )}&\le C (f, h) \varepsilon ^{-m-\frac{1}{2}}, \nonumber \\ \Vert p_\varepsilon \Vert _{L^2(\gamma _\varepsilon )}&\le C(f, h) \varepsilon ^{-\frac{1}{2}}, \nonumber \\ \Vert \nabla p_\varepsilon \Vert _{L^2(\gamma _\varepsilon )}&\le C(f, h) \varepsilon ^{-\frac{1}{2}}, \end{aligned}$$

(4.14)

where C(f, h) depends on m, f and h, but not on $\varepsilon$.

Proof

Recall that

$$\begin{aligned} \Sigma = \cup _{\ell =1}^L \partial \Omega ^\ell \setminus \partial \Omega . \end{aligned}$$

It follows that $\gamma _\varepsilon =\cup _{\ell =1}^L \gamma _\varepsilon ^\ell$, where

$$\begin{aligned} \gamma _\varepsilon ^\ell = \big \{ x\in \partial \Omega ^\ell : \ \text {dist} (x, \partial \Omega )\ge \varepsilon \big \}. \end{aligned}$$

Thus, it suffices to prove (4.14) with $\gamma _\varepsilon ^\ell$ in the place of $\gamma _\varepsilon$. Let

$$\begin{aligned} D^\ell _\varepsilon =\left\{ x\in \Omega ^\ell : \text { dist} \left( x, \gamma _\varepsilon ^\ell \right) < c\, \varepsilon \right\} . \end{aligned}$$

Using the assumption that $\Omega ^\ell$ is a bounded Lipschitz domain, one may show that

$$\begin{aligned} \int _{\gamma _\varepsilon ^\ell } |\nabla ^ m u_\varepsilon |^2\, \mathrm{{d}}\sigma&\le \frac{C}{\varepsilon } \int _{D_\varepsilon ^\ell } |\nabla ^m u_\varepsilon |^2 \, \mathrm{{d}}x + C \varepsilon \int _{D_\varepsilon ^\ell } |\nabla ^{m+1} u_\varepsilon |^2\, \mathrm{{d}}x\nonumber \\&\le \frac{C}{\varepsilon ^{1+2m}} \left\{ \int _{\Omega _\varepsilon } |u_\varepsilon |^2\, \mathrm{{d}}x + C(f) \right\} , \end{aligned}$$

(4.15)

where C(f) depends on f. We point out that the second inequality in (4.15) follows by covering $D_\varepsilon ^\ell$ with balls of radius $c\varepsilon$ and using (4.12). This, together with the energy estimate (3.6), yields

$$\begin{aligned} \Vert \nabla ^m u_\varepsilon \Vert _{L^2(\gamma _\varepsilon ^\ell )} \le C (f, h) \varepsilon ^{-m -\frac{1}{2}}, \end{aligned}$$

where C(f, h) depends on f and h. Next, using the equation $-\varepsilon ^2 \Delta u_\varepsilon +\nabla p_\varepsilon =f$, we obtain

$$\begin{aligned} \Vert \nabla p_\varepsilon \Vert _{L^2(\gamma _\varepsilon ^\ell )}&\le \varepsilon ^2 \Vert \Delta u_\varepsilon \Vert _{L^2(\gamma _\varepsilon ^\ell )} + \Vert f\Vert _{L^2(\gamma _\varepsilon ^\ell )}\\&\le C (f, h) \varepsilon ^{-1/2}. \end{aligned}$$

Finally, observe that

$$\begin{aligned} \int _{\gamma _\varepsilon ^\ell } |p_\varepsilon |^2\, \mathrm{{d}}\sigma&\le \frac{C}{\varepsilon } \int _{D_\varepsilon ^\ell } |p_\varepsilon |^2\, \mathrm{{d}}x + C \varepsilon \int _{D_\varepsilon ^\ell } |\nabla p_\varepsilon |^2\, \mathrm{{d}}x\\&\le \frac{C}{\varepsilon } \int _{\Omega _\varepsilon } | p_\varepsilon |^2 \, \mathrm{{d}}x + C \varepsilon ^ 5 \int _{D_\varepsilon ^\ell } |\Delta u_\varepsilon |^2\, \mathrm{{d}}x + C (f)\\&\le \frac{C}{\varepsilon } \int _{\Omega _\varepsilon } |p_\varepsilon |^2\, \mathrm{{d}}x + C \varepsilon \int _{\Omega _\varepsilon } |u_\varepsilon |^2\, \mathrm{{d}}x + C (f). \end{aligned}$$

This, together with the energy estimate (3.6), yields the second inequality in (4.14).

$\square$

The following is the main technical lemma in the proof of Theorem 4.1.

Lemma 4.6

Let $(u_{\varepsilon _k}, p_{\varepsilon _k})$, $P_{\varepsilon _k}$, and (u, P) be the same as in Lemma 4.3. Also assume that $f\in C^\infty ({\mathbb {R}}^d; {\mathbb {R}}^d)$. Let $P^\ell$ denote the trace of P, as a function in $H^1 (\Omega ^\ell )$, on $\partial \Omega ^\ell$. Then, for any $\varphi \in C_0^\infty (\Omega )$,

$$\begin{aligned} \int _{\partial \Omega ^\ell } n_j P^\ell \varphi \, \mathrm{{d}}x =\lim _{k \rightarrow \infty } \int _{\partial \Omega ^\ell } n_j p_{\varepsilon _k} \varphi \, \mathrm{{d}}\sigma , \end{aligned}$$

(4.16)

where $1\le \ell \le L$, $1\le j\le d$, and $n=(n_1, n_2, \dots , n_d)$ denotes the outward unit normal to $\partial \Omega ^\ell$.

Proof

For notational simplicity we use $\varepsilon$ to denote $\varepsilon _k$. Fix $1\le j\le d$ and $1\le \ell \le L$. Let $\varphi \in C_0^\infty (\Omega )$. Then

$$\begin{aligned}&\varepsilon ^2\int _{\Omega _\varepsilon ^\ell } \nabla u_\varepsilon \cdot \nabla \left( W_j^\ell (x/\varepsilon ) \varphi \right) \, \mathrm{{d}}x\\&\quad =\varepsilon \int _{\Omega _\varepsilon ^\ell } \nabla u_\varepsilon \cdot \nabla W_j^\ell (x/\varepsilon ) \varphi \, \mathrm{{d}}x +\varepsilon ^2 \int _{\Omega _\varepsilon ^\ell } \nabla u_\varepsilon \cdot W_j^\ell (x/\varepsilon ) (\nabla \varphi )\, \mathrm{{d}}x, \end{aligned}$$

and by integration by parts,

$$\begin{aligned}&\varepsilon ^2\int _{\Omega _\varepsilon ^\ell } \nabla u_\varepsilon \cdot \nabla \left( W_j^\ell (x/\varepsilon ) \varphi \right) \, \mathrm{{d}}x\\&\quad =\int _{\Omega ^\ell } f \cdot W_j^\ell (x/\varepsilon ) \varphi \, \mathrm{{d}}x +\int _{\Omega ^\ell } P_\varepsilon W_j^\ell (x/\varepsilon ) \cdot \nabla \varphi \, \mathrm{{d}}x +\int _{\partial \Omega ^\ell } \frac{\partial u_\varepsilon }{\partial \nu } \cdot W_j^\ell (x/\varepsilon ) \varphi \, \mathrm{{d}}\sigma , \end{aligned}$$

where

$$\begin{aligned} \frac{\partial u_\varepsilon }{\partial \nu } =\varepsilon ^2 \frac{\partial u_\varepsilon }{\partial n} - p_\varepsilon n. \end{aligned}$$

By letting $\varepsilon \rightarrow 0$ we obtain

$$\begin{aligned}&\lim _{\varepsilon \rightarrow 0} \varepsilon \int _{\Omega _\varepsilon ^\ell } \nabla u_\varepsilon \cdot \nabla W_j^\ell (x/\varepsilon ) \varphi \, \mathrm{{d}}x\nonumber \\&\quad =\int _{\Omega ^\ell } f \cdot K_j^\ell \varphi \, \mathrm{{d}}x +\int _{\Omega ^\ell } P K_j^\ell \cdot \nabla \varphi \, \mathrm{{d}}x +\lim _{\varepsilon \rightarrow 0} \int _{\partial \Omega ^\ell } \frac{\partial u_\varepsilon }{\partial \nu } \cdot W_j^\ell (x/\varepsilon ) \varphi \, \mathrm{{d}}\sigma .\nonumber \\ \end{aligned}$$

(4.17)

It follows by Lemma 2.1 that $\Vert W_j^\ell (x/\varepsilon ) \Vert _{L^2(\partial \Omega ^\ell )} \le C$. This, together with the first inequality in (4.14) with $m=1$, show that

$$\begin{aligned} \left| \varepsilon ^2 \int _{\partial \Omega ^\ell } \frac{\partial u_\varepsilon }{\partial n} \cdot W_j^\ell (x/\varepsilon ) \varphi \, \mathrm{{d}}\sigma \right| \le C \varepsilon ^2 \Vert (\nabla u_\varepsilon ) \varphi \Vert _{L^2(\partial \Omega ^\ell )} =O(\varepsilon ^{1/2}). \end{aligned}$$

Hence, by (4.17),

$$\begin{aligned}&\lim _{\varepsilon \rightarrow 0} \varepsilon \int _{\Omega _\varepsilon ^\ell } \nabla u_\varepsilon \cdot \nabla W_j^\ell (x/\varepsilon ) \varphi \, \mathrm{{d}}x\nonumber \\&\quad =\int _{\Omega ^\ell } f \cdot K_j^\ell \varphi \, \mathrm{{d}}x +\int _{\Omega ^\ell } P K_j^\ell \cdot \nabla \varphi \, \mathrm{{d}}x -\lim _{\varepsilon \rightarrow 0} \int _{\partial \Omega ^\ell } p_\varepsilon n \cdot W_j^\ell (x/\varepsilon ) \varphi \, \mathrm{{d}}\sigma .\nonumber \\ \end{aligned}$$

(4.18)

Next, note that

$$\begin{aligned}&\varepsilon ^2 \int _{\Omega _\varepsilon ^\ell } \nabla \left( W_j^\ell (x/\varepsilon ) \right) \cdot \nabla (u_\varepsilon \varphi )\, \mathrm{{d}}x\nonumber \\&\quad =\varepsilon \int _{\Omega _\varepsilon ^\ell } \nabla W_j^\ell (x/\varepsilon ) \cdot (\nabla u_\varepsilon ) \varphi \, \mathrm{{d}}x + \varepsilon \int _{\Omega _\varepsilon ^\ell } \nabla W_j^\ell (x/\varepsilon ) \cdot u_\varepsilon (\nabla \varphi )\, \mathrm{{d}}x. \end{aligned}$$

(4.19)

Choose a cut-off function $\eta _\varepsilon$ such that supp$(\eta _\varepsilon ) \subset \{ x\in {\mathbb {R}}^d: \text {dist}(x, \partial \Omega ^\ell ) \le 2C \varepsilon \}$, $\eta _\varepsilon (x)=1$ if dist$(x, \partial \Omega ^\ell ) \le C\varepsilon$, and $|\nabla \eta _\varepsilon | \le C \varepsilon ^{-1}$. Thenv

$$\begin{aligned}&\varepsilon ^2 \int _{\Omega _\varepsilon ^\ell } \nabla \left( W_j^\ell (x/\varepsilon ) \right) \cdot \nabla (u_\varepsilon \varphi )\, \mathrm{{d}}x\nonumber \\&\quad = \varepsilon ^2 \int _{\Omega _\varepsilon ^\ell } \nabla \left( W_j^\ell (x/\varepsilon ) \right) \cdot \nabla (u_\varepsilon (1-\eta _\varepsilon ) \varphi )\, \mathrm{{d}}x + \varepsilon ^2 \int _{\Omega _\varepsilon ^\ell } \nabla \left( W_j^\ell (x/\varepsilon ) \right) \cdot \nabla (u_\varepsilon \eta _\varepsilon \varphi )\, \mathrm{{d}}x\nonumber \\&\quad =J_1 + J_2. \end{aligned}$$

(4.20)

Using (4.19), (4.20), and

$$\begin{aligned} |J_2|&\le C \varepsilon \left( \int _{\{ x\in {\mathbb {R}}^d: \, \text {dist}(x, \partial \Omega ^\ell ) \le C \varepsilon \} } |\nabla W_j^\ell (x/\varepsilon )|^2\, \mathrm{{d}}x \right) ^{1/2}\left\{ \Vert \nabla u_\varepsilon \Vert _{L^2(\Omega )} + \varepsilon ^{-1} \Vert u_\varepsilon \Vert _{L^2(\Omega )} \right\} \\&\le C \varepsilon ^{3/2} \left\{ \Vert \nabla u_\varepsilon \Vert _{L^2(\Omega )} + \varepsilon ^{-1} \Vert u_\varepsilon \Vert _{L^2(\Omega )} \right\} \\&\le \varepsilon ^{1/2} C (f, h), \end{aligned}$$

we obtain

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} \varepsilon \int _{\Omega _\varepsilon ^\ell } \nabla W_j^\ell (x/\varepsilon ) \cdot (\nabla u_\varepsilon ) \varphi \, \mathrm{{d}}x =\lim _{\varepsilon \rightarrow 0} J_1. \end{aligned}$$

(4.21)

To handle the term $J_1$, we use integration by parts as well as the fact that

$$\begin{aligned} -\varepsilon ^2 \Delta \left( W_j^\ell (x/\varepsilon ) \right) +\nabla \left( \varepsilon \pi _j^\ell (x/\varepsilon ) \right) =e_j \end{aligned}$$

in the set $\{ x\in \Omega _\varepsilon ^\ell : \textrm{dist}(x, \partial \Omega ^\ell )\ge C \varepsilon \}$, to obtain

$$\begin{aligned} J_1&=\int _{\Omega _\varepsilon ^\ell } \varepsilon \pi _j^\ell (x/\varepsilon ) u_\varepsilon \cdot \nabla ( (1-\eta _\varepsilon ) \varphi )\, \mathrm{{d}}x +\int _{\Omega ^\ell } e_j \cdot u_\varepsilon \varphi (1-\eta _\varepsilon )\, \mathrm{{d}}x\\&=J_{11} +J_{12}, \end{aligned}$$

where we have used the fact div$(u_\varepsilon )=0$ in $\Omega _\varepsilon$. Since

$$\begin{aligned} |J_{11}|&\le C \left( \int _{\{ x\in {\mathbb {R}}^d: \, \text {dist}(x, \partial \Omega ^\ell ) \le C \varepsilon \} } | \pi _j^\ell (x/\varepsilon )|^2\, \mathrm{{d}}x \right) ^{1/2}\Vert u_\varepsilon \Vert _{L^2(\Omega ^\ell )} + C \varepsilon \Vert u_\varepsilon \Vert _{L^2(\Omega ^\ell )}\\&\le C \varepsilon ^{1/2} C (f, h), \end{aligned}$$

we see that

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} J_1 =\lim _{\varepsilon \rightarrow 0} J_{12} =\int _{\Omega ^\ell } e_j \cdot u \varphi \, \mathrm{{d}}x. \end{aligned}$$

(4.22)

In view of (4.18), (4.21) and (4.22), we have proved that

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} \int _{\partial \Omega ^\ell } p_\varepsilon n \cdot W_j^\ell (x/\varepsilon )\varphi \, \mathrm{{d}}\sigma =\int _{\Omega ^\ell } f\cdot K_j^\ell \varphi \, \mathrm{{d}}x + \int _{\Omega ^\ell } P K_j^\ell \cdot \nabla \varphi \, \mathrm{{d}}x -\int _{\Omega ^\ell } e_j \cdot u \varphi \, \mathrm{{d}}x. \end{aligned}$$

(4.23)

Recall that $K^\ell =(K^\ell _{ij})$ is symmetric and by Lemma 4.3,

$$\begin{aligned} u= K^\ell (f-\nabla P) \quad \text { in } \Omega ^\ell . \end{aligned}$$

Thus, by (4.23),

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} \int _{\partial \Omega ^\ell } p_\varepsilon n \cdot W_j^\ell (x/\varepsilon )\varphi \, \mathrm{{d}}\sigma =\int _{\partial \Omega ^\ell } P^\ell ( n\cdot K_j^\ell ) \varphi \, \mathrm{{d}}\sigma , \end{aligned}$$

(4.24)

where $P^\ell$ denotes the trace of P on $\partial \Omega ^\ell$.

Finally, we use Lemma 2.2 to obtain

$$\begin{aligned} n\cdot \left( W^\ell _j (x/\varepsilon ) -K^\ell _j \right) =\frac{\varepsilon }{2} \left( n_\beta \frac{\partial }{\partial x_\alpha } -n_\alpha \frac{\partial }{\partial x_\beta }\right) \left( \phi ^\ell _{\alpha \beta j} (x/\varepsilon )\right) , \end{aligned}$$

(4.25)

where the repeated indices $\alpha$ and $\beta$ are summed from 1 to d. Since $n_\beta \frac{\partial }{\partial x_\alpha } -n_\alpha \frac{\partial }{\partial x_\beta }$ is a tangential derivative on $\partial \Omega ^\ell$, we obtain

$$\begin{aligned}&\left| \int _{\partial \Omega ^\ell } p_\varepsilon n \cdot \left( W_j^\ell (x/\varepsilon ) -K^\ell _j \right) \varphi \, \mathrm{{d}}\sigma \right| \\&\quad = \frac{\varepsilon }{2} \left| \int _{\partial \Omega ^\ell } \phi ^\ell _{\alpha \beta j} (x/\varepsilon ) \left( n_\beta \frac{\partial }{\partial x_\alpha } -n_\alpha \frac{\partial }{\partial x_\beta } \right) (p_\varepsilon \varphi )\, \mathrm{{d}}\sigma \right| \\&\quad \le C \varepsilon \Vert \nabla (p_\varepsilon \varphi ) \Vert _{L^2(\partial \Omega ^\ell )}\\&\quad \le C(f, h) \varepsilon ^{1/2}, \end{aligned}$$

where we have used (2.8) for the first inequality and (4.14) for the last. This, together with (4.24), yields

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} \int _{\partial \Omega ^\ell } p_\varepsilon \left( n \cdot K_j^\ell \right) \varphi \, \mathrm{{d}}\sigma =\int _{\partial \Omega ^\ell } P^\ell \left( n\cdot K_j^\ell \right) \varphi \, \mathrm{{d}}\sigma . \end{aligned}$$

(4.26)

Since the constant matrix $K^\ell =(K_{ij}^\ell )$ is invertible, the desired Eq.(4.16) follows readily from (4.26). $\square$

We are now in a position to give the proof of Theorem 4.1.

Proof of Theorem 4.1

We first prove Theorem 4.1 under the additional assumption $f\in C^\infty ({\mathbb {R}}^d; {\mathbb {R}}^d)$. Let $\{ \varepsilon _k\}$ be a sequence such that $\varepsilon _k \rightarrow 0$, $u_{\varepsilon _k} \rightarrow u$ weakly in $L^2(\Omega ; {\mathbb {R}}^d)$ and $P_{\varepsilon _k} \rightarrow P$ strongly in $L^2(\Omega )$. By Lemma 4.3, $P\in H^1(\Omega ^\ell )$ and $u=K^\ell (f-\nabla P)$ in $\Omega ^\ell$ for $1\le \ell \le L$. It suffices to show that $P\in H^1(\Omega )$. This would imply that P is a weak solution of the Neumann problem,

$$\begin{aligned} \left\{ \begin{aligned}&\textrm{div} (K (f-\nabla P)) =0 \quad \text { in } \Omega ,\\&n \cdot K(f-\nabla P) =n \cdot h \quad \text { on } \partial \Omega . \end{aligned}\right. \end{aligned}$$

(4.27)

As a result, we may deduce that as $\varepsilon \rightarrow 0$, $u_\varepsilon \rightarrow u_0$ weakly in $L^2(\Omega ; {\mathbb {R}}^d)$ and strongly in $L^2(\Omega )$, where $u_0= K (f-\nabla P_0)$ in $\Omega$ and $P_0$ is the unique weak solution of (4.27) with $\int _\Omega P_0\, \mathrm{{d}}x=0$.

To prove $P\in H^1(\Omega )$, we use the assumption $f\in C^\infty ({\mathbb {R}}^d; {\mathbb {R}}^d)$ and Lemma 4.6 to obtain

$$\begin{aligned} \sum _{\ell =1}^L \int _{\partial \Omega ^\ell } n_j P^\ell \varphi \, \mathrm{{d}}\sigma =\lim _{k \rightarrow \infty } \sum _{\ell =1}^L \int _{\partial \Omega ^\ell } n_j p_{\varepsilon _k} \varphi \, \mathrm{{d}}\sigma , \end{aligned}$$

for any $\varphi \in C_0^\infty (\Omega )$ and $1\le j \le d$, where $P^\ell$ denotes the trace of P, as a function in $H^1(\Omega ^\ell )$, on $\partial \Omega ^\ell$. Since $p_\varepsilon$ is continuous in $\Omega _\varepsilon$, we have

$$\begin{aligned} \sum _{\ell =1}^L \int _{\partial \Omega ^\ell } n_j p_{\varepsilon } \varphi \, \mathrm{{d}}\sigma =0. \end{aligned}$$

It follows that

$$\begin{aligned} \sum _{\ell =1}^L \int _{\partial \Omega ^\ell } n_j P^\ell \varphi \, \mathrm{{d}}\sigma =0 \end{aligned}$$

for $1\le j \le d$ and for any $\varphi \in C_0^\infty (\Omega )$. This, together with the fact that $P\in H^1(\Omega ^\ell )$ for $1\le \ell \le L$, gives

$$\begin{aligned} \int _\Omega P\frac{\partial \varphi }{\partial x_j}\, \mathrm{{d}}x&=\sum _{\ell =1}^L \int _{\Omega ^\ell } P\frac{\partial \varphi }{\partial x_j}\, \mathrm{{d}}x\\&=-\sum _{\ell =1}^L \int _{\Omega ^\ell } \frac{\partial P}{\partial x_j} \varphi \, \mathrm{{d}}x +\sum _{\ell =1}^L \int _{\partial \Omega ^\ell } n_j P^\ell \varphi \, \mathrm{{d}}\sigma \\&=-\sum _{\ell =1}^L \int _{\Omega ^\ell } \frac{\partial P}{\partial x_j} \varphi \, \mathrm{{d}}x. \end{aligned}$$

As a result, we obtain $P\in H^1(\Omega )$.

In the general case $f\in L^2(\Omega ; {\mathbb {R}}^d)$, we choose a sequence of functions $\{ f_m \}$ in $C^\infty ({\mathbb {R}}^d; {\mathbb {R}}^d)$ such that $\Vert f_m - f\Vert _{L^2(\Omega )} \rightarrow 0$ as $m \rightarrow \infty$. Let $(u_{\varepsilon , m}, p_{\varepsilon , m})$ denote the weak solution of (4.1) with $f_m$ in the place of f and with $\int _{\Omega _\varepsilon } p_{\varepsilon , m} \, \mathrm{{d}}x=0$. By the energy estimates (3.6) and (3.8) we obtain

$$\begin{aligned} \Vert u_\varepsilon - u_{\varepsilon ,m} \Vert _{L^2(\Omega )} + \Vert P_\varepsilon -P_{\varepsilon , m} \Vert _{L^2(\Omega )} \le C \Vert f- f_m\Vert _{L^2(\Omega )}, \end{aligned}$$

(4.28)

where $P_{\varepsilon , m}$ denotes the extension of $p_{\varepsilon , m}$, defined by (2.21). Let $u_{0, m}=K (f_m -\nabla P_{0, m})$, where $P_{0, m}$ is the unique solution of (4.27) with $f_m$ in the place of f and with $\int _\Omega P_{0, m} \, \mathrm{{d}}x =0$. Note that

Since in $L^2(\Omega )$, as $\varepsilon \rightarrow 0$, we see that

By letting $m\rightarrow \infty$, we obtain in $L^2(\Omega )$, as $\varepsilon \rightarrow 0$.

Finally, let $v \in L^2(\Omega ; {\mathbb {R}}^d)$. Note that

$$\begin{aligned}&\Big | \int _\Omega (u_\varepsilon -u_0) v\, \mathrm{{d}}x \Big |\\&\quad \le \Big | \int _{\Omega } (u_\varepsilon - u_{\varepsilon , m} ) v\, \mathrm{{d}}x\Big | + \Big | \int _\Omega (u_{\varepsilon , m} -u_{0, m }) v \, \mathrm{{d}}x\Big | +\Big | \int _\Omega (u_{0, m} - u_0) v \, \mathrm{{d}}x\Big |\\&\quad \le \Vert u_\varepsilon -u_{\varepsilon , m} \Vert _{L^2(\Omega )} \Vert v \Vert _{L^2(\Omega )} + \Big | \int _\Omega (u_{\varepsilon , m} -u_{0, m }) v \, \mathrm{{d}}x\Big | + \Vert u_{0, m} - u_0 \Vert _{L^2(\Omega )} \Vert v\Vert _{L^2(\Omega )}\\&\quad \le C \Vert f-f_m\Vert _{L^2(\Omega )} \Vert v\Vert _{L^2(\Omega )} + \left| \int _\Omega (u_{\varepsilon , m} -u_{0, m }) v \, \mathrm{{d}}x\right| . \end{aligned}$$

By letting $\varepsilon \rightarrow 0$ and then $m \rightarrow \infty$, we see that $u_\varepsilon \rightarrow u_0$ weakly in $L^2(\Omega ; {\mathbb {R}}^d)$. $\square$

5 Convergence Rates and Proof of Theorem 1.2

Throughout the rest of this paper, unless indicated otherwise, we will assume that $\Omega ^\ell , 1\le \ell \le L$, are $C^{2, 1/2}$ domains satisfying the interface condition (1.12). Given $f\in L^2 (\Omega ; {\mathbb {R}}^d)$, let $P_0\in H^1(\Omega )$ be the weak solution of

$$\begin{aligned} \left\{ \begin{aligned}&-\textrm{div} \left( K (f-\nabla P_0) \right) =0 \quad \text { in } \Omega ,\\&n\cdot K(f-\nabla P_0) =0 \quad \text { on } \partial \Omega , \end{aligned}\right. \end{aligned}$$

(5.1)

with $\int _\Omega P_0\, \mathrm{{d}}x=0$, where the coefficient matrix K is given by (1.10). Since the interface $\Sigma$ and $\partial \Omega$ are of $C^{2, 1/2}$, it follows from [15, Theorem 1.1] that

$$\begin{aligned} \begin{aligned} \Vert \nabla P_0 \Vert _{C^{\alpha }(\Omega )}&\le C \Vert f\Vert _{C^{ \alpha }(\Omega )},\\ \Vert \nabla P_0\Vert _{C^{1, \beta }(\Omega )}&\le C \Vert f \Vert _{C^{1, \beta }(\Omega )}, \end{aligned} \end{aligned}$$

(5.2)

for $0< \alpha < 1$ and $0< \beta \le 1/2$.

Let

$$\begin{aligned} V_\varepsilon (x)= \sum _{\ell =1}^L W^\ell (x/\varepsilon ) (f-\nabla P_0) \chi _{\Omega ^\ell } \quad \text { in } \Omega , \end{aligned}$$

(5.3)

where the 1-periodic matrix $W^\ell (y)$ is defined by (2.1). Note that $V_\varepsilon =0$ in $\Gamma _\varepsilon$. For each $\ell$, using

$$\begin{aligned} -\varepsilon ^2 \Delta \left\{ W_j^\ell (x/\varepsilon )\right\} +\nabla \left\{ \varepsilon \pi _j^\ell (x/\varepsilon ) \right\} = e_j \quad \text { in } \bigcup _{z\in {\mathbb {Z}}^d} \varepsilon \left( z+{Y^\ell _f}\right) , \end{aligned}$$

(5.4)

one may show that for any $\psi \in H^1(\Omega ^\ell _\varepsilon ; {\mathbb {R}}^d)$ with $\psi =0$ on $\Gamma ^\ell _\varepsilon$,

$$\begin{aligned} \begin{aligned}&\Big | \varepsilon \int _{\Omega ^\ell _\varepsilon } \nabla W_j^\ell (x/\varepsilon ) \cdot \nabla \psi \, \mathrm{{d}}x-\varepsilon \int _{\Omega _\varepsilon ^\ell } \pi _j ^\ell (x/\varepsilon ) \, \text {div}(\psi )\, \mathrm{{d}}x -\int _{\Omega _\varepsilon ^\ell } \psi _j \, \mathrm{{d}}x \Big |\\&\quad \le C \varepsilon ^{3/2} \Vert \nabla \psi \Vert _{L^2(\Omega ^\ell _\varepsilon )}. \end{aligned} \end{aligned}$$

(5.5)

To see (5.5), let

$$\begin{aligned} {\mathcal {O}}_\varepsilon ^\ell = \bigcup _z \varepsilon \left( z+ Y_f^\ell \right) , \end{aligned}$$

where $z\in {\mathbb {Z}}^d$ and the union is taken over those z’s for which $\varepsilon (z + Y)\subset \Omega ^\ell$. Using $|\Omega _\varepsilon ^\ell {\setminus } {\mathcal {O}}_\varepsilon ^\ell | \le C \varepsilon$ and $\Vert \psi \Vert _{L^2(\Omega ^\ell _\varepsilon )} \le C \varepsilon \Vert \nabla \psi \Vert _{L^2(\Omega ^\ell _\varepsilon )}$, one may show that each integral in the left-hand side of (5.5), with $\Omega _\varepsilon ^\ell {\setminus } {\mathcal {O}}^\ell _\varepsilon$ in the place of $\Omega _\varepsilon ^\ell$, is bounded by the right-hand side of (5.5). By using integration by parts and (5.4), it follows that the left-hand side of (5.5) with ${\mathcal {O}}_\varepsilon ^\ell$ in the place of $\Omega _\varepsilon ^\ell$ is bounded by

$$\begin{aligned}&C \varepsilon \left( \int _{\partial {\mathcal {O}}_\varepsilon ^\ell } \left( |\nabla W^\ell (x/\varepsilon )| +|\pi ^\ell (x/\varepsilon )|\right) ^2 \, \mathrm{{d}}\sigma \right) ^{1/2} \left( \int _{\partial {\mathcal {O}}_\varepsilon ^\ell } |\psi |^2 \, \mathrm{{d}}\sigma \right) ^{1/2}\\&\quad \le C \varepsilon ^{3/2} \Vert \nabla \psi \Vert _{L^2(\Omega ^\ell _\varepsilon )}, \end{aligned}$$

where we have used (2.5) and the observation,

$$\begin{aligned} \Vert \psi \Vert _{L^2(\partial {\mathcal {O}}_\varepsilon ^\ell )}&\le C \varepsilon ^{-1/2} \Vert \psi \Vert _{L^2(\Omega _\varepsilon ^\ell )} + C \varepsilon ^{1/2} \Vert \nabla \psi \Vert _{L^2(\Omega _\varepsilon ^\ell )}\\&\le C \varepsilon ^{1/2} \Vert \nabla \psi \Vert _{L^2(\Omega _\varepsilon ^\ell )}. \end{aligned}$$

From (5.5) we deduce further that

$$\begin{aligned}&\Big | \varepsilon \int _{\Omega ^\ell _\varepsilon } \nabla W_j^\ell (x/\varepsilon ) \cdot \nabla \psi \, \mathrm{{d}}x -\int _{\Omega _\varepsilon ^\ell } \psi _j \, \mathrm{{d}}x \Big |\nonumber \\&\quad \le C \varepsilon ^{1/2} \left\{ \varepsilon \Vert \nabla \psi \Vert _{L^2(\Omega ^\ell _\varepsilon )} + \varepsilon ^{1/2} \Vert \textrm{div}(\psi ) \Vert _{L^2(\Omega ^\ell _\varepsilon )}\right\} \end{aligned}$$

(5.6)

for any $\psi \in H^1(\Omega ^\ell _\varepsilon ; {\mathbb {R}}^d)$ with $\psi =0$ on $\Gamma ^\ell _\varepsilon$.

Theorem 5.1

Let $(u_\varepsilon , p_\varepsilon )\in H_0^1(\Omega _\varepsilon ; {\mathbb {R}}^d)\times L^2_0(\Omega _\varepsilon )$ be a weak solution of (1.1). Let $V_\varepsilon$ be given by (5.3). Then

$$\begin{aligned}&\Big |\varepsilon ^2\sum _{\ell =1}^L \int _{\Omega ^\ell _\varepsilon } (\nabla u_\varepsilon -\nabla V_\varepsilon ) \cdot \nabla \psi \, \mathrm{{d}}x -\int _{\Omega _\varepsilon } ( p_\varepsilon -P_0 ) \, \textrm{div} (\psi )\, \mathrm{{d}}x \Big |\nonumber \\&\quad \le C \varepsilon ^{1/2} \Vert f \Vert _{C^{1, 1/2}(\Omega )} \left\{ \varepsilon \Vert \nabla \psi \Vert _{L^2(\Omega _\varepsilon )} + \varepsilon ^{1/2} \Vert \textrm{div}(\psi )\Vert _{L^2(\Omega _\varepsilon )} \right\} , \end{aligned}$$

(5.7)

for any $\psi \in H_0^1(\Omega _\varepsilon ; {\mathbb {R}}^d)$.

Proof

We apply (5.6) with $\psi (f_j -\frac{\partial P_0}{\partial x_j})$ in the place of $\psi$. Using

$$\begin{aligned}&| \varepsilon ^2 \nabla V_\varepsilon \cdot \nabla \psi - \varepsilon \nabla W^\ell (x/\varepsilon ) \cdot \nabla \left( \psi (f-\nabla P_0) \right) |\\&\le C \left\{ \varepsilon ^2 |W^\ell (x/\varepsilon )| |\nabla \psi | + C \varepsilon |\nabla W^\ell (x/\varepsilon )| |\psi |\right\} | \nabla (f-\nabla P_0)| \end{aligned}$$

in $\Omega ^\ell _\varepsilon$, we obtain

$$\begin{aligned}&\Big | \varepsilon ^2 \int _{\Omega _\varepsilon ^\ell } \nabla V _\varepsilon \cdot \nabla \psi \, \mathrm{{d}}x -\int _{\Omega _\varepsilon ^\ell } (f-\nabla P_0)\cdot \psi \, \mathrm{{d}}x \Big |\\&\quad \le C\varepsilon ^{3/2} \left( \Vert f\Vert _\infty + \Vert \nabla f\Vert _\infty + \Vert \nabla P_0\Vert _\infty + \Vert \nabla ^2 P_0 \Vert _\infty \right) \Vert \nabla \psi \Vert _{L^2(\Omega ^\ell _\varepsilon )}\\&\qquad + C \varepsilon (\Vert f\Vert _\infty + \Vert \nabla P_0 \Vert _\infty ) \Vert \textrm{div}(\psi )\Vert _{L^2(\Omega _\varepsilon ^\ell )}. \end{aligned}$$

This, together with

$$\begin{aligned} \int _{\Omega _\varepsilon } (f-\nabla P_0) \cdot \psi \, \mathrm{{d}}x =\varepsilon ^2 \int _{\Omega _\varepsilon }\nabla u_\varepsilon \cdot \nabla \psi \, \mathrm{{d}}x -\int _{\Omega _\varepsilon } (p_\varepsilon -P_0) \, \textrm{div}(\psi )\, \mathrm{{d}}x, \end{aligned}$$

gives (5.7). $\square$

Let

$$\begin{aligned} U_\varepsilon =V_\varepsilon + \Phi _\varepsilon , \end{aligned}$$

(5.8)

where $\Phi _\varepsilon$ is a corrector to be constructed so that $U_\varepsilon \in H_0^1(\Omega _\varepsilon ; {\mathbb {R}}^d)$,

$$\begin{aligned} \Vert \textrm{div} (U_\varepsilon ) \Vert _{L^2(\Omega _\varepsilon )} \le C \varepsilon ^{1/2} \Vert f\Vert _{C^{1, 1/2} (\Omega )}, \end{aligned}$$

(5.9)

and that

$$\begin{aligned} \varepsilon \Vert \nabla \Phi _\varepsilon \Vert _{L^2(\Omega ^\ell _\varepsilon )} \le C \varepsilon ^{1/2} \Vert f\Vert _{C^{1, 1/2}(\Omega )} \end{aligned}$$

(5.10)

for $1\le \ell \le L$.

Assuming that such corrector $\Phi _\varepsilon$ exists, we give the proof of Theorem 1.2.

Proof of Theorem 1.2

By letting $\psi =u_\varepsilon -U_\varepsilon =u_\varepsilon -V_\varepsilon -\Phi _\varepsilon \in H_0^1(\Omega _\varepsilon ; {\mathbb {R}}^d)$ in (5.7), we obtain

$$\begin{aligned}&\varepsilon ^2 \Vert \nabla u_\varepsilon -\nabla V_\varepsilon \Vert ^2_{L^2(\Omega _\varepsilon )}\\&\quad \le \varepsilon ^2 \Vert \nabla u_\varepsilon -\nabla V_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} \Vert \nabla \Phi _\varepsilon \Vert _{L^2(\Omega _\varepsilon )} + \Vert p_\varepsilon -P_0-\beta \Vert _{L^2(\Omega _\varepsilon )} \Vert \textrm{div} (U_\varepsilon ) \Vert _{L^2(\Omega _\varepsilon )}\\&\qquad + C \varepsilon ^{1/2} \ \Vert f\Vert _{C^{1, 1/2}(\Omega )} \left\{ \varepsilon \Vert \nabla u_\varepsilon -\nabla V_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} +\varepsilon \Vert \nabla \Phi _\varepsilon \Vert _{L^2(\Omega _\varepsilon )} + \varepsilon ^{1/2} \Vert \textrm{div} (U_\varepsilon ) \Vert _{L^2(\Omega _\varepsilon )} \right\} \\&\quad \le C \varepsilon ^{3/2} \Vert f\Vert _{C^{1, 1/2} (\Omega )} \Vert \nabla u_\varepsilon -\nabla V_\varepsilon \Vert _{L^2(\Omega _\varepsilon )}\\&\qquad + C \varepsilon ^{1/2} \Vert f \Vert _{C^{1, 1/2} (\Omega )} \Vert p_\varepsilon -P_0-\beta \Vert _{L^2(\Omega _\varepsilon )} + C \varepsilon \Vert f\Vert _{C^{1, 1/2} (\Omega )}^2, \end{aligned}$$

for any $\beta \in {\mathbb {R}}$, where we have used (5.9) and (5.10) for the last inequality. By the Cauchy inequality, this implies that

$$\begin{aligned} \varepsilon ^2 \Vert \nabla u_\varepsilon -\nabla V_\varepsilon \Vert ^2_{L^2(\Omega _\varepsilon )} \le C \varepsilon \Vert f\Vert ^2_{C^{1, 1/2}(\Omega )} + C \varepsilon ^{1/2} \Vert f\Vert _{C^{1, 1/2}(\Omega )} \Vert p_\varepsilon -P_0 -\beta \Vert _{L^2(\Omega _\varepsilon )}.\nonumber \\ \end{aligned}$$

(5.11)

We should point out that both $V_\varepsilon$ and $\Phi _\varepsilon$ are not in $H^1(\Omega _\varepsilon ; {\mathbb {R}}^d)$. In the estimates above (and thereafter) we have used the convention that

$$\begin{aligned} \Vert \ \nabla \psi \Vert _{L^2(\Omega _\varepsilon )} =\left( \sum _{\ell =1}^L \Vert \nabla \psi \Vert ^2_{L^2(\Omega _\varepsilon ^\ell )} \right) ^{1/2}, \end{aligned}$$

where $\psi \in H^1(\Omega _\varepsilon ^\ell )$ for $1\le \ell \le L$.

Next, we choose . By Lemma 2.6, there exists $v_\varepsilon \in H^1_0 (\Omega _\varepsilon ; {\mathbb {R}}^d)$ such that

$$\begin{aligned}&\textrm{div}(v_\varepsilon ) = p_\varepsilon -P_0 -\beta \quad \text { in } \Omega _\varepsilon , \\&\varepsilon \Vert \nabla v_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} \le C \Vert p_\varepsilon -P_0 -\beta \Vert _{L^2(\Omega _\varepsilon )}. \end{aligned}$$

By letting $\psi _\varepsilon =v_\varepsilon$ in (5.7), we obtain

$$\begin{aligned} \Vert p_\varepsilon -P_0 -\beta \Vert _{L^2(\Omega _\varepsilon )} \le C \varepsilon \Vert \nabla u_\varepsilon -\nabla V_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} +C \varepsilon ^{1/2} \Vert f\Vert _{C^{1, 1/2}(\Omega )}. \end{aligned}$$

(5.12)

By combining (5.11) with (5.12), it is not hard to see that

$$\begin{aligned} \varepsilon \Vert \nabla u_\varepsilon -\nabla V_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} + \Vert p_\varepsilon -P_0 -\beta \Vert _{L^2(\Omega _\varepsilon )} \le C \varepsilon ^{1/2} \Vert f\Vert _{C^{1, 1/2} (\Omega )}. \end{aligned}$$

(5.13)

This, together with $\Vert u_\varepsilon -V_\varepsilon \Vert _{L^2(\Omega _\varepsilon ^\ell )} \le C \varepsilon \Vert \nabla u_\varepsilon -\nabla V_\varepsilon \Vert _{L^2(\Omega ^\ell _\varepsilon )}$, gives the bound for the first term in (1.13). Also, note that

$$\begin{aligned} \Vert \varepsilon \nabla V_\varepsilon -\nabla W^\ell (x/\varepsilon ) (f-\nabla P_0) \Vert _{L^2(\Omega _\varepsilon ^\ell )} \le C \varepsilon \Vert \nabla (f-\nabla P_0)\Vert _\infty . \end{aligned}$$

Thus,

$$\begin{aligned} \Vert \varepsilon \nabla u_\varepsilon - \nabla W^\ell (x/\varepsilon ) (f-\nabla P_0)\Vert _{L^2(\Omega _\varepsilon ^\ell )} \le C \varepsilon ^{1/2} \Vert f\Vert _{C^{1, 1/2}(\Omega )}. \end{aligned}$$

Finally, to estimate the pressure, we let $Q_\varepsilon$ be the extension of $(P_0+\beta )|_{\Omega _\varepsilon }$ to $\Omega$, using the formula in (2.21). Note that

where the sum is taken over those $(\ell , z)$’s for which $z \in {\mathbb {Z}}^d$ and $\varepsilon (Y+z) \subset \Omega ^\ell$. It follows that

$$\begin{aligned} \Vert Q_\varepsilon - (P_0+\beta )\Vert _{L^2(\Omega )}&\le C \varepsilon \Vert \nabla P_0 \Vert _{L^\infty (\Omega )}\\&\le C \varepsilon \Vert f\Vert _{C^{1, 1/2}(\Omega )}. \end{aligned}$$

As a result, by (5.13), we obtain

$$\begin{aligned} \Vert P_\varepsilon - P_0 -\beta \Vert _{L^2(\Omega )}&\le \Vert P_\varepsilon - Q_\varepsilon \Vert _{L^2(\Omega )} + \Vert Q_\varepsilon - (P_0 +\beta )\Vert _{L^2(\Omega )}\\&\le C \Vert p_\varepsilon - P_0 -\beta \Vert _{L^2(\Omega _\varepsilon )} + C \varepsilon \Vert f\Vert _{C^{1, 1/2} (\Omega )}\\&\le C \varepsilon ^{1/2} \Vert f \Vert _{C^{1, 1/2}(\Omega )}, \end{aligned}$$

where . Clearly, we may replace $\beta$ by . This gives the bound for the second term in (1.13). $\square$

To complete the proof of Theorem 1.2, it remains to construct a corrector $\Phi _\varepsilon$ such that $V_\varepsilon +\Phi _\varepsilon \in H_0^1(\Omega _\varepsilon ; {\mathbb {R}}^d)$ and (5.9)–(5.10) hold. This will be done in the next three sections. More precisely, we let

$$\begin{aligned} \Phi _\varepsilon = \Phi _\varepsilon ^{(1)} + \Phi _\varepsilon ^{(2)} + \Phi _\varepsilon ^{(3)}, \end{aligned}$$

(5.14)

where $\Phi _\varepsilon ^{(1)}$ is a corrector for the divergence operator with the properties that

$$\begin{aligned} \left\{ \begin{aligned}&\Phi _\varepsilon ^{(1)} \in H_0^1 (\Omega _\varepsilon ; {\mathbb {R}}^d),\\&\varepsilon \Vert \nabla \Phi _\varepsilon ^{(1)} \Vert _{L^2(\Omega _\varepsilon )} \le C \varepsilon ^{1/2} \Vert f\Vert _{C^{1, 1/2} (\Omega )}, \\&\Vert \textrm{div}(\Phi _\varepsilon ^{(1)} +V_\varepsilon ) \Vert _{L^2(\Omega _\varepsilon ^\ell )} \le C \varepsilon ^{1/2}\Vert f\Vert _{C^{1, 1/2}(\Omega )}, \end{aligned}\right. \end{aligned}$$

(5.15)

$\Phi _\varepsilon ^{(2)}$ is a corrector for the boundary data of $V_\varepsilon$ on $\partial \Omega$ with the properties that

$$\begin{aligned} \left\{ \begin{aligned}&\Phi _\varepsilon ^{(2)} \in H^1 (\Omega _\varepsilon ; {\mathbb {R}}^d) \quad \text { and } \quad \Phi ^{(2)}_\varepsilon =0 \quad \text { on } \Gamma _\varepsilon ,\\&\Phi _\varepsilon ^{(2)} +V_\varepsilon =0\quad \text { on } \partial \Omega ,\\&\varepsilon \Vert \nabla \Phi _\varepsilon ^{(2)} \Vert _{L^2(\Omega _\varepsilon )} + \Vert \textrm{div} (\Phi _\varepsilon ^{(2)}) \Vert _{L^2(\Omega _\varepsilon )} \le C \varepsilon ^{1/2} \Vert f\Vert _{C^{1, 1/2} (\Omega )}, \end{aligned}\right. \end{aligned}$$

(5.16)

and $\Phi _\varepsilon ^{(3)}$ is a corrector for the interface $\Sigma$ with the properties that

$$\begin{aligned} \left\{ \begin{aligned}&\Phi _\varepsilon ^{(3)} \in H^1 (\Omega ^\ell _\varepsilon ; {\mathbb {R}}^d) \quad \text { and } \quad \Phi _\varepsilon ^{(3)}= 0 \quad \text { on } \partial \Omega _\varepsilon ,\\&V_\varepsilon + \Phi _\varepsilon ^{(3)}\in H^1(\Omega _\varepsilon ; {\mathbb {R}}^d),\\&\varepsilon \Vert \nabla \Phi _\varepsilon ^{(3)} \Vert _{L^2(\Omega ^\ell _\varepsilon )} + \Vert \textrm{div} (\Phi _\varepsilon ^{(3)}) \Vert _{L^2(\Omega _\varepsilon ^\ell )} \le C \varepsilon ^{1/2} \Vert f\Vert _{C^{1, 1/2} (\Omega )}, \end{aligned}\right. \end{aligned}$$

(5.17)

for $1\le \ell \le L$. It is not hard to verify that the desired property $V_\varepsilon +\Phi _\varepsilon \in H_0^1(\Omega _\varepsilon ; {\mathbb {R}}^d)$ as well as the estimates (5.9) and (5.10) follows from (5.15)and(5.17).

6 Correctors for the Divergence Operator

Let $V_\varepsilon$ be given by (5.3). Note that since div$(W_j^\ell (x/\varepsilon ))=0$ in ${\mathbb {R}}^d$,

$$\begin{aligned} \textrm{div} (V_\varepsilon ) =W^\ell (x/\varepsilon ) \nabla (f-\nabla P_0) \quad \text { in } \Omega ^\ell _\varepsilon . \end{aligned}$$

(6.1)

In this section we construct a corrector $\Phi _\varepsilon ^{(1)}$ that satisfies (5.15). The approach is similar to that used in [11, 14].

For $1\le \ell \le L$ and $1\le \, i, j \le d$, let $\Theta _{ij}^\ell = (\Theta ^\ell _{1ij}, \dots , \Theta ^\ell _{dij})$ be a 1-periodic function in $H^1_{loc}({\mathbb {R}}^d; {\mathbb {R}}^d)$ such that

$$\begin{aligned} \left\{ \begin{aligned}&\textrm{div} (\Theta ^\ell _{ij}) = -W^\ell _{ij} + | Y_f|^{-1} K^\ell _{ij} \quad \text { in } Y_f,\\&\Theta _{ij}^\ell =0 \quad \text { in } Y_s. \end{aligned}\right. \end{aligned}$$

(6.2)

Fix $\varphi \in C_0^\infty (B(0, 1/8))$ such that $\varphi \ge 0$ and $\int _{{\mathbb {R}}^d} \varphi \, \mathrm{{d}}x =1$. Define

$$\begin{aligned} S_\varepsilon (\psi ) (x) =\psi * \varphi _\varepsilon (x)=\int _{{\mathbb {R}}^d} \psi (y) \varphi _\varepsilon (x-y)\, \mathrm{{d}}y, \end{aligned}$$

(6.3)

where $\varphi _\varepsilon (x)=\varepsilon ^{-d} \varphi (x)$. Let $\Phi _\varepsilon ^{(1)} =( \Phi _{\varepsilon , 1}^{(1)}, \dots , \Phi _{\varepsilon , d}^{(1)} )$, where, for $x\in \Omega _\varepsilon ^\ell$,

$$\begin{aligned} \Phi _{\varepsilon , k} ^{(1)} (x) =\varepsilon \eta ^\ell _\varepsilon (x) \Theta ^\ell _{kij} (x/\varepsilon ) \frac{\partial }{\partial x_i} S_\varepsilon \left( f_j -\frac{\partial P_0}{\partial x_j} \right) , \end{aligned}$$

(6.4)

and $P_0$ is the solution of (5.1). The function $\eta _\varepsilon ^\ell$ in (6.4) is a cut-off function in $C_0^\infty (\Omega ^\ell )$ with the properties that $|\nabla \eta _\varepsilon ^\ell |\le C\varepsilon ^{-1}$ and

$$\begin{aligned} \left\{ \begin{aligned}&\eta _\varepsilon ^\ell (x) =0 \quad \text { if dist} (x, \partial \Omega ^\ell )\le 2d \varepsilon ,\\&\eta ^\ell _\varepsilon (x)=1 \quad \text { if } x\in \Omega ^\ell \text { and dist} (x, \partial \Omega ^\ell )\ge 3d \varepsilon . \end{aligned}\right. \end{aligned}$$

As a result, $\Phi _\varepsilon ^{(1)}$ vanishes near $\partial \Omega ^\ell$.

Theorem 6.1

Let $\Phi _\varepsilon ^{(1)}$ be defined by (6.4). Then (5.15) holds.

Proof

Clearly, $\Phi _\varepsilon ^{(1)} \in H_0^1(\Omega _\varepsilon ; {\mathbb {R}}^d)$. Note that

$$\begin{aligned} \Vert \nabla \Phi _\varepsilon ^{(1)}\Vert _{L^2(\Omega _\varepsilon ^\ell )}&\le C \varepsilon ^{1/2} \Vert \nabla S_\varepsilon (f-\nabla P_0) \Vert _{L^\infty (N_{3d\varepsilon }\setminus N_{2d\varepsilon })} + C \Vert \nabla S_\varepsilon (f-\nabla P_0)\Vert _{L^\infty (\Omega ^\ell \setminus N_{2d\varepsilon })}\\&\quad + C \varepsilon \Vert \nabla ^2 S_\varepsilon (f-\nabla P_0)\Vert _{L^\infty (\Omega ^\ell \setminus N_{2d\varepsilon })}, \end{aligned}$$

where $N_r =\{ x\in \Omega ^\ell : \textrm{dist}(x, \partial \Omega ^\ell ) < r \}$. This, together with the observation that $\nabla S_\varepsilon (\psi )=S_\varepsilon ( \nabla \psi )$ and

yields

$$\begin{aligned} \varepsilon \Vert \nabla \Phi _\varepsilon ^{(1)} \Vert _{L^2(\Omega _\varepsilon ^\ell )}&\le C \varepsilon \Vert \nabla (f-\nabla P_0) \Vert _{L^\infty (\Omega ^\ell )}\\&\le C \varepsilon \Vert f \Vert _{C^{1, 1/2}(\Omega )}. \end{aligned}$$

Next, note that in $\Omega ^\ell _\varepsilon$,

$$\begin{aligned} \textrm{div} (\Phi _\varepsilon ^{(1)})&=\varepsilon (\nabla \eta _\varepsilon ^\ell ) \Theta ^\ell (x/\varepsilon ) \nabla S_\varepsilon (f-\nabla P_0) - \eta _\varepsilon ^\ell W^\ell (x/\varepsilon ) \nabla S_\varepsilon (f-\nabla P_0)\\&\quad +\varepsilon \eta _\varepsilon ^\ell \Theta ^\ell (x/\varepsilon ) \nabla ^2 S_\varepsilon (f-\nabla P_0), \end{aligned}$$

where we have used the fact that $\textrm{div} (K^\ell (f-\nabla P_0)) =0$ in $\Omega _\varepsilon ^\ell$. It follows that

$$\begin{aligned}&\Vert \textrm{div} (\Phi _\varepsilon ^{(1)}) + W^\ell (x/\varepsilon ) \nabla (f-\nabla P_0) \Vert _{L^2(\Omega _\varepsilon ^\ell )}\\&\quad \le C \varepsilon ^{1/2} \Vert \nabla (f-\nabla P_0)\Vert _{L^\infty (\Omega ^\ell )} + \Vert W^\ell (x/\varepsilon ) \left\{ \nabla (f-\nabla P_0) -\eta _\varepsilon ^\ell \nabla S_\varepsilon (f-\nabla P_0)\right\} \Vert _{L^2(\Omega _\varepsilon ^\ell )}\\&\qquad + C \varepsilon \Vert \nabla ^2 S_\varepsilon (f-\nabla P_0) \Vert _{L^\infty (\Omega _\varepsilon ^\ell \setminus N_{2d\varepsilon }) }\\&\quad \le C \varepsilon ^{1/2} \Vert \nabla (f-\nabla P_0)\Vert _{L^\infty (\Omega ^\ell )} + \Vert \nabla (f-\nabla P_0) -\nabla S_\varepsilon (f-\nabla P_0) \Vert _{L^\infty (\Omega ^\ell \setminus N_{2d\varepsilon })}\\&\qquad + C \varepsilon \Vert \nabla ^2 S_\varepsilon (f-\nabla P_0) \Vert _{L^\infty (\Omega ^\ell \setminus N_{2d\varepsilon }) }\\&\quad \le C \varepsilon ^{1/2} \Vert \nabla (f-\nabla P_0) \Vert _{C^{1/2} (\Omega ^\ell )}\\&\quad \le C \varepsilon ^{1/2} \Vert f\Vert _{C^{1, 1/2}(\Omega )}, \end{aligned}$$

where we have used (5.2) for the last inequality. In the third inequality above we also used the observation that

$$\begin{aligned} \nabla S_\varepsilon (\psi ) (x)= -\int _{{\mathbb {R}}^d} \left( \psi (x-y) -\psi (x)\right) \nabla _y (\varphi _\varepsilon (y) ) \, \mathrm{{d}}y, \end{aligned}$$

which gives

$$\begin{aligned} |\nabla S_\varepsilon (\psi ) (x)| \le C \varepsilon ^{\alpha -1}\Vert \psi \Vert _{C^{0, \alpha } (B(x, \varepsilon ))}. \end{aligned}$$

This completes the proof of (5.15). $\square$

7 Boundary Correctors

To construct the boundary corrector $\Phi _\varepsilon ^{(2)}$, we consider the Dirichlet problem,

$$\begin{aligned} \left\{ \begin{aligned}&-\varepsilon ^2 \Delta u_\varepsilon +\nabla p_\varepsilon =0 \quad \text { in } \Omega _\varepsilon \\&\textrm{div}(u_\varepsilon ) =\gamma \quad \text { in } \Omega _\varepsilon ,\\&u_\varepsilon =0 \quad \text { on } \Gamma _\varepsilon ,\\&u_\varepsilon =h \quad \text { on } \partial \Omega , \end{aligned}\right. \end{aligned}$$

(7.1)

where $\Omega _\varepsilon$ is given by (1.4) and

$$\begin{aligned} \gamma =\frac{1}{|\Omega _\varepsilon |} \int _{\partial \Omega } h \cdot n \, \mathrm{{d}}\sigma . \end{aligned}$$

(7.2)

Let $\Phi _\varepsilon ^{(2)} \in H^1(\Omega _\varepsilon ; {\mathbb {R}}^d)$ be the solution of (7.1) with boundary value,

$$\begin{aligned} h= -V_\varepsilon \quad \text { on } \partial \Omega , \end{aligned}$$

(7.3)

where $V_\varepsilon$ is given by (5.3). Thus, if $\partial \Omega \cap \partial \Omega ^\ell \ne \emptyset$ for some $1\le \ell \le L$,

$$\begin{aligned} \Phi _\varepsilon ^{(2)} =- W^\ell (x/\varepsilon ) (f-\nabla P_0) \quad \text { on } \partial \Omega \cap \partial \Omega ^\ell . \end{aligned}$$

(7.4)

Theorem 7.1

Let $\Phi _\varepsilon ^{(2)}$ be defined as above. Then $\Phi _\varepsilon ^{(2)}$ satisfies (5.16).

To show Theorem 7.1, we first prove some general results, which will be used also in the construction of correctors for the interface.

Theorem 7.2

Let $\Omega$ be a bounded Lipschitz domain in ${\mathbb {R}}^d$, $d\ge 2$. Assume that $\Omega ^\ell$ and $Y_s^\ell$ with $1\le \ell \le L$ are subdomains of $\Omega$ and Y, respectively, with Lipschitz boundaries. Let $(u_\varepsilon , p_\varepsilon )$ be a weak solution in $H^1(\Omega _\varepsilon ; {\mathbb {R}}^d) \times L_0^2(\Omega _\varepsilon )$ of (7.1), where $h\in H^1(\partial \Omega ; {\mathbb {R}}^d)$ and

$$\begin{aligned} h\cdot n =0 \quad \text { on } \partial \Omega . \end{aligned}$$

(7.5)

Then

$$\begin{aligned} \varepsilon \Vert \nabla u_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} + \Vert u_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} +\Vert p_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} \le C \sqrt{\varepsilon } \left\{ \Vert h \Vert _{L^2(\partial \Omega )} +\varepsilon \Vert \nabla _{\tan } h \Vert _{L^2(\partial \Omega )} \right\} , \end{aligned}$$

(7.6)

where $\nabla _{\tan } h$ denotes the tangential gradient of h on $\partial \Omega$.

Proof

This theorem was proved in [14, Theorem 4.1] for the case $L=1$. The proof only uses the energy estimate (3.6) and the fact that

$$\begin{aligned} -\varepsilon ^2 \Delta u_\varepsilon +\nabla p_\varepsilon = 0 \quad \text { and } \quad \textrm{div}(u_\varepsilon )=0 \end{aligned}$$

in the set $\{ x\in \Omega :\ \textrm{dist} (x, \partial \Omega )< c\, \varepsilon \}$. As a result, the same proof works equally well for the case $L\ge 2$. We mention that the argument relies on the Rellich estimates in [7] for the Stokes equations in Lipschitz domains. The condition (7.5) allows us to drop the pressure $p_\varepsilon$ term in the conormal derivative $\partial u_\varepsilon /{\partial \nu }$ for $u_\varepsilon$ on $\partial \Omega$. We omit the details. $\square$

In the next theorem we consider the case where

$$\begin{aligned} h\cdot n =\varepsilon \ (\nabla _{\tan } \phi _\varepsilon ) \cdot g \quad \text { on } \partial \Omega . \end{aligned}$$

(7.7)

By using integration by parts on $\partial \Omega$, we see that

$$\begin{aligned} |\gamma |&\le C \Big |\int _{\partial \Omega } h\cdot n\, \mathrm{{d}}\sigma \Big |\nonumber \\&\le C\varepsilon \Vert \phi _\varepsilon \nabla _{\tan } g \Vert _{L^2(\partial \Omega )}. \end{aligned}$$

(7.8)

Theorem 7.3

Let $\Omega$ be a bounded $C^{2, \alpha }$ domain in ${\mathbb {R}}^d$, $d\ge 2$. Let $(u_\varepsilon , p_\varepsilon )$ be a weak solution in $H^1(\Omega _\varepsilon ; {\mathbb {R}}^d)\times L_0^2(\Omega )$ of (7.1), where $h\in H^1(\partial \Omega )$ and $h\cdot n$ is given by (7.7). Then

$$\begin{aligned}&\varepsilon \Vert \nabla u_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} +\Vert u_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} + \Vert p_\varepsilon \Vert _{L^2(\Omega _\varepsilon )}\nonumber \\&\quad \le C \sqrt{\varepsilon } \left\{ \Vert h\Vert _{L^2(\partial \Omega )} + \varepsilon \Vert \nabla _{\tan } h \Vert _{L^2(\partial \Omega )} +\Vert \phi _\varepsilon g \Vert _{L^2(\partial \Omega )} + \varepsilon ^{1/2} \Vert \phi _\varepsilon \nabla _{\tan } g \Vert _{L^2(\partial \Omega )}\right\} . \end{aligned}$$

(7.9)

Proof

A version of this theorem was proved in [14, Theorem 5.1] for the case $L=1$. We give the proof for the general case, using a somewhat different argument.

We first note that by writing

$$\begin{aligned} h= (h - (h\cdot n) n) + (h\cdot n) n \end{aligned}$$

and applying Theorem 7.2 to the solution of (7.1) with boundary data $h- (h\cdot n) n$, we may reduce the problem to case where $h=(h\cdot n) n$ on $\partial \Omega$.

Next, by the energy estimate (3.3) and (7.8),

$$\begin{aligned}&\varepsilon \Vert \nabla u_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} +\Vert u_\varepsilon \Vert _{L^2(\Omega _\varepsilon )} + \Vert p_\varepsilon \Vert _{L^2(\Omega _\varepsilon )}\nonumber \\&\quad \le C \left\{ \Vert H \Vert _{L^2(\Omega )} + \Vert \textrm{div}(H)\Vert _{L^2(\Omega )} + \varepsilon \Vert \nabla H \Vert _{L^2(\Omega )} + \varepsilon \Vert \phi _\varepsilon \nabla _{\tan } g \Vert _{L^2(\partial \Omega )} \right\} , \end{aligned}$$

(7.10)

where H is any function in $H^1(\Omega ; {\mathbb {R}}^d)$ with $H=h$ on $\partial \Omega$. We choose $H=H_1+ \gamma (x-x_0) /d$, where $x_0 \in \Omega$ and $H_1$ is the weak solution of

$$\begin{aligned} -\Delta H_1 +\nabla q =0 \quad \text { and } \quad \textrm{div}(H_1)=0 \quad \text { in } \Omega , \end{aligned}$$

with the boundary value $H_1=h- \gamma (x-x_0)/d$ on $\partial \Omega$. It follows that

$$\begin{aligned}&\varepsilon \Vert \nabla u_\varepsilon \Vert _{L^2(\Omega )} +\Vert u_\varepsilon \Vert _{L^2(\partial \Omega )} + \Vert p_\varepsilon \Vert _{L^2(\Omega )}\nonumber \\&\quad \le C \left\{ \Vert H _1\Vert _{L^2(\Omega )} + \varepsilon \Vert \nabla H_1 \Vert _{L^2(\Omega )} + \varepsilon \Vert \phi _\varepsilon \nabla _{\tan } g \Vert _{L^2(\partial \Omega )}\right\} , \end{aligned}$$

(7.11)

where we have used (7.8). By the energy estimates for the Stokes equations in $\Omega$,

$$\begin{aligned} \Vert \nabla H_1 \Vert _{L^2(\Omega )}&\le C \left\{ \Vert h \Vert _{H^{1/2}(\partial \Omega )} +|\gamma |\right\} \\&\le C\left\{ \Vert h\Vert _{L^2(\partial \Omega )}^{1/2} \Vert h \Vert ^{1/2}_{H^1(\partial \Omega )} + |\gamma | \right\} \\&\le C \left\{ \varepsilon ^{-1/2} \Vert h\Vert _{L^2(\partial \Omega )} + \varepsilon ^{1/2} \Vert \nabla _{\tan } h \Vert _{L^2(\partial \Omega )} + |\gamma |\right\} . \end{aligned}$$

It follows that

$$\begin{aligned} \varepsilon \Vert \nabla H_1 \Vert _{L^2(\Omega )} \le C\sqrt{\varepsilon } \left\{ \Vert h \Vert _{L^2(\partial \Omega )} + \varepsilon \Vert \nabla _{\tan } h \Vert _{L^2(\partial \Omega )} + \varepsilon \Vert \phi _\varepsilon \nabla _{\tan } g \Vert _{L^2(\partial \Omega )} \right\} . \end{aligned}$$

(7.12)

To bound $\Vert H_1\Vert _{L^2(\Omega )}$, we use the following nontangential-maximal-function estimate,

$$\begin{aligned} \Vert (H_1)^* \Vert _{L^2(\partial \Omega )} \le C \Vert H_1 \Vert _{L^2(\partial \Omega )}, \end{aligned}$$

(7.13)

where the nontangential maximal function $(H_1)^*$ on $\partial \Omega$ is defined by

$$\begin{aligned} (H_1)^*(x)=\sup \big \{ |H_1(y)|: \ y\in \Omega \text { and } |y-x|< C_0\, \text {dist}(y, \partial \Omega ) \big \} \end{aligned}$$

for $x\in \partial \Omega$. The estimate (7.13) was proved in [7] for a bounded Lipschitz domain $\Omega$. Let

$$\begin{aligned} N_r =\big \{ x\in \Omega : \ \text {dist}(x, \partial \Omega )< r\big \}. \end{aligned}$$

It follows from (7.13) that

$$\begin{aligned} \Vert H_1 \Vert _{L^2(N_\varepsilon )}&\le C \sqrt{\varepsilon } \Vert (H_1)^*\Vert _{L^2(\partial \Omega )}\nonumber \\&\le C \sqrt{\varepsilon } \left\{ \Vert h \Vert _{L^2(\partial \Omega )} +\varepsilon \Vert \phi _\varepsilon \nabla _{\tan } g \Vert _{L^2(\partial \Omega )} \right\} . \end{aligned}$$

(7.14)

It remains to bound $\Vert H_1 \Vert _{L^2(\Omega \setminus N_\varepsilon )}$. To this end, we consider the Dirichlet problem,

$$\begin{aligned} \left\{ \begin{aligned}&-\Delta G +\nabla \pi =F \quad \text { in } \Omega ,\\&\textrm{div} (G) =0 \quad \text { in } \Omega ,\\&G =0 \quad \text { on } \partial \Omega , \end{aligned}\right. \end{aligned}$$

where $F \in C_0^\infty (\Omega {\setminus } N_\varepsilon )$ and $\int _{ \Omega } \pi \, \mathrm{{d}}x =0$. Under the assumption that $\partial \Omega$ is of $C^{2, \alpha }$, we have the $W^{2, 2}$ estimates,

$$\begin{aligned} \Vert G \Vert _{H^2(\Omega )} +\Vert \pi \Vert _{H^1(\Omega )} \le C \Vert F \Vert _{L^2(\Omega )}. \end{aligned}$$

(7.15)

This implies that

$$\begin{aligned} \Vert \nabla G \Vert _{L^2(\partial \Omega )} + \Vert \pi \Vert _{L^2(\partial \Omega )} \le C \Vert F \Vert _{L^2(\Omega )}. \end{aligned}$$

(7.16)

Moreover, since $F=0$ in $N_\varepsilon$, by covering $\partial \Omega$ with balls of radius $c\varepsilon$, one may show that

$$\begin{aligned} \int _{\partial \Omega } \left( |\nabla ^2 G |^2 + |\nabla \pi |^2 \right) \, \mathrm{{d}}\sigma \le C \varepsilon ^{-1} \Vert F \Vert _{L^2(\Omega )}^2. \end{aligned}$$

(7.17)

To see this, we use the Green function representation for G to obtain

$$\begin{aligned} |\nabla ^2 G(x)| \le C \int _{\Omega \setminus N_\varepsilon } \frac{|F(y)|}{|x-y|^d } \, \mathrm{{d}}y \end{aligned}$$

(7.18)

for $x\in \partial \Omega$. See e.g. [8] for estimates of Green functions for the Stokes equations. Choose $\alpha , \beta \in (0, 1)$ such that $\alpha +\beta =1$, $\alpha >(1/2)$ and $\beta > (1/2)-(1/2d)$. It follows by the Cauchy inequality that for $x\in \partial \Omega$,

$$\begin{aligned} |\nabla ^2 G(x)|^2&\le C \left( \int _{\Omega \setminus N_\varepsilon } \frac{\mathrm{{d}}y}{|x-y|^{2\mathrm{{d}}\alpha }}\right) \left( \int _{\Omega \setminus N_\varepsilon } \frac{|F(y)|^2}{|x-y|^{2\mathrm{{d}}\beta }} \, \mathrm{{d}}y \right) \\&\le C \varepsilon ^{d-\mathrm{{d}}d\alpha } \int _{\Omega \setminus N_\varepsilon } \frac{|F(y)|^2}{|x-y|^{2\mathrm{{d}}\beta }} \, \mathrm{{d}}y, \end{aligned}$$

where we have used the conditions $\alpha +\beta =1$ and $\alpha >(1/2)$. Hence,

$$\begin{aligned} \int _{\partial \Omega } |\nabla ^2 G|^2\, \mathrm{{d}}\sigma&\le C \varepsilon ^{d-2d\alpha } \int _{\Omega \setminus N_\varepsilon } |F(y)|^2\, \mathrm{{d}}y \sup _{y\in \Omega \setminus N_\varepsilon } \int _{\partial \Omega } \frac{\mathrm{{d}}\sigma (x)}{|x-y|^{2d\beta }}\\&\le C \varepsilon ^{-1}\int _{\Omega } |F(y)|^2\, \mathrm{{d}}y, \end{aligned}$$

where we have used the condition $\beta >(1/2)-(1/2d)$. This gives the estimate for $|\nabla ^2 G|$ in (7.17). The estimate for $\nabla \pi$ follows from the equation $-\Delta G+\nabla \pi =0$ near $\partial \Omega$.

Finally, using integration by parts, we see that

$$\begin{aligned} \int _\Omega H_1\cdot F\, \mathrm{{d}}x&= \int _\Omega H_1 \cdot (-\Delta G + \nabla \pi )\, \mathrm{{d}}x \\&=- \int _{\partial \Omega } H_1 \cdot \Big (\frac{\partial G}{\partial n} -n\pi \Big )\, \mathrm{{d}}\sigma \\&=-\int _{\partial \Omega } \Big ( \varepsilon ( (\nabla _{\tan } \phi _\varepsilon ) \cdot g ) n - \gamma (x-x_0)/d \Big ) \cdot \Big (\frac{\partial G}{\partial n} -n\pi \Big )\, \mathrm{{d}}\sigma .\\ \end{aligned}$$

It follows by using integration by parts on $\partial \Omega$ that

$$\begin{aligned}&\Big | \int _\Omega H_1 \cdot F\, \mathrm{{d}}x \Big |\\&\quad \le C\varepsilon \int _{\partial \Omega } |\phi _\varepsilon |\left( |\nabla g| |\nabla G| +|g| |\nabla ^2 G| + |g| |\nabla G| + |\nabla g| |\pi | + |g| |\nabla \pi | + |g| |\pi | \right) \, \mathrm{{d}}\sigma \\&\qquad + |\gamma | \int _{\partial \Omega } \left( |\nabla G| + |\pi |\right) \, \mathrm{{d}}\sigma \\&\quad \le C \varepsilon \Vert \phi _\varepsilon g \Vert _{L^2(\partial \Omega )} \left\{ \Vert \nabla ^2 G \Vert _{L^2(\partial \Omega )} + \Vert \nabla G \Vert _{L^2(\partial \Omega )} + \Vert \nabla \pi \Vert _{L^2(\partial \Omega )} + \Vert \pi \Vert _{L^2(\partial \Omega )} \right\} \\&\qquad + C \varepsilon \Vert \phi _\varepsilon \nabla _{\tan } g \Vert _{L^2(\partial \Omega )} \left\{ \Vert \nabla G\Vert _{L^2(\partial \Omega )} + \Vert \pi \Vert _{L^2(\partial \Omega )}\right\} ,\\ \end{aligned}$$

where we have used the Cauchy inequality and (7.8). This, together with (7.16) and (7.17), gives

$$\begin{aligned} \Big | \int _\Omega H_1 \cdot F\, \mathrm{{d}}x \Big | \le C \varepsilon ^{1/2} \Vert F \Vert _{L^2(\Omega )} \left\{ \Vert \phi _\varepsilon g \Vert _{L^2(\partial \Omega )} + \varepsilon ^{1/2} \Vert \phi _\varepsilon \nabla _{\tan } g \Vert _{L^2(\partial \Omega )} \right\} . \end{aligned}$$

By duality we obtain

$$\begin{aligned} \Vert H_1 \Vert _{L^2(\Omega \setminus N_\varepsilon )} \le C \varepsilon ^{1/2} \left\{ \Vert \phi _\varepsilon g \Vert _{L^2(\partial \Omega )} + \varepsilon ^{1/2} \Vert \phi _\varepsilon \nabla _{\tan } g \Vert _{L^2(\partial \Omega )} \right\} . \end{aligned}$$

(7.19)

The desired estimate (7.9) follows from (7.10), (7.12), (7.14) and (7.19). $\square$

Proof of Theorem 7.1

Clearly, by its definition, $\Phi _\varepsilon ^{(2)} \in H^1(\Omega _\varepsilon ; {\mathbb {R}}^d)$, $\Phi _\varepsilon ^{(2)}=0$ on $\Gamma _\varepsilon$, and $\Phi _\varepsilon ^{(2)}+V_\varepsilon =0$ on $\partial \Omega$. Using the fact that $n \cdot K^\ell (f-\nabla P_0) =0$ on $\partial \Omega \cap \partial \Omega ^\ell$, we obtain

$$\begin{aligned} n \cdot h&=-n \cdot W^\ell (x/\varepsilon ) (f-\nabla P_0)\nonumber \\&=-n \cdot (W^\ell (x/\varepsilon ) -K^\ell ) (f-\nabla P_0)\nonumber \\&= -\frac{\varepsilon }{2} \left( n_i \frac{\partial }{\partial x_k} - n_k\frac{\partial }{\partial x_i}\right) \left( \phi ^\ell _{kij} (x/\varepsilon ) \right) \left( f_j -\frac{\partial P_0}{\partial x_j} \right) \end{aligned}$$

(7.20)

on $\partial \Omega \cap \partial \Omega ^\ell$. It follows that

$$\begin{aligned} \Big | \int _{\partial \Omega } n \cdot h \, \mathrm{{d}}\sigma \Big | \le C\varepsilon \Vert \nabla (f-\nabla P_0) \Vert _{L^\infty (\partial \Omega )}. \end{aligned}$$

Hence,

$$\begin{aligned} \Vert \textrm{div}(\Phi _\varepsilon ^{(2)}) \Vert _{L^2(\Omega _\varepsilon )}&\le C |\gamma | \le C \varepsilon \Vert \nabla ( f-\nabla P_0)\Vert _{L^\infty (\partial \Omega )}\\&\le C \varepsilon \Vert f\Vert _{C^{1, 1/2} (\Omega )}. \end{aligned}$$

Finally, in view of (7.20), we apply Theorem 7.3 to obtain

$$\begin{aligned} \varepsilon \Vert \nabla \Phi _\varepsilon ^{(2)} \Vert _{L^2(\Omega )}&\le C \varepsilon ^{1/2} \left\{ \Vert f-\nabla P_0\Vert _{L^\infty (\partial \Omega )} + \varepsilon ^{1/2} \Vert \nabla (f-\nabla P_0) \Vert _{L^\infty (\partial \Omega )} \right\} \\&\le C \varepsilon ^{1/2} \Vert f \Vert _{C^{1, 1/2} (\Omega )}. \end{aligned}$$

$\square$

8 Interface Correctors

In this section we construct a corrector $\Phi _\varepsilon ^{(3)}$ for the interface $\Sigma$ and thus completes the proof of Theorem 1.2. Let $D=\Omega ^\ell$ and $D_\varepsilon =\Omega ^\ell _\varepsilon$ for some $1\le \ell \le L$. Assume that $\partial D$ has no intersection with the boundary of the unbounded connected component of ${\mathbb {R}}^d\setminus \overline{\Omega }$. Consider the Dirichlet problem,

$$\begin{aligned} \left\{ \begin{aligned}&-\Delta u_\varepsilon +\nabla p_\varepsilon =0 \quad \text { in } D_\varepsilon ,\\&\textrm{div} (u_\varepsilon ) =\gamma \quad \text { in } D_\varepsilon ,\\&u_\varepsilon =0 \quad \text { on } \Gamma _\varepsilon ^\ell , \\&u_\varepsilon = h \quad \text { on } \partial D, \end{aligned}\right. \end{aligned}$$

(8.1)

where $\Gamma _\varepsilon ^\ell =\Gamma _\varepsilon \cap D$ and

$$\begin{aligned} \gamma =\frac{1}{|D_\varepsilon |}\int _{\partial D} h \cdot n \, \mathrm{{d}}\sigma . \end{aligned}$$

Let $W^+(y)=W ^\ell (y)$. Fix $1\le j\le d$, the boundary data h on $\partial D$ in (8.1) is given as follows. Let $\partial D= \cup _{k=1}^{k_0} \Sigma ^k$, where $\Sigma ^k$ are the connected component of $\partial D$. On each $\Sigma ^k$, either

$$\begin{aligned} h=0 \end{aligned}$$

(8.2)

or

$$\begin{aligned} h=W^-_j (x/\varepsilon ) -W^+_j (x/\varepsilon ) -W^-_{i} (x/\varepsilon ) (K^-_{mj } -K^+_{mj}) \frac{ n_i n_m}{\langle nK^-, n\rangle }, \end{aligned}$$

(8.3)

where $W^-(y)$ denotes the 1-periodic matrix defined by (2.1) for the subdomain on the other side of $\Sigma ^k$, and

$$\begin{aligned} K^+ =\int _Y W^+ (y) \, \mathrm{{d}}y, \quad K^- =\int _Y W^- (y)\, \mathrm{{d}}y. \end{aligned}$$

In particular, if $\Sigma ^ k\subset \partial \Omega$, we let $h=0$ on $\Sigma ^k$. Note that the repeated indices i, m in (8.3) are summed from 1 to d.

Lemma 8.1

Let D be a bounded $C^{2, \alpha }$ domain in ${\mathbb {R}}^d$, $d\ge 2$. Let $(u_\varepsilon , p_\varepsilon )$ be a weak solution of (8.1) with $\int _{D_\varepsilon } p_\varepsilon \, \mathrm{{d}}x =0$, where h is given by (8.2) and (8.3). Then

$$\begin{aligned} \varepsilon \Vert \nabla u_\varepsilon \Vert _{L^2(D_\varepsilon )}+ \Vert u_\varepsilon \Vert _{L^2(D_\varepsilon )} + \Vert p_\varepsilon \Vert _{L^2(D_\varepsilon )}\le C \sqrt{\varepsilon }, \end{aligned}$$

(8.4)

and

$$\begin{aligned} \Vert \textrm{div}(u_\varepsilon )\Vert _{L^2(D_\varepsilon )} \le C \varepsilon . \end{aligned}$$

(8.5)

Proof

We apply Theorem 7.3 with $\Omega =D$ to establish (8.4). First, observe that by (2.5),

$$\begin{aligned} \Vert h \Vert _{L^2(\partial D)} + \varepsilon \Vert \nabla _{\tan } h \Vert _{L^2(\partial D)} \le C. \end{aligned}$$

(8.6)

Next, we compute $u\cdot n$ on $\Sigma ^k$, assuming h is given by (8.3). Note that

$$\begin{aligned} h\cdot n&= n_t W_{tj}^- (x/\varepsilon )-n_t W^+_{tj} (x/\varepsilon ) -n_t W^-_{ti} (x/\varepsilon ) (K_{mj}^- -K_{mj}^+) \frac{n_i n_m}{\langle n K^-, n \rangle }\nonumber \\&= n_t \left( W_{tj}^- (x/\varepsilon ) -K_{tj}^-\right) -n_t \left( W^+_{tj} (x/\varepsilon ) -K_{tj}^+ \right) \nonumber \\&\quad -n_t \left( W^-_{ti}(x/\varepsilon ) - K_{ti}^-\right) (K_{mj}^- -K_{mj}^+) \frac{n_i n_m}{\langle n K^-, n \rangle }, \end{aligned}$$

(8.7)

where the repeated indices t, i, m are summed from 1 to d. We use Lemma 2.2 to write

$$\begin{aligned} n_t \left( W_{ti}^\pm (x/\varepsilon ) -K_{ti}^\pm \right) =\frac{\varepsilon }{2} \left( n_t \frac{\partial }{\partial x_s} -n_s\frac{\partial }{\partial x_t} \right) \left( \phi ^\pm _{st i} (x/\varepsilon ) \right) . \end{aligned}$$

(8.8)

As a result, the function in the right-hand side of (8.7) may be written in the form $\varepsilon (\nabla _{\tan } \phi _\varepsilon ) \cdot g$ with $(\phi _\varepsilon , g)$ satisfying

$$\begin{aligned} \Vert \phi _\varepsilon \Vert _{L^2(\partial D)} + \Vert g\Vert _\infty + \Vert \nabla _{\tan } g \Vert _\infty \le C. \end{aligned}$$

Consequently, the estimate (8.4) follows from (7.9) in Theorem 7.3. Finally, note that (8.7) and (8.8) yield

$$\begin{aligned} \Vert \textrm{div} (u_\varepsilon ) \Vert _{L^2(D_\varepsilon )}&\le C \Big | \int _{\partial D} h\cdot n \, \mathrm{{d}}\sigma \Big |\\&\le C \varepsilon . \end{aligned}$$

$\square$

Define

$$\begin{aligned} \Phi ^{(3)}_\varepsilon = \sum _{\ell =1}^L I_\varepsilon ^\ell (x) (f-\nabla P_0) \chi _{\Omega _\varepsilon ^\ell } \quad \text { in } \Omega _\varepsilon , \end{aligned}$$

(8.9)

where $I^\ell _\varepsilon =(I_{\varepsilon , 1} ^\ell , \dots , I_{\varepsilon , d}^\ell )$ is a solution of (8.1) in $D_\varepsilon =\Omega ^\ell _\varepsilon$ with h given by (8.2) and (8.3). To fix the boundary value h for each subdomain, we assume that the unbounded connected component of ${\mathbb {R}}^d\setminus \overline{\Omega }$ shares boundary with $\Omega ^1$, and let $h=0$ on $\partial \Omega ^1$. Thus, $I^1_\varepsilon (x) = 0$ and $\Phi _\varepsilon ^{(3)} =0$ in $\Omega ^1$. Next, for each subdomain $\Omega ^\ell$ that shares boundaries with $\partial \Omega ^1$, we use the boundary data (8.3) for the common boundary with $\partial \Omega ^1$ and let $h=0$ on other components of $\partial \Omega ^\ell$. We continue this process. More precisely, at each step, we use (8.3) on the connected component $\Sigma ^k$ of $\partial \Omega ^\ell$ if $\Sigma ^k$ is also the connected component of the boundary of a subdomain considered in the previous step, and let $h=0$ on the remaining components. We point out that at each interface $\Sigma ^k$, the nonzero data (8.3) is used only once. Also, $h=0$ on $\partial \Omega$.

Lemma 8.2

Let $\Phi ^{(3)} _\varepsilon$ be given by (8.9) with $f\in C^{1, 1/2} ({\Omega ; {\mathbb {R}}^d})$. Then $V_\varepsilon +\Phi _\varepsilon ^{(3)} \in H^1(\Omega _\varepsilon ; {\mathbb {R}}^d)$.

Proof

Let $\Psi _\varepsilon =V_\varepsilon + \Phi _\varepsilon ^{(3)}$. Since $f\in C^{1, 1/2}(\Omega )$ implies that $\nabla ^2 P_0$ is bounded in each subdomain, it follows that $\Psi _\varepsilon \in H^1(\Omega _\varepsilon ^\ell ; {\mathbb {R}}^d)$ for $1\le \ell \le L$. Thus, to show $\Psi _\varepsilon \in H^1(\Omega _\varepsilon ; {\mathbb {R}}^d)$, it suffices to show that the trace of $\Psi _\varepsilon$ is continuous across each interface $\Sigma ^k$.

Suppose that $\Sigma ^k$ is the common boundary of subdomains $\Omega ^+$ and $\Omega ^-$. Let $\Psi _\varepsilon ^\pm$ denote the trace of $\Psi _\varepsilon$ on $\Sigma ^k$, taken from $\Omega ^\pm$ respectively. Recall that in the definition of $\{ I_\varepsilon ^\ell \}$, the non-zero data (8.3) is used once on each interface. Assume that the non-zero data on $\Sigma ^k$ is used for $\Omega ^+$. Then

$$\begin{aligned} \Psi _\varepsilon ^+ -\Psi _\varepsilon ^- =\left( W^+ (x/\varepsilon ) + I^+ _\varepsilon (x)\right) (f-\nabla P_0)^+ -W^- (x/\varepsilon ) (f-\nabla P_0)^-, \end{aligned}$$

where $I^+_\varepsilon$ is given by (8.3). It follows that

$$\begin{aligned} \Psi _\varepsilon ^+ -\Psi _\varepsilon ^-&=\left( W_j^- (x/\varepsilon ) -W_i^-(x/\varepsilon ) ( K_{mj}^- -K_{mj}^+) \frac{n_i n_m}{\langle n K^-, n \rangle } \right) \left( f_j -\frac{\partial P_0}{\partial x_j} \right) ^+\\&\quad -W^-_j (x/\varepsilon ) \left( f_j -\frac{\partial P_0}{\partial x_j} \right) ^-\\&=W_j^- (x/\varepsilon ) \left\{ \left( \frac{\partial P_0}{\partial x_j} \right) ^- -\left( \frac{\partial P_0}{\partial x_j} \right) ^+ -\frac{n_j n_m}{\langle nK^-, n\rangle } K_{mi}^- \left( f_i -\frac{\partial P_0}{\partial x_i} \right) ^+\right\} \\&\quad +W_j^-(x/\varepsilon ) \frac{n_j n_m}{\langle n K^-, n \rangle } K_{mi}^- \left( f_i -\frac{\partial P_0}{ \partial x_i} \right) ^- , \end{aligned}$$

where we have used the observation that

$$\begin{aligned} n_m K_{mi}^+ \left( f_i -\frac{\partial P_0}{\partial x_i} \right) ^+ =n_m K_{mi}^- \left( f_i -\frac{\partial P_0}{\partial x_i} \right) ^- \end{aligned}$$

(8.10)

on the interface. Thus,

$$\begin{aligned} \Psi _\varepsilon ^+ -\Psi _\varepsilon ^-&=W_j^-(x/\varepsilon ) \left\{ \left( \frac{\partial P_0}{\partial x_j} \right) ^- -\left( \frac{\partial P_0}{\partial x_j}\right) ^+ -\frac{n_j n_m}{\langle n K^-, n \rangle } K_{mi}^- \left( \left( \frac{\partial P_0}{\partial x_i} \right) ^- -\left( \frac{\partial P_0}{\partial x_i} \right) ^+ \right) \right\} \\&=W_j^-(x/\varepsilon )\left\{ \delta _{ij}-\frac{n_j n_m}{\langle n K^-, n \rangle } K_{mi}^- \right\} \left( \left( \frac{\partial P_0}{\partial x_i} \right) ^- -\left( \frac{\partial P_0}{\partial x_i} \right) ^+ \right) . \end{aligned}$$

Since

$$\begin{aligned} n_i \left\{ \delta _{ij} -\frac{n_j n_m}{\langle n K^-, n \rangle } K_{mi}^- \right\} =0 \end{aligned}$$

and $(\nabla _{\tan } P_0)^+ = (\nabla _{\tan } P_0)^-$ on $\Sigma ^k$, we obtain $\Psi _\varepsilon ^+ =\Psi _\varepsilon ^-$ on $\Sigma ^k$. $\square$

Theorem 8.3

Let $\Phi _\varepsilon ^{(3)}$ be defined by (8.9) with $f\in C^{1, 1/2} (\Omega ; {\mathbb {R}}^d)$. Then $V_\varepsilon + \Phi _\varepsilon ^{(3)}\in H^1(\Omega ; {\mathbb {R}}^d)$ and

$$\begin{aligned} \varepsilon \Vert \nabla \Phi _\varepsilon ^{(3)} \Vert _{L^2(\Omega ^\ell _\varepsilon )} +\Vert \textrm{div} (\Phi _\varepsilon ^{(3)} ) \Vert _{L^2(\Omega ^\ell _\varepsilon )} \le C \varepsilon ^{1/2} \Vert f \Vert _{C^{1, 1/2}(\Omega )} \end{aligned}$$

(8.11)

for $1\le \ell \le L$.

Proof

By Lemma 8.2, we have $V_\varepsilon + \Phi _\varepsilon ^{(3)} \in H^1(\Omega ; {\mathbb {R}}^d)$. Note that by Lemma 8.1,

$$\begin{aligned} \varepsilon \Vert \nabla I_\varepsilon ^\ell \Vert _{L^2(\Omega _\varepsilon ^\ell )} + \Vert I_\varepsilon ^\ell \Vert _{L^2(\Omega _\varepsilon ^\ell )} + \Vert \textrm{div} (I_\varepsilon ^\ell )\Vert _{L^2(\Omega _\varepsilon ^\ell )} \le C \varepsilon ^{1/2} \end{aligned}$$

for $1\le \ell \le L$. It follows that

$$\begin{aligned} \varepsilon \Vert \nabla \Phi _\varepsilon ^{(3)} \Vert _{L^2(\Omega _\varepsilon ^\ell )}&\le \varepsilon \Vert \nabla I_\varepsilon ^\ell \Vert _{L^2(\Omega _\varepsilon ^\ell )} \Vert f -\nabla P_0\Vert _{L^\infty (\Omega _\varepsilon ^\ell )} + \varepsilon \Vert I_\varepsilon ^\ell \Vert _{L^2(\Omega _\varepsilon ^\ell )} \Vert \nabla (f-\nabla P_0) \Vert _{L^\infty (\Omega _\varepsilon ^\ell )}\\&\le C \varepsilon ^{1/2} \Vert f\Vert _{C^{1, 1/2}(\Omega )}, \end{aligned}$$

and

$$\begin{aligned} \Vert \textrm{div} (\Phi _\varepsilon ^{(3)} ) \Vert _{L^2(\Omega _\varepsilon ^\ell )}&\le \Vert \textrm{div}(I_\varepsilon ^\ell ) \Vert _{L^2(\Omega ^\ell _\varepsilon )} \Vert f-\nabla P_0 \Vert _{L^\infty (\Omega ^\ell )} + \Vert I^\ell _\varepsilon \Vert _{L^2(\Omega _\varepsilon ^\ell )} \Vert \nabla (f-\nabla P_0) \Vert _{L^\infty (\Omega _\varepsilon ^\ell )}\\&\le C \varepsilon ^{1/2} \Vert f \Vert _{C^{1, 1/2} (\Omega )}. \end{aligned}$$

$\square$