1 Introduction

Tungsten heavy alloys (WHAs) have excellent mechanical properties such as high strength, high density, considerable ductility, better corrosion resistance, and high radiation absorption coefficient. These alloys are mainly used for kinetic energy penetrators (KEPs) and fragmentation devices [1]. Moreover, other applications include counterweights, rotating inertia members, X­ray and γ-radiation shields, and rigid tools for machining [2]. The main focus in the design of KEPs is to achieve greater depth of penetration (DOP) to defeat the protection capability of armour systems on battle tanks [3]. In the continuous process of achieving higher DOP, enhancing the ballistic performance of KEPs is the foremost priority. The ballistic performance, on the other hand, depends mainly on the mechanical properties of WHAs. The improvement in the mechanical response of WHAs is to be analysed when the KEP is launched at different strain rates over the armour target during the ballistic impact [4]. Therefore, it becomes necessary to study the plastic deformation behaviour of WHA material subjected to different strain rates.

The material is affected by the combination of strain, strain rates, and temperatures during the ballistic impact. Therefore, it becomes highly challenging to predict plastic flow behaviour [5]. To understand the thermo-mechanical flow behaviour of WHAs at different strain rates and temperatures, various constitutive models have been developed so far that give plastic flow stress relation as the function of combined strain rate, strain, and temperature. Over the years, considerable efforts have been made to develop several constitutive models to describe the material behaviour at different strain rates and temperatures. However, accurate prediction of flow stress behaviour is challenging. Furthermore, the accuracy of finite element simulations of physical systems highly depends on trustworthy constitutive model behaviour [6].

Constitutive models are categorised into three types, viz., (i) phenomenological models [7, 8], (ii) physical-based models [9, 10], and (iii) predictive models such as artificial neural networks (ANN) [11, 12]. Phenomenological models are based on empirical relations consisting of mathematical functions which lack physical background. These models are more sensitive to data and strongly rely on model structures and assumptions. However, the development of these types of models is comparatively easier. However, the applicability of these models is limited to particular cases only. On the other hand, physical-based models focus on physical aspects of material behaviour like thermodynamics theory, thermally activated dislocation movement, and slip kinetics. However, determining these physical aspects is challenging, making developing these alloys difficult. In recent times, with the progress and continuous development of computer science and technology, predictive-based modelling like ANN and support vector machine (SVM) is getting attention because of better prediction capabilities and ease of development. Nevertheless, accurate predictions require careful training and testing for an extensive range of data.

Over the years, the Johnson–Cook (JC) phenomenological-based model has been widely used to predict the hot deformation behaviour of a material. Additionally, JC models have been incorporated in many commercially available finite element (FE) simulation software, which helps researchers efficiently implement the model in simulations [13, 14]. The original JC model considers the work hardening, strain rate, and temperature effect independent of flow stress prediction, which may affect the prediction capability. Few researchers have proposed modifications in the original JC model for accurate flow stress prediction [15,16,17,18,19,20].

Zhang et al. [15] coupled the strain hardening coefficient with homologous temperature, showing the variation of yield stress and hardening with respect to temperature change for Ni–Al-based superalloy under tensile tests at strain rates (0.00001–0.01 s−1) and temperatures (25–800 ℃). Vural & Caro [16] modified the JC model for 2139-T8 alloy. They coupled the coefficient of strain hardening with thermal softening and the strain rate sensitivity term, which demonstrate the promising prediction capabilities for 2139-T8 alloy. Shin & Kim [17] decoupled strain hardening, strain rate hardening, and thermal softening terms describing the exponential rise of flow stress with logarithmic strain rate. They proposed a modified JC model which is used to predict the thermal softening of many metals at low and high temperatures. Lin & Chen [18] combined the JC and ZA models, which combine the yield and strain hardening portion of the JC model with the temperature and strain rate portion of the ZA model to represent the coupled behaviour of the temperature and strain rate effect of typical high-strength alloy steel under uniaxial compression at strain rates 1–50 s−1 and temps 850–1150 °C. Another work by Lin & Chen [19] considered the coupled effects of strain, strain rate, and deformation temperature to describe the tensile behaviour of the studied alloy steel under uniaxial tensile tests at strain rates 0.0001–0.01 s−1 and temps 850–900 ℃. Recently, Shen et al. [20] replaced the strain term of the JC model with the Voce hardening model and corrected the strain rate sensitivity coefficient and thermal softening exponent for 6061 aluminium alloy subjected to uniaxial tensile tests. The proposed modification demonstrated promising results compared with the original JC model.

Considerable work on flow stress prediction using various constitutive models has been reported. Based on the nature of flow stress curves, few researchers proposed modifications in the original JC model. However, many changes were mainly focused on increasing the number of coefficient terms for better prediction of flow stress behaviour. Recently, Shen et al. [20] demonstrated the effective use of the suitable hardening model to accurately replace the strain term in the JC model to predict the flow stress behaviour of 6061 aluminium alloy. This study provides new insight into modifying the JC model with suitable hardening equations to predict flow stress behaviour accurately. Therefore, to improve the prediction accuracy of the hot deformation behaviour of a 92W–5Co–3Ni alloy, this work establishes an improved JC model by replacing the strain term with the Ludwigson hardening equation. The present work mainly proposes an improvement in the original JC model, which replaced the strain term with Ludwigson’s work hardening equation. At the same time, to verify the accuracy of the newly proposed improved JC model (i-JC), JC and m-JC models were developed, and the prediction accuracy of the i-JC model was compared with these two models.

2 Experimental details

The as-received 92W–5Co–3Ni alloy was used for compression testing. The chemical composition is displayed in Table 1. The specimen was cut by wire electro-discharge machining for better surface finish and accuracy. For the compression test, the samples were made with a cylindrical geometry of sample length of 15 mm and diameter of 10 mm, maintaining (l/d) of 1.5 as per ASTM-E9 standards. The uniaxial compression tests at different strain rates and elevated temperatures were performed on the Gleeble-3800 Closed Loop thermo-mechanical simulator, as shown in Fig. 1a–c. The samples were subjected to various strain rates and temperatures, as shown in Table 2.

Table 1 Chemical composition of elements in 92W–5Co–3Ni alloy
Full size table
Fig. 1
figure 1

Gleeble 3800 thermo-mechanical simulator a thermocouple welder b thermocouples attached to the specimen c sample loaded in wedge gap between anvils

Full size image
Table 2 Plan of compression testing experiments at different strain rates and temperatures
Full size table

K-type thermocouples made of nickel–chrome–aluminium were spot welded at 30 V voltage to the sample to get embedded with them using a Gleeble Thermocouple welder as shown in Fig. 1a. The ends of the sample were polished with a suitable amount of nickel paste before being placed in the wedge gap between the anvils of the simulator to avoid end friction between tungsten carbide anvil edges and sample ends. The thermocouple-embedded sample polished with Ni paste was sandwiched between anvils in a horizontal position, as shown in Fig. 1b, c. This ensured perfect gripping by adjusting the stroke and jaw ends of the anvils. During compression testing, graphite foils were used between specimens and anvils to reduce friction between the contact surfaces.

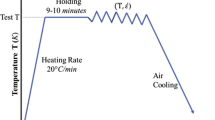
The experimental process for compression testing is illustrated in Fig. 2. The samples were heated to a required test temperature at a heating rate of 10 ℃/s and a holding time of 3 min for uniform temperature distribution over the sample. Hot compression tests were conducted at strain rates and temperatures, as in Table 2, up to 50% deformation. All the tests are repeated three times to ensure the repeatability of the results. The average values of all three tests are further considered for the analysis. After compression, the specimen was water quenched to retain the microstructure.

Fig. 2
figure 2

Schematic diagram of the 92W–5Co–3Ni alloy hot compression test

Full size image

The central portion of the compressed specimens was analysed using optical microscopy and electron backscatter diffraction (EBSD) analysis. For optical microscopy, the sample’s cross-section was initially polished using different grades of emery papers. Furthermore, the specimens were polished using a diamond paste to achieve a smooth finish. After optical microscopy, the sample was prepared for EBSD analysis. The sample was polished with 0.05-micron colloidal silica in a Vibromet (Buehler) polisher for 8 h. The EBSD was performed in FEI™ Quanta 3D-field emission gun at velocity detector by EDAX-OIM™ system with a step size of 0.5 µm. The detailed EBSD analysis was performed to check the grain size distribution of 92W–5Co–3Ni alloy using TSL OIM software.

3 Results and discussion

3.1 Original microstructure

The microstructure of the as-received sample is characterised by two phases, one tungsten (W) phase as the main constituent, forming the basic internal structure of 92W alloy with Co/Ni as the continuous matrix phase, as shown in Fig. 3. The microstructure comprises predominant spherical coarse and fine W grains of BCC lattice embedded in ductile Co/Ni matrix of FCC lattice. The structure is homogeneous and uniform, without any voids and abnormal grain growth.

Fig. 3
figure 3

Microstructure of as-received 92W sample

Full size image

The various important parameters such as tungsten grain size, tungsten/tungsten contiguity (W/W Contiguity), tungsten/tungsten connectivity (W/W connectivity), dihedral angle, neck length, solid volume fraction, and matrix volume fraction were evaluated as presented in Table 3. The tungsten grain size was calculated using the line intercept method. It was found to be approximately 27 µm. It can be seen that the tungsten grains are in contact with each other called tungsten/tungsten interfaces (W/W interfaces), as well as in contact with the matrix called tungsten/matrix interfaces (W/M interfaces), as shown in Fig. 4a. The ratio of number of tungsten/tungsten interfaces (W/W interfaces) to the sum of tungsten/tungsten interfaces (W/W interfaces) and tungsten/matrix interfaces (W/M interfaces) is called tungsten/tungsten contiguity (W/W contiguity), denoted by CWW as mentioned in Eq. (1) [21]. Based on this equation, the contiguity (\({C}_{ww}\)) value was found as 0.625.

$${\text{Contiguity }(C}_{ww})=\frac{2{N}_{ww}}{2{N}_{ww}+{N}_{wm}},$$
(1)

where \({N}_{ww}\) = Number of W/W interfaces per unit length of given intercept;

Table 3 Microstructural parameters of as-received sample
Full size table
Fig. 4
figure 4

Microstructural parameters a number of W/W contacts & W/M contacts b dihedral angle c neck length

Full size image

\({N}_{wm}\) = Number of W/M interfaces per unit length of given intercept.

The W/W connectivity is defined as the number of neighbouring W grains around considered W grains. This was found to be approximately 2. The dihedral angle is the angle between two W grains in mutual contact and contact between W grains with the matrix. It is the triple point angle between the W grains and the matrix, as illustrated in Fig. 4b. The dihedral angle was found to be approximately 57.6°. Neck length is the contact length of two W grains [22]. This was found approximately to be 14 µm, as shown in Fig. 4c. The solid volume fraction was found using the point count method proposed by A. Panchal et al. [22]. The solid volume fraction was calculated based on Eq. (2) mentioned below. The summary of all calculated microstructural parameters is represented in Table 3.

$${v}_{s}=\frac{{N}_{s}}{{N}_{s}+{N}_{L}}.$$
(2)

Further detailed EBSD analysis Fig. 5a, b shows the inverse pole figure (IPF) distribution map and grain size distribution map of the as-received specimen. The tungsten grains are non-dendritic and equiaxed with homogeneity. It is distributed finely over the Co/Ni matrix in the microstructure.

Fig. 5
figure 5

EBSD observation of as-received specimen a inverse pole figure (IPF) distribution map b grain size distribution map

Full size image

3.2 True stress–strain curve analysis

The schematic of flow stress behaviour with different deformation stages is illustrated in Fig. 6. The representative true stress vs true strain graphs at particular temperatures and different strain rates are illustrated in Fig. 7a–d. Also, the true stress vs true strain graphs at particular strain rates and different temperatures are demonstrated in Fig. 8a–e. It has been noticed that flow stress variation is sensitive to both strain rate and temperature change. As expected, the flow stress increases as the strain rate increases for particular temperature conditions and decreases with temperature increases for particular strain rate conditions. The influence of temperature change on flow stress behaviour is significant compared with the strain rate change. The variation of flow stress is considerably high when the temperature changes from 323 to 473 K. However, the marginal change has been noticed in the flow stress change when temperature increases from 673 to 873 K.

Fig. 6
figure 6

Schematic representation of the nature of flow stress–strain curve

Full size image
Fig. 7
figure 7

True stress–strain plots at different strain rates and particular temperatures a 323 K b 473 K c 673 K d 873 K

Full size image
Fig. 8
figure 8

True stress–strain plots at different temperatures and particular strain rate a 1 s−1 b 25 s−1 c 50 s−1 d 75 s−1 e 100 s−1

Full size image

The true stress–strain curves are dominated by both work hardening and work softening mechanisms. Initially, the flow stress increases rapidly up to critical strain (εc) (less than 0.1 strain), and then flow stress increases gradually up to peak strain (εp) (0.1). This can be due to the rapid generation of several internal dislocations causing tangling or trapping of dislocations inside the material. This results in rapid work hardening of the material. Up to deformation from critical strain to peak strain, the flow stress increase becomes gradual as the rate of dislocation multiplication slows down. This resulted in a gradual rise in flow stress, as shown in Fig. 6. On further deformation beyond 0.1 strain, the annihilations of dislocations cause the trapped or pinned dislocations to mobilise, resulting in softening of the material. This can be observed mainly at low temperatures like 323 K and 473 K and high strain rates (25 to 100 s−1).

On further increases in temperature to 673 K and 873 K, the flow stress increases rapidly up to critical strain, and then flow stress increases gradually up to peak strain. At the peak strain, the generation of dislocations completely slows down and reaches dynamic equilibrium, with dislocation annihilation, where the generation and annihilation of dislocations counteract each other. This indicates equilibrium between work hardening and work softening once strain exceeds 0.1, resulting in a steady or constant flow of flow stress as shown in Fig. 6. This region is the dynamic recovery stage.

3.3 Johnson–Cook (JC) model

The original JC model is given by Eq. (3):

$$\sigma =\left(A+B{\varepsilon }^{n}\right)\left(1+C\mathit{ln}{\dot{\varepsilon }}^{*}\right)\left(1-T*m\right),$$
(3)

where \(\upsigma\) is equivalent flow stress, ɛ is equivalent plastic strain, \(A\) is the yield strength of the material at reference temperature 323 K and reference strain rate 1 s−1, \(B\) is the coefficient of strain hardening, \(n\) is strain hardening exponent, C, m are material constants represent coefficient of strain rate hardening and thermal softening exponent, \({\dot{\varepsilon }}^{*}\) is dimensionless strain rate which is given by \({\dot{\varepsilon }}^{*}=\frac{\dot{\varepsilon }}{{\dot{\varepsilon }}_{0}}\); \(\dot{\varepsilon }\)= strain rate (s−1), \({\dot{\varepsilon }}_{0}\) = reference strain rate (s−1), and T* is the dimensionless temperature given by\({T}^{*}=\frac{T-{T}_{r}}{{T}_{m}-{T}_{r}}\), where, \(T\) is temperature in K, \({T}_{r}\) = reference temperature in K, and \({T}_{m}\) = melting temperature in K. The three terms in the JC model \(\left(A+B{\varepsilon }^{n}\right)\) describes the work hardening effect on the material, \(\left(1+C\mathit{ln}{\dot{\varepsilon }}^{*}\right)\) describes the strain rate effect, and \(\left(1-T*m\right)\) describes the temperature effect on the material, respectively. The strain rates and temperatures used for the analysis are presented in Table 2.

The reference strain rate \({(\dot{\varepsilon }}_{0})\) is taken as 1 s−1 and reference temperature \({(T}_{r})\) is taken as 323 K. The term \(A\) is the yield stress obtained as 1430 MPa at the reference strain rate and reference temperature. The melting temperature of Tungsten heavy alloy, \({T}_{m},\) is 1730 K [13].

3.3.1 Determination of constants B and n in the first term

When the strain rate is the reference strain rate 1 s−1 and the deformation temperature is the reference temperature 323 K, the JC equation is reduced to Eq. (4):

$$\sigma =\left(A+B{\varepsilon }^{n}\right).$$
(4)

Taking logarithm on both sides of Eq. (3) we get Eq. (5):

$$\mathit{ln}\left(\sigma -A\right)=\mathit{ln}B+n\mathit{ln}\varepsilon .$$
(5)

Substituting the \(A\) value 1430 MPa, flow stress, and strain values in Eq. (5), it obtains the slope \(n\) and intercept \(\mathit{ln}B\) from the linear variation of \(\mathit{ln}\left(\sigma -A\right)\) vs \(\mathit{ln}\varepsilon\) as shown in Fig. 9. The slope of the graph \(n\) as − 0.7 and the intercept, \(B\) as 23.3 MPa. The negative value of \(n\) is because of the declining trend of flow stress with the plastic strain.

Fig. 9
figure 9

\(\mathit{ln}\left(\sigma -A\right)\) vs \(\mathit{ln}\varepsilon\) plot

Full size image

3.3.2 Determination of constant \(\mathbf{C}\) in the second term

The material constant \(C\) is the strain rate hardening coefficient can be found from the plot of \(\frac{\sigma }{\left(A+B{\varepsilon }^{n}\right)}\) vs \(\mathit{ln}{\dot{\varepsilon }}^{*}\). \(C\) can be obtained when deformation temperature is taken as the reference temperature 323 K, and the JC equation is reduced to as expressed in Eq. (6). The plot of \(\frac{\sigma }{\left(A+B{\varepsilon }^{n}\right)}\) vs \(\mathit{ln}{\dot{\varepsilon }}^{*}\) is a linear fit with intercept 1 as shown in Fig. 10. We obtain \(C\) as 0.004.

Fig. 10
figure 10

\(\frac{\sigma }{\left(A+B{\varepsilon }^{n}\right)}\) vs \(\mathit{ln}{\dot{\varepsilon }}^{*}\) plot

Full size image
$$\frac{\sigma }{\left(A+B{\varepsilon }^{n}\right)}=1+C\mathit{ln}{\dot{\varepsilon }}^{*} .$$
(6)

3.3.3 Determination of constant m in the third term

The material constant \(m\) is the thermal softening exponent is obtained from the plot of \(ln[1-\frac{\sigma }{\left(A+B{\varepsilon }^{n}\right)}]\) vs \(m ln{T}^{*}\) as shown in Fig. 11. When the strain rate is taken as the reference strain rate 1 s−1, the JC equation is reduced to Eq. (7):

Fig. 11
figure 11

\(ln\left[1-\frac{\sigma }{\left(A+B{\varepsilon }^{n}\right)}\right]\) vs \(ln{T}^{*}\) plot

Full size image
$$\frac{\sigma }{\left(A+B{\varepsilon }^{n}\right)}=1- {{T}^{*}}^{m}.$$
(7)

Taking logarithm on both sides we obtain Eq. (8):

$$ln\left[1-\frac{\sigma }{\left(A+B{\varepsilon }^{n}\right)}\right]= m ln{T}^{*}.$$
(8)

Substituting four different temperatures (323 K, 473 K, 673 K, and 873 K) and flow stress at different plastic strain we obtain value of \(m\) as 1.1.

The JC parameters determined are presented in Table 4.

Table 4 JC parameters for 92W–5Co–3Ni alloy
Full size table

The comparison of predicted and experimental flow stress curves is shown in Fig. 12a–e. The JC model had poor accuracy in predicting experimental flow stress, as observed. The predicted flow stress decreased with increase in temperature at particular strain rate. The predicted JC flow stress showed rapid softening initially up to strain of 0.1 and on increase in deformation up to 0.6, the degree of softening got declined gradually. This resulted in poor prediction of experimental flow stress at 323 K and 473 K after 0.1 deformation, where there was large decline in flow stress up to 0.6 strain at all strain rates. On the other side, constant flow stress was observed for all strain rates at temperatures 673 K and 873 K after 0.1 deformation. Due to prediction of gradual decrease in softening from 0.1 to 0.6 strain, the experimental flow stress at these temperature zones got predicted with large error between experimental and predicted flow stress.

Fig. 12
figure 12

Comparison of experimental with JC predicted flow stress for different temperatures at strain rate a 1 s−1 b 25 s−1 c 50 s−1 d 75 s−1 e 100 s.−1

Full size image

The possible reasons for poor prediction of JC model is mentioned below:

  • The first term strain term \(\left(A+B{\varepsilon }^{n}\right)\) is coupled with second and third terms individually, to obtain \(C\) and \(m\) constants. \(A\), \(B,\) and \(n\) are taken as constants in the strain term of JC model. These constants in the strain term remains unchanged at all test strain rates and test temperatures. It resulted in either predicting a complete strain hardening or thermal softening which contradicts the experimental results.

  • The parameter \(C\), coefficient of strain rate hardening which was taken constant in original JC model, is actually dependent on strain rate and plastic strain and \(C\) has non-linear variation with strain rate and plastic strain.

3.4 Modification to the original Johnson–Cook (m-JC) model

Over the years, various modifications have been proposed in the JC model. The one of the popular models proposed by Lin & Chen in 2010 [19] is used in this work. They coupled effects of strain, strain rate, and deformation temperature. The modified JC model (m-JC) equation Eq. (8) is mentioned below:

$$\sigma =\left(A+{B}_{1}\varepsilon +{B}_{2}{\varepsilon }^{2}\right)\left(1+C\mathit{ln}{\dot{\varepsilon }}^{*}\right)\mathit{exp}\left[\left({\lambda }_{1}+{\lambda }_{2}\mathit{ln}{\dot{\varepsilon }}^{*}\right)\left(T-{T}_{r}\right)\right].$$
(8)

3.4.1 Determination of \(\mathbf{A}\), \({\mathbf{B}}_{1},\) and \({\mathbf{B}}_{2}\)

The reference strain rate and temperature are taken as 1 s−1 and 323 K, respectively; then Eq. (8) will be deduced to Eq. (9):

$$\sigma =\left(A+{B}_{1}\varepsilon +{B}_{2}{\varepsilon }^{2}\right),$$
(9)

where \(A\), \({B}_{1}\), \({B}_{2}\), \(C\), \({\lambda }_{1,}\) and \({\lambda }_{2}\) are the material constants. The values of \(A\), \({B}_{1},\) and \({B}_{2}\) are obtained by a second-order polynomial curve fitting as shown in Fig. 13 and are found \(A\) is 1665.98 MPa, \({B}_{1}\) is − 583.53 MPa, and \({B}_{2}\) is 112.84 MPa.

Fig. 13
figure 13

Second-order polynomial fit

Full size image

3.4.2 Determination of \(\mathbf{C}\)

When the reference temperature is taken 323 K, Eq. (8) is deduced to Eq. (10):

$$\frac{\sigma }{\left(A+{B}_{1}\varepsilon +{B}_{2}{\varepsilon }^{2}\right)}=\left(1+C\mathit{ln}{\dot{\varepsilon }}^{*}\right).$$
(10)

The linear fit of all strain rates and corresponding flow stress gives the slope; \(C\) of Eq. (10) is found to be 0.0039 and shown in Fig. 14.

Fig. 14
figure 14

Determination of \(C\)

Full size image

3.4.3 Determination of \({{\varvec{\uplambda}}}_{1}\) and \({{\varvec{\uplambda}}}_{2}\)

When the reference strain rate 1 s−1 is taken and taking λ = \({\lambda }_{1}+{\lambda }_{2}\mathit{ln}{\dot{\varepsilon }}^{*}\), Eq. (8) is deduced to Eq. (11) as shown. Taking logarithm on both sides,

$$\text{ln}\left\{\frac{\sigma }{\left[\left(A+{B}_{1}\varepsilon +{B}_{2}{\varepsilon }^{2}\right)*\left(1+C\mathit{ln}{\dot{\varepsilon }}^{*}\right)\right]}\right\}=\uplambda \left(T-{T}_{r}\right).$$
(11)

The linear fit of \(\frac{\sigma }{\left[\left(A+{B}_{1}\varepsilon +{B}_{2}{\varepsilon }^{2}\right)*\left(1+C\mathit{ln}{\dot{\varepsilon }}^{*}\right)\right]}\) and \(\left(T-{T}_{r}\right)\) gives the slope \(\uplambda\) = -0.0005. The \(\uplambda\) equation is the linear fit of \(\uplambda\) and \(\mathit{ln}{\dot{\varepsilon }}^{*}\) whose slope \({\lambda }_{2}\) = 0.0000023 and intercept \({\lambda }_{1}\) = -0.00041 are found as shown in Fig. 15.

Fig. 15
figure 15

Determination of \({\lambda }_{1}\) and \({\lambda }_{2}\)

Full size image

The m-JC parameters obtained are presented in Table 5.

Table 5  m-JC parameters for 92W–5Co–3Ni alloy
Full size table

The comparison of predicted and experimental flow stress curves is displayed in Fig. 16a–e. Like the JC model, m-JC model also predicted decrease in flow stress with increase in temperature at all strain rates. The m-JC model predicted gradual softening throughout the strain up to 0.6 for all strain rates and temperatures. This resulted in slightly better prediction of experimental flow stress at 323 K and 473 K. But, after 0.3 strain, the predictability declined at 323 K for all strain rates. However, at 473 K temperature, prediction was better and predictability increased with increase in strain rates. On the other side, prediction was observed poor at temperatures 673 K and 873 K. The gradual decline in the predicted flow stress contradicted the steady experimental flow stress at all strain rates and at temperatures 673 K and 873 K.

Fig. 16
figure 16

Comparison of experimental with m-JC predicted flow stress for different temperatures at strain rate a 1 s−1 b 25 s−1 c 50 s−1 d 75 s−1 e 100 s.−1

Full size image

3.5 An improved Johnson–Cook (i-JC) model

The new modification of the original JC model follows the replacement of the strain term with the suitable work hardening model. In the present work, Ludwigson’s work hardening model has been used to replace the strain term in the JC model. The Ludwigson equation is the modified Hollomon equation, given by Eq. (12):

$$\sigma ={k}_{1}{\varepsilon }^{{n}_{1}}+\mathit{exp}\left({k}_{2}+{n}_{2}\varepsilon \right),$$
(12)

where \({k}_{1}\) and \({n}_{1}\) are the strength coefficient and strain hardening exponent similar to k and n in the Hollomon equation. \({k}_{2}\) and \({n}_{2}\) are the constants added as the modification parameters. The term \(\mathit{exp}\left({k}_{2}+{n}_{2}\varepsilon \right)\) is the positive deviation coefficient (\(\Delta\)), which helps in correcting the stress–strain response in the material. The hardening exponent (\({n}_{1}\)) for the Ludwigson equation is determined for every strain rate and temperature in a similar fashion previously for the Hollomon equation.

In this modification, the parameter strain rate sensitivity coefficient, \(C,\) has a non-linear variation with both strain rate and plastic strain and can be expressed as the binary quadratic polynomial with plastic strain and strain rate.

3.5.1 Replacing the strain term with a suitable work hardening model

The strain term in JC is unsuitable to describe the stress–strain behaviour under reference conditions. So, it is necessary to replace the strain term with a suitable work hardening model which fits best the experimental plastic stress–strain data. Therefore, the strain term \(\left(A+B{\varepsilon }^{n}\right)\) is replaced with Ludwigson work hardening model which is given by Eq. (12), where, \({k}_{1}, {n}_{1}, {k}_{2}, and {n}_{2}\) are obtained by non-linear fitting of experimental plastic data at reference conditions. These constants in the new strain term are varied at every strain rate and temperature conditions. Under reference strain rate (1 s−1) and reference temperature (323 K), the i-JC measured flow stress would deduce to Ludwigson hardening equation. The Ludwigson hardening curve fitting the flow stress behaviour under reference conditions is shown in Fig. 17a. The Ludwigson hardening equation is in good agreement with experimental flow stress curve with maximum correlation coefficient of 0.9971 and least error and standard deviation of 0.37% and 0.29%, as shown in Fig. 17b. Thus, the plastic stress–strain relationship under reference conditions can be accurately represented by the Ludwigson hardening curve. The material constants of Ludwigson model obtained are mentioned in Table 6.

Fig. 17
figure 17

Comparison between Ludwigson hardening curve and experimental curve at reference strain rate 1 s−1 and reference temperature 323 K

Full size image
Table 6 Material constants of Ludwigson model
Full size table

3.5.2 Modification of parameter \(\mathbf{C}\)

The parameter \(C\) can be obtained at reference temperature. So, the i-JC model is deduced with the coupling of the Ludwigson equation with the strain rate effect term given by Eq. (13):

$$\sigma ={[k}_{1}{\varepsilon }^{{n}_{1}}+\mathit{exp}\left({k}_{2}+{n}_{2}\varepsilon \right)]\left(1+C\mathit{ln}{\dot{\varepsilon }}^{*}\right).$$
(13)

The \(C\) is obtained by simplifying the above equation as given by Eq. (14):

$$C=\frac{\frac{\sigma }{\left[{k}_{1}{\varepsilon }^{{n}_{1}}+\mathit{exp}\left({k}_{2}+{n}_{2}\varepsilon \right)\right]}-1}{\mathit{ln}{\dot{\varepsilon }}^{*}}.$$
(14)

The parameter \(C\) is not constant, but varies non-linearly with plastic strain, \(\varepsilon\), having a quadratic relationship as shown in Fig. 18a, as well as \(C\) is a quadratic function of strain rate \({\dot{\varepsilon }}^{*}\) as shown in Fig. 18b. Therefore, the strain rate sensitivity coefficient, \(C,\) can be expressed as the binary quadratic polynomial with plastic strain and strain rate as shown in Eq. (15). Then, non-linear surface fit has been plotted for the value of C with plastic strain and strain rate variation. The coefficients of C are presented in Table 7.

Fig. 18
figure 18

Variation of parameter \(C\) with a plastic strain, \(\varepsilon\) b strain rate, \({\dot{\varepsilon }}^{*}\)

Full size image
Table 7 Values of coefficients of \(C\)
Full size table
$$C={C}_{0}+{C}_{1}\varepsilon +{C}_{2}{\varepsilon }^{2}+{C}_{3}\dot{\varepsilon }+{C}_{4}{\dot{\varepsilon }}^{2}+{C}_{5}\varepsilon \dot{\varepsilon }.$$
(15)

At reference temperature, 323 K, with increase in strain rates 25 s−1–100 s−1, i-JC is deduced to Eq. (16):

$$\sigma ={[k}_{1}{\varepsilon }^{{n}_{1}}+\mathit{exp}\left({k}_{2}+{n}_{2}\varepsilon \right)]\left[1+\left({C}_{0}+{C}_{1}\varepsilon +{C}_{2}{\varepsilon }^{2}+{C}_{3}\dot{\varepsilon }+{C}_{4}{\dot{\varepsilon }}^{2}+{C}_{5}\varepsilon \dot{\varepsilon }\right)\mathit{ln}{\dot{\varepsilon }}^{*}\right].$$
(16)

3.5.3 Determination of parameter \(\mathbf{m}\)

At reference strain rate, 1 s−1, the first term Ludwigson equation is coupled to the temperature effect term of original JC model as shown in Eq. (17):

$$\sigma ={[k}_{1}{\varepsilon }^{{n}_{1}}+\mathit{exp}\left({k}_{2}+{n}_{2}\varepsilon \right)]\left(1-{{T}^{*}}^{m}\right).$$
(17)

Taking \(ln\) on both sides, we get Eq. (18):

$$\mathit{ln}\left[1-\frac{\sigma }{\left[{k}_{1}{\varepsilon }^{{n}_{1}}+\mathit{exp}\left({k}_{2}+{n}_{2}\varepsilon \right)\right]}\right]=mln{T}^{*},$$
(18)

where \({T}^{*}=\) \(\frac{T-{T}_{ref}}{{T}_{m}-{T}_{ref}}\). \({T}_{m}\) is melting point temperature of WHA taken as 1730 K. \({T}_{ref}\) is reference temperature taken as 323 K. \(T\) is the operating temperature.

Equation (18) is linear with slope \(m\) and intercept 0. Slope \(m\) is determined similar to the original JC model which remains constant. Slope \(m\) is obtained 4.486. Now, with the above coupling of Ludwigson equation with temperature term, we obtain prediction of reference strain rate 1 s−1, at different temperatures, 473 K, 673 K, and 873 K.

The strain rates of 25 s−1, 50 s−1, 75 s−1, and 100 s−1 at different temperatures of 473 K, 673 K, and 873 K can be obtained from the final new modified JC model as given by Eq. (19):

$$\sigma ={[k}_{1}{\varepsilon }^{{n}_{1}}+\mathit{exp}\left({k}_{2}+{n}_{2}\varepsilon \right)]\left[1+\left({C}_{0}+{C}_{1}\varepsilon +{C}_{2}{\varepsilon }^{2}+{C}_{3}\dot{\varepsilon }+{C}_{4}{\dot{\varepsilon }}^{2}+{C}_{5}\varepsilon \dot{\varepsilon }\right)\mathit{ln}{\dot{\varepsilon }}^{*}\right]\left(1-{{T}^{*}}^{m}\right).$$
(19)

The predicted flow stress was compared with the experimental data and is shown in Fig. 19a–e. Due to replacement of the strain term of JC model with Ludwigson equation, the declining trend of experimental flow stress at 323 K as well as 473 K temperature had better prediction in complete strain range 0–0.6. The variation of Ludwigson parameters in every experimental condition helped give best fitting of experimental flow stress. Also, the variation of coefficient of strain hardening with plastic strain and strain rate contributed to better prediction of experimental flow stress at all strain rates and temperatures.

Fig. 19
figure 19

Comparison of experimental with i-JC predicted flow stress for different temperatures at strain rate a 1 s−1 b 25 s−1 c 50 s−1 d 75 s−1 e 100 s.−1

Full size image

3.6 Models comparison with statistical parameters

The prediction ability of constitutive models has been evaluated by various statistical measures mainly correlation coefficient (R), average absolute relative error (AARE), and its standard deviation (δ). The R value may be biased towards higher or lower values [23]. Therefore, it is essential to check the other error parameters too [24]. These parameters are calculated based on Eq. (20), Eq. (21), Eq. (22):

$$Correlation Coeffiecnt \left(R\right)=\frac{\sum_{i=1}^{n}\left({x}_{i}-\overline{x }\right)\left({y}_{i}-\overline{y }\right)}{\sqrt{\sum_{i=1}^{n}{\left({x}_{i}-x\right)}^{2}\sum_{i=1}^{n}{\left({y}_{i}-y\right)}^{2}}},$$
(20)
$$Average Absloute Relative Error \left(AARE\right)=\sum_{i=1}^{n}\left|\frac{{x}_{i}-{y}_{i}}{{x}_{i}}\right|\times 100\%,$$
(21)
$$\text{Standard Deviation},\updelta = \sqrt{\frac{1}{n}\sum_{\dot{i}=1}^{n}{\left({x}_{i}-\overline{x }\right)}^{2},}$$
(22)

where \({x}_{i}\) = experimental flow stress data; \({y}_{i}\) = predicted flow stress data; \(\overline{x}\) = mean experimental flow stress data; \(\overline{y}\) = mean predicted flow stressdata; \(n\) = total number of data points.

The correlation coefficient (R) for all three models are shown in Fig. 20. It can be seen from Fig. 20 that JC model demonstrates poor flow stress prediction capability with R value as 0.7715. However, the prediction capability slightly improves for m-JC model with R values as 0.7925. However, the significant improvement in the R value (0.9891) has noticed in case of newly proposed i-JC model. The percentage increase in the correlation coefficients are 28.20% and 24.80% in comparison with JC and m-JC models, respectively. Further, average absolute relative error (AARE) and their standard deviation (δ) are evaluated and shown in Table 8. The highest percentage of AARE (8.72%) and standard deviation (7.82%) are found in JC model which proves again the poor prediction capability. However, the slight decrease in AARE (6.91%) and standard deviation (5.57%) have seen in case of m-JC model. The AARE and standard deviation decrease significantly for i-JC model which demonstrate the accurate flow stress prediction behaviour.

Fig. 20
figure 20

Correlation coefficient, R, of three models a JC b m-JC c i-JC

Full size image
Table 8 Statistical parameters values
Full size table

4 Conclusions

The flow stress behaviour of 92W–5Co–3Ni alloy was predicted using phenomenological-based constitutive models, namely, JC, m-JC, and i-JC models, over a wide range of strain rates (1 s−1, 25 s−1, 50 s−1, 75 s−1, and 100 s−1) and temperatures (323 K, 473 K, 673 K, 873 K). The important conclusions from the study is as follows:

  • The JC model demonstrates poor flow stress prediction capability with correlation coefficient of 0.7715 and average absolute error of 8.72%. Particularly, at high strain rates and high temperatures, the absolute error and standard deviation abruptly rose. This is due to considering the coefficient of strain rate hardening and thermal softening exponent as constants.

  • Also, the modified JC (m-JC) model shows poor flow stress prediction capability with correlation coefficient of 0.7925 and average absolute error of 6.91%. Specifically, the model captures the decline trend of flow stress behaviour in some extent. However, the model displays poor flow prediction when flow stress stabilises at 673 K and 873 K.

  • The newly proposed modification to JC (i-JC) model replaced the strain term with Ludwigson hardening equation and considering coefficient of strain rate hardening term as variable. The i-JC model exhibits better prediction accuracy with correlation coefficient of 0.9891 and average absolute error of 1.35%.