1 Introduction

Magnesium and its alloys are considered the lightest structural metallic materials with low density and high specific strength. They are commonly employed in weight-saving applications in the automotive and aerospace industries [1]. However, a few sliding systems at room temperature reduce their ductility, leading to a brittle fracture [2]. This phenomenon is due to the difference in critically resolved shear stresses (CRSS) between the basal and non-basal sliding systems. The different thermo-mechanical processing techniques, e.g. rolling, forging and extrusion, introduce the basal texture in magnesium alloys, further hampering the wrought magnesium alloy’s forming ability [3]. The primary modes of slipping in Mg alloys were basal slipping, non-basal slipping (mainly prismatic and pyramidal I and II), and tension and compression twinning. The low CRSS of basal slipping would not be enough to meet von Mises’ standards for plastic deformation. However, due to the high CRSS, activating the non-basal slip at ambient conditions was not easy [4]. The hot deformation behaviour of any metallic materials can be captured in terms of force–displacement plots through various experiments such as uniaxial stretching, uniaxial compression, shear and torsion. Over the years, different constitutive models have been presented to forecast the flow behaviour of various metallic materials. The best-predicted model is implemented in numerical simulations to analyse the complex behaviour of metal-forming processes [5]. The complexity in deformation behaviour can be understood by the nature of stress–strain curves at diverse temperatures and strain rates, for which most metals and alloys exhibit a substantial dependency. Hence, there is a need to develop constitutive mathematical equations that can predict the experimental tensile behaviour of various metallic materials, which can be used in finite element (FE) simulations to evaluate their suitability for industrial applications [6].

Lin and Chen [7] addressed the applicability of various constitutive relationships for different metallic materials in detail. The three major types of constitutive models were noted: “phenomenological-based, physical-based and neural network-based”. The phenomenological-based models received much attention due to their simple mathematical equations and the few numbers of materials constant required for flow stress prediction. On the other hand, the physical constitutive models require information related to microstructural evolution, dislocation motion and slip theory, among others. Many material constants and critical mathematical calculations are needed to explain the flow behaviour of metallic alloys. The neural network-based models demand high-quality data sets to further estimate the flow curve prediction.

Several researchers used many phenomenological-based models [8,9,10]. The famous scientists’ Johnson and Cook proposed one such model capable of predicting the flow stress behaviour of various metallic alloys at high strain, strain rates and temperatures. The J–C model's materials constants were reasonably simple to calculate and put into practice for predicting flow stress. Over the years, many modifications of the J–C model have been developed for better prediction ability with low relative error. Ulacia et al. [11] implemented a modified J–C model to forecast the hardening behaviour of AZ31 alloy between 25 and 250 °C temperatures and quasi-static and dynamic strain rates conditions. The authors only considered the prediction of flow stresses till hardening without incorporating the softening behaviour of magnesium alloy. The suggested modifications of J–C models did not predict the decrement in flow stresses after the ultimate strength. Hou and Wang [12] proposed a modification in temperature terms by introducing an exponential function to predict the dynamic compression of hot-extruded Mg–Gd-based alloy. In their work, the absolute temperature term in modified J–C was lower than the reference temperature. Mirza et al. [13] used a modified J–C model to predict the uniaxial tensile flow stress and observed the hardening behaviour of rare earth magnesium alloy. The modified J–C predicted well with a less than 2% standard deviation. Zhou et al. [14] studied the hot compressive behaviour of Mg–Gd alloy at 703–773 K under quasi-static strain rate conditions. The authors introduced the modified Arrhenius model and processing maps to ensure the prediction ability and minimum standard deviation (less than 2%) under favourable operating conditions.

Abbasi-Bani et al. [15] employed J–C and Arrhenius equations to estimate the hot compressive deformation behaviour of AZ61 alloy from 250 to 400 °C under quasi-static strain rates. The predictive power of J–C was poor in constant strain rate conditions, whereas Arrhenius predicted the flow behaviour reasonably well. Ahmad and Shu [16] conducted the compression tests of AZ31B alloy in dynamic conditions. The authors used a simple J–C model to predict the compressive flow stress behaviour. However, the J–C model could not describe the nature of flow curves in compression. To counter the unpredictability of magnesium alloy's softening behaviour, Zhang et al. [17] proposed a modification in the temperature term of the J–C equation. The authors predicted the dynamic compression behaviour of AZ31 alloy using the modified version of J–C and successfully employed the equations in the FE simulation of a hat-shaped specimen. However, the outcome of their work is limited to 250 °C deformation temperature.

Over the years, different modifications of the J–C model have been implemented to predict the flow behaviour of various metallic materials. Souza et al. [18] combined the J–C model with Avrami equations to predict the flow behaviour of Inconel 625 alloy at 900–1100 °C with a strain rate from 0.01 to 1 s−1. The study correlated the microstructural evolution with the constitutive model and FE simulations. Trimble and O'Donnell [19] used different constitutive models to predict the flow behaviour of aluminium-based alloys. They proposed a model based on the strain hardening and softening behaviour of Al alloy and compared the results with different constitutive models.

In another work by Lin et al. [20], a phenomenological-based model is incorporated to predict the hot tensile behaviour of Al–Cu–Mg alloy at different strain rates and temperatures. The combined effect of strain rate, hardening and softening region, and deformation temperature were considered for better prediction. The work related to cast magnesium alloy AZ91 and its flow behaviour is discussed by Mei et al. [21]. Their work focused on implementing piecewise function and its comparison with strain compensated Arrhenius model for the flow stress behaviour in quasi-static strain rate conditions. Chen et al. [22] studied the hot compression behaviour and its prediction with sine hyperbolic and modified J–C models for the cast magnesium alloy AZ80 at 523–673 K and 0.001–1 s−1 conditions. The hyperbolic model predicted the flow curve before the peak stress, whereas the modified J–C predicted the peak stress. The recent study of Wang et al. [23] investigated the tensile behaviour of AA7075 alloy using the new Johnson–Cook constitutive model under cryogenic conditions. The new J–C model predicted the flow stress at cryogenic temperature conditions with a relative error of less than 0.80%. The dynamic flow behaviour of Ni- and W-based super-alloys can be described by a modification related to the exponential temperature term in J–C, as was recently used in the work of Xie et al. [24]. The authors introduced a thermal softening parameter and compared their results with the simple J–C model.

Based on extensive literature reviews, the authors have solely concentrated on predicting the hardening behaviour of various magnesium alloys at varying temperatures and strain rates. However, there is still much scope to implement the J–C model and its modifications to anticipate the AZ31B alloys’ thermal softening and hardening regimes. The current study predicts both regimes with three distinct versions of J–C models. As most of the studies are restricted to 250 °C, the experimental observation suggests that the thermal softening of AZ31B alloy is more dominant after the deformation temperature of 250 °C. Hence, it is worth investigating the suitability of different J–C models for flow stress behaviour predictions.

2 Materials and Method

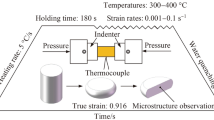
The combination of hot- and cold-rolled AZ31B alloy with major chemical compositions of 2.67% (wt.) Al, 0.87% Zn, 0.34% Mn and balanced magnesium was used in this study. The 1-mm-thick sheet was employed for the hot tensile test. The microstructural characterization was performed on a small specimen of size 8 mm × 8 mm in the RD-TD plane. Here, the RD and TD represent the rolling and transverse direction in the AZ31B alloy sheet. Several grades of silicon carbide (SiC) wet sandpaper in series of #1200, #1500 and #2000 were polished to acquire the microstructure. It was then followed by cloth polishing using diamond paste and electrochemical etching. The acetic-picral solution was used as an etching agent to get the microstructure in an optical microscope. Figure 1a shows the initial as-received microstructure, and the grain size was calculated through the line intercept method. The approximate average grain size was 10 µm. The electron back-scattered diffraction (EBSD) technique was also employed to check the exact grain size distribution of AZ31B alloy. The EBSD was performed in FEI™ Quanta 3D-field emission gun and EDAX-OIM™ system with a step size of 0.5 µm. Electro-polishing was carried out at 20 V. The tensile samples were fabricated by wire-cut electric discharge machining (EDM) following ASTM E8/E8M-11 standards.

Fig. 1
figure 1

a Optical microstructure of as-received AZ31B alloy. b Zwick Roell mechanical testing setup

Full size image

The specimen has an overall dimension of 100 mm long and 10 mm wide. However, for measuring load and displacement while subjected to tensile stress, the gauge length was 30 mm, and its width was 6 mm. The samples obtained from EDM were loaded in a tensile testing machine and then heated at 10 °C/min to a fixed temperature, i.e. 473–623 K. Once the desired temperature was reached, the specimen was kept for 10 min to ensure uniform temperature distribution within the sample. The Zwick Roell Z100 of 100 kN capacity mechanical testing machine, fitted with box-type furnace, was used for uniaxial stretching of specimens at 473 and 523 K till fracture, as depicted in Fig. 1b.

In contrast, a different set-up with three zones split furnace was used for 573 and 623 K to capture the load–displacement data. The quasi-static strain rate of 0.001, 0.01 and 0.1 s−1 was selected. Three tests were conducted for each deformation temperature and strain rate, and the average stress–strain data were plotted.

3 Results and Discussion

3.1 Hot Deformation Mechanism

In this section, we have discussed the hot deformation behaviour of AZ31B alloy at various temperatures and strain rates. Figure 2 illustrates transforming the “force and displacement data” from tensile tests into “true stress–strain curves”.

Fig. 2
figure 2

Tensile flow curves at different temperatures and strain rates

Full size image

The true stress–strain flow curves have been divided into two parts for further analysis.

  • The effect of temperature at a constant strain rate (Fig. 2a–c)

  • Effect of strain rate at constant temperature (Fig. 2d–g)

During the initial stretching of specimens, the stress increases as the strain progresses, which also denotes the work hardening (W–H) stage. This phenomenon occurs due to the generation of dislocations and their interaction with other dislocations. Afterwards, single peak stresses were observed at all the temperatures and strain rates, followed by the W–H stage. Meanwhile, the stresses decreased with further stretching of specimens until fracture.

The development of dynamically recrystallized (DRX) grains was most likely the cause of the decrease in stresses. In some cases, dynamic recovery (DRV) was also observed in the hot stretching of AZ31B alloy. The separate discussion is described in “Sects. 3.1.1 and 3.1.2” in brief.

3.1.1 Temperature Effect at Constant Strain Rate

The effect of temperature at a constant strain rate on the hot stretching of AZ31B alloy is illustrated in Fig. 2a–c. The strength of the alloy decreases with the increase in the deformation temperature. At 473 and 523 K, the typical WH and DRV behaviour is observed at strain rates of 0.1 and 0.01 s−1. Once the flow stress attained a peak value, the steady-state condition was reached for a small value of plastic strains. Afterwards, the flow stress gradually drops till the fracture of the specimen. For all strain rates, the abrupt decrease in flow stresses was observed at temperatures of 573 and 623 K. This phenomenon was attributed to the typical DRX behaviour.

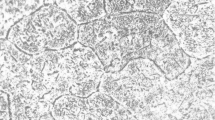
Figure 3 shows the inverse pole figure and grain size distribution maps at two deformation conditions. Figure 3a exhibits the as-received specimen's IPF and grain size variation. The microstructure of the as-received specimen consists of fully recrystallized equiaxed grains with heterogeneity. The average grain size was calculated through OIM software. The measured grain size of the as-received specimen was 9.40 µm.

Fig. 3
figure 3

a IPF and average grain distribution of as-received specimen. b IPF and average grain distribution of fractured specimen at 523 K and 0.01 s−1

Full size image

On the other hand, Fig. 3b presents the IPF and grain size variation of fractured specimens at 523 K–0.01 s−1 deformation conditions. The DRX grains were formed along the grain boundaries of deformed grains. The average grain size was dropped to 5.89 µm. The reduction in grain size indicated the initiation of DRX behaviour during the hot deformation of AZ31B alloy.

3.1.2 The Strain Rate Effect at a Constant Temperature

The strain rate effect is depicted in Fig. 2d–g. During the hot tensile stretching of the specimen at 473 and 523 K for all the strain rates, the flow stress gradually increased by maintaining a steady-state condition. Then, it decreased at a constant strain rate until fracture. The sudden drop in the flow stresses at 573 and 623 K for 0.1 s−1 strain rate was noticed. This phenomenon is due to the rapid generation of dislocation with the plastic strain that restricts further deformation leading to early fracture. The increment in strain rate causes a decrement in the ductility of AZ31B alloy. However, the drop in strain rate provides more time for DRX and DRV grains to pop up and grow, further reflecting the increment in ductility.

4 Flow Stress Prediction and Constitutive Modelling

The tensile behaviour of various metallic materials during hot deformation is complex and depends upon multiple factors, e.g. work hardening and thermal softening. These factors are related to the temperature, strain, strain rate and microstructure of metals and alloys. The flow stress behaviour of an alloy is predicted through different constitutive models. The predicted model is then used in performing the numerical simulations for sheet metal forming. The appropriate selection of constitutive models is necessary to explain the nature of the deformation behaviour of different metallic materials. Johnson and Cook have introduced a phenomenological-based model to mimic the flow behaviour of metals and alloys. The three modifications of the J–C models are discussed in the upcoming sections.

4.1 Johnson–Cook (J–C) Model

Johnson and Cook’s model used the effect of plastic strain, strain rate and deformation temperature on the flow stress behaviour of metals and alloys. It considered all three parameters to be independent of each other. The J–C model used Eq. (1) to explain the dependency of flow stress with these parameters.

$$\begin{aligned}\sigma & = \left( {\sigma_{{{\text{ref}}}} + \left( {B*\varepsilon_{{\text{p}}} } \right)^{n} } \right) * \left( {1 + C\ln \frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{{{\text{ref}}}} }}} \right) \\ &\quad * \left( {1 - \left( {\frac{{T - T_{{{\text{ref}}}} }}{{T_{{\text{m}}} - T_{{{\text{ref}}}} }}} \right)^{q} } \right) \end{aligned}$$
(1)

Here, \(\sigma\) and \({\varepsilon }_{\mathrm{p}}\) is the flow stress in tension and plastic strain, respectively. The first parameter in Eq. (1) describes the work hardening behaviour at reference conditions. The reference temperature and strain rate were 473 K and 0.001 s−1, respectively, whereas the yield stress at reference conditions can be obtained from the flow curve. Similarly, the second and third parameter relates the strain rate sensitivity and the effect of deformation temperature on flow stress behaviour. Furthermore, B, n, C and q are the material's constants representing the work hardening coefficient, hardening exponent, strain rate hardening coefficient and thermal softening exponent, respectively. The melting temperature (\(T_{{\text{m}}}\)) of AZ31B alloy is 923 K, and T is the current temperature of hot deformation. The material parameters in the J–C model can be evaluated by applying some of the mathematical tools. The natural logarithmic operation is used from the first parameter to get the values of B and n at reference conditions.

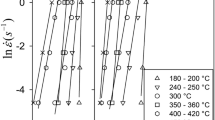
$$\ln \left( {\sigma - \sigma_{{{\text{ref}}}} } \right) = \ln B + n\ln \varepsilon_{{\text{p}}}$$
(2)

The slope and intercept from Eq. (2) represent the value of n and lnB, respectively. The values can be obtained from the linear fitting of Eq. (2) as shown in Fig. 4. Afterwards, the C value can be obtained at T = Tref for different strain rates as depicted in Eq. (3).

$$\frac{\sigma }{{\left( {\sigma_{{{\text{ref}}}} + \left( {B*\varepsilon_{{\text{p}}} } \right)^{n} } \right)}} = \left( {1 + C\ln \frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{{{\text{ref}}}} }}} \right)$$
(3)
Fig. 4
figure 4

Linear fitting for n and \(\ln B\)

Full size image

The slope of Fig. 5 represents the value of C with an intercept of 1 at various plastic strains and strain rates.

Fig. 5
figure 5

Linear fitting for C

Full size image

At \(\dot{\varepsilon }\) = \(\dot{\varepsilon }_{{{\text{ref}}}}\), the last parameter can be evaluated at reference strain rate condition as shown in Eq. (4). The flow stress becomes independent of softening behaviour term C.

$$\frac{\sigma }{{\left( {\sigma_{{{\text{ref}}}} + \left( {B*\varepsilon_{{\text{p}}} } \right)^{n} } \right)}} = \left( {1 - \left( {\frac{{T - T_{{{\text{ref}}}} }}{{T_{{\text{m}}} - T_{{{\text{ref}}}} }}} \right)^{q} } \right)$$
(4)

The q value can be obtained by taking a natural logarithm in Eq. (4) with zero intercepts as shown in Eq. (5). As illustrated in Fig. 6, the linear fitting was done to determine the q value at various plastic strains and temperatures.

$$\ln \left( {1 - \frac{\sigma }{{\left( {\sigma_{{{\text{ref}}}} + \left( {B*\varepsilon_{{\text{p}}} } \right)^{n} } \right)}}} \right) = q\ln \left( {\frac{{T - T_{{{\text{ref}}}} }}{{T_{{\text{m}}} - T_{{{\text{ref}}}} }}} \right)$$
(5)
Fig. 6
figure 6

Linear fitting for q

Full size image

Finally, all the material parameters for the J–C model were calculated and listed in Table 1. The predicted flow stress was formulated in Eq. (6).

$$\begin{aligned}\sigma &= \left( {102.20 + \left( {121.01*\varepsilon_{{\text{p}}} } \right)^{0.33} } \right) * \left( {1 + 0.0547\ln \frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{{{\text{ref}}}} }}} \right) \\ &\quad * \left( {1 - \left( {\frac{{T - T_{{{\text{ref}}}} }}{{T_{{\text{m}}} - T_{{{\text{ref}}}} }}} \right)^{0.271} } \right)\end{aligned}$$
(6)
Table 1 J–C’s material constant
Full size table

4.2 Predictive Behaviour of Flow Stress under the J–C Model

The J–C model predicted the experimentally obtained flow stress curve, and their comparison is shown in Fig. 7. It has been observed that the J–C model was appropriate for predicting the work hardening behaviour of AZ31B alloy at elevated temperatures. J–C’s predictive power is suitable for a small plastic strain range (0.01–0.07), especially at the reference temperature and strain rate. However, it overpredicts the softening behaviour of AZ31B alloy, particularly at 573 and 623 K, for all the strain rates. The solid and dashed lines represent the experimental and predictive stresses, respectively.

Fig. 7
figure 7

Comparison of experimental stress and prediction stress (J–C) at a 0.1 s−1, b 0.01 s−1, c 0.001 s−1

Full size image

A similar observation has been reported for the hot compressive behaviour of AZ61 alloy by Abbasi-Bani et al. [15]. The shortcomings of the J–C model lie in its assumptions, i.e. considering all three parameters in Eq. (1) to be independent of each other. Hence, there is a need for clubbing those parameters for better prediction.

4.3 Modified Johnson–Cook (m J–C) Model

Lin et al. [25] first consider the modification of J–C, in which the authors have clubbed the effects of strain rate and temperature in the following equation.

$$\begin{aligned} \sigma &= \left( {A + A_{1} \varepsilon_{{\text{p}}} + A_{2} \varepsilon_{{\text{p}}}^{2} } \right) * \left( {1 + C_{1} \ln \frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{{{\text{ref}}}} }}} \right) \\ &\quad * \exp \left( {\left( {\lambda_{1} + \lambda_{2} \ln \frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{{{\text{ref}}}} }}} \right)\left( {T - T_{{{\text{ref}}}} } \right)} \right) \end{aligned}$$
(7)

Here, \(A\), \(A_{1}\), \(A_{2}\), \(C_{1}\), \(\lambda_{1}\) and \(\lambda_{2}\) are the material constants. The first parameter is the polynomial equation of second order in terms of \(A\), \(A_{1}\), \(A_{2}\) and yield stress (\(\sigma_{{{\text{ref}}}}\)) at the reference temperature and strain rate, which is the same as considered in the J–C model. These constants can be evaluated based on second-order polynomial curve fitting, as illustrated in Fig. 8.

Fig. 8
figure 8

Second-order polynomial fit for A, A1, A2

Full size image

Similarly, the value of C1 is calculated by considering the strain rate effect at reference temperature (473 K) using Eq. (8).

$$\frac{\sigma }{{\left( {A + A_{1} \varepsilon_{{\text{p}}} + A_{2} \varepsilon_{{\text{p}}}^{2} } \right)}} = \left( {1 + C_{1} \ln \frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{{{\text{ref}}}} }}} \right)$$
(8)

Figure 9 shows the linear fitting of the curve plotted from Eq. (8).

Fig. 9
figure 9

Linear fitting for C1

Full size image

The material constants associated with the third parameter can be evaluated by considering the average values of the new arbitrary constant for each strain rate. The value of this new constant is given in Eq. (9) along with its substitution in Eq. (10).

$$\lambda = \lambda_{1} + \lambda_{2} \ln \frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{{{\text{ref}}}} }}$$
(9)
$$\frac{\sigma }{{\left( {A + A_{1} \varepsilon_{{\text{p}}} + A_{2} \varepsilon_{{\text{p}}}^{2} } \right)*\left( {1 + C_{1} \ln \frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{{{\text{ref}}}} }}} \right)}} = \exp \left( {\lambda *\left( {T - T_{{{\text{ref}}}} } \right)} \right)$$
(10)

Equation (10) shows changed to Eq. (11), by taking the logarithm on both sides.

$$\ln \left[ {\frac{\sigma }{{\left( {A + A_{1} \varepsilon_{{\text{p}}} + A_{2} \varepsilon_{{\text{p}}}^{2} } \right)*\left( {1 + C_{1} \ln \frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{{{\text{ref}}}} }}} \right)}}} \right] = \left( {\lambda *\left( {T - T_{{{\text{ref}}}} } \right)} \right)$$
(11)

The three values are obtained from the linear fitting of Eq. (11) at different strain rates and temperatures, as depicted in Fig. 10.

Fig. 10
figure 10

Linear fitting for λ

Full size image

The modified Johnson–Cook model’s material parameters are systematically evaluated using different boundary conditions listed in Table 2.

Table 2 m J–C’s materials constant
Full size table

4.4 Predictive Behaviour of Flow Stress Under Modified J–C Model

The evaluated constants in Table 2 are used to predict the flow behaviour of AZ31B alloy using a modified J–C model under various process parameters. This model has the best predictive capability at the reference temperature (473 K) and strain rate (0.001 s−1). Unlike the J–C model, it predicted the softening behaviour of magnesium alloy at 473, 573 and 623 K for all the strain rates reasonably well, as shown in Fig. 11. The m J–C uses a second-order polynomial equation to predict the strain hardening behaviour, as shown in Fig. 8. It accurately fits the flow stresses for the plastic strain range of (0.01–0.25). The nature of predicted stress by m J–C matches the flow curve for all three strain rates and temperatures. The significant deviation between the predicted and experimental stresses was observed at (523–623 K) and 0.1 s−1 condition, as shown in Fig. 11a. However, the m J–C was able to reproduce the flow curve at (473 K–0.1 s−1) deformation conditions.

Fig. 11
figure 11

Comparison of experimental stress and prediction stress (m J–C) at a 0.1 s−1, b 0.01 s−1, c 0.001 s−1

Full size image

Similarly, for 0.01 s−1, except at 523 K, the m J–C conforms to the flow behaviour of AZ31B alloy, as depicted in Fig. 11b. The inability of the m J–C’s prediction at 523 K–0.01 s−1 conditions can be explained by the complex microstructural activity, e.g. DRX and DRV. Figure 3b explains the change in grain size due to the formation of dynamically recrystallized grains. At this stage, the microstructure evolution affects the flow curve behaviour of AZ31B alloy. It may be the possible reason for the deviation between the predicted and experimental stress at 523 K. A similar trend was also observed at 523 K temperature and 0.1 and 0.001 s−1 strain rate conditions. Instead of the complexities in the flow behaviour of AZ31B alloy, the m J–C has the best prediction ability with a coefficient of determination of 0.99 at different temperatures and a low strain rate of 0.001 s−1. This model can be further used to simulate the hot tensile behaviour of AZ31B alloy in commercially available software like LS-Dyna, Abaqus, etc.

4.5 New Johnson–Cook Model (n J–C)

Hou and Wang [12] altered the temperature term in the original “Johnson Cook model” to predict the extruded Mg-based alloy's dynamic behaviour. The author implemented the model based on the availability of reference temperature Tref, sometimes less than the absolute temperature T. The present work employs n J–C model to observe the effect of flow and predictive stress at various temperatures and strain rates. The equation for the n J–C is written in Eq. (12).

$$\begin{aligned} \sigma & = \left( {\sigma_{{{\text{ref}}}} + \left( {B*\varepsilon_{{\text{p}}} } \right)^{n} } \right) * \left( {1 + C\ln \frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{{{\text{ref}}}} }}} \right) \\ &\quad * \left( {1 - \left( {\lambda \frac{{\exp \left( {T/T_{{\text{m}}} } \right) - \exp \left( {T_{{{\text{ref}}}} /T_{{\text{m}}} } \right)}}{{\exp (1) - \exp \left( {T_{{{\text{ref}}}} /T_{{\text{m}}} } \right)}}} \right)} \right)\end{aligned}$$
(12)

The calculation of material constants B, n and C is the same as the original Johnson–Cook model. The λ is used instead of q as the coefficient of thermal softening. The value of λ is evaluated based on reference strain rate at different temperatures for various plastic strains. At reference strain rate, \(\dot{\varepsilon }\) = \(\dot{\varepsilon }_{{{\text{ref}}}}\) = 0.001 s−1, Eq. (12) becomes Eq. (13).

$$1 - \sigma /\left( {\sigma_{{{\text{ref}}}} + \left( {B*\varepsilon_{{\text{p}}} } \right)^{n} } \right) = \left( {\left( {\lambda \frac{{\exp \left( {T/T_{{\text{m}}} } \right) - \exp \left( {T_{{{\text{ref}}}} /T_{{\text{m}}} } \right)}}{{\exp (1) - \exp \left( {T_{{{\text{ref}}}} /T_{{\text{m}}} } \right)}}} \right)} \right)$$
(13)

The linear fitting between \(1 - \sigma /\left( {\sigma_{{{\text{ref}}}} + (B*\varepsilon_{{\text{p}}} )^{n} } \right)\) and \(\frac{{\exp (T/T_{{\text{m}}} ) - \exp (T_{{{\text{ref}}}} /T_{{\text{m}}} )}}{{\exp (1) - \exp (T_{{{\text{ref}}}} /T_{{\text{m}}} )}}\) at various plastic strain ranges (0.01–0.3) gives the average value of λ, as shown in Fig. 12.

Fig. 12
figure 12

Linear fitting for λ

Full size image

The material parameters of n J–C are shown in Table 3.

Table 3 Materials constant of n J–C
Full size table

4.6 Predictive Behaviour of Flow Stress Under the New J–C Model

The material constants from Table 3 were used in Eq. (12) to predict the deformation behaviour of AZ31B alloy. The first four constants were the same as in the original J–C model. The introduction of new constant λ and the modification in temperature term significantly affect the predictive power of n J–C. The comparison between the experimental and n J–C 's predicted stress is shown in Fig. 13.

Fig. 13
figure 13

Comparison of experimental stress and prediction stress (n J–C) at a 0.1 s−1, b 0.01 s−1, c 0.001 s−1

Full size image

The n J–C model has the best prediction ability at 473 and 623 K for 0.001 s−1 strain rate. However, when compared with the J–C model, the softening behaviour of AZ31B alloy was more precisely predicted by n J–C. The fitting accuracy can further be described in Fig. 12. The coefficient of determination (R) was 0.91, and a fixed value of λ was obtained. However, the fitting accuracy of m J–C has an edge over the J–C and n J–C models at all the strain rates and deformation temperatures. Work hardening and thermal softening were predicted separately at 573 K and 0.1 s−1 deformation conditions to further analyse the difference between the three models. Section 4.6.1 explains the three constitutive models' prediction ability and relative error estimation.

4.6.1 Work Hardening and Thermal Softening Prediction Regime

The traditional J–C model and the comparison among its two modifications for the hardening regime (0.01–0.07) and softening regime (0.09–0.25) at 573 K temperature and 0.1 s−1 strain rate were compared. The two statistical parameters, namely, the coefficient of determination (R) and average absolute relative error (AARE), were evaluated for a better understanding of the flow behaviour at high temperatures. Equations (14) and (15) are used to calculate the AARE and R values, respectively. Figure 14 compares the three models for the work hardening and softening regimes.

Fig. 14
figure 14

Comparison of experimental stress and its prediction by three models at a–c 573 K, 0.1 s−1 and b–d Variation of AARE with plastic strain

Full size image

Figure 14b shows that the average absolute relative error is 4.06% for n J–C. Introducing an exponential term in the J–C model’s temperature effect enhances the hardening regime's prediction ability. Moreover, the predictive stress by J–C and m J–C shows a more significant deviation in the work hardening regime. The coefficient of determination is found to be 0.93 for n J–C and 0.86 for m J–C in the hardening regime. However, as the plastic strain progressed, the flow curve decreased continuously, and softening was dominant at a 0.1 s−1 strain rate. The n J–C poorly predicts the softening regime, whereas the nature of predicted stress by m J–C showed a downward trend to minimize the relative error (~ 41.96%), as shown in Fig. 14c. An exponential term in the n J–C model increases the gap between experimental and predicted flow stress, further enhancing the relative error variation.

4.7 Correlation Maps for J–C, m J–C and n J–C

The type of “flow stress” is predicted in several load conditions to implement several constitutive models, and a more precise model has been selected with low deviation among the predicted and tested flow stress in high temperatures. The average absolute relative error (AARE) and coefficient of determination (R) are calculated based on the values of stresses at various plastic strains. Equations (14) and (15) mention the AARE and R, respectively.

$${\text{AARE}}(\% ) = \sum\limits_{j = 1}^{N} {\frac{{E_{j} - P_{j} }}{{E_{j} }}}$$
(14)
$$R = \frac{{\sum_{j = 1}^{N} {\left( {E_{j} - E_{m} } \right)*\left( {P_{j} - P_{m} } \right)} }}{{\sqrt {\sum_{j = 1}^{N} {\left( {E_{j} - E_{m} } \right)^{2} *\sum_{j = 1}^{N} {\left( {P_{j} - P_{m} } \right)^{2} } } } }}$$
(15)

Here, \(E_{j}\) and \(P_{j}\) are the experimental and predicted stress, respectively. \(E_{{\text{m}}}\) and \(P_{{\text{m}}}\) is the mean stress associated with experiments and modelling. N is the number of plastic strain data used in the investigation. The values of AARE and R are calculated for all three developed models and are shown in Table 4.

Table 4 AARE and R values for J–C, m J–C and n J–C
Full size table

The correlation maps were also plotted to represent the model’s applicability for the hot deformation behaviour of AZ31B alloy, as depicted in Fig. 15. There is a significant improvement in error (%) of the n J–C model (31.65) concerning its original version (J–C, 39.02). The precision of constitutive models depends on the nearness of those data points with the linear fitting of predictive stress and experimental stress.

Fig. 15
figure 15

Correlation maps for constitutive relations: a Johnson–Cook (J–C), b modified Johnson–Cook (m J–C), c new Johnson–Cook (n J–C)

Full size image

It has been pointed out that, at 0.001 s−1 strain rate, the modified J–C shows precise prediction with an R-value greater than 0.98 for all the hot deformation temperatures (473–623 K). This strain rate suits the stress state developed in sheet metal-forming operations. Moreover, most of the tensile test is performed at 0.001 s−1 strain rate. Due to the clubbing of strain rate and temperatures, the overall predictive power of the m J–C model is well, with a coefficient of determination 0.96 and AARE 16.42% for all the strain rates. This combined effect makes it possible for better prediction ability than the other two J–C models.

The J–C model has poor prediction ability because the flow stress independently varies with strain, strain rates and temperature. However, the n J–C model predicts better with the coefficient of determination 0.95 and AARE 31.65% for all the strain rates.

Recently, Xie et al. [26] have used the n J–C model to predict the dynamic behaviour of Ni- and W-based alloys at high temperatures. The authors modified the term λ into λ/ɛ and calculated the variation of λ with plastic strains. In their work, the prediction of n J–C was better than the original J–C. The error variation between the experimental and predictive stresses is represented at a particular value of strain rate (0.001 s−1), and temperature ranges from 473 to 623 K, as illustrated in Fig. 16.

Fig. 16
figure 16

Variation of AARE with plastic strains for a J–C model, b m J–C model, c n J–C model

Full size image

The J–C model fails to predict the overall flow behaviour of AZ31B alloy at 573 and 623 K. The AARE increases for all values of plastic strains. The difference between the experimental and predictive stress is greater than 200%. However, the J–C predicts well for temperatures of 473 and 523 K with a maximum AARE of 18%, as shown in Fig. 16a.

On the contrary, the modified J–C has a mixed variation of AARE except for a 473 K temperature. At 523 K, the m J–C model’s maximum error was 27%; this error decreased as the plastic strain increased. So far, the modified J–C model has better prediction capability than J–C and n J–C. The erratic behaviour of AARE was observed in the case of the n J–C model at 573 K. The value of AARE suddenly increased and reached a maximum of 168%. A similar trend was observed for the 523 K, whereas the difference between predicted and experimental stress was found to be a minimum of 0.61% and a maximum of 25.7% at 623 K.

5 Conclusion

The present work investigated the hot tensile behaviour of AZ31B alloy under various temperatures and strain rates. The flow behaviour of the AZ31B alloy at high temperatures was predicted using modifications to the J–C model, and a new J–C model (n J–C) was adopted. The following were the key conclusions of this study:

  • The flow behaviour of the alloy displayed a sharp peak at 573 and 623 K for all strain rates. After attaining the peak, there was an abrupt decrease in flow stress. This phenomenon was attributed to the emergence of DRX grains reflected in the IPF map at 523 K temperature and 0.01 s−1 strain rate condition.

  • The experimental and predicted flow stress values were compared with statistical parameters. The n J–C model accurately predicts the hardening behaviour of the AZ31B alloy with a relative error of 4.06% at a deformation state of 573 K–0.1 s−1. Out of three constitutive models, the m J–C model has a good predictive performance with an average absolute error (AARE) of 16.42% and a higher correlation coefficient (R) of 0.96.

  • For a typical experimental strain rate of 0.001 s−1, the percentage error variation with plastic stresses was plotted to evaluate the performance of each constitutive model. The J–C model exhibits more error variation with plastic strain, but the m J–C model has displayed considerably less error variation across all temperatures.