A parametric analysis of free vibration and bending behavior of sandwich beam containing an open-cell metal foam core

Abstract

Free vibration and bending behavior of sandwich beams containing open-cell metal foam core are studied in the present work using zigzag theory. Hamilton’s principle and the principle of minimum potential energy are applied for determining the governing equations for free vibration and bending behavior, respectively. Three types of distribution of pores are used during the present study. The influence of the distribution of pores, end condition, thickness of the core, foam coefficients on beam behavior is studied in detail. The face sheets are assumed to be made up of the same material like foam. It was noticed that the nature of the distribution of pores and the end conditions widely determine the behavior of the beam.

1 Introduction

Because of the excellent properties of sandwich structures, such as lower self-weight, high strength, and stiffness, they are used widely in aerospace, civil, aeronautical, marine, defense, automobile industries, etc. [1]. Sandwich structures are the layered structures embedding a softcore [2]. Due to the presence of softcore, it is difficult to analyze these structures because they are weak in shear [3].

Several theories are available in the literature for the analysis of porous soft core sandwich structures [4]. These porous structures are used for constructing hydrological structures, marine structures, aerospace structures, etc. [5]. Ashby et al. [6] in their book, provided the guidelines for designing the metal foam structures. Hohe [7] presented stochastic homogenization of polymeric sandwich foam structures. Kesler and Gibson [8] performed bending analysis of sandwich metal foam core beams subjected to point load experimentally. Howson and Zare [9] derived an exact stiffness matrix for 3-layered sandwich beams. Classical plate theory [10], the earliest one, cannot predict the behavior of sandwich structures accurately [11]. Single-layer theories expand the in-plane displacement field as the first-order variation in the form of unknowns defined at the reference plane. This theory is called first-order shear deformation theory (FSDT) or Timoshenko beam theory. Magnucka-Blandzi [12] proposed modification in Timoshenko beam theory for bending analysis of metallic soft core sandwich beams. Chen et al. [13] carried out elastic buckling, free and forced vibration [14] analysis of porous beams using the Ritz method [15] based on Timoshenko beam theory. Later, a similar methodology was reformed for buckling and free vibration analysis of graphene reinforced porous plates by Yang et al. [16] and Kitipornchai et al. [17]. Wang and Zhao [18] proposed Chebyshev collocation method-based FSDT solutions for free vibration analysis of sandwich metallic foam core beams resting upon elastic foundations. Bamdad et al. [19] carried out magneto-electro-elastic-based buckling and vibration analysis of sandwich porous Timoshenko beams. The requirement of the shear correction factor is a major drawback of this theory, whose value is affected by several parameters, such as end conditions, material properties, etc. [20].

To avoid the incorporation of the shear correction factor, higher-order shear deformation theories (HSDT) were developed, incorporating warping of the beam’s cross section. Misiurek K, Śniady [21] carried out vibration analysis of beams under moving loading conditions. Wattanasakulpong et al. [22] carried out a vibration analysis of functionally graded porous beams using the Galerkin method based on HSDT. Wang et al. [23] proposed HSDT-based transient analysis of functionally graded porous soft core sandwich beam loaded with a moving mass. Chinh et al. [24] employed third-order SDT for bending analysis of porous core sandwich beams with functionally graded face sheets along with a mesh-free method. With the help of the Galerkin method, Dat et al. [25] carried out vibration analysis of porous sandwich beams. Ebrahimi et al. [26] carried out vibration analysis of porous metal plates resting on the viscoelastic foundation. Using higher-order sandwich panel theory, Shahedi and Mohammadimehr [27] carried out vibration analysis of rotating metallic soft core sandwich beams under hygrothermal conditions. Analytical solutions were presented by Yaghoobi and Taheri [28] for analysis of porous sandwich plates. However, HSDTs fail to predict transverse shear stress-free conditions at the beams' top and bottom surfaces and continuity of transverse shear stress at interfaces [29].

Layerwise theories (LWT) analyze each layer separately, and then the results are integrated over the whole domain. Loja [30] employed LWT for dynamic analysis of sandwich structures with metallic core with graphene reinforced skin faces using the finite element method. However, discrete LWTs are computationally costly as with an increase in layers, the number of unknowns increases. In the case of zigzag theories, the number of unknowns is independent of the number of layers. Application of zigzag theories for the analysis of functionally graded soft core sandwich structures is available in the works of Neves et al. [31], Garg et al. [32], Di Sciuva and Sorrenti [33]. Swaminathan et al. [34] presented a detailed review on the analysis of functionally graded plates. Carrera [35] presented a detailed review of the use of zigzag theories for the analysis of laminated sandwich plates and shells. Noor and Burton [36] presented an assessment of various theories for the analysis of laminated sandwich structures under thermal conditions. Reddy [37] presented a detailed review of available models for the analysis of sandwich structures. Sayyad and Ghugal [38] reviewed available methods for the analysis of sandwich plates and beams subjected to different kinds of loadings. Liew et al. [39] presented a review of layerwise theories available for the analysis of laminated structures. Garg et al. [40] presented a review on the analysis of carbon nanotubes reinforced structures. Garg et al. [41] presented a detailed review of available literature on the analysis of nanocomposites.

It has been noticed that the free vibration analysis of sandwich porous metallic softcore beams is carried out using FSDT. Bending analysis of the same beams is also absent in the literature to the authors’ best knowledge. In the present work, free vibration and bending analysis of sandwich porous metallic softcore beam are carried out using higher-order zigzag theory (HOZT). The influence of foam coefficients, end conditions, nature of the distribution of pores, core height is carried out in detail. The proposed model’s efficiency is checked by comparing present results with those reported already. Several new results are also reported.

2 Theoretical formulation

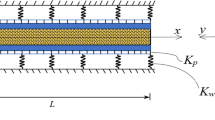
For a beam of length $\fancyscript{l}$ units and thickness $\fancyscript{h}$ units (Fig. 1), the displacement fields are expressed as

Fig. 1

The geometry of sandwich beam with open-cell metal foam core

$${\mathcal{U}}_{\left({\fancyscript{x}}\right)}={\fancyscript{u}}^{\left(0\right)}+{\mathbb{z}}{\psi }^{\left({\fancyscript{x}}\right)}+{\mathbb{z}}^{2}{\eta }^{\left({\fancyscript{x}}\right)}+{\mathbb{z}}^{3}{\varphi }^{\left({\fancyscript{x}}\right)}+{\mathbb{z}}^{4}{\xi }^{\left({\fancyscript{x}}\right)}+{\sum }_{{\fancyscript{p}}=1}^{{\mathbb{N}}^{\left({\fancyscript{u}}\right)}-1}\left({\mathbb{z}}-{\mathbb{z}}_{\fancyscript{p}}^{\left({\fancyscript{u}}\right)}\right)S\left({\mathbb{z}}-{\mathbb{z}}_{\fancyscript{p}}^{\left({\fancyscript{u}}\right)}\right){\uptheta }_{\fancyscript{p}}^{\left({\fancyscript{x}}_{\fancyscript{u}}\right)}$$

$$+\sum_{\fancyscript{q}=1}^{{\mathbb{N}}^{(\fancyscript{l})}-1}\left({\mathbb{z}}-{\mathbb{z}}_{\fancyscript{q}}^{\left(\fancyscript{l}\right)}\right)S\left(-{\mathbb{z}}+{\mathbb{z}}_{\fancyscript{q}}^{\left(\fancyscript{l}\right)}\right){\uptheta }_{\fancyscript{q}}^{\left({\fancyscript{x}}_{\fancyscript{l}}\right)},$$

(2.1)

$${\fancyscript{W}}_{\left({\mathbb{z}}\right)}={\fancyscript{w}}^{\left(0\right)}+{\mathbb{z}}{\psi }^{\left({\mathbb{z}}\right)}+{\mathbb{z}}^{2}{\eta }^{\left({\mathbb{z}}\right)}+{\mathbb{z}}^{3}{\varphi }^{\left({\mathbb{z}}\right)}+{\mathbb{z}}^{4}{\xi }^{\left({\mathbb{z}}\right)}+\sum_{{\fancyscript{p}}=1}^{{\mathbb{N}}^{\left(\fancyscript{u}\right)}-1}\left({\mathbb{z}}-{\mathbb{z}}_{\fancyscript{p}}^{\left(u\right)}\right)S\left({\mathbb{z}}-{\mathbb{z}}_{\fancyscript{p}}^{\left({\fancyscript{u}}\right)}\right){\uptheta }_{\fancyscript{p}}^{\left({\mathbb{z}}_{\fancyscript{u}}\right)}$$

$$+\sum_{\fancyscript{q}=1}^{{\mathbb{N}}^{(\fancyscript{l})}-1}\left({\mathbb{z}}-{\mathbb{z}}_{\fancyscript{q}}^{\left(\fancyscript{l}\right)}\right)S\left(-{\mathbb{z}}+{\mathbb{z}}_{\fancyscript{q}}^{\left(\fancyscript{l}\right)}\right){\uptheta }_{\fancyscript{q}}^{\left({\mathbb{z}}_{\fancyscript{l}}\right)}.$$

(2.2)

In the above equations, mid-plane displacements and rotations are denoted by $\left({\fancyscript{u}}^{\left(0\right)},{\fancyscript{w}}^{\left(0\right)}\right)$ and $\left({\psi }^{\left(\fancyscript{x}\right)},{\psi }^{\left({\mathbb{z}}\right)}\right)$ respectively. The slope of $\fancyscript{p}$th and $\fancyscript{q}$th layer is represented by $\uptheta$,  $\eta ,\varphi$ and $\xi$ are higher-order unknowns. $S\left({\mathbb{z}}-{\mathbb{z}}_{\fancyscript{p}}^{\left(\fancyscript{u}\right)}\right)$ and $S\left(-{\mathbb{z}}+{\mathbb{z}}_{\fancyscript{q}}^{\left(\fancyscript{l}\right)}\right)$ are unit step functions. The number of lower and upper layers is denoted by ${\mathbb{N}}^{\left(\fancyscript{u}\right)}$ and ${\mathbb{N}}^{(\fancyscript{l})}$ respectively.

The generalized stress–strain relationship is written as:

$$\left\{\begin{array}{c}{\sigma }_{\fancyscript{x}\fancyscript{x}}\\ {\sigma }_{zz}\\ {\sigma }_{\fancyscript{x}z}\end{array}\right\}=\left[\begin{array}{ccc}{Q}_{11}& {Q}_{12}& 0\\ {Q}_{21}& {Q}_{22}& 0\\ 0& 0& {Q}_{66}\end{array}\right]\left\{\begin{array}{c}{\varepsilon }_{\fancyscript{x}\fancyscript{x}}\\ {\varepsilon }_{zz}\\ {\gamma }_{\fancyscript{x}z}\end{array}\right\} or \left\{\sigma \right\}=\left[Q\right]\left\{\varepsilon \right\}.$$

(2.3)

The unknowns are stated in Eqs. (2.1) and (2.2) can be obtained in form of displacement-based terms ${\fancyscript{u}}^{\left(0\right)},{\fancyscript{w}}^{\left(0\right)},{\psi }^{\left(\fancyscript{x}\right)},{\psi }^{\left({\mathbb{z}}\right)},{\fancyscript{u}}^{\left(\fancyscript{u}\right)},{\fancyscript{w}}^{\left(\fancyscript{u}\right)},{\fancyscript{u}}^{\left(\fancyscript{l}\right)},{\fancyscript{w}}^{\left(\fancyscript{l}\right)}$ using the following conditions: (a) At ${\mathbb{z}}=\fancyscript{h}/2$, ${\sigma }_{\fancyscript{x}z}$ = 0, ${\mathcal{U}}_{\left(\fancyscript{x}\right)}$ = ${\fancyscript{u}}^{\left(\fancyscript{u}\right)}$, ${\mathcal{W}}_{\left({\mathbb{z}}\right)}$ = ${\fancyscript{w}}^{\left(\fancyscript{u}\right)}$; (b) At ${\mathbb{z}}=-\fancyscript{h}/2$, ${\sigma }_{\fancyscript{x}z}$ = 0, ${\mathcal{U}}_{\left(\fancyscript{x}\right)}$ = ${\fancyscript{u}}^{\left(\fancyscript{l}\right)}$, ${\fancyscript{W}}_{\left({\mathbb{z}}\right)}$ = ${\fancyscript{w}}^{\left(\fancyscript{l}\right)}$; (c) At the interface: ${\sigma }_{\fancyscript{x}z}^{\fancyscript{p}}={\sigma }_{\fancyscript{x}z}^{\fancyscript{p}+1}$, ${\sigma }_{zz}^{\fancyscript{p}}={\sigma }_{zz}^{\fancyscript{p}+1}$.

$$\left\{\mathcal{K}\right\}=\left[{\mathbb{E}}\right]\left\{\mathcal{D}\right\}$$

(2.4)

where

$$\left\{\mathcal{K}\right\}=\begin{array}{c}\{{\eta }^{\left(\fancyscript{x}\right)}{\varphi }^{\left(\fancyscript{x}\right)}{\xi }^{\left(\fancyscript{x}\right)}{\eta }^{\left({\mathbb{z}}\right)}{\varphi }^{\left({\mathbb{z}}\right)}{\xi }^{\left({\mathbb{z}}\right)}{\uptheta }_{1}^{\left({\fancyscript{x}}_{\fancyscript{u}}\right)}{\uptheta }_{2}^{\left({\fancyscript{x}}_{\fancyscript{u}}\right)}\dots {\uptheta }_{{\mathbb{N}}^{\left(\fancyscript{u}\right)}-1}^{\left({\fancyscript{x}}_{\fancyscript{u}}\right)}{\uptheta }_{1}^{\left({\mathbb{z}}_{\fancyscript{u}}\right)}{\uptheta }_{2}^{\left({\mathbb{z}}_{\fancyscript{u}}\right)}\dots {\uptheta }_{{\mathbb{N}}^{\left(\fancyscript{u}\right)}-1}^{\left({\mathbb{z}}_{\fancyscript{u}}\right)}\\ {\uptheta }_{1}^{\left({\fancyscript{x}}_{\fancyscript{l}}\right)}{\uptheta }_{2}^{\left({\fancyscript{x}}_{\fancyscript{l}}\right)}\dots {\uptheta }_{{\mathbb{N}}^{\left(\fancyscript{l}\right)}-1}^{\left({\fancyscript{x}}_{\fancyscript{l}}\right)}{\uptheta }_{1}^{\left({\mathbb{z}}_{\fancyscript{l}}\right)}{\uptheta }_{2}^{\left({\mathbb{z}}_{\fancyscript{l}}\right)}\dots {\uptheta }_{{\mathbb{N}}^{\left(\fancyscript{l}\right)}-1}^{\left({\mathbb{z}}_{\fancyscript{l}}\right)}\frac{\partial {\fancyscript{w}}^{\left(\fancyscript{u}\right)}}{\partial x}\frac{\partial {\fancyscript{w}}^{\left(\fancyscript{l}\right)}}{\partial x}{\}}^{T}\end{array}$$

(2.5)

is a vector of unknowns, $\left\{\mathcal{D}\right\}$ is a vector of displacement components as stated above and $\left[{\mathbb{E}}\right]$ is a matrix whose elements depend on material properties and thickness of the concerned layer.

The last two derivative terms are explained easily with respect to displacement components; therefore, Eq. (2.4) will no longer require C−1 continuity conditions.

Now, with the aid of Eq. (2.4), Eqs. (2.1) and (2.2) can be re-written as

$${\mathcal{U}}_{\left(\fancyscript{x}\right)}={\fancyscript{c}}^{\left(1\right)}{\fancyscript{u}}^{\left(0\right)}+{\fancyscript{c}}^{\left(2\right)}{\fancyscript{w}}^{\left(0\right)}+{\fancyscript{c}}^{\left(3\right)}{\psi }^{\left(\fancyscript{x}\right)}+{\fancyscript{c}}^{\left(4\right)}{\psi }^{\left({\mathbb{z}}\right)}+{\fancyscript{c}}^{\left(5\right)}{\fancyscript{u}}^{\left(\fancyscript{u}\right)}+{\fancyscript{c}}^{\left(6\right)}{\fancyscript{w}}^{\left(\fancyscript{u}\right)}$$

$$+{\fancyscript{c}}^{\left(7\right)}{\fancyscript{u}}^{\left(\fancyscript{l}\right)}+{\fancyscript{c}}^{(8)}{\fancyscript{w}}^{\left(\fancyscript{l}\right)},$$

(2.6)

$${\mathcal{W}}_{\left({\mathbb{z}}\right)}={\fancyscript{d}}^{\left(1\right)}{\fancyscript{u}}^{\left(0\right)}+{\fancyscript{d}}^{\left(2\right)}{\fancyscript{w}}^{\left(0\right)}+{\fancyscript{d}}^{\left(3\right)}+{\fancyscript{d}}^{\left(4\right)}{\varphi }^{\left(z\right)}+{\fancyscript{d}}^{\left(5\right)}{\fancyscript{u}}^{\left(\fancyscript{u}\right)}+{\fancyscript{d}}^{\left(6\right)}{\fancyscript{w}}^{\left(\fancyscript{u}\right)}$$

$$+{\fancyscript{d}}^{\left(7\right)}{\fancyscript{u}}^{\left(\fancyscript{l}\right)}+{\fancyscript{d}}^{(8)}{\fancyscript{w}}^{\left(\fancyscript{l}\right)}.$$

(2.7)

In the above equations, ${\fancyscript{c}}^{\left(\mathrm{s}\right)}$ and ${\fancyscript{d}}^{\left(\mathrm{s}\right)}$ depend on unit step function, thickness, and material property.

Generalized displacement vector for three-noded beam element having eight degrees of per node $\left\{\mathcal{D}\right\}$ is stated as

$$\left\{\mathcal{D}\right\}=\left[{N}_{i}\right]\left\{{\mathcal{D}}_{i}\right\},$$

(2.8)

where ${N}_{i}$ is the nodal shape function.

Using Eqs. (2.1)–(2.4), linear strain–displacement relation can be written as:

$$\left\{\varepsilon \right\}=\left\{\begin{array}{c}\frac{\partial {\fancyscript{U}}_{\left(\fancyscript{x}\right)}}{\partial x}\\ \frac{\partial {\mathcal{W}}_{\left({\mathbb{z}}\right)}}{\partial z}\\ \frac{\partial {\mathcal{U}}_{\left(\fancyscript{x}\right)}}{\partial z}+\frac{\partial {\mathcal{W}}_{\left({\mathbb{z}}\right)}}{\partial z}\end{array}\right\}\quad \mathrm{or} \quad \left\{\overline{\varepsilon }\right\}=\left[\mathcal{H}\right]\left\{\varepsilon \right\},$$

(2.9)

where

$$\left\{\varepsilon \right\}=\begin{array}{c}\{{\fancyscript{u}}^{\left(0\right)}{\fancyscript{w}}^{\left(0\right)}{\psi }^{\left(\fancyscript{x}\right)}{\psi }^{\left({\mathbb{z}}\right)}{\fancyscript{u}}^{\left(\fancyscript{u}\right)}{\fancyscript{w}}^{\left(\fancyscript{u}\right)}{\fancyscript{u}}^{\left(\fancyscript{l}\right)}{\fancyscript{w}}^{\left(\fancyscript{l}\right)}\frac{\partial {\fancyscript{u}}^{\left(0\right)}}{\partial x}\frac{\partial {\fancyscript{w}}^{\left(0\right)}}{\partial x}\frac{\partial {\psi }^{\left(\fancyscript{x}\right)}}{\partial x}\frac{\partial {\psi }^{\left(z\right)}}{\partial x}\frac{\partial {\fancyscript{u}}^{\left(\fancyscript{u}\right)}}{\partial x}\\ \frac{\partial {\fancyscript{w}}^{\left(\fancyscript{u}\right)}}{\partial x}\frac{\partial {\fancyscript{u}}^{\left(\fancyscript{l}\right)}}{\partial x}\frac{\partial {\fancyscript{w}}^{\left(\fancyscript{l}\right)}}{\partial x}\frac{\partial {\fancyscript{u}}^{\left(0\right)}}{\partial z}\frac{\partial {\fancyscript{w}}^{\left(0\right)}}{\partial z}\frac{\partial {\psi }^{\left(\fancyscript{x}\right)}}{\partial z}\frac{\partial {\psi }^{\left({\mathbb{z}}\right)}}{\partial z}\frac{\partial {\fancyscript{u}}^{\left(\fancyscript{u}\right)}}{\partial z}\frac{\partial {\fancyscript{w}}^{\left(\fancyscript{u}\right)}}{\partial z}\frac{\partial {\fancyscript{u}}^{\left(\fancyscript{l}\right)}}{\partial z}\frac{\partial {\fancyscript{w}}^{\left(\fancyscript{l}\right)}}{\partial z}\},\end{array}$$

and matrix $\left[\mathcal{H}\right]$ is a function of layer thickness and unit step function.

Applying Eq. (2.8) in Eq. (2.9), we will arrive at Eq. (2.10), which is stated as

$$\left\{\varepsilon \right\}=\left[\mathcal{B}\right]\left\{\mathcal{D}\right\},$$

(2.10)

where $\left[B\right]$ is strain–displacement relationship matrix.

2.1 For free vibration problems

Considering a mass $m$ moving from one point to another along $x$-axis, taking a certain time, the time-independent potential ${P}_{\left(x\right)}$ can be explained as:

$$m\ddot{x}=-\frac{\mathrm{d}{P}_{\left(x\right)}}{\mathrm{d}x}.$$

(2.11)

Multiplying both sides of the above equations with a small infinitesimal time function:

$$m\ddot{x}\times \delta x\left(t\right)=-\frac{\mathrm{d}{P}_{\left(x\right)}}{\mathrm{d}x}\delta x\left(t\right).$$

(2.12)

Adopting the analogy with Fermat’s principle, $\delta x\left(t\right)$ can be pictured as an infinitesimal deviation in a path from Newton’s trajectory, $x\left(t\right)\to x\left(t\right)+\delta x\left(t\right)$ and adopting variations at fixed ends as zero i.e., $\delta x\left({t}_{1}\right)=\delta x\left({t}_{2}\right)=0$.

Rewriting the Eq. (2.11) and integrating over the time domain, we get

$${\int }_{{t}_{1}}^{{t}_{2}}\left(-m\ddot{x}\left(t\right)-\frac{\mathrm{d}{P}_{\left(x\left(t\right)\right)}}{\mathrm{d}x}\right)\delta x\left(t\right)\mathrm{d}t=0,$$

(2.13)

$$-{\int }_{{t}_{1}}^{{t}_{2}}m\ddot{x}\left(t\right)\delta x\left(t\right)\mathrm{d}t-{\int }_{{t}_{1}}^{{t}_{2}}\frac{\mathrm{d}{P}_{\left(x\left(t\right)\right)}}{\mathrm{d}x}\delta x\left(t\right)\mathrm{d}t=0.$$

(2.14)

Performing integration by parts on the first term and trivial integration on the second term, we get

$$-{\int }_{{t}_{1}}^{{t}_{2}}m\ddot{x}\left(t\right)\delta x\left(t\right)\mathrm{d}t{\int }_{{t}_{1}}^{{t}_{2}}m\dot{x}\left(t\right)\delta \dot{x}\left(t\right)\mathrm{d}t={\int }_{{t}_{1}}^{{t}_{2}}m\dot{x}\left(t\right)\delta \dot{x}\left(t\right)\mathrm{d}t$$

$$={\int }_{{t}_{1}}^{{t}_{2}}\delta \left(\frac{1}{2}m{\dot{x}}^{2}\left(t\right)\right)\mathrm{d}t={\int }_{{t}_{1}}^{{t}_{2}}\delta T\left(x\left(t\right)\right)\mathrm{d}t,$$

(2.15a)

$$-{\int }_{{t}_{1}}^{{t}_{2}}\frac{\mathrm{d}{P}_{\left(x\left(t\right)\right)}}{\mathrm{d}x}\delta x\left(t\right)\mathrm{d}t=-{\int }_{{t}_{1}}^{{t}_{2}}\delta P\left(x\right)\mathrm{d}t.$$

(2.15b)

Now substituting Eq. (2.15a, b) in Eq. (2.14), we will get Hamilton’s principle (without considering work done by external forces and damping) stated as

$${\int }_{0}^{t}\delta \left(T-P\right)\mathrm{d}t=0.$$

(2.16)

In the above equation, $T$ represents kinetic energy, which is calculated as

$$T=\frac{1}{2}\int \rho \left({\dot{U}}_{\left(x\right)}^{2}+{\dot{U}}_{\left(z\right)}^{2}\right)\mathrm{d}v,$$

(2.17)

$\rho$ stands for the density of material and ${\dot{U}}_{\left(x\right)}$ and ${\dot{U}}_{\left(z\right)}$ are the derivatives of ${U}_{\left(x\right)}$ and ${U}_{\left(z\right)}$, respectively. $P$ in Eq. (2.16) represents potential energy which is expressed as

$$P=\frac{1}{2}\int \left({\sigma }_{xx}{\varepsilon }_{xx}+{\sigma }_{zz}{\varepsilon }_{zz}+{\sigma }_{xz}{\varepsilon }_{xz}\right)\mathrm{d}v,$$

or

$$P=\frac{1}{2}\sum_{i=1}^{n}{\left\{\overline{\varepsilon }\right\}}^{T}\left[{\overline{Q} }_{i}\right]\left\{\overline{\varepsilon }\right\}\mathrm{d}x\mathrm{d}z.$$

(2.18)

The dynamic equations for a system given by Hamilton’s principle are

$$\left[M\right]\left\{\frac{{\partial }^{2}\overline{\mathcal{D}}}{\partial {t }^{2}}\right\}+\left[K\right]\left\{\overline{\mathcal{D}}\right\}=\{0\}.$$

(2.19)

In the above equation $\left[M\right]$, $\left\{\frac{{\partial }^{2}\overline{\mathcal{D}}}{\partial {t }^{2}}\right\}$, $\left[K\right]$ and $\left\{\overline{\mathcal{D}}\right\}$ represent global mass matrix, nodal acceleration vector of system, global stiffness matrix, and unknown nodal vector, respectively. The frequency $\lambda$ can be evaluated using (Governing equation)

$$\left[K\right]\overline{\mathcal{D}}={\lambda }^{2}\left[M\right]\left\{\overline{\mathcal{D}}\right\}.$$

(2.20)

At any point within the beam, displacement due to free vibration can be written as

$$\left\{\frac{{\partial }^{2}\overline{\mathcal{D}}}{\partial {t }^{2}}\right\}= -{\upomega }^{2}\left\{\begin{array}{c}{U}_{\left(x\right)}\\ \begin{array}{c}{U}_{\left(z\right)}\end{array}\end{array}\right\},$$

(2.21)

or

$$\left\{\frac{{\partial }^{2}\overline{\mathcal{D}}}{\partial {t }^{2}}\right\}=- {\upomega }^{2}\left[F\right]\left\{\mathcal{D}\right\},$$

(2.22)

where the matrix $\left[F\right]$ is similar to $\left[\mathcal{H}\right]$ that contains terms in form of $z$ and the unit step function. The consistent elemental mass matrix for an element can be stated as

$$\left[{m}^{e}\right]=\sum_{i=1}^{{\mathbb{N}}^{\left(\fancyscript{u}\right)}+{\mathbb{N}}^{(\fancyscript{l})}}\int {\rho }_{i}{\left[N\right]}^{T}{\left[F\right]}^{T}\left[N\right]\left[F\right]\mathrm{d}x\mathrm{d}z=\int {\left[N\right]}^{T}\left[L\right]\left[N\right]\mathrm{d}x,$$

(2.23)

where ${\rho }_{i}$ is the mass density of the ith layer and $\left[N\right]$ is the shape function matrix and the matrix $\left[L\right]$ is

$$\left[L\right]=\sum_{i=1}^{nu+nl}\int {\rho }_{i}{\left[F\right]}^{T}\left[F\right]\mathrm{d}z.$$

(2.24)

Elemental stiffness, mass, and load matrix are assembled to form corresponding global matrices by taking into account the behavior of all the elements. Finally, the free vibration problem is solved as an eigenvalue problem. The skyline technique has been used to store the global stiffness matrix in a single array and the simultaneous iteration technique of Corr and Jennings [42] is used in free vibration analysis.

2.2 For bending study

Stating the total potential energy of the beam subjected to static loading as:

$${\Pi }_{e}={U}_{s}-{W}_{ext}$$

(2.25)

where ${U}_{s}$ is the beam’s strain energy and ${W}_{ext}$ is the energy due to external loading

$${U}_{s}=\frac{1}{2}\sum_{k=1}^{n}\iint {\left\{\overline{\varepsilon }\right\}}^{T}\left[Q\right]\left\{\overline{\varepsilon }\right\}\mathrm{d}x\mathrm{d}z,$$

(2.26)

$${U}_{s}=\begin{array}{c}\frac{1}{2}\int \left[{\left\{\varepsilon \right\}}^{T}\left[\mathcal{J}\right]\left\{\varepsilon \right\}\right]\mathrm{d}x\end{array},$$

(2.27)

where

$$\left[\mathcal{J}\right]=\sum_{k=1}^{n}\int {\left[H\right]}^{T}\left[Q\right]\left[H\right]\mathrm{d}z,$$

$${W}_{ext}=\int w q \mathrm{d}x \quad \mathrm{or} \quad {W}_{ext}=\int {\left\{\delta \right\}}^{T}{\left[{N}_{td}\right]}^{T}\fancyscript{q}\mathrm{d}x.$$

(2.28)

Now, the total elemental potential energy can be written as:

${\Pi }_{e}=\frac{1}{2}\int {\left\{\mathcal{D}\right\}}^{T}{\left[B\right]}^{T}\left[\mathcal{J}\right]\left[B\right]\left\{\mathcal{D}\right\}\mathrm{d}x-\frac{1}{2}\int {\left\{\mathcal{D}\right\}}^{T}{\left[{N}_{td}\right]}^{T}\fancyscript{q}\mathrm{d}x$ or

$${\Pi }_{e}=\frac{1}{2}{\left\{\mathcal{D}\right\}}^{T}\left[{K}_{e}\right]\left\{\mathcal{D}\right\}-\frac{1}{2}{\left\{\mathcal{D}\right\}}^{T}\left[{P}_{e}\right],$$

(2.29)

where the elemental stiffness matrix $\left[{K}_{e}\right]$ is written as $\int {\left[B\right]}^{T}\left[D\right]\left[B\right]\mathrm{d}x$. $\left[{P}_{e}\right]$ is elemental mechanical load vector $\iint {\left[{N}_{td}\right]}^{T}q\mathrm{d}x\mathrm{d}y$. $\left[{N}_{td}\right]$ is the shape function like matrix.

By minimizing Eq. (2.29) with $\left\{\mathcal{D}\right\}$, one gets (Governing equation)

$$\left[{K}_{e}\right]\left\{\mathcal{D}\right\}=\left[{P}_{e}\right].$$

(2.30)

Now taking the effect of all the elements, and determining the global stiffness matrix, load vector, and displacements can be worked out from there along with the application of suitable boundary conditions. Stresses can be determined using Eq. (2.3). The discussed methodology is coded in FORTRAN and the results are drawn out which are stated in the subsequent section. The Gaussian decomposition scheme is adopted for the solution.

Boundary conditions: Clamped: All degrees of freedom are restrained at the clamped end of the beam; Free: All degrees of freedom are allowed at the free end of the beam. For simply supported beam, at one end, following degrees of freedom are restrained: ${\fancyscript{u}}^{\left(0\right)},{\fancyscript{w}}^{\left(0\right)},{\fancyscript{u}}^{\left(\fancyscript{u}\right)},{\fancyscript{w}}^{\left(\fancyscript{u}\right)},{\fancyscript{u}}^{\left(\fancyscript{l}\right)},{\fancyscript{w}}^{\left(\fancyscript{l}\right)}$, whereas at another end, the following degrees of freedom are restrained: ${\fancyscript{u}}^{\left(0\right)},{\fancyscript{u}}^{\left(\fancyscript{u}\right)},{\fancyscript{u}}^{\left(\fancyscript{l}\right)}$.

3 Material modeling

Young’s modulus $E$ and density $\rho$ of metal foam core at any height ${\mathbb{z}}$ are given by:

Type-A foam (Fig. 2a) [13]:

Fig. 2

Various types of distribution of pores/cells within the metallic foam core

$$\begin{array}{c}E\left({\mathbb{z}}\right)={E}_{1}\left[1-{\kappa }_{o} \mathrm{cos}\left(\pi {\mathbb{z}}/{\fancyscript{h}}_{\fancyscript{c}}\right)\right],\\ \rho \left({\mathbb{z}}\right)={\rho }_{1}\left[1-{\kappa }_{d}\mathrm{cos}\left(\pi {\mathbb{z}}/{\fancyscript{h}}_{\fancyscript{c}}\right)\right].\end{array}$$

(3.1)

Type-B foam (Fig. 2b) [16]:

$$\begin{array}{c}E\left({\mathbb{z}}\right)={E}_{1}\left[1-{\kappa }_{o}^{*}\left\{1-\mathrm{cos}\left(\pi {\mathbb{z}}/{\fancyscript{h}}_{\fancyscript{c}}\right)\right\}\right],\\ \rho \left({\mathbb{z}}\right)={\rho }_{1}\left[1-{\kappa }_{d}^{*}\left\{1-\mathrm{cos}\left(\pi {\mathbb{z}}/{\fancyscript{h}}_{\fancyscript{c}}\right)\}\right.\right].\end{array}$$

(3.2)

Type-C foam (Fig. 2c) [18]:

$$\begin{array}{c}E\left({\mathbb{z}}\right)={E}_{1}\psi ,\\ \rho \left({\mathbb{z}}\right)={\rho }_{1}{\psi }^{*},\end{array}$$

(3.3)

where ${E}_{1}$ and ${\rho }_{1}$ are Young’s modulus and density of metal from which the foam is made up of $({\kappa }_{o},{\kappa }_{o}^{*},\psi )$ and $\left({\kappa }_{d},\right.{\kappa }_{d}^{*}, {\psi }^{*})$ are the foam coefficients for Young’s modulus and density, respectively, Type-A, B, and C foams.

For open-cell metal foams, Gibson and Ashby [43] published the following relationship between density and Young’s modulus given by

$$\frac{E\left({\mathbb{z}}\right)}{{E}_{1}}={\left(\frac{\rho \left({\mathbb{z}}\right)}{{\rho }_{1}}\right)}^{2}.$$

(3.4)

The following equations exhibit the relationship between the coefficient of mass density and the coefficient of Young’s modulus [18]

$$\begin{array}{c}1-{\kappa }_{d}\mathrm{cos}\left(\pi {\mathbb{z}}/{\fancyscript{h}}_{\fancyscript{c}}\right)=\sqrt{1-{\kappa }_{o}\mathrm{cos}\left(\pi {\mathbb{z}}/{\fancyscript{h}}_{\fancyscript{c}}\right)}\quad \text{For Type-A foam},\\ 1-{\kappa }_{d}^{*}\left[1-\mathrm{cos}\left(\pi {\mathbb{z}}/{\fancyscript{h}}_{\fancyscript{c}}\right)\right]=\sqrt{1-{\kappa }_{o}^{*}\left[1-\mathrm{cos}\left(\pi {\mathbb{z}}/{\fancyscript{h}}_{\fancyscript{c}}\right)\right]}\quad \text{For Type-B foam},\\ {\psi }^{*}=\sqrt{\psi }\quad\text{For Type-C foam}.\end{array}$$

(3.5)

For comparative-based study between the three types of foams, the masses of all foams are assumed the same for which the following relationship is used [18], which is used to find out the values for ${\kappa }_{o}^{*}$ and $\psi$ for a particular value of ${\kappa }_{o}$

$$\underset{0}{\overset{{\fancyscript{h}}_{\fancyscript{c}}/2}{\int }}\sqrt{1-{\kappa }_{o}\mathrm{cos}\left(\pi {\mathbb{z}}/{\fancyscript{h}}_{\fancyscript{c}}\right)}\mathrm{d}z=\underset{0}{\overset{{\fancyscript{h}}_{\fancyscript{c}}/2}{\int }}\sqrt{1-{\kappa }_{o}^{*}\left[1-\mathrm{cos}\left(\pi {\mathbb{z}}/{\fancyscript{h}}_{\fancyscript{c}}\right)\right]}\mathrm{d}z=\underset{0}{\overset{{\fancyscript{h}}_{\fancyscript{c}}/2}{\int }}\sqrt{\psi }\mathrm{d}z.$$

(3.6)

With the help of Eq. (3.6), Chen et al. [13] and Wang and Zhao [18] and suggested the values for ${\kappa }_{o}\in \left[0, 0.6\right]$. The values for foam coefficients are given in Table 1.

Table 1 Metal foam coefficients for different foam distributions

4 Results and discussion

The proposed mathematical model is applied for free vibration and static analysis of sandwich beams containing metallic foam core made up of steel. The influence of foam coefficients, geometric properties, end conditions, core thickness, and nature of the distribution of pores on the static, free vibration, and buckling behavior is presented in detail. The material properties for steel areas ${E}_{1}=200 \,\mathrm{GPa}$, $\nu =0.33$, ${\rho }_{1}=7850 \,\mathrm{kg}/{\mathrm{m}}^{3}$.

4.1 Free vibration study

4.1.1 Convergence and validation studies

For choosing the optimum mesh size and validating the proposed model, free vibration analysis of metal foam (Type-A) beams is carried out (i.e., ${\fancyscript{h}}_{\fancyscript{c}}=1$). Both ends clamped (CC) and cantilever (CF) end conditions are adopted. Dimensionless natural frequency $\left(\overline{\lambda }=\lambda \fancyscript{l}\sqrt{{\rho }_{1}/{E}_{1}}\right)$ is shown in Table 2. Dimensionless natural frequency converges when the number of beam elements reaches 10 (Fig. 3). Therefore, the same mesh size is adopted. Present results are validated with dimensionless natural frequencies calculated using Timoshenko beam theory along with the Ritz method by Chen et al. [14] and the Chebyshev collocation method by Wang and Zhao [18]. Present results are found to be in good agreement.

Table 2 Dimensionless natural frequency for metal foam Type-A beam with different end conditions (E.C.) ${\kappa }_{o}=0.5$

Fig. 3

Convergence study for dimensionless natural frequency for metal foam Type-A beam with both ends clamped for different numbers of finite elements $({\kappa }_{o}=0.5, \fancyscript{l}/\fancyscript{h}=10)$

4.1.2 Free vibration study on sandwich beam containing open-cell metal foam core

In this section, free vibration analysis of sandwich beam with open-cell metal foam core is carried out. In Table 3, variation of dimensionless natural frequency is reported for various values of ${\fancyscript{h}}_{\fancyscript{c}}/\fancyscript{h}$. For Type-A beam, the values of ${\kappa }_{o}$ are taken as 0.1, 0.2 and 0.3. Corresponding values for ${\kappa }_{o}^{*}$ and $\psi$ are taken for Type-B and Type-C beams as reported in Table 1. By doing this, for a value of ${\kappa }_{o}$, the mass of core will remain constant for Type-A, B, and C cases. With an increase in thickness of the core, the values for dimensionless natural frequency decrease. With an increase in the thickness of the core, the amount of distribution of pores across the thickness increases, resulting in a decrease in the beam's stiffness. Hence, the natural frequency of the beam decreases. The nature of the distribution of pores also affects the behavior of the beam. Maximum value for frequency is observed for Type-A case and minimum for Type-B case. Thus, the beam with Type-A configuration has greater stiffness followed by Type-C. Type-B configuration gives minimum stiffness value. With the increase in metal foam coefficient, the dimensionless natural frequency decreases for Type-B and C beams but increases for Type-A beam. This behavior is in accordance with the results given by Wang and Zhao [24] for sandwich foam core beams resting on elastic foundations.

Table 3 Dimensionless natural frequency for sandwich beam containing open-cell metal foam core for different thicknesses of cores having CC ends $(\fancyscript{l}/\fancyscript{h}=10)$

Figure 4 shows the variation of dimensionless natural frequencies for thick sandwich beams containing metallic foam core with different end conditions, namely, both ends clamped (CC), cantilever (CF), and both ends simply supported (SS) for different foam coefficients. Equivalent foam coefficients are used during the present study as reported in Sect. 2. In the present study, it is observed that with an increase in the value of ${\kappa }_{o}$ for Type-A beam, the dimensionless natural frequency decreases for all end conditions which is opposite to the behavior as observed in Table 3, in which the dimensionless natural frequency increases. A similar type of behavior is observed for both Type-B and Type-C beams. Thus, the vibration behavior of a thick metallic foam beam is different from a moderately thick beam. The amount of decrease is more in the case of CC and CF beams than the SS beam for Type-A and C beams. For the Type-B beam, a noticeable decrease in natural frequency is observed for all the end conditions.

Fig. 4

Variation of dimensionless natural frequencies for different types of thick sandwich beams containing metallic foam core with different end conditions (${\fancyscript{h}}_{\fancyscript{c}}/\fancyscript{h}=0.8$, $\fancyscript{l}/\fancyscript{h}=4$)

Figure 5 shows the first ten-mode shapes metal foam Type-A porous sandwich beam $({\kappa}_{\mathrm{o}}=0.1, \fancyscript{l}/\fancyscript{h}=4,{\fancyscript{h}}_{\fancyscript{c}}/\fancyscript{h}=0.8)$ for CC, SS, and CF end conditions. In Fig. 6, the first ten-mode shapes are shown for metal foam Type-B porous sandwich beam $({\kappa }_{o}^{*}=0.1738, \fancyscript{l}/\fancyscript{h}=4)$ whereas, Fig. 7 shows the same for metal foam Type-C porous sandwich beam $(\psi =0.9361, \fancyscript{l}/\fancyscript{h}=4)$. Mode shapes for all three types of CC and SS beams are similar, whereas, for a beam with CF end condition, mode shapes are different for all three cases, especially at higher vibration modes.

Fig. 5

First ten-mode shapes for (a) CC, (b) SS, and (c) CF ended metal foam Type-A porous sandwich beam $({\kappa }_{o}=0.1, \fancyscript{l}/\fancyscript{h}=4,{\fancyscript{h}}_{\fancyscript{c}}/\fancyscript{h}=0.8)$

Fig. 6

First ten-mode shapes for (a) CC, (b) SS, and (c) CF ended metal foam Type-B porous sandwich beam $({\kappa }_{o}^{*}=0.1738, \fancyscript{l}/\fancyscript{h}=4,{\fancyscript{h}}_{\fancyscript{c}}/\fancyscript{h}=0.8)$

Fig. 7

First ten-mode shapes for (a) CC, (b) SS, and (c) CF ended metal foam Type-C porous sandwich beam $(\psi =0.9361, \fancyscript{l}/\fancyscript{h}=4,{\fancyscript{h}}_{\fancyscript{c}}/\fancyscript{h}=0.8)$

4.2 Bending analysis

4.2.1 Convergence and validation studies

Table 4 shows the variation of dimensionless maximum deflection $\left(\overline{w }\left(l,0\right)=w/\fancyscript{h}\right)$ and stresses $\left({\tilde{\sigma }}_{xx}\left\{0,\fancyscript{h}/2\right\}={\sigma }_{xx}/\fancyscript{q},{\tilde{\sigma }}_{xz}\left\{\mathrm{0,0}\right\}={\sigma }_{xz}/\fancyscript{q}\right)$ for porous Type-A $\left({\fancyscript{h}}_{\fancyscript{c}}=1\right)$ CF beam subjected to uniformly distributed load of intensity $\left(\fancyscript{q}\right)$ 1 × 10⁴ N/m. It can be seen that the values for dimensionless maximum deflection converge when the number of beam elements equals 60, which is taken for further studies. Obtained results are found to be in good agreement with those published by Chen et al. [14] using FSDT with shear correction factor equals 5/6.

Table 4 Dimensionless displacement and stresses for metal foam Type-A porous beam with CF end and ${\kappa }_{o}=0.5$

4.2.2 Bending study on sandwich beam containing open-cell metal foam core

Under this section, a bending analysis of sandwich beam containing metallic foam core subjected to sinusoidal loading is carried out. Next are the relations adopted for transforming dimensional quantities into respective dimensionless ones: $\overline{w }\left(l/\mathrm{2,0}\right)=w\left(l/\mathrm{2,0}\right){E}_{1}{\fancyscript{h}}^{3}/{\fancyscript{l}}^{4}$, ${\tilde{\sigma }}_{xx}\left(l/2,\fancyscript{h}/2\right)={{\sigma }}_{xx}\left(l/2,\fancyscript{h}/2\right)/\fancyscript{l}{\fancyscript{q}}_{0}$, ${\tilde{\sigma }}_{xz}\left(\mathrm{0,0}\right)={{\sigma }}_{xz}\left(\mathrm{0,0}\right)/{\fancyscript{q}}_{0}$, $\overline{u }\left(0,\fancyscript{h}/2\right)=10\times u\left(0,h/2\right){E}_{1}{\fancyscript{h}}^{3}/{\fancyscript{l}}^{4}$.

Type-A sandwich beam with metal soft core foam: Table 5 shows the variation of dimensionless transverse displacement for Type-A sandwich beam containing metal soft core foam having simply supported end for different values of foam coefficient $({\kappa }_{o})$, $\fancyscript{l}/\fancyscript{h}$ and ${\fancyscript{h}}_{\fancyscript{c}}/\fancyscript{h}$. It can be seen that as the value for ${\kappa }_{o}$ increases, dimensionless transverse deflection of beam increases. Thus, the beam is losing its stiffness as the value for ${\kappa }_{o}$ increases. With an increase in the thickness of the core, dimensionless transverse deflection increases. Table 6 shows the variation of dimensionless in-plane displacement for the same beam. Also, the in-plane displacement of the beam increases with the increase in ${\kappa }_{o}$ value. Thus, as the foam coefficient for Type-A configuration increases, the beam starts losing its both in-plane and transverse stiffness. Tables 7 and 8 show the variation of dimensionless in-plane stress and dimensionless transverse shear stress for the same beam. With the increase in the value for ${\kappa }_{o}$, the value for ${\tilde{\sigma }}_{xx}$ increases and ${\tilde{\sigma }}_{xz}$ decreases. Figure 8 shows the variation of dimensionless stresses across the thickness for SS Type-A beam having $\fancyscript{l}/\fancyscript{h}=4$ with ${\kappa }_{o}$ = 0.1 and 0.6. It is observed that with an increase in foam coefficient, non-linearity in dimensionless in-plane stress increases. However, the nature of variation of transverse shear stress almost remains the same.

Table 5 Dimensionless transverse displacement $(\overline{w })$ for a sandwich beam with Type-A metal soft core foam having SS ends subjected to sinusoidal load

Table 6 Dimensionless in-plane displacement $(-\overline{u })$ for a sandwich beam with Type-A metal soft core foam having SS ends subjected to sinusoidal load

Table 7 Dimensionless in-plane stress $({\tilde{\sigma }}_{xx})$ for a sandwich beam with Type-A metal soft core foam having SS ends subjected to sinusoidal load

Table 8 Dimensionless transverse shear stress $({\tilde{\sigma }}_{xz})$ for a sandwich beam with Type-A metal soft core foam having SS ends subjected to sinusoidal load

Fig. 8

Variation of dimensionless stresses across the thickness for a sandwich beam with Type-A metal soft core foam having SS ends subjected to sinusoidal load $(\fancyscript{l}/\fancyscript{h}=4)$

Type-B sandwich beam with metal soft core foam: Tables 9 and 10 present the values for dimensionless transverse and in-plane displacements for Type-B sandwich beam containing metal soft core foam with SS ends for different values of foam coefficient $({\kappa }_{o}^{*})$, $\fancyscript{l}/\fancyscript{h}$ and ${\fancyscript{h}}_{\fancyscript{c}}/\fancyscript{h}$. With an increase in the value for ${\kappa }_{o}^{*}$, the values for both types of displacements show an increasing trend, which informs about a decrease in the value for stiffness of the beam. With an increase in the thickness of the core, the values for dimensionless deflections also increase. Tables 11 and 12 exhibit the variation of dimensionless in-plane stress and transverse shear stress for the same beam. With an increase in the thickness of the core, values for ${\tilde{\sigma }}_{xx}$ increase. For ${\tilde{\sigma }}_{xz}$, the values first decrease and then increase. Figure 9 shows the variation of dimensionless stresses across the thickness for SS Type-B beam having ${\kappa }_{o}^{*}$ = 0.1738 and 0.9612. It is observed that with an increase in the value of foam coefficient, non-linearity in the distribution of stresses increases. Thus, for better prediction of stresses, a zigzag effect must be incorporated.

Table 9 Dimensionless transverse displacement $(\overline{w })$ for a sandwich beam with Type-B metal soft core foam having SS ends subjected to sinusoidal load

Table 10 Dimensionless in-plane displacement $(-\overline{u })$ for a sandwich beam with Type-B metal soft core foam having SS ends subjected to sinusoidal load

Table 11 Dimensionless in-plane stress $({\tilde{\sigma }}_{xx})$ for a sandwich beam with Type-B metal soft core foam having SS ends subjected to sinusoidal load

Table 12 Dimensionless transverse shear stress $({\tilde{\sigma }}_{xz})$ for a sandwich beam with Type-B metal soft core foam having SS ends subjected to sinusoidal load

Fig. 9

Variation of dimensionless stresses across the thickness for a sandwich beam with Type-B metal soft core foam having SS ends subjected to sinusoidal load $(\fancyscript{l}/\fancyscript{h}=4)$

Type-C sandwich beam with metal soft core foam: Bending behavior of SS Type-C sandwich beam containing metallic softcore foam is studied in this part. Results for dimensionless transverse and in-plane displacements are reported in Tables 13 and 14, respectively. Even for this case, with an increase in the value for $\psi$, the beam starts losing its both in-plane and transverse stiffness. Tables 15 and 16 show the variation of dimensionless in-plane stress and transverse shear stress for Type-C beam. With an increase in value for $\psi$, the value for ${\tilde{\sigma }}_{xx}$ increases and ${\tilde{\sigma }}_{xz}$ decreases. Figure 10 shows the nature of dimensionless stress distribution across the thickness for SS Type-C beam $(\fancyscript{l}/\fancyscript{h}=4)$ with $\psi$ = 0.9361 and 0.6047. The nature of stress distribution for Type-C beam is found similar to Type-A beam.

Table 13 Dimensionless transverse displacement $(\overline{w })$ for a sandwich beam with Type-C metal soft core foam having SS ends subjected to sinusoidal load

Table 14 Dimensionless in-plane displacement $(-\overline{u })$ for a sandwich beam with Type-C metal soft core foam having SS ends subjected to sinusoidal load

Table 15 Dimensionless in-plane stress $({\tilde{\sigma }}_{xx})$ for a sandwich beam with Type-C metal soft core foam having SS ends subjected to sinusoidal load

Table 16 Dimensionless transverse shear stress $({\tilde{\sigma }}_{xz})$ for a sandwich beam with Type-C metal soft core foam having SS ends subjected to sinusoidal load

Fig. 10

Variation of dimensionless stresses across the thickness for a sandwich beam with Type-C metal soft core foam having SS ends subjected to sinusoidal load $(\fancyscript{l}/\fancyscript{h}=4)$

5 Conclusions

In the present work, free vibration and bending analysis of sandwich beams containing metallic foam core are investigated using finite element-based HOZT. Three different configurations of distribution of pores are assumed. The influence of porosities, end conditions, geometric properties, foam coefficients, and core thickness is studied in detail. Following points are noted during present investigations:

• The free vibration behavior of a thick sandwich beam with metallic foam is different from a moderately thick sandwich beam containing metallic foam core for a Type-A case.

• Type-A beam shows the maximum value for stiffness followed by Type-C and Type-B cases.

• With an increase in thickness of the core, the value for dimensionless natural frequency decreases.

• The end condition also determines the free vibration behavior of the sandwich beam with a metallic core. A large decrease in dimensionless natural frequency decreases for simply supported Type-B beams, whereas, for Type-A and C beams, the dimensionless natural frequency remains almost constant.

• Mode shapes for SS and CC Type-A, B, and C beams are similar, whereas, for CF end condition, mode shapes are different for all three types of beams, especially at higher modes.

• With an increase in the value for foam coefficient, all types of beams lose their in-plane and transverse stiffnesses.

• With an increase in the thickness of the metallic foam core, dimensionless displacements, and in-plane stress increases, and dimensionless transverse stress decrease for all types of beams. However, for the Type-B beam, variation of transverse shear stress with an increase in thickness first shows an increasing trend and then decreases.

• The present model can predict zero transverse shear stress at the top and bottom surfaces of the beam.

• Type-B beam gives a highly non-linear distribution of stresses across its thickness. The amount of non-linearity increases with increases in the value for foam coefficient.