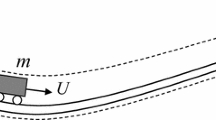1 Introduction

Plates, beams, and shells as the most famous continuous structures can be found as building blocks of many mechanical/civil systems; Polus and Szumigala [1] analysed aluminium–concrete composite beams using a three-dimensional finite element technique and found very good agreement between experiments and theory. Domagalski [2] considered periodically inhomogeneous beams and examined the vibration behaviour in the absence of loadings and subject to external loadings via the Galerkin techniques for frequency–amplitude responses. In some applications, their nonlinear response becomes important. Loads applied to these structures have different natures such as randomly/harmonically varying magnitude. There are also mechanisms where the applied load changes its position; for instance, Mohanti et al. [3] employed a single-mode approximation in the framework of the method of multiple scales in the presence of a moving mass and obtained the corresponding time histories. One famous application is in bridges, where the moving cars and passengers could be considered as moving loads and depending on the value and sequence of them the dynamics could be analysed.

For a supported–supported beam-mass system, a geometric type of nonlinearity due to stretching influences becomes important in the nonlinear dynamical behaviour. Another feature is the couplings of linear/nonlinear type between the transverse/longitudinal displacements/inertia; none of these have been ignored in the modelling/simulations.

Investigations into the moving-load-caused dynamics of beams may be categorised into linear and nonlinear. In the first class, the geometric nonlinearity is assumed to be small for near-equilibrium dynamics; for instance, Dimitrovova [4] formulated a viscoelastically supported beam subject to a moving harmonic load using the Bernoulli–Euler theory and developed a semi-analytical solution by means of the integral transform and contour integration methods. Esen [5] used a modified version of the finite element technique for the linear dynamics analysis of functionally graded Timoshenko beams subject to a variable-velocity moving mass and obtained the deflection-velocity curves. Roy et al. [6] considered an infinitely long beam under a uniform-speed harmonically moving force and analysed its dynamics. Yang and Wang [7] obtained the dynamical behaviour of an inclined beam under a moving vertical force and conducted stability analysis. Yang et al. [8], for bi-directional functionally graded beams, conducted a dynamic response analysis using a boundary-domain integral equation technique and analysed the natural frequencies and forced vibrations. Sarparast and Ebrahimi-Mamaghani [9] conducted forced/free vibrations analysis due to moving loads on laminated curved beams via the Galerkin method and obtained the fundamental frequency and displacements.

There are a limited number of investigations in the literature which considered nonlinearities [2, 10,11,12]. Correa et al. [13], for an Euler–Bernoulli beam under a moving load, developed a dynamic model using the finite element (FE) model in the pressure of non-smooth frictional damping. In a study by Chen et al. [14], the thermo-mechanical dynamic responses of a laminated beam under a harmonically moving force by means of the finite difference method and time histories were obtained. Zupan and Zupan [15] employed a three-dimensional framework for the dynamic analysis of beams with a moving mass through use of a finite element formulation. Khurshudyan and Ohanyan [16] considered a nonlinear Bernoulli–Euler beam excited by two moving loads in opposite directions and analysed the nonlinear vibrations using the Bubnov–Galerkin procedure.

This article is the first to study the moving-load-caused local nonlinear coupled dynamical response of beam-mass systems. Two coupled partial differential equations describing the coupled transverse/longitudinal motion are formulated using a Hamilton-based technique. A load with a constant magnitude with a harmonically changing position excites the beam-mass system. The corresponding work contribution is formulated. Mass kinetic energy together with that of the beam as well as the energy stored in the beam after deflection is formulated. Using Hamilton’s principle results in the moving-load-caused nonlinear dynamics model of the beam-mass structure. A 20-DOF system is obtained via a weighted-residual-based discretisation scheme; this is numerically integrated by means of continuation/time-integration techniques. The nonlinear and resonance dynamical behaviour in frequency, time, and spatial domains is investigated. A FEA model is developed for a simple linear version for linear natural frequency verifications.

2 Coupled model for moving-load-caused dynamics of beam-mass structure

As illustrated in Fig. 1, the beam-mass system assembly consists of a straight beam with a mass M attached to it at a distance ξM from the left end with the following assumptions:

  • The beam is considered of an Euler–Bernoulli type; hence, the shear deformation/rotary inertia are neglected.

  • Large rotations and stretching nonlinearities are considered.

  • The motion is considered to be planar.

  • The beam is considered perfectly straight.

  • The mass is assumed to be a point mass; hence, there are no rotary inertia influences.

  • The mass is attached to the centreline of the beam.

  • A Lagrangian system of movement description is used.

  • The beams is considered to be homogenous with uniform properties.

  • The moving load is considered as a point force.

Fig. 1
figure 1

A beam-mass system with a moving load

Full size image

EI, EA, L, and A are the flexural rigidity, axial stiffness, length, and cross-sectional area of the beam, respectively. m is beam’s mass per unit length. A constant-magnitude moving point force \(F\) is applied to the beam whose distance from the left end, ξ0(t), is given by

$$ \xi_{0} (t) = \frac{L}{2}\left( {1 - s_{f} \cos \left( {\omega_{f} t} \right)} \right), $$
(1)

where ωf is the frequency of the position change and sf is a parameter determining the boundaries of the position of the moving load. The virtual work of this moving load is given by

$$ \delta W_{F} = \int_{0}^{L} {F\delta_{{{\text{Dirac}}}} \left( {\xi - \xi_{0} (t)} \right)\delta \chi_{2} {\text{d}}\xi } , $$
(2)

where \(\chi_{2}\) is the displacement in transverse direction.

Defining \(\chi_{1}\) as the displacements in axial direction and ρ as the centreline rotation, the strain term (incorporating both stretching and curvature nonlinearities) can be written as [17]

$$ \varepsilon_{\xi \xi } \left( {t,\xi ,z} \right) = \sqrt {\left( {\frac{{\partial \chi_{1} (t,\xi )}}{\partial \xi } + 1} \right)^{2} + \left( {\frac{{\partial \chi_{2} (t,\xi )}}{\partial \xi }} \right)^{2} } - 1 - z\frac{\partial \rho (t,\xi )}{{\partial \xi }}, $$
(3)

resulting in the potential energy of the beam as [18]

$$ \begin{aligned} \delta U = & \int_{0}^{L} {\int_{A} {E\left[ {\sqrt { \left( {\frac{{\partial \chi_{2} (t,\xi )}}{\partial \xi }} \right)^{2} + \left( {\frac{{\partial \chi_{1} (t,\xi )}}{\partial \xi } + 1} \right)^{2} } - 1 - \left( {\frac{\partial \rho (t,\xi )}{{\partial \xi }}} \right)z} \right]} } \\ & \; \times \delta \left[ {\sqrt { \left( {\frac{{\partial \chi_{2} (t,\xi )}}{\partial \xi }} \right)^{2} + \left( {\frac{{\partial \chi_{1} (t,\xi )}}{\partial \xi } + 1} \right)^{2} } - 1 - \left( {\frac{\partial \rho (t,\xi )}{{\partial \xi }}} \right)z} \right]{\text{d}}A{\text{d}}\xi . \\ \end{aligned} $$
(4)

Defining a linear viscous damping of coefficient c for the motion, the dissipative work is formulated as [19]

$$ \delta W_{d} = - \int_{0}^{L} {\left( {c\left( {\frac{{\partial \chi_{1} }}{\partial t}} \right)\delta \chi_{1} + c\left( {\frac{{\partial \chi_{2} }}{\partial t}} \right)\delta \chi_{2} } \right){\text{d}}\xi } . $$
(5)

Formulation of the motion energy gives

$$ T = \frac{1}{2}\int\limits_{0}^{L} {\left( {m + M\delta_{{{\text{Dirac}}}} (\xi - \xi_{M} )} \right)\left( {\frac{{\partial \chi_{1} }}{\partial t}} \right)^{2} {\text{d}}\xi + \frac{1}{2}\int\limits_{0}^{L} {\left( {m + M\delta_{{{\text{Dirac}}}} (\xi - \xi_{M} )} \right)\left( {\frac{{\partial \chi_{2} }}{\partial t}} \right)^{2} {\text{d}}\xi } .} $$
(6)

Hamilton’s work/energy principle for Eqs. (2), (4), (5), and (6) gives

$$ \left( {1 + \gamma \delta_{{{\text{Dirac}}}} (\xi - \xi_{M} )} \right)\frac{{\partial^{2} \chi_{1} }}{{\partial \tau^{2} }} - \Pi \frac{{\partial^{2} \chi_{1} }}{{\partial \xi^{2} }} - \frac{\Pi }{S}\frac{{\partial^{2} \chi_{2} }}{{\partial \xi^{2} }}\frac{{\partial \chi_{2} }}{\partial \xi } - \frac{1}{S}\left( {\frac{{\partial^{3} \chi_{2} }}{{\partial \xi^{3} }}\frac{{\partial^{2} \chi_{2} }}{{\partial \xi^{2} }} + \frac{{\partial^{4} \chi_{2} }}{{\partial \xi^{4} }}\frac{{\partial \chi_{2} }}{\partial \xi }} \right) + c_{d} \frac{{\partial \chi_{1} }}{\partial \tau } = 0, $$
(7)
$$ \begin{aligned} & \left( {1 + \gamma \delta_{{{\text{Dirac}}}} (\xi - \xi_{M} )} \right)\frac{{\partial^{2} \chi_{2} }}{{\partial \tau^{2} }} + \frac{{\partial^{4} \chi_{2} }}{{\partial \xi^{4} }} + c_{d} \frac{{\partial \chi_{2} }}{\partial \tau } - f_{m} \delta_{{{\text{Dirac}}}} \left[ {\xi - \frac{1}{2}\left( {1 - s_{f} \cos \left( {\Omega_{f} \tau } \right)} \right)} \right] - \frac{\Pi }{S}\left( {\frac{3}{2S}\left( {\frac{{\partial \chi_{2} }}{\partial \xi }} \right)^{2} \frac{{\partial^{2} \chi_{2} }}{{\partial \xi^{2} }} + \frac{{\partial \chi_{2} }}{\partial \xi }\frac{{\partial^{2} \chi_{1} }}{{\partial \xi^{2} }} + \frac{{\partial \chi_{1} }}{\partial \xi }\frac{{\partial^{2} \chi_{2} }}{{\partial \xi^{2} }}} \right) \\ & \quad \quad - \frac{1}{S}\left( {2\frac{{\partial \chi_{1} }}{\partial \xi }\frac{{\partial^{4} \chi_{2} }}{{\partial \xi^{4} }} + 4\frac{{\partial^{2} \chi_{1} }}{{\partial \xi^{2} }}\frac{{\partial^{3} \chi_{2} }}{{\partial \xi^{3} }} + \frac{{\partial^{4} \chi_{1} }}{{\partial \xi^{4} }}\frac{{\partial \chi_{2} }}{\partial \xi } + 3\frac{{\partial^{3} \chi_{1} }}{{\partial \xi^{3} }}\frac{{\partial^{2} \chi_{2} }}{{\partial \xi^{2} }} + \frac{1}{S}\left\{ {2\left( {\frac{{\partial^{2} \chi_{2} }}{{\partial \xi^{2} }}} \right)^{3} + 8\frac{{\partial^{2} \chi_{2} }}{{\partial \xi^{2} }}\frac{{\partial \chi_{2} }}{\partial \xi }\frac{{\partial^{3} \chi_{2} }}{{\partial \xi^{3} }} + 2\frac{{\partial^{4} \chi_{2} }}{{\partial \xi^{4} }}\left( {\frac{{\partial \chi_{2} }}{\partial \xi }} \right)^{2} } \right\}} \right) = 0, \\ \end{aligned} $$
(8)

in which the following non-dimensionalisations have been performed

$$ \begin{aligned} \left\langle {\xi ^{*} ,\xi _{M}^{*} ,\chi _{1}^{*} ,\chi _{2}^{*} ,S} \right\rangle =& \left\langle {\frac{\xi }{L},\frac{{\xi _{M} }}{L},\frac{{\chi _{1} }}{h},\frac{{\chi _{2} }}{h},\frac{L}{h}} \right\rangle , \\ \Omega _{f} =& \omega _{f} L^{2} \sqrt {\frac{m}{{EI}}} ,\tau = \frac{t}{{L^{2} }}\sqrt {\frac{{EI}}{m}} , \\ c_{d} =& \frac{{cL^{2} }}{{EI}}\sqrt {\frac{{EI}}{m}} ,\prod = \frac{{AL^{2} }}{T},f_{m} = \frac{{FL^{2} }}{{EIh}},\gamma = \frac{M}{{mL}} \\ \end{aligned}$$
(9)

and the asterisk is dropped for brevity.

One way of dealing with Eqs. (7) and (8), which are complex/coupled in nonlinear ways, and solving them together for time/frequency domains is to discretise them; however, it is important to retain enough number of discretisation terms (here 20 modes) to get reliable/converged results; in a nonlinear sense, this makes numerical integrations expensive and time-consuming. So, defining series expansion of

$$ \left[ \begin{gathered} \chi_{1} \hfill \\ \chi_{2} \hfill \\ \end{gathered} \right] = \sum\limits_{k = 1}^{10} {\left[ \begin{gathered} \left( {r_{k} (\tau )\Delta_{k} (\xi )} \right) \hfill \\ \left( {\Gamma_{k} (\xi )p_{k} (\tau )} \right) \hfill \\ \end{gathered} \right]} , $$
(10)

with

$$ \begin{gathered} \left[ \begin{gathered} \Delta_{k} \hfill \\ \Gamma_{k} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} \left( {\sin \left( {k\pi \xi } \right)} \right) \hfill \\ \left[ { - \cos \left( {\alpha_{k} \xi } \right) + \theta_{k} \sin \left( {\alpha_{k} \xi } \right)} \right] - \left[ {\theta_{k} \sinh \left( {\alpha_{k} \xi } \right) - \cosh \left( {\alpha_{k} \xi } \right)} \right] \hfill \\ \end{gathered} \right] \hfill \\ \theta_{k} = \left( {\sinh \alpha_{k} - \sin \alpha_{k} } \right)^{ - 1} \left( {\cosh \alpha_{k} - \cos \alpha_{k} } \right) \hfill \\ \end{gathered} $$
(11)

and weakening Eqs. (7) and (8) via a weighted-residual approach gives

$$ \left\{ {\begin{array}{*{20}l} {\ddot{r}_{k} \leftrightarrow \sum\limits_{k = 1}^{10} {\left[ {\int_{0}^{1} {\Delta_{j} \Delta_{k} \left( {1 + \gamma \delta_{{{\text{Dirac}}}} (\xi - \xi_{M} )} \right){\text{d}}\xi } } \right]} } \hfill \\ {\dot{r}_{k} \leftrightarrow + c_{d} \sum\limits_{k = 1}^{10} {\left( {\int_{0}^{1} {\Delta_{j} \Delta_{k} {\text{d}}\xi } } \right)} } \hfill \\ {r_{k} \leftrightarrow - \Pi \sum\limits_{k = 1}^{10} {\left( {\int_{0}^{1} {\Delta_{k}^{\prime \prime } \Delta_{j} {\text{d}}\xi } } \right)} } \hfill \\ {p_{k} p_{l} \leftrightarrow - \frac{\Pi }{S}\sum\limits_{k = 1}^{10} {\sum\limits_{l = 1}^{10} {\left( {\int_{0}^{1} {\Delta_{j} \Gamma_{k}^{\prime \prime } \Gamma_{l}^{\prime } {\text{d}}\xi } } \right) - \frac{1}{S}\sum\limits_{k = 1}^{10} {\sum\limits_{l = 1}^{10} {\left[ {\int_{0}^{1} {\left( {\Gamma_{k}^{\prime \prime \prime } \Gamma_{l}^{\prime \prime } + \Gamma_{k}^{\prime \prime \prime \prime } \Gamma_{l}^{\prime } } \right)\Delta_{j} {\text{d}}\xi } } \right]} } } } = 0} \hfill \\ {j = 1, \, 2, \ldots , \, 10} \hfill \\ \end{array} } \right\}, $$
(12)
$$ \left\{ {\begin{array}{*{20}l} {\ddot{p}_{k} \leftrightarrow \sum\limits_{k = 1}^{10} {\left( {\int_{0}^{1} {\left( {1 + \gamma \delta_{{{\text{Dirac}}}} (\xi - \xi_{M} )} \right)\Gamma_{k} \Gamma_{j} {\text{d}}\xi } } \right)} } \hfill \\ {\dot{p}_{k} \leftrightarrow + c_{d} \sum\limits_{k = 1}^{10} {\left( {\int_{0}^{1} {\Gamma_{k} \Gamma_{j} {\text{d}}\xi } } \right)} } \hfill \\ {p_{k} \leftrightarrow + \sum\limits_{k = 1}^{10} {\left( {\int_{0}^{1} {\Gamma_{k}^{\prime \prime \prime \prime } \Gamma_{j} {\text{d}}\xi } } \right)} } \hfill \\ {r_{k} p_{l} \leftrightarrow - \frac{\Pi }{S}\sum\limits_{k = 1}^{10} {\sum\limits_{l = 1}^{10} {\left( {\int_{0}^{1} {\left[ {\Delta_{k}^{\prime } \Gamma_{l}^{\prime \prime } + \Delta_{k}^{\prime \prime } \Gamma_{l}^{\prime } } \right]\Gamma_{j} {\text{d}}\xi } } \right)} } - \frac{1}{S}\sum\limits_{k = 1}^{10} {\sum\limits_{l = 1}^{10} {\left( {\int_{0}^{1} {\left[ {2\Delta_{k}^{\prime } \Gamma_{l}^{\prime \prime \prime \prime } + \Delta_{k}^{\prime \prime \prime \prime } \Gamma_{l}^{\prime } + 4\Delta_{k}^{\prime \prime } \Gamma_{l}^{\prime \prime \prime } + 3\Delta_{k}^{\prime \prime \prime } \Gamma_{l}^{\prime \prime } } \right]\Gamma_{j} {\text{d}}\xi } } \right)p_{k} p_{l} } } } \hfill \\ {p_{k} p_{l} p_{m} \leftrightarrow - \frac{1}{{S^{2} }}\sum\limits_{k = 1}^{10} {\sum\limits_{l = 1}^{10} {\sum\limits_{m = 1}^{10} {\left( {\int_{0}^{1} {\left[ {2\Gamma_{k}^{\prime \prime \prime \prime } \Gamma_{l}^{\prime } \Gamma_{m}^{\prime } + 2\Gamma_{k}^{\prime \prime } \left( {\Gamma_{l}^{\prime \prime } \Gamma_{m}^{\prime \prime } + 4\Gamma_{l}^{\prime } \Gamma_{m}^{\prime \prime \prime } } \right)} \right]\Gamma_{j} {\text{d}}\xi } } \right)p_{k} p_{l} p_{m} - \frac{3}{2}\frac{\Pi }{{S^{2} }}\sum\limits_{k = 1}^{10} {\sum\limits_{l = 1}^{10} {\sum\limits_{m = 1}^{10} {\left( {\int_{0}^{1} {\Gamma_{k}^{\prime \prime } \Gamma_{l}^{\prime } \Gamma_{m}^{\prime } \Gamma_{j} {\text{d}}\xi } } \right)} } } - f_{m} \left( {\int_{0}^{1} {\delta_{{{\text{Dirac}}}} \left[ {\xi - \frac{1}{2}\left( {1 - s_{f} \cos \left( {\Omega_{f} \tau } \right)} \right)} \right]\Gamma_{j} {\text{d}}\xi } } \right) = 0} } } } \hfill \\ {j = 1,2, \ldots ,10} \hfill \\ \end{array} } \right\} $$
(13)

Solving this coupled set of 20 nonlinear equations using a continuation/time-integration technique along with Floquet theory for stability gives time histories as well as force/frequency diagrams and determines stability and bifurcation types. As this procedure is time-consuming and computationally expensive, the computer codes for each to be well optimised regarding run-times and cores required.

3 Verifications for linear free dynamics

Before proceeding with the coupled/nonlinear results, a linear FEA free dynamics model is developed in ANSYS® (version 19.0, ANSYS Inc., Canonsburg, PA, USA) by keeping the point mass; for the linear system parameters in Sect. 4, the FEA gives the fundamental frequency of ω1 = 21.4519 which when compared to ω1 = 21.3204 shows the error percentage of 0.6. The mode shapes are also presented in Fig. 2 for the first four ones.

Fig. 2
figure 2

FEA free linear dynamics with point mass: first four mode shapes

Full size image

4 Frequency/time domain dynamics

The frequency/time domain dynamics of a beam-mass structure of length-to-thickness ratio of 100 is examined in this section. The damping ratio of ζ = 0.01 is selected; ω1 is the first non-dimensional natural frequency. For all cases, ξM = 0.5. In Figs. 3, 6, 8, 9, 10, and 11, dashed and solid line styles indicate unstable and stable periodic responses, respectively.

Fig. 3
figure 3

Frequency–amplitude diagrams of the moving-load excited beam; a maximum χ2 at ξ = 0.5; b maximum χ1 at ξ = 0.66. fm = 10.0, γ = 0.04, sf = 1.0, ω1 = 21.3204

Full size image

For fm = 10.0, γ = 0.04, and sf = 1.0, the frequency–amplitude diagrams in the moving-load-caused nonlinear resonance of the beam-mass structure are shown in Fig. 3, where (a) shows frequency–amplitude of the transverse motion and (b) that of axial one. The fundamental natural frequency of ω1= 21.3204 is obtained for the transverse motion. It is interesting that a nonlinear resonance of hardening type for transverse/longitudinal motions is observed when the frequency of the force position approaches half of beam-mass’s fundamental frequency. Apart from the main saddle-node bifurcation points (at Ωf/ω1 = 0.6425 and 0.5315), there are two small-amplitude ones in the vicinity of Ωf/ω1 = 0.59. Highlighted in Fig. 4 are the time response and phase plane of the motion beam-mass system at peak oscillation amplitude, showing the complexity of the longitudinal motion due to nonlinear couplings. The spatial domain distribution of the motion at its largest amplitude is shown in Fig. 5, highlighting the fact of symmetry-breaking and travelling-type motion for the moving-load excited system.

Fig. 4
figure 4

Motion details for Fig. 2 at Ωf/ω1 = 0.6422 (which is peak amplitude). a, b Time response and phase plane of χ2 at ξ = 0.5, respectively; (c, d) those of χ1 at ξ = 0.66, respectively. τn indicates time normalised by oscillation period

Full size image
Fig. 5
figure 5

Transverse moving-load-caused dynamics of the beam-mass structure of Fig. 3 in one period at Ωf/ω1 = 0.6422

Full size image

Another interesting aspect of the nonlinear dynamic characteristics of the beam-mass system under a moving load is shown in Fig. 6, highlighting the presence of modal interactions and internal resonances. As seen, as a result of strong modal interactions and modal energy transfer, additional peaks appear in the frequency–amplitude of the p2.

Fig. 6
figure 6

Frequency–amplitude diagrams of the first two transverse generalised coordinates of the system of Fig. 3

Full size image

Effects of the amplitude of the constant load position on the resonance dynamics of the beam-mass system under a moving load are highlighted in Fig. 7 for fm = 10.0, γ = 0.04. For both the transverse/longitudinal motions, the overall motion amplitude is larger for larger position amplitudes; hence, the peak nonlinear resonance occurs at larger frequencies. Additionally, it is seen that the modal interactions become stronger at larger values of sf leading to extra peaks and bifurcation points.

Fig. 7
figure 7

Effect of the parameter sf on frequency–amplitude diagrams of the moving-load excited beam; a maximum χ2 at ξ = 0.5; b maximum χ1 at ξ = 0.66. fm = 10.0, γ = 0.04, ω1 = 21.3204

Full size image

Shown in Fig. 8 are the force–amplitude diagrams of the moving-load-caused coupled nonlinear dynamics of the beam-mass system for Ωf/ω1 = 0.59 γ = 0.04, sf = 1.0, ω1 = 21.3204. The system initially displays two saddle-node bifurcations at fm = 17.68 and 8.70, which are the results of internal modal interactions; Fig. 9 illustrates the strong modal energy transfer in the vicinity of these two bifurcation points, leading to strong energy transfer from mode 1 to mode 2 which in turn results in a sudden local increase in second mode’s amplitude. Returning to Fig. 8, by further increasing the moving-load magnitude, the beam-mass system displays two torus bifurcations at fm = 32.59 and 41.70. Increasing the moving-load magnitude slightly further, a saddle-node bifurcation occurs at fm = 41.87 causing the system to lose stability and jump to a larger-amplitude stable limit-cycle. In all the sub-figures of Figs. 8 and 9, similar to the case of Fig. 8a, the saddle-node bifurcations are responsible for these jumps as the solution branch becomes unstable and there is no way for the system rather than jumping to the closest stable branch.

Fig. 8
figure 8

Force–amplitude diagrams of the moving-load excited beam; a maximum χ2 at ξ = 0.5; b maximum χ1 at ξ = 0.66. Ωf/ω1 = 0.59 γ = 0.04, sf = 1.0, ω1 = 21.3204

Full size image
Fig. 9
figure 9

Force–amplitude diagrams of the first two transverse generalised coordinates of the system of Fig. 8

Full size image

The purpose of presenting the plots of Fig. 10 is to show how different the frequency–amplitude diagrams in the moving-load-caused nonlinear dynamics of the system are to those of dynamic force with a constant position. Interestingly, the first nonlinear resonance occurs in the vicinity of the frequency ratio of 0.25 and the second in the vicinity of 0.5, third one 0.6, fourth one 0.9, then fifth around 1, and 1.35 and 1.4 for the last two one; all of them, if sufficiently large, are hardening type. To better illustrate the contribution of each generalised coordinate to the resonance response of the beam-mass system under a moving load, Fig. 11 is constructed showing the frequency–amplitude diagrams for the first three transverse modes. As seen, the first mode reaches its peak amplitude in the vicinity of the frequency ratio of 0.5. For the second generalised coordinate, the peak amplitude occurs around Ωf/ω1 = 1.0; this ratio is 1.4 for the third generalised coordinate. This figure highlights the significant contributions of higher modes to the nonlinear dynamical response of the beam-mass system under a moving load. Hence, to study the nonlinear dynamical response of a system with a moving load accurately, it is essential to consider many modes in the discretisation procedure.

Fig. 10
figure 10

Wideband frequency–amplitude diagrams of the moving-load excited beam; a–d the maximum transverse displacement at ξ = 0.2, 0.3, 0.4 and 0.5, respectively. fm = 10.0, γ = 0.04, sf = 1.0, ω1 = 21.3204

Full size image
Fig. 11
figure 11

Wideband frequency–amplitude diagrams of the first three transverse generalised coordinates of the system of Fig. 10

Full size image

Depicted in Fig. 12 are the transverse/longitudinal motions for several mass ratio parameters. As seen, increasing the mass ratio causes a shift in the resonance region to the left. Additionally, the peak transverse oscillation amplitude increases as the mass ratio is increased. The nonlinear behaviour of the system seems not to be influenced by varying the mass ratio.

Fig. 12
figure 12

Effect of the parameter γ on frequency–amplitude diagrams of moving-load excited beam; a maximum χ2 at ξ = 0.5; b maximum χ1 at ξ = 0.66. fm = 10.0

Full size image

5 Conclusions

The moving-load-caused nonlinear coupled dynamics of beam-mass systems has been investigated. The moving load considered is of a constant magnitude which changes position harmonically. Energy stored in the beam after deflection and the beam-mass kinetic energy were formulated. A virtual work formulation was used for the energy contribution of the moving load. The discretised equations of the beam-mass system with 20 degree of freedom were numerically integrated via continuation/time-integration techniques. A linear natural frequency verifications in the presence of point mass was performed using the FEA.

It was found that once the frequency of the force position approaches half the system’s first transverse natural frequency, the system reaches its peak nonlinear resonance showing two saddle-node bifurcations. Additional saddle-node bifurcations were displayed by the system as a result of modal energy transfer and interactions. Symmetry-breaking and travelling-type motion were also displayed by the beam-mass system. Regarding the force–amplitude diagrams of the beam-mass system, there are two torus bifurcations apart from the two main saddle-node bifurcations. Frequency–amplitude diagrams for a wider range of frequency sweep showed that the first nonlinear resonance takes place in the vicinity of the frequency ratio of 0.25. Additionally, it was shown that the peak oscillation amplitude for the first three transverse generalised coordinates occurs near frequency ratio of 0.5, 1.0, and 1.4, respectively. Examining the effect of the mass ratio showed that increasing the mass ratio results in an increase in the peak resonance transverse amplitude but does not affect the nonlinear characteristics much.