1 Introduction

The modular multilevel converter (MMC) is considered to be one of the most promising topologies for medium-voltage high-power industrial applications, such as the powertrains of electric vehicle motor drives, due to its modularity, scalable voltage level, single DC bus, etc. [1,2,3].

However, the MMC has an inherent issue with the SM capacitor voltage low-frequency ripple components dramatically increasing when the operating line frequency is reduced, which can adversely affect the system performance and lifetime. This issue limits the application of MMCs in variable-speed machine drives [4].

Several approaches have been proposed in the literature to address this serious issue [5,6,7,8,9,10,11]. In [5, 6, 9, 10], different power-balancing channels were proposed to balance the voltage ripple between the MMC arms by transferring the ripple power from the arm that has the largest ripple to the other arms, which can increase the circuit components ratings. In addition, several of these techniques only compensate the fundamental frequency ripple power component when the double-fundamental frequency component is kept uncompensated. In [7, 8], an additional active power filter was connected to each of the SMs of a MMC to direct the ripple power to a low-frequency capacitor. However, the increase in the part count was significant. In addition, these approaches use large LF capacitors.

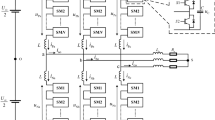
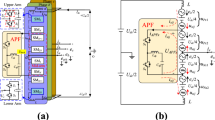
In this paper, a frequency-independent magnetic power decoupling circuit (PDC) is proposed to replace the LF SM capacitor. The proposed approach compensates for both the fundamental and the double-fundamental ripple power components in the MMC arms. Figure 1 shows a MMC with a power decoupling configuration. The MMC-SM is a two-half-bridge (HB) with a very small high-frequency film capacitor as a DC link. Each of the symmetrically modulated adjacent-arm SMs is magnetically coupled to decouple the three-phase ripple power. The PDC is realized through a three-winding HFT with three-port half-bridge (THB) converters interfacing each of the three-phase contiguous SMs. The three-phase PDC is theoretically based on the flux cancelation method. Its basic idea is to eliminate the three-phase symmetrical modulation ripple powers since their instantaneous sum is zero. Instantaneous three-phase ripple power gathering occurs magnetically in the HFT core.

Fig. 1
figure 1

MMC with a THB-based power decoupling circuit

Full size image

The amount of ripple power sent to the HFT through the power de-coupler depends on the leakage inductance of the transformer and the phase shift. A phase-shift controller is needed to drive the pulsating power toward the HFT to ensure an acceptable capacitor voltage ripple level. Different ripple rejection control methods were proposed in [12,13,14,15,16]. One of these methods involved a dual control loop [12], where the outer loop provides voltage with a crossover frequency far below that of the ripple component frequency, and the inner loop provides current feedback with a wider bandwidth. The narrow bandwidth of the voltage loop degrades the dynamic response of the system and introduces instability. In [13], a notch filter was inserted into the voltage loop to enhance the voltage loop bandwidth. However, this added a large negative phase shift in some frequencies lower than the filter cut-off frequency, which can reduce the phase margin of the system [14]. Other papers have proposed a converter impedance-shaping method to block the ripple components [15, 16]. These approaches were designed for a specific frequency, which makes them unsuitable for variable frequency applications and variable-speed applications. Furthermore, some of the aforementioned approaches degrade the dynamic performance of the system. All of these approaches use a linear controller, which has limitations in terms of robustness and stability.

This paper proposes a sliding mode controller (SMC) that regulates the wide variations in the system parameters, and it is more suitable for variable structure systems such as power electronic converters [17,18,19,20,21,22,23,24,25]. The SMC for a PDC is designed to shape the input impedance of the THB converter, and it enforces the delivery of ripple power to the high-frequency transformer to be canceled on the HFT core. The SMC is independent of the MMC ripple frequency, unlike conventional methods such as proportional resonance (PR) controllers, which are designed for the ripple frequency. The proposed SMC can keep the capacitor voltage ripple of the SM narrow from standstill to full speed, without the need for a filtering stage. This means it does not suffer from stability limitations as with conventional control methods. The proposed SMC method ensures system robustness against variations in the circuit parameters. Furthermore, it has a faster transient response with negligible overshoots and undershoots. The control design is also introduced in this paper. Additionally, the system stability under SMC is analyzed. The robustness of the proposed control against system parameter variations is demonstrated.

1.1 Motivations

The SM capacitor voltage of a MMC suffers from LF ripple components, where their magnitude is inversely proportional to the line frequency of the converter. Therefore, utilizing a MMC in adjustable-speed applications is a challenge. Employing a magnetic PDC instead of a bulky SM capacitor is a solution for this issue. A fast and robust ripple rejection control is needed for the PDC. The main issue with variable-speed motor drive applications is that there is a need for variable frequency control. Therefore, conventional PR-based controllers are problematic since a large number of PR controllers are needed, or a large number of complex adaptive filters are needed if d–q control was used. The conventional linear ripple rejection methods suffer from bandwidth and stability limitations. Additionally, at near-zero-speed operation, the PR controller has slower dynamics. Therefore, a fast nonlinear ripple rejection control is proposed for the PDC. The proposed control is independent of the ripple frequency. Therefore, the proposed scheme can drive medium-voltage high-power variable-speed machines from standstill to full speed with a narrow SM capacitor voltage ripple.

1.2 Challenges

  1. 1.

    Modeling a three-port power decoupling circuit is a challenge since the circuit has three input ports and zero output ports.

  2. 2.

    Keeping the conventional MMC sensing points the same without adding extra sensing points is difficult.

  3. 3.

    Designing a nonlinear ripple rejection control that can overcome linear control limitations is challenging.

1.3 Contributions

  1. 1.

    The proposed scheme solves the issue of wide fluctuations of the low-frequency voltage ripple components in SM capacitors, especially under low-speed operations without using a bulky ripple power capacitor.

  2. 2.

    The proposed scheme succeeds in keeping the SM capacitor voltage ripple narrow regardless of the converter line frequency.

  3. 3.

    The modeling of the THB-based power decoupling circuit has the following enhancements.

    1. (a)

      A novel transient model was applied to the THB-based power decoupling circuit, which is based on the state space generalized average modeling.

    2. (b)

      This model provides a highly accurate modeling of the system dynamics.

  4. 4.

    The proposed sliding mode control offers the following enhancements.

    1. (a)

      Conventional ripple rejection controllers are designed with a crossover frequency that is far below that of the ripple component which can degrade the system dynamics and introduce instability, especially under low-frequency operation. However, the proposed control has nonlinear design that is independent of the ripple frequency, which solves these issues.

    2. (b)

      There is no need for adaptive filters or a large number of PR controllers, which makes it less complicated in comparison with conventional methods.

    3. (c)

      It compensates both the differential mode and the common mode ripple components of the SM capacitors.

    4. (d)

      No extra sensors are required since it is current sensor-less control.

    5. (e)

      Robust control against system parameter variations.

    6. (f)

      It is a frequency-independent control. Therefore, it suitable for both adjustable-speed and low-speed operations.

The remainder of this paper is organized as follows. Section 2 introduces the proposed model of a power decoupling circuit-based THB converter. Section 3 describes the proposed sliding mode controller. In Sect. 4, the proposed scheme performance is verified by simulation and experimental tests. Section 5 discusses the system volume reduction when compared to conventional methods. Section 6 provides some concluding remarks.

2 Proposed circuit modeling

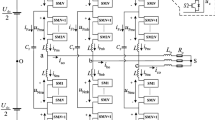
Figure 2 shows a detailed circuit diagram of a THB-based power decoupling circuit in symmetrically modulated three-phase MMC legs. The THB extracts the instantaneous ripple power from the SMs, and pushes it to the HFT. The ripple power flows from each of the THB ports to the three-winding HFT are canceled out in the magnetic core.

Fig. 2
figure 2

Three contiguous MMC arm SMs

Full size image

The modeling procedures of the power decoupling circuit are proposed, and the derived model is used to estimate the transformer currents. Due to three-phase symmetry, the circuit in Fig. 2 is modeled, and the model is extended to any group of three contiguous arm SMs. In the proposed THB, the ripple power flows from all three of the ports to the single three-winding HFT. To date, no literature reports have addressed the modeling of this type of circuit. Figure 3 shows an equivalent circuit of the three-port PDC shown in Fig. 2. The inverter side of the MMC is modeled with three parallel current sources \({i}_{\mathrm{s}J}\) with a resistance \({R}_{J}\). The HFT is modeled with a T-model. The HFT windings are modeled with their leakage inductance \({L}_{J}\), and the core is modeled with the magnetizing inductance \({L}_{\mathrm{m}}\), which has a current \({i}_{\mathrm{m}}\) and a voltage drop \({v}_{n}\). The equivalent circuit shown in Fig. 3 has two operational modes. The combined form of the switched model can be defined as follows:

$$\frac{\mathrm{d}{i}_{\mathrm{T}J}}{\mathrm{d}t}=\frac{1}{2{L}_{J}}{u}_{J}{v}_{\mathrm{c}J}-\frac{1}{{L}_{J}}{v}_{n},$$
(1)
$$\frac{\mathrm{d}{v}_{cJ}}{\mathrm{d}t}=\frac{2}{{c}_{\mathrm{f}}}{i}_{\mathrm{s}J}-2\frac{{v}_{\mathrm{c}J}}{{R}_{J}{c}_{\mathrm{f}}}-\frac{1}{{c}_{\mathrm{f}}}{u}_{J}{i}_{\mathrm{T}J},$$
(2)
$$\frac{\mathrm{d}{i}_{\mathrm{m}}}{\mathrm{d}t}=\frac{1}{{L}_{\mathrm{m}}}{v}_{\mathrm{n}}.$$
(3)

where \(u=[\mathrm{1,0}]\) and J = {a, b, c}.

Fig. 3
figure 3

Equivalent circuit of the three-phase contiguous SMs of a MMC

Full size image

GAM is used to average the previously derived switched model, as can be seen in (1)–(3). The GAM is based on waveform representation employing the complex Fourier series [26]. After a mathematical derivation, the complex state space representation per phase of the circuit in Fig. 3 is obtained as follows:

$$\frac{\mathrm{d}{i}_{\mathrm{T}JR}}{\mathrm{d}t}=\frac{1}{\pi {L}_{J}}{v}_{\mathrm{c}J}\mathrm{sin}\left({\varnothing }_{J}\right)-\frac{1}{{L}_{J}}{v}_{\mathrm{nR}}+{\omega }_{\mathrm{s}}{i}_{TJI}$$
(4)
$$\frac{\mathrm{d}{{i}_{\mathrm{m}}}_{\mathrm{R}}}{\mathrm{d}t}=\frac{1}{{L}_{\mathrm{m}}}{v}_{\mathrm{nR}}+{\omega }_{\mathrm{s}}{{i}_{\mathrm{m}}}_{\mathrm{I}}$$
(5)
$$\frac{\mathrm{d}{v}_{cJ}}{\mathrm{d}t}=\frac{2}{{c}_{\mathrm{f}}}{i}_{\mathrm{s}J}-2\frac{{v}_{cJ}}{{R}_{J}{c}_{\mathrm{f}}}-\frac{4}{\pi {c}_{\mathrm{f}}}\mathrm{sin}\left({\varnothing }_{J}\right){i}_{\mathrm{T}J\mathrm{R}}+\frac{4}{\pi {c}_{\mathrm{f}}}\mathrm{cos}\left({\varnothing }_{J}\right){i}_{\mathrm{T}J\mathrm{I}}$$
(6)
$$\frac{\mathrm{d}{i}_{\mathrm{T}J\mathrm{I}}}{\mathrm{d}t}=-\frac{1}{\pi {L}_{J}}{v}_{\mathrm{c}J}\mathrm{cos}\left({\varnothing }_{J}\right)-\frac{1}{{L}_{J}}{v}_{\mathrm{nI}}-{\omega }_{\mathrm{s}}{i}_{\mathrm{T}JR}$$
(7)
$$\frac{\mathrm{d}{{i}_{\mathrm{m}}}_{\mathrm{I}}}{\mathrm{d}t}=\frac{1}{{L}_{\mathrm{m}}}{v}_{\mathrm{nI}}-{\omega }_{\mathrm{s}}{{i}_{\mathrm{m}}}_{\mathrm{R}}$$
(8)

where \({\upomega }_{\mathrm{s}}=2\pi {f}_{\mathrm{s}}\), and \({f}_{\mathrm{s}}\) is the switching frequency. \({\varnothing }_{J}\) is the phase shift angle. \({i}_{\mathrm{T}J\mathrm{R}}\), \({{i}_{\mathrm{m}}}_{\mathrm{R}}\), and \({v}_{\mathrm{nR}}\) are the real parts of the first harmonic component of the transformer current, the transformer magnetizing current, and the transformer magnetizing voltage, respectively. \({i}_{\mathrm{T}J\mathrm{I}}\), \({{i}_{\mathrm{m}}}_{\mathrm{I}}\), and \({v}_{\mathrm{nI}}\) are the imaginary parts of the first harmonic component of the transformer current, transformer magnetizing current, and transformer magnetizing voltage, respectively.

Normally, current is used as a control variable to design a fast response controller. However, the transformer currents are high-frequency currents. Sensing high-frequency currents requires high bandwidth sensors and a fast DSP, which increases the cost of the system. A solution is to estimate the currents rather than sense them. For this estimation, (4)–(8) can be rewritten as:

$$\frac{\mathrm{d}{i}_{TJR}}{\mathrm{d}t}={X}_{J1}{\mathrm{sin}\left({\varnothing }_{a}\right)v}_{\mathrm{c}a}+{X}_{J2}{\mathrm{sin}\left({\varnothing }_{b}\right)v}_{\mathrm{c}b} {+{X}_{J3}\mathrm{sin}\left({\varnothing }_{\mathrm{c}}\right)v}_{\mathrm{cc}}+{X}_{J4}{i}_{\mathrm{T}j\mathrm{I}}$$
(9)
$$\frac{\mathrm{d}{i}_{TJI}}{\mathrm{d}t}=-{X}_{J1}{\mathrm{cos}\left({\varnothing }_{a}\right)v}_{ca}-{X}_{J2}{\mathrm{cos}\left({\varnothing }_{b}\right)v}_{cb}-{{X}_{J3}\mathrm{cos}\left({\varnothing }_{c}\right)v}_{cc}-{X}_{J4}{i}_{TjR}$$
(10)

where\({X}_{a1}={X}_{b2}={X}_{c3}=\frac{1}{\pi L}(\frac{L+2{L}_{\mathrm{m}}}{L+3{L}_{\mathrm{m}}})\),\({X}_{a1}={X}_{b2}={X}_{c3}={\omega }_{\mathrm{s}}\), and\({X}_{a\mathrm{2,3}}={X}_{b\mathrm{1,3}}={X}_{c\mathrm{1,3}}=-\frac{1}{\pi L}(\frac{1}{L+3{L}_{\mathrm{m}}})\). For the sake of simplicity, \({L}_{a}={L}_{b}={L}_{c}=L\) was chosen. A block diagram of the current estimator per phase is shown in Fig. 4.

Fig. 4
figure 4

Block diagram of a transformer currents estimator

Full size image

3 Proposed sliding mode control

Figure 5 shows the proposed control scheme for a MMC drive three-phase machine. The overall control scheme can be divided into the following three main parts. (1) Motor control is applied to control the motor operation characteristics (torque and speed). (2) MMC control is applied to control the MMC performance. (3) PDC control is applied to keep the SM capacitor voltage ripple narrow. In this section, sliding mode control is introduced for the PDC. The other control parts are described in [3,4,5,6,7,8,9,10, 27]. The sliding mode controller is proposed for the THB circuit to force the ripple power to flow to the HFT to be canceled out in the core. Sliding mode control is a variable structure control that is resistant to system disturbances and parameter uncertainties. Its implementation is less complex when compared to other nonlinear controls. In the following, the sliding mode control design steps are given.

Fig. 5
figure 5

Proposed control scheme (the subscripts “u” and “l” stand for upper and lower arms, respectively)

Full size image

3.1 Proposed control design

To design the proposed sliding mode controller, the sliding surface should be selected according to the control objectives. In this paper, the sliding surface \({s}_{J}\) is chosen as a function of the transformer current as follows:

$${s}_{J}=-{k}_{1}\frac{\mathrm{d}{i}_{TJR}}{\mathrm{d}t}-\frac{1}{{k}_{2}}\int {i}_{TJR}\mathrm{d}t-{k}_{3}{i}_{TJR}$$
(11)

where \({k}_{1}\),\({k}_{2}\), and \({k}_{3}\) are design parameters. Once the state trajectory reaches the sliding surface, it should slide along the surface toward the equilibrium point. The sliding mode phase operation can be described by constant dynamics [19]:

$$\frac{\mathrm{d}{s}_{J}}{\mathrm{d}t}=0$$
(12)

where the time derivative of \({s}_{J}\) is:

$$\frac{\mathrm{d}{s}_{J}}{\mathrm{d}t}=-{k}_{1}\frac{{\mathrm{d}}^{2}{i}_{TJR}}{{\mathrm{d}t}^{2}}-\frac{1}{{k}_{2}}{i}_{TJR}-{k}_{3}\frac{\mathrm{d}{i}_{TJR}}{\mathrm{d}t}$$
(13)

Replacing \(\frac{\mathrm{d}{i}_{TJR}}{\mathrm{d}t}\) in (13) with (4) yields the following equation:

$$\frac{\mathrm{d}{s}_{J}}{\mathrm{d}t}=-{k}_{1}\frac{{\mathrm{d}}^{2}{i}_{TJR}}{{\mathrm{d}t}^{2}}-\frac{1}{{k}_{2}}{i}_{TJR}-{k}_{3}\left(\frac{1}{\pi {L}_{J}}{v}_{cJ}\mathrm{sin}\left({\varnothing }_{J}\right)-\frac{{v}_{\mathrm{nR}}}{{L}_{J}}+{\omega }_{\mathrm{s}}{i}_{TJI}\right)$$
(14)

In addition, using (12) and (14), the equivalent control part is obtained as follows:

$${{\varnothing }_{J}}_{\mathrm{eq}}={\mathrm{sin}}^{-1}\left(\frac{\pi {L}_{J}}{{v}_{cJ}}\left(-\frac{{k}_{1}}{{k}_{3}}\frac{{\mathrm{d}}^{2}{i}_{TJR}}{{\mathrm{d}t}^{2}}-\frac{1}{{k}_{3}{k}_{2}}{i}_{TJR}+\frac{{v}_{nR}}{{L}_{J}}-{\omega }_{s}{i}_{TJI}\right)\right)$$
(15)

The reaching dynamics have been chosen as follows:

$$\frac{\mathrm{d}{s}_{J}}{\mathrm{d}t}=-\Gamma {s}_{J}-\alpha \cdot \mathrm{sign}({s}_{J})$$
(16)

which ensures that the state trajectory reaches \(s=0\) in a finite time. The phase-shift expiration is then:

$${\varnothing }_{J}={\mathrm{sin}}^{-1}\left(\frac{\pi {L}_{J}}{{v}_{cJ}}\left(-\frac{{k}_{1}}{{k}_{3}}\frac{{\mathrm{d}}^{2}{i}_{TJR}}{{\mathrm{d}t}^{2}}-\frac{1}{{k}_{3}{k}_{2}}{i}_{TJR}+\frac{1}{{L}_{J}}{v}_{\mathrm{nR}}-{\omega }_{\mathrm{s}}{i}_{TJI}+\Gamma {s}_{J}+\alpha \mathrm{sign}({s}_{J})\right)\right)$$
(17)

The following condition must always be investigated:

$$-1\le \frac{\pi {L}_{J}}{{v}_{cJ}}\left(-\frac{{k}_{1}}{{k}_{3}}\frac{{\mathrm{d}}^{2}{i}_{TJR}}{{\mathrm{d}t}^{2}}-\frac{1}{{k}_{3}{k}_{2}}{i}_{TJR}+\frac{1}{{L}_{J}}{v}_{\mathrm{nR}}-{\omega }_{\mathrm{s}}{i}_{TJI}+\Gamma {s}_{J}+\alpha \mathrm{sign}({s}_{J})\right)$$
(18)

Figure 6 shows a block diagram of the proposed sliding mode control, as can be seen in (17).

Fig. 6
figure 6

Block diagram of the proposed sliding mode control for a THB circuit

Full size image

To ensure that the sliding surface is an attractor to the state trajectory, the following existence conditions should be valid in the neighborhood of the sliding manifold. This allows it to fulfill the local reachability condition [21].

$${s}_{J}\frac{\mathrm{d}{s}_{J}}{\mathrm{d}t}<-\eta \left|{s}_{J}\right|, \eta >0$$
(19)

Recalling the reaching dynamics (16), the local reachability condition is:

$${s}_{J}\frac{\mathrm{d}{s}_{J}}{\mathrm{d}t}=-\left(\Gamma \left|{s}_{J}\right|+\alpha \right)\left|{s}_{J}\right|$$
(20)

Comparing (19) with (20), yields \(\eta \ge \Gamma \left|{s}_{J}\right|+\alpha\). Thus, the existence condition for the sliding mode is \(\eta >\Gamma \left|{s}_{J}\right|+\alpha\) at\(\Gamma ,\alpha >0\).

3.2 Sliding mode stability analysis

The following ideal sliding-mode dynamics represent the reduced-order dynamics of the system on the sliding surface.

$$\frac{\mathrm{d}{v}_{cJ}}{\mathrm{d}t}=-2\frac{{v}_{cJ}}{{R}_{J}{c}_{f}}-\frac{4}{\pi }{c}_{f}\mathrm{sin}\left({{\mathrm{\varnothing }}_{J}}_{\mathrm{eq}}\right){i}_{TJR}+\frac{4}{\pi {c}_{f}}\mathrm{cos}\left({{\mathrm{\varnothing }}_{J}}_{\mathrm{eq}}\right){i}_{TJI}$$
(21)
$$\frac{\mathrm{d}{i}_{TJI}}{\mathrm{d}t}=-\frac{1}{\pi {L}_{J}}{v}_{cJ}\mathrm{cos}\left({{\varnothing }_{J}}_{\mathrm{eq}}\right)-{\omega }_{\mathrm{s}}{i}_{TJR}-\frac{1}{{L}_{J}}{v}_{\mathrm{nI}}$$
(22)

The equilibrium point can be obtained by forcing the left side of (21) and (22) to be equal to zero. Then the two equations are solved to obtain the steady state value of the two components of the transformer current (\({I}_{TJI}\) and \({I}_{TJR}\)), where the steady values of \({v}_{\mathrm{c}J}\), \({v}_{\mathrm{nI}}\), \({v}_{\mathrm{nR}}\), and \({{\varnothing }_{J}}_{\mathrm{eq}}\) are \({V}_{\mathrm{c}J}\), \({V}_{\mathrm{nI}}\), \({V}_{\mathrm{nR}}\), and \({{\Psi }_{J}}_{\mathrm{eq}}\), respectively. The Routh-Hurwitz stability criterion is applied to (21) and (22) to verify the system stability on the sliding phase. The linearized (21) and (22) around the equilibrium point is:

$$\left[\begin{array}{c}\frac{\mathrm{d}{v}_{cJ}}{\mathrm{d}t}\\ \frac{\mathrm{d}{i}_{TJI}}{\mathrm{d}t}\end{array}\right]=A\left[\begin{array}{c}{\widehat{v}}_{cJ}\\ {\widehat{i}}_{TJI}\end{array}\right]$$
(23)

where A is the Jacobean matrix of the system around the equilibrium point and for some (\({k}_{1}, {k}_{2} , {k}_{3}\)). A is the following matrix (see the bottom of this page (24)). The A matrix in (24) can be rewritten in a more general form as follows:

$$A=\left[\begin{array}{cc}{a}_{11}& {a}_{12}\\ {a}_{21}& {a}_{22}\end{array}\right]$$
$$A=\left[\begin{array}{cc}-\frac{2}{{R}_{J}{c}_{\mathrm{f}}}+\frac{4\mathit{tan}({{\Psi }_{J}}_{\mathrm{eq}})}{\pi {c}_{f}{V}_{cJ}}\left({I}_{\mathit{TJR}}\mathrm{cos}\left({{\Psi }_{J}}_{eq}\right)+{I}_{TJI}\mathrm{sin}\left({{\Psi }_{J}}_{\mathrm{eq}}\right)\right)& \frac{4}{\pi {c}_{\mathrm{f}}}\mathrm{cos}\left({{\Psi }_{J}}_{\mathrm{eq}}\right)+\frac{4{L}_{J}{\omega }_{\mathrm{s}}}{{c}_{f}{V}_{cJ}}\left({I}_{TJR}+{I}_{TJI}\mathrm{tan}({{\Psi }_{J}}_{\mathrm{eq}})\right)\\ -\frac{1}{\pi {L}_{J}}\mathrm{cos}\left({{\Psi }_{J}}_{\mathrm{eq}}\right)-\frac{1}{\pi {L}_{J}}\mathrm{sin}\left({{\Psi }_{J}}_{\mathrm{eq}}\right)\mathrm{tan}({{\Psi }_{J}}_{\mathrm{eq}})& -{\omega }_{\mathrm{s}}\mathrm{tan}({{\Psi }_{J}}_{\mathrm{eq}})\end{array}\right]$$
(24)

The characteristic equation of the system (|\(\lambda\)I − A|= 0) is:

$${\lambda }^{2}- \left({a}_{11}s+{a}_{22}\right)\lambda +{a}_{11}{a}_{22}-{a}_{12}{a}_{21}=0$$
(25)

Finally, by applying the Routh–Hurwitz stability criterion to this second-order linear polynomial, it is found that all of the coefficients must be positive, i.e., \({k}_{1}, {k}_{2},{k}_{3}>0,\) to ensure that all of the eigenvalues of the system have a negative real part [20].

Figure 7 shows the locus of the eigenvalues (\({\lambda }_{1}\),\({\lambda }_{2}\)) with increasing sliding surface gains, where \(k={k}_{2}{k}_{3}\). In addition, \({k}_{1}\) has a negligible effect. It can be observed that the system is stable since all of the eigenvalues are in the left side plane. Therefore, for low values of (k), the eigenvalues are real and negative. Thus, the system is critically damped [20]. This indicates that the system performs better at low values of (k).

Fig. 7
figure 7

Locus of eigenvalues with changing sliding surface gains

Full size image

3.3 THB Impedance shaping

To highlight the effectiveness of the proposed sliding mode control, it is shown how the sliding mode control shapes the input side impedance (\({Z}_{\mathrm{in}}\)) of the THB converter to bypass the ripple power to the HFT. Referring to (23) and (24), \({Z}_{\mathrm{in}}\) in the frequency domain can be defined as follows:

$${Z}_{\mathrm{in}}=\frac{\frac{4}{\pi {c}_{f}}\mathrm{cos}\left({{\Psi }_{J}}_{\mathrm{eq}}\right)+\frac{4{L}_{J}{\omega }_{s}}{{c}_{f}{V}_{cJ}}\left({I}_{TJR}+{I}_{TJI}\mathrm{tan}({{\Psi }_{J}}_{\mathrm{eq}})\right)}{\lambda +\frac{2}{{R}_{J}{c}_{f}}-\frac{4\mathrm{tan}({{\Psi }_{J}}_{eq})}{\pi {c}_{f}{V}_{cJ}}\left({I}_{\mathit{TJR}}\mathit{cos}\left({{\Psi }_{J}}_{\mathrm{eq}}\right)+{I}_{TJI}\mathrm{sin}\left({{\Psi }_{J}}_{\mathrm{eq}}\right)\right)}$$
(26)

where \(\lambda\) is a complex number, and \({Z}_{\mathrm{in}}=\frac{{\widehat{v}}_{cJ}}{{\widehat{i}}_{TJI}}\). To obtain the common mode impedance (\({Z}_{\mathrm{CM}}\)) and the differential mode impedance (\({Z}_{\mathrm{DM}}\)), \(\lambda\) is replaced in (26) with the fundamental line frequency and double the line frequency, respectively. Figure 8 shows \({Z}_{\mathrm{DM}}\) and \({Z}_{\mathrm{CM}}\) versus the sliding surface gains (k). From Fig. 8 it can be concluded that the sliding mode control can shape \({Z}_{\mathrm{in}}\). By varying the sliding surface gains, the amount of ripple power transferred through the THB can be controlled. This graphical approach can be used to design the sliding surface gains to achieve optimal values of \({Z}_{\mathrm{DM}}\) and \({Z}_{\mathrm{CM}}\).

Fig. 8
figure 8

Shaping the input side impedance (\({Z}_{\mathrm{in}}\)) of a THB converter by changing the sliding surface gains at (\({V}_{cJ}=260\mathrm{ V},{c}_{f}=30\mathrm{ \mu F},\mathrm{ and }L=100\mathrm{ \mu H}\))

Full size image

3.4 Robustness analysis

A robustness analysis is performed in the presence of uncertainty in the HFT leakage inductance (\({L}_{J}\)). The aim of this analysis is to determine whether the sliding phase \({s}_{J}=0\) is established despite system parameter uncertainty. The sliding phase starts after the local reachability condition is satisfied, and the local reachability condition is defined in Eq. (19). For this, it is necessary to recall Eq. (14) and replace \(\left({L}_{J}\right)\) with \(\left({L}_{J}+\Delta {L}_{J}\right)\), where \(\left(\Delta {L}_{J}\right)\) is the uncertainty in \(\left({L}_{J}\right)\). Then Eq. (14) can be rewritten as follows:

$$\frac{\mathrm{d}{s}_{J}}{\mathrm{d}t}=-{k}_{1}\frac{{\mathrm{d}}^{2}{i}_{TJR}}{{\mathrm{d}t}^{2}}-\frac{1}{{k}_{2}}{i}_{TJR}-{k}_{3}\left(\frac{1}{\pi \left({L}_{J}+\Delta {L}_{J}\right)}{v}_{cJ}\mathrm{sin}\left({\varnothing }_{J}\right)-\frac{{v}_{nR}}{\left({L}_{J}+\Delta {L}_{J}\right)}+{\omega }_{\mathrm{s}}{i}_{TJI}\right)$$
(27)

Using Eqs. (13) and (17), Eq. (27) is:

$$\frac{\mathrm{d}{s}_{J}}{\mathrm{d}t}=\left(\frac{{L}_{J}}{\left({L}_{J}+\Delta {L}_{J}\right)}-1\right)\left(-{\dot{s}}_{J}-{k}_{3}\frac{\mathrm{d}{i}_{TJR}}{\mathrm{d}t}+{k}_{3}{\omega }_{\mathrm{s}}{i}_{TJI}\right)-\frac{{L}_{J}}{\left({L}_{J}+\Delta {L}_{J}\right)}\Gamma {s}_{J}-\frac{{L}_{J}}{\left({L}_{J}+\Delta {L}_{J}\right)}\alpha \mathrm{sign}\left({s}_{J}\right)$$
(28)

which leads to:

$$\frac{{L}_{J}}{\left({L}_{J}+\Delta {L}_{J}\right)}\frac{\mathrm{d}{s}_{J}}{\mathrm{d}t}=\left(\frac{\Delta {L}_{J}}{\left({L}_{J}+\Delta {L}_{J}\right)}\right){k}_{3}\frac{\mathrm{d}{i}_{TJR}}{\mathrm{d}t}+\left(\frac{-\Delta {L}_{J}}{\left({L}_{J}+\Delta {L}_{J}\right)}\right){k}_{3}{\omega }_{\mathrm{s}}{i}_{TJI}-\frac{{L}_{J}}{\left({L}_{J}+\Delta {L}_{J}\right)}\Gamma {s}_{J}-\frac{{L}_{J}}{\left({L}_{J}+\Delta {L}_{J}\right)}\alpha \mathrm{sign}\left({s}_{J}\right)$$
(29)

Dividing both sides of Eq. (29) by \(\frac{{L}_{J}}{\left({L}_{J}+\Delta {L}_{J}\right)}\) yields \(\frac{\mathrm{d}{s}_{J}}{\mathrm{d}t}\) as follows:

$$\frac{d{\mathrm{s}}_{\mathrm{J}}}{\mathrm{d}t}=\Delta x-\Gamma {s}_{J}-\alpha \mathrm{sign}\left({s}_{J}\right)$$
(30)

where \(\Delta x=\frac{\Delta {L}_{J}}{{L}_{J}}{k}_{3}\frac{\mathrm{d}{i}_{TJR}}{\mathrm{d}t}-\frac{\Delta {L}_{J}}{{L}_{J}}{k}_{3}{\omega }_{\mathrm{s}}{i}_{TJI}\).

The robustness of the control against system parameter variations is ensured if the local reachability condition, as shown in (19), is satisfied. Using Eq. (30), the left term of Eq. (19) is as follows:

$${s}_{J}\frac{\mathrm{d}{s}_{J}}{\mathrm{d}t}={s}_{J}\left(\Delta x-\Gamma {s}_{J}-\alpha \mathrm{sign}\left({s}_{J}\right)\right)$$
(31)

Since \({s}_{J}\mathrm{sign}\left({s}_{J}\right)=\left|{s}_{J}\right|\), Eq. (30) is:

$${s}_{J}\frac{\mathrm{d}{s}_{J}}{\mathrm{d}t}=-\left(-\frac{\Delta x}{\mathrm{sign}\left({s}_{J}\right)}+\Gamma \left|{s}_{J}\right|+\alpha \right)\left|{s}_{J}\right|$$
(32a)
$${s}_{J}\frac{\mathrm{d}{s}_{J}}{\mathrm{d}t}=-{\eta }^{^{\prime}}\left|{s}_{J}\right|$$
(32b)

where \({\eta }^{\mathrm{^{\prime}}}=\left(-\frac{\Delta x}{\mathrm{sign}\left({s}_{J}\right)}+\Gamma \left|{s}_{J}\right|+\alpha \right)\).

The reachability condition is satisfied at \({\upeta }^{\mathrm{^{\prime}}}>0\). It is assumed that \(\Delta x={\rho }_{\mathrm{max}}\) is the maximum tolerable uncertainty in the system parameters. When using (32) and \({\upeta }^{\mathrm{^{\prime}}}>0\), the following condition must be fulfilled:

$$\left|{\rho }_{\mathrm{max}}\right|<\left|\Gamma \left|{s}_{J}\right|+\alpha \right|$$
(33)

When \(\alpha >{\rho }_{\mathrm{max}}\) is chosen, the condition given by (33) is satisfied.

4 Verifications

The performance of the proposed scheme is verified using a megawatt simulation system and a downscaled laboratory hardware prototype. The performance is investigated under different operation conditions.

4.1 Simulation verification

The PSIM circuit parameters are shown in Table 1. The circuit has two SMs per phase. Figure 9 shows circuit waveforms at the fundamental frequency, where they exhibit the three-phase voltage and three-phase load current, which varies smoothly at 60 Hz. Then the SM capacitor voltages are balanced with a ± 8% voltage ripple. This voltage ripple value is achieved with a 15 μF film capacitor. Meanwhile, conventionally, a 1000 μF is needed for the same ripple. The figure also shows that the DC source produces a pure DC current. Additionally, it shows the MMC arm current for phase A. It can be seen that the arm currents are free from the 120 Hz and 240 Hz components. Therefore, the circulating current is almost a pure DC current. Figure 10 shows the performance of the proposed scheme at a 50% imbalance between the HFT leakage inductances. The proposed sliding mode control succeeded in compensating the imbalance, which results in the SM capacitor voltage ripples being balanced. The simulation investigated the robustness of the proposed control against circuit parameter variations.

Table 1 Simulation circuit parameter values
Full size table
Fig. 9
figure 9

Simulation waveforms of the proposed scheme under its rated parameters

Full size image
Fig. 10
figure 10

Performance of the proposed scheme at a 50% imbalance in the HFT leakage inductances

Full size image

Figure 11 shows SM capacitor voltage waveforms with and without the sliding mode control (SMC). The circuit started without the SMC. Then at 0.15 s, the sliding mode control is activated. The transient time is less than half of a cycle of the fundamental frequency with negligible overshoot and undershoot. The proposed control compensated more than 88% of the SM capacitor voltage ripple with a significantly small settling time. This cannot be achieved with normal ripple rejection control due to bandwidth limitations.

Fig. 11
figure 11

Simulation waveforms of SM capacitor voltages with and without the sliding mode control (SMC)

Full size image

The main enhancement of the proposed scheme is replacing the low-frequency SM capacitor with a frequency-independent power decoupling scheme, which solves the issue of wide voltage fluctuations in the SM capacitor under low-speed operation. To investigate this, the circuit was tested under low-frequency operation at a constant load current. The load resistance was changed linearly to keep the load current constant, which represents the constant torque condition. The control parameters were maintained the same without any change as the rated frequency control parameters. Figure 12 shows circuit waveforms at a 5 Hz operating frequency.

Fig. 12
figure 12

Performance of the proposed scheme under a 5 Hz fundamental line frequency

Full size image

They indicate that the THB power decoupling scheme can keep the voltage ripple constant (± 8%) under a near-zero-speed operation. This voltage ripple is achieved with a 15 μF film capacitor, while a 12,000 μF is normally needed at 5 Hz. Employing the proposed scheme reduces the required SM capacitance. Figure 13 shows the dynamic performance of the proposed scheme when driving a 3-phase machine from standstill to full speed under a constant torque condition. The SM capacitor voltage ripple is nearly constant over a wide range of frequency variations. The proposed scheme shows a very smooth transient response with a negligible transient time.

Fig. 13
figure 13

Transient response of the proposed scheme under continuous frequency variations

Full size image

4.2 Experimental verification

A hardware prototype was built to validate the proposed scheme. All of the MMC-SM capacitors in the circuit were metalized-polypropylene film-type capacitors from Vishay, with a capacitance of 30 µF and a rating of 500 V DC. The load power for the three phases was 1.3 kW. All of the switches used in the circuit were silicon-carbide switches chosen to improve efficiency. Two lab-made high-frequency transformers with 1:1:1 turn ratios were used with a sandwich winding method. Six 100 μH inductors were connected in series with transformer windings. The control configurations were implemented on a TMS320F28335 with an XDS100v1 development board. Detailed information on the prototype is listed in Table 2, and the circuit setup is shown in Fig. 14.

Table 2 Experimental circuit parameter values
Full size table
Fig. 14
figure 14

Lab prototype circuit

Full size image

To highlight the enhancement of the proposed MMC scheme, the circuit has been tested under a low operating frequency (Figs. 15, 16 and 17). Figures 18 and 19 show circuit waveforms at 30 Hz and 10 Hz converter line frequencies, respectively. The load current is regulated to be constant at the different operating frequencies. The control parameters are kept the same without any changes of the rated frequency control parameters. The SM capacitor voltage ripples are ± 8.49% and ± 9.43% at 30 Hz and 10 Hz, respectively. Figure 20 shows experimental waveforms at a 5 Hz operating frequency. This figure shows that the SM capacitor voltage ripples are ± 10% under near-zero-speed operating. These voltage ripples are achieved with an SM capacitance of 15 μF. There is very little high-frequency chattering in the SM voltage due to the sliding mode control action. The SM capacitor voltage ripple is nearly constant over a wide range of frequencies.

Fig. 15
figure 15

Experimental waveforms of the proposed scheme under its rated parameters

Full size image
Fig. 16
figure 16

Experimental waveforms of SM capacitor voltages under HFT external inductors La = 100 µH, Lb = 100 µH, and Lc = 75 µH

Full size image
Fig. 17
figure 17

Experimental waveforms of SM capacitor voltages with and without the sliding mode control (SMC)

Full size image
Fig. 18
figure 18

Experimental waveforms of the proposed scheme under a 30 Hz fundamental line frequency

Full size image
Fig. 19
figure 19

Experimental waveforms of the proposed scheme under a 10 Hz fundamental line frequency

Full size image
Fig. 20
figure 20

Experimental waveforms of the proposed scheme under near-zero-speed operation

Full size image

Figure 21 shows power decoupling circuit-based THB waveforms under the rated operation conditions. The HFT current contains the switching frequency component with a low-frequency envelop. The low-frequency components are transferred to be canceled out in the transformer core. This demonstrates that the power decoupling circuit works as expected. The switching component of the transformer currents shows that the proposed sliding mode control works as expected since the three currents have the fundamental waveform at the switching frequency, and are shifted to cause the transformer to absorb more voltage ripple. The transformer rated current is nearly half the phase current, which demonstrates the quality of the proposed scheme.

Fig. 21
figure 21

Experimental waveforms of HFT currents under its rated parameters

Full size image

5 Discussion

In this section, circuit volumes are used for a comparison of the proposed scheme, two other schemes [9, 10], and the conventional MMC. The design specifications for the four topologies are a ± 5% voltage ripple at a near-zero speed, a total power of 10 MW, and an average SM voltage of 2.5 kV. The results for one sub-module are shown below.

For a conventional MMC, a 13 mF, 2500 V SM capacitor is required [9]. A 1300 µF, 1320 V capacitor (TDK) with a volume of 14.84 L is commercially available, which means the total volume of the required capacitors is 593.6 L [28].

Two 2 mF, 1300-V SM capacitors are needed for the topologies in [9] and [10]. Using the aforementioned commercial capacitors, the total volume of the capacitors is 59.36 L. This represents a 90% reduction in capacitor volume relative to the conventional MMC. However, for the proposed scheme, two 30 µF, 1300 V SM capacitors are required. A 30 µF, 1400 V capacitor (CDE) with a volume of 0.3 L is commercially available [29]. The total volume of the capacitors is 1.2 L, which represents a 99% reduction in the capacitor volume (again relative to conventional MMCs).

In [10], the power decoupling branch has four semiconductor switches, and 5SNA0650J450300 IGBTs (4.5 kV, 650 A, ABB) are used. The volume of one IGBT is 0. 87 L, and the total volume of the switches in the power decoupling branch is 3.48 L. In both [9], and the proposed scheme, the power decoupling branch has two semiconductor switches. Therefore, the total volume of the switches in the power decoupling branches is 1.74 L. 5SNA1200G450350 IGBT semiconductors (4.5 kV, 1200 A, ABB) are used for the MMC branch, and the volume of one IGBT is 1.28 L. Thus, the total volume of the switches in the MMC branch is 2.56 L. The total volume of the switches in the conventional MMC is 2.56 L, and the overall switch volume in [10] is 6.04 L. Thus, the switching device volume is increased by 136% when compared to a conventional MMC. However, in [9] and in the proposed scheme, the overall switch volume is 4.3 L. Therefore, the switching device volume is increased by 68% over that of a conventional MMC.

In [10], each of the SMs requires an HF transformer. In [9], the two submodules use an HF transformer. In the proposed scheme, each of the three SMs requires a HF transformer. The design procedures of the HF transformer for MV and high-power applications are discussed in [30], where it is noted that the transformer specifications are 1.25 kV, 330 A, and 17 L. Therefore, the transformer volume requirements for the topologies in [9, 10] and the proposed scheme are 8.5 L, 17 L, and 6 L, respectively.

Figure 22 shows a comparison of the component volumes for the four topologies with SM component switching devices (IGBT), IGBT heat sinks, HF transformers, and SM capacitors. The proposed scheme, [9], and [10] reduce the overall volume of the conventional MMC by 97%, 88%, and 86%, respectively. This reduction in the system volume is due to eliminating the LF SM capacitor.

Fig. 22
figure 22

Component volume comparison per SM of the proposed scheme, the scheme in [9], the scheme in [10], and the conventional MMC

Full size image

6 Conclusion

A medium-voltage high-power machine drive system has been proposed based on a MMC with a three-port power decoupling approach. The proposed scheme solves the issue of the low-frequency ripple components in the sub-module (SM) capacitor voltage, where their magnitude is inversely proportional with respect to the converter line frequency, which limits employing a MMC in applications operating at a low-speed. The power decoupling approach employs a THB converter to extract the three-phase ripple power from the SMs. Then it delivers this power to the three-winding high-frequency transformer where the three-phase ripple power is dissipated magnetically regardless of the ripple frequency. To ensure that the SM capacitor voltage has acceptable ripple components, a ripple rejection-based sliding mode control has been proposed. The proposed control is independent of the converter line frequency. Therefore, it is suitable for adjustable-speed applications. The proposed control shows a fast transient response with negligible overshoots and undershoots at continuous speed adjusting, which overcomes conventional methods drawbacks, such as bandwidth limitations and frequency dependence. The main advantages of employing the proposed scheme can be summarized as follows. (1) The proposed scheme is suitable for low-speed and continuous adjusting speed operations. (2) The proposed scheme is totally free from SM ripple power capacitors. Therefore, a significant reduction in the overall volume of the system is possible in comparison to conventional MMCs. (3) In fault cases, the possibility of the switching devices exploding is small since there are no large energy storage units in the circuit and the inrush current is small. (4) The proposed scheme succeeds in keeping the SM capacitor voltage ripple narrow regardless of the converter line frequency. (5) The proposed scheme is believed to be the best solution for variable-speed drives based on MMCs. It has the lowest rated and the smallest number of circuit components among the related SM ripple power decoupling methods. In addition, it does not increase the magnitude of the arm current relative to those of other circulating current injection techniques. The performance of the proposed scheme has been verified for MV high-power variable-speed applications with simulations and downscaled hardware experiments under various operating conditions.