1 Introduction

The modular multilevel converter (MMC) has been extensively researched in HVDC transmission system and motor drives [1,2,3] because of its efficiency, highly modularity and extensibility, and superior output signal quality [4]. When compared with conventional converters like flying capacitor and cascaded H-bridge (CHB) converters, the utilization of the MMC topology enables the preservation of substantial reactive components in medium/high voltage high power ranges, including line transformers, harmonic filters, and dc bus capacitors [5].

The extensive use of sub-module (SM) capacitors causes heavier weight and higher cost, which hinders the further application of MMC. What is worse, the voltage fluctuation of the SM is in a reverse ratio with the operating frequency. Thus, a large capacitor is required to restrain the voltage ripple when operating at low frequencies. It is evident from actual engineering application that SM capacitors occupy approximately half of the system volume and most of the system weight [6]. Hence, capacitor voltage ripple must be reduced, resulting in a smaller capacitance [7].

Since the MMC topology was first proposed in [8], a great deal of research has been done on diminishing SM voltage fluctuation, and this research is mainly divided into two kinds of methods, adding control variable degrees of freedom and adding hardware degrees of freedom [9,10,11,12,13,14,15,16,17,18]. In terms of adding control variable degrees of freedom, in [9] and [10], a second-order circuiting current was infused to arms of each phase to suppress the voltage ripple in the SM. Methods for injecting second-order and fourth-order circuiting currents into arm currents were proposed in [11] and [12]. The aforementioned methods are effectual when the voltage modulation index is high [13]. However, they are not applicable for motor drive systems that require wide range adjustment [11]. Moreover, the above methods only handle even-order frequency powers. However, these are not the critical portions that cause voltage fluctuation [12]. A mixed injection strategy of high-frequency sinusoidal current with voltage was initially put forth in [14] to handle the base frequency power in SM capacitors. Capacitor voltage fluctuation can be effectively decreased using this method. However, the current stress and power dissipation on the switch devices are significantly increased, particularly when the voltage modulation index is low [6]. To diminish the maximum of arm current, other high-frequency component waveforms are introduced, such as square wave [15,16,17]. However, a related high-frequency voltage emerges in the arm voltage reference value, that could result in overmodulation [6, 18]. In addition, the infused voltage produces electromagnetic interference and even causes motor insulation breakdown [19].

To avert the above drawbacks of adding control variable degrees of freedom, the suppression of SM voltage fluctuation is achieved by adding hardware degrees of freedom to the MMC [20,21,22,23,24,25,26]. In [20, 21], a novel active power filtering decoupling circuit was proposed, which utilizes inductors and capacitors as energy storage devices and adds a power switching arm. Through the precise control of the additional arm and the MMC main circuit, the ripple suppression of the SM capacitor was successfully achieved. It is worth noting that these methods involve coupling effects between the active power filter circuit and the MMC main topology, leading to additional switching actions and ultimately increasing the total power loss of the system. Meanwhile, the authors of [22,23,24,25] proposed an independent decoupling circuit for active power filters, which uses inductors or capacitors as energy storage components and is connected in parallel at both ends of the dc bus capacitor. However, due to the relatively low energy storage density of inductors, additional active power filter decoupling circuits often occupy a larger volume, reducing the power density of the system. In [26], it was proposed that an active power filter (APF) circuit be inserted to the per phase of the MMC, which is called APF-MMC. This topology addresses only the even-order frequency powers in SMs.

In this paper, an extension of the APF-MMC introduced in [26] is presented. The basic principle is to manage the two control degrees of freedom of the injected high-frequency component to achieve SM voltage ripple suppression, and to use the hardware degree of freedom of the additional APF circuit to mitigate the impact of the injected high-frequency voltage with the external characteristics. The frequency of the control degrees of freedom in the APF-MMC can be controlled, which means they can better adapt to operation in a wide frequency range and avoid overmodulation.

2 Proposed APF-MMC topology

2.1 Basic configuration of the APF-MMC

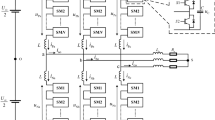
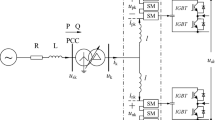
Figure 1a presents the APF-MMC topology, which is made up of phases x (x = a, b, c). Every phase includes two duplicate arms, called the upper arm and the lower arm, and one parallel-connected Buck-type APF branch. Every arm is equipped with an inductor L and 2N half-bridge SMs. Furthermore, each of the arms can be further divided into a top sub-arm and a bottom sub-arm, each consisting of N SMs. The lower-half arm located in the upper arm and the upper-half arm situated in the lower arm are called middle arms (Mid-arms), as depicted in Fig. 1a. Both the APF circuit and the SM can be substituted with various topology structures [27]. In addition, the Mid-SM does not exert any substantial influence on the ac output side.

Fig. 1
figure 1

APF-MMC topology: a configuration; b equivalent model

Full size image

It is assumed that the output voltage ex and the output current ix of the APF-MMC circuit are

$$\left\{ \begin{gathered} e_x = E_x \sin (\omega t + \theta_x ) \hfill \\ i_x = I_x \sin (\omega t + \theta_x - \varphi ) \hfill \\ \end{gathered} \right.,$$
(1)

where Ex and Ix (subscript x = a, b, c) are the peak output voltage and the peak current, respectively. ω is the output angular frequency of the fundamental, and θx and φ are the phase angle and the power factor angle, respectively.

By disregarding the voltage drop across the arm inductor [28], the arm voltages uPx and uNx of the APF-MMC are described as

$$\left\{ \begin{gathered} u_{Px} = \frac{1}{2}U_{dc} - e_x = \frac{1}{2}U_{dc} - E_x \sin (\omega t + \theta_x ) \hfill \\ u_{Nx} = \frac{1}{2}U_{dc} + e_x = \frac{1}{2}U_{dc} + E_x \sin (\omega t + \theta_x ). \hfill \\ \end{gathered} \right.$$
(2)

Similarly, the corresponding arm currents iPx and iNx are

$$\left\{ \begin{gathered} i_{Px} = \frac{1}{3}I_{dc} [1 + m\sin (\omega t + \theta_x - \varphi )] + I_{2f} \cos (2\omega t + 2\theta_x - \varphi ) \hfill \\ i_{Nx} = \frac{1}{3}I_{dc} [1 - m\sin (\omega t + \theta_x - \varphi )] + I_{2f} \cos (2\omega t + 2\theta_x - \varphi ). \hfill \\ \end{gathered} \right.$$
(3)

2.2 Operating principle of the APF-MMC

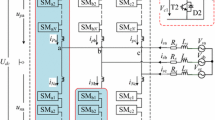
For convenient understanding of the operating principle, the equivalence structure of the APF-MMC is exhibited in Fig. 1b. In the model, controlled voltage sources are used to substitute for the sub-arms, and the desirable sub-arm output voltages uPx1, uPx2, uNx1, and uNx2 in each phase are postulated to be composed of three dominant elements of dc voltage components (Udc/4), fundamental frequency ac voltage (ex/2), and high-frequency ac voltage uxij. To keep the dc voltage consistent, the dc components of the sub-arm in each phase are set to identical directions, while the ac voltages of the arm are arranged in contrary directions to generate differential voltage to be sent to the output.

As signified in Fig. 1b, the sign of the injected high-frequency voltage of the top and bottom arms is inverted in each arm to prevent the high-frequency voltage from affecting the topology output side. The sub-arm voltage can be realized by controlling the modulation wave of the corresponding sub-arm [6]. In addition, the expressions of sub-arm voltages are

$$\left\{ \begin{gathered} u_{Px1} = \frac{{U_{dc} }}{4} - \frac{e_x }{2} - u_{xij} \\ u_{Px2} = \frac{{U_{dc} }}{4} - \frac{e_x }{2} + u_{xij} \\ u_{Nx1} = \frac{{U_{dc} }}{4} + \frac{e_x }{2} - u_{xij} \\ u_{Nx2} = \frac{{U_{dc} }}{4} + \frac{e_x }{2} + u_{xij}. \\ \end{gathered} \right.$$
(4)

There are three degrees of freedom in the APF-MMC circuit, which are the high-frequency voltage uxij, the high-frequency ac current ixij, and the APF circuit branch, to reconstruct the fluctuation power of the sub-arm and to eliminate the effect of high-frequency voltage on the ac output voltage. Similar to the methods in [14] and [15], the high-frequency components uxij and ixij are used as two degrees of freedom to convert low-frequency fluctuation powers into high-frequency ripple powers to diminish the capacitor voltage fluctuation. In addition, the APF circuit is taken as a hardware degree of freedom, supplies a route for the current ixij in the Mid-SMs and eliminates the effects of the injected voltage uxij on the external features of the MMC.

Due to the presence of the arm inductor L, the high-frequency current ixij of the top sub-arm and the bottom sub-sum can be generated by controlling the voltage on the relevant arm inductor L [4]:

$$i_{xij} = \frac{1}{L}\int {u_{Lxij} } {\text{d}}t,$$
(5)

where uLxij is the drop voltage on the arm inductor L. In addition, the currents of the top sub-arm in the upper arm and the bottom sub-sum in the lower arm iPx1 and iNx2 can be derived as

$$\left\{ \begin{gathered} i_{Px1} = \frac{{I_{{\text{dcir}}} }}{3} + \frac{i_x }{2} + i_{xij} \\ i_{Nx2} = \frac{{I_{{\text{dcir}}} }}{3} - \frac{i_x }{2} + i_{xij} \\ \end{gathered} \right.,$$
(6)

where Idcir is the circuiting current, which is calculated as

$$I_{{\text{dcir}}} = I_{{\text{dc}}} + 3i_{{\text{cir}}} .$$
(7)

The second-order circuiting current icir can be effectively eliminated through the utilization of a circuiting current suppression controller (CCSC) [29]. Assuming that there is no second-order component in the circuiting current, Idcir can be rewritten as

$$I_{{\text{dcir}}} = I_{{\text{dc}}} .$$
(8)

The high-frequency current ixij of the Mid-SMs can be generated by controlling the APF circuit current iAPFx.

$$i_{{\text{APF}}x} = 2i_{xij} .$$
(9)

On the basis of Kirchhoff’s current law, the arms currents iPx2 and iNx1 are derived as

$$\left\{ \begin{gathered} i_{Px2} = \frac{{I_{{\text{dc}}} }}{3} + \frac{i_x }{2} - i_{xij} \\ i_{Nx1} = \frac{{I_{{\text{dc}}} }}{3} - \frac{i_x }{2} - i_{xij}. \\ \end{gathered} \right.$$
(10)

In the APF-MMC, the momentary energies within the sub-arms are acquired through the multiplication of the sub-arm current and voltage. The powers are obtained as

$$\left\{ \begin{gathered} p_{Px1} = u_{Px1} i_{Px1} = p_1 + p_2 + p_3 \\ P_{Px2} = u_{Px2} i_{Px2} = p_1 + p_2 - p_3 \\ p_{Nx1} = u_{Nx1} i_{Nx1} = p_1 - p_2 - p_3 \\ P_{Nx2} = u_{Nx2} i_{Nx2} = p_1 - p_2 + p_3, \\ \end{gathered} \right.$$
(11)

where pPx1 and pPx2 are the powers of the upper arm. pNx1 and pNx2 are the powers of top and bottom sub-arm in the lower arm, respectively. In addition, p1, p2, and p3 can be expressed as (12):

$$\left\{ \begin{gathered} \begin{aligned} & p_1 = \frac{{U_{{\text{dc}}} I_{{\text{dc}}} }}{12} - \frac{E_x I_x }{8}\cos \varphi + \frac{E_x I_x }{8}\cos (2\omega t + 2\theta_x - \varphi ) \\ & p_2 = \frac{{U_{{\text{dc}}} I_x }}{8}\sin (\omega t + \theta_x - \varphi ) - \frac{{E_x I_{{\text{dc}}} }}{6}\sin (\omega t + \theta_x ) - u_{xij} i_{xij} \\ & p_3 = \frac{{U_{{\text{dc}}} i_{xij} }}{4} - \frac{{u_{xij} I_{{\text{dc}}} }}{3} - \frac{{E_x i_{xij} }}{2}\sin (\omega t + \theta_x ) - \frac{{u_{xij} I_x }}{2}\sin (\omega t + \theta_x - \varphi ). \\ \end{aligned} \end{gathered} \right.$$
(12)

In (12), the initial two components of p1 correspond to the direct current (dc) powers of the system. It is imperative for these values to be zero to maintain system stability [30], and the third term of p1 is the second-order fluctuation power. In addition, the first two terms of p2 are the base frequency powers, which are the major causes of the voltage ripple, and the third term of p2 consists of two controllable variable degrees of freedom. Similarly, each term of p3 contains a controllable variable degree of freedom. Because each degree of freedom is a high-frequency variable, its impact on the SM capacitor voltage ripple is relatively small and negligible [31].

According to [14] and [29], square waves and other waveforms can be selected as the injected high-frequency components to diminish the arm current amplitude. For the convenience of analysis, a sine waveform is selected as the infused high-frequency voltage, as follows:

$$u_{xij} = U_{xij} \sin (\omega_h t + \theta_h ){ = }U_{xij} \sin (2\pi f_h t + \theta_h ),$$
(13)

where ωh is the angular velocity, and θh and fh are the initial phase angle and the output angular frequency. To significantly diminish the capacitor voltage ripple, fh is generally specified as 4–10 times the working frequency f. At the same time, fh ought to be no higher than 1/10 of the tantamount switch frequency of the MMC topology to accurately control the high-frequency variables [13].

By controlling the two degrees of freedom of the infused high-frequency voltage and current, the base frequency power in the sub-arms is converted to high-frequency power, realizing the suppression of voltage ripple [14]. Then the high-frequency current is expressed as [31]

$$i_{xij} = \left[ {\frac{{E_x I_{{\text{dc}}} }}{3}\sin (\omega t + \theta_x ) - \frac{{U_{{\text{dc}}} I_x }}{4}\sin (\omega t + \theta_x - \varphi )} \right]U_{xij}^{ - 1} \sin (\omega_h t + \theta_h ).$$
(14)

Substituting (14) into (12), p2 can be obtained as

$$p_2 = \left[ {\frac{{U_{{\text{dc}}} I_x }}{8}\sin (\omega t + \theta_x - \varphi ) - \frac{{E_x I_{{\text{dc}}} }}{6}\sin (\omega t + \theta_x )} \right]\cos (2\omega_h t + 2\theta_h ).$$
(15)

As indicated by Eq. (14), the value of ixij is reversed proportional to the maximum value of the high-frequency voltage. To reduce the amplitude of the injected high-frequency current and to prevent overmodulation, [29] suggests calculating the amplitude value of the high-frequency voltage based on the instantaneous magnitude of the output voltage. The amplitude should meet the following mathematical relations:

$$U_{xij} = \frac{{U_{{\text{dc}}} }}{4} - \frac{{\max \left( {\left| {e_a } \right|,\left| {e_b } \right|,\left| {e_c } \right|} \right)}}{2},$$
(16)

where max (|ex|) is meant to take the largest value of |ex|.

When the value of the injected high-frequency voltage is gained by (16), although the infused current can be minimized, the calculation of the variable voltage amplitude aggravates the complicacy and affects the robustness and redundancy of the system [13]. For this reason, the most commonly used expression for calculating the infused voltage is

$$U_{xij} = \frac{{U_{{\text{dc}}} }}{4} - \frac{E_x }{2}.$$
(17)

On the basis of the above discussion, the equations for the injected high-frequency elements are as follows:

$$\left\{ \begin{gathered} u_{xij} = \frac{{U_{{\text{dc}}} - 2E_x }}{4}\sin (\omega_h t + \theta_h ) \hfill \\ i_{xij} = \frac{{{[}4E_x I_{{\text{dc}}} \sin (\omega t + \theta_x ) - {3}U_{{\text{dc}}} I_x \sin (\omega t + \theta_x - \varphi )]\sin (\omega_h t + \theta_h )}}{{3U_{{\text{dc}}} - 6E_x }} \hfill \\ \end{gathered} \right..$$
(18)

Substituting (18) into (12), the sub-arm powers can be derived as

$$\left\{ \begin{gathered} p_1 = \frac{E_x I_x }{8}\cos (2\omega t + 2\theta_x - \varphi ) \\ p_2 = \left[ {\frac{{U_{{\text{dc}}} I_x }}{8}\sin (\omega t + \theta_x - \varphi ) - \frac{{E_x I_{{\text{dc}}} }}{6}\sin (\omega t + \theta_x )} \right]\cos (2\omega_h t + 2\theta_h ) \\ p_3 = \frac{{U_{{\text{dc}}} i_{xij} }}{4} - \frac{{u_{xij} I_{{\text{dc}}} }}{3} - \frac{{E_x i_{xij} }}{2}\sin (\omega t + \theta_x ) - \frac{{u_{xij} I_x }}{2}\sin (\omega t + \theta_x - \varphi ) \\ \end{gathered} \right..$$
(19)

Comparing (12) with (19), the basic frequency fluctuation power in the arm is completely replaced by the high-frequency fluctuation powers. Then the ripple powers in arms are basically constituted of second-order and high-frequency parts. Unlike the classical MMC arm powers, because ωh is greater than ω, the high-frequency ripple powers in (19) significantly increase the charging and discharge frequency of the arm capacitor, greatly alleviating the variability in the capacitor voltage, and the smaller the angular frequency ω, the better the capacitor voltage ripple suppression effect [19].

2.3 Operating principle of the APF branch

According to Fig. 1b, the voltage UAPFx is equal to Udc/2. Subsequently, the power pAPFx assimilated by the capacitor Cdp in the APF circuit is shown in (20):

$$p_{{\text{APF}}x} = \frac{{U_{{\text{dc}}} i_{{\text{APF}}x} }}{2}.$$
(20)

Substituting (18) into (20), pAPFx can be re-calculated as

$$\begin{aligned} p_{{\text{APF}}x} & = \frac{{4E_x U_{{\text{dc}}} I_{{\text{dc}}} \sin (\omega t + \theta_x )\sin (\omega_h t + \theta_h )}}{{3U_{{\text{dc}}} - 6E_x }} \\ & \qquad - \frac{{U_{{\text{dc}}}^2 I_x \sin (\omega t + \theta_x - \varphi )\sin (\omega_h t + \theta_h )}}{{U_{{\text{dc}}} - 2E_x }}. \\ \end{aligned}$$
(21)

Only when the buck-type APF branch is controlled to operate in the boundary conduction mode (BCM) or the discontinuous current mode (DCM) mode [32], the power shown in (21) is completely absorbed by the capacitor Cdp in the APF branch so that

$$C_{{\text{dp}}} \frac{{{\text{d}}v_{{\text{dp}}} }}{{{\text{d}}t}}v_{{\text{dp}}} = p_{{\text{APF}}x} ,$$
(22)

where vdp represents the capacitor voltage of Cdp. In addition, the integral (22), the APF branch energy WAPF is expressed as

$$W_{{\text{APF}}} = \frac{1}{2}C_{{\text{dp}}} v_{{\text{dp}}}^2 = \int {p_{{\text{APF}}x} {\text{d}}t = W_{{\text{APF}}x} + W_{{\text{APF}}0} } ,$$
(23)

where WAPFx is the fluctuation energy of every phase. WAPF0, a constant intricately associated with the energy storage efficiency, governs the direct current deviation of vdp [6].

Combining (21) and (23), the expressions of vdp and idp are described as (24) and (25), respectively:

$$v_{\text{dp}} = \sqrt{\frac{2}{C_{\text{dp}}}(W_{\text{APFx}} + W_{\text{APF0}}} = \sqrt{\begin{aligned} &\frac{4U_{\text{dc}}E_{\text{x}} I_{\text{dc}} \sin[(\omega _h - \omega )t + \theta _h - \theta _x]}{3U_{\text{dc}} - 6E_x) C _{\text{dp}} (\omega _h - \omega)} - \frac{U_{\text{dc}}^2 I_x \sin [(\omega _h - \omega)t + \theta _h - \theta _x + \varphi]}{U_{\text{dc}} - 2E_x) C _{\text{dp}} (\omega _h - \omega)} \\ & + \frac{U_{\text{dc}}^2 I_x \sin [(\omega _h + \omega)t + \theta _h + \theta _x - \varphi]}{U_{\text{dc}} - 2E_x) C _{\text{dp}} (\omega _h + \omega)} - \frac{4U_{\text{dc}}E_{\text{x}} I_{\text{dc}} \sin[(\omega _h + \omega )t + \theta _h + \theta _x]}{3U_{\text{dc}} - 6E_x) C _{\text{dp}} (\omega _h + \omega)} + \frac{2W_{\text{dp0}}}{C _{\text{dp}}}\end{aligned},}$$
(24)
$$i_{{\text{dp}}} = \frac{{p_{{\text{APF}}x} }}{{v_{{\text{dp}}} }}.$$
(25)

In addition, to effectively suppress the switching harmonics, it is crucial to ensure that the resonant frequency fLC of the APF circuit is approximately 1/10 ~ 1/5 of the switching frequency fAPF. Furthermore, the switching frequency fAPF is independent of the switching frequency of the SMs.

$$f_{{\text{LC}}} = \frac{1}{{2\pi \sqrt {{L_{{\text{dp}}} C_{{\text{dp}}} }} }} = \lambda f_{{\text{APF}}} ,(1/10 < \lambda < 1/5).$$
(26)

3 Control and analysis of the APF circuit

The primary objective of the APF is the generation of the required high-frequency current ixij in the Mid-arms. Since the switching frequency of the APF circuit is much higher than the operating frequency that needs to be controlled to generate the high-frequency current, the input voltage UAPF and the decoupling capacitor voltage vdp in the APF branch can be considered as constants in one switching period TAPF. At this time, the decoupling inductor Ldp in the APF circuit can be regarded as linear charging or linear discharge in one switching cycle. Thus, the change rate of inductor current can be considered a constant, as shown in Fig. 2.

Fig. 2
figure 2

Working mode of the APF circuit: a MMC transfers energy to the APF circuit; b APF circuit transfers energy to the MMC

Full size image

Figure 2a displays the charging process from the MMC to the inductor Ldp and the capacitor Cdp of the APF circuit. At t = t1, the power switching device S3 turns on and S4 turns off, and the APF circuit works in the Buck state. At this time, the inductor current idp in the APF circuit increases linearly. Equation (27) indicates the mathematical logic between the capacitor voltage vdp and the current idp in the APF circuit. In addition, the change rate of the inductor current k1 is shown in (28). At t = t2, the power switching device S3 turns off and S4 turns on. The inductor Ldp in the APF circuit begins to release energy to the capacitor Cdp, and when t = t3, the energy in the inductor Ldp is conveyed to the capacitor Cdp. At this time, the voltage vdp and the current idp of the capacitor have the mathematical relationship shown in (29). TAPF is the switching period of the APF circuit, and its calculation is shown in (30):

$$U_{{\text{buck}}} - v_{{\text{dp}}} = L_{{\text{dp}}} \frac{{\Delta I_{{\text{dp}}} }}{t_2 - t_1 },$$
(27)
$$k_1 = \frac{{U_{{\text{buck}}} - v_{{\text{dp}}} }}{{L_{{\text{dp}}} }},$$
(28)
$$v_{{\text{dp}}} = L_{{\text{dp}}} \frac{{\Delta I_{{\text{dp}}} }}{t_3 - t_2 },$$
(29)
$$T_{{\text{APF}}} = t_4 - t_1 .$$
(30)

In one switching cycle, the energy releasing process of the inductor and capacitor from the APF circuit to the MMC is displayed in Fig. 2b. At t = t5, S3 turns off and S4 turns on, the APF circuit works in the Boost state, and the capacitor Cdp begins to release energy to the inductor Ldp. At this time, the inductor current idp in the APF circuit increases linearly, and the mathematical relationship of the voltage vdp and the current idp in the APF circuit is shown in (31), and the change rate of the inductor current k2 is shown in (32). At t = t6, the power switching device S3 turns on and S4 turns off, and the inductor and capacitor in the APF circuit begin to release energy to the MMC. When t = t7, the energy is all transferred to the MMC. In addition, the capacitor current idp and the voltage vdp have the mathematical relationship shown in (33). The switching period TAPF is obtained as (34):

$$v_{{\text{dp}}} = L_{{\text{dp}}} \frac{{\Delta I_{{\text{dp}}} }}{t_6 - t_5 },$$
(31)
$$k_2 = \frac{{v_{{\text{dp}}} }}{{L_{{\text{dp}}} }},$$
(32)
$$U_{{\text{buck}}} - v_{{\text{dp}}} = L_{{\text{dp}}} \frac{{\Delta I_{{\text{dp}}} }}{t_7 - t_6 },$$
(33)
$$T_{{\text{APF}}} = t_8 - t_5 .$$
(34)

According to energy conservation and the impulse area equivalent law, in one switching period, the following results can be obtained, respectively:

$$\left\{ \begin{gathered} \frac{1}{2}k_1 (t_2 - t_1 )(t_3 - t_1 ) = \overline{{i_{{\text{dp}}} }}T_{{\text{APF}}} \hfill \\ \frac{1}{2}k_2 (t_6 - t_5 )(t_7 - t_5 ) = \overline{{i_{{\text{dp}}} }}T_{{\text{APF}}} \hfill \\ \end{gathered} \right.,$$
(35)

where idp is the average current in each switch period TAPF.

According to (35), the duty factor D1 of the switching device S3 when the MMC transfers energy to the APF circuit, and the duty factor D2 of S3 when the APF circuit transfers energy to the MMC can be obtained as (36):

$$\left\{ \begin{gathered} D_1 = \sqrt {{\frac{{2L_{{\text{dp}}} v_{{\text{dp}}} \overline{{i_{{\text{dp}}} }}}}{{U_{{\text{buck}}} (U_{{\text{buck}}} - v_{{\text{dp}}} )T_{{\text{APF}}} }}}} \hfill \\ D_2 = \sqrt {{\frac{{2L_{{\text{dp}}} (U_{{\text{buck}}} - v_{{\text{dp}}} )v_{{\text{dp}}} \overline{{i_{{\text{dp}}} }}}}{{U_{{\text{buck}}} v_{{\text{dp}}} T_{{\text{APF}}} }}}} \hfill \\ \end{gathered} \right..$$
(36)

Equation (36) dictates the duty factor of the switch device S3 when there is energy interaction within the MMC and APF topology. According to the duty factor of the power device S3 in the APF, the terminal voltage of the capacitor in the APF circuit can track the reference voltage shown in (24).

4 Simulations and experimental results

4.1 Experimental results

To verify that the capacitor voltage fluctuation suppression approach is applicable to the APF-MMC topology, experimental results obtained with the APF-MMC and the conventional MMC are compared on the single-phase experimental prototype platform depicted in Fig. 3. With reference to the experimental parameters outlined in [19] and [31], Table 1 showcases the comprehensive prototype platform parameters, while Figs. 4, 5, 6, 7, 8, 9, 10, 11, and 12 present the corresponding results.

Fig. 3
figure 3

Pictures of experimental platform

Full size image
Table 1 Experimental and simulation parameters
Full size table

4.1.1 Experimental comparison at f = 10 Hz

Figure 4a illustrates the SM capacitor oscillation voltage of the conventional MMC, with a peak value of approximately 20.3 V. For comparison, when the frequency of the infused components fh = 100 Hz, the voltage ripple of the top sub-arm capacitor of the APF-MMC upper arm is 9.3 V, as displayed in Fig. 4b. In a similar fashion, Fig. 4c, d portrays the voltage magnitudes of the lower sub-arm capacitors in the APF-MMC. These values measure 9.6 V and 9.7 V, respectively. When comparing Fig. 4a with Fig. 4b–d, it becomes evident that the voltage ripple observed in the capacitor of the APF-MMC is diminished to a mere 46.8% of the corresponding ripple in conventional MMC, which is achieved through the injection application of high-frequency voltage and current.

Fig. 4
figure 4

Comparison of the SM capacitor voltage at f = 10 Hz: a traditional MMC; b top sub-arm SM of the upper arm in the APF-MMC topology; c bottom sub-arm SM of the upper arm in the APF-MMC topology; d bottom sub-arm SM of the lower arm in the APF-MMC topology

Full size image

As displayed in Fig. 5a, the maximum of the arms current in the conventional MMC topology is about 3.3 A, which is constituted of the base frequency part (at this time, f = 10 Hz). The arms current of the APF-MMC is described in Fig. 7b, and the maximum amplitude is about 9.2 A. Comparing Fig. 5a with Fig. 5b, it is evident that the growth of arms current amplitude of the APF-MMC is a result of the injection of high-frequency current, which results in additional power dissipation and current stress of the power switch devices in the SM.

Fig. 5
figure 5

Comparison of the upper and lower arm currents at f = 10 Hz: a traditional MMC topology; b APF-MMC topology

Full size image

4.1.2 Experimental comparison at f = 5 Hz

In Fig. 6a, it is illustrated that the classical MMC capacitors experience a maximum voltage fluctuation of 33.2 V. However, when high-frequency components with a frequency of fh = 100 Hz are introduced, Fig. 6b showcases the voltage fluctuations of the top sub-arm capacitor in the upper arm of the APF-MMC, with a peak ripple value of approximately 11.9 V. Similarly, Fig. 6c, d reveals the capacitor voltage of the top sub-arm in the Mid-arm and the bottom sub-arm in the lower arms of the APF-MMC, with ripple amplitudes of 12.1 V. Combining Fig. 6a–d, it can be seen that as a result of the injected components, the capacitor voltage fluctuation of the APF-MMC circuit is decreased to 36.14% of that of the traditional MMC. When compared to the base frequency of f = 10 Hz, it is observed that the APF-MMC topology with a base frequency of 5 Hz exhibits a higher rate of change in the SM voltage ripple. This observation further validates the validity of the APF-MMC in suppressing the voltage ripple of SM capacitors during low-frequency operation.

Fig. 6
figure 6

Comparison of the SM capacitor voltage at f = 5 Hz: a traditional MMC; b top sub-arm SM of the upper arm in the APF-MMC topology; c bottom sub-arm SM of the upper arm in the APF-MMC topology; d bottom sub-arm SM of the lower arm in the APF-MMC topology

Full size image

In Fig. 7a, the arm current of the classical MMC is depicted. These currents comprise the base frequency component, operating at a frequency of 5 Hz, with a maximum amplitude reaching approximately 2.88 A. Figure 7b displays arm currents of the improved topology, of which the amplitude is about 10.1 A. When comparing Fig. 7a with Fig. 7b, it becomes evident that as a result of the injected current, the maximum value of the arm current for the APF-MMC experiences a significant increase, resulting in increases of the power dissipation and current stress in the SM power switch parts. Given the brief ramp-up time of the motor, the additional power dissipation from the synchronous machine remains minimal throughout the entire operating cycle. Therefore, the impact of the elevated arm currents on the system can be disregarded. The amplitude of arm currents can be diminished by optimizing the high-frequency components in practical applications.

Fig. 7
figure 7

Comparison of the upper and lower arm currents at f = 5 Hz: a traditional MMC topology; b APF-MMC topology

Full size image

4.1.3 Output voltage and current of the APF-MMC

To ascertain the elimination of the impact of the high-frequency voltage on the external characteristics of the MMC topology, an additional APF circuit is utilized as a hardware degree of freedom. The experimental findings, depicted in Fig. 8a, b, present the external characteristics at fundamental frequencies of 5 Hz and 10 Hz, respectively. Concurrently, Fig. 9a, b showcases the respective output voltage waveforms of the APF. Notably, it can be observed that high-frequency harmonics with significant amplitudes are absent, underscoring the successful mitigation of the injected component influence on the external characteristics of the topology.

Fig. 8
figure 8

Output wave of the APF-MMC: a f = 10 Hz; b f = 5 Hz

Full size image
Fig. 9
figure 9

Output voltage of the APF circuit: a f = 10 Hz; b f = 5 Hz

Full size image

Based on the aforementioned experimental findings, it can be concluded that the APF-MMC topology, in comparison to the conventional MMC topology, exhibits a noteworthy reduction in voltage ripples across the SM capacitors. Furthermore, the injected high-frequency voltage does not influence the external output characteristics of the APF-MMC topology.

4.2 Motor drive simulation results

A simulation of a PMSM is conducted using PLECS software, since the availability of an experimental motor drive is limited. The PMSM is regulated by both an inner vector control loop and an outer speed control loop, and the d-axis current id is set to 0. Notably, the voltage level applied in motor drive applications typically does not surpass 10 kV. The motor parameter is outlined in Table 1.

Simulation waveforms for the conventional MMC from standstill (0 Hz) to 150 r/min (10 Hz) are shown in Fig. 10. It can be obtained from Fig. 10 that the traditional MMC topology has a large capacitor voltage ripple with low-frequency operation, which requires a large capacitor value to suppress the voltage ripple, which limits its application. In contrast, the APF-MMC simulation results with the introduced operation approach are displayed in Fig. 11.

Fig. 10
figure 10

Simulated run-up waveforms of a PMSM driven by the traditional MMC

Full size image
Fig. 11
figure 11

Simulated run-up waveforms of a PMSM driven by the APF-MMC

Full size image

Obviously, the SM capacitor voltage fluctuation amplitude is considerably suppressed. It can be obtained from Figs. 10 and 11 that the lower the working frequency, the better the suppression of the SM voltage fluctuation. In addition, by controlling the additional APF topology, the impact caused by the infused high-frequency voltage to the output characteristics of the MMC topology can be removed. Furthermore, due to the short start-up time of the motor, the power losses caused by the large arm current can be ignored.

To verify the transient characteristics of the APF-MMC topology with the introduced control approach, the mechanical torque of the motor is reduced from the rated torque to a light torque and then back to the rated torque. The corresponding simulation outcomes are given in Fig. 12. There is no marked over-shoot at the moment of torque switching, and the APF-MMC with the introduced control method can achieve a new stable state in a few basic cycles. In addition, it has been confirmed that the introduced APF-MMC topology with the suggested regulation approach can effectively drive the motor under low-frequency operation.

Fig. 12
figure 12

Simulated waveforms of the APF-MMC when the load changes

Full size image

5 Conclusion

This study presented an APF-MMC topology for low-frequency operation. It accomplished suppression of SM capacitor voltage ripples by incorporating two adjustable degrees of freedom for the injected high-frequency voltage and current. Additionally, the hardware degrees of freedom within the APF circuit were shown to effectively mitigate the influence of the injected high-frequency voltage on the output characteristics of the topology.

The composition and analogous representation of the APF-MMC circuit were meticulously expounded upon and minutely scrutinized. Subsequently, a control technique was proposed for the APF branch, ensuring the seamless operation of this topology. Finally, prototypes of both the APF-MMC and the conventional MMC were constructed and subjected to meticulous comparative experimentation. Furthermore, the utilization of the three-phase APF-MC for motor drive applications was assessed via a comprehensive simulation platform. Upon direct comparison with the traditional MMC, the APF-MMC circuit was shown to exhibit commendable performance, particularly in low-frequency scenarios, as substantiated by meticulous simulation and exhaustive experimental evaluations.