Finding preferential paths by numerical simulations of reactive non-darcy flow through porous media with the Lattice Boltzmann method

Abstract

Preferential flow is still an elusive phenomenon in porous media, impacting the oil industry, micro- and nanofluidic applications, and soil sciences. The Lattice Boltzmann Method (LBM) with the Pore-Scale approach is a robust mesoscopic tool for modeling flows in complex geometries, detailing velocity fields, and identifying preferred pathways. Since preferential flow has several causes, it is hard to distinguish and evaluate the different contributions to the phenomenon. However, a starting simplification assumes that geometrical features are its primary cause. In this work, we discuss some insights about preferential flow and verify the validity of a previous tortuosity-dependent resistance model in a non-Darcy regime. Initially, we demonstrate that the Pore-Scale LBM recovers the Forchheimer empirical model. Although the tortuosity model reasonably predicts many preferred pathways, the inertial contributions in the Forchheimer regime make the porous pattern, grain shape, and path deflections disturb those predictions. The simulations indicate that paths with minor flow resistances affect the neighboring flow preferences. Dead zones arise by imposing clogging conditions, and the flow field and preferred paths change. Wondering how the observed preferential routes impact the evolution of a reactive flow, a mass transport analysis was carried out to track the porosity evolution during the reactive dissolution of the solid structures. As a result, the matrix porosity increases over time, especially under diffusion- and kinetic-dominated conditions.

Introduction

Understanding fluid flow in porous media and mathematically describing its dynamics are still current challenges in research. The relevance of the problem is evidenced by a broad range of applications, from enhanced oil recovery (EOR) in the oil industry to pharmaceutical, geological, and environmental studies. In many cases, one is particularly interested in determining the preferential paths of the flow, which are defined as the higher flow rates in specific sections of the matrix, such as fractures and fingers (Nimmo 2009).

In pharmaceutical industries and farming, for instance, knowledge of the preferential flow allows for the design of microfluidic devices (Bhagat et al. 2009), and the targeted delivery of biochemicals and microbes (Wang et al. 2014; Fishkis et al. 2020). In soil sciences, preferential flow influences the aeration and contamination of soils (Kozuskanich et al. 2014; Xiao et al. 2019), the design of geological reservoirs for $\text{CO}_{2}$ sequestration (Gor et al. 2013), and also the formation of subsurface stormflow, which causes urban flooding and erosions (Dusek et al. 2012). In the oil industry, when preferential paths are considered, the reservoir oil displacement can be optimized, e.g., through micro- and nanoparticle control in EOR (Donath et al. 2019). Additionally, the loss of drilling fluid as a result of fracture formation during drilling operations can be perhaps prevented, since those fractures deflect the flow to preferential paths through the rocks (Calçada et al. 2015). Hence, an improved understanding of the preferential flow dynamics could have a positive impact on diverse sets of problems.

Preferential flows have several causes, including (i) topological features [e.g., presence of macropores (Guo et al. 2019) and differences in pore configurations (Clothier et al. 2008)], (ii) physical and chemical properties of the fluid and solid phases along with their interactions (e.g., capillarity, surface tension, and spatial variability of matrix properties (Dusek et al. 2012)), and (iii) flow dynamics [e.g., unstable wetting front (Parlange and Hill 1976)]. Because of the complexity of the problem, researchers have usually investigated each separate contribution to establish their relative importance.

Regarding the influence of topology, some authors have identified critical geometry factors for better predictions of the preferential flow, like tortuosity (Viberti et al. 2020), channel size, and pore-to-pore alignment (Yeates et al. 2020). Ju et al. (2018) proposed and validated a tortuosity-dependent model derived from Darcy’s law to predict preferential trajectories in porous media. However, the geometry features have been mostly restricted to creeping flows with extremely low Reynolds numbers [i.e., the flow rate is a relevant factor (Liu et al. 2019a)]. Since the preferential flow depends on several aspects, the current literature still lacks a unifying or generalized theory to determine it (Weiler 2017; Fan et al. 2022).

Some studies experimentally evaluate the preferential paths through tracer tests (Yao et al. 2017) or measurements of isotope signatures (Ma et al. 2017). However, experimental investigation of preferential flows is often problematic because it causes clogging and interferes with the flow patterns (Parvan et al. 2020), decreasing permeability (Liu et al. 2019b) and changing the outlet pressure (Shen and Ni 2017). Hence, a helpful alternative is the use of theoretical modeling and simulation.

Depending on the length scale, there are two major modeling approaches for porous media flow: the Representative Element Volume (REV) (Zhang et al. 2000) and the Pore-Scale (Blunt et al. 2013) approaches. Macroscopic properties, such as permeability, and continuum models using standard computational fluid dynamic tools characterize the REV simulations. On the other hand, in Pore-Scale simulations, the proper matrix is treated with connections and discrete models at a microscopic level (Sharma et al. 2019). REV is easy to implement but uses semi-empirical models (e.g., drag forces), oversimplifies the descriptions, and fails to provide crucial clues for preferential flow determination, such as the local information about the flow. Pore-Scale is precise and detailed, but it is also computationally expensive (He et al. 2019; Sharma et al. 2019).

A promising and recent approach in computational fluid dynamics is the Lattice Boltzmann Method (LBM), a kinetic-based numerical tool developed from the Lattice Gas Automata (Higuera et al. 1989). The LBM can model a variety of engineering problems (Sharma et al. 2020). Rothman (1988) presented one of the first works about LBM in porous media flow. Since then, several works applying LBM have appeared in the literature investigating, for instance, the effects of pore configuration in the flow (Sharma et al. 2018; Ju et al. 2020), multiphase flows (Kashyap and Dass 2018; Lourenço et al. 2022), and so on (Sharma et al. 2019). REV-LBM, the most popular approach, represents the porous media through a resistance field model (He et al. 2019). One successful example is the Guo-Zhao model, which proposed adding the porosity and a forcing term in the LB methodology (Guo and Zhao 2002). Nevertheless, it still relies on macroscopic empirical models, unsuitable for the preferential flow determination problem.

In this context, the Pore-Scale LBM emerges as a powerful and computationally efficient method to model flows through porous media (He et al. 2019). This method implements the no-slip boundary condition without necessarily using mesh refinement and it is easily extended to complex geometries (Sharma et al. 2019). Hence, in this work, we use the Pore-Scale LBM simulations to investigate the geometry and topological effects of a bidimensional matrix on the preferential flow configuration. We initially detail the theoretical background, such as the governing equations for porous media flow and the LBM approach. Next, we present the methodology used, including the initialization process and parameter adjustments. Finally, we discuss the results observed from simulations and summarize the main contributions of this work.

Theoretical background

Here we present an overview of the mathematical modeling behind the simulations in this paper. The first sections characterize fluid flow in porous media by enumerating the main physical properties and governing equations, respectively. Then, the LBM concepts are introduced and lattice equations for fluid flow and mass transport are presented for a bidimensional domain. Next, we explain how heterogeneous reactions are included in this work and discuss the evolution of the porous structures over time due to reaction degradation. Finally, we close the theoretical background with important aspects of boundary conditions.

Physical properties

The most relevant physical properties used to characterize porous media are permeability, porosity, and tortuosity. The permeability $K$ measures how easy it is for any fluid to percolate the porous pattern independent of its properties. It is generally associated with the fraction of empty space in the matrix, i.e., the porosity or voidage. Among different types of porosity, we can identify the overall porosity ($\phi$) as the ratio between the void (${V}_{v}$) and bulk volumes (${V}_{b}$) of the porous media (Guo 2019),

$$\phi =\frac{{V}_{v}}{{V}_{b}} .$$

(1)

Although permeability and porosity are related to flow magnitude, in this work, we consider tortuosity ($\tau$) as the most crucial matrix property to predict preferential flow. It measures how sinuous the trajectories are inside a porous medium, and it can be defined as $\tau ={L}_{e}/L$, where ${L}_{e}$ is the sinuous length through the porous structures, and $L$ is the linear distance from inlet to outlet of the media (Clennell 1997). The relevance of this geometrical parameter for preferential flow will become clearer in the following section.

Additionally, the most relevant parameter to characterize fluid flow is the Reynolds number ($Re$). This dimensionless parameter is often used to identify the flow regime by recognizing the balance of inertial and viscous forces. Especially for porous media flow, $Re$ can be defined using the Blunt diameter as the characteristic length (${l}_{c}$),

$$Re=\frac{\rho \left|\varvec{u}\right|{l}_{c}}{\mu } ,$$

(2)

$${l}_{c}=\frac{\pi {V}_{b}}{{A}_{w}} ,$$

(3)

where $\mu$ is the shear viscosity, $\varvec{u}$ is the macroscopic velocity, $\rho$ is the macroscopic density, ${V}_{b}$ is the total volume of the porous media, and ${A}_{w}$ is the wetted surface (Blunt 2017; Viberti et al. 2020).

Governing equations in porous media

In systems described by small $Re$, i.e., Stokes or creeping flows ($Re<25$), only viscous forces control the flow (Mckibbin 1998). In this case, the velocity is directly proportional to the pressure drop but inversely proportional to the matrix length, as suggested by Darcy’s law,

$$\nabla p=-\frac{\mu }{K}\varvec{u} .$$

(4)

The integral form of Eq. (4), which is the simplest equation for modeling one-phase flow in porous media, makes the dependence of the velocity flow on pressure $p$ and porous media length ${L}_{PM}$ even more evident,

$$\left|\varvec{u}\right|=\frac{K}{\mu }\frac{\delta p}{{L}_{PM}} .$$

(5)

Because the velocity must be inversely proportional to the flow resistance $G$, we can define $G=\mu {L}_{PM}/K$ (Ju et al. 2018). Given, however, that the permeability of the matrix is usually a function of tortuosity (Clennell 1997; Guo 2012), the flow resistance through a uniform cross-sectional area can be written as

$$G=\mathbb{C}\mu {L}_{PM}{{\uptau }}^{2} ,$$

(6)

where $\mathbb{C}$ is a constant related to the chosen permeability model. Here, we identify Eq. (6) as the Ju et al. model since it is similar to Darcy’s flow resistance equation derived in their work (Ju et al. 2018). When modeling a specified fluid through settled porous structures, the fluid and matrix properties are fixed. Consequently, the flow resistance is only dependent on the tortuosity. In these conditions, small tortuosities (i.e., small flow resistances) indicate the preferential paths of the porous medium.

As the flow rate increases, the inertial forces become stronger and the application of Darcy’s law at the so-called inertial regime ($25<Re<375$) becomes unfeasible. For systems with larger $Re$, the Forchheimer equation is a semi-empirical model that seeks to describe the further complexity of the porous media flow. Hence, the resistance in this model admits contributions from both viscous forces (first term) and inertial forces (second term) (Mckibbin 1998),

$$-\nabla p=\frac{\mu }{K}\left(1+\frac{\beta \rho K}{\mu }\left|\varvec{u}\right|\right)\varvec{u} ,$$

(7)

where $\beta$ is a constant which, despite some model proposals to predict it (Takhanov 2011), is easily obtained experimentally (Iriarte et al. 2018).

The Forchheimer equation successfully recovers Darcy’s law for small $Re$ when the second term is much smaller than the first term, i.e., when $\beta \rho K\left|\varvec{u}\right|/\mu \ll 1$. Thus, it is convenient to give a proper name to this dimensionless term: the permeability Reynolds number $R{e}_{K}=\beta \rho K\left|\varvec{u}\right|/\mu$. Hence, when $R{e}_{K}\ll 1$, the inertial contributions become unimportant and the Forchheimer equation reduces to Darcy’s law (Mckibbin 1998; Dukhin and Goetz 2009).

Again, to inspect the dependence of velocity on the pressure gradient, the Forchheimer equation can be rewritten in more attractive form by defining the apparent permeability ${K}_{app}=-\mu \left|\varvec{u}\right|/|\nabla p|$ (Huang and Ayoub 2008),

$$\frac{1}{{K}_{app}}=\frac{1}{K}+\frac{\beta \rho \left|\varvec{u}\right|}{\mu } ,$$

(8)

which provides a linear relationship between the velocity $\varvec{u}$ and $1/{K}_{app}$ (Iriarte et al. 2018).

Lattice Boltzmann method (LBM)

The LBM is a mesoscopic approach, where we consider a statistical description of the particles in the system. LBM uses the density distribution function $f(\mathbf{x},\mathbf{v},t)$ to track the distributions of molecules, which describes the probability of finding a particle with velocity $\mathbf{v}$ at an infinitesimal space and time interval around $\mathbf{x}$ and $t$. In the absence of an external force field, the advection of $f(\mathbf{x},\mathbf{v},t)$ is governed by the simplified Boltzmann Transport Equation (BTE),

$$\left[{\partial }_{t}+\mathbf{v}\cdot {\nabla }_{\mathbf{x}}\right]f\left(\mathbf{x},\mathbf{v},t\right) ={\Omega }\left(f\right) ,$$

(9)

where ${\Omega }$ is the collision operator, which describes the complex dynamical interactions during particle collisions. The linear model known as the Bhatnagar-Gross-Krook (BGK) operator is broadly used in the LBM literature because of its simplicity (Bhatnagar et al. 1954). Alternatively, more robust collision schemes can be implemented, such as the Multiple-Relaxation-Time (MRT) model proposed by d’Humières (1992). Here, we implement the MRT model for fluid flow to ensure viscosity-independent permeabilities (Pan et al. 2006) and use the BGK model for mass transport to save computational time.

LBM for fluid flow

The insertion of the MRT model into the BTE discretized in space ($\mathbf{x}$), velocity (${\mathbf{e}}_{{\upalpha }}$), and time ($t$) originates the LB-MRT equation for each discrete lattice direction ${\mathbf{e}}_{{\upalpha }}$,

$${f}_{{\upalpha }}\left(\mathbf{x}+{\mathbf{e}}_{{\upalpha }}\delta t,t+\delta t\right)- {f}_{{\upalpha }}\left(\mathbf{x},t\right)=-{\mathbf{M}}^{-1}\varvec{\Lambda }\mathbf{M}\left[{f}_{{\upalpha }}\left(\mathbf{x},t\right)-{f}_{{\upalpha }}^{eq}\left(\mathbf{x},t\right)\right]\delta t ,$$

(10)

which, after Chapman-Enskog expansion, recovers both the Navier-Stokes and the continuity equations without external forces. We note that $\alpha$ is the index of the direction ${\mathbf{e}}_{{\upalpha }}$ and $\delta t$ is the time interval that arises after discretization.

The purpose of $\mathbf{M}$ is to map ${f}_{{\upalpha }}$ from the population space into the moment space by a similarity transformation. These moments (averages) are the statistical descriptors of the particle distribution. The collisions are then executed in the moment space. The matrix $\mathbf{M}$ expressed in Eq. (11) was calculated by implementing the orthogonal-based Gram-Schmidt approach to satisfy the hydrodynamic moments. The main difference to the BGK operator is that the moments can be individually relaxed. Afterward, they can be mapped back onto the population space by computing the inverse transformation ${\mathbf{M}}^{-1}$.

Therefore, $\mathbf{M}$ and $\varvec{\Lambda }$ are, respectively, the transformation and relaxation matrices,

$$\mathbf{M}=\left[\begin{array}{ccccccccc}1& 1& 1& 1& 1& 1& 1& 1& 1\\ -4& -1& -1& -1& -1& 2& 2& 2& 2\\ 4& -2& -2& -2& -2& 1& 1& 1& 1\\ 0& 1& 0& -1& 0& 1& -1& -1& 1\\ 0& -2& 0& 2& 0& 1& -1& -1& 1\\ 0& 0& 1& 0& -1& 1& 1& -1& -1\\ 0& 0& -2& 0& 2& 1& 1& -1& -1\\ 0& 1& -1& 1& -1& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 1& -1& 1& -1\end{array}\right] ,$$

(11)

$$\varvec{\Lambda }=diag\left({\omega }_{\rho },{\omega }_{e},{\omega }_{\upepsilon},{\omega }_{j},{\omega }_{q},{\omega }_{j},{\omega }_{q},{\omega }_{\nu },{\omega }_{\nu }\right) ,$$

(12)

where $\omega$ is the relaxation rate ($\omega \equiv 1/\tau$), $\tau$ is the relaxation time, ${\omega }_{\rho }$ and ${\omega }_{j}$ are the relaxation rates for the conserved moments (i.e., density and momentum), ${\omega }_{\upepsilon}$ and ${\omega }_{q}$ are free parameters adjusted to keep the method stable, ${\omega }_{e}$ is related to the bulk viscosity (or dilatational viscosity) $\kappa$, and ${\omega }_{\nu }$ is related to the shear viscosity $\mu$ (D’Humierès 1992; Jiang et al. 2022),

$$\kappa =\rho {c}_{s}^{2}\left(\frac{1}{{\omega }_{e}}-\frac{\delta t}{2}\right)-\frac{\mu }{3} ,$$

(13)

$$\mu =\rho {c}_{s}^{2}\left(\frac{1}{{\omega }_{\nu }}-\frac{\delta t }{2}\right) ,$$

(14)

where ${c}_{s}$ is the speed of sound.

The matrix $\mathbf{M}$ also transforms the equilibrium distribution function ${f}_{{\upalpha }}^{eq}$, represented by the Maxwell-Boltzmann distribution function,

$${f}_{{\upalpha }}^{eq}\left(\mathbf{x},t\right)={\omega }_{{\upalpha }} \rho \left[1+\frac{{\mathbf{e}}_{{\upalpha }} . \mathbf{u}}{{c}_{s}^{2}}+\frac{{\left({\mathbf{e}}_{{\upalpha }} . \mathbf{u}\right)}^{2}}{{2c}_{s}^{4}}-\frac{{\mathbf{u}}^{2}}{2{c}_{s}^{2} }\right] ,$$

(15)

into the moment space. Note that ${\omega }_{{\upalpha }}$ are the weights specified for each different lattice model after expressing the equilibrium distribution as a Hermite polynomial. For the D2Q9 model (a bidimensional model with nine discrete velocities), ${c}_{s}^{2}=\frac{1}{3}{\left(\frac{\delta x}{\delta t}\right)}^{2}$ and the weights are

$$\omega _{\alpha } = \left\{ {\begin{array}{*{20}c} {4/9} & {\alpha = 1} \\ {1/9} & {\alpha = 1,\;2,\;3,\;4} \\ {1/36} & {\alpha = 5,\;6,\;7,\;8} \\ \end{array} ,} \right.$$

(16)

in which the discrete velocities are

$$\left\{\left(\begin{array}{c}{{\text{e}}_{0}}_{\text{x}}\\ {{\text{e}}_{0}}_{\text{y}}\end{array}\right),\dots ,\left(\begin{array}{c}{{\text{e}}_{8}}_{\text{x}}\\ {{\text{e}}_{8}}_{\text{y}}\end{array}\right)\right\}=\left\{\left(\begin{array}{c}0\\ 0\end{array}\right), \left(\begin{array}{c}1\\ 0\end{array}\right), \left(\begin{array}{c}0\\ 1\end{array}\right),\left(\begin{array}{c}-1\\ 0\end{array}\right),\left(\begin{array}{c}0\\ -1\end{array}\right),\left(\begin{array}{c}1\\ 1\end{array}\right),\left(\begin{array}{c}-1\\ 1\end{array}\right),\left(\begin{array}{c}-1\\ -1\end{array}\right),\left(\begin{array}{c}1\\ -1\end{array}\right)\right\}\left(\frac{\delta x}{\delta t}\right) .$$

(17)

Finally, the macroscopic density and flow velocity are recovered as the first moments of the density distribution function,

$$\rho \left(\mathbf{x},t\right)=\sum _{\alpha }{f}_{\alpha }\left(\mathbf{x},t\right) ,$$

(18)

$$\mathbf{u}\left(\mathbf{x},t\right)=\frac{1}{\rho }\sum _{\alpha }{f}_{\alpha }\left(\mathbf{x},t\right){\mathbf{e}}_{{\upalpha }} .$$

(19)

LBM for mass transport

The BTE can also be implemented to solve the mass transport with the BGK collision scheme. Thus, the LB-BGK equation for each discrete lattice direction ${\mathbf{e}}_{{\upalpha }}$ is

$${g}_{{\upalpha }}\left(\mathbf{x}+{\mathbf{e}}_{{\upalpha }}\delta t,t+\delta t\right)- {g}_{{\upalpha }}\left(\mathbf{x},t\right)=-\frac{\delta t}{{\tau }_{g}}\left[{g}_{{\upalpha }}\left(\mathbf{x},t\right)-{g}_{{\upalpha }}^{eq}\left(\mathbf{x},t\right)\right] ,$$

(20)

where ${g}_{\alpha }$ is the concentration distribution function, and ${\tau }_{g}$ is the relaxation time. Because the macroscopic convection-diffusion equation is linear in velocity, the equilibrium distribution function ${g}_{{\upalpha }}^{eq}\left(\mathbf{x},t\right)$ can be written in simpler form compared to Eq. (15):

$${g}_{{\upalpha }}^{eq}\left(\mathbf{x},t\right)=C\left(\mathbf{x},t\right)\left[{J}_{\alpha }+\frac{{\mathbf{e}}_{{\upalpha }} . \mathbf{u}\left(\mathbf{x},t\right)}{2}\right] .$$

(21)

Hence, after Chapman-Enskog expansion, Eqs. (20) and (21) recover the macroscopic convection-diffusion equation with Fick’s law. It is worth noting that source terms (e.g., homogeneous reactions) are neglected in this analysis. The concentration field $C\left(\mathbf{x},t\right)$ is obtained from the zeroth-moment:

$$C\left(\mathbf{x},t\right)=\sum _{\alpha }{g}_{\alpha }\left(\mathbf{x},t\right) .$$

(22)

Unlike for the fluid flow methodology, the D2Q5 model is considered here to discretize the spatial domain, in which only the discrete velocities in the range [${\mathbf{e}}_{0},\dots ,{\mathbf{e}}_{4}$] are used. In this case, the rest fraction ${J}_{\alpha }$ is chosen as

$$J_{\alpha } = \left\{ {\begin{array}{*{20}c} {J_{0} ,} & {\alpha = 0} \\ {{{\left( {1 - J_{0} } \right)} \mathord{\left/ {\vphantom {{\left( {1 - J_{0} } \right)} {4,}}} \right. \kern-\nulldelimiterspace} {4,}}} & {\alpha = 1,\;2,\;3,\;4} \\ \end{array} } \right.$$

(23)

where ${J}_{0}$ ($0\le {J}_{0}\le 1$) is either given or obtained from a known diffusion coefficient $\mathcal{D}$ calculated by the formula

$$\mathcal{D}=\frac{\left(1-{J}_{0}\right)}{2}\left({\tau }_{g}-\frac{1}{2}\right)\frac{{\left(\delta x\right)}^{2}}{\delta t} .$$

(24)

For advection-diffusion problems, the Péclet dimensionless number ($Pe$) determines if the system is primarily controlled by advection ($Pe\gg 1$) or diffusion ($Pe\ll 1$), where

$$Pe=\frac{{u}_{x}{l}_{c}}{\mathcal{D}} .$$

(25)

Heterogeneous reactions

Heterogeneous reactions can be implemented to evaluate the effect and significance of preferential paths. Here, the degradation of the solid porous structures is modeled by a first-order reaction,

$$Pm_{{\left( s \right)}} + Rc_{{\left( {aq} \right)}} \xrightarrow{{k_{r} }}Pd_{{\left( {aq} \right)}} ,$$

(26)

where $Pm$ represents the chemical component in the porous matrix (solid phase), $Rc$ and $Pd$ represent the reactant and the product soluble in the fluid phase, respectively, and ${k}_{r}$ is the forward reaction rate constant. The arbitrary components in Eq. (26) can represent, for instance, an acid attack in carbonate rocks. Based on Eq. (26), the elementary rate of reactant consumption is

$$r=-{k}_{r}\left[Rc\right] ,$$

(27)

where the concentration of the reactant $\left[Rc\right]$ at each time and position is computed from the mass transport.

Additionally, the dimensionless parameter known as Damköhler number ($Da$) can be used to distinguish between heterogeneous reactions controlled by kinetic ($Da\gg 1$) or diffusion ($Da\ll 1$) rates, since

$$Da=\frac{{k}_{r}{l}_{c}^{2}}{\mathcal{D}} .$$

(28)

Volume of pixel (VOP)

The Volume of Pixel (VOP) method can be used to track the evolution of the solid phase when heterogeneous reactions take place. In this method, the degradation rate of the solid phase is (Kang et al. 2006)

$$\frac{\partial {V}_{s}\left(\mathbf{x}\right)}{\partial t}=A{V}_{m}r ,$$

(29)

where ${V}_{s}\left(\mathbf{x}\right)$ is the solid volume at the node $\mathbf{x}$, $A$ is the area of the solid-liquid interface, and ${V}_{m}$ is the solid molar volume. After first-order time discretization, the volume at the time step $t+\delta t$ is calculated by

$${V}_{s}\left(\mathbf{x},t+\delta t\right)={V}_{s}\left(t\right)+A{V}_{m}r\delta t .$$

(30)

${V}_{s}\left(\mathbf{x},t=0\right)$ is initialized with a constant value ${{V}_{s}}_{0}$. Adjusting the time and space intervals ($\delta t$ and $\delta x$) to be the same as used in the LB simulations, the volume of the solid gradually decreases according to Eq. (30), since $r<0$. When it locally reaches ${V}_{s}\left(\mathbf{x},t+\delta t\right)=0$, the node is updated as a fluid node and, consequently, the fluid properties must be set. In this work, density and concentration are initialized to average values from neighboring fluid nodes; velocities are initialized to zero since the node is near to the stationary solid phase (no-slip condition); and the distribution functions are initialized to their equilibrium values.

Boundary conditions

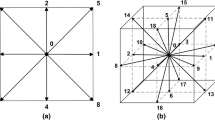
Figure 1 presents an illustration of the system simulated in this work, where the inlet ($x=0$) and the outlet ($x=2{L}_{PM}$) are open boundaries. Considering that the isothermal equation of state that emerges from the LB approach is $p\left(\mathbf{x}\right)=\rho \left(\mathbf{x}\right){c}_{s}^{2}$, a pressure drop $\delta p$ was imposed to ensure fluid flow:

Fig. 1

Simulated domain with artificial porous media. White and black areas represent, respectively, fluid and grain regions, while ${\text{L}}_{\text{PM}}$ is the length of the porous medium

$$\delta p=\left[\rho \left(x=0\right)-\rho \left(x=2{L}_{PM}\right)\right]{c}_{s}^{2}={c}_{s}^{2}\delta \rho .$$

(31)

By setting an average density $\langle{\rho }\rangle$ inside the domain, the macroscopic densities are specified on the open boundaries:

$$\rho \left(x=0\right)=\langle{\rho }\rangle+0.5\delta \rho ,$$

(32)

$$\rho \left(x=2{L}_{PM}\right)=\langle{\rho }\rangle-0.5\delta \rho .$$

(33)

A periodic condition ${f}_{{\upalpha }}^{neq}\left(x=0,y,t\right)={f}_{{\upalpha }}^{neq}\left(\text{x}=2{L}_{PM},y,t\right)$, where ${f}_{{\upalpha }}^{neq}={f}_{{\upalpha }}-{f}_{{\upalpha }}^{eq}$ is the non-equilibrium distribution function, is set at the open boundaries. This type of boundary condition guarantees that the information (e.g., momentum) exiting from one side of the domain enters the opposite side. Thus, the periodic condition with pressure variation (Kim and Pitsch 2007) is

$${f}_{{\upalpha }}\left(x=0,y,t\right)=\,{f}_{{\upalpha }}^{eq}\left[\rho \left(x=0,{y}_{{\upalpha }},t\right),\mathbf{u}\left(x=2{L}_{PM},{y}_{{\upalpha }},t\right)\right]+{f}_{{\upalpha }}\left(\text{x}=2{L}_{PM},{y}_{{\upalpha }},t\right)-{f}_{{\upalpha }}^{eq}\left(\text{x}=2{L}_{PM},{y}_{{\upalpha }},t\right) ,$$

(34)

$${f}_{{\upalpha }}\left(\text{x}=2{L}_{PM},y,t\right)=\,{f}_{{\upalpha }}^{eq}\left[\rho \left(x=2{L}_{PM},{y}_{{\upalpha }},t\right),\mathbf{u}\left(x=0,{y}_{{\upalpha }},t\right)\right]+{f}_{{\upalpha }}\left(x=0,{y}_{{\upalpha }},t\right)-{f}_{{\upalpha }}^{eq}\left(x=0,{y}_{{\upalpha }},t\right) ,$$

(35)

where ${y}_{{\upalpha }}=y+{{\text{e}}_{{\upalpha }}}_{y}\delta t.$

The halfway bounce-back scheme (Ladd 1994) was adopted to model the solid boundary conditions for fluid flow and mass transport (for non-reactive solids) because it yields exact mass conservation and second-order accuracy. Kang’s scheme (Kang et al. 2007) is implemented for reactive boundaries, through which the distribution function ${g}_{\alpha }({\mathbf{x}}_{\mathbf{s}},t)$ coming into the fluid domain is calculated by

$${g}_{\alpha }\left({\mathbf{x}}_{\mathbf{s}},t\right)-{g}_{\stackrel{-}{\alpha }}\left({\mathbf{x}}_{\mathbf{s}},t\right)=-\mathcal{D}\frac{\partial C}{\partial {x}_{\alpha }} ,$$

(36)

where $\stackrel{-}{\alpha }$ is the opposite orientation of $\alpha$.

Finally, it is assumed that the mass flux at the liquid-solid interface equals the rate of generated species from the chemical reaction. This boundary condition can be written as

$$\mathcal{D}\frac{\partial C}{\partial {x}_{\alpha }}=r\delta {x}_{\alpha } .$$

(37)

Methodology

For reader’s convenience, we describe the setup of the numerical simulations step by step in the following separate sections. The algorithm was developed in-house in C + + language and implemented for serial processing. The hardware is an Intel processor (11th Gen Intel® Core(TM) i7-11700 @ 2.50 GHz) and 16 GB of memory (RAM DDR4). The computational time for the slowest reactive case ($Pe=10.0$ and $Da=1.0$) was 92 min.

Porous media construction

We consider an artificial square computational domain filled with a porous medium of length ${L}_{PM}=1 \text{m}\text{m}$, as shown in Fig. 1. Aiming to work with irregular paths and sudden flow changes, we intentionally generated the porous structure from a freehand sketch and converted it into a bidimensional array identifying fluid and solid nodes. This matrix was then filtered for fluid nodes that could cause unstable LB simulations, such as fluid nodes surrounded by solids. The final lattice resolution after processing was $366 \times 366$.

Preferential paths in a single-component fluid flow

Water at $25^\circ C$ ($\rho =0.997 \text{g}/\text{c}\text{m}^{2}$, $\mu =0.890 \text{c}\text{P}$, and $\kappa =2.4 \text{c}\text{P}$ (Dukhin and Goetz 2009)) was initialized as a stationary fluid. The single-component flow was ensured by ten different settings of the pressure drop equivalent to varying heights of the water column $H=[2 \text{m},20 \text{m}]$ by $2 \text{m}$ increments. We highlight that the LBM algorithm is solved by considering its proper units (lattice units) rather than the physical ones. Therefore, the D2Q9-LBM was implemented with the common choice of $\delta x=1$ and $\delta t=1$, and $\langle{\rho }\rangle=$ 1 in order to adopt the periodic condition with pressure variation. Solid-fluid interaction forces were neglected. Parameters related to the conserved moments were set as unity while the remaining parameters were set to keep the method stable (${\tau }_{\nu }=0.513$, ${\tau }_{\upepsilon}=0.7$, and ${\tau }_{q}=0.6$). We implemented the flow dynamics for both the orientation displayed in Fig. 1 as well as the opposite direction. The simulations were interrupted when the velocity field inside the porous media reached stationary state with an absolute error of less than ${10}^{-5}$.

Given that fluid properties are assumed to be constant, and the minimum areas of each channel are considered similar, only the tortuosity governs the preferential path. Therefore, the preferential paths are first theoretically predicted by Eq. (6) (Ju et al.’s model), in which the smallest resistance $G$ (i.e., smallest ${\tau }^{2}$) reveals the preferred routes (the reader can find more details in the supplementary material). Since the preferential paths coincide with the channels that develop the highest flow velocities (Liu et al. 2019a), we could also measure the main paths from simulations by evaluating the velocity field and, consequently, compare the initial predictions with the simulation results. Lastly, Fig. 2 enumerates some pores and outlets for identification.

Fig. 2

Identification of pores, channels, inlets, outlets, and regions in the considered porous media that supports discussion. The complete numbering can be found in the supplementary material

Preferential paths with reactive-mass transport

At this moment, we are interested in discussing how preferred routes inside a porous matrix can impact the evolution of a reactive flow. As a result, after identifying the preferential paths using the previous methodology, the mass transport analysis was carried out to track the porosity evolution in different sections of the porous matrix. For this purpose, the matrix was virtually subdivided into three regions (regions 1, 2, and 3), as identified in Fig. 2. However, we must normalize the porosity in each region first to further compare its evolution over time. The normalized overall porosity $\bar{\phi }\left(t\right)$ at time $t$ and in a given region is

$$\bar{\phi }\left(t\right)=\frac{\phi \left(t\right)}{{\phi }_{0}} ,$$

(38)

where ${\phi }_{0}$ is the initial overall porosity at that region.

Based on Eq. (38), the normalized porosity is limited to the range $1\le \bar{\phi }\left(t\right)\le {\bar{\phi }}_{max}=1/{\phi }_{0}$. Then, by imposing a new definition to standardize the range, we obtain

$${\upeta }\left(t\right)=\frac{\bar{\phi }\left(t\right)-1}{{\bar{\phi }}_{max}-1} ,$$

(39)

where we call ${\upeta }\left(t\right)$ the rescaled normalized porosity, which is limited to the range $0\le {\upeta }\left(t\right)\le 1$.

Similarly, to facilitate the comparison between the regions for the given flow conditions, we define a rescaled time ${t}_{R}$,

$${t}_{R}=\frac{t-{t}_{0}}{{t}_{f}-{t}_{0}} ,$$

(40)

where ${t}_{0}$ and ${t}_{f}$ are the beginning and final reference times, and ${t}_{R}$ is limited to the range $0\le {t}_{R}\le 1$. Consequently, we can write that ${\upeta }={\upeta }\left({t}_{R}\right)$.

The evolution of ${\upeta }\left({t}_{R}\right)$ is tracked for each flow and reactive condition, specified by varying the Péclet and Damköhler numbers. The D2Q5-LBM was implemented for mass transport with $\delta x=1$ and $\delta t=1$. The inlet concentration is set as $C=1$, the relaxation time as ${\tau }_{g}=1$ and, based on a previous work (Zhang et al. 2019), the molar volume of the solid is set as ${V}_{m}=1.303 \times 10^{-4}$ m³/mol, and ${{V}_{s}}_{0}={V}_{m}$. The D2Q9-LBM is implemented with a height of water column equal to $H=4$ m ($Re=92.4$). The diffusion coefficient and reaction constant are calculated by Eqs. (25) and (28) for a given $Pe$ and $Da$. Then, ${J}_{0}$ is obtained from Eq. (24).

At $t=0$, only at the inlet is there reactant. The chemical reaction displayed in Eq. (26) only starts when the reactant reaches the matrix due to its advection and diffusion. This interval of time without reaction is sufficient for the velocity and density profiles inside the porous media achieving the stationary state.

Results and discussion

Preferential paths in a single-component fluid flow

This section discusses the preferential paths that emerge with a single-component fluid flow. First, we consider the original porous matrix for the analysis; then, we add some structural modifications.

Flow in the original porous media

The ten different heights considered here generated flows within a Reynolds range of $Re=\left[55.4, 274.2\right]$. Initially, to demonstrate the LBM potential with the Pore-Scale approach and achieve the matrix permeability, we plotted the relationship between the inverse of the apparent permeability (${K}_{app}$) and the average velocity in Fig. 3. A linear regression of the data shows that the method recovers the linearized Forchheimer equation ($1/{K}_{app}=\left(0.72 u+1.37\right)\times {10}^{10}$) with a permeability of $K=0.76 {\dot{A}}^{2}$ and strong correlation (${R}^{2}=0.998$). Additionally, the Blunt diameter and the overall porosity are ${l}_{c}=$ 0.08 mm and $\phi =$ 0.45, respectively.

Fig. 3

Linear regression of the calculated points (circles) with the linearized Forchheimer equation (dashed line): $\frac{1}{{K}_{app}}=\left(0.72u+1.37\right)\times {10}^{10}$ with ${R}^{2}=0.998$

After establishing the physical properties and flow characteristics, this section will focus on a sample case at $H=10 \text{m}$ with $R{e}_{K}=1.11 \sim 1$, which suggests that the inertial forces contribute to describing the flows in our simulations (Forchheimer regime). Figure 4a presents the velocity profile considering the flow from left to right, while Fig. 4b shows the flow in the opposite direction. Both velocity profiles confirm that most paths agree with the theoretical predictions and, in agreement with Ju et al.’s model, suggest that the main preferential paths may be independent of the flow orientation.

Fig. 4

Velocity field of the flow simulation for H = 10 m in the original porous media. In case (a) the flow is from left to right, and in case (b) is the opposite. The circles evidence some channels with their flow preference altered after changing the flow orientation

This observation, however, becomes locally distorted and is exemplified, for instance, by the flow around pores 2 and 3. The velocity magnitudes in Fig. 4a are equivalent in pores 2 and 3. This happens because the flow from inlet 9 splits into two paths, in which one of them influences the flow coming from inlet 1 and directs it to pore 2. On the other hand, Fig. 4b indicates that pore 2 is favored in the path A-1 since the grain shape and channel orientation are favorable to the flow direction. In both situations, Ju et al.’s model is incapable of discerning which pore (2 or 3) is preferred. Hence, in the Forchheimer regime, the inertial effects propagated due to sudden flow changes and geometry shapes locally influence the preferred pore.

A controlled flow configuration, sketched in Fig. 5a, is simulated to illustrate this discussion and investigate the importance of the local shape. The artificial pore region has a solid triangle with length $L=100$ lattice nodes at the center. The two dashed rectangles in Fig. 5b indicate regions with the same lattice area $3 L/5$, through which the fluid must stream. At those regions, the velocity magnitudes can be compared. Although Ju et al.’s model predicts that the path under the triangle (${\tau }^{2}=1.13$) is favored rather than the path above it (${\tau }^{2}=1.28$), Fig. 5b shows that the velocities are higher in the dashed rectangle at the top. Thus, the route above the triangle is favored.

Fig. 5

Flow simulation through a rectangular pore with a triangle with length L in the center. The sketch is presented in a, where the solid (—) and dashed (– –) lines are the shortest paths passing under and above the triangle, respectively. The flow is presented in b, where the white rectangles specify the two regions with the same area

Therefore, both the pore configuration and its orientation relative to the velocity field are crucial to determining which path will be chosen. Additionally, some small recirculation zones can emerge in the pore due to entrainment, jet effects, and transitional regimes, affecting the preferential paths. These drawbacks make Ju et al.’s model unviable to predict the preferential flow in the Forchheimer regime accurately, but it is sufficient to discern the main possible trajectories. As additional examples, some channels preferred in Fig. 4a (circled regions) are not preferred in Fig. 4b after only changing the flow orientation.

Flow with clogging

In the last section, Fig. 4a shows that some global preferential paths arise in the matrix, such as paths 1-A in region 1 and 59-G/H in region 3, since they locally present small flow resistances. In region 2, although some preferred channels agree with the theoretical prediction, it is difficult to identify one global preferential path. Instead, the flow is divided into several channels with representative velocity magnitudes. The outlet E, however, is a significant outlet for this region.

Wondering how clogging might affect the preferential paths, we blocked some pores, channels, or outlets and performed flow simulations with these modified porous matrices. Four main observations from these simulations are: (i) paths with minor flow resistance influence the flow preferences; (ii) many routes have their flow locally changed when an obstruction happens; (iii) some pores, channels, or outlets can lose their applicability after clogging; and (iv) dead zones can arise near an obstructed region.

Figure 6 presents some velocity fields that illustrate these observations. Firstly, Fig. 6a shows that the velocity magnitudes in route 22-B/C increases when outlet A is blocked. This is expected because the fluid must find an alternative route if the original path is blocked. However, what is remarkable here is that the paths with minor flow resistance in the original matrix significantly impact the preferred route, a condition that can be altered with clogging. Secondly, Fig. 6b illustrates what is affirmed in (ii) by blocking outlet E. In this situation, some routes have their flow locally changed, such as the disappearing flow in connections 30–34 and the decreasing flow in connections 40–41. Thirdly, Fig. 6c confirms statements (iii) and (iv). The consequence of closing pore 32 is the flow reduction in 51-F. Although outlet F is still open in this case, it drastically loses its applicability because the main contribution to the flow in F comes from pore 32. Moreover, this case illustrates the formation of dead zones near the obstructed pore. Since the flow is close to zero in these regions, it could, for instance, reinforce the surface runoff in soils or even influence the displacement of oil in geological reservoirs.

Fig. 6

Velocity field of the flow simulation with H = 10 m and the a outlet A, b outlet E, and c pore 32 closed

Preferential paths with reactive-mass transport

Here, we discuss the influence of preferential paths for reactive-mass transport in porous media. First, we consider the original porous matrix for the analysis; then, we consider some structural modifications.

Porosity evolution in the original porous matrix

The reader can follow the evolution of the concentration field and the solid degradation in Fig. 7 for $Pe=10$ and $Da=10$. The spatial differences in the porous structures developed some preferred connections, as discussed previously, making the concentration field advance heterogeneously through the matrix. The circles identify some local dead zones that were also noticed in Fig. 4 and that are only accessed by the reactant through diffusion, which can affect the porosity evolution in the matrix.

Fig. 7

Concentration field and solid degradation for $Pe=10$ and $Da=10$ at the following dimensionless times: a $t/{t}_{f}=0.4$, b $t/{t}_{f}=0.8$, and c $t/{t}_{f}=1.0$. The white circles evidence dead zones accessed by diffusion

Figure 8 shows the changes in the overall porosity for the whole original porous matrix, varying $Pe$ and $Da$. The reference time T for comparison is chosen based on the presence of reactant in the outflow. Hence, we found $T=15,200$ l.u., which is the minimum observed time when the reactant concentration is different than zero in the outflow. In Fig. 8a, the changes in $\phi$ start earlier ($t/T=0.5$) for $Pe=1.0$ than for the other two cases ($t/T =0.8$), which are explained by the noticeable diffusion condition at $Pe=1.0$ that allows the reactant to reach more zones in the porous media. For advection-dominated conditions (i.e., higher $Pe$), the reactants are readily advected through the channels, making the time related for advection insufficient to achieve large reactive conversions (observed through the $\phi$-profile). Hence, by increasing $Pe$, the overall porosities decrease due to the difference in the characteristic time scale between the phenomena and the complication of the reactant reaching specific parts of the matrix.

Fig. 8

Overall porosity evolution in the whole matrix for different a $Pe$ and b $Da$ numbers. $Da$ and $Pe$ are fixed respectively in cases a $Da=7.7$ and b $Pe=10$. The lines are plotted to help guide the eye, and the reference time is set as $T=15,200$ l.u.

On the other hand, Fig. 8b shows that the porosity increases with $Da$. In contrast to the case in Fig. 8a, it is inconsistent to explain the changes in porosity for $Da$ variation in terms of diffusion effect because, if so, $Pe$ or $Re$ would vary, hindering the investigation. Instead, the phenomenon is explained by the modification of the reaction rate. Hence, the increase of $Da$ (kinetic-dominated or diffusion-controlled condition) intensifies the heterogeneous reaction, causing larger values of $\phi$ to arise. Furthermore, the changes in $\phi$ start almost at the same time ($t/T\approx 0.7$), whereby we understand that the diffusion has a smaller impact within the studied range of $Da$ compared to the range of $Pe$.

To understand how much different regions of the matrix and their preferential paths contribute to the porosity evolution, we plot ${\upeta }\left({t}_{R}\right)$ in Fig. 9. We first point out that with contrasting degrees, distinct regions of the matrix, having their own structural properties and local preferential paths, individually contribute to the global porosity evolution. This is illustrated by Fig. 9, which shows that region 1 most contributes to the advancement of ${\upeta }\left({t}_{R}\right)$ and has its relevance accentuated by $Pe$, while region 3 produces the smallest contributions for the three different $Pe$ cases. Interestingly, we observe that the role of region 2 in porosity evolution changes with $Pe$. Although region 2 contributes similarly to region 1 at $Pe=1$ (a gap of ${\Delta }{\upeta }=0.092$), its importance gradually declines with $Pe$, achieving a gap of ${\Delta }{\upeta }=0.169$ at $Pe=100$ and ${\upeta }\left({t}_{R}\right)$ comparable to those of region 3. Hence, some zones of a porous media (in our case, region 2) are more significantly affected under diffusion-dominated conditions (i.e., lower $Pe$) than others (e.g., region 1).

Fig. 9

Rescaled normalized porosity evolution for each region in the original porous media at $Da=7.7$, for a $Pe=1$, b $Pe=10$, and c $Pe=100$. ${t}_{R}$ is computed assuming ${t}_{0}$ as the first time when ${\upeta }\left(t\right)$ changes and ${t}_{f}$ as the time when the reactant first reaches the outlet of the matrix. The lines are plotted to help guide the eye

We can see the kinetic effect in Fig. 10 for a fixed advection-diffusion condition of $Pe=10$. Regions 1 and 3 still provide major and minor contributions to the porosity evolution for all the $Da$ cases, and the relevance of region 2 only slightly alters their contributions, resulting in similar gaps in each case. In general, the relative contributions to the porosity evolution remain kinetically independent, which implies that the solid amount is gradually available over the studied $Da$ range.

Fig. 10

Rescaled normalized porosity evolution for each region in the original porous media at $Pe=10$, for a $Da=5$, b $Da=10$, and c $Da=15$. ${t}_{R}$ is computed assuming ${t}_{0}$ as the first time when ${\upeta }\left(t\right)$ changes and ${t}_{f}$ the time when the reactant first reaches the outlet of the matrix. The lines are plotted to help guide the eye

Porosity evolution in an obstructed porous matrix

Now, we insert some structural modifications in the reactive-mass transport issue to check how far they hinder the matrix dissolution at fixed conditions ($Pe=10$ and $Da=10$). We observed that the reactive-mass transport through the original structure delivers a maximum $\phi$ for each time. The overall porosities from the matrix with modifications are always lower than this upper value since the blocked pores or outlets invariably alter the flow and create dead zones.

However, the clogging effect in the reactive conversion is negligible for the modifications tested. For instance, the reactive flow with closed pore 32 originates the lowest $\phi$ (2.72% lesser than for the original matrix), while the flow with blocked outlet A produces the closest $\phi$ compared to the original matrix (1.00% lesser than for the original matrix). Obviously, this remark results from specific considerations employed in this work, such as the given matrix, individual topological alterations, and reactive-transport conditions.

In other words, the reactive conversion could either stay unaltered or be strongly affected, depending on the studied case and the extent of the modifications. To illustrate this point and reinforce that diversified modifications affect the matrix dissolution differently, we plot Fig. 11, which separates the contribution of each region for the entire porosity evolution. For instance, the blocked pore 32 affects the regions where it is located (i.e., regions 2 and 3) as well as the distant region 1. This impact, however, is not observed for the restrictions of outlet A and pore 4, since they mainly influence the region where they are located (i.e., region 1) and originate slight porosity variations in the other regions.

Fig. 11

Rescaled normalized porosity evolution at $Pe=10$ and $Da=10$ for the regions a 1, b 2, and c 3, considering different structural changes in the porous matrix. Here, ${t}_{R}$ is computed assuming ${t}_{0}=8400$ l.u. and ${t}_{f}=17,500$ l.u

Conclusion

Preferential flow is a phenomenon that affects a vast range of problems and needs to be better understood. Because of the attractive advantages of the Pore-Scale LBM approach (e.g., the absence of empirical models), Lattice Boltzmann is an inviting method to model the flow in porous media and search for preferential pathways. Performing a geometric investigation of the matrix is a typical and simplified numerical way to predict these paths. Hence, in this work, we discussed some insights about preferential flow and tested the Ju et al. model, a tortuosity-dependent resistance model, to measure the preferential paths in a non-Darcy flow through an artificial square porous medium.

LBM naturally recovers the Forchheimer equation for the established range of Reynolds. The Ju et al. model successfully indicates many preferential paths independent of the flow orientation, but its accuracy is more substantial for Darcy flows. This deficiency is related to the inertial effects in the Forchheimer regime, which the model fails to account for. Therefore, geometric characteristics like grain shape and pore-to-pore alignment (deflections of the paths) are highlighted features to describe this kind of flow. When clogging occurs, we observe that paths with lower flow resistance affect the flow preferences in the neighboring sections. Additionally, depending on the position of the blocked pores, not only the flow configuration, but also preferred paths, and reaction rates may change. Dead zones in the porous medium can also arise, and some are only accessed by diffusion.

The reactive flow through the original matrix delivers a maximum overall porosity, below which the porosities from the clogged matrix stand. The porosity of the entire matrix increases when reducing the Péclet (diffusion-dominated condition) or enlarging the Damköhler numbers (kinetic-dominated condition). Different regions considered in this work contribute separately to the porosity evolution, having kinetic-independent relative contributions. However, some are more significantly affected under diffusion-dominated conditions than others.