Optimizing Structure and Internal Unit Weights of Echo State Network for an Efficient LMS-Based Online Training

Abstract

Echo state network (ESN) is a special type of recurrent neural networks (RNN) wherein a dynamic reservoir is used in the hidden layer, the weight of internal units of ESN is kept fix during training process, and output weights are the only trainable weights. Therefore, network training in an offline mode can be changed into a linear regression equation which is simply solved, although it is required to use online training of ESN in some applied problems. The least mean square (LMS) algorithm can provide an easy and constant method for online training of ESN; however, the huge eigenvalue spreads of the correlation matrix of internal network states reduce the speed of the algorithm convergence. In this study, harmony search algorithm (HSA) is used to optimally produce the structure and weight of internal network units. It is possible to significantly reduce the eigenvalue spreads of the correlation matrix of network states by means of this algorithm. Thereafter, the LMS algorithm is used for the online training of ESN built with the help of HSA. Already-obtained simulation results show that the eigenvalue spreads of the correlation matrix are reduced millions of times, and the LMS algorithm increases the online training speed of the network several times with an acceptable precision of training.

1 Introduction

An echo state network (ESN) is a new type of recurrent neural network (RNN) that uses a large dynamic reservoir in the hidden layer. The weights of the reservoir connections are randomly generated and remain fixed during the training process. Therefore, it is possible to use more units in the reservoir to produce more dynamics. This feature of ESN has attracted the attention of many researchers. The important research done so far on ESN includes detailed scrutiny of intrinsic plasticity in ESN [1, 2], an augmented ESN for nonlinear adaptive filtering of complex noncircular signals [3], using leaky integrator neurons in ESN [4, 5], and echo state Gaussian process [6]. Some other scientists studied various ESN schemes [7,8,9,10,11,12] and several researchers attended to echo state property (ESP) [13,14,15,16].

The simple use as well as the ability to model dynamic systems make ESN an appropriate alternative for modeling unknown dynamic systems. ESN has been successfully used in solving many problems such as chaotic time-series prediction [17,18,19], speech recognition [20], grammatical structure learning [21], communication channel equalization [22], dynamical pattern recognition [20, 23], power system monitoring [24,25,26,27], and energy consumption forecasting [28, 29]. However, in some practical problems where the parameters change during operation or the network needs output feedback, it is necessary to train the network online [30].

The least mean square (LMS) is one of the simple algorithms for online training of RNN. However, the convergence of this algorithm is very slow or may not converge due to the eigenvalues spread of the autocorrelation matrix of network states [22]. To tackle this issue, several structures were used to construct ESN [31, 32], but none of these structures have a significant effect on the eigenvalues spread of the autocorrelation matrix. Therefore, other algorithms such as recursive least squares (RLS) [33], particle swarm optimization (PSO) [34, 35], and harmony search algorithm (HSA) [36] have been used for the purpose of ESN online training, although these algorithms require complex calculations and much time is spent for online training. It has been tried to provide the possibility of using the LMS algorithm for online training of the network by building an appropriate reservoir [22].

A mixed method for the optimization of the reservoir and then online training of ESN will be introduced in this study. In this approach, HSA will be used to optimize an ESN so that the eigenvalues spread of the autocorrelation matrix is reduced, then the LMS algorithm will be used to train the optimized ESN online. In the following, the obtained results will be compared with PSO, HS, and RLS algorithms.

ESN, its conventional structure as well as its offline training will be explained in the section “Echo State Network”. LMS and HSA will be briefly introduced in sections “Least Mean Square (LMS) Algorithm” and “Harmony Search Algorithm (HSA),” respectively. In the section “Main Results”, a mixed method for the construction and online training of ESN will be proposed. With the help of some examples, the efficiency of the proposed method will be illustrated in the section “Simulation”. Finally, the results obtained from simulations will be referred to, and some applied suggestions will be made for the construction and online training of ESN.

2 Echo State Network

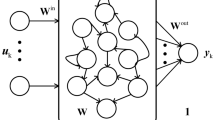
ESN is a discrete-time network, which contains three layers, namely input, hidden, and output. These layers consist of K, N, and L units, respectively. The size of input units at time n is represented by $u(n)=\left({u}_{1}\left(n\right),{u}_{2}\left(n\right). . . , {u}_{K}\left(n\right)\right)$, the size of reservoir states is represented by $x(n)=({x}_{1}\left(n\right),{x}_{2}\left(n\right),\dots ,{x}_{N}\left(n\right))$, and the size of output units is represented by $y(n)=({y}_{1}\left(n\right),{y}_{2}\left(n\right),\dots ,{y}_{L}\left(n\right)$. The weight of the connections entering into the reservoir in an N × K matrix is ${W}^{in}=({w}_{ij}^{in})$, the weight of the internal connections of the reservoir in an N × N matrix is $W=({w}_{ij})$, the weight of connections returning from output to the reservoir in an N × L matrix is ${W}^{back}=({w}_{ij}^{back})$, and the weight of connections entering into the output in an L × (K + N + L) matrix is ${W}^{out}=({w}_{ij}^{out})$. These weights are all gathered together. In ESN, the size of units and weight of network connections are real values and input can directly enter into the output [37,38,39]. Figure 1 shows the structure of the echo state neural network.

Fig. 1

Block figure of echo state network

Reservoir states in ESN are calculated using Eq. (1):

$$x\left(n+1\right) =f\left(\begin{array}{c}{W}^{in}.u\left(n+1\right)+W.x\left(n\right)\\ +{W}^{back}.y\left(n\right)\end{array}\right)$$

(1)

In the above equation, $\mathrm{f}=\left({\mathrm{f}}_{1},{\mathrm{f}}_{2},\dots ,{\mathrm{f}}_{\mathrm{N}}\right)$ is the performance function of reservoir units and is usually selected as a sigmoidal function (or tanh), and network outputs are obtained through the following relation:

$$\mathrm{y}\left(\mathrm{n}+1\right)={\mathrm{f}}^{\mathrm{out}}\left({\mathrm{W}}^{\mathrm{out}}.\mathrm{\emptyset}\left(\mathrm{n}+1\right)\right)$$

(2)

In the above equation, ${\mathrm{f}}^{\mathrm{out}}=({\mathrm{f}}_{1}^{\mathrm{out}},{\mathrm{f}}_{2}^{\mathrm{out}},\dots ,{\mathrm{f}}_{\mathrm{L}}^{\mathrm{out}})$ represents the performance function of output units and is selected as a linear or sigmoidal function and $\mathrm{\emptyset}\left(\mathrm{n}+1\right)=\left[\begin{array}{ccc}\mathrm{u}\left(\mathrm{n}+1\right)& \mathrm{x}\left(\mathrm{n}+1\right)& \mathrm{y}\left(\mathrm{n}\right)\end{array}\right]$ is obtained from the combination of input, reservoir, and output vectors of the previous moment [36].

2.1 Echo State Property

A main condition for the correct performance of ESN (as the name is clear) is that reservoir states be a function (echo) of the history of the inputs operated on the network. This condition is called echo state property. Although the investigation of necessary and sufficient conditions to make certain about the satisfaction of echo state property is a difficult task, the network can satisfy echo state property on each input and all states of x ∈ [− 1, 1] only if the spectral radius of the reservoir (the highest eigenvalue of matrix W is called reservoir spectral radius) is smaller than one [12, 36].

2.2 ESN Construction

Production of a suitable dynamic reservoir is necessary to build an echo state neural network. Although there is no precise method for determining network units, the number of network units could be selected in a range from one-tenth to half of the training data size. In addition to the size of the reservoir, the level of scattering in connections also affects the precision and convergence speed of the ESN. In many practical applications, the level of scattering could be considered to be 10% [9]. Once the number of reservoir units and the scatter level are set, it is time to propose the reservoir weight matrix so that the network maintains its echo state characteristic. The following steps provide a systematic method to construct an echo state neural network [40]:

• 1. Produce Wⁱⁿ, W^back, and W0 matrices with optional spread and at random.

• 2. Divide the W0 matrix by the largest spectral radius of itself to get matrix W1 with the spectral radius of one, ${W}_{1}=\frac{{W}_{0}}{\left|{\lambda }_{max}\right|}$.

• 3. Multiply an appropriate value of α within the range of $0<a<1$ to get the matrix W with an optional value of the spectral radius, i.e., $\mathrm{W}=\mathrm{\alpha }.{\mathrm{W}}_{1}$ [36, 38].

2.3 Offline ESN Training

The purpose of neural network training is to determine the weight of network connections so that a minimum deviation from the desired output could be achieved. There are two general methods for the training of a neural network: supervised and unsupervised learning. Generally, for the training of echo state neural networks, the supervised learning method is used in both offline and online modes. In this study, a step-by-step method is proposed for offline training. Although, an online training method is also suggested in the following sections:

• First step: produce Wⁱⁿ, W^back, and W matrices randomly.

• Second step: sample network dynamics with the operation of training data on the network, this step includes the following:

  • 1. First determine the initial states of the reservoir arbitrarily.

  • 2. Operate the network by training data and bringing it up-to-date through (1).

  • 3. Put d (0) = 0 at the beginning time of n = 0 where d(0) has not been defined.

  • 4. Put the network states in a row matrix of M states.

  • 5. Put the reverse of the performance function of output units $({\mathrm{f}}^{-1}(\mathrm{d}(\mathrm{n}))$ in matrix T, similar to the previous stage.

    To eliminate the effect of the initial states of the reservoir, we should omit the first sample from M and T matrices and store x(n) and $({\mathrm{f}}^{-1}(\mathrm{d}(\mathrm{n}))$ vectors in M and T matrices simultaneously.

• Third step: calculate the weight matrix of output connections W^out, multiply the pseudo-inverse matrix of M by matrix T, and get transpose of them to obtain W^out.

  $$W^{out}=\left(M^{-1}\;.\;T\right)^T$$

  (3)

• Fourth step: now, the obtained echo state neural network (W^out, W, Wⁱⁿ, and W^back) is ready to be used for solving new problems [2, 35, 36].

3 Least Mean Square (LMS) Algorithm

LMS is an adaptive algorithm, which uses an error gradient vector for the estimation of weight vectors. This algorithm has been made up of a repetitive structure for the movement of weight vectors towards the symmetry of the error gradient vector and finally minimizes the mean squared error. Compared to the RLS algorithm, the calculations of this algorithm are very simple. This algorithm does not need the correlation matrix and matrix inversion [41, 42]. Assume to calculate the network output via Eq. (4).

For the symmetric gradient vector error

$$\mathrm{y}\left(\mathrm{n}\right)={\mathrm{W}}^{\mathrm{out}}\mathrm{\emptyset}\left(\mathrm{n}\right)$$

(4)

In the above relation, the output function has been assumed a linear one, and the current matrix of $\mathrm{\emptyset}\left(\mathrm{n}\right)=\left[\begin{array}{ccc}\mathrm{u}\left(\mathrm{n}+1\right)& \mathrm{x}\left(\mathrm{n}+1\right)& \mathrm{y}\left(\mathrm{n}\right)\end{array}\right]$ has been considered as the algorithm input. Then, the weight matrix of W^out is estimated with the help of this algorithm and based on reducing the maximum gradient in order to minimize the mean squared error. The equation of weight estimation is expressed as the following simplified Eq. (5).

$${\mathrm{W}}^{\mathrm{out}}\left(\mathrm{n}+1\right)={\mathrm{W}}^{\mathrm{out}}\left(\mathrm{n}\right)+\upmu .\, \mathrm{\emptyset}\left(\mathrm{n}\right).\, \mathrm{e}\left(\mathrm{n}\right)$$

(5)

In the above relation, e(n) represents the error of real network output from the desired degree, and $\upmu$ is the step size of the algorithm and determines its convergence. We need to select $0<\mu <\frac{1}{{\uplambda }_{\mathrm{max}}}$ to make certain about the convergence algorithm. If a large value is selected for the step size of the algorithm, its convergence will be endangered and the small step size will reduce the speed of algorithm convergence. In this study, $\mu =\frac{1}{2.{\lambda }_{max}}$ is considered to keep a balance between speed and algorithm precision. The convergence speed of the algorithm depends on the eigenvalue spreads of the correlation matrix corresponding to reservoir states which will be minimized using the harmony search algorithm in the next section.

The goal of the harmony search algorithm is to minimize the S gain. In these cases, the largest spectral radius of the autocorrelation matrix of the network states is minimized, and therefore, a larger $\mu$ can be selected for the LMS algorithm. Also, in this method, eigenvalues close to zero of the autocorrelation matrix of the network states are removed. As a result, the training speed and convergence of this algorithm improved together.

4 Harmony Search Algorithm (HSA)

HSA has been designed based on composers’ performance for making better music. As composers search different nets to achieve beautiful music, engineers search appropriate weight vectors for the optimization of objective functions [43, 44].

Harmony memory (HM), harmony memory size (HMS), harmony memory considering rate (HMCR), and pitch adjusting rate (PAR) constitute the parameters of this algorithm for optimization. To use the algorithm, we should store the number of HMSs of the feasible vector in HM and then produce a new harmony by means of PAR and HMCR. If the new harmony outweighs the worst harmony in harmony memory, it can replace it. This process should be repeated until an acceptable vector for the optimization of the objective function is achieved [45, 46].

The harmony search algorithm is operationalized using the following steps:

• Step 1: First select the algorithm parameters and optimization problem. Then determine PAR, HMCR, HMS, a suitable objective function, and a small neighborhood radius of bw, and an allowed range of D for the vector values in this step.

• Step 2: Then store as much as the capacity of harmony memory of the produced vector along with the values of the objective function for each vector.

• Step 3: Based on Eq. (6), a new vector (harmony) is produced; each component of the new vector is selected with the probability of HMCR out of the components of existing vectors in harmony memory and with the probability of 1-HMCR out of the allowed range.

  $$\begin{aligned}&\mathrm {x^\prime}_{\mathrm i}^{\mathrm j}\in\left\{\mathrm x_{\mathrm i}^1,\mathrm x_{\mathrm i}^2,\dots,\mathrm x_{\mathrm i}^{\mathrm{HMS}}\right\} \quad \mathrm{HMCR}\\&{\mathrm x^\prime}_{\mathrm{i}}^{\mathrm{j}}\in \mathrm{D}\quad\quad\quad\quad\quad\quad\;\,\;1-\mathrm{HMCR}\end{aligned}$$

  (6)

  Then the selected components from harmony memory will be regulated with the probability of PAR, and the components selected from the allowed range will remain unchanged. Equation (7) shows how vector components have been regulated.

  $${\mathrm{x^\prime}}_{\mathrm{i}}^{\mathrm{j}}={\mathrm{x^\prime}}_{\mathrm{i}}^{\mathrm{j}}+\mathrm{bw}*\mathrm{rand \quad PAR}$$

  (7)

• Step 4: In this case, the new objective function of the vector (harmony) outweighs the worst existing vector in harmony memory; the new vector and value of the related objective function are replaced in harmony memory.

• Step 5: Steps 3 and 4 will be repeated until an acceptable answer is reached [12].

Due to the efficiency of HSA in problems with extensive search space, we have used this algorithm for the construction of a proper dynamic reservoir with a small s rate. Then we train the weight of network output connections by means of the LMS algorithm in an online state.

5 Main Results

In this paper, a mixed method for ESN training and construction is proposed, which consists of two substantial steps. The former is the optimization of the structure and weight of internal connections while the latter is online training of the weight of output connections. In the first step, HSA for the optimization of the structure and weight of internal connections of ESN is used to provide the conditions for the convergence of online training of ESN by means of the LMS algorithm. In this way, we should have the lowest possible value for eigenvalue spreads of the state correlation matrix. This step is aimed at optimizing the structure and weight of internal connections of the network; therefore, the weight of output connections remains unchanged and is determined by means of the LMS algorithm after network optimization. To use the HS algorithm, we should introduce the evaluation function at first. Here, s rate is introduced as the evaluation function. In other words, the purpose of the algorithm is to reduce eigenvalue spreads of the state autocorrelation matrix.

$$\mathrm{R}=\mathrm{E}\left[\mathrm{\emptyset}(\mathrm{n}){\mathrm{\emptyset}}^{\mathrm{T}}(\mathrm{n})\right]$$

(8)

$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{s}=\left|\frac{{\uplambda }_{\mathrm{max}}(\mathrm{R})}{{\uplambda }_{\mathrm{min}}(\mathrm{R})}\right|$$

(9)

In the above relations, the expression of $\left(\mathrm{n}\right)=[\begin{array}{ccc}\mathrm{u}\left(\mathrm{n}\right)& \mathrm{x}\left(\mathrm{n}\right)& \mathrm{y}(\mathrm{n}-1\end{array})]$ holds true, and ${\uplambda }_{\mathrm{max}}(\mathrm{R})$ and ${\uplambda }_{\mathrm{min}}(\mathrm{R})$ are representative of the maximum and minimum values of the correlation matrix corresponding to R, respectively. In order to use time in a better way, it is suggested that we construct an optimized echo state neural network for use within an extensive range of applied issues. Thereafter, we can use this network for each specific application with a slight modification. The relevant modifications can also be made by means of HSA with fewer repetitions.

In the second step, the network constructed by HSA is trained in an online state by means of the LMS algorithm. For the training of ESN, the step size of the algorithm $(\upmu )$ is selected. The step size is set as $\mu =\frac{1}{2.{\lambda }_{max}}$ to make a balance between algorithm speed and precision. Then, training data are operated on the optimized network, reservoir states are calculated through (1), and the weight of output connections of the network are regulated through Eq. (5). Flowchart 1 shows the proposed method briefly. Using the LMS, the algorithm not only increases the speed of training and needs a very smaller memory, but also it increases the network stability via proper step sizes.

Flowchart 1

Brief description of the proposed method.

6 Simulation

One of the most common applications of ESNs is the prediction of chaotic time series. In this paper, we have used this network for the prediction of the Rossler, Mackey–Glass, and Lorenz time series. To this end, we should determine the number of reservoir units and their spectral radius. In this paper, 500 units in the reservoir network and a spectral radius of 0.90 have been used. The size of training data sets in all simulations has been considered 4000 where the first 500 samples are ignored to nullify the effect of the initial states of the reservoir. The next 3000 ones are used for training and the remaining 500 ones are used for performance evaluation. All the simulations have been made in the Matlab environment version of 2013 by means of a personal computer with INTEL CORETM i7-3470 CPU to make certain about the correctness of obtained results.

6.1 Mackey–Glass Time Series

Mackey–Glass time series is obtained through the following differential equation:

$$\frac{dx}{dt}=\beta \, x\left(t\right)+\frac{\alpha \, x(t-\delta )}{1+{x(t-\delta )}^{10}}$$

(10)

In the above equation, x(t) represents the value of the Mackey–Glass time series at time t; in order for the time series to be chaotic, we have selected equation parameters as δ = 17, β =  − 0.1, and α = 0.2. This time, the series is constructed by means of the second-order Runge–Kutta method with a step size of 0.01 [41, 47].

6.2 Lorenz Time Series

The following three-variable differential (11) is used for the construction of the Lorenz time series.

$$\left\{\begin{array}{l}\frac{dx}{dt}=-a \, x\left(t\right)+a \, y\left(t\right) \\ \frac{dy}{dt}=b \, x\left(t\right)-y\left(t\right)-x\left(t\right)z(t)\\ \frac{dz}{dt}=x\left(t\right)y\left(t\right)-c \, z\left(t\right)\end{array}\right.$$

(11)

To ensure that the obtained series is chaotic, we should select parameters as a = 10, b = 28, and $c=\frac{8}{3}$, and we produce data sets using the fourth-order Runge–Kutta method with a step size of 0.02 and initial states of x (0) = 12, y (0) = 2, and z(0) = 9.

6.3 Rossler Time Series

The following differential (12) is used for the construction of the Rossler time series.

$$\left\{\begin{array}{l}\frac{dx}{dt}=-z\left(t\right)-y\left(t\right) \\ \frac{dy}{dt}=x\left(t\right)+d \, y\left(t\right) \\ \frac{dz}{dt}=e+z(t)(x\left(t\right)-f)\end{array}\right.$$

(12)

To produce data sets out of the above chaotic time series, we should consider d = 0.15, e = 0.2, and f = 10 and use the fourth-order Runge–Kutta method with a step size of 0.01.

After the production of training data sets, we use the proposed optimized ESN for the construction and training of the network. In the first step, weights of the network reservoir should be produced in a way that correlation matrix eigenvalues of the reservoir have the least possible spreads. Algorithm parameters have also been selected as HMS = 10, HMCR = 0.85, PAR = 0.2, bw = 0.4, NI = 100000, and $X\in \left\{-0.4,-0.2, 0, 0.2, 0.4\right\}$. In this step, three training data sets are operated on the input network simultaneously, and the algorithm is repeated NI times. Table 1 shows eigenvalue spreads of the correlation matrix of network internal states constructed with compromise structures, of the network constructed with the conventional random method, and of the network constructed with HSA. It clearly shows the performance of HSA in the optimization construction of ESN.

Table 1 Eigenvalue spreads different structures

In Table 1, short expressions of LMS-ESN have been used for the proposed method. As it is seen, the S rate has been reduced 106 times through HAS compared to the available methods. The algorithm is also repeated $\frac{NI}{10}$ other times for each time series. The obtained results are briefly illustrated in Table 2.

Table 2 Eigenvalue spreads of the network state matrix

The obtained results show that training online conditions of ESN have been provided using the LMS algorithm; therefore, in the second step, the LMS algorithm is used for online training of ESN. In this paper, mean squared error for training (MSEtrain) and for testing (MSEtest) and spent time during network training (t) are used as performance criteria of each training method.

$$\mathrm{MSE}=\frac{1}{T}{\sum }_{n=1}^{T}{\Vert D\left(n\right)-Y(n)\Vert }^{2}$$

(13)

Tables 3, 4, and 5 show the results obtained from Mackey–Glass, Lorenz, and Rossler time series, respectively.

Table 3 Prediction results of Mackey glass time series

Table 4 Prediction results of Lorenz time series

Table 5 Prediction results of Rossler time series

As it is seen in the above tables, the speed of the proposed method for online training of echo state network is higher than other methods, and the precision of this method is also higher than that of PSO and HS. Furthermore, this proposed method guarantees network stability with selecting a proper step size and uses a very shorter memory compared to existing methods.

7 Conclusion

In this paper, a mixed method using LMS and HS algorithm has been introduced to tackle the issue and pitfalls of online training of ESN. In this proposed method, the structure and weight of internal connections of echo state neural network are produced so that we have the lowest possible value for eigenvalue spreads of the internal state correlation matrix. Then, the network is trained in an online state by means of an LMS algorithm. Simulation results clearly indicate that spent time during network training through the proposed method is much lower than that of other methods while the precision of outputs is acceptable. In addition, the proposed method is advantageous over the other two methods because it has simple calculations, guarantees network stability, and uses less memory. It is also possible to construct an echo state neural network by means of HSA and apply it within an extensive range of problems. Although the training time has been improved in this method, the process of optimizing reservoir connections is a time-consuming and complex process. In the future, other methods of improving reservoir performance can be studied and investigated (Appendix: Table 6).

Appendix

Table 6 Index and parameters description