Extended Random Assignment Mechanisms on a Family of Good Sets

Abstract

For the problem of allocating indivisible goods to agents, we recently generalized the probabilistic serial (PS) mechanism proposed by Bogomolnaia and Moulin (J Econ Theory 100(2):295–328, 2001). We generalized the constraints with the fixed quota on each good to a set of inequality constraints induced by a polytope called polymatroid (Fujishige et al. in ACM Trans Econ Comput 6(1):1–28, 2018. https://doi.org/10.1145/3175496; Math Program 178(1–2):485–501, 2019). The main contribution of this paper was to extend the previous mechanism to allow indifference among goods. We show that the extended PS mechanism is ordinally efficient and envy-free. We also characterize the mechanism by lexicographic optimization. Finally, a lottery, an integral decomposition mechanism is outlined.

1 Introduction

We consider the problem of allocating a set of indivisible goods to agents according to their ordinal preferences for goods. A common fair mechanism used in practice is the random serial dictatorship: agents are randomly ordered (with a uniform distribution over permutations), and they successively pick their favorite good from those available in a realized order.

In a seminal paper, Bogomolnaia and Moulin proposed an efficient and fair mechanism called probabilistic serial (PS), which allocates goods to agents through the simultaneous eating algorithm with uniform speed [1]. The PS mechanism can be outlined as follows.

Consider each good as an infinitely divisible object with a quota that agents eat during some time intervals.

• Step 1. Each agent eats away from his/her favorite good at the same unit speed, then proceeds to the next step when some of the favorite goods are completely exhausted.

• Step $s>1$. Each agent eats away from his/her remaining favorite good at the same unit speed, then proceeds to the next step when some of the favorite goods are completely exhausted.

Since then PS mechanism has been significantly studied; see, for example, [2,3,4,5,6,7,8,9,10] and references therein for more details.

PS mechanism was extended by Fujishige et al. by generalizing the constraint with the fixed quota on each good to a system of linear inequalities induced by a polytope called polymatroid [11, 12]. The extension also included multi-unit demands by agents and a lottery on indivisible goods. The present study aims to complete the generalized PS mechanism given by Fujishige et al. by allowing agents’ indifference among goods.

1.1 Motivation and Related Work

The main contribution of the work given by Fujishige et al. [11, 12] is to enlarge the constraint on goods from a fixed set to a family of sets. Figure 1 illustrates an example containing three (type of) goods $\{a,b,c\}$ to show the difference of the settings of goods in the assignment given by Bogomolnaia and Moulin [1], and the one given by Fujishige et al. [12]. In the left graph, each good has a fixed quota $q_a = q_b = g_c =1$, which is the assignment problem considered by Bogomolnaia and Moulin. The area bounded by the thick lines of the right graph is the base polyhedron (defined in Sect. 2) considered by Fujishige et al. [12]. Apparently, that the left set of goods is a special case of the right one. For a more detailed explanation of the motivation of the extended assignment mechanism with submodularity, their applications, or other related topics, refer to numerous examples (mainly expressed in the matching and flows) and the discussions provided in [12].

Fig. 1

The settings of goods considered in the assignment problems: (left) the fixed set (the circle point); (right) a family of sets (the area bounded by thick lines), the base polyhedron B defined in Sect. 2

The well-known Birkhoff–von Neumann theorem that every bistochastic matrix can be expressed as a convex combination of permutation matrices plays a crucial role in implementing the PS mechanism developed by Bogomolnaia and Moulin [1]. Our extended PS mechanism depends on the results of submodular optimization, such as the integrality of the independent flow polyhedra [13, 14]. There are other generalizations of the PS mechanism. For example, Budish et al. [5] considered the laminar constraint called a bihierarchy on both the set of agents and the set of goods. Fixing a set E, a family ${\mathcal {F}}$ is called laminar if for all $X, Y \in {\mathcal {F}}$ we have $X \subseteq Y, Y \subseteq X$, or $X \cap Y = \emptyset$. We draw an example for goods $\{a_1,a_2,b\}$ in Fig. 2 with the laminar structure $\{\{a_1\},\{a_1,a_2\},\{b\}\}$, where the quotas $q_{a_1},q_{\{a_1,a_2\}}, q_b$ are integers, and good $a_1$ should be allocated to a sub-group of agents in [5]. The laminar structure of the good setting is different from the base polyhedron, the latter is more general in the assignment, as indicated in [12].

Fig. 2

The setting of goods (the thick line) under a laminar structure $\{\{a_1\},\{a_1,a_2\},\{b\}\}$ with quotas $q_{a_1},q_{\{a_1,a_2\}}, q_b$

Moreover, the PS mechanism allowing indifference among goods was generalized by Katta and Sethuraman [8]. The following is an example of the assignment problem treated by Katta and Sethuraman [8] with the set of agents $\{1,2,3\}$, the set of goods $\{a,b,c\}$, and the preference profile defined as follows:

$$\begin{aligned} \begin{array}{cccc} 1 \qquad &{} \{a,b\} \,\, &{} &{} \,\, c \\ 2 \qquad &{} a \, &{} b &{} \,\, c \\ 3 \qquad &{} a\,&{} c &{} \, \ b \end{array} \end{aligned}$$

Agent 1 is indifferent between a and b, but prefers both of them to c; agent 2 prefers a to b to c, and agent 3 prefers a to c to b. They handled the problem by solving the parametric max-flow problems in succession and using the matching under dichotomous preference proposed by Bogomolnaia and Moulin [15].

The present study aims to complete the extension of the PS mechanism with multi-unit demands and submodular constraints on goods given by Fujishige et al. [11, 12] by generalizing the preference profile on the full domain, including indifference among goods. Instead of the max-flow problem, we need to treat the independent flow problem given by Fujishige in [13]. Our extended mechanism and other related works are summarized in Sect. 1.2.

Bogomolnaia and Moulin [15] suggested that in the mechanism design, the three enduring goals are efficiency, incentive-compatibility, and fairness. It was shown by Katta and Sethuraman that the above example of three agents, three goods, including indifferent preference cannot be ordinal efficient, envy-free, and (weakly) strategy-proof.¹ As shown in Fig. 1, since our work is an extension of the one given by Bogomolnaia and Moulin as well as Katta and Sethuraman, on the incentive front, the proposed mechanism is not strategy-proof, even in weakly meaning. We also discuss the strategy-proof in Concluding remarks.

1.2 Our Contributions

First, we define some notations and introduce informally the concepts used to evaluate the assignment mechanism.

Let $N=\{1,\ldots ,n\}$ be a set of agents and E be a set of goods. For $i \in N$, $a,b \in E$, we write $a \succ _i b$ if agent i prefers good a to b. Let $U(\succ _i,e)\equiv \{e' \in E \mid e' \succ _i e \} \cup \{e\}$ be the upper contour set of good e at $\succ _i$. An assignment is a matrix $P\in {\mathbb {R}}^{N \times R}_{\ge 0}$, where the entry $P(i,e)\ge 0$ denotes the portion or the probability of good e agent i obtained.

Sd-dominance, ordinally efficiency, sd-envy-freeness: Fix an agent set N, a good set E and a preference profile $(\succ _i | i \in N)$. For any two assignments P and Q, we say that P sd-dominates Q if $\sum _{e' \in U(\succ _i,e)} P(i,e') \ge \sum _{e' \in U(\succ _i,e)} Q(i,e')$ for all $e \in E$ and $i \in N$. We say that an assignment is ordinally efficient if it is not sd-dominated by any other assignment. Ordinal efficiency is also related to other efficiencies [16]. We say that assignment P is sd-envy-free if $\sum _{e' \in U(\succ _i,e)} P(i,e') \ge \sum _{e' \in U(\succ _i,e)} P(j,e')$ for all $i,j \in N$. Envy-freeness is a criterion of fairness among various concepts, which are summarized in the concluding chapter of the handbook by Thomson [18].

Totally lexicographical optimization: This is the concept suggested by Bogomolnai [4] to characterize the PS mechanism. For each agent i, we define $r_i(k)$ to be the sum of P(i, e) for agent i’s top preference up to kth one over goods. Rearrange $r_i(k)$ for all i and all k in the non-increasing order, denote it as a vector ($r_i(k)$). Then, an allocation with the lexicographical maximizer, ($r^*_i(k))$, is the totally lexicographical optimization allocation.

In our problem setting, constraints on goods can be a polyhedron called polymatroid. Budish et al. also extended the PS mechanism on a family of sets [5]. They assume a layer structure; ours include and generalize their mechanism as discussed in [12].

Now, the contributions of the paper can be outlined as follows:

• We propose two algorithms: In Algorithm I, agents only provide the top preferences, or goods that are accessible to each agent. Algorithm II is a generalization of the PS mechanism provided by Bogomolnaia and Moulin [1] with full preference domains. We show that our mechanisms keep the main desired properties, ordinal efficiency and sd-envy-freeness.

• Totally lexicographical optimization, maximin or leximin maximizer, is a unified characterization of PS presented by Bogomolnaia [4]. Lexicographical optimization related to submodular functions has been solved by Fujishige [19]. We also show the lexicographical characterization of our mechanism.

• The mechanism of the lottery outlined for allocating indivisible goods is a generalization of the decomposition of the doubly stochastic matrices. The result can also be applied to the generalization of some assignments’ efficiencies as studied by Doğan et al. [16].

• Our mechanism is based on some preliminary results. One key fact is that the composition function of the adjacency of a graph and monotonic submodular functions keeps submodularity. The result certainly applies to other cases.

1.3 Organization of the Paper

The remainder of the paper is organized as follows. In Sect. 2, we describe the problem, notations, independent flows, and preliminary results. Sections 3 and 4 provide algorithms. The efficiency and fairness of the proposed mechanism are presented in Sect. 5. Section 6 gives a lexicographical characterization. Section 7 provides a mechanism of the lottery for assigning indivisible goods. Section 8 gives the concluding remarks.

2 Definitions and Preliminaries

2.1 Model Description and Fundamentals

Let $N=\{1,2,\ldots ,n\}$ be a set of agents and E be a set of goods. Each agent $i\in N$ has a preference relation $\succeq _i$. Let $\succ _i$ and $\sim _i$ be the strict preference and the indifference binary relations, respectively, induced by $\succeq _i$. Let $\succeq =(\succeq _i \mid i \in N)$ denote the preference profile. Each agent $i \in N$ wants to obtain a certain number of goods $d(i) \in {\mathbb {Z}}_{>0}$ of any types at most in total. We refer to d(i) as the demand upper bound of agent i. Denote agents’ total demand vector by $\mathbf{d}=(d(i) \mid i \in N) \in {\mathbb {Z}}^N_{>0}$. Constraints on goods are defined as follows.

A pair $(E, \rho )$ of a set E and a function $\rho : 2^E \rightarrow {\mathbb {R}}_{\ge 0}$ is called a polymatroid if the following three conditions hold (see [14, 17]):

• (a) $\rho (\emptyset )=0.$

• (b) For any $X,Y \in 2^E$ with $X \subseteq Y$ we have $\rho (X) \le \rho (Y)$.

• (c) For any $X,Y \in 2^E$ we have $\rho (X) + \rho (Y) \ge \rho (X \cup Y)+\rho (X \cap Y)$.

The submodular function $\rho$ is called the rank function of the polymatroid $(E, \rho )$. We assume $\rho (E) > 0$ in the sequel. For a given polymatroid $(E, \rho )$, the submodular polyhedron $\mathrm{P}(\rho )$ of $(E, \rho )$ is defined by

$$\begin{aligned} \;\;\; \mathrm{P}(\rho )=\{x\in {\mathbb {R}}^E \mid \forall X\subseteq E: x(X)\le \rho (X)\} \end{aligned}$$

and its base polyhedron by

$$\begin{aligned} \mathrm{B}(\rho )=\{x\in \mathrm{P}(\rho )\mid x(E)=\rho (E)\}, \end{aligned}$$

where $x(X)=\sum _{e\in X}x(e)$ for all $X\subseteq E$. The submodular inequality implies that the intersection of $\mathrm{B}(\rho )$ with each constraint equality is nonempty, in other words,

$$\begin{aligned} \rho (X)=\max \{x(X)\mid x \in \mathrm{B}(\rho ) \}, \quad \forall X \subseteq E. \end{aligned}$$

(1)

For a polymatroid $(E,\rho )$, it should be noted that $\mathrm{B}(\rho ) \subseteq {\mathbb {R}}^E_{\ge 0}$ and $\mathrm{B}(\rho ) \ne \emptyset$ (refer to [12, 14] for more details). The polytope $\mathrm{P}_{(+)}(\rho ) \equiv \mathrm{P}(\rho ) \cap {\mathbb {R}}^E_{\ge 0}$ is called the independent polytope of a polymatroid $(E,\rho )$, and each vector in $\mathrm{P}_{(+)}(\rho )$ is called an independent vector (see Fig. 3).

Fig. 3

Base polyhedral $\mathrm{B}(\rho )$ and independent polytopes $\mathrm{P}_{(+)}(\rho )$, where the thick line or the area bounded by thick lines are base polyhedral

Next we denote a random assignment problem by $\mathbf{RA}=(N,E,\succeq ,\mathbf{d}, (E,\rho ))$. Given a $\mathbf{RA}$, an assignment, also called an expected allocation, is a nonnegative matrix $P \in {\mathbb {R}}_{\ge 0}^{N\times E}$ satisfying

• (i) $\sum _{e \in E} P(i,e) \le d(i)$ for all $i \in N,$

• (ii) $\sum _{i \in N} P^i \in \mathrm{B}(\rho ),$

where P(i, e) represents the number of copies of good e agent i obtained, and ith row denoted by $P^i$ is the total goods allocated to agent i. We assume $\sum _{i\in N} d(i) \ge \rho (E)$ indicating that the goods are in high demand or non-disposal. By our problem setting, a random assignment problem is finding a matrix P with vector $(p_e \mid e \in E)\in \mathrm{B}(\rho )$ to satisfy efficiency and fairness, where $p_e=\sum _{i \in N} P(i,e)$.

When we rewrite the submodular inequality as

$$\begin{aligned} \rho (X) -\rho (X \cap Y) \ge \rho (X \cup Y) -\rho (Y) , \; \forall X,Y \in 2^E, \end{aligned}$$

(2)

(2) is called “diminishing return,” economies of scale, or economies of scope. Submodular functions are used in various disciplines, such as combinatorics, operations research, information theory, and machine learning. The concept of the base polyhedron of a polymatroid is equivalent to the core of a convex game due to Shapley [21]. Well-known submodular functions include cut functions of graphs and hypergraphs, entropy, mutual information, coverage functions, and budget additive functions. It is also known that any set function can be expressed as the difference of two monotone nondecreasing submodular functions [20]. For an assignment problem $\mathbf{RA}=(N,E,\succeq ,\mathbf{d}, (E,\rho ))$, submodular property (2) allows preferred goods sharing more portion of total resources if preferred goods are chosen earlier. For example, when assigning a task to a person, submodularity means higher specialty bringing higher effect. Consider the following Example 1.

In the following, we write one element set $\{e\}$ as e for simplicity.

Example 1

Consider agent set $N=\{1,2,3,4\}$ and good get $E=\{a,b,c\}$ with an all “1” demand vector 1. The most preferred goods for all agents are given as follows. They are called acceptable goods under dichotomous preference (Bogomolnaia and Moulin [15]).

Suppose that a rank function $\rho$ on goods E is given by (see Fig. 4)

$$\begin{aligned} \rho (X)={\left\{ \begin{array}{ll} |X |&{}{ if} \; X\in 2^E \setminus \{\{a,b\},E \} \\ |X |-1 \quad &{} { if} \; X \in \{\{a,b\},E \} \end{array}\right. } \end{aligned}$$

Fig. 4

Graph $G=(V,E)$ with edge set $\{a,b,c\}$ and rank 2

An expected allocation is the following nonnegative matrix

Since $\sum _{i \in N}P^i =(p_a, p_b, p_c) =(1/3, 2/3, 1) \in \mathrm{B}(\rho )$, P is an assignment according to our definition. We show that assignment P is efficient and fair in the following sections.

The following lemma is fundamental in the theory of polymatroids and submodular functions.

Lemma 1

Given a vector $x \in \mathrm{P}(\rho )$ and $X,Y \subseteq E$, if $x(X)=\rho (X)$ and $x(Y)=\rho (Y)$, then we have $x(X\cup Y)=\rho (X\cup Y)$ and $x(X\cap Y)=\rho (X\cap Y)$. That is, the x-tight sets are closed with respect to the set union and intersection.

For a polymatroid $(E, \rho )$ and a non-empty subset $F \subseteq E$, define $\rho _F: 2^{E \setminus F} \rightarrow {\mathbb {R}}$ by $\rho _F(X)=\rho (X \cup F)-\rho (F)$ for all $X \subseteq E \setminus F$. We call $(E \setminus F, \rho _F)$ a contraction of the polymatroid $(E , \rho )$ by F. Moreover, define $\rho ^F: 2^ F \rightarrow {\mathbb {R}}$ by $\rho ^F(X)=\rho (X)$ for all $X \subseteq F$. We call $(F,\rho ^F)$ a reduction of $(E, \rho )$ by F. For any nonempty $F_1,F_2 \subseteq E$ with $F_1 \subset F_2$ we put $\rho _{F_1}^{F_2}=(\rho ^{F_2})_{F_1}$, which is called a minor of $(E,\rho )$. The following result is well known.

Proposition 1

A minor of a polymatroid is also a polymatroid.

The mechanisms proposed in the following sections are the iteration of taking minors of $(E,\rho )$. By Proposition 1, we have the invariance of submodularity under minors.

2.2 Independent Flows

To treat the problem with indifference preference, we need to solve the independent flow problems during the extended algorithms provided in Sects. 3.2 and 4.2 .

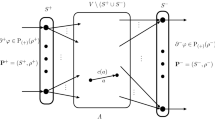
Consider a (directed) graph $G=(V,A)$ with a vertex set V and arc set A, which has a set $S^+$ of entrances and a set $S^-$ of exists, where $S^+$ and $S^-$ are disjointed subsets of V (see Fig. 5 and refer to the paper given by Fujishige et al. [22]). Each arc $a \in A$ has a capacity $c(a)>0$. We also have a polymatroid $\mathbf{P}^+=(S^+,\rho ^+)$ on a set $S^+$ of entrances and another polymatroid $\mathbf{P}^-=(S^+,\rho ^-)$ on a set $S^-$ of exits. Denote the present network by $\mathcal{N}=(G=(V,A),S^+,S^-,c, \mathbf{P}^+=(S^+,\rho ^+), \mathbf{P}^-=(S^-,\rho ^-))$. A function $\varphi : A \rightarrow {\mathbb {R}}_{\ge 0}$ is called an independent flow if it satisfies

$$\begin{aligned}&0 \le \varphi (a) \le c(a) \quad \forall a \in A, \end{aligned}$$

(3)

$$\begin{aligned}&\partial \varphi (v)=0 \quad \forall v \in V \setminus (S^+ \cup S^-), \ \partial ^+ \varphi \in \mathrm{P}_{(+)}(\rho ^+), \partial ^- \varphi \in \mathrm{P}_{(+)}(\rho ^-), \end{aligned}$$

(4)

where $\partial \varphi \in {\mathbb {R}}^V$ is the boundary of $\varphi$ defined by

$$\begin{aligned} \partial \varphi (v)=\sum _{(v,w)\in A} \varphi (v,w) - \sum _{(w,v)\in A} \varphi (w,v) \quad \forall v \in V, \end{aligned}$$

(5)

and $\partial ^+ \varphi \in {\mathbb {R}}^{S^+}$ and $\partial ^- \varphi \in {\mathbb {R}}^{S^-}$ are defined by

$$\begin{aligned} \partial ^+ \varphi (v)= \partial \varphi (v) \, \forall v \in S^+, \quad \partial ^- \varphi (v)= -\partial \varphi (v) \, \forall v \in S^-. \end{aligned}$$

(6)

Some examples of independent flows are given in [12].

Fig. 5

Independent flow network $\mathcal{N}$

The independent flow considered in each iteration of Algorithms I & II (in the case of divisible goods) is based on an underlying bipartite graph $G=(V,A)$ with vertex set $V=N \cup E$ and arc set $A \subseteq N \times E$. Here $N=S^+$ and $\rho ^+$ is a modular function defined by a demand upper bound vector $\mathbf{d}\in {\mathbb {R}}^N_{> 0}$, while $S^-=E$ and $\rho ^- =\rho$ (note that $V \setminus (S^+ \cup S^-)= \emptyset$). The capacity is $c(a)=\infty$ for all arc $a \in A$. For simplicity, we have the following notations $\mathcal{N}=(G=(V,A),S^+,S^-,c,(S^+,\rho ^+), (S^-,\rho ^-))$ as $\mathcal{N}=(G=(N \cup E,A),\mathbf{d},(E,\rho ))$ (see Fig. 6).

Fig. 6

Independent flow network $\mathcal{N}$ with an underlying bipartite graph

The following fact is closely related to Sect. 7, a lottery of assigning indivisible goods to agents (see, for example, [12, 14]).

Theorem 1

Let $(E, \rho )$ be a polymatroid with integer-valued rank function $\rho \in {\mathbb {Z}}^E$. Then $\mathrm{B}(\rho )$ (resp. $\mathrm{P}_{(+)}(\rho ))$ is an integral polyhedron, i.e., the convex hull of integral vectors.

Theorem 2

Let $P^* \subset {\mathbb {R}}^A$ be the set of all independent flows $\varphi$ in a network $\mathcal{N}=(G=(V,A),S^+,S^-,c,(S^+,\rho ^+), (S^-,\rho ^-))$. Suppose the capacity function c and the rank functions $\rho ^{+}$ and $\rho ^-$ are integer-valued, then $P^*$ is an integral polytope. Moreover, the same integrality property holds if we consider the set of independent flows of fixed integral value $\partial ^+ \varphi (S^+)$ or $\partial ^- \varphi (S^-)$.

2.3 Bipartite Graphs

Fix a bipartite graph $G=(N \cup E,A)$. Let $\varGamma : 2^N \rightarrow 2^E$, and for $X \subseteq N$, $\varGamma (X)$ denotes the set of vertices E adjacent to at least one vertex of X, i.e.,

$$\begin{aligned} \varGamma (i)= & {} \{ e \in E \mid (i,e) \in A \}, \end{aligned}$$

(7)

$$\begin{aligned} \varGamma (X)= & {} \bigcup _{i \in X} \varGamma (i). \end{aligned}$$

(8)

Lemma 2

Given a bipartite graph $G=(N \cup E,A)$, for any $X,Y \subseteq N$, we have

$$\begin{aligned}&\varGamma (X \cup Y) = \varGamma (X) \cup \varGamma (Y), \end{aligned}$$

(9)

$$\begin{aligned}&\varGamma (X \cap Y) \subseteq \varGamma (X) \cap \varGamma (Y). \end{aligned}$$

(10)

Proof

We only show the latter case. The first one can be done following the same approach.

If $e \in \varGamma (X \cap Y)$, we have at least one $i \in X \cap Y$, which means that good e is adjacent to both X and Y. Therefore $e \in \varGamma (X) \cap \varGamma (Y).$²$\square$

Lemma 3

Fix a bipartite graph $G=(N \cup E,A)$. If $\rho$ is a monotone submodular function on E, then the composition $\rho \circ \varGamma : 2^N \rightarrow {\mathbb {R}}$ of functions $\varGamma$ and $\rho$ is also a monotone submodular function on N.

Proof

For $\forall X,Y \subseteq N$, we have

$$\begin{aligned}&\rho (\varGamma (X))+\rho (\varGamma (Y)) \ge \rho (\varGamma (X)\cup \varGamma (Y)) + \rho (\varGamma (X)\cap \varGamma (Y)) \\&\quad \ge \rho (\varGamma (X\cup Y)) + \rho (\varGamma (X\cap Y)), \end{aligned}$$

where the first inequality follows from the submodularity of $\rho$, and the second one follows from Lemma 2 and the monotonicity of $\rho$.

The monotonicity of composition function $\rho \circ \varGamma$ is obvious. $\square$

3 Random Assignment with Top Preferences

In Sect. 2.1, we define the random assignment problem, $\mathbf{RA}=(N,E,\succeq ,\mathbf{d}, (E,\rho ))$. In this section, we consider a special case, the model with two choices for goods, acceptable (top preference) or not (or others).³ The allocation for a general model is basically the algorithm iteration provided in this section. For simplicity, we assume that the demand upper bound vector d is all “1” entries denoted by 1 (we will treat the general case in the next section).

3.1 Maximal Saturated Sets and the Social Welfare Concept

For the problem considered here, a special case has been solved by Katta and Sethurama [8]. They treated the problem through the maximal flow in a network. A natural generalization is the constraints of polymatroids on goods as follows (see Fig. 7).

Fig. 7

Independent flow network $\mathcal{N}(\lambda )$

Considering a network $\mathcal{N}(\lambda ) \equiv (G=(N \cup E,A),\lambda {\mathbf {1}}, (E,\rho ))$ with a parameter $\lambda \ge 0$, where $(i,e) \in A$ if and only if good e is the top preference of agent i and agent i may have more than one good as top preference. Let $\varphi _{\lambda }: A\rightarrow {\mathbb {R}}_{\ge 0}$ denote an independent flow in $\mathcal{N}(\lambda )$. We increase the parameter $\lambda$ $=\partial ^+{\varphi _\lambda }(i)$ $(\forall i\in N)$ to maximize the goods shared by agents while keeping constraints on goods $\partial ^- \varphi _{\lambda } \in \mathrm{P}_{(+)}(\rho )$. These can be formulated as:

$$\begin{aligned} {{\bar{\lambda }}}=\max \{ \lambda >0 \mid \partial ^-{\varphi _\lambda } \in \mathrm{P}_{(+)}(\rho ) \}. \end{aligned}$$

(11)

Note that ${{\bar{\lambda }} }$ in (11) is equivalent to

$$\begin{aligned} {{\bar{\lambda }} }= \min \{ \lambda >0 \mid \partial ^- \varphi _{\lambda }(Z)=\rho (Z),\; \; Z \subseteq E \}. \end{aligned}$$

(12)

In (12), Z is the set of goods “blocking”⁴ the increasing of $\lambda$. Then there exists $Z \ne \emptyset$ such that $\varphi _{\lambda }(Z)=\rho (Z)$ if $\lambda >0$.

For ${{\bar{\lambda }}}$ in ${\mathcal {N}}({{\bar{\lambda }}})$, let ${{\bar{Y}}}$ be defined as

$$\begin{aligned} {{\bar{Y}}} = \max \{ Y \subseteq E \mid \partial ^- \varphi _{{\bar{\lambda }}}(Y)=\rho (Y) \}, \end{aligned}$$

(13)

where ${{\bar{Y}}}$ is unique by Lemma 1.

Lemma 4

Let ${{\bar{Y}}}$ and ${\varphi _{{\bar{\lambda }}}}$ be defined as above, and let

$$\begin{aligned} {{\bar{X}}} = \{ i \in N \mid \varGamma (i) \subseteq {{\bar{Y}}} \}=\varGamma ^{-1}({\bar{Y}}). \end{aligned}$$

(14)

Then, we have

$$\begin{aligned} {{\bar{\lambda }}} |{{\bar{X}}} |= \partial ^- {\varphi _{{\bar{\lambda }}}}(\varGamma ({{\bar{X}}}))=\rho (\varGamma ({ {\bar{X}}}))=\rho ({{\bar{Y}}}) . \end{aligned}$$

(15)

Proof

Consider the following relations (see Fig. 8 for more illustration):

$$\begin{aligned} {{\bar{\lambda }}} |{{\bar{X}}} | \le \partial ^- { \varphi _{{\bar{\lambda }}}}(\varGamma ({{\bar{X}}})) \le \rho (\varGamma ({{\bar{X}}})) \le \rho ({{\bar{Y}}})=\partial ^- { \varphi _{{\bar{\lambda }}}}({{\bar{Y}}}). \end{aligned}$$

(16)

The first inequality in (16) follows from the definition of ${{\bar{X}}}$, i.e., no flow of ${{\bar{\lambda }}} |{{\bar{X}}} |$ can leave $\varGamma ({{\bar{X}}})$, but there may be some flows from $N \setminus {{\bar{X}}}$ to $\varGamma ({{\bar{X}}})$. The second one is the independent flow constraint in (11). For the third inequality in (16), we have $\varGamma ({{\bar{X}}}) \subseteq {{\bar{Y}}}$ by the definition of ${{\bar{X}}}$. The inequality comes from the maximality of ${{\bar{Y}}}$ and the monotonicity assumption of $\rho$. The last equality follows from the definition (13) of ${{\bar{Y}}}$.

Fig. 8

Illustrative network for (16) and Remark 1

Next we show that for each $i \in N \setminus {{\bar{X}}}$, the independent flow ${ \varphi _{{\bar{\lambda }}}}$ satisfies ${ \varphi _{{\bar{\lambda }}}}(i,e)= 0$ for every $e \in {{\bar{Y}}}$. Otherwise, we can decrease a small amount flow $\epsilon > 0$ of arc (i, e) and increase the same value $\epsilon > 0$ of $(i,e')$, the existence of arc $(i,e')$ follows from $i \notin {{\bar{X}}}$. This is possible since ${{\bar{Y}}}$ is the maximal saturated set that does not contain $e'$. However, this contradicts the saturation of ${{\bar{Y}}}$ with ${{\bar{\lambda }}}$. Hence, we have

$$\begin{aligned} {{\bar{\lambda }}} |{{\bar{X}}} | = \partial ^-{ \varphi _{{\bar{\lambda }}}}({{\bar{Y}}}). \end{aligned}$$

(17)

Thus, all the inequalities in (16) are satisfied with equalities. $\square$

We can introduce an egalitarianism social welfare concept by Dutta and Ray [23] and mentioned by Bogomolnaia and Moulin [15]. Let ${{\bar{X}}}^* \subseteq N$ be a maximal set satisfying

$$\begin{aligned} {{\bar{X}}}^* \in \arg \min _{\emptyset \ne X \subseteq N} \frac{ \rho (\varGamma (X)) }{|X|}. \end{aligned}$$

(18)

Here ${{\bar{X}}}^*$ is unique because of Lemma 3.⁵ Define ${{\bar{\lambda }}}^*(>0)$ by

$$\begin{aligned} {{\bar{\lambda }}}^* \equiv \frac{ \rho (\varGamma ({{\bar{X}}}^*)) }{|{{\bar{X}}}^*|}=\min _{\emptyset \ne X \subseteq N} \frac{ \rho (\varGamma (X)) }{|X|}. \end{aligned}$$

(19)

From the above discussions and Lemma 4, we obtain:

Proposition 2

Given a network $\mathcal{N}(\lambda )=(G,\lambda {\mathbf {1}},(E,\rho ))$, let ${{\bar{X}}}^*$ and ${{\bar{\lambda }}}^*$ be defined as in (18) and (19), respectively, and let $\varphi _{{{\bar{\lambda }}}^*}$ be an independent flow in $\mathcal{N}({{\bar{\lambda }}}^*)=(G,{{\bar{\lambda }}}^*{\mathbf {1}},(E,\rho ))$. Then we have

$$\begin{aligned} \rho (\varGamma ({{\bar{X}}}^*)) = \partial ^-\varphi _{{{\bar{\lambda }}}^*}(\varGamma ( {{\bar{X}}}^*))={{\bar{\lambda }}}^* |{{\bar{X}}}^*|, \end{aligned}$$

(20)

and (${{\bar{\lambda }}}^*, {{\bar{X}}}^*$) coincides with (${{\bar{\lambda }}}, {{\bar{X}}}$) in (11) and (13).

Observation 1

Suppose that $\lambda (i)>0$ ($i \in N$) is the boundary of vertex (agent) i in $\mathcal{N}(\lambda )$. Then (19) becomes

$$\begin{aligned} {{\bar{\lambda }}}^* \in \;\; \;\;\arg \max _{ {\mathcal {N}}(\lambda (i)) } \min _{i \in N} \lambda (i), \end{aligned}$$

(21)

i.e., each $\lambda (i)$ ($i \in N$) receiving the same value, the average determined by (18). If some agents obtain more portion, then there exists at least one agent who gets less allocation than ${{\bar{\lambda }}}^*$ determined by (21). Maximizing the minimizer of $\lambda (i)$ ($i \in N$) is the principle of (extended) PS mechanism, and the lexicographic optimum is generalized in Sect. 6.

3.2 Algorithm

During the execution of the following Algorithm I, we construct a network $\mathcal{N}_p(\lambda )$ ($1 \le p \le \min \{|N|,|E|\}$) in each iteration on smaller sets $N_p\subseteq N$ and $E_p \subseteq E$.

Algorithm I6
Intput: A random assignment problem RA$=(N,E,\succeq ,\mathbf{1},(E,\rho ))$.
Output: An expected allocation matrix $P\in {\mathbb {R}}^{N\times E}_{\ge 0}$.
Step 0: Put $N_1 \leftarrow N$, $E_1 \leftarrow E$, $\rho _1 \leftarrow \rho$. Put $p \leftarrow 1.$
Step p: Construct ${\mathcal {N}}_p(\lambda )=(G=(N_p \cup E_p,A_p), \lambda {\mathbf {1}},(E_p,\rho _p ))$. Compute
${\lambda }_p = \max \{ \lambda >0\mid \partial ^+\varphi = \lambda \mathbf{1}, \; \partial ^-\varphi \in \mathrm{P}_{(+)}(\rho _p) \}$
by solving the associated independent flow ${ \varphi }_{\lambda _p}$ of ${\mathcal {N}}_p(\lambda _p)$.
Let $T_p \subseteq E_p$ be the maximal saturated set of $\partial ^-{\varphi }_{\lambda _p}$ and $X_p =\varGamma ^{-1}(T_p)$. Put
$P(i,e) \leftarrow \varphi _{\lambda _p}(i,e) \;\ \mathrm{for } \;e \in T_p \qquad \qquad \mathrm{if} \; i \in X_p$
$N_{p+1} \leftarrow N_p \setminus X_p, \; E_{p+1} \leftarrow E_p \setminus T_p \qquad \mathrm{otherwise}.$
If $$E_{p+1} \ne \emptyset ,$$ E p + 1 ≠ ∅ , 7 put $$\rho _{p+1} \leftarrow \rho _{T_1 \cup \ldots \cup T_p}$$ ρ p + 1 ← ρ T 1 ∪ … ∪ T p and go to the beginning of Step p.
Otherwise stop and return P.

Note that by Proposition 2, we have $0={ \lambda }_0< { \lambda }_{1}< \ldots < { \lambda }_{k}$ for some $k \le |E|$ during the execution of Algorithm I.

Remark 1

By a little abuse of language, from Proposition 2, if we take a cut ${{\bar{X}}} \cup \varGamma ({{\bar{X}}})$ in $\mathcal{N}^T({{\bar{\lambda }}})$ such that no arc with infinite capacity leaving the cut, then the capacity of the cut is ${{\bar{\lambda }}} (|N|-|{{\bar{X}}}|) + \rho (\varGamma ({{\bar{X}}}))\ne \infty$. Moreover, the flow entering the cut is zero. Then, we have $\varGamma ({{\bar{X}}}) \subseteq {{\bar{Y}}}$ and $\rho (\varGamma ({{\bar{X}}})) =\rho ({{\bar{Y}}})$. (Refer to Fig. 8.) Hence, the associated nonzero flows of each agent are saturated within the same step p. Precisely, if $P(i,e)>0$ and $P(i,e')>0$ with $e\sim _i e'$, then $\{e,e'\}\subseteq T_p$. The fact is crucial in the sequential proofs later for the preference profile including the indifference relation.

Example 1 (Continue): For $p=1$, $\mathcal{N}_1(\lambda )$ is constructed and an independent flow in $\mathcal{N}_1(\lambda _1)$ is shown in Fig. 9.

Fig. 9

Independent flow ${ \varphi }_{\lambda _1}$ of $\mathcal{N}_1(\lambda _1)$ in Example 1

We obtain the saturated set $T_1$, $X_1 =\varGamma (T_1)$ and the maximal $\lambda _1$ to satisfy the constraints on goods as follows,

$$\begin{aligned} { T_1=\{a,b\}, \quad X_1=\{1,3,4\}, \quad \lambda _1=\frac{1}{3}}. \end{aligned}$$

Note that $a \sim _1 b$ with $P(1,a) \ge 0$ and $P(1,b) \ge 0$, both a and b are saturated at Step 1 as stated in Remark 1. All flows entering node 2 are toward c and the flow to $a \in T_1$ is zero making $\lambda _1$ reach the maximum 1/3. This is the fact discussed in Observation 1 and the proof of Lemma 4.

For $p=2$, the corresponding $\mathcal{N}_2(\lambda _2)$ is shown in Fig. 10. Thus we obtain

$$\begin{aligned} T_2=\{c\}, \quad X_2=\{2\}, \quad \lambda _2=1. \end{aligned}$$

Fig. 10

Independent flow ${\varphi }_{\lambda _2}$ of $\mathcal{N}_2(\lambda _2)$ in Example 1

We note that the allocation is not unique, unlike in the case of a strict preference profile. This occurs when two, or more goods saturate simultaneously.

For the efficiency and fairness of Algorithm I, we will show them in a more general case for Algorithm II.⁸

It is worth noting that a similar scheme treating a general case is provided in [19] as an extension of the one in [24].

4 Random Assignments on Full Preference Domains

This section provides a mechanism for our original model, i.e., assign goods among agents over a preference profile ${\succeq }=(\succeq _i \mid i \in N)$ and a demand upper bound vector $\mathbf{d}=(d(i) \mid i \in N)\in {\mathbb {Z}}^N_{> 0}$ with submodular constraints on goods.

4.1 A Corollary of Proposition 2

Similar to the discussion of Sect. 3.1, the parametric network $\mathcal{N}(\lambda )=(G=(N \cup E,A), \lambda \mathbf{d} ,(E,\rho ))$ is given in Fig. 11.⁹ Let ${{\bar{X}}}^*$ be the maximal set satisfying

$$\begin{aligned} {{\bar{X}}}^* \in \arg \min _{\emptyset \ne X \subseteq N} \frac{ \rho (\varGamma (X)) }{\sum _{i \in X}d(i)}, \end{aligned}$$

(22)

and let ${{\bar{\lambda }}}^* (>0)$ be defined by

$$\begin{aligned} {{\bar{\lambda }}}^*=\frac{ \rho (\varGamma ({{\bar{X}}}^*)) }{\sum _{i \in {{\bar{X}}}^*}d(i)}. \end{aligned}$$

(23)

Corollary 1

Let ${{\bar{X}}}^*$ and ${{\bar{\lambda }}^*}$ be defined as in (22) and (23), respectively, and let $\varphi _{{\bar{\lambda }}^*}$ be the associated independent flow in $\mathcal{N}({{\bar{\lambda }}}^*)$. Then we have

$$\begin{aligned} \rho (\varGamma ({{\bar{X}}}^*)) =\partial ^- \varphi _{{\bar{\lambda }}^*}(\varGamma ( {{\bar{X}}}^*)) = \sum _{i \in {{\bar{X}}}^*} d(i) {{\bar{\lambda }}}^*. \end{aligned}$$

(24)

Proof

We can view each agent i containing d(i) subagents, and the result follows from Proposition 2$\square$

Fig. 11

Independent flow network $\mathcal{N}(\lambda )=(G=(N \cup E,A), \lambda \mathbf{d},(E,\rho ))$

4.2 Algorithm

Here, agents’ available top preferred goods are added in each iteration after saturated goods being removed, unlike Algorithm I, and also the agents’ set is N throughout Algorithm II. Moreover, a cumulated capacity function ${c}_p \in {\mathbb {R}}_{\ge 0}^N$ is introduced and updated to compensate those agents, not in the inverse of the saturated good set in the later steps (also refer to Example 2).

Algorithm II
Input: A random assignment problem $\mathbf{RA}=(N,E,{\succeq },\mathbf{d},(E,\rho ))$.
Output: An expected allocation matrix $P\in {\mathbb {R}}^{N\times E}_{\ge 0}$.
Step 0: Put $c_1 \leftarrow \mathbf{0} \in {\mathbb {R}}^N$, $p \leftarrow 1.$ Let $E_1$ contain agents’ most preferred goods.
Step p: Construct $\mathcal{N}_p(\lambda )=(G=(N \cup E_p, A_p), \lambda \mathbf{d}, \mathbf{c}_p, (E_p,\rho _p))$, where $A_p=$
$\{(i,e) \mid e$ is i’s most preferred good in $E_p\}$ (see Fig. 12). Compute $\lambda _p$ by
solving independent flow ${\varphi }_{\lambda _p}$ as follows,
$\,\lambda _p = \max \{ \lambda >0 \mid \partial ^+\varphi _{\lambda } = (d(i)(c_p(i) +\lambda ) \mid i \in N), \; \partial ^-\varphi _{\lambda } \in \mathrm{P}_{(+)}(\rho _p) \}.$
Let $T_p \subseteq E_p$ be the maximal saturated set of $\partial ^-\varphi _{\lambda _p}$ and $X_p =$ $\varGamma ^{-1} (T_p)$. Put
$P(i,e) \leftarrow \varphi _{\lambda _p}(i,e) \; \mathrm{for } \;e \in T_p, \; c_{p}(i)\leftarrow 0 \qquad \mathrm{if} \; i \in X_p,$
$c_{p+1}(i) \leftarrow c_p(i)+ \lambda _p \hspace{37.5mm} \mathrm{if}\; i \in N \setminus X_p,$
$E_{p+1}\leftarrow (E_p \setminus T_p) \cup \{e \mid e \mathrm{\, is \, agents' \, most \, preferred \, available \, good} \} .$
If $E_{p+1} \ne \emptyset$, put $\rho _{p+1} \leftarrow \rho _{T_1 \cup \ldots \cup T_p}$, then go to the beginning of Step p.
Otherwise, ($E_{p+1} = \emptyset )$ return P.

Note that the capacity vector $\mathbf{c}_p$ makes the agents in the inverse of saturated goods get more portion (larger $\lambda _p$) without sacrificing other agents’ allocation because of indifference among these goods. The same concept is stated in Remark 1.

Fig. 12

Independent flow network $\mathcal{N}_p(\lambda )$ for Algorithm II

Example 2

Consider agent set $N=\{1,2,3,4\}$, good set $E=\{a,b,c,d\}$ and demand upper bound vector $\mathbf{d}=\mathbf{1}$. Agents’ preference profile is given as follows.

$$\begin{aligned}\begin{array}{cc} 1 \quad &{} a \sim _1 b \succ _1 c \succ _1 d \\ 2 \quad &{} a \sim _2 c \succ _2 b \succ _2 d \\ 3 \quad &{} a \succ _3 c \succ _3 d \succ _3 b \\ 4 \quad &{} b \succ _4 a \succ _4 d \succ _4 c \end{array}\end{aligned}$$

The polymatroid ($E,\rho$) constraint on goods is defined by

$$\begin{aligned} \rho (X)={\left\{ \begin{array}{ll} |X |-1 &{}{ if} \; \{a,b\} \subseteq X \subseteq E \\ |X |\quad &{} { if} \; \{a,b\} \nsubseteq X \subset E \end{array}\right. } \end{aligned}$$

For Step $p=1$, network $\mathcal{N}_1(\lambda _1)$ and its independent flow are shown in Fig. 13. The step is the same as in Example 1 (Continue) shown in Fig. 9.

Fig. 13

Independent flow $\varphi _1$ of $\mathcal{N}_1(\lambda _1)$ in Example 2

We have saturated set $T_1$ and in-flow $\lambda _1$ for parameter $\lambda$ as

$$\begin{aligned} {T_1= \{a,b\} \quad \lambda _1=\frac{1}{3}}. \end{aligned}$$

Then saturated set $\{a,b\}$ is removed. The most preferred good for agents 1 and 2 are good c and agent 4’s most available preferred good d is added. Although agent 2 does not get an allocation of good a in Step 1, the same amount 1/3 is accumulated to the capacity function to get the allocation of good c indifferent to good a later.

When $p=2$, we have $\mathcal{N}_2(\lambda _2)$ as Fig. 14, where agent 2 has an accumulated capacity 1/3. We obtain

Fig. 14

Independent flow $\varphi _2$ of $\mathcal{N}_2(\lambda _2)$ in Example 2

$$\begin{aligned} {T_2= \{c\} \quad \lambda _2=\frac{2}{9}. } \end{aligned}$$

Following the same arguments, we have

$$\begin{aligned} T_3= \{d\} \quad \lambda _3=\frac{7}{36}. \end{aligned}$$

The output of Algorithm II is the following expected allocation:

Example 3

Consider $N=\{1,2,3,4\}$ and $E=\{a,b,c,d\}$ again. The preference profile is given by

$$\begin{aligned}\begin{array}{cc} 1 &{} a\succ _1 b \succ _1 c \succ _1 d \\ 2 &{} a \sim _2 c \succ _2 b \succ _2 d \\ 3 &{} a \succ _3 c \succ _3 d \succ _3 b \\ 4 &{} b \succ _4 a \succ _4 d \succ _4 c \end{array}\end{aligned}$$

The demand upper bound vector is given by $\mathbf{d}=(4,2,1,1) \in {\mathbb {Z}}^N_{\ge 0}$. The polymatroid ($E,\rho$) is defined by

$$\begin{aligned} \rho (X)={\left\{ \begin{array}{ll} 4 |X |&{}\mathrm{if} \; |X |\le 2 \\ 8 \quad &{} \mathrm{if} \; |X |> 2 \end{array}\right. } \quad (\forall X \subseteq E). \end{aligned}$$

(25)

We have the independent flows of $\mathcal{N}_1(\lambda _1)$ and $\mathcal{N}_2(\lambda _2)$ shown in Figs. 15 and 16, and

$$\begin{aligned} {T_1= \{a\} \quad \lambda _1=\frac{4}{5}}, \quad {T_2= \{b,c,d\} \quad \lambda _2=\frac{1}{5} } \end{aligned}$$

are the associated saturated sets $T_p$ and parametric values $\lambda _p$ for $p=1,2$.

Fig. 15

An independent flow $\varphi _1$ of $\mathcal{N}_1(\lambda _1)$ in Example 3

Fig. 16

An independent flow $\varphi _2$ of $\mathcal{N}_2(\lambda _2)$ in Example 3

The following matrix P is the expected allocation obtained,

5 Properties of the Mechanisms

5.1 Ordinal Efficiency

Next we present the properties of the proposed mechanisms, the first and prominent one, efficiency.

Fix a random assignment problem $\mathbf{RA}=(N,E,{\succeq },\mathbf{d},(E,\rho ))$. Let $U(\succeq _i,e)\equiv \{e' \in E \mid e' \succeq _i e \}$ be the upper contour set of good e at $\succeq _i$. Given expected allocation matrices P and Q, we say that P ordinally dominates Q if for each agent i with preference relation $\succeq _i$, ith row $P^i$ of P sd-dominates¹⁰ith row $Q^i$ of Q,

$$\begin{aligned} P^i \succeq _i^\mathrm{sd} Q^i \quad \Longleftrightarrow \;\; \sum _{e \in U(\succeq _i,e)} P(i,e) \ge \sum _{e \in U(\succeq _i,e)}Q(i,e), \quad \forall e \in E, \end{aligned}$$

(26)

with strict inequality for some i. We say that P is ordinally efficient if P is not ordinally dominated by any other allocation.

Recall Remark 1, the key point in the following proofs for the mechanism over full domain preferences is the indifference goods of each agent with positive allocation saturated within an iteration.¹¹ Thus, the proof schemes in the following are the same as those in [11, 12].

Theorem 3

The expected allocation computed by Algorithm II is ordinally efficient.

Proof

By Algorithm II, we obtain a random assignment P, a partition $T_1,\ldots ,T_{p^*}$ of E. Let Q be an arbitrary expected allocation, and suppose that Q ordinally dominates P, or for each $i \in N$ we have

$$\begin{aligned} \sum _{e \in U(\succeq _i,e)} P(i,e) = \sum _{e \in U(\succeq _i,e)}Q(i,e), \quad \forall e \in E, \end{aligned}$$

(27)

It suffices to prove (27).

Let us denote $E^i_q$ as agent i’s most available preferred goods at Step q, and let $Q(i,E^i_q)$ and $P(i,E^i_q)$ be defined respectively by

$$\begin{aligned} Q(i,E^i_q)= \sum _{e \in E^i_q} Q(i,e), \quad P(i,E^i_q)= \sum _{e \in E^i_q} P(i,e). \end{aligned}$$

(28)

Suppose that for some integer $q^*\ge 1$ we have

$$\begin{aligned} Q(i,E^i_q) = P(i,E^i_q)\qquad (\forall q=1,\ldots ,q^*-1,\, \forall i\in X_q) \end{aligned}$$

(29)

and we execute $q^*$th step (here recall that $X_q=\varGamma ^{-1}(T_q)$). Then, from Algorithm II we have

$$\begin{aligned} \sum _{i\in X_{q}}P(i,E^i_q) =\rho _q( T_q) \qquad (q=1,\ldots ,q^*). \end{aligned}$$

(30)

Since Q ordinally dominates P, it follows from (29) that $Q(i,E^i_{q^*})\ge P(i,E^i_{q^*})$ for all $i\in X_{q^*}$. Hence, from (29) and (30) we obtain

$$\begin{aligned} Q(i,E^i_{q^*})= P(i,E^i_{q^*})\qquad (\forall i\in X_{q^*}), \end{aligned}$$

(31)

since $\sum _{i\in X_{q^*}}Q(i,E^i_{q^*})\le \rho _q(T_q)$, and when $q^*=1$, Eq. (29) is void (thus holds) by induction. (Here, recall that $\sum _{q=1}^{q^*}\sum _{i\in X_q}Q(i,E^i_q)\le \rho (T_1 \cup \ldots \cup T_{q^*})$.) From the discussions before Theorem 3, and Algorithm II which always selects agent i’s most preferred available goods, we have

$$\begin{aligned} \sum _{e \in U(\succeq _i,e)} P(i,e) = \sum _{e \in E^i_1 \cup \ldots \cup E^i_k} P(i,e) = \sum _{e \in E^i_1 \cup \ldots \cup E^i_k} Q(i,e) = \sum _{e \in U(\succeq _i,e)} Q(i,e), \,\, \forall e \in E, \end{aligned}$$

(32)

for some $k\ge 1$. Then the proof is complete. $\square$

5.2 Envy-Freeness

We say that an expected allocation P is normalized envy-free (see [25]) with respect to a preference profile ${\succeq }=(\succeq ^i \mid i \in N)$ if

$$\begin{aligned} \frac{1}{d(i)} P^i \succeq _i^\mathrm{sd} \frac{1}{d(j)} P^j \quad (\forall i,j \in N), \end{aligned}$$

(33)

where d(i) and d(j) are the integral demand upper bound of agents $i,j \in N$.

Theorem 4

The expected allocation computed by Algorithm II is normalized envy-free.

Proof

It suffices to show that for each $i \in N$ and $e \in E$, we have

$$\begin{aligned} \frac{1}{d(i)} \sum _{e \in U(\succeq _i,e)} P(i,e) \ge \frac{1}{d(j)} \sum _{e \in U(\succeq _i,e)} P(j,e), \quad \forall j \in N. \end{aligned}$$

(34)

Define

$$\begin{aligned} t^i_e = \frac{1}{d(i)} \sum _{e \in U(\succeq _i,e)} P(i,e). \end{aligned}$$

(35)

When goods in $\{e' \mid e' \sim e)$ are removed during the execution of Algorithm II, all goods $U(\succeq _i,e)$ have been removed from E (refer to the description and the footnote before Theorem 3). It follows that for $\forall j \in N$ the time spent by agent j to eat $U(\succeq _i,e)$ given by the possible value $\frac{1}{d(j)}\sum _{e \in U(\succeq _i,e)} P(j,e)$ is less than $t^i_e$. Hence, we obtain

$$\begin{aligned} t^i_e \ge \frac{1}{d(j)} \sum _{e \in U(\succeq _i,e)} P(j,e) \quad \forall j \in N. \end{aligned}$$

(36)

$\square$

Following the same arguments as above, we obtain the following theorem.

Theorem 5

The expected allocation computed by Algorithm I is ordinally efficient and normalized envy-free.

6 Lexicographic Characterization and Submodularity

For simplicity, we assume that the demand upper bound vector is an all “1” vector $\mathbf{1}$. As stated above, we can view an agent $i \in N$ with an integer demand upper bound $d(i)>1$ as d(i) subagents if needed.

The lexicographic property, maximin or lexmin maximizer, presented by Bogomolnaia [4] is a unified characterization of PS mechanism proposed by Bogomolnaia and Moulin [1]. The related problem, solutions of the lexicographically optimal base of a polymatroid was solved by Fujishge [19].

Let Q be any expected allocation matrix, define for each pair (i, e) with $i \in N$ and $e\in E$

$$\begin{aligned} Q(i,{{\hat{U}}}^i(e))\equiv \sum _{e\in U(\succeq _i,e)} Q(i,e). \end{aligned}$$

(37)

Moreover, denote $\mathbf{T}(Q(i,{{\hat{U}}}^i(e))\mid i\in N, e\in E)$ the linear arrangement of values $Q(i,{{\hat{U}}}^i(e))$ for all $i\in N$ and $e \in E$ in nondecreasing order of magnitude. For simplicity, we denote $\mathbf{T}(Q(i,{{\hat{U}}}^i(e))\mid i\in N, e\in E)$ as $\mathbf{T}(Q(i,{{\hat{U}}}^i(e)))$ in the sequel.

The lexicographic order among $\mathbf{T}(Q(i,{{\hat{U}}}^i(e)))$ for all expected allocation matrices Q is defined as usual. For any two expected allocation matrices P and Q, suppose that $\mathbf{T}(P(i,{{\hat{U}}}^i(e)))=(p_1,\ldots ,p_{k})$ and $\mathbf{T}(Q(i,{{\hat{U}}}^i(e)))=(q_1,\ldots ,q_{k})$ for some k. Then we say that $\mathbf{T}(P(i,{{\hat{U}}}^i(e)))$ is lexicographically greater than $\mathbf{T}(Q(i,{{\hat{U}}}^i(e)))$ if there exists an integer $\ell \in \{1,\ldots ,k\}$ such that $p_i=q_i$ for all $i=1,\ldots ,\ell -1$ and $p_\ell >q_\ell$.

We have the following theorem, the proof follows the approach for assignment problem studied by Bogomolnaia [4]. It is also a generalization of the result presented by Fujishige et al. [11].

Theorem 6

The expected allocation P obtained by Algorithm II is exactly the lexicographic maximizer of $\mathbf{T}(Q(i,{{\hat{U}}}^i(e))\mid i\in N, e \in E)$ among all expected allocation matrices Q.

(Proof) Let Q be an arbitrary expected allocation matrix such that $\mathbf{T}(Q(i,{{\hat{U}}}^i(e)))\ne \mathbf{T}(P(i,{{\hat{U}}}^i(e)))$. It suffices to show that $\mathbf{T}(Q(i,{{\hat{U}}}^i(e)))$ is lexicographically smaller than $\mathbf{T}(P(i,{{\hat{U}}}^i(e)))$.

Since $\mathbf{T}(Q(i,{{\hat{U}}}^i(e)))\ne \mathbf{T}(P(i,{{\hat{U}}}^i(e)))$, there exists a pair of $i\in N$ and $e \in E$ such that $Q(i,{{\hat{U}}}^i(e)) \ne P(i,{{\hat{U}}}^i(e))$. Let $(i^*,e^*)$ be such a pair (i, e) with the minimal value of $Q(i,{{\hat{U}}}^i(e)).$

Let $r_{d}=\sum _{p=0}^{d} \lambda _p$, where $\lambda _p$ is given in Algorithm II. Suppose that $E^{i^*}_{e^*}$ appears in $p^*$th iteration of Algorithm II. By our assumption, we have $Q(i,{{\hat{U}}}^i(e)) = P(i,{{\hat{U}}}^i(e))$ for all (i, e) such that $P(i,{{\hat{U}}}^i(e))\le r_{p^*-1}$, we define $P(i, {{\hat{U}}}^i(\emptyset )) = 0$.

For every $i \in N$, we can verify, step by step, that at each iteration p $(p=0,1, \ldots ,{p^*-1})$,

$$\begin{aligned} Q(i,{{\hat{U}}}^i(e)) = P(i,{{\hat{U}}}^i(e))=r_p < r_{p^*}, \quad \forall i \in N, \; e \succeq e^i, \end{aligned}$$

(38)

where $e^i$ is the least preferred good of agent i which saturated (lastly) during first ${p^*-1}$ iterations of Algorithm II.

In iteration $p^*$, if $\{e' \mid e' \sim e \} \subseteq T_{p^*}$, we have $P(i,{{\hat{U}}}(e))=r_{p^*}$. Otherwise $P(i,{{\hat{U}}}^i(e)) > r_{p^*}$, this is true for all $i \in N$. Hence, we have

$$\begin{aligned} P(i,{{\hat{U}}}^i(e)) \ge r_{p^*} \quad \forall i \in N. \end{aligned}$$

(39)

By Lemma 4, Corollary 1, and Observation 1, $\lambda _{p^*}$ (and then also $r_{p^*}$) is the maximal possible value satisfying the constraints. For Q, by our assumption of $(i^*,e^*)$, agent $i^*$ consumes some less preferred goods, i.e.,

$$\begin{aligned} Q(i^*,{{\hat{U}}}^{i^*}(e^*))< r_{p^*}=P(i^*,{{\hat{U}}}^{i^*}(e^*)). \end{aligned}$$

(40)

Therefore, (38)–(40) imply that $\mathbf{T}(Q(i,{{\hat{U}}}^i(e)))$ is lexicographically smaller than $\mathbf{T}(P(i,{{\hat{U}}}^i(e)))$. $\square$

The relation of lexicographic preference order with simultaneous eating mechanism was developed by Schulman and Vazirani [26]. Moreover, dl- (downward lexicographic) and ul-(upward lexicographic) extensions are also investigated in [27].

7 Designing a Lottery

Consider the following expected allocation P

$$\begin{aligned} P= \begin{pmatrix} {\tfrac{16}{5}}&{} {\tfrac{4}{5} } &{} 0 &{} 0\\ 0 &{} 0 &{} {\tfrac{8}{5} +\tfrac{2}{5}} &{} 0 \\ {\tfrac{4}{5}} &{} 0 &{} {\tfrac{1}{5}} &{} 0 \\ 0 &{} {\tfrac{4}{5}}+ {\tfrac{1}{5}}&{} 0 &{}0 \end{pmatrix} \end{aligned}$$

(41)

of Example 3. The probability distribution of integral allocations can be

$$\begin{aligned} P=\frac{4}{5}\begin{pmatrix} 3 &{} 1 &{} 0 &{} 0\\ 0 &{} 0 &{} 2 &{} 0 \\ 1 &{} 0 &{} 0&{} 0 \\ 0 &{} 1 &{} 0 &{}0 \end{pmatrix} + \frac{1}{5}\begin{pmatrix} 4 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 2 &{} 0 \\ 0 &{} 0 &{} 1&{} 0 \\ 0 &{} 1 &{} 0 &{}0 \end{pmatrix}. \end{aligned}$$

(42)

It is easy to check that both integral allocations in (42) satisfy demand bound $\mathbf{d}=(4,2,1,1)$ and submodular constraints (25). These are independent flows discussed in Sect. 2.2.

Next we show how to decompose the expected allocation P obtained by Algorithm II as a probability distribution (or a convex combination) of integral expected allocations, i.e.,

$$\begin{aligned} P=\sum _{k \in K} \nu _k Q^{(k)}, \end{aligned}$$

(43)

for some $K\ge 1$, where, $Q^{(k)} \in {\mathbb {Z}}^{N \times E}_{\ge 0}$ are expected allocations and $\nu _k >0$ for $\forall k \in K$ and $\sum _{k \in K} \nu _k =1$.

The randomized decomposition mechanism is based on the network presented by Fujishige et al. [22]. We present it for completeness. Figure 17 shows the following is a special case of Fig. 5 given in Sect. 2.2.

Let ${{\bar{E}}}^i_e \equiv \{e' \mid e' \sim e \}$ represent the class equivalent to good e, and we suppose that there are $k_i$ equivalent classes with $1\le k_i \le |E|$ for each $i \in N$. Then we can write ${{\bar{E}}}^i_e$ ($e\in E$) as ${{\bar{E}}}^i_\ell$ for some $\ell \in \{1,\ldots , k_i\}.$ Now we define a directed graph $G=(V,A)$ with a vertex set V and arc set A by

$$\begin{aligned} V= & {} N \cup W \cup E, \end{aligned}$$

(44)

$$\begin{aligned} W= & {} \{v_{\ell } ^i \mid i \in N,\ell \in \{1,\ldots , k_i\}\}, \end{aligned}$$

(45)

$$\begin{aligned} A= & {} B_1 \cup B_2, \end{aligned}$$

(46)

$$\begin{aligned} B_1= & {} \{(i,v_\ell ^i )\mid i\in N,\ell \in \{1,\ldots , k_i\}\}, \end{aligned}$$

(47)

$$\begin{aligned} B_2= & {} \{(v_{\ell }^i,e')\mid i\in N,\ell \in \{1,\ldots , k_i\}, \forall e' \in {{\bar{E}}}^i_{\ell }\}. \end{aligned}$$

(48)

Here, W represents the total equivalent classes for all agents. The number of arcs of $B_1$ is the number of these classes and the arcs of $B_2$ means the goods contained in each class.

Let $\varphi : A \rightarrow {\mathbb {R}}$ be an independent flow in the network $\mathcal{N}=(G=(V,A),S^+=N,S^-=E,\mathbf{d}, (E,\rho ))$ satisfying

• (a) $\forall v \in W : \partial \varphi (v)=0,$

• (b) $\partial ^+\varphi \le \mathbf{d}$ and $\partial ^- \varphi \in \mathrm{P}_{(+)} (\rho )$.

Recall that we omitted the capacity function in $\mathcal{N}$ if it is $\infty$.

Fig. 17

Independent flow network $\mathcal{N}$ for the decomposition mechanism

The decomposition mechanism¹² can be given as presented by Fujishige et al. [12] since the mechanism does not depend on the structure of graph G in $\mathcal{N}$. Here, we give an outline as follows.

Let P be an expected allocation associated with the network ${\hat{\mathcal{N}}}_{\varphi _P}$ of Fig. 17, and let

$$\begin{aligned} {{\hat{A}}}^0= & {} \{a \in A \mid \varphi _P(a)=0 \}, \end{aligned}$$

(49)

$$\begin{aligned} {{\hat{A}}}^+= & {} { A} \setminus {{\hat{A}}}^0, \end{aligned}$$

(50)

$$\begin{aligned} {{\hat{I}}}= & {} \{i \in N \mid \partial ^+ \varphi _P(i)=d(i) \}. \end{aligned}$$

(51)

Recall the definition of polytope $P^* \in {\mathbb {R}}^A$ in Theorem 2. Define the minimal¹³ face of a polyhedron $P^*$ containing $\varphi _P$ by

$$\begin{aligned} P^* (\varphi _P) = \{ \varphi \in P^* \mid \forall i \in {{\hat{I}}}: \partial ^+ \varphi (i)=d(i), \forall a \in {{\hat{A}}}^0: \varphi (a)=0, \partial ^- \varphi \in \mathrm{B}(\rho ) \}. \end{aligned}$$

(52)

¹⁴ Let P be an expected allocation. We begin with an independent flow ${{\hat{\varphi }}}_1=\varphi _P$ in the network ${\hat{\mathcal {N}}}_{\varphi _P}$. Do the following (i) and (ii) until integral solution ${{\hat{\varphi }}}_{t+1}$ is obtained on the boundary of polytope $P^*$:

• (i) Find an integer-valued independent flow $\varphi _t$ in ${\hat{\mathcal {N}}}_{{{\hat{\varphi }}}_t}$.

• (ii) Compute

  $$\begin{aligned} \beta ^*_t=\max \{ \beta >0 \mid {{\hat{\varphi }}}_t + \beta ({{\hat{\varphi }}}_t -{ \varphi }_t) \in P^*({{\hat{\varphi }}}_t) \}. \end{aligned}$$

  (53)

Put ${{\hat{\varphi }}}_{t+1} \leftarrow {{\hat{\varphi }}}_t + \beta _t^* ({{\hat{\varphi }}}_t -{ \varphi }_t)$.

If ${{\hat{\varphi }}}_{t+1}$ is not integer-valued, then put $t \leftarrow t+1$ and go to (i).

Two key points in the above iteration are: First, ${{\hat{\varphi }}}_t$ is in the relative interior of the unique minimal face of $P^*({{\hat{\varphi }}}_t)$, then we have $\beta ^*_t>0$. Second, the maximum of $\beta ^*_t$ in (53) means that the associated ${{\hat{\varphi }}}_{t+1}$ reaches some boundary of flow polytope $P^*$, arcs in (49) or vertices in (51) increases at least by one. Therefore, the number of iterations is a polynomial of |N||A| of the underlying graph. Thus (43) can be obtained by a simple arithmetic calculation. Refer to paper [12] for details.

8 Concluding Remarks

For random assignment problems with the constraint of a polytope defined by submodular inequalities on goods, we complete our former allocation mechanism by allowing agents’ indifference among goods.

• 1. Supported by our preliminary results, Lemma 3, Proposition 2 and its corollary, the PS mechanism of Bogomolnaia and Moulin [1] and its extension by Katta and Sethuraman [8] can naturally be extended to the allocation problem with submodular constraints on goods. We realized the extended PS mechanism by Algorithm I and Algorithm II.

• 2. Theorems 3 and 4 show that the mechanisms, Algorithm I and Algorithm II, are ordinally efficient and normalized envy-free.

• 3. The lexicographic characterization of the PS mechanism provided by Bogomolnaia [4] is also possible for our extended mechanism (Theorem 6).

• 4. The lottery randomized mechanisms based on our previous papers, Fujishige et al. [12] and [22], is outlined to assign indivisible goods for the problem settings of this paper.

Several other generalizations of allocation mechanisms with additional conditions or hybrid types have been developed, refer to the papers [2, 3, 6, 9, 10, 28] and reference therein. Allocating resource summation, similar to the base equality of polymatroids, is treated in a recent paper by Bochet and Tumennasan [29], which is related to single-peakedness, Zhan [30]. Finally, in the case of the dichotomous domain with a matroidal family of goods, we expect the strategy-proofness property to be kept. Strategy-proofness is more delicate with submodularity. More general resource summation, the single-peakedness and strategy-proofness in assignment problems will be our further work.