The Lipschitz injective hull of Lipschitz operator ideals and applications

Abstract

We introduce and study the Lipschitz injective hull of Lipschitz operator ideals defined between metric spaces. We show some properties and apply the results to the ideal of Lipschitz p-nuclear operators, obtaining the ideal of Lipschitz quasi p-nuclear operators. Also, we introduce in a natural way the ideal of Lipschitz Pietsch p-integral operators and show that its Lipschitz injective hull coincide with the ideal of Lipschitz p-summing operators defined by Farmer and Johnson. Finally, we consider both ideals as Lipschitz operator ideals between a metric space and a Banach space, showing that these ideals are not of composition type. Their maximal hull and minimal kernel are also studied.

1 Introduction

Inspired by the work of Farmer and Johnson [10], where the notion of p-summing linear operator is extended to the Lipschitz setting, many authors have introduced different notions of Lipschitz operators between pointed metric spaces which, in some sense, extend different kind of ideals of (linear) operators between Banach spaces (see e.g. [1,2,3, 8] and the references therein). On the other hand, given a Banach linear operator ideal, Stephani in [16] defined a procedure which assign new Banach operator ideals from a given one, named the injective hull. In the present work, we extend this notion to the Lipschitz case. This is, we define the Lipschitz injective hull of a Lipschitz operator ideal between pointed metric spaces. We give some properties of this procedure and apply our results to the Lipschitz ideal of p-nuclear operators defined in [8], obtaining the class of quasi p-nuclear Lipschitz operators.

The article is divided as follows. In Sect. 1 we introduce and study the Lipschitz injective hull of Lipschitz operator ideals defined between pointed metric spaces. We give some characterizations (which can be seeing as a generalization of the linear case) and apply our results to some known Lipschitz operator ideals. We show that the Lipschitz injective hull of the Lipschitz p-integral operators (defined in [10]) and Lipschitz Pietsch p-integral operators (see definition below) coincide with the Lipschitz p-summing operators of Farmer and Johnson. We also introduce the ideal of Lipschitz quasi p-nuclear operators between pointed metric spaces and show that it coincide with the Lipschitz injective hull of the ideal of Lipschitz p-nuclear operators. In Sect. 2 we deal with the ideal of Lipschitz quasi p-nuclear operators and Lipschitz Pietsch p-integral operators between a pointed metric space and a Banach space. We show that both ideals are not of composition type, implying that they cannot be obtained from linear Banach operator ideals. We show that the maximal hull of the Lipschitz quasi p-nuclear operators coincide with the ideal of p-summing operators and also we characterize the minimal kernel of the Lipschitz Pietsch p-integral operators. Finally, we compare the Lipschitz injective hull procedure with the injective hull procedure of Banach Lipschitz operator ideals, defined in [3, Definition 2.2]. We use our results to show that both procedure are, in general, different.

Our notation is standard. X and Y will be pointed metric spaces with a base point denoted by 0 and the metric will be denoted by d. We denote by $B_{X}=\{x \in X :d(x,0)\le 1\}$. Also, E and F will stand for Banach spaces over the same field ${\mathbb {K}}$ (either ${\mathbb {R}}$ or ${\mathbb {C}}$) with dual spaces $E^*$ and $F^*$. A Banach space E will be considered as pointed metric spaces with distinguished point 0 and distance $d(x,x')=\Vert x-x'\Vert$. With $Lip_{0}(X,Y)$ we denote the set of all Lipschitz mappings from X to Y such that maps 0 to 0 and we put

$$\begin{aligned} Lip( T) =\inf \{C>0:d(T(x),T(x'))\le Cd(x,x');\ \forall x,x'\in X\}. \end{aligned}$$

In particular, $Lip_{0}(X,E)$ is the Banach space of all Lipschitz mappings T from X to E that vanish at 0, under the Lipschitz norm $Lip(\cdot )$. When $E={\mathbb {K}}$, $Lip_{0}(X,{\mathbb {K}})$ is denoted by $X^{\#}$ and it is called the Lipschitz dual of X. We consider $B_{X^{\#}}$ endowed with the pointwise topology. Is well known that, with this topology, $B_{X^{\#}}$ is a compact Hausdorff space. The space of all linear operators from E to F is denoted by ${\mathcal {L}}(E,F)$ and it is a Banach space with the usual supremum norm. It is clear that ${\mathcal {L}}(E,F)$ is a subspace of $Lip_0(E,F)$ and, in particular, $E^*$ is a subspace of $E^{\#}$. Let $p\ge 1,$ we write $p'$ the conjugate index of p, that is $1/p+1/p'=1$. As usual, when $p=1, p'=\infty$. For a Banach space E,  $\ell _{p}(E)$ denotes the Banach space of all absolutely p-summable sequences $(x_n)_n$ in E with the norm $\Vert (x_n)_n\Vert _p=(\sum _{n=1}^{\infty }\Vert x_n\Vert ^{p})^{\frac{1}{p}}$.

All the other relevant terminology and preliminaries as well as the definitions of the ideals that we will use are given in corresponding sections. For the theory (Banach) of operator ideals we refer to the book of Pietsch [13] and for the theory of Lipschitz mappings to the book of Weaver [18].

2 Lipschitz injective hull of Lipschitz operator ideals between metric spaces

Before start, as far as we know, there are different notions of Lipschitz operator ideals between pointed metric spaces which we may consider, (see for instance [1, Definition 5.2], [6, Proposition 6.3] and [7, Definition 1.1]). Although our results and examples fits in all the definition we know, we are going to specify the notion that we are going to use. By an ideal of Lipschitz maps ${\mathcal {I}}_{Lip}$ between pointed metric spaces we mean an assignment for each pair of pointed metric spaces X and Y of a family of mappings ${\mathcal {I}}_{Lip}(X,Y)\subset Lip_0(X,Y)$, together with a real-valued function $\Vert \cdot \Vert _{{\mathcal {I}}_{Lip}}$ which satisfies:

• 1. If $Y=E$ is a Banach space, then for any $f\in X^{\#}$ and $e\in E$, the map $fe:x\mapsto f(x)e \in {\mathcal {I}}_{Lip}(X,E)$.

• 2. For every $T\in {\mathcal {I}}_{Lip}(X,Y), Lip(T)\le \Vert T\Vert _{{\mathcal {I}}_{Lip}}$.

• 3. The ideal property: If $R\in Lip_0(U,X)$, $T\in {\mathcal {I}}_{Lip}(X,Y)$ and $S\in Lip_0(Y,V)$, then $STR \in {\mathcal {I}}_{Lip}(U,V)$ and $\Vert STR\Vert _{{\mathcal {I}}_{Lip}}\le Lip(S)\Vert T\Vert _{{\mathcal {I}}_{Lip}} Lip(R)$.

Following [16, Satz 4.1], for a Banach operator ideal ${\mathcal {A}}$, a linear operator $T:E\rightarrow F$ belongs to the injective hull of ${\mathcal {A}}$, ${\mathcal {A}}^{inj}$, if there is a Banach space G and a linear operator $S\in {\mathcal {A}}(E,G)$ such that $\Vert Tx\Vert \le \Vert Sx\Vert$ for all $x \in E$. The operator ideal ${\mathcal {A}}^{inj}$ is a Banach operator ideal endowed with the norm

$$\begin{aligned} \Vert T\Vert _{{\mathcal {A}}^{inj}}=\inf \{\Vert S\Vert _{\mathcal {A}}:S\in {\mathcal {A}}(E,G) \ \text{ with } \ \Vert Tx\Vert \le \Vert Sx\Vert , \forall x \in E\}. \end{aligned}$$

Now, we propose a definition of the injective hull of a Lipschitz operator ideal which extend that introduced by Stephani for the linear case.

Definition 1.1

Let ${\mathcal {I}}_{Lip}$ be a Lipschitz operator ideal between pointed metric spaces. For pointed metric spaces X and Y, a Lipschitz operator $T\in Lip_0(X,Y)$ belongs to the Lipschitz injective hull of ${\mathcal {I}}_{Lip}$ if there exists a pointed metric space Z and a Lipschitz operator $S\in {\mathcal {I}}_{Lip}(X,Z)$ such that $d(Tx,Tx')\le d(Sx,Sx')$ for all $x, x'\in X$. The class of all operators from X to Y which belongs to the Lipschitz injective hull of ${\mathcal {I}}_{Lip}$ will be denoted by ${\mathcal {I}}_{Lip}^{Linj}(X,Y)$.

For any Lipschitz operator ideal ${\mathcal {I}}_{Lip}$, we may assign to ${\mathcal {I}}_{Lip}^{Linj}$ a real valued function $\Vert \cdot \Vert _{{\mathcal {I}}^{Linj}_{Lip}}$ as follows. For pointed metric spaces X and Y and $T\in {\mathcal {I}}_{Lip}^{Linj}(X,Y)$,

$$\begin{aligned} \begin{array}{ll} \Vert T\Vert _{{\mathcal {I}}_{Lip}^{Linj}}=&{}\\ \inf \{\Vert S\Vert _{{\mathcal {I}}_{Lip}} :S\in {\mathcal {I}}_{Lip}(X,Z) \ \text{ with } \ d(Tx,Tx')\le d(Sx,Sx'),\ \forall x,x' \in X\}.&{} \end{array} \end{aligned}$$

Since the proof of the next proposition follows in the same way as in the linear case we omit it.

Proposition 1.1

Let ${\mathcal {I}}_{Lip}$ be a Lipschitz operator ideal between metric spaces.

• (a) ${\mathcal {I}}_{Lip}^{Linj}$ together with $\Vert \cdot \Vert _{{\mathcal {I}}_{Lip}^{Linj}}$ is a Lipschitz operator ideal.

• (b) ${\mathcal {I}}_{Lip} \subset {\mathcal {I}}_{Lip}^{Linj}$and$\Vert \cdot \Vert _{{\mathcal {I}}_{Lip}^{Linj}}\le \Vert \cdot \Vert _{{\mathcal {I}}_{Lip}}$.

• (c) $({\mathcal {I}}_{Lip}^{Linj})^{Linj}={\mathcal {I}}_{Lip}^{Linj}$and$\Vert \cdot \Vert _{({\mathcal {I}}_{Lip}^{Linj})^{Linj}}= \Vert \cdot \Vert _{{\mathcal {I}}_{Lip}^{Linj}}$.

In particular, we say that a Lipschitz operator ideal is injective if it coincide with its Lipschitz injective hull. Before give our first characterization of injective Lipschitz operator ideal, recall that every metric space X is isometric to a subset of $\ell _{\infty }(\varGamma )$ for some set $\varGamma$ (see for instance [5, Lemma 1.1]). The embedding is a Lipschitz map denoted by $\iota _{X}^{L}:X\longrightarrow \ell _{\infty }(\varGamma )$. In the case of X being a pointed metric space, one may consider a isometry which maps 0 to 0, denoted by $\iota _{X}^{L_{0}}:X\longrightarrow \ell _{\infty }(\varGamma )$.

The following result can be seen as generalization of a well known characterization of the injective hull of a Banach linear operator ideal, which first appear in [16].

Proposition 1.2

Let${\mathcal {I}}_{Lip}$be a Lipschitz operator ideal between pointed metric spaces and let$T\in Lip_0(X,Y)$. The following are equivalent.

• (i) For all (or some) Lipschitz 1-injective metric spaceZand all isometric embedding$\iota :Y\longrightarrow Z$we have$\iota T\in {\mathcal {I}}_{Lip}(X,Z)$.

• (ii) $\iota _Y^{L_0}T\in {\mathcal {I}}_{Lip}(X,\ell _{\infty }(\varGamma ))$.

• (iii) $T \in {\mathcal {I}}^{Linj}_{Lip}(X,Y)$.

Moreover,

$$\begin{aligned} \Vert T\Vert _{{\mathcal {I}}_{Lip}^{Linj}}=\Vert \iota _Y^{L_0} T\Vert _{{\mathcal {I}}_{Lip}}=\inf \{\Vert \iota T\Vert _{{\mathcal {I}}_{Lip}}:Z \, \text{ and } \ \iota :Y\rightarrow Z \ \text{ as } \, in \, \mathrm{(i)}\}. \end{aligned}$$

Proof

Since $\ell _{\infty }(\varGamma )$ is a Lipschitz 1-injective metric space (see [5, Lemma 1.1 (b)]), is clear that (i) implies (ii). Now suppose that (ii) holds. Since $\iota _{Y}^{L_0}:Y \rightarrow \ell _{\infty }(\varGamma )$ is an isometric embedding, for all $x,x'\in X$ we have that $d(Tx,Tx')=d(\iota _{Y}^{L_0}Tx,\iota _{Y}^{L_0}Tx')$. Then (iii) follows. Moreover, $\Vert T\Vert _{{\mathcal {I}}_{Lip}^{Linj}}\le \Vert \iota _Y^{L_0}T\Vert _{{\mathcal {I}}_{Lip}}$. Finally we show that (iii) implies (i). Fix Z a Lipschitz 1-injective metric space and take $\iota :Y\longrightarrow Z$ an isometric embedding and $\varepsilon >0$. There exist a metric space W and a Lipschitz operator $S\in {\mathcal {I}}_{Lip}(X,W)$ such that $d(Tx,Tx')\le d(Sx,Sx')$ for all $x,x'\in X$ and $\Vert S\Vert _{{\mathcal {I}}_{Lip}}\le (1+\varepsilon )\Vert T\Vert _{{\mathcal {I}}_{Lip}^{Linj}}$. Consider $M=S(X)$ which is a subset of W and define the function $U:M\rightarrow Y$ as $Uw=Tx$ if $w=Sx$. Routine arguments shows that U is well defined and a Lipschitz function with $Lip(U)\le 1$. Since $\iota U:M\longrightarrow Z$ is Lipschitz and Z is a Lipschitz 1-injective metric space, there exists a Lipschitz function ${\widetilde{U}}:W\rightarrow Z$ such that $Lip({\widetilde{U}})\le 1$ and ${\widetilde{U}}|_{M}=\iota U$ [5, Proposition 1.2]. Then, for $x\in X$, we have

$$\begin{aligned} \iota Tx=\iota U Sx={\widetilde{U}}Sx. \end{aligned}$$

Since ${\mathcal {I}}_{Lip}$ is a Lipschitz operator ideal, we conclude that $\iota T\in {\mathcal {I}}_{Lip}(X,Z)$. Moreover,

$$\begin{aligned} \Vert \iota T\Vert _{{\mathcal {I}}_{Lip}}=\Vert {\widetilde{U}}\circ S\Vert _{{\mathcal {I}}_{Lip}}\le Lip({\widetilde{U}})\Vert S\Vert _{{\mathcal {I}}_{Lip}}\le (1+\varepsilon )\Vert T\Vert _{{\mathcal {I}}_{Lip}^{Linj}}, \end{aligned}$$

and the proof follows. $\square$

Farmer and Johnson introduced the concept of Lipschitz p-summing and Lipschitz p-integral operators [10], extending the p-summing and p-integral linear operators to the Lipschitz case. For pointed metric spaces X and Y, a mapping $T\in Lip_0(X,Y)$ is called Lipschitz p-summing, $1\le p <\infty$, if there exists a constant $C>0$ such that regardless of the choice of points $x_1,\ldots , x_n,x'_1,\ldots , x'_n$ in X

$$\begin{aligned} \sum _{i=1}^{n} (d(Tx_i,Tx'_i))^p\le C^p\underset{f\in B_{X^{\#}}}{\sup }\sum _{i=1}^{n} |f(x_i)-f(x'_{i})|^p. \end{aligned}$$

(1)

In this case we put $\pi _{p}^{L}(T)=\inf \left\{ C:\text{ satisfying } (1)\right\}$. The set of all Lipschitz p-summing operators from X to Y is denoted by $\varPi _{p}^{L}(X,Y)$. On the other hand, the mapping $T\in Lip_0(X,Y)$ is said to be Lipschitz p-integral, $1\le p <\infty$, if there exists a probability measure space $(\varOmega ,\varSigma ,\mu )$ and two Lipschitz mappings $A\in Lip_{0}(L_{p}(\mu ),(Y^{\#})^{*})$ and $B\in Lip_{0}(X,L_{\infty }(\mu ))$ such that the following diagram commute

where $i_{p}:L_{\infty }(\mu )\longrightarrow L_{p}(\mu )$ is the canonical mapping and $k_{Y}:Y\longrightarrow (Y^{\#})^{*}$ is the evaluation map $k_{Y}(y)(g)=g(y)$, for $y \in Y$ and $g \in Y^{\#}$. The set of all Lipschitz p-integral mappings from X to Y is denoted by ${\mathfrak {I}}_{p}^{L}(X,Y)$. With each $T\in {\mathfrak {I}}_{p}^{L}(X,Y)$ we associate its Lipschitz p-integral quantity, $i_{p}^{L}(T)=\inf \{Lip(A)Lip(B)\},$ where the infimum is taken over all $\mu ,$A and B as above.

It is well known that in the linear case, the injective hull of p-integral and Pietsch p-integral operators (also known as strictly p-integral operators) coincides with ideal of p-summing operator. So now, we introduce the class of Lipschitz Pietsch p-integral operators in a natural way. Then we show that this last result can be extended to the Lipschitz case.

Definition 1.2

Let X and Y be pointed metric spaces and $1\le p< \infty$. A Lipschitz mapping $T\in Lip_{0}(X,Y)$ is Lipschitz Pietsch p-integral if there is a probability measure space $(\varOmega ,\varSigma ,\mu )$ and two Lipschitz mappings $A \in Lip_0(L_{p}(\mu ), Y)$ and $B\in Lip_0(X,L_{\infty }(\mu ))$ giving rise to the following commutative diagram:

The class of all Lipschitz Pietsch p-integral mappings from X to Y is denoted by ${\mathcal {P}}{\mathfrak {I}}_{p}^{L}(X,Y)$. Also, the Lipschitz Pietsch p-integral function $pi^L_{p}(T)$ of T is the infimum of Lip(A)Lip(B), taken over all factorization as above.

It follows from the definition that the Lipschitz Pietsch p-integral operators are a Lipschitz operator ideal. Also, note that a Lipschitz map $T\in Lip_{0}(X,Y)$ is p-integral if and only if $k_{Y}T:Y\rightarrow (Y^{\#})^{*}$ is Lipschitz Pietsch p-integral. Also, from the factorization of Lipschitz p-summing operators obtained in [10, Theorem 1], a map T is Lipschitz p-summing if and only if $\iota _Y^{L_0}T:X\rightarrow \ell _{\infty }(\varGamma )$ is Lipschitz Pietsch p-integral. Summarizing, as an application of Proposition 1.2 we obtain the following result.

Proposition 1.3

Let$1\le p < \infty$, then

$$\begin{aligned} \left( {\mathcal {P}}{\mathfrak {I}}_p^L\right) ^{Linj}=({\mathfrak {I}}_p^L)^{Linj}=\varPi _p^L. \end{aligned}$$

Moreover, for any pointed metric spacesXandYand$T\in \varPi _p^{L}(X,Y)$, we have

$$\begin{aligned} \Vert T\Vert _{({\mathcal {P}}{\mathfrak {I}}_p^L)^{Linj}}=\Vert T\Vert _{({\mathfrak {I}}_p^L)^{Linj}}=\pi _p^L(T). \end{aligned}$$

The notion of quasi p-nuclear operator was introduced by Persson and Pietsch in [12]. For $1\le p <\infty$, a linear map T between Banach spaces E and F is said to be quasi p-nuclear if there exists a sequence $(x^*_n)_n$ in $\ell _{p}(E^{*})$ such that $\Vert Tx\Vert \le \Vert \left( x_n^{*}(x)\right) _n\Vert _p$ for all $x\in E$. This class, which is denoted by ${\mathcal {QN}}_{p}$, endowed with the norm $\nu _{p}^{Q}$ defined as the infimum of $\Vert (x^*_n)_n\Vert _p$ taken over all the sequences $(x^*_n)_n$ satisfying the above inequality, became a Banach operator ideal. Now, we extend this notion to the Lipschitz case.

Definition 1.3

Let X and Y be pointed metric spaces and $1\le p<\infty$. A mapping $T\in Lip_{0}(X,Y)$ is called Lipschitz quasi p-nuclear if there exists a sequence $(f_n)_n\in \ell _{p}(X^{\#})$ such that

$$\begin{aligned} d(T(x),T(x'))\le \left( \sum _{n=1}^{\infty }|f_n(x)-f_n(x')|^{p}\right) ^{\frac{1}{p}} \end{aligned}$$

(2)

for all $x,x'\in X$. In such case, we put

$$\begin{aligned} \nu _{p}^{QL}(T)=\inf \left\{ \left( \sum _{n=1}^{\infty } Lip(f_n)^{p}\right) ^{1/p}:(f_n)_n \text{ satisfying } (2)\right\} \end{aligned}$$

We denote by ${\mathcal {QN}}_{p}^{\,L}(X,Y)$ the space of all quasi p-nuclear Lipschitz mappings between pointed metric spaces X and Y.

The next proposition is clear and we omit the proof.

Proposition 1.4

For$1\le p <\infty$, ${\mathcal {QN}}_{p}^{\,L}$is a Lipschitz operator ideal.

The rest of this section is devoted to show that most of the properties of linear quasi p-nuclear operators can be extended to the Lipschitz setting. First, recall that the ideal of linear quasi p-nuclear operators coincide with injective hull of the Banach operator ideal of p-nuclear operators [12, Satz 38]. On the other hand, the Lipschitz p-nuclear operators were introduced by Chen and Zheng in [8] and can be extended in a verbatim way to Lipschitz maps between pointed metric spaces. For pointed metric spaces X and Y, a Lipschitz mapping $T\in Lip_{0}(X,Y)$ is called Lipschitz p-nuclear, if there exist two Lipschitz mappings $A\in Lip_{0}(\ell _{p},Y)$ and $B\in Lip_{0}(X,\ell _{\infty })$ and a sequence $\lambda \in \ell _{p}$ such that the following diagram commute

(3)

where $D_{\lambda }:\ell _{\infty }\longrightarrow \ell _{p}$ is the diagonal operator induced by the sequence $\lambda \in \ell _p$. The set of all Lipschitz p-nuclear operators from X to Y is denoted by ${\mathcal {N}}_{p}^{\,L}(X,Y)$. To the class ${\mathcal {N}}_p^{L}(X,Y)$ we will assign the function $\nu _{p}^{L}$ defined, for $T\in {\mathcal {N}}_p(X,Y)$, as the infimum of $Lip(A)\Vert \lambda \Vert _{p} Lip(B)$ over all factorizations as in (3). It follows that ${\mathcal {N}}_{p}^{\,L}$ is Lipschitz operator ideal.

Now we are ready to give our first characterization of Lipschitz quasi p-nuclear operators.

Theorem 1.1

LetXandYbe pointed metric spaces and$1\le p <\infty$. For a mapping$T\in Lip_{0}(X,Y)$, the following are equivalent.

• (i) $T\in {\mathcal {QN}}_{p}^{\,L}(X,Y)$

• (ii) There exist subsets$M\subset \ell _{\infty }$with$0\in M$and$N\subset \ell _{p}$with$0\in N$, a sequence$\lambda \in \ell _{p}$and two Lipschitz maps$A\in Lip_0(N,Y)$and$B\in Lip_0(X, M)$such that following diagram commute

  

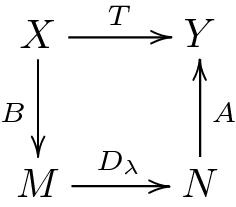
  where$D_{\lambda }$is the diagonal operator.

• (iii) For all (or some) Lipschitz 1-injective pointed metric spaceZand all isometric embedding$\iota :Y\longrightarrow Z$, $\iota T\in {\mathcal {N}}_{p}^{\,L}(X,Z)$.

• (iv) There exist a pointed metric spaceZtogether with a Lipschitz operator$S\in {\mathcal {N}}_{p}^{\,L}(X,Z)$such that$d(Tx,Tx^{\prime })\le d(Sx,Sx^{\prime })$for all$x,x^{\prime }\in X$.

Moreover,

$$\begin{aligned} \nu _{p}^{QL}(T)=\inf \{Lip(A)Lip(B)\Vert \lambda \Vert _p\}=\nu _{p}^{L}(\iota T)=\inf \{\nu _{p}^{L}(S)\}. \end{aligned}$$

Proof

The proof follows in an analogous way of that of the linear case. We sketch the proof. Suppose that T is a Lipschitz quasi p-nuclear and fix $\varepsilon >0$. There exists a sequence $(f_n)_n\in \ell _{p}(X^{\#})$ with $\Vert (Lip(f_n))_n\Vert _p\le (1+\varepsilon )\nu _{p}^{QL}(T)$ such that $d(Tx,Tx')\le (\sum _{n=1}^{\infty }|f_n(x)-f_n(x')|^{p}) ^{\frac{1}{p}}$ for all $x,x'\in X$. Define the mapping $B\in Lip_{0}(X,\ell _{\infty })$ by $\displaystyle Bx:=\left( f_n(x)/Lip(f_n)\right) _n$ and set $M=B(X)$. Note that $0\in M$ and that $Lip(B)\le 1$. Also, set $\lambda =(Lip(f_n))_n$, which belongs to $\ell _{p}$, and $N=D_{\lambda }(B(X))$ which is a subset of $\ell _{p}$ containing 0. Finally, define the operator $A:N\rightarrow Y$ by $A\beta =Tx$, if $\beta =D_{\lambda }(Bx)$. The reader may check that A is a well-defined Lipschitz mapping with $A(0)=0$ and $Lip(A)\le 1.$ Then is clear that $T=A D_{\lambda } B$ and $Lip(A)Lip(B)\Vert \lambda \Vert _{p}\le \Vert \lambda \Vert _{p}\le (1+\varepsilon )\nu _{p}^{QL}(T)$. Then (ii) follows.

Suppose that (ii) holds and take a Lipschitz 1-injective pointed metric space Z and an isometric embedding $\iota :Y\rightarrow Z$. For $\varepsilon >0$, take a factorization of T as in statement (ii), with $Lip(A)=Lip(B)=1$ and $\Vert \lambda \Vert _{p}\le (1+\varepsilon )\inf \{Lip(A)Lip(B)\Vert \lambda \Vert _{p}\}$, where the infimum is taken over all the factorization. To see that the mapping $\iota T$ is Lipschitz p-nuclear, note that by [5, Proposition 1.2] we can extend the Lipschitz operator $\iota A$ to a Lipschitz mapping ${\widetilde{A}}\in Lip_{0}(\ell _{p},Z)$ such that $Lip(A)=1$. Also, extend B to ${{\widetilde{B}}}:X \rightarrow \ell _{\infty }$ and, since the diagonal operator $D_{\lambda }$ is defined over all $\ell _{\infty }$, we obtain that $\iota T={{\widetilde{A}}}D_{\lambda }{{\widetilde{B}}}$, implying that $\iota T\in {\mathcal {N}}_{p}^{\,L}(X,Z)$ and

$$\begin{aligned} \nu _{p}^{L}(\iota T)\le Lip(A)\left\| \lambda \right\| _{p}Lip(B)\le (1+\varepsilon )\inf \{Lip(A)Lip(B)\Vert \lambda \Vert _{_{p}}\}, \end{aligned}$$

and (iii) follows. From Proposition 1.2 we get that (iii) is equivalent to (iv).

Finally, suppose that (iv) holds. Take a Lipschitz operator $S\in {\mathcal {N}}^L_p(X,Z)$ as in (3) and, for $\varepsilon >0$, factorize S as $S=A D_{\lambda }B$ with $A\in Lip_{0}(\ell _{p},Y)$ and $B\in Lip_{0}(X,\ell _{\infty })$, $Lip(A)=Lip(B)=1$ and $\Vert \lambda \Vert _p\le (1+\varepsilon )\nu _{p}^{L}(S)$. For all $x,x'\in X$ we have that

$$\begin{aligned} \begin{array}{rl} d(Tx,Tx')\le &{} d(AD_{\lambda }Bx,AD_{\lambda }Bx') \\ \le &{}\displaystyle Lip(A)\Vert D_{\lambda }(Bx-Bx')\Vert _p \\ = &{} \displaystyle \left( \sum _{n=1}^{\infty }|\lambda _{n}e_{n}^*(Bx-Bx')|^p\right) ^{\frac{1}{p}}\\ = &{}\displaystyle \left( \sum _{n=1}^{\infty }|\lambda _ne_n^*(Bx)-\lambda _ne_n^*(Bx')|^p\right) ^{\frac{1}{p}}. \end{array} \end{aligned}$$

Here, $(e_n^*)_n$ stands for the sequence of coordinate functional on $\ell _{\infty }$. Denoting by $f_n=\lambda _n e_n^*B$, it follows that $(f_n)_n\in \ell _{p}(X^{\#})$, which implies that T is quasi p-nuclear and $\nu _{p}^{QL}(T)\le \Vert \lambda \Vert _p\le (1+\varepsilon )\nu _{p}^{L}(S)$. The proof conclude. $\square$

As a direct consequence of Proposition 1.2 and Theorem 1.1 we have the following results which extend the results of the linear case.

Proposition 1.5

For$1\le p <\infty$, the Lipschitz quasip-nuclear operators coincide with the Lipschitz injective hull of the Lipschitzp-nuclear operators. This is

$$\begin{aligned} ({\mathcal {N}}_{p}^{\,L})^{Linj}= {\mathcal {QN}}_{p}^{\,L} \quad \text{ and } \quad \Vert \cdot \Vert _{({\mathcal {N}}_p^L)^{Linj}}=\nu _p^{QL}(\cdot ). \end{aligned}$$

Corollary 1.1

LetXandYbe pointed metric spaces such thatYis Lipschitz 1-injective. For$1\le p <\infty$, a Lipschitz mapping$T\in Lip_{0}(X,Y)$is quasip-nuclear if and only ifTis Lipschitzp-nuclear. Moreover, $\nu _p^{QL}(T)=\nu _p^{L}(T)$.

In [12, Satz 43] it is shown that every quasi p-nuclear operator is p-summing and that the quasi p-nuclear norm and the p-summing norm coincide. We have an analogous results in the Lipschitz setting.

Proposition 1.6

LetXandYbe pointed metric spaces and$1\le p <\infty$. If a Lipschitz operator$T\in {\mathcal {QN}}_{p}^{\,L}(X,Y)$, then$T\in \varPi _{p}^{L}(X,Y)$. Moreover, $\pi _{p}^{L}(T)=\nu _{p}^{QL}(T)$.

Proof

Take $T\in {\mathcal {QN}}_{p}^{\,L}(X,Y)$ and fix $\varepsilon >0$. Choose a sequence $(f_n)_n\in \ell _{p}(X^{\#})$ with $\Vert (f_n)_n\Vert _p\le \nu _{p}^{QL}(T)+\varepsilon$ such that $d(Tx,Tx')\le (\sum _{n=1}^{\infty }|f_n(x)-f_n(x')|^p) ^{\frac{1}{p}},$ for all $x,x'\in X$. Define the probability measure $\mu$ on $B_{X^{\#}}$ by $\mu =\sum _{n=1}^{\infty }\alpha _n\delta _n$ where $\alpha _n=\frac{|Lip(f_n)|^p}{\Vert (f_n)_n\Vert _p^p}$ and $\delta _n$ is the Dirac measure at $f_n/Lip(f_n)$ for $n\ge 1$. We have

$$\begin{aligned} d(Tx,Tx')\le & {} \left( \sum _{i=1}^{\infty }|f_n(x)-f_n(x')|^{p}\right) ^{\frac{1}{p}} \\= & {} \Vert (f_n)_n\Vert _p\left( \sum _{n=1}^{\infty }\frac{|Lip(f_n)|^{p}}{\Vert (f_n)_n\Vert _p}\left| \frac{f_n(x)}{Lip(f_{n})}-\frac{f_n(x')}{Lip(f_n)}\right| ^{p}\right) ^{\frac{1}{p}} \\= & {} \Vert (f_n)_n\Vert _p\left( \int \nolimits _{B_{X^{\#}}}|f(x)-f(x')|^{p}d\mu (f)\right) ^{\frac{1}{p}}. \end{aligned}$$

Consequently, by the Pietsch domination theorem for the class $\varPi _{p}^{L}$ ([10, Theorem 1]), T is Lipschitz p-summing and $\pi _{p}^{L}(T)\le \Vert (f_n)_n\Vert _p\le \nu _{p}^{QL}(T)+\varepsilon$. Then it follows that $\pi _{p}^{L}(T)\le \nu _{p}^{QL}(T)$. To see the equality of the norms, note that as in the same way that Farmer and Johnson noticed in the proof of [10, Theorem 2], the quasi p-nuclear and the p-summing norm of an operator can be obtained by considering just finite metric subsets of X. This means that for $T\in {\mathcal {QN}}^{L}_p(X,Y)$,

$$\begin{aligned} \nu _{p}^{QL}(T)=\sup _{\begin{array}{c} X_{0}\subset X \\ X_{0}\ \text{ finite } \end{array}}\nu _{p}^{QL}(T i_{X_{0}})\quad \text{ and }\quad \pi _{p}^{L}(T)=\sup _{\begin{array}{c} X_{0}\subset X \\ X_{0}\ \text{ finite } \end{array}}\pi _{p}^{L}(T i_{X_{0}}), \end{aligned}$$

where $i_{X_{0}}:X_{0}\rightarrow X$ is the inclusion map. Hence, the proof will follow if we show that $\nu _{p}^{QL}(Ti_{X_{0}})=\pi _{p}^{L}(T i_{X_{0}})$ for every $X_{0}$ finite metric space.

Now, by Theorem 1.1, $\nu _{p}^{QL}(T i_{X_{0}})=\nu _{p}^{L}(\iota _{Y}^{L_{0}}Ti_{X_{0}})$. By [8, Theorem 4.1], since $X_{0}$ is a finite metric space and the range of the Lipschitz operator $\iota _{Y}^{L_{0}}T i_{X_{0}}$ is the Banach space $\ell _{\infty }(\varGamma )$, the Lipschitz p-nuclear and Lipschitz p-integral norms coincide. This is

$$\begin{aligned} \nu _{p}^{L}(\iota _{Y}^{L_{0}}T i_{X_{0}})=i_{p}^{L}(\iota _{Y}^{L_{0}}T i_{X_{0}}). \end{aligned}$$

Since by Proposition 1.3 and Proposition 1.5 Lipschitz p-summing operators and Lipschitz quasi p-nuclear operators coincides with the Lipschitz injective hull of Lipschitz p-integral operators and of Lipschitz p-nuclear operators respectively, by Proposition 1.2 we obtain the equality $\pi _{p}^{L}(Ti_{X_{0}})=\nu _{p}^{Q}(Ti_{X_{0}})$ which completes the proof. $\square$

We finish this section by showing another property of Lipschitz quasi p-nuclear operators which can be seen as an extension of the linear case. Recall that, for $1\le p <\infty$ a linear operator $T:E\rightarrow F$ is p-compact in the sense of Sinha and Karn [15] if there exists a sequence $(y_n)_n \in \ell _p(F)$ such that

$$\begin{aligned} T(B_{E})\subset \left\{ \sum _{n=1}^{\infty } \alpha _n y_n :(\alpha _n)_n \in B_{\ell _{p'}}\right\} . \end{aligned}$$

(4)

The p-compact norm of a p-compact operator is $\kappa _p(T)=\inf \{\Vert (y_n)_n\Vert _p :(4) \ \text{ holds }\}$. In [9, Corollary 3.4], was established the relation between p-compact operators and quasi p-nuclear operators. A linear operator $T:E\rightarrow F$ is quasi p-nuclear if and only if its adjoint $T^{*}: F^{*}\rightarrow E^{*}$ is p-compact and $\Vert T\Vert _{{\mathcal {QN}}_p}=\kappa _p(T^{*})$.

On the other hand, for $T\in Lip_{0}(X,Y)$, we will consider the Lipschitz adjoint of T, defined by Sawashima [14], but extended to the metric space setting. That is, $T^{\#}\in {\mathcal {L}}(Y^{\#},X^{\#})$ is the linear operator given by $T^{\#}(g)=g{\,}T$ for all $g\in Y^{\#}$.

Proposition 1.7

LetXandYbe pointed metric spaces and$1\le p <\infty$. For an operator$T\in Lip_{0}(X,Y)$, if$T^{\#}:Y^{\#}\longrightarrow X^{\#}$is ap-compact linear operator, then$T\in {\mathcal {QN}}_p^{L}(X,Y)$and$\nu _{p}^{QL}(T)\le \kappa _p(T^{\#})$.

Proof

Notice first that, for any $y,y' \in Y$, $d(y,y')=\sup _{g\in B_{Y^{\#}}}|g(y)-g(y')|$. The supremum is attained when we consider the Lipschitz function $g_y(z)=d(z,y)-d(y,0)$, $z \in Y$. In particular, for all $x,x'\in X$ we have

$$\begin{aligned} d(Tx,Tx')=\sup _{g\in B_{Y^{\#}}}|g(Tx)-g(Tx')|=\sup _{g\in B_{Y^{\#}}}|(T^{\#}g)(x)-(T^{\#}g)(x')|. \end{aligned}$$

Now, suppose that $T^{\#}$ is p-compact and take $\varepsilon >0$. Choose a sequence $(f_n)_n\in \ell _{p}(X^{\#})$ such that $T^{\#}(B_{Y^{\#}})\subset \{\sum _{n=1}^{\infty }\alpha _n f_n:(\alpha _n)_n \in B_{\ell _{p'}}\}$ and $\Vert (f_n)_n\Vert _p\le \varepsilon +\kappa _{p}(T^{\#})$. For a fixed $g\in B_{Y^{\#}}$ there exists a sequence $(\alpha _n)_n\in B_{\ell _{p'}}$, such that $T^{\#}g=\sum _{n=1}^{\infty }\alpha _nf_n$. An application of Hölder’s inequality reveals that

$$\begin{aligned} |(T^{\#}g)(x)-(T^{\#}g)(x')|= & {} |\sum _{n=1}^{\infty }\alpha _{n}f_{n}(x)-\sum _{i=1}^{\infty }\alpha _{n}f_{n}(x')| \\= & {} |\sum _{n=1}^{\infty }\alpha _{n}(f_{n}(x)-f_{n}(x')| \\\le & {} \left( \sum _{n=1}^{\infty }|f_{n}(x)-f_{n}(x^{\prime })|^{p}\right) ^{\frac{1}{p}}. \end{aligned}$$

By taking the supremum over all $g\in B_{Y^{\#}}$ we obatin that $T\in {\mathcal {QN}}_{p}^{\,L}(X,Y)$ with $\nu _{p}^{QL}(T)\le \Vert (f_n)_n\Vert _p\le \varepsilon +\nu _{p}^{Q}(T^{\#})$ and the proof follows. $\square$

3 Lipschitz injective hull of Banach Lipschitz operator ideals between a metric space and a Banach space

Now we center our study in the case when the Lipschitz operators are consider from a pointed metric spaces to Banach spaces. We decided to consider this case in a different section because the theory of Lipschitz operator ideals between a pointed metric space and a Banach space is richer. First of all, in the literature, there just one definition of Lipschitz operator ideal between pointed metric space and Banach space that is considered. Following [3] or [6] a Lipschitz operator ideal between a pointed metric space and Banach space ${\mathcal {I}}_{Lip}$ is a subclass of $Lip_{0}$ such that for every pointed metric space X and every Banach space E the components

$$\begin{aligned} {\mathcal {I}}_{Lip}(X,E):=Lip_{0}(X,E)\cap {\mathcal {I}}_{Lip} \end{aligned}$$

satisfy

• (i) ${\mathcal {I}}_{Lip}(X,E)$ is a linear subspace of $Lip_{0}(X,E)$.

• (ii) For any $f\in X^{\#}$ and $e\in E$, the map $fe:x\mapsto f(x)e \in {\mathcal {I}}_{Lip}(X,E)$.

• (iii) The ideal property: if $S\in Lip_{0}(Y,X)$, $T\in {\mathcal {I}}_{Lip}(X,E)$ and $w\in {\mathcal {L}}(E,F)$, then the composition wTS is in ${\mathcal {I}}_{Lip}(Y,F)$.

A Lipschitz operator ideal ${\mathcal {I}}_{Lip}$ is a normed (Banach) Lipschitz operator ideal if there is $\Vert \cdot \Vert _{{\mathcal {I}}_{Lip}}:{\mathcal {I}}_{Lip}\longrightarrow [0,+\infty [$ that satisfies

• (i’) For every pointed metric space X and every Banach space E, the pair $({\mathcal {I}}_{Lip}(X,E),\Vert \cdot \Vert _{{\mathcal {I}}_{Lip}})$ is a normed (Banach) space and $Lip(T)\le \Vert T\Vert _{{\mathcal {I}}_{{L}ip}}$ for all $T\in {\mathcal {I}}_{{L}ip}(X,E)$.

• (ii’) $\Vert Id_{{\mathbb {K}}}:{\mathbb {K}} \longrightarrow {\mathbb {K}}\Vert _{{\mathcal {I}}_{Lip}}=1$, where $Id_{{\mathbb {K}}}$ is the identity map of ${\mathbb {K}}$.

• (iii’) If $S\in Lip_{0}(Y,X)$, $T\in {\mathcal {I}}_{Lip}(X,E)$ and $w\in {\mathcal {L}}(E,F)$, the inequality $\Vert wTS\Vert _{{\mathcal {I}}_{Lip}}\le Lip(S)\Vert T\Vert _{{\mathcal {I}}_{Lip}}\Vert w\Vert$ holds.

Note that the concept of Lipschitz operator ideal between pointed metric spaces that we consider in the previous section and Banach Lipschitz operator ideal between a pointed metric space and a Banach space may be different. First of all, the condition of ${\mathcal {I}}_{Lip}(X,E)$ being a vector space has no sense if we consider Lipschitz ideal between pointed metric spaces. So, as first glance, there could be a Lipschitz operator ideal between pointed metric spaces which are not a Lipschitz operator ideal between a pointed metric space and a Banach space. Also, in the case of Lipschitz operator ideal between pointed metric spaces, the ideal property allows outer composition by Lipschitz maps, meanwhile now we consider just linear maps. If the Banach Lipschitz operator ideal between a pointed metric space and a Banach space that the ideal property is considered with both Lipschitz operator, it is said to be a strong Lipschitz operator ideal (see [1, Definition 5.1] and [6, Definition 6.1]).

However, in our case, all the ideals we consider in Section 1 are also Banach Lipschitz operator ideals. The proof is straightforward and we omit it.

Proposition 2.1

Let$1\le p <\infty$, then$({\mathcal {QN}}_{p}^{\,L},\nu _{p}^{QL})$and$({\mathcal {P}}{\mathfrak {I}}_p^L,pi_p^L)$are a Banach Lipschitz operator ideal.

Under some requirements, the notion of Lipschitz quasi p-nuclear operator can be consider as generalization of the concept of linear quasi p-nuclear operator, as the following result shows.

Proposition 2.2

Let$1\le p<\infty$, EandFBanach spaces and$T\in {\mathcal {L}}(E,F)$. IfTis a quasip-nuclear linear operator thenTis Lipschitz quasip-nuclear. The converse is true ifEis separable. Moreover, the norms$\nu _{p}^{QL}$and$\nu _{p}^{Q}$coincide.

Proof

The first implication follows from the inclusion $\ell _{p}(E^{*})\subset \ell _{p}(E^{\#})$. For the converse, suppose that E is separable and T is Lipschitz quasi p-nuclear. We consider the linear isometry $\iota _{F}:F\longrightarrow \ell _{\infty }(B_{F^{*}})$, then by Theorem 1.1, the mapping $\iota _{F}T:E\rightarrow \ell _{\infty }(B_{F^{*}})$ is a linear operator which is Lipschitz p-nuclear operator with $\nu _{p}^{L}(\iota _{F}T)=\nu _{p}^{QL}(T)$. Since E is separable and $\ell _{\infty }(B_{F^{*}})$ is a dual space, by [8, Theorem 2.1], $\iota _{F}T$ is a p-nuclear linear operator, with $\nu _{p}(\iota _{F}T)=\nu _{p}^{L}(\iota _{F}T)$, which implies that T is a quasi p-nuclear linear operator with $\nu _{p}^{Q}(T)=\nu _{p}^{QL}(T)$. The proof is finished. $\square$

In analogy with the linear case, in [6, Definition 2.5] was introduced the concept of maximal hull, meanwhile in [17, Definition 4.3] was introduced the concept of minimal kernel of a Lipschitz Banach operator ideal. Loosely speaking, for a Banach Lipschitz operator ideal ${\mathcal {I}}_{Lip}$, the maximal hull $({\mathcal {I}}_{Lip})^{max }$ and the minimal kernel ${\mathcal {I}}_{Lip}^{min}$ are the biggest and the smallest Banach Lipschitz operator ideals which coincide with ${\mathcal {I}}_{Lip}$ over finite pointed metric spaces and finite dimensional Banach spaces.

Following [6], given a Banach Lipschitz operator ideal ${\mathcal {I}}_{Lip}$, a pointed metric space X and a Banach space E, a Lipschitz map $T\in Lip_0(X,E)$ belongs to ${\mathcal {I}}_{Lip}^{max}(X,E)$ if

$$\begin{aligned} \sup \{\Vert Q_{L}^E \circ T \circ \iota _{X_0}^X\Vert _{{\mathcal {I}}_{Lip}}\} <\infty , \end{aligned}$$

where the supremum is taken over all pointed finite metric subset $X_0$ of X and every cofinite subspace L of E. Here $\iota _{X_0}^{X}:X_0\rightarrow X$ and $Q^{E}_L:E\rightarrow L$ denotes the inclusion of $X_0$ into X and $Q^{E}_L$ the natural quotient map from E to L, respectively. Is worth mention that, as far as we know, there is no explicit definition of the minimal kernel of a Lipschitz Banach operator ideal. However, both (the maximal hull and the minimal kernel of ${\mathcal {I}}_{Lip}$) can be determined as the only Banach Lipschitz operator ideals such that

$$\begin{aligned} {\mathcal {I}}_{Lip}^{min}(X_{0},N)={\mathcal {I}}_{Lip}(X_{0},N)={\mathcal {I}}_{Lip}^{max}(X_{0},N) \quad isometrically, \end{aligned}$$

for every finite metric space $X_{0}$ and any finite dimensional Banach space N and, if ${\mathcal {J}}_{Lip}$ is a Banach Lipschitz operator ideal such that ${\mathcal {J}}_{Lip}(X_{0},N)={\mathcal {I}}_{Lip}(X_{0},N)$ for every finite metric space $X_{0}$ and any finite dimensional Banach space N, then

$$\begin{aligned} {\mathcal {I}}_{Lip}^{min}(X,E)\subset {\mathcal {J}}_{Lip}(X,E)\subset {\mathcal {I}}_{Lip}^{max}(X,E), \end{aligned}$$

for all pointed metric space X and Banach space E.

Proposition 2.3

Let$1\le p < \infty$. Then

• (a) $({\mathcal {QN}}_{p}^{\,L})^{max}=\varPi _{p}^{L}$isometrically.

• (b) $({\mathcal {P}}{\mathfrak {I}}_{p}^{L})^{min}=({\mathcal {N}}_{p}^{\,L})^{min}$isometrically.

Proof

First recall that the p-summing Lipschitz operator ideal is maximal Lipschitz operator ideal (see [6, Page 600]). Then by Proposition 1.6 we have that ${\mathcal {QN}}_{p}^{\,L}(X_0,N)=\varPi _{p}^{L}(X_0,N)$ for every finite metric space $X_0$ and for every finite dimensional space N. Thus, an application of [6, Lemma 2.4] completes the proof of (a). To see (b), take N a finite dimensional space. Since $N=N^{**}$ is 1-complemented in $(N^{\#})^{*}$, for every pointed metric space X, the equality ${\mathcal {P}}{\mathfrak {I}}_{p}^{L}(X,N)={\mathfrak {I}}_{p}^{L}(X,N)$ holds, in particular for $X_0$ a finite pointed metric space. By [8, Theorem 4.1], we have ${\mathcal {P}}{\mathfrak {I}}_{p}^{L}(X_0,N)={\mathcal {N}}_{p}^{\,L}(X_0,N)$ for every finite metric space $X_0$ and every finite dimensional space N. Then the second equality holds. $\square$

In [3, Definition 3.1], was introduced a technique to construct a (Banach) Lipschitz operator ideal from a (Banach) linear operator ideal using the linearization of Lipschitz maps, that we now describe briefly.

For a pointed metric space X, Banach space E and an operator $T\in Lip_{0}(X,E)$, there exists a unique linear map $T_{L}:$Æ(X) $\longrightarrow E$ such that $T=T_{L}\delta _{X}$ and $\Vert T_{L}\Vert =Lip(T)$, where Æ(X) stands for the Arens-Eells space Æ(X), introduced in [4] and $\delta _{X}:X\rightarrow$ Æ(X) is the canonical Lipschitz injection. The operator $T_{L}$ is referred to as the linearization of T (see for instance [18, Theorem 2.2.4 (b)]). The correspondence $T\longleftrightarrow T_{L}$ establishes an isometric isomorphism between the Banach spaces $Lip_{0}(X,E)$ and ${\mathcal {L}}$(Æ(X),E). In particular, the spaces $X^{\#}$ and Æ(X)$^{*}$ are isometrically isomorphic.

The Arens-Eells space is also known as the Lipschitz-free Banach space of a metric space X. For more of this space, we refer the reader to the manuscript [11] and the reference therein.

Now, let ${\mathcal {A}}$ be a linear Banach operator ideal. A Lipschitz mapping $T\in Lip_{0}(X,E)$ belongs to the composition Lipschitz operator ideal${\mathcal {A}}\circ Lip_{0}$ if its linearization $T_{L}$ belongs to ${\mathcal {A}}$(Æ(X),E). Moreover, ${\mathcal {A}}\circ Lip_0$ endowed with the norm $\Vert T\Vert _{{\mathcal {A}}\circ Lip_0}=\Vert T_L\Vert _{\mathcal {A}}$ is a Banach Lipschitz operator ideal. This way to obtain a Banach Lipschitz operator ideal from a Banach operator ideal is called composition method and the Lipschitz Banach operator ideals obtained in this way are called ideals of composition type.

In [3], the authors introduced the injective hull of a Banach Lipschitz operator ideal. For this, recall that for a Banach space E, we may consider the linear isometry $\iota _{E}:E\longrightarrow \ell _{\infty }(B_{E^{*}})$. Then, following [3, Definition 2.2], for a Banach Lipschitz operator ideal ${\mathcal {I}}_{Lip}$, a pointed metric space X and a Banach space E, a Lipschitz operator $T:X\rightarrow E$ belongs to ${\mathcal {I}}_{Lip}^{inj}(X,E)$ if and only if $\iota _{E}T$ belongs to ${\mathcal {I}}_{Lip}(X,\ell _{\infty }(B_{E^{*}}))$ with $\Vert T\Vert _{{\mathcal {I}}_{Lip}^{inj}}=\Vert \iota _{E}T\Vert _{{\mathcal {I}}_{Lip}}$. If ${\mathcal {I}}_{Lip}$ is a Lipschitz operator ideal, then ${\mathcal {I}}^{inj}_{Lip}$ is also a Lipschitz operator ideal and

$$\begin{aligned} {\mathcal {I}}_{Lip}^{inj}\subset {\mathcal {I}}_{Lip}^{L inj}. \end{aligned}$$

In general, the equality does not hold. To show this, first we need the following propositions which are of interest for themselves.

The first result describe the injective hull of a Banach Lipschitz operator ideal of composition type.

Proposition 2.4

Let${\mathcal {A}}$be a Banach linear operator ideal. Then

$$\begin{aligned} ({\mathcal {A}}\circ Lip_0)^{inj} = {\mathcal {A}}^{inj} \circ Lip_0 \quad isometrically. \end{aligned}$$

In particular, if${\mathcal {I}}_{Lip}$is a Banach Lipschitz operator ideal of composition type, then so is also${\mathcal {I}}^{inj}_{Lip}$.

Proof

Fix X and E and take $T \in ({\mathcal {A}}\circ Lip_0)^{inj}(X,E)$. Consider the following diagram

Note that, since $\iota _E:E\rightarrow \ell _{\infty }(B_{E^{*}})$ is a linear operator, the uniqueness of the linearization maps gives that $(\iota _ET)_L=\iota _ET_L\in {\mathcal {A}}$(Æ(X),$\ell _{\infty }(B_{E^{*}}))$. Then, we have that $T \in ({\mathcal {A}}\circ Lip_0)^{inj}(X,E)$ if and only if $\iota _ET \in ({\mathcal {A}}\circ Lip_0)(X,\ell _{\infty }(B_{E^{*}}))$ if and only if $(\iota _ET)_L \in {\mathcal {A}}$(Æ(X),$\ell _{\infty }(B_{E^{*}}))$. This is equivalent to the fact that operator $\iota _E T_L$ belongs to ${\mathcal {A}}$(Æ(X),$\ell _{\infty }(B_{E^{*}}))$, or, in other words, to $T_L\in {\mathcal {A}}^{inj}$(Æ(X),E). But this last is, by definition the same to $T\in {\mathcal {A}}^{inj} \circ Lip_0(X,E)$. The isometry follows in the same way. $\square$

From the definitions it is straightforward to see that, for $1\le p <\infty$ the inclusions

$$\begin{aligned} {\mathcal {QN}}_{p}\circ Lip_{0}\subset {\mathcal {QN}}_{p}^{\,L}\quad \text{ and }\quad {\mathcal {P}}{\mathfrak {I}}_{p}\circ Lip_{0}\subset {\mathcal {P}}{\mathfrak {I}}_{p}^{L} \end{aligned}$$

holds, where ${\mathcal {QN}}_p$ and ${\mathcal {P}}{\mathfrak {I}}_p$ stands for the Banach linear operators ideals of quasi p-nuclear and Pietsch p-integral operators. However, the equality is not true in general, for both cases. Moreover, we have

Proposition 2.5

For$1\le p<\infty$, the Lipschitz Banach operator ideals${\mathcal {QN}}_{p}^{\,L}$and${\mathcal {P}}{\mathfrak {I}}_{p}^{L}$are not of composition type.

Proof

Recall that from [17, Proposition 3.18] we have that $\varPi _p^{L}$ is not of composition type and that, by Proposition 2.3, $({\mathcal {QN}}_{p})^{max}=\varPi _p^{L}$. Then if ${\mathcal {QN}}_{p}^{\,L}$ were of composition type, by [17, Proposition 4.1] we obtain that $\varPi _p^{L}$ is of composition type, arriving to a contradiction.

To see that ${\mathcal {P}}{\mathfrak {I}}_{p}^{L}$ is not of composition type follows with the same pattern. Recall that from [17, Proposition 4.13] that $({\mathcal {N}}_p^{L})^{min}$ is not of composition type and that, by Proposition 2.3, $({\mathcal {P}}{\mathfrak {I}}_{p}^{L})^{min}=({\mathcal {N}}_p^{L})^{min}$. If ${\mathcal {P}}{\mathfrak {I}}_{p}^{L}$ were of composition type, by [17, Theorem 4.8] $({\mathcal {N}}_p^{L})^{min}$ is also of composition type, which is also a contradiction. $\square$

Moreover, in order to compare ${\mathcal {QN}}_p^{L}$ with Banach Lipschitz operator ideals of composition type, we have

Proposition 2.6

Let$1\le p < \infty$, then

• (i) ${\mathcal {N}}_p^L \subset ({\mathcal {N}}_p \circ Lip_0)^{Linj}$.

• (ii) ${\mathcal {QN}}_p^{L}\subset ({\mathcal {N}}_p \circ Lip_0)^{Linj}$.

Proof

First, fix a pointed metric space X, a Banach space E and take $T \in {\mathcal {N}}_p^{L}(X,E)$. Then there exist two Lipschitz operators $A \in Lip_0(X,c_0)$, $B\in Lip_0(\ell _p,E)$ and a diagonal operator $D_{\lambda }(c_0,\ell _p)$ such that $T=BD_{\lambda }A$, where $\lambda \in \ell _p$. If we consider the operator $U=D_{\lambda }A$, since $D_\lambda$ is a p-nuclear linear operator, by [3, Proposition 3.2] $U\in {\mathcal {N}}_p\circ Lip_0(X,\ell _p)$. Thus, for all $x, x' \in X$ we have

$$\begin{aligned} \Vert Tx-Tx'\Vert =\Vert BUx-BUx'\Vert \le Lip(B) \Vert Ux-Ux'\Vert , \end{aligned}$$

and then (i) follows.

Now, (ii) follows from (i) in combination with Proposition 1.1 and Proposition 1.5. $\square$

To finalize the article, we use our results to show that the Lipschitz injective hull procedure and the injective hull procedure of Banach Lipschitz operator ideals, defined in [3, Definition 2.2] are, in general, different.

Proposition 2.7

Let$1\le p <\infty$. Then$({\mathcal {N}}_p \circ Lip_0)^{inj} \subsetneq ({\mathcal {N}}_p \circ Lip_0)^{Linj}$and the inclusion is strict.

Proof

If $({\mathcal {N}}_p \circ Lip_0)^{inj}= ({\mathcal {N}}_p \circ Lip_0)^{Linj}$, then by Proposition 2.6 (ii), we obtain that ${\mathcal {QN}}_p^{L} \subset ({\mathcal {N}}_p \circ Lip_0)^{inj}$ which, by Proposition 2.4 give that ${\mathcal {QN}}_p^{L} \subset {\mathcal {QN}}_p \circ Lip_0$. Since the other inclusion always holds, we obtain that ${\mathcal {QN}}_p^{L} ={\mathcal {QN}}_p \circ Lip_0$, which contradicts Proposition 2.5. $\square$