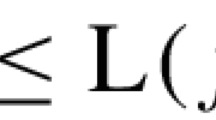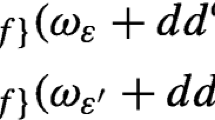Derivations and cohomologies of Lipschitz algebras

Abstract

For a compact metric space (M, d), ${\mathrm {Lip}}M$ denotes the Banach algebra of all complex-valued Lipschitz functions on (M, d). Motivated by a classical result of de Leeuw, we give a canonical construction of a compact Hausdorff space ${\hat{M}}$ and a continuous surjection $\pi :{\hat{M}} \rightarrow M$ which may viewed as a metric analogue of the unit sphere bundle over a Riemannian manifold. It is shown that, for each $n \ge 1$ the continuous Hochschild cohomology ${\mathrm {H}}^{n}({\mathrm {Lip}}M, C({\hat{M}}))$ has the infinite rank as a ${\mathrm {Lip}}M$-module, if the metric space (M, d) admits a local geodesic structure, for example, if M is a compact Riemannian manifold or a non-positively curved metric space. Here $C({\hat{M}})$ denotes the algebra of all complex-valued continuous functions on ${\hat{M}}$. On the other hand, if the coefficient $C({\hat{M}})$ is replaced with C(M), then it is shown that ${\mathrm {H}}^{1}({\mathrm {Lip}}M,C(M)) = 0$ for each compact Lipschitz manifold M.

1 Introduction, main result and preliminaries

For a Banach algebra A and a Banach A-bimodule X, let $C^{n}(A,X)$ be the continuous n-cochains of A to X

$$\begin{aligned} C^{n}(A,X) =\left\{ f:A^{n} \rightarrow X~|~f ~\text{ is } \text{ a } \text{ bounded }~n\text{-linear } \text{ map }\right\} \end{aligned}$$

with $C^{0}(A,X) = X$. The coboundary operator $\delta ^{n}:C^{n}(A,X) \rightarrow C^{n+1}(A,X)$ is defined by

$$\begin{aligned} \delta ^{n} f(a_{1}, \ldots a_{n+1})= & {} a_{1}\cdot f(a_{2}, \ldots ,a_{n+1}) +\sum _{i=1}^{n}(-1)^{i}f(a_{1}, \ldots ,a_{i}a_{i+1}, \ldots ,a_{n+1})\nonumber \\&+ (-1)^{n+1}f(a_{1},\ldots ,a_{n})\cdot a_{n+1} \end{aligned}$$

(1.1)

for $f \in C^{n}(A,X)$ and $a_{1}, \ldots , a_{n+1} \in A$. Then $\delta ^{n+1}\circ \delta ^{n} = 0$ and $Z^{n}(A,X) = {\mathrm {Ker}}~\delta ^{n} \supset B^{n}(A,X) = {\mathrm {Im}}~\delta ^{n-1}$. The continuous Hochschild cohomology of A with coefficient X is defined by ${\mathrm {H}}^{n}(A,X) = Z^{n}(A,X)/B^{n}(A,X)$ (see [1, 5, 6]). When A is a commutative Banach algebra, $C^{n}(A,X)$ is a left A-module by the action

$$\begin{aligned} (a\cdot f)(a_{1},\ldots , a_{n}) = a\cdot f(a_{1},\ldots , a_{n}),~~ f \in A,~a, a_{1}, \ldots , a_{n} \in A \end{aligned}$$

and the coboundary operator $\delta ^{n}:C^{n}(A,X) \rightarrow C^{n+1}(A,X)$ is an A-module homomorphism, which induces a left A-module structure on ${\mathrm {H}}^{n}(A,X)$.

For a Banach algebra A and a Banach A-bimodule X, a bounded linear operator $D:A \rightarrow X$ is called a derivation if it follows the Leibniz rule:

$$\begin{aligned} D(ab) = a \cdot Db + Da \cdot b,\quad a,b \in A. \end{aligned}$$

(1.2)

The space of all continuous derivations $A \rightarrow X$ is denoted by ${\mathfrak {D}}(A,X)$. An inner derivation is a derivation $D:A \rightarrow X$ defined by $Da = a \cdot x - x \cdot a ~(a \in A)$ for some $x \in X$. The first cohomology ${\mathrm {H}}^{1}(A,X)$ is isomorphic to the space of derivations modulo the inner derivations.

The present paper studies continuous Hochschild cohomologies of Lipschitz algebras over compact metric spaces. For a compact metric space (M, d), let ${\mathrm {Lip}}M$ be the Banach algebra of all complex-valued Lipschitz functions $f:M \rightarrow {\mathbb {C}}$ with the norm

$$\begin{aligned} \Vert f \Vert _{L} = \Vert f \Vert _{\infty }+ L(f) \end{aligned}$$

where $\Vert f\Vert _{\infty } = \sup _{p \in M}|f(p)|$, the sup norm, and

$$\begin{aligned} L(f): = \sup \left\{ \frac{|f(x)-f(y)|}{d(x,y)}~|~x,y \in X, ~x \ne y \right\} , \end{aligned}$$

the Lipschitz constant of f. In a previous paper [8] the author proved that, for each $n\ge 1$, ${\mathrm {H}}^{n}({\mathrm {Lip}}M, {\mathbb {C}})$ is an infinite dimensional ${\mathbb {C}}$-linear space when M contains a certain point-sequence which converges to a point $p \in M$. Here ${\mathbb {C}}$ is endowed with a ${\mathrm {Lip}}M$-bimodule structure given by:

$$\begin{aligned} f\cdot z = z\cdot f = f(p) z,\quad f \in {\mathrm {Lip}}M,\quad z \in {\mathbb {C}}. \end{aligned}$$

(1.3)

The above result relies only on the local geometry of M at p and a question arises whether the same holds if the coefficient ${\mathbb {C}}$ is replaced with an appropriate continuous function algebra over M with a ${\mathrm {Lip}}M$-module structure. The present paper gives an answer to the question.

For a compact metric space (M, d), let ${\tilde{M}} = M \times M {\setminus } \Delta M$, where $\Delta M = \{ (x,x)~|~ x \in M\} \subset M \times M$. Let $\beta {\tilde{M}}$ be the Stone–Čech compactification of ${\tilde{M}}$ (see [20]). Since $M\times M$ is another compactification of ${{\tilde{M}}}$, there exists a continuous surjection $\pi :\beta {\tilde{M}} \rightarrow M \times M$ such that $\pi | \pi ^{-1}({\tilde{M}}): \pi ^{-1}({\tilde{M}}) \rightarrow {\tilde{M}}$ is a homeomorphism. Let

$$\begin{aligned} \begin{aligned} \begin{array}{ll} \qquad \qquad \quad \qquad \qquad {\hat{M}} = \pi ^{-1}(\Delta M) \\ \text { with the restriction of the map }~\pi , ~ \pi |{\hat{M}}:{\hat{M}} \rightarrow \Delta M. \end{array} \end{aligned} \end{aligned}$$

(1.4)

The restriction $\pi |{\hat{M}}$ is also denoted by $\pi :{\hat{M}} \rightarrow \Delta M$. In what follows we identify the space $\Delta M$ with M via the diagonal map $\Delta _{M}:M \rightarrow \Delta M$ and the map $(\Delta _{M})^{-1}\circ \pi$ is also denoted by $\pi :{\hat{M}} \rightarrow M$. As will be explained in Sect. 3, the space ${\hat{M}}$ may be regarded as an analogue of the unit sphere bundle of the tangent bundle over a Riemannian manifold. For a point $\omega \in {\hat{M}}$, a point derivation $D_{\omega }:{\mathrm {Lip}}M \rightarrow {\mathbb {C}}$ is defined as an analogue of the directional derivative of smooth functions.

The Banach space $C({\hat{M}})$ of all complex-valued continuous functions on ${\hat{M}}$ with the sup norm admits a Banach ${\mathrm {Lip}}M$-bimodule structure given by

$$\begin{aligned} \begin{aligned} (f \cdot \varphi )(\omega )=&{} (\varphi \cdot f)(\omega ) = f(\pi (\omega )) \varphi (\omega ), \\ f \in {\mathrm {Lip}}M,&~\varphi \in {} C({\hat{M}}), ~ \omega \in {\hat{M}}. \end{aligned} \end{aligned}$$

(1.5)

Our first result is on the continuous Hochschild cohomology ${\mathrm {H}}^{*}({\mathrm {Lip}}M,C({\hat{M}}))$. A map $\gamma :[a,b] \rightarrow M$ of the interval [a, b] to a metric space (M, d) is called a geodesic if $d(\gamma (s),\gamma (t)) = |s-t|$ for each $s,t\in [a,b]$. By abuse of terminology the image of $\gamma$, denoted by ${\mathrm {Im}}\gamma$, is also called a geodesic.

Definition 1.1

A metric space (M, d) is said to satisfy the condition (G) if there exists a positive number $\delta >0$ such that

$(*)$  for each $x, y \in M$ with $d(x,y) \le \delta$, there exists a unique geodesic $\gamma _{xy}:[0,d(x,y)] \rightarrow M$ such that $\gamma _{xy}(0) = x, \gamma _{xy}(d(x,y)) = y.$

Besides Riemannian manifolds, all CAT($\kappa$) metric spaces (see [3]) are examples of spaces satisfying the condition (G).

Theorem 1.2

Let (M, d) be a compact metric space satisfying the condition (G). Then for each $n \ge 1$, the cohomology ${\mathrm {H}}^{n}({\mathrm {Lip}}M,C({\hat{M}}))$ has the infinite ${\mathrm {Lip}}M$-rank in the sense that, for each $N \ge 1$, there exist ${\mathrm {Lip}}M$-linearly independent N elements in ${\mathrm {H}}^{n}({\mathrm {Lip}}M,C({\hat{M}}))$.

The main result of [8] may be viewed as a local version of the above theorem. The above theorem should also be compared with the homological dimension theorems of Ogneva [14, 15], Kleshchev [10] and Pugach [18]; the global homological dimension of the Frechét algebra $C^{\infty }(M)$ of the smooth functions on a smooth manifold M is equal to $\dim M$ [14, 15], while the global homological dimension of $C^{n}(M)$ of the Banach algebra of the $C^n$-functions on M is infinity for each $n,~1 \le n < \infty$. A long standing open problem is to decide the global homological dimension of $C([0,1]) = C^{0}([0,1])$ [5, Chap.V, section 2.5].

Our proof is conceptually motivated by the classical Hochschild–Kostant–Rosenberg theorem [13, 16, 17]. The space ${\mathfrak {D}}({\mathrm {Lip}}M,C({\hat{M}}))$ of all derivations ${\mathrm {Lip}}M \rightarrow C({\hat{M}})$ is a ${\mathrm {Lip}}M$-module under the action

$$\begin{aligned} (f\cdot D)g(\omega ) = f(\pi (\omega )) Dg(\omega ),~~f,g \in {\mathrm {Lip}}M, \omega \in {\hat{M}}. \end{aligned}$$

We take the n-fold exterior product $\wedge _{{\mathrm {Lip}}M}^{n}{\mathfrak {D}}({\mathrm {Lip}}M, C({\hat{M}}))$ of the ${\mathrm {Lip}}M$-module ${\mathfrak {D}}({\mathrm {Lip}}M, C({\hat{M}}))$, define a homomorphism $\Omega _{n}{:}\wedge _{{\mathrm {Lip}}M}^{n}{\mathfrak {D}}({\mathrm {Lip}}M, C({\hat{M}})) \rightarrow {\mathrm {H}}^{n}({\mathrm {Lip}}M, C({\hat{M}}))$ by

$$\begin{aligned}&\Omega _{n}(D_{1}\wedge \cdots \wedge D_{n})(a_{1},\ldots ,a_{n}) = \det ((D_{i}a_{j})_{1\le i,j \le n}),\nonumber \\&D_{1},\ldots ,D_{n} \in {\mathfrak {D}}({\mathrm {Lip}}M,C({\hat{M}})), a_{1},\ldots ,a_{n} \in {\mathrm {Lip}}M \end{aligned}$$

(1.6)

and prove that the image ${\text {Im}}\Omega _{n}$ contains arbitrarily large number of ${\mathrm {Lip}}M$-linearly independent elements of ${\mathrm {H}}^{n}({\mathrm {Lip}}M, C({\hat{M}}))$ when the space M satisfies the condition (G). The notion of alternating n-cocycle due to Johnson [7] plays the crucial role in the proof.

The above idea naturally leads to the study of the cohomology with C(M)-coefficient ${\mathrm {H}}^{n}({\mathrm {Lip}}M,C(M))$. The situation is rather different than that of the smooth-function setup and we prove the following theorem. A homeomorphism $h:S_{1}\rightarrow S_{2}$ between metric spaces $(S_{1},d_{1})$ and $(S_{2},d_{2})$ is called a bi-Lipschitz homeomorphism (a lipeomorphism in [11]) if h and $h^{-1}$ are both Lipschitz maps. A topological embedding $\alpha :D \rightarrow M$ of a metric space D into a metric space M is called a bi-Lipschitz embedding if $\alpha :D \rightarrow {\mathrm {Im}}\alpha$ is a bi-Lipschitz homeomorphism. Throughout ${\mathbb {R}}^{m}$ is assumed to be endowed with the standard Euclidean metric. Let $D^{m} = \{ x \in {\mathbb {R}}^{m}~|~\Vert x \Vert \le 1\}$ and ${\mathrm {int}}D^{m} = \{x\in D^{m}~|~\Vert x \Vert <1\}$.

Theorem 1.3

Let (M, d) be a compact metric space such that, for each point $p \in M$, there exists a bi-Lipschitz embedding $\alpha : D^{m(p)} \rightarrow M$ of $D^{m(p)}$ into M (m(p) may depend on p) such that $p \in \alpha (D^{m})$ and $\alpha ({\mathrm {int}}D^{m(p)})$ is open in M. Then we have

$$\begin{aligned} {\mathrm {H}}^{1}({\mathrm {Lip}}M,C(M)) = {\mathfrak {D}}({\mathrm {Lip}}M,C(M)) = 0. \end{aligned}$$

In particular the conclusion holds for each compact Lipschitz manifold M.

Theorem 1.2 is proved in Sect. 2 and Theorem 1.3 is proved in Sect. 3 after developing the sphere-bundle-analogue mentioned above.

The rest of this section fixes notation and recalls some basic results. For a compact metric space (M, d), let $\pi :{\hat{M}}\rightarrow \Delta M$ be the map defined in (1.4). For a Lipschitz function $f:M \rightarrow {\mathbb {C}}$, let $\Phi _{f}:{\tilde{M}} \rightarrow {\mathbb {C}}$ be the function defined by

$$\begin{aligned} \Phi _{f}(x,y) = \frac{f(x)-f(y)}{d(x,y)},\quad (x,y) \in {\tilde{M}}. \end{aligned}$$

By the Lipschitz condition, $\Phi _{f}$ is a bounded continuous function on ${\tilde{M}}$ and hence admits the unique extension, called the de Leeuw map [2, 4, 19, 22]

$$\begin{aligned} \beta {\Phi }_{f}:\beta {{\tilde{M}}} \rightarrow {\mathbb {C}}, \end{aligned}$$

to the Stone-Čech compactification of ${\tilde{M}}$ which restricts to the map

$$\begin{aligned} {\hat{\Phi }}_{f}:= \beta \Phi _{f}|{\hat{M}}:{\hat{M}}\rightarrow {\mathbb {C}} \end{aligned}$$

(1.7)

on the space ${\hat{M}}$. This defines a pairing ${\hat{\Phi }}:{\hat{M}}\times {\mathrm {Lip}}M \rightarrow {\mathbb {C}}$ by

$$\begin{aligned} {\hat{\Phi }}(\omega ,f) = {\hat{\Phi }}_{f}(\omega ),\quad \omega \in {\hat{M}}, f \in {\mathrm {Lip}}M \end{aligned}$$

such that

$$\begin{aligned} |{\hat{\Phi }}(\omega ,f)| \le L(f) \le \Vert f \Vert _{L},\quad \omega \in {\hat{M}}, f\in {\mathrm {Lip}}M. \end{aligned}$$

(1.8)

It is convenient to introduce the notation

$$\begin{aligned} D_{\omega }f = {\hat{\Phi }}_{f}(\omega ),\quad \omega \in {\hat{M}},~f \in {\mathrm {Lip}}M. \end{aligned}$$

(1.9)

The map ${\hat{\Phi }}$ (or $D_{\omega }$ in the above notation) induces two maps

$$\begin{aligned} D:{\mathrm {Lip}}M \rightarrow C({\hat{M}}),\quad T:{\hat{M}} \rightarrow ({\mathrm {Lip}}M)^{*} \end{aligned}$$

defined by

$$\begin{aligned} Df(\omega )= & {} D_{\omega }f = {\hat{\Phi }}_{f}(\omega ),\nonumber \\ T(\omega )(f)= & {} D_{\omega }f = {\hat{\Phi }}_{f}(\omega ),\quad \omega \in {\hat{M}},\quad f \in {\mathrm {Lip}}M. \end{aligned}$$

(1.10)

Observe that (1.8) guarantees that $T(\omega ) \in ({\mathrm {Lip}}M)^{*}$ for each $\omega \in {\hat{M}}$. The map D is a $\Vert \cdot \Vert _{L}-\Vert \cdot \Vert _{\infty }$-bounded linear operator and T is continuous if $({\mathrm {Lip}}M)^{*}$ is endowed with the weak*-topology. We use the map D in the proof of Theorem 1.2 and T will be used in the discussion on the space ${{\hat{M}}}$ in Sect. 3. It follows from the proof of [19, Theorem 9.8] that $D:{\mathrm {Lip}}M \rightarrow C({\hat{M}})$ satisfies

$$\begin{aligned} D(fg) = (\pi ^{*}g) Df + (\pi ^{*}f) Dg,\quad f,g \in {\mathrm {Lip}}M, \end{aligned}$$

(1.11)

that is, D is a derivation of ${\mathrm {Lip}}M$ to the ${\mathrm {Lip}}M$-module $C({\hat{M}})$ (cf. 1.5). A point derivation$D:{\mathrm {Lip}}M \rightarrow {\mathbb {C}}$ at a point $p\in M$ is a bounded linear functional on ${\mathrm {Lip}}M$ such that

$$\begin{aligned} D(fg) = f(p)Dg + g(p)Df,\quad f,g \in {\mathrm {Lip}}M. \end{aligned}$$

The space of all point derivations at p is denoted by ${\mathfrak {D}}_{p}({\mathrm {Lip}}M)$. The next result, which also follows from of [19, Theorem 9.8], explains the role of the operator defined by (1.9).

Theorem 1.4

(cf. [19, Theorem 9.8] ) Let (M, d) be a compact metric space and let $\pi :{\hat{M}} \rightarrow M$ be the map defined in (1.4).

• 1. For each $p \in M$ and for each $\omega \in \pi ^{-1}(p) \subset {\hat{M}}$, $D_{\omega }:{\mathrm {Lip}}M \rightarrow {\mathbb {C}}$ is a continuous point derivation at p.

• 2. The weak $*$-closure of the linear span of $\{ D_{\omega }~|~\omega \in \pi ^{-1}(p) \}$ is equal to the space ${\mathfrak {D}}_{p}({\mathrm {Lip}}M)$.

We use the classical extension theorem of McShane [12].

Theorem 1.5

[12] Let (K, d) be a metric space and let E be a subset of K. For each bounded real-valued Lipschitz function $f:E \rightarrow {\mathbb {R}}$, there exists a Lipschitz function $F:K \rightarrow {\mathbb {R}}$ such that

• 1. $F|E = f$,

• 2. $\Vert F \Vert _{\infty } = \Vert f \Vert _{\infty }$ and $L(F) = L(f)$.

Next we recall the notion of alternating cocycles due to Johnson. Let ${\mathfrak {S}}_{n}$ be the nth symmetric group. For a Banach algebra A and a Banach A-bimodule X, the continuous n-cochains $C^{n}(A,X)$ is an ${\mathfrak {S}}_n$-module by the action

$$\begin{aligned} (\sigma F)(a_{1}, \ldots , a_{n}) = F(a_{\sigma (1)}, \ldots , a_{\sigma (n)}),\quad \sigma \in {\mathfrak {S}}_{n},~ a_{1}, \ldots , a_{n} \in A. \end{aligned}$$

An n-chain F is said to be alternating if $\sigma F = ({\mathrm {sgn}}\sigma )F$, where ${\mathrm {sgn}}~\sigma$ denotes the signature of $\sigma \in {\mathfrak {S}}_{n}$. The subspace of all continuous alternating n-cocycles is denoted by $Z^{n}_{\mathrm {alt}}(A,X)$. An n-chain $F \in C^{n}(A,X)$ is called an n-derivation if

$$\begin{aligned}&F(a_{1}, \ldots , a_{i-1},b_{i}c_{i},a_{i+1}, \ldots , a_{n}) \nonumber \\&\quad =b_{i} \cdot F(a_{1}, \ldots , a_{i-1},c_{i},a_{i+1}, \ldots , a_{n}) \nonumber \\&\qquad + F(a_{1}, \ldots , a_{i-1}, b_{i},a_{i+1}, \ldots , a_{n}) \cdot c_{i} \end{aligned}$$

(1.12)

for each $i=1, \ldots , n$ and for each $a_{1}, \ldots , a_{i-1}, a_{i+1}, \ldots , a_{n}, b_{i}, c_{i} \in A$.

Theorem 1.6

[7, Theorem 2.3, Propostion 2.9, Corollary 2.10] Let A be a commutative Banach algebra and let X be a symmetric Banach A-bimodule.

• 1. An n-cochain $F \in C^{n}(A,X)$ is an alternating n-cocycle if and only if it is an alternating n-derivation.

• 2. The restriction $q_{n}| Z^{n}_{\mathrm {alt}}(A,X): Z^{n}_{\mathrm {alt}}(A,X) \rightarrow H^{n}(A,X)$ of the natural quotient map $q_{n}:Z^{n}(A,X) \rightarrow H^{n}(A,X)$ to $Z^{n}_{\mathrm {alt}}(A,X)$ is injective.

2 Proof of Theorem 1.2

This section is devoted to prove Theorem 1.2. The proof is divided into several steps. In Step 1, we give a construction of derivations ${\mathrm {Lip}}M \rightarrow C({\hat{M}})$. Step 2 supplies a construction of Lipschitz functions associated with a convergent point-sequence of M. Step 3 proves the theorem for $n=1$ and the proof for $n >1$ will be given in Step 4.

We start with a general discussion on maps induced on the Stone–Čech compactification of a space. Let M be a compact metric space and let $\pi :\beta {\tilde{M}} \rightarrow M\times M$ be the continuous surjection defined in (1.4) with the restriction $\pi :{\hat{M}} \rightarrow M$ (recall the identification $M \approx \Delta M$). Let N be a closed, hence compact, neighborhood of the diagonal set $\Delta M$ and let $F:N \rightarrow N$ be a continuous map such that $F(\Delta M) = F^{-1}(\Delta M) = \Delta M$. Let ${\tilde{N}} = N {\setminus } \Delta M$ and let ${\tilde{F}}= F|{\tilde{N}}:{\tilde{N}} \rightarrow {\tilde{N}}$ be the restriction of F. The map ${{\tilde{F}}}$ admits a unique extension $\beta {{{\tilde{F}}}}:\beta {\tilde{N}} \rightarrow \beta {\tilde{N}}$. Since N is another compactification of ${{\tilde{N}}}$, there exists the canonical continuous surjection $\pi _{N}:\beta {{{\tilde{N}}}} \rightarrow N$ such that $\pi _{N}|\pi _{N}^{-1}({\tilde{N}}): \pi _{N}^{-1}({\tilde{N}}) \rightarrow {\tilde{N}}$ is a homeomorphism. Notice that $\beta {{\tilde{F}}}$ is the unique map such that

$$\begin{aligned} \beta {{\tilde{F}}}|\pi _{N}^{-1}({\tilde{N}}) = \pi _{N}^{-1}\circ {\tilde{F}} \circ \pi _{N}|\pi _{N}^{-1}({\tilde{N}}). \end{aligned}$$

(2.1)

Lemma 2.1

• 1. We have the inclusion

  $$\begin{aligned} {\hat{M}} = \pi ^{-1}(\Delta M) \subset \beta {\tilde{N}} \subset \beta {\tilde{M}} \end{aligned}$$

  and $\pi _{N} = \pi |\beta {\tilde{N}}$.

• 2. $\pi _{N} \circ \beta {\tilde{F}} = F \circ \pi _{N}.$

• 3. The restriction $\beta {\tilde{F}}|{\hat{M}}$ of $\beta {{\tilde{F}}}$ to ${{\hat{M}}}$ induces a map ${\hat{F}}:{\hat{M}} \rightarrow {\hat{M}}$ such that $\pi \circ {\hat{F}} = (F|\Delta M) \circ \pi$.

Proof

• 1. Since N is closed in M, ${\tilde{N}}$ is closed in ${{\tilde{M}}}$ and by [20, Proposition 1.48], the Stone-Čech compactification $\beta {\tilde{N}}$ is the closure of ${{\tilde{N}}}$ in $\beta {\tilde{M}}$: $\beta {\tilde{N}} = {\mathrm {cl}}_{\beta {\tilde{M}}}{\tilde{N}}$. In particular $\beta {\tilde{N}} \subset \beta {\tilde{M}}$ and we have $\pi _{N} = \pi |\beta {\tilde{N}}$. It follows from this that $\pi ^{-1}(\Delta M) \subset \beta {\tilde{N}}$.

• 2. We have from (2.1) that $\pi _{N} \circ \beta {\tilde{F}}|\pi _{N}^{-1}({\tilde{N}}) = {\tilde{F}} \circ \pi _{N}|\pi _{N}^{-1}({\tilde{N}})$ and the desired equality follows from the denseness of $\pi _{N}^{-1}({\tilde{N}})$ in $\beta {\tilde{M}}$.

• 3. is a direct consequence of (1) and (2).

$\square$

For a map $F:N \rightarrow N$ as above, we define a bounded linear map $F^{*}D:{\mathrm {Lip}}M \rightarrow C({\hat{M}})$ by

$$\begin{aligned} ((F^{*}D)f)(\omega ) = D_{{{{\hat{F}}}}(\omega )}f,\quad \omega \in {\hat{M}},~f \in {\mathrm {Lip}}M. \end{aligned}$$

Lemma 2.2

If $F|\Delta M = {\mathrm {id}}_{\Delta M}$, then the operator $F^{*}D:{\mathrm {Lip}}M \rightarrow C({\hat{M}})$ is a derivation.

Proof

It suffices to verify the Leibniz rule. Fix Lipschitz functions $f,g \in {\mathrm {Lip}}M$ and a point $\omega \in {\hat{M}}$. We have, by (1.11), the assumption $F|\Delta M = {\mathrm {id}}_{\Delta M}$ and (3) of Lemma 2.1, the following equalities:

$$\begin{aligned} ((F^{*}D)fg)(\omega )= & {} D_{{{{\hat{F}}}}(\omega )}fg\\= & {} \pi ^{*}f({\hat{F}}(\omega )) D_{{{{\hat{F}}}}(\omega )}g + \pi ^{*}g({\hat{F}}(\omega )) D_{{{{\hat{F}}}}(\omega )}f \\= & {} f(\pi ({\hat{F}}(\omega )) D_{{{{\hat{F}}}}(\omega )}g + g(\pi ({\hat{F}}(\omega )) D_{{{{\hat{F}}}}(\omega )}f \\= & {} f(\pi (\omega )) (F^{*}D)g (\omega ) + g(\pi (\omega )) (F^{*}D)f(\omega ). \end{aligned}$$

Recalling the ${\mathrm {Lip}}M$-module structure of $C({\hat{M}})$ ((1.5)) we obtain the conclusion. $\square$

Proof of Theorem 1.2

Step 1. Let (M, d) be a compact metric space satisfying the condition (G) with a positive number $\delta >0$ that meets the condition $(*)$ of Definition 1.1. We may and will assume that $\delta < 1$. Let

$$\begin{aligned} W=\left\{ (x,y)~|~d(x,y) \le \delta \right\} \end{aligned}$$

(2.2)

and for each $(x,y) \in W$, let $\gamma _{xy}$ be the unique geodesic joining x with y. In what follows it is convenient to take the parametrization of $\gamma _{xy}$ as

$$\begin{aligned} \gamma _{xy}:\left[ -\frac{d(x,y)}{2}, \frac{d(x,y)}{2}\right] \rightarrow M,~~\gamma _{xy}\left( -\frac{d(x,y)}{2}\right) =x,~\gamma _{xy}\left( \frac{d(x,y)}{2}\right) =y. \end{aligned}$$

Also let $m_{xy} = \gamma _{xy}(0)$, the midpoint of x and y. For $w(x,y) = d(x,y)/2$, the above parametrization of $\gamma _{xy}$ is given by

$$\begin{aligned} \gamma _{xy}:[-w(x,y),w(x,y)] \rightarrow M.\quad \gamma _{xy}(-w(x,y)) = x, \gamma _{xy}(w(x,y)) = y. \end{aligned}$$

We make a convention that $\gamma _{xx} = m_{xx} = \{x\}$ and $w(x,x) = 0$. Let $\kappa :[0,\delta ] \rightarrow [0,1]$ be the function defined by

$$\begin{aligned} \kappa (t) = t/\delta , \quad t \in [0,\delta ]. \end{aligned}$$

(2.3)

It satisfies

$$\begin{aligned} \kappa ^{-1}(0) = \{0\},\quad \kappa ^{-1}(1) = \{\delta \},\quad \kappa '(t) > 0. \end{aligned}$$

(2.4)

The argument in Step 1 depends only on (2.4) and the explicit form (2.3) will be used in later steps. Let $H:W \rightarrow W$ be the map defined by

$$\begin{aligned} H(x,y) = \bigl (\gamma _{xy}(-w(x,y)\kappa (w(x,y))), \gamma _{xy}(w(x,y)\kappa (w(x,y)))\bigr ),\quad (x,y) \in W.\nonumber \\ \end{aligned}$$

(2.5)

Let $\xi (x,y) = \gamma _{xy}(-w(x,y)\kappa (w(x,y)))$ and $\eta (x,y) = \gamma _{xy}(w(x,y)\kappa (w(x,y)))$ so that $H(x,y) = (\xi (x,y),\eta (x,y)).$ The map H has the following properties.

• (a) For each $(x,y) \in W$, we have

  • (a.1) the points $\xi (x,y), \eta (x,y)$ are on the geodesic $\gamma _{xy}$,

  • (a.2) $m_{\xi (x,y)\eta (x,y)} = m_{xy}$,

  • (a.3) $w(\xi (x,y),\eta (x,y)) = d(\xi (x,y), m_{xy}) = d(\eta (x,y),m_{xy}) = \kappa (w(x,y))w(x,y)$,

  • (a.4) $\gamma _{\xi (x,y)\eta (x,y)} = \gamma _{xy}|[-\kappa (w(x,y))w(x,y),\kappa (w(x,y))w(x,y)]$.

• (b) $H|\Delta M = {\mathrm {id}}_{\Delta M},~H|\partial W = {\mathrm {id}}_{\partial W}$ and $H^{-1}(\Delta M) = H(\Delta M) = \Delta M$,

• (c) If $d(x,y) < \delta$, then $\lim _{n\rightarrow \infty }H^{n}(x,y) = (m_{xy},m_{xy})$, where $H^{n}$ denotes the n-fold iteration of H.

$\square$

Proof

(a.1)–(a.3) are direct consequences of the definition. (a.4) follows from the uniqueness of the geodesic joining $\xi (x,y)$ and $\eta (x,y)$. (b) follows from the definition (2.5) and (2.4). Note that $d(x,y) = \delta$ if $(x,y) \in \partial W$. To verify (c) let $w^{i} = w(H^{i}(x,y))$. By induction we can see directly that $w^{i+1} < w^{i}$ and $\kappa (w^{i+1}) < \kappa (w^{i})$ due to (2.4). Then we see from (a.3) that

$$\begin{aligned} w^{i+1}= & {} \kappa (w^{i})w^{i} = \kappa (w^{i})\kappa (w^{i-1}) \cdots \kappa (w^{1})w^{1} \\\le & {} \kappa (w^{1})^{i}w^{1}. \end{aligned}$$

Since $w(x,y) = d(x,y)/2 \le \delta /2 < 1$, we have $\kappa (w^{1}) = \kappa (w(x,y)) <1$ and $\lim _{i}w^{i} = 0$. This and (a.2) imply the condition (c).

We apply Lemma 2.1 to the map $H:W \rightarrow W$ defined on the closed neighbourhood W of $\Delta M$ and obtain a sequence of linear operators

$$\begin{aligned} \left\{ (H^{n})^{*}D:{\mathrm {Lip}}M \rightarrow C({\hat{M}})~|~n\ge 1\right\} . \end{aligned}$$

We see from Lemma 2.2 and the condition (b) that $(H^{n})^{*}D$ is a derivation. Our goal is to prove that the above forms a ${\mathrm {Lip}}M$-linearly independent sequence of derivations.

Step 2. Fix a point p of M and take a geodesic $\gamma :[0,\delta ] \rightarrow M$ such that $\gamma (0) = p$. Take a sequence $S_{0} = \{x_{k}, y_{k}~|~k \ge 1\}$ of points on the geodesic ${\mathrm {Im}}\gamma$ which satisfies the following conditions:

• (d.1) $\lim _{k}x_{k} = \lim _{k}y_{k} =p$, $x_{k}\ne y_{k}$ for each k,

• (d.2) $d(x_{1},p) < \delta$ and, for each $k\ge 1$, $d(x_{k+1},p)< d(y_{k},p) < d(x_{k},p)$,

• (d.3) for each $k\ge 1$, $d(x_{k+1},y_{k+1}) < d(x_{k},y_{k}).$

For a fixed integer $N \ge 1$, we examine the sequence $\{H^{\nu }(x_{k},y_{k})~|~k \ge 1,~1 \le \nu \le N\}$ of points of W. The following statements are consequences of (a)–(c) above and will be used later.

• (e) For each k, the geodesic $\gamma _{x_{k}y_{k}}$ is the geodesic segment in $\gamma$ joining $x_{k}$ and $y_{k}$, denoted by $\overline{x_{k}y_{k}}$ for simplicity.

• (f) For $i \ge 0$, let $(x_{k}^{i},y_{k}^{i}) = H^{i}(x_{k},y_{k})$ with $(x_{k}^{0},y_{k}^{0}) = (x_{k},y_{k})$. Then the points $x_{k}^{i+1}$ and $y_{k}^{i+1}$ are on the geodesic $\overline{x_{k}^{i}y_{k}^{i}}$ so that $d(x_{k}^{i},m_{k}) \downarrow 0$ and $d(y_{k}^{i},m_{k}) \downarrow 0$ as $i \rightarrow \infty$.

The next lemma describes a general procedure to find a Lipschitz function that detects the derivation $(H^{i})^{*}D$.

Lemma 2.3

(cf. [8, Lemma 2.2]) Under the above notation, for each $N \ge 1$ and for each $i \in \{1,\ldots , N\}$, there exist an integer $k_{0} \ge 1$ and a real-valued Lipschitz function $f \in {\mathrm {Lip}}M$ such that

• 1. $L(f) = 1$,

• 2. for each $k \ge k_{0}$ we have $|\Phi _{f}(x_{k}^{i},y_{k}^{i})| \ge 1/4$ for each $i=1,\ldots , N$,

• 3. for each $k \ge k_{0}$ and for each $j \in \{1,\ldots ,N\}$ with $j \ne i$, we have $\Phi _{f}(x_{k}^{j},y_{k}^{j}) = 0$.

Proof

First we make some preliminary estimates on the distance $d(x_{k}^{i},y_{\ell }^{j})$. Let $d_{k} = d(x_{k},y_{k}),$$w_{k} = w(x_{k},y_{k}) = d_{k}/2$ and $m_{k} = m_{x_{k}y_{k}}$. Also for $j \ge 1$, let $w_{k}^{j} = d(x_{k}^{j},y_{k}^{j})/2 = d(x_{k}^{j},m_{k}) = d(y_{k}^{j},m_{k})$. Under this notation we have

$$\begin{aligned} w_{k}^{j} = \delta (w_{k}/\delta )^{2^i} \end{aligned}$$

(2.6)

In fact, $w_{k}^{1} = \kappa (w(x_{k},y_{k}))w(x_{k},y_{y}) = w_{k}^{2}/\delta$, and $w_{k}^{j+1}= \kappa (w_{k}^{j})w_{k}^{j} = \delta ^{-1}(w_{k}^{j})^{2}$, from which (2.6) follows by an induction. Let

$$\begin{aligned} \varepsilon _{k}^{j} = \frac{d(x_{k}^{j},x_{k}^{j+1})}{d(x_{k},y_{k})}= \frac{d(x_{k}^{j},x_{k}^{j+1})}{d_{k}},\quad j \ge 0. \end{aligned}$$

(2.7)

We have by (2.6)

$$\begin{aligned} \varepsilon _{k}^{j}= & {} \frac{1}{d_k}\left( d\left( x_{k}^{j},m_{k}\right) -d\left( x_{k}^{j+1},m_{k}\right) \right) \nonumber \\= & {} \frac{1}{d_k}\delta \left( \frac{w_{k}}{\delta }\right) ^{2^j} \left( 1-\left( \frac{w_{k}}{\delta }\right) ^{2^j}\right) . \end{aligned}$$

(2.8)

Let $r_{k} = w_{k}/\delta$. We use (2.8) to see

$$\begin{aligned} \frac{\varepsilon _{k}^{j}}{\varepsilon _{k}^{j-1}} = (r_{k})^{2^{j-1}} \cdot \frac{1-r_{k}^{2^j}}{1-r_{k}^{2^{j-1}}} \end{aligned}$$

for each $j \ge 1$. Since $w_{k} = d(x_{k},y_{k})/2 < d(x_{k},p)/2 \le \delta /2$, we see $0< r_{k} < 1$ and thus, for each $j\ge 1$, we obtain

$$\begin{aligned} \lim _{k\rightarrow \infty }\frac{\varepsilon _{k}^{j}}{\varepsilon _{k}^{j-1}} = 0. \end{aligned}$$

Also by (d.1) we see $\lim _{k}w_{k} = 0$. Take a large $k_{0} \ge 1$ such that

$$\begin{aligned} \begin{array}{ll} \frac{\varepsilon _{k}^{j}}{\varepsilon _{k}^{j-1}} \le 1,\quad k \ge k_{0},~1 \le j \le N\quad \text{ and } \\ r_{k} = w_{k}/\delta \le 1/2,\quad k \ge k_{0}. \end{array} \end{aligned}$$

(2.9)

Fix an integer $N \ge 1$, let $S_{k}^{N} = \{x_{k}^{j},y_{k}^{j}~|~0 \le j \le N\}$ and $S^{N} = \cup _{k\ge k_{0}}S_{k}^{N} \cup \{p\}$. We fix $i \in \{1, \ldots , N\}$ and define a function $f:S^{N} \rightarrow [0,\infty )$ by:

$$\begin{aligned} \begin{array}{ll} f(p) = 0,\\ f(x_{k}^{i}) = \varepsilon _{k}^{i}d_{k} = d\left( x_{k}^{i},x_{k}^{i+1}\right) ,\quad (\text{ see }~(2.7))\\ f(y_{k}^{i}) = 0,\\ f(x_{k}^{j}) = f(y_{k}^{j}) = 0,\quad k \ge k_{0}, 0 \le j \le N, j \ne i. \end{array} \end{aligned}$$

(2.10)

We first verify that the function f is a Lipschitz function on $S^N$ with the Lipschitz constant 1 which satisfies the condition (2) and (3).

In order to estimate

$$\begin{aligned} \Phi _{f}(x_{k}^{i},x_{\ell }^{j}) = \frac{f(x_{k}^{i})-f(x_{\ell }^{j})}{d(x_{k}^{i},x_{\ell }^{j})}, \end{aligned}$$

we may assume that $k \le \ell$. First we observe

$$\begin{aligned} \Phi _{f}(x_{k}^{i},x_{k}^{i+1}) = \frac{f(x_{k}^{i})-f(x_{k}^{i+1})}{d(x_{k}^{i},x_{k}^{i+1})} = 1 \end{aligned}$$

(2.11)

and by (2.9)

$$\begin{aligned} 0 \le \Phi _{f}(x_{k}^{i},x_{k}^{i-1}) = \frac{f(x_{k}^{i})-f(x_{k}^{i-1})}{d(x_{k}^{i},x_{k}^{i-1})} = \frac{\varepsilon _{k}^{i}}{\varepsilon _{k}^{i-1}} \le 1. \end{aligned}$$

(2.12)

For j with $0 \le j \le i-2$, we see $d(x_{k}^{i},x_{k}^{j}) = d(x_{k}^{i},x_{k}^{i-1})+d(x_{k}^{i-1}, x_{k}^{j}) \ge d(x_{k}^{i},x_{k}^{i-1})$ by (f). Hence we have by (2.12),

$$\begin{aligned} 0 \le \Phi _{f}(x_{k}^{i},x_{k}^{j}) = \frac{f(x_{k}^{i})-f(x_{k}^{j})}{d(x_{k}^{i},x_{k}^{j})} \le \frac{f(x_{k}^{i})}{d(x_{k}^{i},x_{k}^{i-1})} \le 1 \end{aligned}$$

(2.13)

Similarly by using (2.11) we have for j with $i+2 \le j \le N$,

$$\begin{aligned} 0 \le \Phi _{f}\left( x_{k}^{i},x_{k}^{j}\right) \le 1. \end{aligned}$$

(2.14)

Next we estimate $\Phi _{f}(x_{k}^{i},x_{\ell }^{j})$ for $\ell > k$. By definition $|\Phi _{f}(x_{k}^{i},x_{\ell }^{i})| = \frac{|\varepsilon _{k}^{i}d_{k} - \varepsilon _{\ell }^{i}d_{\ell }|}{d(x_{k}^{i},x_{\ell }^{i})},$ and we see

$$\begin{aligned} \varepsilon _{k}^{i}d_{k} \ge \varepsilon _{\ell }^{i}d_{\ell }. \end{aligned}$$

In fact, we have, by (2.8), $\varepsilon _{k}^{i} d_{k} = \delta r_{k}^{2^i}(1-r_{k}^{2^i})$ and $\varepsilon _{\ell }^{i}d_{\ell } = \delta r_{\ell }^{2^i}(1-r_{\ell }^{2^i})$. Also by (2.9) we have $r_{\ell } = w_{\ell }/\delta \le w_{k}/\delta = r_{k} \le 1/2$ and hence $r_{\ell }^{2^i} \le r_{k}^{2^i} \le 1/2$, from which we obtain the desired inequality.

Also by (d.2) we have $d(x_{k}^{i},x_{\ell }^{i}) = d(x_{k}^{i},x_{k}^{i+1}) + d(x_{k}^{i+1},x_{\ell }^{i}) \ge d(x_{k}^{i},x_{k}^{i+1})$. Hence we obtain, by (2.11),

$$\begin{aligned} |\Phi _{f}(x_{k}^{i},x_{\ell }^{i})|= & {} \frac{|\varepsilon _{k}^{i}d_{k} - \varepsilon _{\ell }^{i}d_{\ell }|}{d(x_{k}^{i},x_{\ell }^{i})} = \frac{\varepsilon _{k}^{i}d_{k} - \varepsilon _{\ell }^{i}d_{\ell }}{d(x_{k}^{i},x_{\ell }^{i})} \nonumber \\\le & {} \frac{\varepsilon _{k}^{i}d_{k}}{d(x_{k}^{i},x_{\ell }^{i})} \le \frac{\varepsilon _{k}^{i}d_{k}}{d(x_{k}^{i},x_{k}^{i+1})} =1. \end{aligned}$$

(2.15)

Similarly we have for $\ell > k$,

$$\begin{aligned} \begin{array}{ll} |\Phi _{f}(x_{k}^{i},x_{\ell }^{j})| \le 1,\quad 0\le j \le N, j\ne i \\ |\Phi _{f}(x_{k}^{i},y_{\ell }^{j})| \le 1,\quad 0\le j \le N. \end{array} \end{aligned}$$

(2.16)

Combining (2.11)–(2.16), we obtain $L(f) = 1$ on $S^N$.

In order to prove (2), we estimate $\Phi _{f}(x_{k}^{i},y_{k}^{i}) = \frac{\varepsilon _{k}^{i}d_{k}}{d(x_{k}^{i},y_{k}^{i})}$. First we see

$$\begin{aligned} d(x_{k}^{i},y_{k}^{i})= & {} d(x_{k}.y_{k}) - \sum _{j=0}^{i-1}\left( d(x_{k}^{j},x_{k}^{j+1})+d(y_{k}^{j},y_{k}^{j+1}) \right) \nonumber \\= & {} d(x_{k},y_{k}) - 2 \sum _{j=0}^{i-1}\varepsilon _{k}^{j}d_{k} = d_{k}\left( 1-2\sum _{j=0}^{i-1}\varepsilon _{k}^{j}\right) . \end{aligned}$$

(2.17)

Using (2.8) with $d_{k} = 2w_{k}$, we compute

$$\begin{aligned} 2\sum _{j=0}^{i-1}\varepsilon _{k}^{j} = \frac{\delta }{w_k}\sum _{j=0}^{i-1}r_{k}^{2^j}(1-r_{k}^{2^j}) =\frac{\delta }{w_k}\left( r_{k} -r_{k}^{2^i}\right) . \end{aligned}$$

Hence we obtain, by $w_{k} = \delta r_{k}$ (see 2.9),

$$\begin{aligned} 2d_{k} \sum _{j=0}^{i-1}\varepsilon ^{j}_{k} = d_{k} \frac{\delta }{w_{k}}\left( r_{k}-r_{k}^{2^i}\right) = d_{k}\left( 1- r_{k}^{2^{i}-1}\right) \end{aligned}$$

and by (2.17), we have

$$\begin{aligned} d(x_{k}^{i},y_{k}^{i}) = d_{k} r_{k}^{2^{i}-1}. \end{aligned}$$

Thus we obtain

$$\begin{aligned} \Phi _{f}(x_{k}^{i},y_{k}^{i})= & {} \frac{\varepsilon _{k}^{i}d_{k}}{d_{k}r_{k}^{2^{i}-1}} = \frac{r_{k}^{2^i}(1-r_{k}^{2^i})}{r_{k}^{2^{i}-1}} \frac{\delta }{d_{k}} \\= & {} \frac{r_{k}}{d_{k}}\delta (1-r_{k}^{2^i}) = \frac{w_{k}(1-r_{k}^{2^i})}{d_{k}} \\= & {} (1-r_{k}^{2^i})/2. \end{aligned}$$

Using $r_{k}^{2^i} =(\frac{w_{k}}{\delta })^{2^{i}} \le \frac{w_{k}}{\delta } \le 1/2$ we see that the last term of the above is at least 1 / 4. Hence we obtain

$$\begin{aligned} \Phi _{f}(x_{k}^{i},y_{k}^{i}) \ge 1/4, \end{aligned}$$

(2.18)

which proves (2). (3) directly follows from the definition (2.10). Finally we apply Theorem 1.5 to the above f to obtain a Lipschitz extension ${\bar{f}}:M \rightarrow {\mathbb {R}}$ such that $L({\bar{f}}) = L(f) = 1$, the desired condition (1). The function ${\bar{f}}$ satisfies (2) and (3) as well. This completes the proof of lemma. $\square$

Step 3. We prove the theorem for $n=1$. Since $C({\hat{M}})$ is a symmetric ${\mathrm {Lip}}M$-module, we have ${\mathrm {H}}^{1}({\mathrm {Lip}}M,C({\hat{M}})) = {\mathfrak {D}}({\mathrm {Lip}}M,C({\hat{M}}))$. In order to prove that ${\mathfrak {D}}({\mathrm {Lip}}M,C({\hat{M}}))$ has the infinite ${\mathrm {Lip}}M$-rank, we take the map $H:M \times M \rightarrow M \times M$ in Step 1, fix an integer $N\ge 1$ and consider the N derivations

$$\begin{aligned} H^{*}D, \ldots , (H^{N})^{*}D:{\mathrm {Lip}}M \rightarrow C({\hat{M}}), \end{aligned}$$

and assume that, for $\varphi _{1},\ldots , \varphi _{N} \in {\mathrm {Lip}}M$, the equality

$$\begin{aligned} \sum _{j=1}^{N}\varphi _{j}(\pi (\omega ))(H^{j})^{*}D_{\omega }f = 0 \end{aligned}$$

(2.19)

holds for each $\omega \in {\hat{M}}$ and for each $f \in {\mathrm {Lip}}M$. We fix $i \in \{1,\ldots , N\}$ and show that $\varphi _{i} \equiv 0$. Pick an arbitrary point $p \in M$, take a geodesic $\gamma$, choose a sequence $\{x_{k},y_{k}~|~k \ge 1\}$ of points on $\gamma$ such that

$$\begin{aligned} \begin{array}{ll} \gamma :[0,\delta ] \rightarrow M, ~\text{ with }~ \gamma (0) = p ~\text{ and } \\ \text{ the } \text{ sequence }~\{x_{k},y_{k}~|~k \ge 1\}~\text{ satisfies } \text{(d.1)-(d.3) }, \end{array} \end{aligned}$$

(2.20)

and apply Lemma 2.3 to find an integer $k_{0} \ge 1$ and a Lipschitz function f satisfying the conditions of the lemma.

Let $\omega$ be an accumulation point of the set $\{ (x_{k},y_{k})~|~k \ge k_{0}\} \subset \beta {\tilde{W}}$. Then $\pi (\omega )$, as a point of $M \times M$, is an accumulation point of the set $\{(x_{k},y_{k})~|~k\ge k_{0}\} \subset M\times M$, that is, the singleton (p, p). Recalling the identification $M \approx \Delta M$ via the diagonal map, we have $\pi (\omega ) = p$. Also ${\hat{H}}^{j}(\omega ) = (\beta {\tilde{H}}^{j})(\omega ) = (\beta {\tilde{H}})^{j}(\omega )$ is an accumulation point of $\{H^{j}(x_{k},y_{k}) = (x_{k}^{j},y_{k}^{j})~|~k \ge k_{0}\}$. This and the conditions 2 and 3 of Lemma 2.3 imply

$$\begin{aligned} \begin{array}{ll} D_{{\hat{H}}^{i}}(\omega )f = \beta \Phi _{f}({\hat{H}}^{i}(\omega )) \ge 1/4 ~\text{ and }\\ D_{{\hat{H}}^{j}}(\omega )f = \beta \Phi _{f}({\hat{H}}^{j}(\omega )) = 0,\quad 1\le j \le N, j\ne i. \end{array} \end{aligned}$$

Therefore from (2.19) we have

$$\begin{aligned} 0 = \sum _{j=1}^{N}\varphi _{j}(\pi (\omega ))((H^{j})^{*}D)_{\omega }f = \varphi _{i}(p)D_{{\hat{H}}^{i}(\omega )}f \end{aligned}$$

which shows $\varphi _{i}(p) = 0$ as required.

This completes the proof of the theorem for $n=1$.

Step 4. This step finishes the proof of theorem, proving the case $n > 1$, by carrying out the idea stated in Sect. 1. Rather than considering the homomorphism $\Omega _n$ in (1.6), we proceed directly as follows. Let $Z_{\mathrm {alt}}^{n}({\mathrm {Lip}}M,C({\hat{M}}))$ be the space of the alternating n-cocycles on ${\mathrm {Lip}}M$ with coefficient $C({\hat{M}})$. By Theorem 1.3 we have an injection $Z_{\mathrm {alt}}^{n}({\mathrm {Lip}}M,C({\hat{M}})) \rightarrow {\mathrm {H}}^{n}({\mathrm {Lip}}M,C({\hat{M}}))$ and thus it suffices to prove that $Z_{\mathrm {alt}}^{n}({\mathrm {Lip}}M,C({\hat{M}}))$ has the infinite ${\mathrm {Lip}}M$-rank.

Fix an arbitrary integer $N\ge 1$. For $\nu =1,\ldots , N$ and $i=1,\ldots , n$, let

$$\begin{aligned} H_{\nu ,i} = H^{(\nu -1)n+i}:W\rightarrow W \end{aligned}$$

and define the n-cochain $d_{\nu } \in C^{n}({\mathrm {Lip}}M,C({\hat{M}}))$ by

$$\begin{aligned} d_{\nu }(a_{1},\ldots ,a_{n})(\omega ) = \det \left( (H_{\nu ,i}^{*}D)a_{j}(\omega )\right) = \det \left( (D_{{\hat{H}}_{\nu ,i}(\omega )}a_{j})_{1\le i,j \le n}\right) .\nonumber \\ \end{aligned}$$

(2.21)

It follows from the definition that $d_{\nu }$ is an alternating cochain. By Lemma 2.2, $D_{{\hat{H}}_{\nu ,i}}(\omega )$ is a derivation, from which it follows that $d_{\nu }$ is an n-derivation. Thus by (1) of Theorem 1.6 we see that $d_{\nu }$ is an alternating cocycle: $d_{\nu } \in Z_{\mathrm {alt}}^{n}({\mathrm {Lip}}M,C({\hat{M}}))$.

Assume that, for $\varphi _{1},\ldots , \varphi _{N} \in {\mathrm {Lip}}M$, the equality

$$\begin{aligned} \sum _{\nu =1}^{N}\varphi _{\nu }(\pi (\omega ))d_{\nu }(a_{1},\ldots ,a_{n})(\omega ) = 0 \end{aligned}$$

(2.22)

holds for each $\omega \in {\hat{M}}$ and for each $a_{1},\ldots ,a_{n} \in {\mathrm {Lip}}M$. We fix $\mu \in \{1,\ldots , N\}$ and show $\varphi _{\mu }\equiv 0$. Take an arbitrary point p of M and choose a geodesic $\gamma$ and a sequence $\{x_{k},y_{k}~|~k \ge 1\}$ as in (2.20). Applying Lemma 2.3 we obtain an integer $k_{0} \ge 1$ and a sequence $\{f_{j}~|~1\le j \le n\}$ of Lipschitz functions such that

$$\begin{aligned} L(f_{j})= & {} 1,\quad 1 \le j \le n, \nonumber \\ |\Phi _{f_j}(H_{\mu ,j}(x_{k},y_{k}))|\ge & {} 1/4,\quad k \ge k_{0},~1 \le j \le n, \end{aligned}$$

(2.23)

$$\begin{aligned} \Phi _{f_j}(H_{\mu ,t}(x_{k},y_{k}))= & {} 0,\quad k \ge k_{0},~1 \le t \le n, t\ne j, \end{aligned}$$

(2.24)

$$\begin{aligned} \Phi _{f_j}(H_{\nu ,t}(x_{k},y_{k}))= & {} 0,\quad k \ge k_{0},~1\le \nu \le N, \nu \ne \mu ,~1\le t \le n. \end{aligned}$$

(2.25)

Let $\omega$ be an accumulation point of $\{(x_{k},y_{k})~|~k \ge k_{0}\} \subset {\tilde{W}}$. As in Step 3, we see $\pi (\omega ) = p$ and ${\hat{H}}_{\nu ,i}(\omega )$ is an accumulation point of $\{H_{\nu ,i}(x_{k},y_{k})~|~k \ge k_{0}\}$ for each $\nu$ and i with $1\le \nu \le N,~1\le i \le n$. Thus by (2.23) and (2.24) we find a nonzero $c_{i}$ such that

$$\begin{aligned} D_{{\hat{H}}_{\mu ,i}(\omega )}f_{j} = {\hat{\Phi }}_{f_j}({\hat{H}}_{\nu ,i}(\omega )) = \beta \Phi _{f_j}({\hat{H}}_{\nu ,i}(\omega )) =\delta _{ij}c_{i}. \end{aligned}$$

Also by (2.25) $D_{{\hat{H}}_{\nu ,i}(\omega )}f_{j} = 0$ for each $\nu \ne \mu$. Hence by (2.22) we have

$$\begin{aligned} 0= & {} \sum _{\nu =1}^{N}\varphi _{\nu }(\pi (\omega ))d_{\nu }(a_{1},\ldots ,a_{n})(\omega )\nonumber \\= & {} \varphi _{\mu }(\pi (\omega ))d_{\mu }(f_{1},\ldots ,f_{n})(\omega ) = \varphi _{\mu }(p) c_{1}\cdots c_{n}, \end{aligned}$$

which implies $\varphi _{\mu }(p) = 0$ as desired.

This completes Step 4 and hence completes the proof of the theorem. $\square$

3 The space ${\hat{M}}$ and Proof of Theorem 1.3

Here we compare the point derivation $D_{\omega }$ for a point $\omega \in {\hat{M}}$ [see (1.9) and Theorem 1.4] with the derivation by tangent vectors of compact smooth manifolds. The comparison indicates that the space ${\hat{M}}$ may be regarded, to certain extent, as a Lipschitz analogue of the unit sphere bundle of a Riemannian manifold.

Let (M, g) be a compact Riemannian manifold with the metric d induced by g. By the compactness of M, there exists a $\delta >0$ such that, for each pair p, q of points of M with $d(p,q) \le \delta$, there exists a unique geodesic $\gamma _{pq}:[0,d(p,q)] \rightarrow M$ such that

$$\begin{aligned} \gamma _{pq}(0) = p,\quad \gamma _{pq}(d(p,q)) = q,\quad \Vert {\dot{\gamma }}_{pq}(t) \Vert \equiv 1. \end{aligned}$$

(3.1)

As in (2.2), let $W =\{(p,q) \in M\times M~|~d(p,q) \le \delta \}$ and let ${\tilde{W}} = W {\setminus } \Delta M$. By Lemma 2.1, we have the inclusion ${\hat{M}} \subset \beta {\tilde{W}} \subset \beta {\tilde{M}}$ and the canonical surjection $\pi _{W}:\beta {\tilde{W}} \rightarrow W$ is the restriction of $\pi :\beta {\tilde{M}} \rightarrow M\times M$. In what follows $\pi _{W}$ is simply denoted by $\pi :\beta {\tilde{W}} \rightarrow W$. Let $\tau :TM \rightarrow M$ be the tangent bundle of M and let $SM =\{ v \in TM~|~\Vert v \Vert = 1\}$, the unit sphere bundle. We define a map $V:{\tilde{W}} \rightarrow SM$ by

$$\begin{aligned} V(p,q) = {\dot{\gamma }}_{qp}(0) \in S_{p}M,\quad (p,q) \in {\tilde{W}}. \end{aligned}$$

(3.2)

By the uniqueness of the geodesic $\gamma _{qp}$ (3.1), the map V is a well-defined continuous map to the compact space SM and hence extends uniquely to the Stone-Čech compactification: $\beta V: \beta {\tilde{W}} \rightarrow SM$ which restricts to:

$$\begin{aligned} {\hat{V}}:= \beta V | {\hat{M}}: {\hat{M}} \rightarrow SM. \end{aligned}$$

As in Sect. 1, let $\Delta _{M}:M \rightarrow \Delta M \subset M\times M$ be the diagonal map. We have

Lemma 3.1

We have the equality

$$\begin{aligned} \Delta _{M} \circ \tau \circ {\hat{V}} = \pi . \end{aligned}$$

Proof

For a point $\omega \in {\hat{M}} \subset \beta {\tilde{W}}$ there exists a net $(p_{\alpha },q_{\alpha })_{\alpha }$ of points of ${\tilde{W}}$ such that $\lim _{\alpha }(p_{\alpha },q_{\alpha }) = \omega$ in $\beta {\tilde{W}}$. By the continuity of $\beta V$ we have

$$\begin{aligned} {\hat{V}}(\omega ) = \lim _{\alpha }V(p_{\alpha },q_{\alpha }) = \lim _{\alpha }{\dot{\gamma }}_{q_{\alpha }p_{\alpha }}(0). \end{aligned}$$

Noticing $\tau ({\dot{\gamma }}_{q_{\alpha }p_{\alpha }}(0)) = q_{\alpha }$, we have

$$\begin{aligned} \Delta _{M}(\tau ({\hat{V}}(\omega ))) = \Delta _{M}\left( \lim _{\alpha } \tau V(p_{\alpha },q_{\alpha })\right) = \left( \lim _{\alpha }q_{\alpha }, \lim _{\alpha }q_{\alpha }\right) . \end{aligned}$$

On the other hand $\pi (\omega ) = \lim _{\alpha }(p_{\alpha },q_{\alpha }) = (\lim _{\alpha } p_{\alpha }, \lim _{\alpha }q_{\alpha })$. Since $\omega \in \pi ^{-1}(\Delta M)$ we have by [19, Lemma 9.6] that $\lim _{\alpha }p_{\alpha } = \lim _{\alpha }q_{\alpha }$. Hence we have $\Delta _{M}(\tau ({\hat{V}}(\omega ))) = \pi (\omega )$, as desired. $\square$

In Sect. 1 the map $T:{\hat{M}} \rightarrow ({\mathrm {Lip}}M)^{*}$ was defined by $(T(\omega ))(f) = D_{\omega }f$ for $\omega \in {\hat{M}},~f \in {\mathrm {Lip}}M$. The map is continuous when $({\mathrm {Lip}}M)^{*}$ is endowed with the weak*-topology. Restricting $T(\omega )$ to the subspace $C^{1}(M)$ of ${\mathrm {Lip}}M$ consisting of the $C^1$-functions on M we obtain a composition

$$\begin{aligned} T:{\hat{M}} \rightarrow ({\mathrm {Lip}}M)^{*} \rightarrow (C^{1}(M))^{*} \end{aligned}$$

which is continuous when $(C^{1}(M))^{*}$ is endowed with the weak*-topology. On the other hand we have a map $\theta :SM \rightarrow (C^{1}(M))^{*}$ given by

$$\begin{aligned} (\theta (v))(f) = vf,\quad v \in SM,\quad f \in C^{1}(M). \end{aligned}$$

(3.3)

See [21, 1.21] for the action of tangent vectors on $C^{1}$-functions. The map $\theta$ is related to the map T by the next lemma. For $\xi \in (C^{1}(M))^{*}$ and $f \in C^{1}(M)$, $\xi (f)$ is also denoted by $\langle \xi ,f \rangle$.

Lemma 3.2

• 1. $\theta \circ {\hat{V}} = T$, that is, for each $\omega \in {\hat{M}}$ and for each $f \in C^{1}(M)$, we have

  $$\begin{aligned} D_{\omega }f = {\hat{V}}(\omega )f. \end{aligned}$$

• 2. ${\text {Im}}\theta = {\text {Im}}T$.

Proof

• 1. For a point $\omega \in {\hat{M}}$ take a net $((p_{\alpha },q_{\alpha }))_{\alpha }$ of points of ${{\tilde{W}}}$ such that $\omega = \lim _{\alpha }((p_{\alpha },q_{\alpha }))$. By the continuity of $\theta$, we have, for each $f \in C^{1}(M)$,

  $$\begin{aligned} \langle (\theta \circ {\hat{V}}) (\omega ),f \rangle= & {} \langle \theta (\lim _{\alpha }V(p_{\alpha },q_{\alpha })),f \rangle \\= & {} \lim _{\alpha } \langle \theta ({\dot{\gamma }}_{q_{\alpha }p_{\alpha }}(0)),f\rangle = \lim _{\alpha } {\dot{\gamma }}_{q_{\alpha }p_{\alpha }}(0)f \\= & {} \lim _{\alpha } \frac{d}{dt}\big |_{t=0}f(\gamma _{q_{\alpha }p_{\alpha }}(t)). \end{aligned}$$

  The complex-valued function f is written as $f = u+iv$ for real-valued $C^1$-functions u and v. Applying the mean value theorem to u and v, we have

  $$\begin{aligned} f(p_{\alpha }) - f(q_{\alpha })= & {} f(\gamma _{q_{\alpha }p_{\alpha }}(d(q_{\alpha },p_{\alpha })))-f(\gamma _{q_{\alpha }p_{\alpha }}(0)) \nonumber \\= & {} \left( \frac{d(u \circ \gamma _{q_{\alpha }p_{\alpha }})}{dt}(\rho _{\alpha }) + i\frac{d(v \circ \gamma _{q_{\alpha }p_{\alpha }})}{dt}(\sigma _{\alpha })\right) d(p_{\alpha },q_{\alpha })\nonumber \\ \end{aligned}$$

  (3.4)

  for some $\rho _{\alpha }, \sigma _{\alpha } \in (0,d(p_{\alpha },q_{\alpha }))$. Since $\omega \in {\hat{M}}$ we have again by [19, Lemma 9.6] that $\lim _{\alpha }d(p_{\alpha },q_{\alpha }) = 0$. By (3.4) we have

  $$\begin{aligned} \begin{aligned} \Phi _{f}(p_{\alpha },q_{\alpha }) = \frac{d(u \circ \gamma _{q_{\alpha }p_{\alpha }})}{dt}(\rho _{\alpha }) + i\frac{d(v \circ \gamma _{q_{\alpha }p_{\alpha }})}{dt}(\sigma _{\alpha }) \end{aligned} \end{aligned}$$

  (3.5)

  Taking the limit in (3.5) and using $\lim _{\alpha }(\frac{d}{dt}u \circ \gamma _{q_{\alpha }p_{\alpha }})(\rho _{\alpha }) = (\frac{d}{dt}u \circ \gamma _{q_{\alpha }p_{\alpha }})(0)$, $\lim _{\alpha }(\frac{d}{dt}v \circ \gamma _{q_{\alpha }p_{\alpha }})(\sigma _{\alpha }) = (\frac{d}{dt}v \circ \gamma _{q_{\alpha }p_{\alpha }})(0)$, we have

  $$\begin{aligned} D_{\omega }f= & {} {\hat{\Phi }}_{f}(\omega ) = \lim _{\alpha }\Phi _{f}(p_{\alpha },q_{\alpha }) \\= & {} \lim _{\alpha } \frac{d(f \circ \gamma _{q_{\alpha }p_{\alpha }})}{dt}(0) = {\hat{V}}(\omega )f. \end{aligned}$$

  This proves (1).

• 2. From (1) we see ${\mathrm {Im}}T \subset {\mathrm {Im}}\theta$. In order to prove the reverse inclusion, let $v \in S_{p}M$ with $\Vert v \Vert = 1$ and take the geodesic $\gamma _{v}:[0,\delta ] \rightarrow M$ such that

  $$\begin{aligned} \gamma _{v}(0) = p,\quad {\dot{\gamma }}_{v}(0) = v. \end{aligned}$$

  Note that the point $(\gamma _{v}(t),p)$ is in ${\tilde{W}}$ for each $t \in (0,\delta ]$. Using $\Vert {\dot{\gamma }}_{v}\Vert \equiv 1$, we see $d(\gamma _{v}(t),p) = t$. Thus for each $f\in C^{1}(M)$ and for each $t \in (0,\delta ]$,

  $$\begin{aligned} \Phi _{f}((\gamma _{v}(t),p))= & {} \frac{f(\gamma _{v}(t)) - f(\gamma _{v}(0))}{d(\gamma _{v}(t),p)} \\= & {} \frac{1}{d(\gamma _{v}(t),p)} \frac{d(f\circ \gamma _{v})}{dt}(\rho _{t}) \cdot d(\gamma _{v}(t),p) \\= & {} \frac{d(f\circ \gamma _{v})}{dt}(\rho _{t}) \end{aligned}$$

  for some $\rho _{t} \in (0,t)$. Let $\omega \in {\hat{M}}$ be an accumulation point of $\{(\gamma _{v}(t),p)~|~t \in (0,\delta ]\}$. Since the net $(\frac{d(f\circ \gamma _{v})}{dt}(\rho _{t}))_{t\in (0,\delta ]}$ converges to $\frac{d(f\circ \gamma _{v})}{dt}(0) = {\dot{\gamma }}(0)f = vf$, we have

  $$\begin{aligned} D_{\omega }f = {\hat{\Phi }}_{f}(\omega ) = vf, \end{aligned}$$

  as desired.

$\square$

In view of these lemmas we may regard ${{\hat{M}}}$ as a Lipschitz-analogue of the unit sphere bundle SM of a Riemannian manifold M. Let $\Gamma (M,SM)$ be the space of smooth sections of the bundle $\tau :SM\rightarrow M$

$$\begin{aligned} \Gamma (M,SM) = \left\{ \sigma :M\rightarrow SM~|~\tau \circ \sigma = {\mathrm {id}}_{M}\right\} \end{aligned}$$

and let $\Theta :\Gamma (M,SM) \rightarrow {\mathfrak {D}}(C^{1}(M),C(M))$ be the map defined by

$$\begin{aligned} \Theta (\sigma )(f)(p) = \sigma (p)f,\quad \sigma \in \Gamma (M,SM), f \in C^{1}(M), p \in M. \end{aligned}$$

(3.6)

A standard argument shows that the image ${\mathrm {Im}}\Theta$ is non-zero and finitely generated as a $C^{1}(M)$-module. The map $\Theta$ yields the map $\theta$ in Lemma 3.2 when localized at a point p: To be more precise, let $\epsilon _{p}:\Gamma (M,SM) \rightarrow S_{p}M$ and $e_{p}:{\mathfrak {D}}(C^{1}(M),C(M)) \rightarrow {\mathfrak {D}}_{p}(M)$ be the evaluation maps defined by

$$\begin{aligned} \begin{array}{ll} \epsilon _{p}(\sigma ) = \sigma (p),\quad \sigma \in \Gamma (M,SM), \\ e_{p}(D)(f) = (Df)(p),\quad D \in \mathfrak {D}(C^{1}(M),C(M)),\quad f \in C^{1}(M). \end{array} \end{aligned}$$

(3.7)

Then we have

$$\begin{aligned} e_{p} \circ \Theta = \theta \circ \epsilon _{p}. \end{aligned}$$

Here the similarity between the spaces ${\hat{M}}$ and SM breaks down: every continuous map $\sigma :M \rightarrow {\hat{M}}$ of a path-connected compact metric space M must be a constant map, because the space ${{\hat{M}}} = \beta {\tilde{M}} {\setminus } {\tilde{M}}$, being a remainder of the Stone–Čech compactification of a non-psuedo-compact Lindelöf space ${\tilde{M}}$, contains no metrizable compact connected subsets which are not singletons [9] and hence the image $\sigma (M)$ must be a singleton. In particular there exists no continuous map $\sigma :M \rightarrow {\hat{M}}$ such that $\pi \circ \sigma = {\mathrm {id}}_{M}$ for such a space. This prevents us from defining a map which corresponds to $\Theta$ (3.6) to obtain elements of ${\mathfrak {D}}({\mathrm {Lip}}M,C(M))$. More strongly, Theorem 1.3 states that there exists no non-zero derivations ${\mathrm {Lip}}M \rightarrow C(M)$ when M is a compact Lipschitz manifold. Combining [8, Theorem 3.5] we see that the map $e_{p}:{\mathfrak {D}}({\mathrm {Lip}}M,C(M)) \rightarrow {\mathfrak {D}}_{p}(M)$ that corresponds to (3.7) reduces to the trivial map $0 \rightarrow$ (an $\infty$-dimensional space).

The rest of this section is devoted to the proof of Theorem 1.3. First the theorem is proved for $M = [0,1]^{m} \subset {\mathbb {R}}^{m}$ and the result is combined with Theorem 1.5 to prove the general case. We start with several lemmas. For simplicity let $I = [0,1]$. For $i\in \{1,\ldots ,n\}$ and $a \in {\mathrm {int}}I$, the subspace $H =\{(t_{1},\ldots ,t_{m}) \in I^{m}~|~ t_{i} = a\}$ is called a coordinate section. For two points $x,y \in I^{m}$, ${\overline{xy}}$ denotes the segment joining x with y. For a subset S of $I^{m}$, ${\mathrm {int}}S$ denotes the interior of S in $I^m$. Notice that for each derivation $D:{\mathrm {Lip}}M \rightarrow C(M)$ we have

$$\begin{aligned} Dc = 0 \end{aligned}$$

(3.8)

for each constant function $c \in {\mathrm {Lip}}M$.

Lemma 3.3

For $a \in {\mathrm {int}}I$ and $i=1,\ldots , m$, let $H^{a,i} =\{(t_{1},\ldots ,t_{m}) \in I^{m}~|~ t_{i} = a\}$ be a coordinate section of $I^m$ and let

$$\begin{aligned} H_{+}^{a,i} = \{(t_{1},\ldots ,t_{m}) \in I^{m}~|~ t_{i} \ge a\},\quad H_{-}^{a,i} = \{(t_{1},\ldots ,t_{m}) \in I^{m}~|~ t_{i} \le a\}. \end{aligned}$$

For a Lipschitz function $f \in {\mathrm {Lip}}I^{m}$ with $f|H^{a,i} \equiv 0$, let

$$\begin{aligned} \begin{aligned} f_{+}(x) = \left\{ \begin{array}{ll} f(x) \quad \text { if }~x \in H_{+}^{a,i}, \\ 0 \quad \quad \text { if }~x \in H_{-}^{a,i}, \end{array} \right. \end{aligned} \end{aligned}$$

(3.9)

and

$$\begin{aligned} \begin{aligned} f_{-}(x) = \left\{ \begin{array}{ll} f(x) \quad \text { if }~x \in H_{-}^{a,i},\\ 0 \quad \text { if }~x \in H_{+}^{a,i}. \end{array} \right. \end{aligned} \end{aligned}$$

(3.10)

Then $f_{+}$ and $f_{-}$ are Lipschitz functions such that $f = f_{+} + f_{-}$ and $f_{+}\cdot f_{-} = 0$.

Proof

Let $x \in H_{+}^{a,i}$ and $y \in H_{-}^{a,i}$ and take the point $m \in {\overline{xy}}\cap H^{a,i}$. We have

$$\begin{aligned} \frac{|f_{+}(x)-f_{+}(y)|}{\Vert x-y \Vert } = \frac{|f_{+}(x)|}{\Vert x-y \Vert } \le \frac{|f_{+}(x)|}{\Vert x-m \Vert } \le L(f). \end{aligned}$$

Thus $f_{+}$ is a Lipschitz function. Similarly $f_{-}$ is a Lipschitz function. The last equalities follow directly from the definition. $\square$

Lemma 3.4

Let $D:{\mathrm {Lip}}I^{m} \rightarrow C(I^{m})$ be a derivation and let B be a convex body in $I^{m}$. For each $f \in {\mathrm {Lip}}I^{m}$ with $f|B \equiv 0$, we have $Df|B \equiv 0$.

Proof

Let $g(x) = d(x,\overline{I^{m}{\setminus } B}),~x \in I^{m}$. It is straightforward to see

$$\begin{aligned} g \in {\mathrm {Lip}}I^{m},\quad g^{-1}(0) = \overline{I^{m}{\setminus } B},\quad fg \equiv 0. \end{aligned}$$

(3.11)

Restricting the equality $0 = D(fg) = f\cdot Dg + g \cdot Df$ to ${\mathrm {int}}B$, we obtain

$$\begin{aligned} (g|{\mathrm {int}}B) \cdot (Df|{\mathrm {int}}B) = 0 \end{aligned}$$

and hence $Df|{\mathrm {int}}B = 0$. By the continuity of Df we have $Df|B = 0$. $\square$

Lemma 3.5

Let H be a coordinate section of $I^{m}$ and let $D:{\mathrm {Lip}}I^{m} \rightarrow C(I^{m})$ be a derivation. For each function $f \in {\mathrm {Lip}}M$ with $f|H \equiv 0$, we have $Df|H \equiv 0$.

Proof

We may assume $H = H^{a,m}= \{(t_{1},\ldots ,t_{m-1},a)~|~t_{i} \in I,1\le i\le m-1\}$ for some $a \in {\mathrm {int}}I$. Let $H_{+} = H_{+}^{a,i}, H_{-} = H_{-}^{a,i}$, and let $f \in {\mathrm {Lip}}M$ with $f|H \equiv 0$. We see that the functions $f_{+}$ and $f_{-}$ defined by (3.9) and (3.10) are Lipschitz such that $f = f_{+}+f_{-}, ~f_{+}f_{-} = 0$ due to Lemma 3.3. From the equality $0 = D(f_{+}f_{-}) = f_{+}Df_{-}+f_{-}Df_{+}$ we see

$$\begin{aligned} f(x) Df_{-}(x)= & {} 0,\quad x \in H_{+}, \end{aligned}$$

(3.12)

$$\begin{aligned} f(y) Df_{+}(y)= & {} 0,\quad y \in H_{-}. \end{aligned}$$

(3.13)

We take an arbitrary $p \in H$ and prove $Df(p) = 0$ by considering two cases.

Case 1. There exists an $\varepsilon >0$ such that, for the rectangular neighbourhood $B_{\varepsilon } = \prod _{i=1}^{m}[p_{i}-\varepsilon ,p_{i}+\varepsilon ]$, we have either

$$\begin{aligned} f|B_{\varepsilon }\cap H_{+}\equiv 0\quad \text{ or }~ f|B_{\varepsilon }\cap H_{-}\equiv 0. \end{aligned}$$

Applying Lemma 3.4 to the convex body $B_{\varepsilon }\cap H_{+}$ or $B_{\varepsilon }\cap H_{-}$, we conclude $Df|B_{\varepsilon }\cap H_{+}\equiv 0$ or $Df|B_{\varepsilon }\cap H_{-}\equiv 0$. In particular we have $Df(p) = 0$.

Case 2. There exist two sequences $(x_{k})_{k\ge 1}$ and $(y_{k})_{k\ge 1}$ such that

• (i) $x_{k} \in H_{+}, y_{k} \in H_{-}$ and $f(x_{k}) \ne 0 \ne f(y_{k})$ for each $k\ge 1$,

• (ii) $\lim _{k}x_{k} = \lim _{k}y_{k} = p$.

By (3.12), (3.13) and (i) above, we have $Df_{-}(x_{k}) = Df_{+}(y_{k}) = 0$ for each k and hence by continuity of $Df_{\pm }$ we see $Df_{-}(p) = Df_{+}(p) = 0$. Then we see $Df(p) = Df_{+}(p) + Df_{-}(p) = 0$.

Since p is an arbitrary point of H we have $Df|H \equiv 0$. $\square$

Remark 3.6

The above lemma holds also for $m=1$ in which case H is a singleton in ${\mathrm {int}}I$.

Proof of Theorem 1.3

Step 1. As before let $I = [0,1]$. First we prove the theorem for $M = I^{m}$ by induction on m.

• (i) $m=1$. Let $D:{\mathrm {Lip}}I \rightarrow C(I)$ be a derivation, let $f \in {\mathrm {Lip}}I$, and take a point $p \in {\mathrm {int}}I$. Let $f_{p}:I \rightarrow {\mathbb {C}}$ be the function defined by $f_{p}(t) = f(t) - f(p), ~t \in I$. By (3.8) we have $Df_{p} = Df$. Since $f_{p}(p) = 0$, we have $(Df_{p})(p) = 0$ by Lemma 3.5 and Remark 3.6. Thus we obtain $Df(p) = Df_{p}(p) = 0$. Since p is an arbitrary point of ${\mathrm {int}}I$ we see by continuity that $Df \equiv 0$ on I.

• (ii)  Assume that theorem holds for m and let $D:{\mathrm {Lip}}I^{m+1}\rightarrow C(I^{m+1})$ be a derivation. Take a point $a = (a_{1},\ldots , a_{m+1}) \in {\mathrm {int}}I^{m+1}$ and take the coordinate section $H=\{(t_{1},\ldots ,t_{m},a_{m+1})~|~t_{i} \in I,1\le i \le m\}$. The space H is isometric to $I^m$ and the inclusion of H into $I^{m+1}$ is denoted by $\iota :H \rightarrow I^{m+1}$. Let $R:I^{m+1} \rightarrow H$ be the projection defined by

  $$\begin{aligned} R(t_{1},\ldots ,t_{m+1}) = (t_{1},\ldots ,t_{m},a_{m+1}),\quad (t_{1},\ldots ,t_{m+1}) \in I^{m+1}. \end{aligned}$$

  The map R is a Lipschitz map. We define an operator $d:{\mathrm {Lip}}H \rightarrow C(H)$ by $d = \iota ^{*}\circ D \circ R^{*}$ which is explicitly given by

  $$\begin{aligned} df = D(f\circ R)|H,\quad f \in {\mathrm {Lip}}H. \end{aligned}$$

  We show that d is a derivation. Indeed using $R|H = {\mathrm {id}}_{H}$ we have

  $$\begin{aligned} d(fg)= & {} D(fg\circ R)|H = D((f\circ R)\cdot (g\circ R))|H\\= & {} (f\circ R|H)\cdot D(g \circ R)|H +(g\circ R|H)\cdot (f \circ R)|H\\= & {} f D(g \circ R)|H + g D(f \circ R)|H = fdg+gdf. \end{aligned}$$

  By the inductive hypothesis and the isometry $H \equiv I^{m}$ we see $d = 0$. Thus for each $h \in {\mathrm {Lip}}H$, we have

  $$\begin{aligned} dh = D(h\circ R)|H = 0. \end{aligned}$$

  (3.14)

  For an arbitrary $f \in {\mathrm {Lip}}I^{m+1}$, consider the function $g_{f}$ given by

  $$\begin{aligned} g_{f} = f - (f|H)\circ R \end{aligned}$$

  which is a Lipschitz function on $I^{m+1}$ such that $g_{f}|H\equiv 0$. By Lemma 3.5 we see $(Dg_{f})|H \equiv 0$ and thus by (3.14) we have

  $$\begin{aligned} Df|H= D((f|H)\circ R)|H =0. \end{aligned}$$

  In particular $Df(a) = 0$. Since a is an arbitrary point of ${\mathrm {int}}I$ we see by continuity of Df that $Df \equiv 0$ on $I^{m+1}$. This finishes the inductive step and Step 1 is completed.

Step 2. For a proof of general M, we use the next lemma. The standard Euclidean metric on $I^m$ is denoted by $\rho$.

Lemma 3.7

Let $D:{\mathrm {Lip}}M \rightarrow C(M)$ be a derivation. Let $\alpha :I^{m} \rightarrow M$ be a bi-Lipschitz embedding of $I^m$ into a compact metric space (M, d) such that $\alpha ({\mathrm {int}}I^{m})$ is open in M. For each $f \in {\mathrm {Lip}}M$ with $f|\alpha (I^{m}) \equiv 0$, we have $Df|\alpha (I^{m}) \equiv 0$.

Proof

For an $\epsilon \in (0,1)$, let $\epsilon I^{m} = [\epsilon ,1-\epsilon ]^{m}$. We define a function $g:M \rightarrow [0,\infty )$ by

$$\begin{aligned} \begin{aligned} g(x) = \left\{ \begin{array}{lr} d(\alpha ^{-1}(x),\overline{I^{m}{\setminus } \epsilon I^{m}}),~\text { if }~x \in \alpha (I^{m}),\\ 0,~~~~~~~\quad \quad \quad \quad \quad \quad \text { if }~x \notin \alpha (I^{m}). \end{array} \right. \end{aligned} \end{aligned}$$

Notice that

$$\begin{aligned} g|\alpha (\overline{I^{m}{\setminus } \epsilon I^{m}}) \equiv 0 \end{aligned}$$

(3.15)

and hence the above function is well-defined.

In order to see that g is a Lipschitz function, first notice that $t \mapsto d(t,\overline{I^{m}{\setminus } \epsilon I^{m}})$ is a Lipschitz function on $I^{m}$. Since $\alpha$ is a bi-Lipschitz embedding we see that $g|\alpha (I^{m})$ is a Lipschitz function. This and (3.15) imply that g is a locally Lipschitz function. By the compactness of M we conclude that $g \in {\mathrm {Lip}}M$ (see [11, p. 85]). Also by the definition $g(q) \ne 0$ for each $q \in \alpha ({\mathrm {int}}(\epsilon I^{m}))$.

For each $f \in {\mathrm {Lip}}M$ with $f|\alpha (I^{m}) \equiv 0$, we have $fg \equiv 0$ and thus

$$\begin{aligned} 0 = D(fg)|\alpha (\epsilon I^{m}) = f\cdot Dg |\alpha (\epsilon I^{m})+g \cdot Df| \alpha (\epsilon I^{m}) = g \cdot Df|\alpha (\epsilon I^{m}), \end{aligned}$$

which implies $Df|\alpha ({\mathrm {int}}(\epsilon I^{m}))=0$. Since $\epsilon$ is an arbitrary number in (0, 1) we see that $Df|\alpha (I^{m}) \equiv 0$. $\square$

In order to finish the proof of Theorem, let M be a compact metric space as in the hypothesis and let $D:{\mathrm {Lip}}M \rightarrow C(M)$ be a continuous derivation. Fix a point $p \in M$. Take a bi-Lipschitz embedding $\alpha :I^{m}\rightarrow M$ such that $p \in \alpha (I^{m})$ and $\alpha ({\mathrm {int}}I^{m})$ is open in M. First we show that there exists a Lipschitz map $R:M \rightarrow \alpha (I^{m})$ such that $R|\alpha (I^{m})= {\mathrm {id}}_{\alpha (I^{m})}$.

To show the above, let ${\mathrm {proj}}_{j}:I^{m}\rightarrow I$ be the projection to the j-th factor ($1\le j \le m$). The map ${\mathrm {proj}}_{j}\circ \alpha ^{-1}:\alpha (I^{m}) \rightarrow I$ is a Lipschitz function and we apply Theorem 1.5 to obtain a Lipschitz function $r_{j}:M\rightarrow I$ such that $r_{j}|\alpha (I^{m}) = {\mathrm {proj}}_{j}\circ \alpha ^{-1}$. Define $r:M \rightarrow I^{m}$ by $r(x) = (r_{j}(x))_{1\le j \le m}$ and let

$$\begin{aligned} R = \alpha \circ r:M \rightarrow \alpha (I^{m}). \end{aligned}$$

Then the map R is the desired Lipschitz map (see [11, Lemma 5.6]).

Take a function $f \in {\mathrm {Lip}}M$ and let $g_{f}$ be the function given by

$$\begin{aligned} g_{f} = f - ((f|\alpha (I^{m}))\circ R) \end{aligned}$$

which is a Lipschitz function such that $g_{f}|\alpha (I^{m}) \equiv 0$. By Lemma 3.7 we see $Dg_{f}|\alpha (I^{m}) \equiv 0$. Thus we see

$$\begin{aligned} Df|\alpha (I^{m}) = D\left( (f|\alpha (I^{m}))\circ R\right) |\alpha (I^{m}). \end{aligned}$$

(3.16)

We notice that the Lipschitz homeomorphism $\alpha :I^{m}\rightarrow \alpha (I^{m})$ induces algebraic isomorphisms $\alpha ^{*}:{\mathrm {Lip}}({\mathrm {Im}}\alpha ) \rightarrow {\mathrm {Lip}}(I^{m})$ and $\alpha ^{*}:C(\alpha (I^{m})) \rightarrow C(I^{m})$. It follows from this and Step 1 that the derivation $d:{\mathrm {Lip}}(\alpha (I^{m})) \rightarrow C({\mathrm {Im}}\alpha )$ defined by

$$\begin{aligned} dg = D(g\circ R)|\alpha (I^{m}),\quad g \in {\mathrm {Lip}}(\alpha (I^{m})) \end{aligned}$$

is the zero-homomorphism. It implies $D(f|\alpha (I^{m}) \circ R)|\alpha (I^{m}) = 0$ for each $f \in {\mathrm {Lip}}M$. Combining this with (3.16) we have $Df|\alpha (I^{m}) = 0$ and thus $Df(p) = 0$, as required.

This completes the proof of theorem. $\square$

For a compact metric space M as in Theorem 1.3 and $n\ge 2$, take an alternating n-cochain $F \in Z^{n}_{\mathrm {alt}}({\mathrm {Lip}}(M), C(M))$. By (1) of Theorem 1.6, F is an n-derivation. Fixing arbitrary Lipschitz functions $f_{1}, \ldots , f_{n-1} \in {\mathrm {Lip}}(M)$, we have the linear operator $f \mapsto F(f_{1},\ldots , f_{n-1},f)$ that is a derivation due to (1.12). It follows from the proof of Theorem 1.3 that the operator is zero and we conclude:

Corollary 3.8

Let M be a compact metric space as in Theorem 1.3. Then we have $Z_{\mathrm {alt}}^{n}({\mathrm {Lip}}(M),C(M)) = 0$ for each $n \ge 2$.

It is not known to the author whether the cohomology ${\mathrm {H}}^{n}({\mathrm {Lip}}(M), C(M))$ is trivial for each $n \ge 2$ and for each compact metric space M in Theorem 1.3.