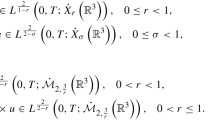Abstract
The paper is concerned with the regularity of solutions of the Boussinesq equations for incompressible fluids without heat conductivity. The main goal is to prove a regularity criterion in terms of the vorticity for the initial boundary value problem in a bounded domain \(\Omega\) of \(\mathbb {R}^{3}\) with Navier-type boundary conditions and we prove that if
where \(\omega :=\)curl u is the vorticity, then the unique local in time smooth solution of the 3D Boussinesq equations can be prolonged up to any finite but arbitrary time.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and main result.
Let \(\Omega\) be a bounded, simply connected domain in \(\mathbb {R}^{3}\) with \(\partial \Omega \in C^{\infty }\) and \(n=(n^{1},n^{2},n^{3})\) be the outward unit normal vector field along boundary \(\partial \Omega\). In this note, we consider the classical problem of regularity conditions for fluid mechanics equations. Precisely, we consider the initial boundary value problem for the 3D Boussinesq equations without heat conductivity modeling the flow of an incompressible fluid with Navier-type boundary conditions :
where \(u=u(x,t)\) and \(\theta =\theta (x,t)\) denote the unknown velocity vector field and the scalar temperature. Initial data \(u_{0}\) is assumed to satisfy a compatibility condition : \(\nabla \cdot u_{0}(x)=0\) in \(\Omega\). \(e_{3}=(0,0,1)^{t}\). \(\pi =\pi (x,t)\) is the pressure of fluid at the point \((x,t)\in \Omega \times (0,\infty )\). The Boussinesq system has important roles in atmospheric sciences (see, e.g., [18]).
When \(\theta =0\), (1.1)\(_{1}\) and (1.1)\(_{3}\) are the well-known Navier-Stokes system. Giga [13], Kim [15] and Kang and Kim [14] have proved some Serrin type regularity criteria.
These type of regularity results are very well-known in literature and they all started with the improvement of Kozono and Taniuchi [16] of the Beale–Kato–Majda criterion for the 3D Euler equations, namely
Here BMO stands for the space of the bounded mean oscillation.
This paper is an improvement on the results contained in the paper [7, 20]. Precisely, in the Reference [20] it is proved that if
holds then the unique local in time smooth solution of the Cauchy problem for the 3D Boussinesq equations with thermal diffusivity can be prolonged up to any finite but arbitrary time. On the other hand in the reference [7] it is proved that if
then the unique local in time smooth solution of the initial boundary value problem for the 3D Boussinesq equations without thermal diffusivity and with Navier boundary conditions can be prolonged up to any finite but arbitrary time.
One may also refer to some interesting results are devoted to find regularity criteria or prove partial regularity for these equations, such as [8] for Boussinesq equations, and [9,10,11,12, 21] for system, in a bounded domain.
Motivated by the result in [7], we will improve (1.2) as
where \(\omega =\nabla \times u\) is the vorticity. More precisely, we will prove
Theorem 1.1
Let \((u_{0},\theta _{0})\in H^{3}(\Omega )\times W^{1,q}(\Omega )\) with \(3<q\le 6\) and \(\nabla \cdot u_{0}=0\) in \(\Omega\) and \(u_{0}\cdot n=0\) , \((\nabla \times u_{0})\times n=0\) on\(\partial \Omega\). Let \((u,\theta )\) be a strong solution of problem (1.1). If (1.3) holds, then the solution \((u,\theta )\) can be extended beyond \(T>0\).
Remark 1.1
This result says that the velocity field of the fluids plays a more dominant role than the temperature \(\theta\) in the regularity theory of the system (1.1). So our theorem is a complement and improvement of the previous results. Therefore, if \(\theta =0\), Theorem 1.1 directly yields an alternative proof of logarithmically improved Beale-Kato-Majda type extension criterion for smooth solutions to the incompressible Navier-Stokes equations, which improves the result in [19].
2 Proof of Theorem 1.1
In this section we prove our main result and to this end, we recall some preliminary results which will be used in the proof.
Lemma 2.1
[4] Let \(\Omega \subset \mathbb {R}^{3}\) be a domain with smooth connected boundary \(\partial \Omega\). Let \(w:\Omega \rightarrow \mathbb {R} ^{3}\) be a smooth vector field and let \(1<s<\infty\). Then
Here \(d\sigma\) denotes the surface measure sur \(\partial \Omega\).
In addition to the classical integration by parts, in some calculations we will also use the following Gauss–Green formula, where \(\omega =\nabla \times u\).
Lemma 2.2
[5] Assume that u is divergence-free and that on \(\partial \Omega\) condition (1.1)\(_{4}\) holds, i.e. \(u\cdot n=0\) and \(\omega \times n=0\). Then
where \(\epsilon _{ijk}\) denotes the totally anti-symmetric tensor such that \((a\times b)_{i}=\epsilon _{ijk}a_{j}b_{k}\).
We shall often make use of the following
Lemma 2.3
(See [1], Lemma 7.44 and [17], Corollary 1.7) Let \(\Omega\) be a smooth and bounded open set in \(\mathbb {R} ^{3}\). Then, there is a constant C depending on \(\Omega\), such that if \(f\in L^{q}(\Omega )\cap W^{1,q}(\Omega )\) with \(1<q<\infty\), then
We need the following Gagliardo–Nirenberg inequality using BMO-norm.
Lemma 2.4
[3] Let \(1\le r<q<\infty\). There exists a constant C depending on \(\Omega\), such that for every \(f\in L^{r}(\Omega )\cap BMO(\Omega )\),
In the sequel, we will use the classical regularity result for the following Stokes problem, see for instance [2].
Lemma 2.5
Let \(\Omega\) be a bounded, simply connected domain in \(\mathbb {R }^{3}\) with \(\partial \Omega \in C^{\infty }\) and let \(m\in \mathbb {Z}\) so that \(m\ge -1\) and \(q\in (1,\infty )\). For any \(f\in W^{m,q}(\Omega )\), there exists a unique solution \((u,\pi )\) of the following Stokes system
such that \(u\in W^{m+2,q}(\Omega )\) and \(\pi \in W^{m+1,q}(\Omega )\). The solution satisfies the estimate
for some constant C depending only on \(\Omega\) and q. In particular, for \(m=0\), we have
and
We need also the following lemma due to [6], (see Theorem 2.6).
Lemma 2.6
[6] Let s be a non-negative real. If \(u\in H^{2}(\Omega )\) such that \(\Delta u\in H^{s}(\Omega )\) and such that
then \(u\in H^{s+2}(\Omega )\) and there is a positive constant C independent of u such that
In particular, for \(s=1\), we have
Now we are in a position to prove our main result.
Proof
We only need to establish a priori estimates. We will show that under the hypotheses of Theorem 1.1, the \(H^{3}\times W^{1,q}-\)norms of both velocity and temperature remain uniformly bounded, hence we can uniquely continue the solution beyond T, contradicting its maximality.
First we observe that, by standard energy method we have
and
Next, we consider the equation for the vorticity \(\omega :\)
By multiplying (2.10) by \(\omega \left| \omega \right| ^{s-2}\) \((1<s<\infty )\), using (1.1)\(_{3}\), (2.1), (2.2), (2.3) and (2.4), we obtain
which gives
Defining
the inequality (2.11) implies that
where \(\epsilon\) is a small constant, such that
By using the standard energy estimate, we can deduce that
Now, testing (1.1)\(_{1}\) by \(\partial _{t}u\), using (1.1)\(_{3}\) and (2.12), we see that
which implies
Here we have used the facts
Now we want to estimate \(\left\| \partial _{t}u\right\| _{L^{2}}\). We take the time derivative of first equation in (1.1), we get
Multiplying (2.14) by \(\partial _{t}u\), using (1.1)\(_{3}\), (2.9), (2.12) and (2.13), it follows that
Here we have used the facts
and also we use the continuity equation (to substitute \(\partial _{t}\theta\) by \(-(u\cdot \nabla )\theta )\)
where in the integration by parts we used the fact that u is divergence-free. In addition, the boundary term vanishes since \((u\cdot n)=0\) on \(\partial \Omega\).
Integrating over \([T_{*},t]\), using (2.12) and (2.13), we obtain
On the other hand, since \((u,\pi )\) is a solution of the Stokes system :
thanks to the \(H^{2}-\)theory of the Stokes system, we obtain by Hölder’s inequality, Sobolev’s inequality, (2.12) and (2.15)
Multiplying (2.14) by \([\nabla (\partial _{t}\pi )-\Delta (\partial _{t}u)]\), using (1.1)\(_{3}\), (2.15) and (2.16), we derive
where we have used the fact : since \(\Omega\) is simply connected and \(u\cdot n=0\) on \(\partial \Omega\) , then
Integrating (2.17) over \((T_{*},t)\) and using (2.15) and (2.16), we have
Here we have used the fact
by the standard energy method.
On the other hand, it follows from (2.8), (2.10), (2.12 ), (2.16) and (2.18) that
Thus we conclude that
By taking the gradient of the continuity equation in (1.1), we get the equation
By multiplying (2.20) by \(\nabla \theta \left| \nabla \theta \right| ^{q-2}\) for \(q>3\) and by integrating by parts, we obtain the following differential inequality
Then, by integrating the above differential inequality with respect to time and by using (2.19), we get that there exists a constant C independent of q such that
This completes the proof of Theorem 1.1.
References
Adams, R.A., Fournier, J.J.F.: Sobolev Spaces. Pure and Applied Mathematics, vol. 140, 2nd edn. Elsevier, Amsterdam (2003)
Amrouche, C., Seloula, N.E.H.: Stokes equations and elliptic systems with nonstandard boundary conditions, C. R. Acad. Sci. Paris Ser. I 349(11–12), 703–708 (2011)
Azzam, J., Bedrossian, J.: Bounded mean oscillation and the uniqueness of active scalar equations. Trans. Am. Math. Soc. 397, 3095–3118 (2015)
Beirão da Veiga, H, Cripo, F.: Sharp inviscid limit results under Navier type boundary conditions. An \(L^{p}\) theory. J. Math. Fluid Mech. 12, 397–411 (2010)
Beirão da Veiga, H., Berselli, L.C.: Navier-Stokes equations : Green’s matrices, vorticity direction, and regularity up to the boundary. J. Differ. Equ. 246, 597–628 (2009)
Bendali, A., Dominguez, J.M., Gallic, S.: A variational approach for the vector potential formulation of the Stokes and Navier-Stokes problems in three dimensional domains. J. Math. Anal. Appl. 107, 537–560 (1985)
Fan, J., Sun, W., Yin, J.: Blow-up criteria for Boussinesq system and MHD system and Landau-Lifshitz equations in a bounded domain. Bound. Value Probl. 2016, 90 (2016). https://doi.org/10.1186/s13661-016-0598-3
Fan, J., Zhou, Y.: A note on regularity criterion for the 3D Boussinesq system with partial viscosity. Appl. Math. Lett. 22, 802–805 (2009)
Fan, J., Jia, X., Zhou, Y.: A logarithmic regularity criterion for 3D Navier-Stokes system in a bounded domain. Appl. Math. 64, 397–407 (2019)
Fan, J., Fukumoto, Y., Zhou, Y.: Logarithmically improved regularity criteria for the generalized Navier-Stokes and related equations. Kinet. Relat. Models 6(3), 545–556 (2013)
Fan, J., Jiang, S., Nakamura, G., Zhou, Y.: Logarithmically improved regularity criteria for the Navier-Stokes and MHD equations. J. Math. Fluid Mech. 13, 557–571 (2011)
Fan, J., Zhang, Z., Zhou, Y.: Regularity criteria for a Ginzburg-Landau-Navier-Stokes in a bounded domain. Bull. Malays. Math. Sci. Soc. 43, 1009–1024 (2020)
Giga, Y.: Solutions for semilinear parabolic equations in \(L^{p}\) and regularity of weak solutions of the Navier-Stokes system. J. Differ. Equ. 62, 186–212 (1986)
Kang, K., Kim, J.: Regularity criteria of the magnetohydrodynamic equations in bounded domains or a half space. J. Differ. Equ. 253, 764–794 (2012)
Kim, H.: A blow-up criterion for the nonhomogeneous incompressible Navier-Stokes equations. SIAM J. Math. Anal. 37, 1417–1434 (2006)
Kozono, H., Taniuchi, Y.: Limiting case of the Sobolev inequality in BMO, with application to the Euler equations. Commun. Math. Phys. 214, 191–200 (2000)
Lunardi, A.: Interpolation theory, 2nd edn. Edizioni della Normale, Pisa, 2009. xiv+191 pp. (distributed by Birkhäuser Verlag, Basel). Third edition. Appunti. Scuola Normale Superiore di Pisa (Nuova Serie) [Lecture Notes. Scuola Normale Superiore di Pisa (New Series)], 16. Edizioni della Normale, Pisa (2018)
Majda, A.: Introduction to PDEs and waves for the atmosphere and ocean. In: Courant Lecture Notes in Mathematics, vol. 9, AMS/CIMS (2003)
Nakao, K., Taniuchi, Y.: An alternative proof of logarithmically improved Beale-Kato-Majda type extension criterion for smooth solutions to the Navier-Stokes equations. Nonlinear Anal. 176, 48–55 (2018)
Yang, X., Zhang, L.: BKM’s criterion of weak solutions for the 3D Boussinesq equations. J. Part. Diff. Equ. 27, 64–73 (2014)
Zhou, Y., Fan, J.: Logarithmically improved regularity criteria for the 3D viscous MHD equations. Forum Math. 24, 691–708 (2012)
Acknowledgements
The part of the work was carried out while the second author was long-term visitor at University of Catania. The hospitality and support of Catania University are graciously acknowledged. The last author wish to thank the support of the RUDN University program 5-100. The authors would like to thank the referees for pointing out some typos and making helpful suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
This article is part of the section “Applications of PDEs” edited by Hyeonbae Kang.
Rights and permissions
About this article
Cite this article
Alghamdi, A.M., Gala, S. & Ragusa, M.A. A logarithmically improved regularity criterion for the Boussinesq equations in a bounded domain. SN Partial Differ. Equ. Appl. 1, 41 (2020). https://doi.org/10.1007/s42985-020-00042-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s42985-020-00042-y