Hybrid Noise Reduction Filter Using the Gaining–Sharing Knowledge-Based Optimization and the Whale Optimization Algorithms

Abstract

Noise reduction is one of the main challenges for researchers. Classical image de-noising methods reduce the image noise but sometimes lose image quality and information, such as blurring the edges of the image. To solve this challenge, this work proposes two optimal filters based on a generalized Cauchy (GC) distribution and two different nature-inspired algorithms that preserve image information while decreasing the noise. The generalized Cauchy filter and the bilateral filter are two parameter-based filters that significantly remove image noise. Parameter-based filters require proper parameter selection to remove the noise and maintain the edge details. To this end, two filters are considered. In the previous works, the parameters of the mask that was made with the GC function were optimized and the mask size was considered fixed. By studying different noisy images, we find that the selected mask size significantly impacts the designed filter performance. Therefore in this paper, a mask is designed using the GC function to formulate the first filter, and despite the optimization of the filter parameters, the selected mask size is also optimized using the peak signal-to-noise ratio (PSNR) as a fitness function. In most metaheuristic-based bilateral filters, only the domain and range parameters, which are based on Gaussian distribution, are optimized and the neighboring radius is a constant value. Filter results on different noisy images show that the neighboring radius has a major effect on the filter performance. Since the filter designed with the GC function causes significant noise removal, this function is effective, and on the other hand, it’s almost similar behavior with the Gaussian function has caused it to be combined with the bilateral filter to design the second filter in this paper. The kernel of the domain and range is considered to be the GC function instead of the Gaussian function. The domain and range parameters and the neighboring radius are optimized using the PSNR as a fitness function. With the help of optimization algorithms such as the whale optimization algorithm and the Gaining sharing knowledge-based optimization algorithm, bilateral filter; and GC filter parameters are optimized. Finally, the performance of the proposed filters is investigated on images corrupted by Gaussian and impulse noise. It is compared with other classical filters, the particle swarm optimization (PSO) based GC filter, and two PSO-based bilateral filters on various images. The experimental findings demonstrate that the suggested filters outperform the others.

Introduction

In recent years, digital images have found numerous applications in various analysis and engineering sciences, such as medical imaging, resonance imaging, computed tomography, satellite observation, etc. However, most sensor-captured images are corrupted by noise [1]. Various types of noises caused by hardware or atmospheric factors affect the image quality [2], so most researchers have considered image de-noising to improve image quality by removing noise from the image while preserving structural information [3]. Noise removal should be done early, not affecting other stages of image analysis, such as image segmentation, image classification, etc. Image de-noising can be done by hardware or software approaches. Despite new advances in optics and hardware to reduce the adverse effects of image noise, software-based methods, including some parameter-based algorithms, have been highly considered because they are device-independent and widespread.

Three types of image de-noising methods exist: filter-based, transform-based, and non-local.

Recently, various filter-based methods have been divided into linear and non-linear categories. Among the linear filters, the Mean filter [4] can be mentioned, which helps eliminate image noise but blurs the edges of the image. Another linear filter that can be said is the Wiener filter [5]. This filter eliminates the noise and blurring of a signal that has damaged the image. It minimizes the square errors associated with inverse filtering and noise removal. Although the Wiener filter can effectively remove Gaussian noise, it loses some details about the image edge. The median filter [6], which is more suitable for salt and pepper noise while reducing noise, is one of the most common non-linear filters. The main idea behind this filter is to insert the current pixel value with median values adjacent to the stated pixel. This filter is complicated and expensive because it takes a long time to calculate the median in each window. The bilateral filter [7] is another non-linear filter, a spatial Mean filter that protects the edges of the image and is an efficient filter for noise removal. The performance of this filter depends on the correct selection of the parameters of the filter, which is not related to the image and requires experimental efforts. Non-linear filters are preferred over linear ones due to their superior image noise removal and edge preservation performance.

Transform-based methods are also efficient for image de-noising [8]. The wavelet transform is one of these transformations. In the transform-based methods, the image domain is first changed by applying some linear transformations on the image. Then, non-linear or multiple operations are performed in this domain, and an inverse linear transformation returns the image domain. One transform-based method is the BLS-GSM method [9], a wavelet domain method. The basic idea of this method is that when the images are split into wavelengths in the multidimensional display, the adjacency of each wavelet coefficient is modeled using Gaussian Scale Mix (GSM), and noise-free coefficients are estimated using Bayesian least squares (BLS). Another transform-based method is three-dimensional block-matching (BM3D) algorithm [10]; for reducing image noise. The idea of using this method to eliminate the noise is to enhance the dispersal of the image, which has scattered representations in the transform domain enhanced by two-dimensional grouping patches similar to the three-dimensional groups. A wavelet-based approach using the least square approach is proposed by Vishnu et al. [11]. The noisy image is considered and given as an input to different filters that perform decomposition and then entered into a Least Square weighted regularization stage. Wavelet-based algorithms have some defects, including a lack of good directionality and calculation complexity, and are time-consuming.

Other noise reduction methods are non-local methods that estimate the intensity of all pixels based on the information about the whole image and thus take advantage of similar patterns and features in an image; in this regard, the Non-Local Mean filter [12] can be mentioned. Unlike local mean filters, which smooth the image by replacing the mean value of a group of pixels located adjacent to the target pixels with the value of the target pixels, the non-local mean method smooths the image by calculating the mean of all the pixels which the amount of similarity between these pixels and the target pixels has weighted. An iterative point filtering algorithm based on the Bayesian non-local mean filter model for ultrasound images is proposed by Zhou et al. [13]. Mehta and Prasad [14] presented a method for speckle noise reduction and entropy minimization of medical contrast-enhanced ultrasound images. Their method has been implemented and tested on different images using a filter bank. The statistical feature of the noise is used to apply the Bayesian non-local mean model to reconstruct the image, obtain the critical probability density function, and provide an iterative filter. For reducing the deviations created in the noise-free patches, the nearest statistical neighbor has been used as a measure of the set of dissimilar neighbors [15]. This method works better for white and color noise than the traditional methods and improves the bilateral filter's image quality. A Gaussian lifting framework for bilateral and non-local filtering is provided by Young et al. [16], which appeals to similarities between separable wavelets transform and Gaussian pyramids. The precise implementation of this filter was important not only for image processing applications but also for several recently proposed bilateral regular inverse problems, in which the accuracy of the answer depends entirely on the precise execution of the filter. Gaussian lifting designs are also examined for bilateral and non-local filters.

Reviewing recent studies on image denoising revealed the drawbacks of various methods and techniques applied in this field. Therefore, new image-denoising methods using metaheuristic algorithms have been proposed. Karami and Tafakori [17] proposed a filter for noise removal. To design this filter, they made a mask with a fixed size and used the GC function in it and found that the GC function could be effective in removing the Gaussian noise. By applying this filter to different noisy images, it can be concluded that the mask size has a major effect on the filter performance. In this paper, a mask is designed, and the GC function parameters as well as the mask size are considered as parameters that should be optimized. Most meta-heuristic algorithms applied to Bilateral filters optimize the intensity and spatial domain parameters in the Gaussian function and assume the neighborhood radius to be constant except for Nabahat et al. [18] methods, or Wang et al. [19] method, which claims that the spatial domain parameter has little effect on the filter performance; therefore, It is assumed to be constant and optimizes the neighborhood radius and intensity domain parameter. In this paper, it is claimed that the neighborhood radius, as well as the spatial and intensity domain parameters, significantly affect the bilateral filter's performance. On the other hand, due to the almost similar behavior, and the effective and better performance of the GC function compared to the Gaussian function in noise reduction, the GC function is used in the spatial and intensity domain of the bilateral filter. Here the WOA and GSK algorithms were applied to solve the Nondeterministic polynomial time (NP) problem, which resulted from the anonymity of the exact values of parameters that must be optimized in the bilateral filter and GC filter. The GC filter parameters as well as mask size and the bilateral filter parameters such as the intensity domain, spatial domain, and spatial neighborhood radius were optimized using the WOA and GSK algorithms. The noise-free image was achieved and compared with classical noise removal filters such as Mean filter, Gaussian filter, Median filter, Wiener filter, Non-local mean filter, and three metaheuristic-based algorithms like PSO-based GC filter [17] (GC_PSO), and two PSO-based bilateral filters (Wang's method [19] ‘BW_PSO’ and Asokan's method [20] ‘BA_PSO’) on various images respectively.

The rest of the paper is organized as follows. “Preliminaries” includes preliminaries (explain the GC distribution, Bilateral filter, PSO, WOA, and GSK algorithms). “Proposed Method” presents the proposed filters based on the GC function. The experimental results and discussion of the proposed method and its description are explained in “Experimental Results and Discussion”, and finally, the conclusions and suggestions for future work are presented in “Conclusion and Future Directions”.

Related Works

By far, there have been several methods proposed for image denoising and restoration. This section reveals the recent studies conducted on image-denoising techniques.

Image denoising’s main goal is to remove the noise effectively and preserve the original image details as much as possible, and to this end, many approaches have been considered [21].

Dhanushree et al. [22] used different filters to remove speckle noise on acoustic images and found that among the available filters, the bilateral filter; followed by the guided filter, further removes speckle noise from acoustic images.

A hierarchical sequence of development and creation of various Gaussian noise removal methods from the primary methods to more sophisticated hybrid techniques are reviewed by Goyal et al. [23]. Other de-noising techniques have been proposed in [24] and [25]. To train high-quality noise reduction models based on an unorganized group of corrupted images, a method described by Laine et al. [24]. This training eliminates the need for reference images using “blind spot” networks in the receiving field and can, therefore, be used in situations where access to such data is costly or impossible. This method also controls situations where the noise model parameters are variable and unclear in training and evaluation data. The model that adequately selects the regularization parameter in the total variation model was proposed by Pan et al. [25]. In this model, an iterative algorithm was used to estimate the optimal upper bound using the stability between the value of the fitting data term and the upper bound. Then, a dual-based method was applied that avoids calculating the Lagrangian coefficient associated with that constraint, to solve the constrained problem.

Various complex background noise and weak desired signals have severely limited the practical application of Distributed Fiber Optic Acoustic Detection (DAS) as a transformative technology in seismic exploration. A residual encoder-decoder deep neural network (RED-Net) enhanced by deep repetitive memory block (DMB) and channel aggregation block (CAB) called Residual Channel Aggregation Encoder-Decoder Network (RCEN) for vertical seismic profile record (VSP) received by DAS is presented for effective noise removal [26]. DMB uses the theory of weight accumulation to improve the feature extraction ability and achieve accurate noise removal; meanwhile, CAB enhances the performance of weak signal storage using multi-channel analysis architecture.

Modifying the measurement index, defining a constraint function, and considering the collision between readers and between readers and tags led to the development of an improved radio-frequency identification (RFID) reader anti-collision model [27]. Since the number of encoded variables increased because of the dense deployment of many readers and caused a high-dimensional problem that traditional algorithms cannot solve, the Distributed Parallel Cooperative Particle Swarm Optimization (DPCCPSO) is used. Inertia weights and learning factors are adjusted during evolution, an improved clustering strategy is obtained, and various combinations of random number generation functions are tested.

A gated attention mechanism and a linear fusion method construct a two-stream interactive recurrent feature transformation network (IRFR-Net) [28]. First, a context extraction module (CEM) is designed to obtain low-level, depth background information. Second, the gated attention fusion module (GAFM) obtains useful RGB depth information (RGB-D) structural and spatial fusion features. Third, adjacent depth information is integrated globally to obtain complementary context features. A Weighted Atrous Spatial Pyramid (WASPP) fusion module extracts multi-scale local information of depth features. Finally, the global and local features are combined in a bottom-up scheme to highlight salient objects effectively.

An image segmentation method based on deep learning to segment key regions in mineral images using morphologic transformation to process mineral image masks is presented by Yang et al. [29]. Four aspects of the deep learning mineral image segmentation model are considered: backbone selection, module configuration, building the loss function, and its application in the classification of the mineral image. A new loss function suitable for mineral image segmentation is also presented, and the formation performance of Convolution neural network (CNN) based segmentation models under various loss functions is compared. Hussain and Vanlalruata [30] de-noised the image using CNN to improve character recognition. By classifying the noise types, they identified the kind of noise to select a specific model of de-noising to increase the image de-noising performance. A noisy and corresponding clean image is fed into the network for training. After that, the generated model de-noises the character image. Chaurasiya and Ganotra [31] have changed the receptive field and investigated its effect on image noise removal. For this purpose, they designed and compared the networks: CNN with expanded kernels, CNN without expansion but with increased kernel size with the same receptive field, and CNN without any expansion and without increasing the kernel size. After reviewing the previous three items, they added a fourth item with an optimized receptive field that improves advanced results.

In recent years, the use of meta-heuristic algorithms has received much attention, which plays an essential role in replacing human inspections and interpreting processed images. Meta-heuristic algorithms have demonstrated their effectiveness in solving high-dimensional optimization problems. Using random initial solutions, these algorithms generate optimal solutions for complex optimization problems [32]. They are divided into four categories. Evolution-based algorithms, swarm-based algorithms, physics-based algorithms, and human-related algorithms. Each category has several algorithms, and they have been used in real-world applications in various fields of engineering and science. The evolutionary algorithms that have gained widespread recognition include genetic algorithm (GA) [33] and differential evolution (DE) [34]. The swarm intelligence algorithms that are most commonly used are Artificial Bee Colony (ABC) [35], Firefly Algorithm (FA) [36], Particle Swarm Optimization (PSO) [37], Moth-Flame Optimization (MFO) [38], Salp Swarm Algorithm (SSA) [39], Grey Wolf Optimizer (GWO) [40], and WOA [41]. The simulated annealing algorithm (SA) [42] is a sample of the physics-based algorithm. Harmony Search (HS) [43], Teaching Learning-Based Optimization (TLBO) [44], and Gaining sharing knowledge-based optimization algorithm (GSK) [45] are the well-known human-based metaheuristic algorithms.

Improved Gray Wolf Optimization (IGWO) addresses the limitations of traditional Grey Wolf Optimization (GWO) by incorporating Dimension Learning-Based Hunting (DLH), inspired by wolf pack dynamics. DLH creates personalized neighborhoods for each wolf, allowing them to exchange information and maintain a balance between local and global search [46]. In response to the limitations of the traditional WOA algorithm, which can converge slowly and get stuck in local optima, a variant called Multi-Population Evolutionary Algorithm (MEWOA) was introduced in [47]. MEWOA divides the population into three subpopulations with different searching strategies: one that searches globally and locally, another that explores randomly, and a third that exploits the search space. This approach helps MEWOA find better solutions and avoid local optima more effectively.

Multi-Trials Vector-Based Differential Evolution (MTDE) [48] is a metaheuristic algorithm that combines multiple search algorithms to evolve better solutions. It uses a novel approach called Multi-Trial Vector (MTV), which adaptively adjusts the movement step size based on past successes. MTV incorporates three different Trial Vector Producer (TVP) strategies: Representative-based, Local Random, and Global Best History. These TVPs share their experiences through an archived database, allowing for more effective solution exploration.

Redundant or irrelevant features in datasets can degrade algorithms' performance. Effective feature selection through nature-inspired metaheuristics like the Aquila optimizer can improve accuracy and decision-making. A wrapper feature selection approach uses the Aquila optimizer to identify the most efficient feature subset, which was tested on medical datasets with binary feature selection methods (S-shaped binary Aquila optimizer (SBAO) and V-shaped binary Aquila optimizer (VBAO)) [49].

In [50], a Discrete Propeller-Flame Optimization Algorithm (DMFO-CD) is proposed for community detection in graphs. It adapts Continuous Moth-Flame Optimization (CMFO) for discrete problems by representing solution vectors, initializing, and moving strategy. DMFO-CD uses a locus-based adjacency representation and considers node relationships during initialization without assuming the number of communities. The movement strategy updates solutions with a two-point crossover for computing movements, a single-point neighbor-based mutation for improving exploration and balancing exploitation and exploration, and a single-point crossover based on modularity in the fitness function.

In “Monkey King Evolution” (MKE) [51], the combination of different methods and control parameters affects the convergence rate and balance between exploration and exploitation. By combining multiple strategies, the Multi-Trial Vector-Based Monkey King Evolution (MMKE) algorithm improves global search performance and avoids early convergence. GSK [45], is a novel algorithm that is derived from the concept of acquisition and distribution of knowledge during the human lifetime. Many efforts have been made in different fields with this algorithm. A binary-based GSK algorithm for feature choice was implemented in [52]. Modifications for the GSK algorithm are done in [53] for its performance enhancement. Agrawal et al. [54] use the GSK algorithm for solving stochastic programming problems.

An Adaptive genetic algorithm (AGA) and bilateral filtering [7] were combined to provide a noise reduction and image restoration filter [55]. The results obtained from this technique indicated that it offered better performance in de-noising all types of noisy images with a higher de-noising Peak signal to noise ratio (PSNR) [56], and it restored all images with high quality. Another automatic PSO-based [37] method for the bilateral filter [7] parameter selection was introduced [19]. The Structural similarity index measure (SSIM) [57] was used as a fitness function to optimize the intensity domain and radius parameters by applying the PSO algorithm. The de-noising performance of the bilateral filter was significantly improved in their method, and the low stability of the bilateral filter without parameter optimization was declared. The parameters of the bilateral filter [7] were also optimized using PSO, cuckoo search [58], and adaptive cuckoo search algorithms to reduce the satellite images that have been affected by Gaussian noise [20]. The proposed adaptive cuckoo search method and traditional filters were compared by evaluating the PSNR, Mean squared error (MSE), Feature Similarity Index (FSIM), Entropy, and CPU time. Their method is an edge-preserving filter with low complexity, and is faster than other optimization algorithms. The parameters of the bilateral filter, including the neighborhood radius, which was considered a parameter, were optimized by the WOA algorithm [41], and the obtained image was restored by optimizing the point spread function in the Richardson-Lucy algorithm (R-L) algorithm [18]. The morphological operation and Multi-objective particle swarm optimization (MOPSO) were used to design a de-noising filter [59]. In their approach, first, a series and parallel compound morphology filter were generated based on an open-close (OC) operation, and a structural element with various sizes aiming to remove all noises in a series link was chosen; after that, MOPSO was combined to solve the parameters’ setting of multiple structural elements. While smoothing the noise, the edges and texture details have been preserved in their methods. An APSO-based R-L algorithm was used for blurry elimination and restoration of the de-noised image using a Fuzzy-based median filter (FMF) [60]. They claimed that their FMF and APSO-RL methods have a higher value regarding PSNR and Second derivative like measure enhancement (SDME) than the other conventional filtering and restoration techniques. Singh et al. [61] used fuzzy linguistic quantifiers to remove impulse noise from images. They claimed that, since the median filter determines the median of a predefined mask, sometimes the estimated intensity of the median filter will again cause noise. The performance of the network can be increased by the size of the receptive field in noise removal. Some features of the GC distribution were used, and a mask was designed that reduces the image noise while preserving the edges and details of the image [17]. The parameters of the GC function optimized by the PSO algorithm [37] and MSE [62] value are selected as a fitness function. The result of this paper claims that maximum PSNR value can be achieved and it is an easily designed method.

Spatial filters include some drawbacks; for instance, these filters smooth the data while decreasing noise and blurring edges in the image. Also, linear filters cannot effectively remove signal-dependent noise. Likewise, spatial frequency filtering and wavelet-based algorithms have some defects, including the calculation complexity and time-consuming. By removing these disadvantages, image denoising and consistency efficiency can be enhanced.

Filter-based denoising techniques can effectively reduce the noise, but they cannot preserve the image quality and useful information; so metaheuristic algorithms which play an important role in replacing human inspections and interpretation of processed images, have been used. Due to the novelty of the GSK algorithm, and the lack of wide applications in image processing, the GSK algorithm is used for noise removal purposes. The WOA and GSK algorithms are used to optimize the parameters due to having a high convergence speed. Since the WOA algorithm has two separate steps of exploration and exploitation in almost half of the iterations that prevent the possibility of getting stuck in local optima. The GSK algorithm's scalability ensures that it can effectively balance exploration and exploitation capabilities. Therefore, the current paper aimed to de-noise images through the WOA and GSK algorithms in the bilateral and GSK filters to optimize the filter parameters. Table 1 details the previous similar efforts and the context of motivating the proposed filters.

Table 1 Details of recently produced filters

The advantages of the proposed method include simple design, significant noise removal, and preservation of image information. However, in the proposed methods, the original noiseless image must be accessible for comparison, which is one of the disadvantages of these methods.

The proposed de-noising filters are applied to the images corrupted with Gaussian and salt & pepper (SAP) noises. The results are compared with each other, and traditional methods such as Mean filter, Gaussian filter, Median filter, Wiener filter, Non-local mean filter, PSO-based GC filter [17] (GC_PSO), and two PSO-based bilateral filters (Wang's method [19] ‘BW_PSO’ and Asokan's method [20] ‘BA_PSO’) on various images that are corrupted by Gaussian noise.

The SSIM, PSNR, Figure of merit (FOM) [63], Edge Preservative Factor (EPF) [64] values, and execution time are calculated for this comparison, and the proposed filters' efficiency is determined.

Preliminaries

At first, we try to explain the applied functions and algorithms. The explanations about the generalized Cauchy distribution and the bilateral filter are given in “The GC Distribution” and “Bilateral Filter”, respectively. Details about PSO, WOA, and GSK algorithms are given in “PSO Algorithm”, “WOA Algorithm”, and “GSK Algorithm”, respectively.

The GC Distribution

The GC distribution is an asymmetric distribution with a bell-shaped density function, similar to the Gaussian distribution, but with a higher mass in the tails and is considered a particular distribution due to the heavy tails. The GC distribution family has properties that depend on the probability density function for the whole family and has algebraic tails that model many impulsive processes in real life [65]. Another parameterization of the GC distribution was performed by Miller and Thomas [66]. Later, the probability density function was given as follows, mainly used to eliminate radio speckle noise [67]. Details about the GC distribution have been described in reference [17].

$$f(x) = \frac{\mu \,\beta \,\Gamma (2/\beta )}{{2(\Gamma (1/\beta ))^{2} }}(\mu^{\beta } + |x - \theta |^{\beta } )^{{ - \,\frac{2}{\beta }}} ,\,\beta ,\mu > 0\,,{\kern 1pt} x,\theta \in {\mathbb{R}},$$

(1)

where $\beta$ corresponds to the tail constant (causes the sharpness or non-sharpness of the peak point of the curve and moving the peak point of the curve up or down), $\mu$ is the scale parameter (causes the tail of the curve to be closer or farther away) and $\theta$ refers to the tail of the curve moving from symmetry and $\Gamma (.)$ is the Gamma function.

Bilateral Filter

As mentioned in [20], the bilateral filter, which was proposed by Tomasi [7], has been a non-linear, edge-preserving, and noise-reducing smoothing filter, which is a combination of range and domain filtering and replaces the intensity of each pixel with the weighted Mean intensity of adjacent pixels. The weights are based on the Gaussian distribution, replaced by the GC distribution in the proposed method. According to the bilateral filter definition, the noisy image is filtered from the following formula:

$$I^{{{\text{filtered}}}} = \frac{1}{W}\mathop \sum \limits_{{x_{i} \in N}} I\left( {x_{i} } \right)f_{{\text{r}}} \left( {I\left( {x_{i} } \right) - I\left( x \right)} \right)g_{{\text{d}}} \left( {x_{i} - x} \right).$$

(2)

The weight $W$ is defined so that adjacent pixels within a neighborhood are compared with the central pixel, and the higher weights are assigned to pixels that are more similar and closer to the center pixel.

$$W = \mathop \sum \limits_{{x_{i} \in N}} \;f_{{\text{r}}} \left( {I\left( {x_{i} } \right) - I\left( x \right)} \right)g_{{\text{d}}} \left( {x_{i} - x} \right),$$

(3)

where $I^{{{\text{filtered}}}}$ and $I$ represent the filtered and noisy images, respectively.$x$ is the current pixel coordinate that needs to be filtered. $N$ is the window centered in, $x$ so $x_{i} \in N$ is another pixel. $f_{{\text{r}}}$ and $g_{{\text{d}}}$ are the range and domain kernel for smoothing the differences in intensities and coordinates.

PSO Algorithm

PSO [37] is a social search algorithm inspired by the social behavior of birds. The algorithm is based on particles representing a potential solution to the optimization problem. The algorithm aims to find the particle location in the response space that obtains the best value for the objective function. Each particle is considered a possible solution to the problem. The improvement in the solution provided by each particle comes from two sources; the first is using the particle's personal experience, called the cognitive component ${\text{(pbest)}}$. The other is to improve the answer in the particle community, which is called the social component ${\text{(gbest)}}$. ${\text{pbest}}$ is the best solution that the particle has received so far from the implementation of the algorithm and ${\text{gbest}}$ is the best solution experienced in the population so far from the implementation of the algorithm. To calculate the velocity of each particle in each location, ${\text{pbest}}$ and ${\text{gbest}}$ are used simultaneously. The cognitive and social components are combined to guide the particle to a better solution to define the particle velocity. The particle velocity in each iteration of the algorithm is calculated as follows.

$$v_{i} \left( {t + 1} \right) = \omega \;v_{i} (t) + c_{1} r_{1} \left( {{\text{pbest}}_{i} \left( t \right) - x_{i} \left( t \right)} \right) + c_{2} r_{2} \left( {{\text{gbest}}\left( t \right) - x_{i} \left( t \right)} \right),$$

(4)

where $x_{i} \left( t \right)$ and $v_{i} (t)$ display the current particle location and current velocity, respectively, and $v_{i} \left( {t + 1} \right)$ indicates the particle's new velocity to move from the current location to the new location. $\omega$ is the inertia weight, $c_{1}$ and $c_{2}$ are the acceleration constant, $r_{1}$ and $r_{2}$ are the random values in the range (0,1). The new location of each particle is obtained from the following equation.

$$x_{i} \left( {t + 1} \right) = x_{i} \left( t \right) + v_{i} \left( {t + 1} \right).$$

(5)

The weight $w$ changes with the number of iterations and can be calculated according to Eq. (6) [68]

$$w = w_{\max } - \frac{{w_{\max } - w_{\min } }}{{{\text{iter}}_{\max } }} \times {\text{iter}}_{{{\text{current}}}} .$$

(6)

Moreover $w_{\min }$, and ${\kern 1pt} w_{\max }$ are the minimum and maximum weights, respectively, ${\text{iter}}_{{{\text{current}}}}$ and ${\text{iter}}_{{{\text{max}}}}$ indicate the current and maximum iterations.

WOA Algorithm

One nature-inspired algorithm that uses the humpback whale hunting strategy is the whale algorithm [41]. The humpback whales usually go 10–15 m underwater and form spiral bubbles to encircle the prey. Afterward, it moves towards the surface of the water and the prey. This type of whale behavior involves two phases exploration and exploitation.

The WOA starts with initializing the search agents (whales) and each search agent's position $Y_{i} \,,i = 1,2, \ldots ,n$, which $n$ indicates the number of search agents. After initialization, the fitness function was evaluated for each search agent, and the best value among them was considered $Y^{*}$. Since the exact location of the prey in the search space is unknown, the best answer $Y^{*}$ is to consider the location of the prey or close to it. The rest of the search agents update their position according to this answer; obtained from the following equations.

$$\overrightarrow {R} = \left| {\overrightarrow {C } \cdot \overrightarrow {{{\kern 1pt} Y }}^{*} \left( u \right) - \overrightarrow {Y } \left( u \right)} \right|,$$

(7)

$$\overrightarrow {Y }^{*} \left( {u + 1} \right) = \overrightarrow {Y }^{*} \left( u \right) - \overrightarrow {A } \cdot \overrightarrow {R} ,$$

(8)

where $u$, $\overrightarrow {Y }^{*}$, $\overrightarrow {Y }$ signifies the current iteration, the position vector of the current best solution, and the position vector respectively, “| |” is the absolute value, “.” is elementwise multiplication, and the vectors $\overrightarrow {A }$ and $\overrightarrow {C }$ are obtained from Eqs. (9) and (10). It should be noted that if there is a better solution, $Y^{*}$ should be updated.

$$\overrightarrow {A } = 2\overrightarrow {m } \cdot \overrightarrow {n } - \overrightarrow {m } ,$$

(9)

$$\overrightarrow {C } = 2\overrightarrow {n } .$$

(10)

In the exploration and exploitation phases, $\overrightarrow {n }$ is a random value in $[0,1][0,1]$, and $\overrightarrow {m }$ decreases from 2 to 0 during the iterations.

Two mechanisms of whale bubble network attack are mathematically modeled as follows:

• The shrinking surrounding mechanism is accomplished by reducing the value of $\overrightarrow {m }$ in Eq. (9); correspondingly, the amount of $\overleftarrow {A\;}$ also decreased.

• The spiral updating position mechanism in which whales imitate the helix-shaped movement to update the position between the prey and the whale is described in Eq. (11).

  $$\overrightarrow {Y } \left( {u + 1} \right) = \overrightarrow {R} ^{\prime } \cdot e^{bl} \cdot {\text{cos}}\left( {2\pi l} \right) + \overrightarrow {{Y ^{*} }} \left( u \right),$$

  (11)

where $\overrightarrow {R} ^{\prime }$, $l$ and $b$ are the distance between the prey and $i{\text{th}}$ whale (current optimal solution $\overrightarrow {{Y ^{*} }}$), a random value in the range of $[ - 1,1]$ and a constant that corresponds to the logarithmic shape of the helix, respectively.

The humpback whales can use both mechanisms simultaneously. Given the same probability of both mechanisms, the mathematical model is as follows.

$$\overrightarrow {Y} \left( {u + 1} \right) = \left\{ {\begin{array}{*{20}l} {\overrightarrow {Y}^{*} \left( u \right) - \overrightarrow {A } \cdot \overrightarrow {R} } & {p < 0.5} \\ {\overrightarrow {{R^{\prime}}} \cdot e^{bl} \cdot \,{\text{cos}}\left( {2\pi l} \right) + \overrightarrow {Y }^{*} \left( u \right)} & {p \ge 0.5} \\ \end{array} } \right.,$$

(12)

where p is a random number in [0, 1].

Changes in $\overrightarrow {A }$ values are considered the exploration phase. In this phase, the humpback whales search arbitrarily according to the location of each one. The arbitrary values are in the range [− 1, 1], forcing the whale to travel far away from the reference whale. In the exploration phase, the position of the whales is updated according to the randomly selected whale.

$$\overrightarrow {R} = \left| {\overrightarrow {C} \cdot \overrightarrow {Y}_{{{\text{rand}}}} \left( u \right) - \overrightarrow {Y} \left( u \right)} \right| ,$$

(13)

$$\overrightarrow { Y} \left( {u + 1} \right) = \overrightarrow {Y}_{{{\text{rand}}}} - \overrightarrow {A} \cdot \overrightarrow {R} .$$

(14)

The WOA algorithm starts to find the best solution by arbitrarily tracing the whales in the search space. The whales update their location in each iteration according to the best or arbitrarily selected search agent. The value $p$ reveals that the whales should have a spiral or shrinkage movement. The WOA algorithm ends when a predetermined termination condition is met.

GSK Algorithm

Gaining sharing knowledge-based optimization algorithm (GSK) [45] is a newly developed metaheuristic algorithm that follows the concept of gaining and sharing knowledge throughout the human lifetime. Let $\left\{ {y_{1} ,y_{2} , \ldots ,y_{M} } \right\}$ be the individuals of the population size $M$. Each individual $y_{j}$ is defined as $y_{j} = \left[ {x_{j1} ,x_{j2} , \ldots ,x_{jc} } \right]$ where $c$ is the branch of knowledge assigned to an individual. In each iteration, individuals are sorted in ascending order according to the value of the objective function and then use the junior gaining and sharing phase and the senior gaining and sharing phase to update the population of individuals together.

Junior GSK Phase

Each $y_{j}$ gains knowledge from the two closest individuals, $y_{j - 1}$ (the best one) and $y_{j + 1}$ (the worst one). It also shares the knowledge of an individual $y_{{{\text{rand}}}}$ randomly. The individuals are updated through Eq. (15).

$$y_{\begin{subarray}{l} {\text{new}} \\ j \end{subarray} } = \left\{ {\begin{array}{*{20}c} {y_{j} + k_{f} .\left[ {\left( {y_{j - 1} - y_{j + 1} } \right) + \left( {y_{{{\text{rand}}}} - y_{j} } \right)} \right],} & { {\text{if}} f\left( {y_{{{\text{rand}}}} } \right) < f\left( {y_{j} } \right)} \\ {y_{j} + k_{f} .\left[ {\left( {y_{j - 1} - y_{j + 1} } \right) + \left( {y_{j} - y_{{{\text{rand}}}} } \right)} \right],} & { {\text{ if}} f\left( {y_{{{\text{rand}}}} } \right) \ge f\left( {y_{j} } \right)} \\ \end{array} } \right.,$$

(15)

where $y_{\begin{subarray}{l} {\text{new}} \\ j \end{subarray} }$ is a trial vector for $y_{j}$, $f$ and $k_{f}$ are the objective function value and knowledge factor, respectively.

Senior GSK Phase

After sorting individuals into ascending order (based on the objective function values) in this phase, the individuals are classified into three categories (best, middle, and worst). The best and worst levels each contain ${\text{n }} \times \, M \, (n \in \left[ {0, \, 1} \right])$ individuals, and the middle level has the rest $\left( {1 \, - \, 2n} \right) \, \times {\text{ M}}$ individuals. For each individual $y_{j}$, it gains knowledge from three individuals of different groups using Eq. (16):

$$y_{\begin{subarray}{l} {\text{new}} \\ j \end{subarray} } = \left\{ {\begin{array}{*{20}c} {y_{j} + k_{f} \cdot \left[ {\left( {y_{{{\text{pb}}}} - y_{{{\text{pw}}}} } \right) + \left( {y_{{\text{m}}} - y_{j} } \right)} \right],} & {{\text{if}} f\left( {y_{{\text{m}}} } \right) < f(y_{j} )} \\ {y_{j} + k_{f} \cdot \left[ {\left( {y_{{{\text{pb}}}} - y_{{{\text{pw}}}} } \right) + \left( {y_{j} - y_{{\text{m}}} } \right)} \right],} & {{\text{if}} f\left( {y_{{\text{m}}} } \right) \ge f\left( {y_{j} } \right)} \\ \end{array} } \right.,$$

(16)

where $y_{{{\text{pb}}}}$, $y_{{{\text{pw}}}}$ and $y_{{\text{m}}}$ are random individuals selected from the best, middle, and worst levels, respectively.

Both phases are done to update the different dimensions of an individual. Note that the numbers of dimensions that will be updated using the junior phase and the senior phase are calculated by the following formulation, respectively:

$$c_{ja} = \left( {1 - \frac{u}{{u_{{{\text{max}}}} }}} \right)^{k} \times c,$$

(17)

$$c_{se} = c - c_{ja}$$

(18)

where $k > 0$, $u$, and $u_{{{\text{max}}}}$ are a knowledge rate, the current iteration, and the maximum number of iterations, respectively. In Algorithms 2 and 4, $k_{r} \in [0,1]$ the knowledge ratio controls the total amount of gained and shared knowledge that will be inherited during generations (the ratio between the current and acquired experience).

Proposed Method

Designing an effective filter that preserves the edges and structural information of the image is one of the challenges most researchers face in image processing. The primary purpose of this paper is to develop two automatic filters to reduce the noise using the GC distribution. The definition of the first and second proposed filters is explained in “Mask Design Using the GC Function” and “Bilateral Filter Using the GC Function (BL-GC)”, respectively.

Mask Design Using the GC Function

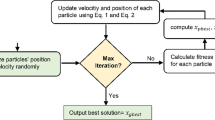
A mask is designed to produce a noiseless image convolved with the noisy image to create an efficient filter. For this purpose, the parameters of the GC function $\beta ,{\kern 1pt} \mu {\kern 1pt} ,{\kern 1pt} \theta$ and mask size $w$ are considered as parameters, and the optimal values of these parameters are found by maximizing the fitness function Eq. (24) defined in “Fitness Function” in the WOA and GSK algorithms. Karami and Tafakori [17] used some features of the GC function and designed a mask that reduces image noise. They optimized the GC distribution parameters by considering the MSE [62] as a fitness function in the PSO [37]. Their method needed to recalculate the PSNR of the filtered image at the end of the algorithm. The selected mask size was considered constant and equal to 3, while in our proposed method, the mask size is regarded as a parameter that should be optimized. By repeating and examining their method on different images with different mask sizes, we found that the selected mask size significantly impacts filter performance, so the proposed method addresses these issues. The diagram of the first proposed method is shown in Fig. 1.

Fig. 1

Diagram of the first proposed method

Considering that $I_{{{\text{input}}}}$ is an $m \times n$ ordered noise-free grayscale image corrupted by an additive Noise, $I_{{{\text{noisy}}}}$ (noisy image) is obtained.

$$I_{{{\text{noisy}}}} = I_{{{\text{input}}}} + {\text{noise}}.$$

(19)

The noisy image is convolved with the designed mask $F$, and the noise-free image is obtained.

$$I_{{{\text{output}}}} = I_{{{\text{noisy}}}} \times F.$$

(20)

To design the mask ‘F’, the bivariate GC function, an extension of the univariate function Eq. (1), is considered Eq. (21).

$$f(x,y) = \left( {\frac{{\mu {\kern 1pt} \beta \,\Gamma (2/\beta )}}{{2(\Gamma (1/\beta ))^{2} }}} \right)^{2} (\mu^{\beta } + |x - \theta |^{\beta } )^{{ - \,\frac{2}{\beta }}} {\kern 1pt} (\mu^{\beta } + |y - \theta |^{\beta } )^{{ - \,\frac{2}{\beta }}} ,\,\beta ,\mu > 0\,,{\kern 1pt} x,y,\theta \in {\mathbb{R}}.$$

(21)

A discretization must be performed to store the continuous generalized Cauchy function in the form of discrete pixels. This process is done, and the mask is produced. The designed mask size has an odd value like 3, 5, etc., which the optimal value is computed through the whale algorithm. For example, the 5 × 5 mask with $\beta = 1$,$\mu = 1$, $\theta = 0$ is as follows:

0.0042	0.0094	0.0375	0.0094	0.0042
0.0094	0.0211	0.0843	0.0211	0.0094
0.0375	0.0843	0.3371	0.0843	0.0375
0.0094	0.0211	0.0843	0.0211	0.0094
0.0042	0.0094	0.0375	0.0094	0.0042

In the WOA (and GSK), each search agent $Y_{i} \,,i = 1,...,n$ (each individual $y_{j} ,j = 1,...,M$) has four parameters $\beta ,{\kern 1pt} \mu {\kern 1pt} ,{\kern 1pt} \theta {\kern 1pt} ,{\kern 1pt} {\kern 1pt} w{\text{size}}$ that the fitness function must optimize. At first, the number of $n$ search agents (M individuals) containing four parameters $\beta ,{\kern 1pt} \mu {\kern 1pt} ,{\kern 1pt} \theta {\kern 1pt} ,{\kern 1pt} {\kern 1pt} w{\text{size}}$ is randomly initialized according to the range of parameters defined in “WOA Algorithm””. Different masks are generated according to these search agents (individuals) and convolved with the noisy image, so different noiseless images are obtained. The fitness function Eq. (24) is evaluated for these output images, and the maximum value is considered the best solution. The WOA (GSK) is continued according to pseudo-codes of Algorithms 1 or 2. Completing the predetermined number of iterations results in a noise-free image with the maximum fitness function. The pseudo-codes of the first proposed filter using the WOA and GSK will be as algorithms 1 and 2.

The pseudo-code of the first proposed WOA-based filter

The pseudo-code of the first proposed GSK-based filter

Bilateral Filter Using the GC Function (BL-GC)

In this section, a filter is designed to reduce the noise using a bilateral filter, in which the GC function is used instead of the Gaussian function.

Assume that the pixel in position $\left( {i,j} \right)$ must be de-noised using the adjacent pixels, and one of the adjacent pixels is in position $\left( {k,l} \right)$; in this case, the weight assigned to the pixel $\left( {k,l} \right)$ for noise reduction of the pixel $\left( {i,j} \right)$ is as follows:

$$w\left( {i,j,k,l} \right) = (\mu_{d}^{{\beta_{d} }} + |(\sqrt {(i - k)^{2} + (j - l)^{2} } {\kern 1pt} ) - \theta_{d} |^{{\beta_{d} }} )^{{ - \frac{2}{\beta }_{d} }} (\mu_{r}^{{\beta_{r} }} + ||I(i,j) - I(k,l)| - \theta_{r} |^{{\beta_{r} }} )^{{ - \frac{2}{\beta }_{r} }} ,$$

(22)

where $\beta_{d} ,{\kern 1pt} \mu_{d} {\kern 1pt} ,{\kern 1pt} \theta {\kern 1pt}_{d}$ are the smoothing parameters in the spatial domain and $\beta_{r} ,{\kern 1pt} \mu_{r} {\kern 1pt} ,{\kern 1pt} \theta {\kern 1pt}_{r}$ are the smoothing parameters in the range domain, and $I\left( {i,j} \right), I\left( {k,l} \right)$ are the intensity of the corresponding pixels. The proposed filter output is calculated as follows:

$$I_{D} \left( {i,j} \right) = \frac{{\mathop \sum \nolimits_{k,l} I\left( {k,l} \right)\,\;w\left( {i,j,k,l} \right)}}{{\mathop \sum \nolimits_{k,l} w\left( {i,j,k,l} \right)}}.$$

(23)

In Eq. (23), the fraction's denominator is the normalization factor and $I_{D}$ is filtered pixel intensity at the location $\left( {i,j} \right)$. Since the optimal values of the smoothing parameters require experimental and manual efforts, the WOA (and GSK) is used to obtain the optimal values of these parameters by considering Eq. (24) in “PSO Algorithm” as a fitness function. In the proposed filter, the neighboring radius $r$ is also considered a parameter that should be optimized, and correspondingly, the window size ($w{\text{size}} = 2r + 1,\;r = 1,2, \ldots$) is obtained. The diagram of the second proposed method is shown in Fig. 2

Fig. 2

Diagram of the second proposed method

In WOA (or GSK), each search agent (each individual) has parameters $\beta_{d} ,{\kern 1pt} \mu_{d} {\kern 1pt} ,{\kern 1pt} \theta {\kern 1pt}_{d} ,\beta_{r} ,{\kern 1pt} \mu_{r} {\kern 1pt} ,{\kern 1pt} \theta {\kern 1pt}_{r} ,r$ that achieve the optimum value according to the fitness function Eq. (24).

Suppose that $I_{{{\text{input}}}}$ is a $m \times n$ noise-free grayscale image corrupted by additive noise and $I_{{{\text{noisy}}}}$ obtained. Equation (23) is applied to all pixels of the noisy image, and the noiseless image is obtained. The noisy image is entered into the WOA (GSK), each search agent (each individual) which contains parameters “$\beta_{d} ,{\kern 1pt} \mu_{d} {\kern 1pt} ,{\kern 1pt} \theta {\kern 1pt}_{d} ,\beta_{r} ,{\kern 1pt} \mu_{r} {\kern 1pt} ,{\kern 1pt} \theta {\kern 1pt}_{r} ,r$“ is initialized randomly in the range defined in “WOA Algorithm”, and according to these parameters, Eq. (23) is applied to all pixels of the noisy image, and different noiseless images are obtained. The fitness of the output images is calculated through Eq. (24), the maximum value is considered the best solution, and the WOA (or GSK) is continued to complete a predetermined number of iterations. A noise-free image with a maximum fitness function is obtained when the algorithm terminates. The pseudo-code of the second proposed method using WOA and GSK will be as Algorithm 3 and 4.

The pseudo-code of the second proposed WOA-based filter

The pseudo-code of the second proposed GSK-based filter

Fitness Function

The goal of optimization problems is to find the optimal solution to the problem. The primary purpose of this paper is to achieve the best results in the proposed filters. The search agents must get better in each iteration. These search agents must be evaluated according to the fitness function in each iteration. The desired fitness function for the first and second proposed filters is the $PSNR$, which is computed using Eq. (24) [62].

$${\text{PSNR}} = 10 \log_{10} \frac{{255^{2} }}{{{\text{MSE}}}},$$

(24)

where MSE is the mean squared error calculated from Eq. (25) [62], $I$ and $I_{D}$ are $M \times N$ ordered original and de-noised images, respectively.

$${\text{MSE}} = \frac{1}{M \times N}\mathop \sum \limits_{x = 1}^{M} \mathop \sum \limits_{y = 1}^{N} \left( {I\left( {x,y} \right) - I_{D} \left( {x,y} \right)} \right)^{2} .$$

(25)

A higher $PSNR$ value indicates a further improvement in the filtered image.

Parameter Setting

Since all meta-heuristic algorithms are parameter-based. Therefore, the analysis of these parameters plays a significant role in determining the optimal solution. According to the parameter values used in meta-heuristic algorithms to solve different types of problems in [41, 45, 46], and also the test results of meta-heuristics-based noise reduction filters on different images, the optimal values of the parameters can be considered as follows. The WOA parameters follow the values given in “WOA Algorithm”, and the PSO parameters are considered $c_{1} ,c_{2} = 2\;,w_{\max } = 0.9\;,w_{\min } = 0.4$. The GSK parameters “$M = 20,\;u_{\max } = 50,k = 10,n = 0.1,k_{f} = 0.5,k_{r} = 0.9$“ are as mentioned in “Experimental Results and Discussion”. In the first proposed filter using WOA (or GSK) and the GC_PSO filter, the maximum number of iterations and the population size are 300 and 50, respectively. The GC function parameters are concluded from [17], so the mask size and GC parameters are set as follows.

$$\beta \in (0,5]{\kern 1pt} \,,{\kern 1pt} \,\mu \in (0,2]{\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} \theta \in [ - 1,1]{\kern 1pt} \,,\,w{\text{size}} \in [3,11].$$

(26)

The WOA (or GSK) obtains the optimal GC function parameters and mask size values. As shown in Table 4, the optimal mask size increases by increasing the Gaussian noise standard deviation. In the second proposed method, BW_PSO; and BA_PSO filters [19, 20], the population size and the maximum number of iterations are considered 20 and 50, respectively. The domain and range parameters of the GC function in the bilateral filter and the neighboring radius have been experimentally obtained by trying on different images and set as follows:

$$\beta_{d} \in (0,1]{\kern 1pt} \,,{\kern 1pt} \,\mu_{d} \in [100,230]{\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} \theta_{d} \in [ - 0.5,0.5]{\kern 1pt} \,,\,\beta_{r} \in [0.01,50]{\kern 1pt} \,,{\kern 1pt} \,\mu_{r} \in [20,150]{\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} \theta_{r} \in [ - 70,70]{\kern 1pt} \,,r \in [1,5].$$

(27)

The domain and range parameters and the radius parameter in the BW_PSO filter [19] are considered as follows:

$${\kern 1pt} \,\sigma_{d} = 10\;{\kern 1pt} ,{\kern 1pt} {\kern 1pt} \sigma_{r} \in [1,200]{\kern 1pt} \,,d \in [1,5].$$

(28)

The domain and range parameters in the BA_PSO filter [20] are considered as follows:

$${\kern 1pt} \,\sigma_{d} = [0.1,10]\;{\kern 1pt} ,{\kern 1pt} {\kern 1pt} \sigma_{r} \in [1,200]{\kern 1pt} \,.$$

(29)

Given the stochastic nature of the proposed methods and PSO-based filters, the presented results are an average of 20 times, the execution of these algorithms.

Experimental Results and Discussion

To demonstrate the efficiency of the proposed filters using WOA and GSK, they are compared with each other, five classical filters, and GC_PSO, BW_PSO, and BA_PSO filters. To this end, six grayscale images such as Barbara “512 × 512”, Boats “512 × 512”, Hill “512 × 512”, Couple “512 × 512”, Peppers “256 × 256”, and House “256 × 256” are considered as data sets. These are noiseless test images with a resolution of 8 bits per pixel and are taken from https://www.kaggle.com/datasets/saeedehkamjoo/standard-test-images. To evaluate the performance of the proposed methods in the presence of noise, each image is corrupted with different standard deviations of Gaussian noise and various densities of SAP noise. These images are corrupted with four standard deviations “$\sigma = 20,30,50,70$“ of the Gaussian noise and three different densities “$d = 0.02, \, 0.03, \, 0.05$“ of SAP noise. Later for all levels of Gaussian noise standard deviation, the classical filters such as Mean filter, Gaussian filter, Median filter, Wiener filter, non-local mean filter (NLM), the GC_PSO filter, BW_PSO, BA_PSO, WOA-based P1_WOA filter (P1_WOA), GSK-based P1_WOA filter (P1_GSK), WOA-based P2_WOA filter (P2_WOA), and GSK-based P2_WOA (P2_GSK) filters are applied to the noisy images, for all densities of SAP noise, Mean filter, Gaussian filter, Median filter, Wiener filter, non-local mean filter, GC_PSO filter, BW_PSO filter, BA_PSO filter, P1_WOA filter, and P2_WOA filter are evaluated. The SSIM [26] value between the filtered image and the original image and the SSIM value between the original image and the noisy image are calculated and are listed in Table 2. The SSIM [57] value is calculated from Eq. (30). Note that the SSIM values between the filtered and the original noiseless images are calculated manually in all methods except for the BW_PSO, which is automatically calculated by the PSO algorithm. In the GC_PSO filter and the BA_PSO, the MSE value between the filtered and original images is calculated automatically, but the SSIM value between the filtered and original images is calculated manually. In the proposed filters, the PSNR value is calculated automatically by WOA (or GSK). To make a fair comparison between the noise reduction filters in all images, the PSNR value between the filtered and the original images is also calculated manually. The results are listed in Table 3.

Table 2 The SSIM results for Gaussian noise reduction

Table 3 The PSNR results for Gaussian noise reduction

The SSIM [57] is a number between zero and one and evaluates the similarity between two images; in contrast, brightness, and structure. The primary purpose is to assess this criterion between the original noiseless image and the filtered output image. Higher values indicate that the structural similarity of the resulting image is close to the original noiseless image, and the filter performance is better.

$${\text{SSIM}} = \frac{{\left( {2\mu_{I} \mu_{{I_{n} }} + c_{1} } \right)\left( {2\sigma_{{I,I_{n} }} + c_{2} } \right)}}{{\left( {\mu_{I}^{2} + \mu_{{I_{n} }}^{2} + c_{1} } \right)\left( {\sigma_{I}^{2} + \sigma_{{I_{n} }}^{2} + c_{2} } \right)}},$$

(30)

where, $\mu_{I} ,\mu_{{I_{n} }}$ and $\sigma_{I}^{2} ,\sigma_{{I_{n} }}^{2}$ are the mean value and variance value of corresponding original and noisy images, and $\sigma_{{I,I_{n} }}$ is the covariance between original and noisy image. $c_{1} = (0.01 \times 255)^{2} ,c_{2} = (0.03 \times 255)^{2}$ are two constants.

As an example, the results of the calculations are shown on some images in Fig. 3, in which the images “${\text{Hill}}\;$, ${\text{Couple}}\;$, ${\text{Barbara}}\;$ and ${\text{Boats}}$“ are corrupted with standard deviations $20, \, 30, \, 50$ and $70$ of the Gaussian noise, respectively. In Fig. 3, “$a, \, b, \, c, \, d, \, e, \, f, \, g, \, h, \, i, \, j,k\;,l,m$ and $n$“ represent the Original, Noisy, Mean filter, Gaussian filter, Median filter, Wiener filter, NLM filter, GC_PSO filter, BW_PSO filter, BA_PSO filter, P1_WOA filter, P2_WOA filter, P1_GSK, and P2_GSK filter images respectively.

Fig. 3

Images before and after Gaussian noise removal

As shown in Tables 2 and 3, higher values are marked in bold, and the P2_GSK filter in almost all images and all standard deviations of the Gaussian noise have better SSIM and PSNR than other methods. After the P2_GSK filter, the P2_WOA filter performs better than other filters. BW_PSO filter has better SSIM and PSNR than others, even compared to the P1_WOA and P1_GSK. The comparison between methods shows that the metaheuristic-based methods have almost better fitness function and SSIM values. The fitness and SSIM value of the proposed filters will be even better than the GC_PSO method. The P2_WOA and P2_GSK filters act better than the P1_WOA and P1_GSK filters. BW_PSO filter acts better than the BA_PSO, P1_WOA, and P1_GSK filters. However, the proposed methods have better results than the classical filters and GC_PSO, which shows the proposed methods' superiority.

After implementing the P1_WOA method and GC_PSO, the corresponding optimal GC distribution parameters and window size values are obtained for each Gaussian noise standard deviation level. The results are placed in Table 4. By plotting the GC function diagram for the optimal parameters obtained from the WOA algorithm and increasing the image noise, the shape of the GC function will be close to the Gaussian function, which reduces undesirable noise effects. Figure 4 shows an example of the GC distribution shape concerning the parameters obtained from the WOA for different noise levels in the ${\text{Hill}}$ image to explain the above claim. Figure 4; $a,{\kern 1pt} \,b,\,{\kern 1pt} c,\,{\text{and}}\;d$ are the GC distribution shape concerning the optimal parameters for $\sigma = 20,30,50,70$ the Gaussian noise in the ${\text{Hill}}$ image, respectively.

Table 4 Optimal parameter values for different images

Fig. 4

Cauchy distribution diagram for optimal parameters for the Hill image

Table 4 shows the PSNR value of the P1_WOA filter and GC_PSO filter for all Gaussian noise standard deviations. All images practically depend on the optimal choice of filter parameters and the selected mask size. For $\sigma = 20$ both methods have almost similar results in all images, and even for some images, the P1_WOA method provides more desirable results. By increasing the Gaussian noise standard deviation, the P1_WOA filter has better PSNR results than the GC_PSO filter. So, the role of the selected mask size in the filter efficiency can be better understood

To assess whether the proposed methods preserve the edges of the image or not, the figure of merit (FOM) [63] and Edge Preservative Factor (EPF) [64] are evaluated. The FOM is a method for quantitative comparison between edge detection algorithms in image processing and has a value between zero and one. The closer the importance of this criterion is to one, the better it shows the edge values and is formulated in Eq. (31) [63].

$$R = \frac{1}{{{\text{Max}}\left( {N_{1} ,N_{2} } \right)}}\mathop \sum \limits_{i = 1}^{{N_{2} }} \frac{1}{{1 + Cd^{2} \left( i \right)}}.$$

(31)

Furthermore $N_{1}$, $N_{2}$ representing the number of actual edges and detected edges achieved by the Sobel edge detector, C represents a constant value equal to 1/9, $d\left( i \right)$ representing the distance between the actual edge and the detected edge.

The EPF is a measure that computes the details preservation ability of the filtered image and is computed from Eq. (32) [64].

$${\text{EPF}} = \frac{{\sum {(I_{L} - \mu_{{I_{L} }} ) \times (DI_{L} - \mu_{{{\text{DI}}_{L} }} )} }}{{\sqrt {\sum {(I_{L} - \mu_{{I_{L} }} )^{2} \times \sum {(DI_{L} - \mu_{{{\text{DI}}_{L} }} )^{2} } } } }},$$

(32)

where $I_{L}$ and ${\text{DI}}_{L}$ are the Laplacian operators of the original and filtered image, respectively, $\mu_{{I_{L} }}$ and $\mu_{{{\text{DI}}_{L} }}$ are the corresponding mean values. The higher EPF value indicates that the filtered image has more details. The FOM and EPF values are calculated for all filtered images and placed in Tables 5 and 6, respectively.

Table 5 The FOM results for Gaussian noise reduction

Table 6 The EPF results for Gaussian noise reduction

A filter with a higher PSNR, SSIM, FOM, and EPF value and less computational complexity and computational time is efficient. The proposed filter's computational time is described in “Bilateral Filter Using the GC Function (BL-GC)”. It is claimed that all de-noising filters produced by meta-heuristic algorithms are convergent, whose convergence is reviewed in “Fitness Function”.

According to Table 5, the highest FOM values are marked in bold, and the FOM value for the P2_GSK filter compared to other filters in most images and almost all Gaussian noise standard deviation levels has the highest value. After P2_GSK, the P2_WOA filter has better performance than the others. In some images, for some levels of Gaussian noise standard deviation, the BW_PSO filter performed better.

As shown in Table 6, the highest EPF values of the filters are marked in bold and vary in different images and different standard deviations of Gaussian noise.

To accurately compare the performance of filters with different images and for different levels of Gaussian noise standard deviation, in terms of criteria like PSNR, SSIM, FOM, and EPF, Friedman's algorithm is used, which is mentioned in “Mask Design Using the GC Function”.

It is clear from Fig. 3 that the images “l” and “n” obtained by P2_WOA and P2_GSK filters respectively; for all standard deviations of Gaussian noise perform better than other images in noise reduction.

The exact process applies to all images with SAP noise. At first, all images are corrupted with a density of 0.02, 0.03, and 0.05 SAP noise. The noisy images are de-noised with the abovementioned filters, and the noiseless images have been obtained. Since the SAP noise affects some pixels of the image, it should not be directly applied to the designed filters. To create a unique procedure with Gaussian-noised images, the proposed filters are also applied to all the pixels of the image contaminated with SAP noise. The PSNR, SSIM, FOM, and EPF values are calculated to compare noise reduction filters.

As shown in Tables 7, 8, 9, 10, according to all criteria, the median filter and the P2_WOA filter have better results in some images and some noise densities. To check the performance of filters in terms of PSNR, SSIM, FOM, and EPF in the presence of SAP noise, Friedman’s algorithm explained in “Mask Design Using the GC Function” is used, the results of which are placed in Table 13.

Table 7 The PSNR results for SAP noise reduction

Table 8 The SSIM results for SAP noise reduction

Table 9 The FOM results for SAP noise reduction

Table 10 The EPF results for SAP noise reduction

Figure 5 displays the practical results in the House, Peppers, and Couple images, which have been corrupted with SAP noise densities of 0.02, 0.03, and 0.05, respectively. In Fig. 5, “$a, \, b, \, c, \, d, \, e, \, f, \, g, \, h, \, i, \, j,k$, and $l$“ are the images represented by “Original,” “Noisy,” “Mean filter,” “Gaussian filter,” “Median filter,” “Wiener filter,” “NLM filter,” “GC_PSO filter,” “BW_PSO filter,” “BA_PSO filter,” “P1_WOA filter,” and “P2_WOA filter” respectively. As shown in Fig. 5, the median and P2_WOA filters not only remove the noise but also maintain image quality, unlike the other methods that cause a loss of image quality. Therefore, it can be concluded that the P2_WOA filter performs better than the other filters after the median filter.

Fig. 5

Images before and after SAP noise reduction

To investigate the effect of the proposed filters on real-world problems, we not only examined their impact on standard images corrupted with Gaussian noise or SAP noise but also considered a medical image (Brains MRI with dimensions of 454 × 448) corrupted by various standard deviations of Gaussian noise. We applied the mentioned filters to the image and calculated criteria such as PSNR, SSIM, FOM, and EPF. The results were then recorded in Table 11.

Table 11 All considered criteria results for Gaussian noise reduction of Brains MRI image

In Table 11, the highest values of the criteria are marked in bold. To determine which filter performs better for all standard deviations of Gaussian noise, Friedman's method is applied for each criterion and the results are listed in Table 14.

Statistical Analysis

Two non-parametric statistical hypothesis tests are utilized to examine the quality and performance of algorithms, such as the Friedman test and the multi-problem Wilcoxon signed-rank test [69]. The null assumption represents no meaningful divergence between the proficiency of the methods, and the alternative assumption is the opposite of the null assumption. According to the obtained p-value, it is decided to reject or accept the null assumption. If the p-value exceeds 0.05, the null assumption is accepted; otherwise, it is rejected.

For all standard deviations of Gaussian noise, the mean rank of the de-noising filters is obtained in different images using the Friedman test regarding the PSNR, SSIM, FOM, and EPF. Columns 2 to 5 and 8 to 12 of Tables 12 and 13 list the mean rank of the filters for all standard deviations of Gaussian noise according to the Friedman test. The 6th and 12th column of Tables 12 and 13 shows the overall mean rank of the filters obtained by Friedman's test, and the 7th and last columns deal with the ranking of the filters. The p-value computed through the Friedman test is zero and less than 0.05. Thus, we can conclude that there is a significant difference between the performances of the algorithms.

Table 12 Friedman test results for Gaussian noise removal

Table 13 Friedman test results for SAP noise reduction

According to the 7th column of the first and second parts of Table 12, P2_GSK, P2_WOA, and BW_PSO filters have the first to third rank, respectively, in terms of SSIM and PSNR. P1_WOA and P1_GSK filters have the fourth rank regarding SSIM and PSNR, respectively. The following ranks are assigned to other filters; the Gaussian filter has the lowest rank. By paying attention to filters with lower rankings, it is understandable that the Gaussian, NLM, and median filters are not appropriate for eliminating Gaussian noise on average. As the first part of Table 12, the last column shows, the P2_GSK filter has the highest Mean ranking in terms of FOM, and P2_WOA, BW_PSO, P1_GSK, and P1_WOA filters have the second to fifth rank, respectively. The BA_PSO and GC_PSO filters have lower rankings on average and perform poorly in terms of FOM. In the last columns of the second section of Table 12, the P2_GSK filter has the highest EPF ranking, and the P2_WOA, P1_GSK, and P1_WOA filters have the second to fourth ranking. Generally, it can be said that the P2_GSK filter has the highest ranking concerning all of the measures, and after that, the P2_WOA filter has a better performance. The BW_PSO filter has the third rank in terms of PSNR, SSIM, and FOM and the fourth rank in terms of EPF. Considering all criteria, filters P2_GSK, P2_WOA, BW_PSO, P1_GSK, P1_WOA, Wiener, BA_PSO, GC_PSO, “Mean = NLM,” Median, and Gaussian, respectively have the best performances. It is clear that the GC_PSO filter has a weaker performance than all the proposed methods, and the P2_GSK and P2_WOA filters have a better performance than all other filters. Generally, it can be said that filters based on evolutionary algorithms work better than other filters. As the results show, the GSK algorithm performs better than the WOA algorithm on the proposed filters, which shows the GSK algorithm's superiority in noise removal.

As shown in column 2, parts 1 and 2 of Table 13, for the noise density of 0.02, on average, in all images, the P2_WOA filter, the Median filter, and the BA_PSO filter have the first to third ranking in terms of PSNR and SSIM, respectively. Similarly, for the noise density of 0.03, the Median filter, the P2_WOA filter, and the BA_PSO filter have the first to third ranking regarding PSNR and SSIM, respectively. For the noise density of 0.05, the Median, the P2_WOA, and the BW_PSO filters have the first to third ranking in PSNR and SSIM, respectively. According to the 6th column, parts 1 and 2 of Table 13, for all noise densities, it is determined that in terms of PSNR and SSIM, the Median, the P2_WOA, and the BA_PSO filters are ranked first to third, respectively. According to parts 1 and 2 of the 7th column of Table 13, for the noise density of 0.02, the FOM and the EPF values of the P2_WOA, the Median, and the NLM filters are ranked first to third, respectively. For the noise density 0.03, on average, the FOM mean rank of the Median and P2_WOA will be the same and equal to one, and the NLM and the BW_PSO filters are ranked second to third, respectively, and in terms of EPF, the P2_WOA, the Median, and the P1_WOA filters are ranked first to third, respectively. For the noise density of 0.05, on average, in terms of FOM, the Median, the P2_WOA, and the NLM are ranked first to third, respectively, and in terms of EPF, the Median filter ranks first, the P1_WOA and P2_WOA filters have the second rank simultaneously, and the NLM filter ranks third. According to section 1 of the last column of Table 13, the Median and the P2_WOA filters both have the first rank in terms of FOM, the NLM and the BW_PSO are located in the second to the third rank, respectively, the BA_PSO has the fourth rank, the Wiener, the Gaussian, the P1_WOA, the Mean, and the GC_PSO filters are placed in the fifth to ninth rank, respectively. On average, the P2_WOA, the Median, and the P1_WOA filters are ranked first to third in terms of EPF, respectively, and the NLM, the GC_PSO, the Gaussian, the BA_PSO, the BW_PSO, the Wiener, and the Mean filters are ranked fourth to tenth, respectively as shown in last column of section 2 of Table 13. Based on all criteria, the Median, the P2_WOA, the BA_PSO, the BW_PSO, the P1_WOA, the NLM, the GC_PSO, the Gaussian, the Wiener, and the Mean filters perform better in reducing SAP noise, respectively. It can be concluded that based on all criteria, the median filter is an efficient filter to remove SAP noise, and after that, the P2_WOA filter is efficient.

Table 14 columns 2 to 5, denotes the mean rank of filters, the higher values are bolded and indicate the filter's better performance. The 6th column of Table 14 shows the mean rank according to all considered criteria, and the last column shows the ranking of the filters. As the last column of Table 14 shows, the P2_GSK method performs better than other filters in Gaussian noise reduction, followed by the P2_WOA filter. In general, the first proposed method was not successful in the noise removal of this image, and bilateral-based filters are better than other filters. Figure 6 shows the results of the proposed filters on the brain MRI image. In that figure, a, b, c, and d represent the original image, noisy (with different standard deviations) images, and filtered-out images with P1_GSK and P2_GSK, respectively.

Table 14 Friedman test results for Gaussian noise reduction in Brains MRI image

Fig. 6

Brains MRI Images before and after Gaussian noise reduction

A multi-problem Wilcoxon signed-rank test is used to check the differences between all algorithms. In this method, S + represents the sum of ranks for all images, which describes the first algorithm performs better than the other one, and S − indicates the opposite of the previous one. Larger ranks indicate more considerable performance differences. The p value is used for comparison. The null hypothesis is rejected if the p value is less than or equal to the assumed significance level of 0.05. The following results show the p values and decisions corresponding to the p values in bold, and the test is performed with SPSS 26.00. For each standard deviation of Gaussian noise, the performance of the GSK-based proposed filters is compared to other filters in terms of SSIM, PSNR, FOM, and EPF using the Wilcoxon method and listed in Tables 15, 16, 17, 18.

Table 15 The results of the Wilcoxon test, according to SSIM

Table 16 The results of the Wilcoxon test, according to PSNR

Table 17 The results of the Wilcoxon test according to FOM

Table 18 The results of the Wilcoxon test, according to EPF

In Tables 15, 16, 17, 18 the 7th and 13th columns (F1?F2) represent the efficiency between two filters. For $\sigma = 20,50,70$ according to the 7th column of Tables 15 and 16, P2_GSK outperforms other filters in terms of SSIM and PSNR except for the P2_WOA filter. For $\sigma = 30$, P2_GSK outperforms all other filters. As the 7th column of Table 17 shows $\sigma = 20$, P2_GSK is better than other filters in terms of FOM, except Wiener and P2_WOA filters. For $\sigma = 30$, P2_GSK is better than other filters, except the BW_PSO filter. For $\sigma = 50$, P2_GSK is better than other filters, except BW_PSO and P2_WOA filters. For $\sigma = 70$, P2_GSK acts better than all other filters.

As the 7th column of Table 18 shows, the following results were obtained in terms of EPF: $\sigma = 20$, P2_GSK is better than other filters, except NLM, BW_PSO, and P2_WOA filters. For $\sigma = 30,50$, P2_GSK is better than other filters, except P1_WOA, P2_WOA, and P1_GSK filters. For $\sigma = 70$, P2_GSK acts better than other filters, except Wiener, P1_WOA, P2_WOA, and P1_GSK filters. In general, it can be concluded that the P2_GSK filter performs better than other methods on average in terms of all criteria, and this shows the superiority of the GSK-based proposed filter.

According to the 13th column of Table 15, which shows the results of the Wilcoxon method for the P1_GSK filter in terms of SSIM, we have: for $\sigma = 20$, P1_GSK is better than Mean, Gaussian and Median filters, but it is weaker than Wiener, BW_PSO, BA_PSO, P2_WOA, and P2_GSK filters, and P1_GSK does not have the significant difference with NLM, GC_PSO, and P1_WOA filters. For $\sigma = 30$, P1_GSK is better than Mean, Gaussian, Median, Wiener, NLM, and GC_PSO filters, but it is weaker than BW_PSO, P2_WOA, and P2_GSK filters, P1_GSK does not have a significant difference with BA_PSO, and P1_WOA filters. For $\sigma = 50$, P1_GSK is better than Mean, Gaussian, Median, Wiener, NLM, GC_PSO, and BA_PSO filters, but it is weaker than BW_PSO, P2_WOA, and P2_GSK filters; it does not have a significant difference with P1_WOA filter. For $\sigma = 70$, P1_GSK is better than Mean, Gaussian, Median, Wiener, NLM, GC_PSO, and BA_PSO filters, but it is weaker than P1_WOA, P2_WOA, and P2_GSK filters, and it does not have a significant difference with BW_PSO filters.

According to the 13th column of Table 16, which shows the results of the Wilcoxon method for the P1_GSK filter in terms of PSNR, we have: for $\sigma = 20$, P1_GSK is better than Mean, Gaussian, Median, and GC_PSO filters, but it is weaker than BW_PSO, BA_PSO, P2_WOA, and P2_GSK filters, and it does not have the significant difference with Wiener, NLM, and P1_WOA filters. For $\sigma = 30$, P1_GSK is better than Mean, Gaussian, Median, Wiener, NLM, GC_PSO, and P1_WOA filters, but it is weaker than BW_PSO, P2_WOA, and P2_GSK filters, and it does not have a significant difference with BA_PSO filter. For $\sigma = 50,70$, P1_GSK is better than Mean, Gaussian, Median, Wiener, NLM, GC_PSO, BA_PSO, and P1_WOA filters, but it is weaker than P2_WOA and P2_GSK filters, and it does not have a significant difference with BW_PSO filter.

According to the 13th column of Table 17, which shows the results of the Wilcoxon method for the P1_GSK filter in terms of FOM, we have: for $\sigma = 20$, P1_GSK is better than Gaussian, and GC_PSO filters, but it is weaker than Mean, Wiener, NLM, BW_PSO, BA_PSO, P2_WOA, and P2_GSK filters, and it does not have the significant difference with Median and P1_WOA filters. For $\sigma = 30$, P1_GSK is better than Gaussian, Median, GC_PSO, BA_PSO, and P1_WOA filters, but it is weaker than BW_PSO, P2_WOA, and P2_GSK filters, and it does not have a significant difference with Mean, Wiener, and NLM filters. For $\sigma = 50$, P1_GSK is better than Mean, Gaussian, Median, Wiener, NLM, GC_PSO, and BA_PSO filters, but it is weaker than BW_PSO, P2_WOA, and P2_GSK filters, and it does not have a significant difference with P1_WOA filter. For $\sigma = 70$, P1_GSK is better than Mean, Gaussian, Median, Wiener, NLM, GC_PSO, BA_PSO, and P1_WOA filters, but it is weaker than P2_WOA and P2_GSK filters, and it does not have a significant difference with BW_PSO filter.

According to the 13th column of Table 18, which shows the results of the Wilcoxon method for the P1_GSK filter in terms of EPF, we have: for $\sigma = 20$, P1_GSK is better than Mean and Median filters. However, it is weaker than NLM, BA_PSO, P2_WOA, and P2_GSK filters, and it does not have a significant difference with Gaussian, Wiener, GC_PSO, BW_PSO, and P1_WOA filters. For $\sigma = 30$, P1_GSK is better than Mean, Gaussian, and Median filters, and it does not have a significant difference with Wiener, NLM, GC_PSO, BW_PSO, BA_PSO, P1_WOA P2_WOA, and P2_GSK filters. For $\sigma = 50$, P1_GSK is better than Mean, Gaussian, Median, NLM, GC_PSO, and BA_PSO filters, and it does not have a significant difference with Wiener, BW_PSO, P1_WOA, P2_WOA, and P2_GSK. For $\sigma = 70$, P1_GSK is better than Mean, Median, GC_PSO, and BA_PSO filters, and it does not have a significant difference with Gaussian, Wiener, NLM, BW_PSO, P1_WOA, P2_WOA, and P2_GSK filters. On average, it can be concluded that the P1_GSK performs better than the P1_WOA and GC_PSO filters.

Algorithms Complexity

The computational complexity of the de-noising filters is described below:

$$O\left( {N_{{{\text{iter}}}} \times N_{{{\text{pop}}}} \times O\left( {{\text{fitness}}} \right)} \right),$$

(33)

where $N_{{{\text{iter}}}}$ and $N_{{{\text{pop}}}}$ indicate the maximum number of iterations and population size, respectively.

In algorithms that neighboring radius “$r$” and mask size “$w$” are considered as optimization parameters like BW_PSO, P1_WOA, P2_WOA, P1_GSK, and P2_GSK $O\left( {fitness} \right)$ is as follows:

$$O\left( {{\text{fitness}}} \right) = O({\text{Image}}_{{{\text{size}}}} \times w_{{{\text{size}}}} )$$

$$w_{{{\text{size}}}} = w \times w\;{\text{or}}\;w_{{{\text{size}}}} = (2r + 1) \times (2r + 1),{\kern 1pt} \,r = 1,2, \ldots$$

(34)

In other algorithms like GC_PSO and BA_PSO, the computational complexity of the fitness function “$O\left( {fitness} \right)$“ is as follows:

$$O\left( {{\text{fitness}}} \right) = O({\text{Image}}_{{{\text{size}}}} )$$

(35)

where ${\text{Image}}_{{{\text{size}}}}$ describes the size of an image.

The execution time of nature-inspired filters depends on factors such as the number of iterations, population size, the number of parameters, the length of variable ranges, and window size, whether fixed or considered an optimization parameter. Therefore, the execution time of P2_WOA and P2_GSK filters will be longer than others because these algorithms must optimize the number of 7 parameters. The execution time of P1_WOA and P1_GSK filters is also more than GC_PSO because the mask size is an optimization parameter. Regardless of the variables range, the execution time of the BW_PSO filter is more extended than BA_PSO since the neighboring radius is an optimization parameter. One of the variable ranges in both BW_PSO and BA_PSO filters is the same. However, the size of the second variable ranges in the BW_PSO filter is smaller than that of the second variable ranges in the BA_PSO filter, increasing the processing speed. However, in the BW_PSO method, the radius of the neighborhood is variable, which increases the evaluation time of this algorithm. In general, considering the same variable ranges for both filters, “BW_PSO and BA_PSO filters,” the execution time of the BW_PSO will be longer due to the variable neighboring radius. The execution time of the filters is listed in Table 19. All computations were implemented and executed using MATLAB R2012b running on a PC with core i5-2410 M (2.30 GHz) CPU and 4 GB RAM running Win7 OS.

Table 19 The execution time of filters

Table 19 shows that the execution time of P2_GSK and P2_WOA filters are more extended than all filters, and subsequently, the execution time of BW_PSO and BA_PSO filters is longer. The execution time of P2_GSK and P1_GSK filters is longer than P2_WOA and P1_WOA, respectively. This shows that the GSK algorithm is faster than WOA.

Convergence Curve

Figure 7 illustrates the convergence attributes based on the fitness of all algorithms to analyze the convergence attitude of algorithms. For instance, the convergence rate of algorithms $\sigma = 20$ in the ‘Couple’ image is represented. In Fig. 7, “a, b, c, d, and e” represent the convergence rates of GC_PSO, BW_PSO, BA_PSO, P1_WOA-P2_GSK, and P1_WOA-P1_GSK filters, respectively. The GSK-based filter convergence velocity is higher in the initial stages of the optimization procedure.

Fig. 7

Convergence curve of the algorithms

In fact, due to the use of the generalized Cauchy function instead of the Gaussian function in the spatial and intensity domain of the bilateral filter, which is a heavy-tailed function compared to the Gaussian function, and neighboring radius optimization, the second proposed filter performs better than other filters. Since the mask size optimization is considered in the first proposed filter, this filter performs better than the GC_PSO filter. On the other hand, this filter has a weaker performance than the second filter because the generated mask is swept over the noisy image and does not consider spatial information of the image pixels. Because the neighborhood radius is optimized in the BW_PSO filter, this filter has a more robust performance than the BA_PSO filter. One of the disadvantages of the second proposed filter is its long execution time compared to the first one.

Conclusion and Future Directions

To summarize, we present two effective WOA-based and GSK-based filters for noise reduction. The GSK's novelty, the lack of widespread application in image processing, and the ability to solve complex and large-scale problems, as well as WOA's ability to solve image processing problems, have led to the use of GSK and WOA in this research. Since the constancy of the selected mask size can affect the efficiency of the filter made by the GC function. First, a mask was designed using the GC function, and the parameters of this function and the size of the chosen mask were optimized by maximizing the PSNR value as the fitness function with WOA and GSK. In most bilateral-based designed filters, the neighborhood radius is constant and the parameters of the intensity and spatial domain, are the Gaussian function parameters that should be optimized. The similar and better performance of the GC function in noise removal, compared to the Gaussian function, as well as the lack of its usage in the bilateral filter in previous works, has caused it to be used in the bilateral filter. So, a hybrid filter was designed by replacing the GC function with a Gaussian function in the bilateral filter, and the domain and range parameters of the GC function, as well as the size of the neighboring radius, were optimized by maximizing the PSNR as a fitness function using WOA and GSK. The GSK and WOA-based proposed filters are compared with each other and classical filters, as well as the PSO-based GC filter and two PSO-based bilateral filters (BW_PSO, BA_PSO) on various images corrupted with a different standard deviation of Gaussian noise. Also, a comparison is made between the WOA-based proposed filters and other filters on images corrupted with various densities of the SAP noise. On average, the superior performance of the P2_GSK and P2_WOA filters is achieved in terms of PSNR and SSIM in Gaussian noise removal. However, the P1_GSK and P2_GSK filters have a more robust performance than those of P1_WOA and P2_WOA in Gaussian noise removal. Following the P2_GSK and P2_WOA filters in terms of PSNR and SSIM, the BW_PSO, P1_GSK, P1_WOA, BA_PSO, and GC_PSO filters work better than traditional methods in Gaussian noise removal. It was also found that as the Gaussian noise standard deviation increased, the parameters of the GC function were quantified by the WOA (or GSK) so that the GC distribution curve was closer to the Gaussian distribution curve. However, the tail was heavier than the Gaussian distribution. Since the mean ranking of the P2_GSK and P2_WOA filters is high in terms of the FOM and EPF, the second proposed method preserves the edges and structural details of the image. The P1_GSK filter performs better than P1_WOA in terms of EPF, and in terms of FOM, it performs better than P1_WOA either. In general, it can be said that the second proposed filter is better than all other filters in terms of PSNR, SSIM, FOM, and EPF. The first proposed filter is also better than all other filters in terms of PSNR, SSIM, and EPF, and in terms of FOM, they are better than other filters after BW_PSO and Wiener.

In the SAP noise removal, after the median filter, the P2_WOA filter is more efficient than other methods, and after these filters, the BA_PSO, the BW_PSO, the P1_WOA, and the GC_PSO methods work better than classical filters in terms of PSNR and SSIM. The P2_WOA filters out the SAP noise and after the median filter is better than all other filters in terms of EPF and FOM.

The P1_WOA filter performs better than other filters in terms of EPF, and in terms of FOM performs weaker than NLM, BW_PSO, BA_PSO, Wiener, and Gaussian filters in SAP noise removal. According to the obtained results, it can be said that the second proposed filter performs better than other filters in SAP noise removal after the median filter, and the first proposed filter is weak in removing the SAP noise compared to other filters. In other words, the proposed filters are not suitable for SAP noise reduction.

The results obtained in “Statistical Analysis” on brain MRI images indicate that the second proposed filter with GSK and WOA algorithm works better than other filters in terms of all criteria. The second proposed filter is ranked fifth with the GSK algorithm and seventh with the WOA algorithm. In general, the proposed filters with the GSK algorithm perform better than the WOA algorithm. However, the first proposed filter is more successful in removing the noise than the second proposed filter.

Since both the neighborhood radius and the parameters of the GC function are optimized instead of the parameters of the Gaussian function in the bilateral filter, and considering that the GC function has a better performance compared to the Gaussian function, the second proposed filter performs better than other filters. The selected mask size is optimized in the first proposed filter, so this filter is better than the GC_PSO method. GSK-based filters get the first ranking among all other filters. Non-parametric tests like Friedman's and Wilcoxon's tests are utilized to statistically evaluate the performance of proposed filters with a significance level of 0.05. The results of the used non-parametric tests show that the GSK-based proposed filters are better than WOA-based filters.

One of the advantages of the proposed filters is the significant noise reduction and their easy design. GSK-based filters are more robust and faster, which is one of their advantages. One of the disadvantages of the second proposed filter is its long execution time, and another disadvantage is the lack of precise upper and lower bounds of the GC function parameters. A method can be investigated for future work to find the exact limits for the parameters. Adaptive meta-heuristic algorithms can also be used to increase the convergence speed. Algorithms can also be used to avoid premature convergence, local optimal trapping, and imbalance between exploration and exploitation. Implementing the proposed method for filtering other noise types, such as speckle noise, is also possible. Also, the proposed methods can be examined on color, ultrasound, and satellite images.