Iterative Respacing of Polygonal Curves

Abstract

A polygonal curve is a collection of m connected line segments specified as the linear interpolation of a list of points $\{p_0, p_1, \ldots , p_m\}.$ In applications it can be useful for a polygonal curve to be equilateral, with equal distance between consecutive points. We present a computationally efficient method for respacing the points of a polygonal curve and show that iteration of this method converges to an equilateral polygonal curve.

Introduction

A polygonal curve (also polygonal chain or polygonal path) is a collection of m connected line segments specified by a sequence of points $\{p_0, p_1, \ldots , p_m\}$ in ${\mathbb {R}}^n$ called vertices. In computer vision, polygonal curves arise as piecewise linear representations of digital curves, and serve as effective tools for shape analysis [8]. A fundamental step in determining these representations is polygonal curve approximation: for a give polygonal curve C,  we must find another polygonal curve ${\overline{C}}$—often subject to constraints or other conditions—which is sufficiently close to C. Polygonal curve approximation is often concerned with minimizing the error between C and ${{\overline{C}}},$ or minimizing the number of vertices in ${{\overline{C}}}.$ Extensive literature is devoted to these objectives; most notably the classical algorithms of Ramer–Douglas–Peucker and Imai and Iri [6, 11, 12, 14].

An equilateral polygonal curve is a polygonal curve for which all Euclidean distances between consecutive points, $\Vert p_{k} - p_{k-1}\Vert ,$ $k = 1, \ldots , m,$ are equal. Equilateral polygonal curves are useful in the context of shape analysis for object reassembly, where they can be directly compared to determine possible congruence [3, 18]. When these equilateral curves represent the boundaries of fragmented objects, these congruences suggest how these objects may fit together. For example, this approach has been used for the automated reassembly of jigsaw puzzles and broken eggs [7, 9, 10].

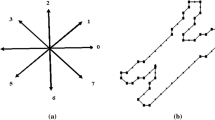
The present work considers a method for polygonal approximation with equilateral (or nearly equilateral) polygonal curves. There is extensive literature on polygonal approximation by curves satisfying various constraints, e.g., [2, 4, 17], but very few that apply an equilateral constraint. One of the few existing works on this topic [15], uses a nonlinear optimization process to compute an equilateral curve that minimizes a weighted distance from vertices of the original curve. In this work, we take a different tack with a similar goal: by sampling a given polygonal curve according to a fixed arclength measurement, we create a new polygonal curve which is close to the original and has more regularly spaced vertices (illustrated in Fig. 1). As we will show, repeating this resampling process creates curves with increasing regularity in the spacing of their vertices, limiting to an equilateral curve. In contrast to most other studies of polygonal approximation, we do not attempt to minimize any kind of distance in the approximation, nor do we impose any constraints on the approximating curve. Instead our goal is to understand the effect of our repeated resampling process from theoretical and empirical viewpoints.

The layout of this paper is as follows. In “The Arclength Respacing Method” we introduce the arclength respacing process for a polygonal curve, outline its implementation, and establish some of its key properties. In “Iteration of the Respacing Method” we consider iteration of arclength respacing and show in Theorem 11 that the iteration tends toward a limiting polygonal curve and that the limit is equilateral. In “Examples” we examine various examples. In “Application” we illustrate the effect of arclength respacing on polygonal curves approximating a shape.

Fig. 1

Unevenly spaced polygonal curve (left) and the polygonal curve that results after one application of arclength respacing (right)

The Arclength Respacing Method

Let C be a polygonal curve with vertices $\{p_0, p_1, p_2, \ldots , p_m\}.$ Curves will be visualized in ${\mathbb {R}}^2,$ but all discussion that follows applies equally to curves in ${\mathbb {R}}^n.$ We make no restrictions on the points that define C; for example, polygonal curves may be closed (have an overlapping startpoint and endpoint) or otherwise have self-intersections or overlapping vertices. Denote by $L(C) = \sum _{k=1}^m \Vert p_k - p_{k-1} \Vert$ the length of C. Let P(s) be the linear interpolation of the vertices of C,  parameterized by arclength s,  such that $0 \le s \le L(C).$ We now define the process that we will study in the following sections: the arclength respacing of a polygonal curve.

Definition 1

The arclength respacing of the polygonal curve C is the polygonal curve f(C) with vertices $\{f(p_0), \ldots , f(p_m) \}$ evenly spaced by arclength along C: 

$$\begin{aligned} f(p_k) = P\left( k \frac{L(C)}{m} \right) , \quad k = 0, \ldots , m. \end{aligned}$$

An example result of arclength respacing is shown in Fig. 2.

Fig. 2

Polygonal curve C and its arclength respacing f(C)

It is important to note that arclength respacing can be performed computationally without costly numerical integration or function inversion typically needed to find an arclength parameterization. The key idea is that piecewise linearity can be exploited to find P(s). Let $d_0 = 0$ and $d_k = \sum _{i=1}^{k} \Vert p_{i}-p_{i-1} \Vert$ the arclength of C up to vertex $d_k$ for $k=1, \ldots , m.$ Then, when $d_k \ne 0,$ for $0 \le t \le 1$ and $k = 1, \ldots , m,$ the parameterizations of segments:

$$\begin{aligned} P\big ( (1-t) d_{k-1} + t d_k \big ) = (1-t) p_{k-1} + t p_{k} \end{aligned}$$

can be combined to provide an arclength parameterization P(s) of C. Thus it is possible to compute f(C) from C quickly using only linear interpolation. We now outline this process in more detail.

Algorithm 2

An outline of the implementation of arclength respacing. An example implementation in Mathematica can be found on the third author’s website [19].

Input: Points $\{p_0, \ldots , p_m\}$ representing the vertices of a polygonal curve C.

Output: Points $\{q_0, \ldots , q_m\}$ representing the arclength respacing f(C) of C.

• 1. Let $d_0 = 0$ and $d_k = \Vert p_k - p_{k-1}\Vert + d_{k-1}$ for $k=1, \ldots m.$ $d_k$ is the piecewise linear arclength distance from $p_0$ to $p_k.$

• 2. Compute the piecewise linear interpolating function $g:[0,d_m] \rightarrow [0,m]$ for the points $(d_k,k),$ $0 \le k \le m.$ This function inverts the arclength measurements, so that $g(d_k) = k.$ Here we require $p_k \ne p_{k+1}$ in order for this inverse to be well defined.

• 3. Compute the piecewise linear interpolating function $h:[0,m] \rightarrow {\mathbb {R}}^2$ for the discrete curve points $p_0, \ldots , p_m.$

• 4. Let $\delta = d_m/m$ and define $q_k = h(g(k \delta ))$ for $k = 0, 1, \ldots , m.$ The points $q_k$ are separated by an arclength distance of $\delta$ along C. These points are the vertices of f(C).

Remark 3

Note that in Step 2 of Algorithm 2, the linear interpolation of the inverted arclength distances is key to avoiding inefficient arclength integral computations when performing arclength respacing. In addition, note that the distance of $\delta$ in Step 4 can be chosen to fit the application. For example, one could choose the same $\delta$ across a collection of curves to have consistent arclength spacing for curve comparison. Finally, since each step of Algorithm 2 involves a fixed time computation done at each of the m points of C,  the algorithm has a run time which is O(m).

Polygonal curves with different vertex sets can have the same arclength parameterized linear interpolation. To account for this ambiguity, we introduce the notion of similar polygonal curves.

Definition 4

A vertex $p_k$ of a polygonal curve is called a basic vertex if it is not equal to the preceding vertex $p_{k-1}$ and does not lie on the line segment between its neighboring vertices $p_{k-1}$ and $p_{k+1}.$ Polygonal curves P and Q are similar, $P \sim Q,$ if they share the same sequence of basic vertices. Note that the initial vertex $p_0$ is always basic.  Two similar polygonal curves are shown in Fig. 3.

Fig. 3

Two similar polygonal curves with different vertices

Lemma 5

Similar polygonal curves have the same arclength parameterized linear interpolation.

Proof

If $p_k$ is a non-basic vertex, either $p_{k-1} = p_k,$ or $p_k$ lies in the image of the line segment connecting $p_{k-1}$ and $p_{k+1}.$ In either case, removing $p_k$ from the vertex set of C will not affect the arclength parameterized linear interpolation (we either remove a segment of length zero or replace two segments with one segment of combined length). Thus the arclength parameterized linear interpolation is determined only by the basic vertices, and similar curves have the same basic vertices. $\square$

We now investigate how the process of arclength respacing changes a polygonal curve. In particular, we find in Proposition 8 that similarity characterizes particular ways that the length and spacing of a polygonal curve change under arclength respacing. We first prove a simple lemma about a more general respacing process we call oriented resampling, of which arclength respacing is a special case.

Definition 6

Let C be a polygonal curve and P(s),  $0 \le s \le L(C),$ the associated arclength parameterized linear interpolation of the vertices of C. Suppose we sample $m+1$ values of arclength $0=s_0 \le s_1 \le \cdots \le s_{m-1} \le s_m = L(C)$ and define a corresponding sample of points $q_0, \ldots , q_m$ along C such that $q_k = P(s_k),$ for $k=0, \ldots , m.$ The polygonal curve D defined by the vertex set ${q_0, \ldots , q_m}$ is called an oriented resampling of P.

Lemma 7

If D is an oriented resampling of C,  then $L(D) \le L(C).$ In particular, $L(f(C)) \le L(C),$ so arclength respacing cannot increase the length of a polygonal curve.

Proof

We use the notation of Definition 6. First observe that $\Vert q_k - q_{k-1}\Vert \le s_k - s_{k-1},$ since $s_k - s_{k-1}$ is the arclength distance between points $q_{k-1}$ and $q_k$ measured along C. Thus

$$\begin{aligned} \begin{aligned} L(D)&= \sum _{k=1}^m \Vert q_k - q_{k-1} \Vert \\&\le \sum _{k=1}^m s_k - s_{k-1} \\&= s_m - s_0 = L(C). \end{aligned} \end{aligned}$$

$\square$

Proposition 8

Let C be a polygonal curve and f(C) the arclength respacing of C. The following properties are equivalent:

• (1) $L(C) = L(f(C)),$

• (2) $C \sim f(C),$

• (3) f(C) is equilateral.

Proof

We first show $(1) \iff (2).$ If $C \sim f(C)$ then $L(f(C)) = L(C)$ by Lemma 5. Suppose then that $f(C) \not \sim C.$ There must then be a vertex $p_k$ of C which is not equal to any vertex of f(C),  nor lies on a line segment connecting two consecutive vertices of f(C). Suppose that $q_n$ and $q_{n+1}$ are the vertices of f(C) immediately preceding and following $p_k$ along C. Let $p_l$ be the vertex of C immediately preceding $q_n$ along C and $p_r$ the vertex immediately following $q_{n+1}$ along C. Let

$$\begin{aligned} {{\overline{C}}} = \{ p_0, \ldots , p_l, q_n, q_{n+1}, p_r, \ldots , p_m\} \end{aligned}$$

be the polygonal curve obtained from C by adding the vertices $q_n, q_{n+1}$ to C and deleting all vertices $p_{l+1},\ldots , p_k,\ldots , p_{r-1}$ between $q_n$ and $q_{n+1}$ along C. Because these deleted vertices do not all lie along the line segment connecting $q_n$ and $q_{n+1}$ (in particular, $p_k$ does not), we have the strict inequality: $L({{\overline{C}}}) < L(C).$ Since the arclength respacing f(C) is also an oriented resampling of ${{\overline{C}}},$ $L(f(C)) \le L({{\overline{C}}})$ by Lemma 7. Combining these two inequalities gives $L(f(C)) < L(C).$

We next show $(2) \iff (3).$ Suppose first that $C\sim f(C).$ Then, by Lemma 5, C and f(C) have the same arclength parameterized linear interpolation. Thus a sampling of points evenly spaced along C by arclength will also be evenly spaced by arclength along f(C),  so f(C) will be equilateral.

Assume now that f(C) is equilateral. Because there are $m+1$ points in f(C) and m line segments in C,  there must be a pair of consecutive vertices $q_k,q_{k+1}$ of f(C) which lie on the same line segment of C. Thus $\Vert q_{k+1}-q_k\Vert = L(C)/m.$ Because f(C) is equilateral, we also have $\Vert q_{k+1}-q_k\Vert = L(f(C))/m.$ Thus $L(C) = L(f(C)),$ and so $C \sim f(C)$, since we have already established that $(1) \implies (2).$ $\square$

We now examine what happens when the arclength respacing process is repeated. First observe that, although the vertices of f(C) are equally spaced by arclength along C,  they are not necessarily equally spaced by arclength along f(C). Thus f(C) is not necessarily an equilateral polygonal curve. Nevertheless, it appears that vertices of f(C) are more evenly spaced than those of C (as seen clearly in Fig. 1). Thus, in an effort to obtain an equilateral curve, we can iterate the arclength respacing process, hoping to obtain polygonal curves that are increasingly close to being equilateral. The result of iterated arclength respacing is considered in the next section.

Iteration of the Respacing Method

Let C be a polygonal curve and denote by $C^n$ the $n^{th}$ iteration of the arclength respacing: $C^n = f^n(C).$ Lemma 7 yields an immediate observation about this iteration: the sequence of lengths of the iterated curves must converge.

Lemma 9

$L(C^n)$ converges as $n \rightarrow \infty .$

Proof

From Lemma 7, the sequence $\left\{ L(C^n) \right\}$ is nonincreasing. This sequence is also bounded below by the distance $\Vert p_m-p_0\Vert$ between the endpoints of C. (Note that this could be 0 for a closed polygonal curve.) Thus $\left\{ L(C^n) \right\}$ is bounded and monotonic and must converge. $\square$

As demonstrated in Proposition 8, arclength respacing yields an equilateral curve only in special cases. However, arclength respacing generally produces a curve that appears closer to being equilateral (as shown in Fig. 2, for example). More precisely, as the respacing is repeated, the iterates will converge to an equilateral curve. We introduce an equivalent definition of equilateral that will be useful in proving this.

Lemma 10

$C =\{p_0, \ldots , p_m \}$ is equilateral if and only if, for $k = 1, \ldots , m:$

$$\begin{aligned} \frac{k L(C)}{m} = \sum _{i=1}^k \Vert p_i - p_{i-1}\Vert . \end{aligned}$$

Theorem 11

For any polygonal curve C,  $\lim _{n \rightarrow \infty }f^n(C)$ exists and is an equilateral curve.

Proof

We will argue that, for each $p_k,$ the sequence $\{f^n(p_k)\}_{n=0}^\infty$ converges, and thus that the limiting polygonal curve is given by $C^* = \{p^*_0, \ldots , p^*_m\},$ where $p_k^* = \lim _{n \rightarrow \infty } f^n(p_k).$ For convenience, we will use the notation $p_k^n = f^n(p_k)$ in what follows.

Let $\epsilon > 0.$ By Lemma 9 there is an N such that for all $n\ge N{:}$

$$\begin{aligned} L(C^{n})-\epsilon < L(C^{n+1}) \le L(C^{n}). \end{aligned}$$

(1)

Consider the distance $\Vert p^{n+1}_{k} - p^{n+1}_{k-1}\Vert .$ This distance must satisfy the inequality:

$$\begin{aligned} \frac{L(C^n)}{m}-\epsilon < \Vert p^{n+1}_{k} - p^{n+1}_{k-1}\Vert \le \frac{L(C^n)}{m} \end{aligned}$$

(2)

for $n\ge N$ and $k =1, \ldots , m.$ The right side of this inequality is by construction, since the points $p^{n+1}_k$ are chosen to be evenly spaced by arclength distance $\frac{L(C^n)}{m}$ along $C^n.$ For the left side, assume that there is some $k^*$ such that $\Vert p^{n+1}_{k^*} - p^{n+1}_{k^*-1}\Vert \le \frac{L(C^n)}{m}-\epsilon .$ Then

$$\begin{aligned} \begin{aligned} L(C^{n+1})&= \sum _{k=1}^m \Vert p^{n+1}_{k}-p^{n+1}_{k-1} \Vert \\&= \Vert p^{n+1}_{k^*} - p^{n+1}_{k^*-1}\Vert + \sum _{k \ne k^*}\Vert p^{n+1}_{k}-p^n_{k-1} \Vert \\&\le \frac{L(C^n)}{m}-\epsilon + (m-1)\frac{L(C^n)}{m}\\&< L(C^{n+1}), \end{aligned} \end{aligned}$$

where the last two inequalities follow from (1). This is a contradiction, and (2) follows.

Next, for $n\ge N$ and $k=1, \ldots , m,$ consider the distance between points on consecutive iterates, $\Vert p^{n+2}_k- p^{n+1}_k\Vert .$ By construction, the point $p^{n+2}_k$ is placed on $C^{n+1}$ an arclength distance of $\frac{k L(C^{n+1})}{m}$ from $p_0^{n+1}$ along $C^{n+1}.$ By definition, the point $p^{n+1}_k$ lies an arclength distance of $\sum _{i=1}^k \Vert p^{n+1}_i - p^{n+1}_{i-1} \Vert$ from $p_0^{n+1}$ along $C^{n+1}.$ Thus, the Euclidean distance $\Vert p^{n+2}_k- p^{n+1}_k\Vert$ is bounded by the difference of these arclength distances along $C^{n+1}$:

$$\begin{aligned} \Vert p^{n+2}_k- p^{n+1}_k\Vert \le \bigg | \frac{k L(C^{n+1})}{m} - \sum _{i=1}^k \Vert p^{n+1}_i - p^{n+1}_{i-1} \Vert \bigg |. \end{aligned}$$

(3)

With some rearrangement we find

$$\begin{aligned} \begin{aligned}&\bigg | \frac{k L(C^{n+1})}{m} - \sum _{i=1}^k \Vert p^{n+1}_i - p^{n+1}_{i-1} \Vert \bigg | \\&= \bigg | \sum _{i=1}^k \frac{ L(C^{n+1})}{m} - \Vert p^{n+1}_i - p^{n+1}_{i-1} \Vert \bigg | \\&\le \sum _{i=1}^k \bigg |\frac{ L(C^{n+1})}{m} - \Vert p^{n+1}_i - p^{n+1}_{i-1} \Vert \bigg |. \end{aligned} \end{aligned}$$

(4)

Now, by (1)

$$\begin{aligned} \frac{L(C^n)}{m} - \epsilon < \frac{L(C^{n+1})}{m} \le \frac{L(C^n)}{m}, \end{aligned}$$

which, combined with (2), yields

$$\begin{aligned} \bigg |\frac{ L(C^{n+1})}{m} - \Vert p^{n+1}_i - p^{n+1}_{i-1} \Vert \bigg |< \epsilon \end{aligned}$$

for $i = 1, \ldots , k.$ Thus

$$\begin{aligned} \begin{aligned} \Vert p^{n+2}_k- p^{n+1}_k\Vert&\le \sum _{i=1}^k \bigg |\frac{ L(C^{n+1})}{m} - \Vert p^{n+1}_i - p^{n+1}_{i-1} \Vert \bigg | \\&< k \epsilon . \end{aligned} \end{aligned}$$

(5)

Since m is fixed in the respacing process, this provides a uniform bound $\Vert p^{n+2}_k- p^{n+1}_k\Vert < m \epsilon$ for $k = 1, \ldots , m$ and $n \ge N,$ and thus $\lim _{n\rightarrow \infty } p_k^n$ converges for $k = 0, \ldots , m.$ (The $k=0$ case is immediate, since the initial point is always fixed.) As before, call the limit $p_k^*$ and the limiting curve $C^* = \{p_0^*, \ldots , p_m^*\}.$

Finally, we show that $C^*$ is equilateral. From (4) and (5) we see that, for $k = 1, \ldots , m,$

$$\begin{aligned} \lim _{n\rightarrow \infty } \bigg | \frac{k L(C^{n+1})}{m} - \sum _{i=1}^k \Vert p^{n+1}_i - p^{n+1}_{i-1} \Vert \bigg | = 0. \end{aligned}$$

Passing the limit, we have

$$\begin{aligned} \bigg | \frac{k L(C^*)}{m} - \sum _{i=1}^k \Vert p^*_i - p^*_{i-1} \Vert \bigg | = 0, \end{aligned}$$

and thus by Lemma 10, $C^*$ is equilateral. $\square$

Examples

Any given polygonal curve will limit to an equilateral curve; however, it appears to be difficult in general to determine the limiting equilateral curve. In this section, we look at some examples, where we know the limiting curve or can determine information about it. We will continue to use the notation $p_k^n = f^n(p_k)$ and $p_k^* = \lim _{n\rightarrow \infty } p_k^n$ from the proof of Theorem 11.

Example 12

There are polygonal curves which become equilateral precisely at iteration n. Consider three colinear vertices $p_0, p_1, p_2,$ with $p_2$ on the line segment connecting $p_0$ and $p_1.$ Let $d =\Vert p_2-p_0\Vert .$ After each iteration, $p_0$ and $p_2$ remain fixed, and $p_1$ moves a distance d/2 closer to $p_0.$ If $L(C) = n\, d,$ then C will become equilateral at precisely iteration n. This example is illustrated in Fig. 4.

Fig. 4

Polygonal curve that becomes equilateral after n iterations

It is not necessary to have colinear vertices to produce an example which becomes equilateral after finitely many iterations. Figure 5 shows a curve which becomes equilateral after exactly two iterations. It is an open question if it is possible to generalize an approach like the one shown in Fig. 5 to work for an arbitrary iteration n.

Fig. 5

Polygonal curve that becomes equilateral after two iterations

Example 13

We next consider triangles, viewed as closed polygonal curves with four vertices $\{p_0,p_1,p_2,p_3=p_0\}.$ By Theorem 11, the only possible limiting polygonal curves are a single point, or an equilateral triangle. We consider starting curves which will realize either of these possibilities.

Consider an isosceles triangle C with angle $\theta > \frac{\pi }{3}$ at $p_0,$ as shown in Fig. 6. The points $p_1$ and $p_2$ will be mapped symmetrically under iteration to points on the side opposite to $p_0.$ The angle $\theta ^n$ at $p_0^n$ will approach $\pi /3$ and C will approach an equilateral triangle.

Fig. 6

Arclength respacing iteration for an isosceles triangle with angle $\theta > \frac{\pi }{3}$ at $p_0$ converges to an equilateral triangle

Next consider a triangle C with an angle $\theta < \frac{\pi }{3}$ at the starting vertex $p_0.$ By construction, this angle does not increase under iteration, so $\theta ^{n+1} \le \theta ^{n},$ where $\theta ^n$ is the angle at the vertex $p_0^n$ of $C^n.$ Thus $C^n$ cannot approach an equilateral triangle, and must converge to a point. A special case of this is the iteration of an isosceles triangle with angle $\theta < \frac{\pi }{3}$ at $p_0,$ which will produce a sequence of similar triangles shrinking to a point, as shown in Fig. 7.

Fig. 7

Arclength respacing iteration for a triangle with angle $\theta < \frac{\pi }{3}$ at $p_0$ converges to a point

Example 14

We consider quadrilaterals, viewed as closed polygonal curves with five vertices $\{p_0,p_1,p_2,p_3,p_4=p_0\}.$ By Theorem 11, a quadrilateral must tend toward an equilateral polygonal curve, in this case a rhombus, degenerate rhombus, or a single point. If the polygonal curve $\{p_0, p_1, p_2\}$ has the same length as the polygonal curve $\{p_2,p_3,p_4\},$ the vertex $p_2$ will remain fixed under iteration. The limiting curve will be a rhombus. A special case of this is the iteration of a parallelogram, shown in Fig. 8.

Fig. 8

Parallelogram will limit towards a rhombus under iteration

Application

In this section, we empirically explore the practical effect arclength respacing has on polygonal curves approximating a given shape. We compute several measurements at the $n^{th}$ iteration of the arclength respacing to quantify this effect. Iterations should tend toward an equilateral curve, so we find the standard deviation $\sigma ^n$ of the collection of distances $d^n_k = \Vert p^n_{k} - p_{k-1}^n\Vert ,$ $k=1, \ldots , m,$ the maximum interpoint distance $\max ^n =$ $\max _{1 \le k \le n} d_k^n,$ and the minimum interpoint distance $\min ^n =$ $\min _{1 \le k \le n} d_k^n,$ as different ways to measure this effect. It is also important to understand how successive iterations retain fidelity to the original polygonal curve. Since the $\epsilon$-tolerance zone—the region consisting of the union of all radius $\epsilon$ disks centered on the polygonal curve—is a standard metric in polygonal curve approximation [5, 11, 13], we compute $\epsilon ^n,$ the smallest $\epsilon$ for which the nth iterate lies within the $\epsilon$-tolerance zone of the original polygonal curve, as measure for the accuracy of our polygonal approximation.

Fig. 9

“Noisy cat” polygonal curve after 0,  1,  and 5 iterations of arclength respacing

Shown in Fig. 9 is a synthetic “noisy cat” curve after 0,  1,  and 5 applications of respacing. The noisy cat curve consists of 65 points, with x, y values in the range $[-1,1].$ The points are visually equilateral after only a few iterations. The ears (and other smaller protrusions) become rounded, causing $\epsilon ^n$ to increase sharply, but this effect quickly diminishes. Note that the jagged point on the right side of the figure does not smooth out; this is an artifact of the choice of starting point for the respacing. As seen in Fig. 10 the standard deviation $\sigma ^n$ appears to decrease exponentially with a factor of about 0.54. After approximately 15 iterations, the standard deviation is essentially 0 and the maximum and minimum are equal up to first five decimal places.

Fig. 10

Measuring the respacing of the “noisy cat” polygonal curve

We next apply arclength respacing to the outline of a jigsaw puzzle piece obtained from image segmentation, shown in Fig. 11. This jigsaw curve consists of 400 points, with x, y values in $[-6,6].$ The vertices have been normalized so that mean interpoint distances are comparable to the “noisy cat” example, with $\delta \approx 0.1.$ One iteration of arclength respacing produces a curve which appears very close to equilateral. In Fig. 12 are the basic statistics for this arclength respacing iteration. Once again, the standard deviation $\sigma ^n$ appears to decrease exponentially, and the standard deviation is 0 and the maximum and minimum are equal up to first five decimal places after approximately 15 iterations. The size $\epsilon ^n$ of the $\epsilon$-tolerance zone settles quickly at a value that is very small relative to the overall size of the original polygonal curve, suggesting that this iteration provides an equilateral approximation with good fidelity.

Fig. 11

Outline of a puzzle piece after 0 and 1 iteration

Fig. 12

Measuring the respacing of a puzzle piece polygonal curve

Conclusions

This paper introduces an arclength respacing method for polygonal curves and establishes general facts about the behavior of polygonal curves under iteration of this respacing. There are several interesting directions for further investigation.

The impetus for this research was the application of arclength respacing to problems in computer vision. For this application it would be very useful to better understand the rate of convergence to an equilateral polygon and the smoothing effect, the latter being especially apparent in Fig. 9. One might also consider replacing the underlying polygonal curve with a higher order interpolating function, as is done in [9], to affect rates of convergence and smoothing.

Simple, concrete examples of limiting polygonal curves are provided in “Examples”, but we found it generally difficult to determine limiting curves exactly. Further investigation may discover ways to obtain information about the limiting curves, e.g., bounds for final locations of vertices or knowledge of whether the vertices will converge to a single point. In addition, one could study stability—ways in which perturbations to the initial vertex configuration affect the limiting curve.

Finally, the arclength respacing iteration bears a resemblance to the pentagram map [16], an operation defined on convex polygons with many interesting properties, including discrete integrability and a continuum limit corresponding to the Boussinesq equation [1, 20]. It would be worthwhile to investigate this resemblance. A first step could be understanding the continuum limit of arclength respacing; does the infinitesimal motion of the vertices produce a non-trivial curve flow? This curve flow would likely be non-local, since the respacing process is non-local.