Introduction

Quality has become one of the most vital market differentiators when it comes to a product or service. With the increasing number of producers for the same consumer product, the market has become highly competitive and manufacturers coming with better quality in their products or service get a competitive advantage. Therefore, manufacturers are focusing on enhancing their product quality to capture the major portion of the demand in the market and give constant satisfaction to their customers. To increase or maintain the quality of their offerings, manufacturers use different statistical process control tools [11]. Control chart, also known as process behavior chart, was first developed by Walter A. Shewhart in the 1920s [26]. The main reason for using control charts is to identify a manufacturing process being in a state of control [33]. However, control charts do not provide any pattern related information if a process deviates from its inherent pattern and follows a particular abnormal pattern [9]. CCPs are important because when any unnatural patterns exist in a process for a long time, it is evident that the unnatural pattern comes from a common source of error or defect. This error can result from machine damage, a problem with raw material, error from workers, etc.

Many authors have already developed different techniques for CCPR over the years. Some of them involve complex algorithms, whereas some have a simple mechanism to recognize CCPs. Cheng [3] developed a method for control chart pattern recognition using a neural network approach. Guh and Hsieh [8] proposed a neural network-based model and in their paper which was used to recognize abnormal patterns. Yang and Yang [31] proposed a fuzzy-soft learning vector quantization to recognize control chart patterns. In contrast with the above-mentioned models that require a complex learning algorithm and large computational effort, Yang and Yang [30] developed a simple mechanism to recognize CCPs using statistical correlation coefficient. In their paper, CCPs were recognized by measuring the statistical correlation between the test data and reference data with a set threshold value. The learning algorithm in this model is simple and requires very low computational effort. However, selecting the threshold value for classifying patterns into a certain class and pattern length of data is a big issue in this model, for which the accuracy to detect correct CCPs is lower than the other complex learning models.

Over the years, SVM has become the most popular model for CCPR because of its ability to control data more effectively and perform a large number of operations such as classification, regression, and distribution. SVM is a powerful machine learning tool that has the capability to represent the non-linear relationship and produce a model that generalizes well to unseen data [4]. Lin et al. [13] proposed an SVM-based approach for CCPR in autocorrelated data. Xanthopoulos and Razzaghi [28] in their research have defined a CCPR as an imbalanced supervised learning problem and used a weighted SVM model to show its benefits over traditional SVMs. Later, SVM has been incorporated with other approaches to develop more efficient models for CCPR. To outperform the traditional SVM model, Zhou et al. [37] used fuzzy SVM incorporated with a hybrid kernel function. To optimize the feature selection, they also used a genetic algorithm (GA). A supervised locally linear embedding algorithm was incorporated with SVM to reduce features of high dimension [35]. Zhang et al. [34] proposed a CCPR method by using fusion feature reduction and fireworks algorithm-based multiclass support vector machine (MSVM). Cuentas et al. [5] proposed an SVM-GA based monitoring system for CCPR of correlated processes.

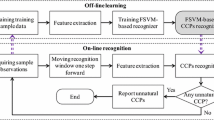
In this paper, a new model is proposed that uses the MIC value to recognize control chart patterns. MIC is based on mutual information analysis (MIA) [7, 27]. Mutual information (MI) is a quantity to estimate a relationship between two random variables, where the relationship between them is either linear or nonlinear [17]. However, using MIA directly to measure non-linear relationships between two datasets is difficult because mutual information computation needs to choose an estimator from a set of existing methods [23]. Moreover, it is difficult to interpret the computed value for MI and compare different obtained values [24]. For these reasons, a statistical tool named MIC was developed by Reshef et al. [20]. It has the same advantages as the MI, since it considers any kind of relationship including non-linear relationships, but has an exact definition, a soft interpretation, and better stability [21]. The main idea of the MIC is that if a relationship exists between a test dataset and a reference dataset, there exists a partition of the data that will allow to include this relationship [36]. Using MIC, a large number of non-linear relationships between the test set and the reference set can be measured [16].

There has been a wide range of applications of MIC in measuring the relationship between datasets. Caban et al. [2] characterized non-linear dependencies among pairs of clinical variables and imaging data using MIC. Tang et al. [25] proposed a cross-platform tool that was used for the rapid computation of MIC to effectively analyze large-scale biological datasets with a substantially reduced computing time through parallel processing. Xu et al. [29] predicted defects from historical data based on MIC with hierarchical agglomerative clustering. Shao et al. [22] used an improved MIC model to analyze railway accidents. MIC has also been used in railway accident analysis. MIC was also used to identify differentially expressed genes by Liu et al. [14].

However, there has not been any application of MIC in CCPR in the existing literature. Being a novel statistical method, MIC has already been used as a robust model to identify different classes with better overall performance, adaptability, and noise immunity from the traditional statistical methods such as SCM [14]. Hence, this paper aims to develop a model to identify the CCPs using MIC, as MIC can capture linear and non-linear relationships, such as cubic, exponential, sinusoidal, etc., and also robust to outliers due to its MI foundation. This makes MIC a feasible approach to identify the relationship between test data and reference data and thus pinpoint the exact pattern of control charts.

The objective of this paper is to illustrate the proposed MIC model along with two existing CCPR methods, namely SCM and SVM with production data of 1.5 gram (g) coffee minipack obtained from a major consumer product manufacturing company. The results obtained from the MIC model are then compared with results obtained from the SCM as well as the SVM model in terms of both computational accuracy and efficiency.

The remainder of this paper is organized as follows. In the following section, we discuss the existing approaches for CCPR. The subsequent section describes the proposed CCPR approach based on MIC and in the section following that we illustrate the proposed methods with numerical examples. The next section provides conclusions and suggestions for future work.

Existing Methodologies

This section discussed two existing methods for CCPR, the SCM, and SVM models. A brief background on the CCPR problem is provided first.

CCPR

CCPR can help to figure out the sources of deviation, if there is information available, and eliminate the error occurring in the future. This facilitates a system to remain in check so that any variations can be easily detected otherwise such alterations will remain hidden in the system thus affecting the whole lot. There might arise six types of abnormal patterns in a process other than the natural normal pattern. Each of them presents a different form of failure or source of error in a process. In this paper, CCPs have been classified into normal (NOR) and abnormal patterns. Abnormal patterns include upward shift (US), downward shift (DS), upward trend (UT), a downward trend (DT), systematic (SYS), and cyclic (CYC) as shown in Fig. 1.

Fig. 1
figure 1

Different types of control chart patterns

Full size image

CCPR Using SCM

The statistical correlation coefficient method, also known as SCM, is the most traditional and simplest method to recognize control chart patterns. In this method, the linear correlation coefficient (r) between a reference dataset and a test dataset is measured to justify if the value of r with a reference set of a certain control chart pattern exceeds a threshold value to match that pattern.

Framework for SCM

SCM determines the linear correlation between two random datasets. If x and y are two random vectors, then the linear correlation between them can be defined as in Eq. (1):

$$r=\frac{\sum ({x}_{i-}\overline{x})({y}_{i}-\overline{y})}{\sqrt{\sum ({{x}_{i-}\overline{x})}^{2}}\sqrt{\sum ({{y}_{i-}\overline{y})}^{2}}}$$
(1)

where, \(\overline{x}\) and \(\overline{y}\) are the mean value of x and y, respectively.

The first step of this method is to develop a training algorithm where each pattern sample has a length of n. Pattern samples can be generated as follows:

Normal pattern:

If n(t) follows a normal distribution then the normal pattern can be described as in Eq. (2).

$$x\left(t\right)=n\left(t\right)$$
(2)

Upward and downward shift patterns:

Upward and downward patterns can be described as in Eq. (3).

$$x\left(t\right)=n\left(t\right) \pm ud$$
(3)

where d is the shift quantity and the values of u are 0 and 1 before and after shifting, respectively.

Upward and downward trend patterns:

Upward and downward trend patterns are described in Eq. (4).

$$x\left(t\right)=n\left(t\right) \pm te$$
(4)

where, e is the value of the slope of the trend.

Cyclic pattern:

The cyclic pattern is shown in Eq. (5).

$$x\left(t\right)=n\left(t\right)+f\mathrm{sin}\left(\frac{2\pi t}{8}\right)$$
(5)

where, f is the value of amplitude.

Systematic pattern:

The systematic pattern can be defined as in Eq. (6).

$$x\left(t\right)=n\left(t\right)+ {(-1)}^{t}f$$
(6)

where f is the value of amplitude.

The first step of using the linear correlation method is to develop a training algorithm. The training algorithm can be implemented as follows:

  • A pattern length of n has to be determined.

  • Using a disturbance level of d, a pattern sample generator is selected. A pattern vector \({x}_{1}\) is generated for a pattern length of n, accordingly \({x}_{2}, {x}_{3}\)…,\({x}_{N}\) pattern vectors are generated.

  • From N samples, an estimated pattern vector is determined by Eq. (7) [30].

    $$E\left(x\right)=\frac{\sum_{i=1}^{N}{x}_{i}}{N}$$
    (7)

Now, to classify the dataset, a classification algorithm is needed. The algorithm is as follows:

  • A processing data sequence containing recent n points is regarded as the pattern size to be recognized. The data sequence is input to the recognizer and calculated its statistical correlation coefficient using six reference vectors to obtain outputs for the upward shift, downward shift, upward trend, downward trend, cyclic pattern, and systematic patterns, respectively.

  • The pattern for which the value of r is maximum is considered as the winner pattern for the model.

CCPR Using MSVM

Support vector machines (SVMs) were previously designed only to solve binary classification problems [10]. With the increasing need for multiclass classification, different methods have been studied. Currently, there are two types of approaches for MSVM, namely the One-against-one (OAO), and the One-against-all (OAA) method. OAO method involves constructing and combining several binary classifiers, whereas the OAA method involves directly considering all data in one optimization formulation [32]. The formulation to solve multiclass SVM problems in one step has variables proportional to the number of classes. Thus, in order to solve problems with multiclass SVM methods, either a larger optimization problem has to be constructed or several binary classifiers have to be formulated. As a result, MSVM is computationally more expensive to solve a multiclass problem than a binary problem with the same amount of data.

The core concept of the SVM model is to classify two different classes of data by constructing an optimal separating hyperplane (OHS) that maximizes the margin between the two nearest data points belonging to two separate classes [18].

If a dataset is represented by \({(x}_{i},{y}_{i}), i=1, 2, \dots ,l, {(x}_{i},{y}_{i})\in {R}^{n+1} ,\) where l is the number of samples and n is the number of features. Each xi is a sample with n features and a class label\(y\in \left\{-1,+1\right\}\). The SVM classifies the data point by identifying a separating hyperplane \({w}^{\mathrm{T}}x+b=0\), where w is the weight vector and b is the bias. If this hyperplane maximizes the margin, then the Eq. (8) below is valid for all input data.

$${y}_{i}\left({w}^{\mathrm{T}}\mathrm{\varnothing }\left({x}_{i}\right)+b\right)\ge 1 \quad \forall i=1, 2,\dots l$$
(8)

where, \(\mathrm{\varnothing }\) is the kernel function.

Using the Kernel function, it is possible to classify non-linear problems. The concept of kernel trick is to map the original data points into a higher dimensional feature space in which they can be separated by a linear classifier. The projection of a linear classifier on the feature space is a non-linear one in the original space.

The separating hyperplane defined by the parameters w and b is used to maximize the margin between two classes by solving the convex optimization problem as shown in Eq. (9).

$$\mathrm{min }\frac{1}{2}\left|\left|{w}^{2}\right|\right|+C \sum_{i=1}^{l}{\xi }_{i}$$
(9)

where, C is the parameter denoting the tradeoff between the margin width and the training error and \({\xi }_{i}\) is the slack variable to allow the margin constraint to be violated.

In this paper, MSVM is used to classify different pattern classes. Between OAA and OAO MSVM methods, OAO is more suitable to use for practical uses than OAA [10]. In OAO, for a P class problem, there are \(\frac{P(P-1)}{2}\) SVM models. Each of the SVMs is trained for separating a class from another [19]. Additionally, the voting result of these SVMs also directs the decision of a testing sample. Whereas in OAA, P class pattern recognition problem is solved. In the first step of OAA, P independent SVMs are to be constructed and each of them is trained to separate one class of samples from all others. The kth SVM is trained with all of the datasets in the kth class with positive labels, and all other examples with negative labels. To test the model after all the SVMs are trained, a sample dataset is an input to all the SVMs. If that sample belongs to a certain class like P1, then only the SVM which has been trained to separate that particular class from the others will give a positive response [6]. Because of the better suitability in the classification of practical problems, this paper uses OAO.

Feature Selection

Major decision-making in the SVM classifier is selecting the number of appropriate features. Selecting the right features in MSVMs facilitates the recognition of CCPs quickly and accurately. Different classes can be characterized by several shape features. There are nine shape features for discrimination of the CCPs [19]. Features should be chosen such that the proposed statistical features can significantly recognize the patterns quickly and accurately. Some features can be described as follows:

Slope (S)

Slope is a feature that represents the least-square line representing the pattern. The magnitude of the slope is approximately zero for normal and cyclic patterns. On the other hand, for trend and shift patterns, the magnitude of the slope is greater or less than zero. As a result, the slope can be a potential feature to differentiate normal and cyclic patterns from shift patterns.

The Number of Mean Crossings (NC1)

It is the number of times a pattern crosses the mean line. The value of NC1 is relatively small for shift and trend patterns. It is the highest for normal patterns. For cyclic patterns, its value is an intermediary between those of normal patterns and shift or trend patterns. Therefore, it can differentiate normal patterns from cyclic patterns as well as normal and cyclic patterns from trend and shift patterns.

The Number of Least-Square Line Crossings (NC2)

NC2 is the highest for normal and trend patterns and the lowest for shift and cyclic patterns. Thus, it is a good differentiator for normal and trend patterns from shift and cyclic patterns.

The Average Slope of the Line Segments (AS)

There are two line segments for each pattern to fit the data starting from either end of the pattern in addition to its least-square line. The average slope of the line segments is higher for the patterns than for normal, cyclic, and shift patterns. Therefore, it is a good feature to differentiate the patterns from the other patterns.

Other than the above-mentioned shape features, statistical features also have distinguishable properties to solve a classification problem. Mean, standard deviation, skewness, etc. are some of the important statistical features used in SVM models. They are shown respectively in Eqs. (10)–(12).

$$\mathrm{mean}= \frac{\sum_{i=1}^{n}{x}_{i}}{n}$$
(10)
$${\text{standard deviation }} (\mathrm{std})= \sqrt{\frac{\sum_{i=1}^{n}{{(x}_{i}-\mathrm{mean})}^{2}}{n}}$$
(11)
$$\mathrm{skewness}= \frac{\sum_{i=1}^{n}{{(x}_{i}-\mathrm{mean})}^{3}}{n{(\mathrm{std})}^{3}}$$
(12)

Using more features in the classification algorithm gives more accurate results. Also, selecting the right features for a particular classification problem is important.

Framework for SVM Model

The SVM model involves two algorithms. Firstly, the model is trained with training datasets. Training algorithm also involves providing the datasets with appropriate features. Training algorithm can be implemented as follows:

  • A pattern length of n has to be determined for each reference dataset.

  • A pattern sample generator is selected from the reference pattern equations in Eqs. (2)–(6). A pattern vector \({x}_{1}\) is generated for a pattern length of n, accordingly \({x}_{2}\), \({x}_{3}\)…, xN pattern vectors are generated. N is the number of samples used for a certain pattern.

  • From N samples, an estimated pattern vector is determined by Eq. (7).

  • Each reference pattern vector is trained with its shape and statistical features. Features are mean, standard deviation, skewness, and the number of crossings.

  • Each reference pattern is labeled with a different number.

After the reference datasets are properly trained, a classification algorithm is implemented as follows:

  • Input test dataset with corresponding features.

  • MSVM model compares the test datasets to all the SVMs trained.

  • The output is the label of the pattern best matched with the test data.

In the following section, we have proposed a new technique to recognize CCPs using the MIC model.

Proposed CCPR Model Using MIC

MIC method uses MI between two random variables to determine non-linear dependence or functional relationship between them. Using MIC, we can identify the functional relationship between a test dataset and a reference dataset. If the MIC value is low, that will signal a weak functional relationship between the two datasets. If the MIC value is close to 1, that will signal a strong relationship between the datasets and identify a dataset following the corresponding pattern.

Framework for MIC Model

MIC is based on MIA. Before describing MIC, some tools of mutual information are discussed first.

Let A be a random variable in space A, B a random variable in space B and \(\mathrm{Pr}\left[E\right]\) is the probability of the event E. The entropy (H) associated with A is defined in Eq. (13).

$$H\left(A\right)=-{\sum }_{a\in A}^{n}\mathrm{Pr}\left[A=a\right]. {\mathrm{log}}_{2}(\mathrm{Pr}[A=a])$$
(13)

The entropy associated with B is defined in Eq. (14).

$$H\left(B\right)=-{\sum }_{b\in B}^{n}\mathrm{Pr}\left[B=b\right]. {\mathrm{log}}_{2}(\mathrm{Pr}[B=b])$$
(14)

The conditional entropy of A given B can be defined by Eq. (15).

$$H\left(A,B\right)=-{\sum }_{a\in A,b\in B}^{n}\mathrm{Pr}\left[A=a, B=b\right]. {\mathrm{log}}_{2}(\mathrm{Pr}[A=a|B=b])$$
(15)

The MI which defines the mutual dependency between random variables can be defined with the help of Eq. (16).

$$\mathrm{MI}\left(A,B\right)=H\left(A\right)-H\left(A\right|B)=H\left(A\right)+H\left(B\right)-H\left(A,B\right)$$
(16)

The maximal value of the MI is \(H\left(A\right)+H\left(B\right)\). This measure can detect if there is any relationship linking the variables regardless it is a linear or a non-linear relationship. If the value of MI is 0, the two variables are independent. On the contrary, if the value of the MI is maximal, it indicates that A and B have the strongest relationship. However, computing the mutual information is tricky, when a continuous variable is involved. The issue with MI is that they overestimate the conditional entropy. This has long been perceived as an issue and huge consideration has been committed to creating alternative methods to nullify this limitation [21]. For these reasons, a new method called maximal information coefficient (MIC) was proposed to estimate the probability density function (PDF) of variables using bins [20].

The objective of MIC is to measure if there exists a relationship between two random variables A and B. A and B are coupled in a set D(A, B). A p-by-q grid is formed that can be called the partition of the couple (A, B). Here, variable A is distributed in p, and variable B is distributed in q bins. There are a lot of different grids of size p-by-q. AG and BG are used to denote the distributions of A and B over the grid G and G(p, q) is the set of all grids of size p-by-q.

For a particular value of p and q, Eq. (17) defines the maximal mutual information over grids p-by-q:

$${I}^{*}\left(D,p,q\right)={\mathrm{max}}_{G\in \left(p,q\right)}(I({A}^{G},{B}^{G} ))$$
(17)

MIC value between the variables A and B can be defined with the help of Eq. (18).

$$\mathrm{MIC}\left(p,q\right)=\mathrm{max}\left(\frac{{I}^{*}\left(D,p,q\right)}{{\mathrm{log}}_{2 }\mathrm{min}\left(p,q\right)}\right)$$
(18)

MIC value is defined by calculating the ratio in Eq. (18) using the data-dependent binning scheme. MIC value is also bounded by the denominator of the ratio, that’s why the range of MIC values is always 0 to 1. MIC can be stated as the estimate of MI, \({I}^{*}\left(D,p,q\right)\) utilizing constrained binning scheme and divided by a normalization factor, \({log}_{2 }\mathit{min}\left(p,q\right)\). It appears that except for highly structured data, MIC values reduce to the estimates of MI as the denominator of the ratio in Eq. (18) becomes 1.

The value of MIC is highly dependent on choosing the number of p and q bins. As the bin sizes affect the value of mutual information, determining the appropriate values of p and q is important. The generality of MIC shares a direct relationship with maximal grid size B(n). If B(n) is set too low, this will result in searching only for simple patterns and weakening the generality. On the other hand, while setting B(n) too high will result in a nontrivial MIC score for independent paired variables under finite samples. Reshef et al. [20] set the p × q ˂ B(n), where B(n) = n0.6 is the maximal grid size restriction and n is the sample size. This grid size has been used to develop the MIC model for CCPR in this paper.

Using this concept, the MIC model takes a reference dataset of one of the seven CCPs as variable A that is distributed in p and the test dataset as variable B distributed in q. The reference dataset for which the MIC gives the highest value is considered as the actual pattern of the test dataset.

An algorithm to generate a reference dataset can be implemented as follows:

  • A pattern length of n is determined for each reference dataset.

  • A pattern sample generator is selected from the reference pattern equations in Eqs. (2)– (6).

  • A pattern vector \({x}_{1}\) is generated for a pattern length of n, accordingly \({x}_{2}\),\({x}_{3},\) …, xN pattern vectors are generated. N is the number of samples used for a certain pattern.

  • From N samples, an estimated pattern vector is determined by Eq. (8)

Pattern recognition algorithm by determining MIC value between reference dataset and test dataset is as follows:

  • Test dataset of pattern length n is imported.

  • MIC value between the test dataset and each reference dataset is determined using Eq. (18).

  • Amongst the MIC values, the highest MIC obtained from the reference dataset is considered as the winner pattern for the test dataset.

In the following section, we illustrate the CCPR methodologies with numerical examples.

Numerical Illustrations

Data Collection

To demonstrate control chart pattern recognition, training datasets, and test datasets are to be incorporated in the model to recognize the patterns of the test datasets. Training datasets are generated randomly using MATLAB using Eqs. (2)–(6). For a better understanding of the classification problem, production data of a consumer product is used as the test dataset. In this paper, production datasets of 1.5 g coffee minipack manufactured in a major manufacturing company 'XYZ' have been used. Data from two different coffee powder filling machines are taken from two production lines. For numerical illustration, a portion of a test dataset from Machine-1 and Machine-2 are presented in Tables 10 and 11 respectively. For SCM, each of the datasets has been normalized and used to measure the correlation coefficient with all 7 training datasets. For SVM, the test datasets have been first normalized and then used to determine the SVM features described in “Feature selection”. For MIC, the same procedure has been followed as in the SCM method. Additionally, for Machine-1, filling capacity has been gradually increased in each batch and shown in Table 10 to validate the credibility of the three models in recognizing an abnormal CCP. Similarly, other test datasets obtained from company ‘XYZ’ have also been used for CCPR.

The selection of pattern length is very important for the datasets because the accuracy of the models depends on it. 1000 randomly generated samples of different patterns where pattern length, n = 70, 80, 100, 150, 200, 300, 400, 500 were taken and these three models were used for pattern recognition. The simulation was repeated ten times for each type of pattern and it was seen that for a pattern length of 400, the accuracy was higher. Therefore, for both training and testing datasets, a pattern length of 400 is selected.

SCM

In SCM, firstly, reference data are generated for all six unnatural control chart patterns as well as for the natural normal pattern using Eqs. (2)–(6). Using Eq. (1), correlation coefficient rnorm, ru.s., rd.s., ru.t, rd.t, rcyc, rsys between test dataset and reference dataset is measured. rnorm, ru.s., rd.s., ru.t, rd.t, rcyc, rsys are correlation coefficients, respectively, for NOR, US, DS, UT, DT, CYC, and SYS patterns. Correlation coefficient values for sample test datasets as given in Tables 1 and 11 (“Appendix”) are shown in Tables 1 and 2, respectively.

Table 1 Correlation coefficient values for Machine-1 dataset
Full size table
Table 2 Correlation coefficient values for Machine-2 dataset
Full size table

From Table 1, it is seen that in every trial, correlation coefficients’ values of upward and downward trends give the highest scores compared to others, thus creating a paradox in recognizing the actual pattern of the datasets. From Table 2, it can be said that correlation coefficients’ values are highest for normal patterns in each trial. The highest value for a pattern in each trial is considered as the winner pattern of the dataset for that trial and the pattern that wins the highest number of trials is considered as the actual pattern of the test dataset. That is to say, SCM cannot confirm the pattern for the dataset from Machine-1, but identity Machine-2 dataset as a normal pattern.

Error Analysis for SCM

50 datasets were taken from two coffee machines from the production floor of company ‘XYZ’ at different times for control chart pattern recognition using all three approaches. Using the SCM model, these 50 datasets have been tested and most of the results were confusing as different trials give different results. By considering the maximum coefficient value, 30% of datasets were correctly recognized and around 70% of results could not accurately recognize the pattern. Hence, the accuracy of this model in recognizing patterns is low as it cannot recognize the nonlinear relations between the datasets. Other factors like randomness in the dataset, data collection methods (timings and frequency), etc., can also affect the accuracy of the SCM model.

SVM Model

In the SVM model, the reference dataset is firstly generated and their appropriate features are determined. In this paper, the mean value is considered as the statistical, feature and the number of crossings is considered as the shape feature. Using these two features, reference datasets are classified into different classes and classes are labeled as shown in Table 3.

Table 3 Class labels
Full size table

After the reference datasets are labeled and classified in different classes, test datasets are used as inputs to the model and their features are calculated. Table 4 shows samples’ feature values for two test datasets.

Table 4 Feature values of test datasets
Full size table

Once the features are determined, datasets are tested against each trained class and the classifications obtained from the model are given in Table 5.

Table 5 Classifications of test datasets
Full size table

From Table 5, it is clear that the SVM model identifies the Machine-1 dataset as upward trend pattern and the Machine-2 dataset as normal pattern, since it gives the same output in all the trials.

Error Analysis for SVM

From the analysis of the test dataset of pattern length n of 400, it is evident that SVM, for its highly developed training algorithm, gives the same classification result in all the trials, thus considered as 100% accurate in recognizing CCPs using appropriate features. The result shows that SVM performs well when there is a distinct margin of class separation. It also uses a subset of the training set in the decision functions called support vectors, so it is also memory efficient. All the 50 test datasets mentioned in “Error analysis for SCM” are checked with the SVM model and the accuracies of the results obtained from other models have been identified using the results obtained from SVM model. However, one of the significant problems of SVM is the trouble to interpret except if the features are interpretable. Values of features in different classes must not intersect with each other. For that reason, the selection of an optimum number of features and their corresponding ranges are necessary and difficult tasks for the proper separation and identification of classes based on those features. In other words, the selection of features for the classification of data is a vital task in SVM. It also tends to be computationally costly and it highly depends on kernel function [1, 15]. All these negative traits of the SVM model in pattern recognition create the need to develop or identify another model to overcome the disadvantages of SVM while maintaining accuracy. Hence, results from the other two methods are compared with the SVM model to search for a method that can replace the SVM model by providing substantial accuracy and overcoming the computational complexity of the SVM model.

MIC Model

Using the test datasets as given in Tables 10 and 11, the MIC model compares the MIC values between the test datasets and training datasets. Using Eq. (18), MIC values are measured for the sample datasets of Machine-1 and Machine-2 as shown in Tables 6 and 7, respectively.

Table 6 MIC values for Machine-1 dataset
Full size table
Table 7 MIC values for Machine-2 dataset
Full size table

As discussed earlier in “Framework for MIC model”, the highest MIC obtained from the reference dataset is considered as the winner pattern for the test dataset. It is seen in Table 6 that, in every trial, the MIC value is the maximum for the upward trend. Therefore, we identify the Machine-1 dataset as upward trend pattern. Similarly, it can be observed in Table 7 that, in every trial, the MIC value is the maximum for the normal pattern. Therefore, the proposed framework identifies the Machine-2 dataset as normal pattern.

Error Analysis for MIC

MIC is an equitable measure of dependence as it has the ability to provide similar scores to relationships with similar noise levels [20]. Because of this property, MIC is more useful in identifying the strongest association among many significant associations in a dataset, compared to other alternatives such as MI estimation, distance correlation, Spearman correlation coefficient, etc. However, all statistical problems do not call for a self-equitable measure of dependence. For example, if data which are to be measured are of a limited type and noise in that data are approximated as Gaussian, squared Pearson correlation R2 gives more accurate results than estimates of mutual information [12]. In the case of larger data with unknown noise, MIC gives more accurate results. After testing 50 test datasets as mentioned in “Error analysis for SCM” with the MIC model, it is seen that it can accurately recognize patterns 85% of the time. MIC model can estimate both linear and nonlinear correlations between datasets considering the noise levels in datasets. Therefore, the accuracy of the MIC model is better than the SCM model. Though its accuracy is slightly less than the SVM model, it still can replace SVM in places where a few errors in the system are acceptable.

Comparison of Results

After recognizing CCPs using the traditional SCM, SVM and MIC, it can be stated that traditional SCM results in 70% error which is the highest among the three models. As it can only measure the linear relationship between two datasets, it gives inaccurate results for most of the cases where linearity cannot properly define the relation between a test and a training dataset. The output obtained from the MIC model clarifies that it performs better in terms of accuracy than the SCM method as it is able to identify the non-linear relationship between any two datasets. MIC model can recognize CCPs having pattern length n of 400 with 85% accuracy. Among the three models, the SVM model is the most advanced and accurate model which recognizes CCPs for this study with a 100% accuracy. The training algorithm and feature selection in the SVM model allow it to perform better than both SCM and MIC models. In Table 8, accuracies for statistical correlation measure and MIC model are shown.

Table 8 Accuracies of the three models in CCPR
Full size table

For the pattern length, n of 400, the computational time for three models was calculated as given in Table 9. From Table 9, it is seen that SCM needs the lowest time for computing the result. However, this model has very low accuracy. MIC model needs 0.31 s to calculate output, whereas the SVM model needs 0.39 s to recognize a certain pattern. It is evident that the MIC model is 20.5% faster than the SVM model in CCPR because of its simpler learning algorithm than SVM.

Table 9 Computational time for three models
Full size table

The comparison among the three models suggests that the MIC model is the most feasible model when 10–15% error can be considered allowable in the output, because of its simplicity, accuracy and decreased computational time.

Conclusions

In this highly competitive market, no product can sustain profitability without maintaining consistent quality. Manufacturing process plays a vital role in maintaining the product quality. As a result, maintaining a highly controlled manufacturing process has become mandatory. Control charts are one of the most useful statistical tools used to monitor a process. With the use of a control chart pattern recognizer, any type of CCP can be recognized very fast and a structured decision can be made to resolve a certain anomaly or defect that may arise in the production process.

In this paper, a new methodology has been proposed for CCPR using MIC values between two datasets. The results obtained from the MIC model are then compared with the results obtained from the traditional SCM and SVM models. Results reveal that the MIC model can be a potential alternative to the SVM model as it can certainly reduce the computational effort and cost and yet can provide satisfactory classification accuracy, whereas the SCM model is not suitable for CCPR.

The existing MIC model begins to fluctuate its output when the sample size is large. The future scope of this research involves using a more optimized MIC model that is able to handle a large number of samples each having a large pattern length without deviating from a constant performance. Another scope is optimizing the p-by-q grid size of the model that can distribute random variables in a more efficient way to recognize control chart patterns accurately in all cases. Moreover, a hybrid MIC model, such as random forest regression-based MIC can also be used for better accuracy in CCPR. If these improvements could be brought in the MIC model, it would be able to successfully replace the SVM model in industrial applications by achieving higher accuracy. Thus, it would be able to reduce the computational effort and cost for CCPR.