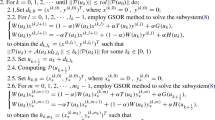Modified Newton-PAGSOR Method for Solving Nonlinear Systems with Complex Symmetric Jacobian Matrices

Abstract

We propose, in this paper, the preconditioned accelerated generalized successive overrelaxation (PAGSOR) iteration method for efficiently solving the large complex symmetric linear systems. To solve the nonlinear systems whose Jacobian matrices are complex and symmetric, treating the PAGSOR method as internal iteration, we construct a modified Newton-PAGSOR (MN-PAGSOR) method to provide an effective approach for solving a wide range of problems in various scientific and engineering fields. Based on the Hölder continuous condition we present the theoretical framework of the modified method, demonstrate its local convergence properties, and provide numerical experiments to validate its effectiveness in solving a class of nonlinear systems.

1 Introduction

Let us consider the solution of a complex nonlinear systems of equations,

$$\begin{aligned} F(u)=0, \end{aligned}$$

(1)

where $F{:}\,\mathbb {D}\subset \mathbb {C}^n\rightarrow \mathbb {C}^n$ is a continuously differentiable nonlinear mapping defined on an open convex subset of the complex linear space $\mathbb {C}^n$, and $F=(F_1,\cdots ,F_n)^{\textrm{T}}$, $F_j=F_j(u)$, $j=1,\cdots ,n$, $u=(u_1,\cdots ,u_n)^{\textrm{T}}$. And the Jacobian matrix $F'(x)$ is large sized, sparse, and complex symmetric. This class of nonlinear systems of equations has widespread applications in various fields, such as quantum mechanics [31], fluid mechanics [24, 25, 41], structural mechanics [1, 27], chemical reaction [32, 38], nonlinear wave [47], mechanical engineering [27], and so on. Assuming that the complex symmetric Jacobian matrix $F'(u)$ has the following form:

$$\begin{aligned} F'(u)=W(u)+\textrm{i}T(u), \end{aligned}$$

(2)

where W(u) and T(u) are real symmetric and positive semi-definite matrices, and $\textrm{i}=\sqrt{-1}$ is the imaginary unit. The effective classical method to solve the nonlinear system of equations (1) is the Newton method [22, 36, 44] with the specific format:

$$\begin{aligned} u_{k+1}=u_k+s_k, \quad F'(u_k)s_k=-F(u_k), \quad k=0,1,\cdots {.} \end{aligned}$$

(3)

With a good choice of the initial guess $u_0$ for the exact solution $u_*$ of the equation (1), the Newton method possesses quadratic convergence speed. However, it becomes challenging to solve exactly the Newton equation $F'(u)s=-F(u)$, especially when the dimension n is large.

To address this issue and raise the efficiency, on one hand, the inexact Newton method [21] was proposed and widely studied. The specific format of the inexact Newton method is as follows:

$$\begin{aligned} \Vert F(u_k)+F'(u_k) s_k\Vert \leqslant \eta _k\Vert F(u_k)\Vert , \quad k=0,1,\cdots , \end{aligned}$$

(4)

note that the parameter $\eta _k\in [0,1)$ here is the forcing term which is used to control the level of accuracy and $F'(u_k)$ represents the Jacobian matrix of the operator F(u) evaluated at the iterate $u_k$. On the other hand, to expedite the solving process of the Newton method, the modified Newton method was presented and studied in [20], which is formulated as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} v_k=u_k-F'(u_k)^{-1}F(u_k),\\ u_{k+1}=v_k-F'(u_k)^{-1}F(v_k),\quad k=0,1,2,\cdots . \end{array}\right. \end{aligned}$$

(5)

The theoretical and numerical analysis shows evidently that the modified Newton method (5) has achieved significant improvements. Compared with the Newton method, it requires only one additional evaluation F per step. However, the modified Newton method has at least R-order three of convergence. Over the years, inner-outer methods have attracted lots of attention for nonlinear systems due to their superior numerical performance, see [12, 18, 28, 34, 50, 53] and references therein. Therefore, for the nonlinear system (1), building on the efficient performance of the modified Newton method as an outer iteration, we need to search for more suitable inner methods for different forms of nonlinear problems to further improve effectiveness. To make the solver faster, we focus on finding efficient inner iterative methods to solve the following linear system.

Actually, we consider the linear system of equations

$$\begin{aligned} Au=b,\quad A\in \mathbb {C}^{n\times n},\ u, \ b\in \mathbb {C}^n, \end{aligned}$$

(6)

where A is a complex matrix with $A=W+\textrm{i}T$, and $W, T \in \mathbb {R}^{n\times n}$ are real symmetric matrices, W being positive definite, and T being positive semi-definite. It is known that (6) is a special case of the generalized saddle-point problem [16, 17] which has broad applications, for instance, in the finite element discretization of constrained optimization problems for elliptic partial differential equations, or distributed control problems [2, 42, 43].

The methods for solving block two-by-two structured real linear equations have garnered significant attention from scholars. Among them, several kinds of preconditioned Krylov subspace methods [19, 45] have shown remarkable performance in handling large sparse matrices, effectively utilizing their structural characteristics to accelerate the solution process. Since 2003, the Hermitian and skew-Hermitian splitting (HSS) methods introduced by Bai et al. [9] have gained considerable attention for their effectiveness in solving large linear systems with non-Hermitian positive definite matrices. Researchers have devoted efforts to studying and refining the HSS-based methods [6, 8, 11, 55], drawn by their elegant formulation and reliable convergence properties. To circumvent the need for complex linear system computations, Bai et al. designed the modified HSS (MHSS) iteration method [3] to tackle the solution of equation (6) without resorting to complex linear system computations. Subsequently, massive improved methods have been proposed both in terms of HSS-version, such as the preconditioned MHSS (PMHSS) method [4] and the double-parameter generalized PMHSS (DGPMHSS) [33], etc., and in terms of SOR-version. However, as for the improved methods in terms of SOR-version, the original idea, and analysis of the generalized successive overrelaxation (GSOR) method were presented early in, 2005 [13] for solving augmented linear systems. Further generalizations and developments were extended by applying the GSOR method to address large sparse generalized saddle-point problems, as exemplified by the Uzawa method [14], and the GSOR-type (SOR-acceleration for HSS) methods were also established in [10]. Nearly 10 years later, certain straightforward applications of the GSOR methods and their accelerations as well as preconditioning were also researched in [23, 29, 46]. Especially inspired also by the preconditioning technique, Huang et al. introduced the preconditioned AGSOR (PAGSOR) method [30] whose aim is to decrease the optimal convergence factor of the AGSOR method and to enhance its convergence efficiency. All the above studies lead us to provide excellent inner iteration methods by developing two variants of the GSOR method, namely the accelerated GSOR (AGSOR) and the preconditioned GSOR (PGSOR) for linear systems.

As for nonlinear systems (1), by making use of the HSS-version iteration as the inner solver for the inexact Newton or modified Newton method, researchers have contributed a lot of excellent algorithms. See, for example, papers [12, 15, 28, 35, 48, 49, 53, 54] and references therein. In recent years the modified Newton-DGPMHSS (MN-DGPMHSS) method [18] and the modified Newton-DSS (MN-DSS) method [52] were also proposed to improve the algorithms. (Note that “D” for the two methods here represents “double” or “double-step”. Do not confuse it with the “D” standing for “deteriorated” used in the initial study related to the HSS-type iteration methods [37]. Abbreviations always have limitations!) Due to the advantages of easy programming, efficient computing, and saving storage for SOR-version iteration and its variants, the modified Newton-GSOR (MN-GSOR) method and the modified Newton-AGSOR (MN-AGSOR) method were introduced [39, 40]. The local convergence properties of these methods were performed under a Hölder condition. The efficiency of their numerical results can be compared with those of the MN-DPMHSS and MN-MPPMHSS methods. In 2021, the modified Newton-PGSOR (MN-PGSOR) method was proposed to solve (1) with block two-by-two complex symmetric Jacobian matrices. It can get a similar conclusion while applying on a 2-torsion free block upper triangular matrix algebra [26]. All these methods have made progress in the study of solving a nonlinear system of equations.

To improve the computational efficiency and expand the range of problems when the Jacobian matrix is symmetric indefinite, we consider the possibility of applying the modified Newton method to solve a nonlinear system of equations while utilizing the preconditioned accelerated successive overrelaxation (PAGSOR) method to solve the Newton equations. Thus, we construct the modified Newton-PAGSOR (MN-PAGSOR) method to solve equations (1). Under proper conditions, the local convergence theorem is provided. Then, we use numerical results to show the feasibility and effectiveness of the method compared with several existing algorithms.

The article is organized as follows. In Sect. 2, we introduce the MN-PAGSOR method for handling (1) while elaborating on the properties of local convergence in Sect. 3. To substantiate its practicality and efficiency, Sect. 4 presents compelling numerical results that validate the effectiveness of the MN-PAGSOR method. Finally, in Sect. 5, a succinct conclusion is provided, summarizing the key findings and contributions of this article.

2 The Modified Newton-PAGSOR (MN-PAGSOR) Method

Consider the following complex linear system:

$$\begin{aligned} Au=b,\quad A\in \mathbb {C}^{n\times n},\quad u,\ b\in \mathbb {C}^n. \end{aligned}$$

(7)

The complex symmetric linear system is structured in the following form:

$$\begin{aligned} Au=(W+\textrm{i}T)(x+\textrm{i}y)=(p+\textrm{i}q)=b, \end{aligned}$$

(8)

where $\textrm{i}=\sqrt{-1}$ is the imaginary unit, $W,T\in \mathbb {R}^{n\times n}$ are real, symmetric, and positive semi-definite matrices, and $x, y, p, q\in \mathbb {R}^n$ are real vectors. To avoid complex number operations, we can derive the equivalent real equations in the two-by-two form:

$$\begin{aligned} \left( \begin{array}{cc} W &{}-T\\ T&{}W \end{array}\right) \left( \begin{array}{cc} x\\ y \end{array}\right) =\left( \begin{array}{cc} p\\ q \end{array}\right) . \end{aligned}$$

(9)

2.1 The PAGSOR Iteration Method

Multiplying (9) to its left by the matrix

$$\begin{aligned} {\mathcal {Z}}_\omega \ =\left( \begin{array}{cc} \omega I &{} I\\ -I&{}\omega I \end{array}\right) , \quad \omega >0, \end{aligned}$$

(10)

we obtain

$$\begin{aligned} \left( \begin{array}{cc} \omega W + T &{}W-\omega T\\ \omega T - W&{}\omega W + T \end{array}\right) \left( \begin{array}{cc} x\\ y \end{array}\right) =\left( \begin{array}{cc} \omega p+q\\ \omega q-p \end{array}\right) :=\widetilde{b}. \end{aligned}$$

(11)

Denote $\widetilde{W}=\omega W + T$, $\widetilde{T}=\omega T - W$, $\widetilde{p}=\omega p+q$, $\widetilde{q}= \omega q-p$, and

$$\begin{aligned} \widetilde{A}\ =\left( \begin{array}{cc} \widetilde{W}&{} -\widetilde{T}\\ \widetilde{T}&{}\widetilde{W} \end{array}\right) . \end{aligned}$$

Then, (9) can be rewritten as

$$\begin{aligned} \widetilde{A} u:=\left( \begin{array}{cc} \widetilde{W} &{}-\widetilde{T}\\ \widetilde{T}&{}\widetilde{W} \end{array}\right) \left( \begin{array}{cc} x\\ y \end{array}\right) =\left( \begin{array}{cc} \widetilde{p}\\ \widetilde{q} \end{array}\right) . \end{aligned}$$

Note that the coefficient matrix $\tilde{A}$ can be naturally split into

$$\begin{aligned} \widetilde{A}\ =\left( \begin{array}{cc} \widetilde{W}&{}\varvec{O}\\ \varvec{O}&{}\widetilde{W} \end{array}\right) -\left( \begin{array}{cc} \varvec{O}&{}\varvec{O}\\ -\widetilde{T}&{}\varvec{O} \end{array}\right) -\left( \begin{array}{cc} \varvec{O}&{}\widetilde{T}\\ \varvec{O}&{}\varvec{O} \end{array}\right) :=\widetilde{D}-\widetilde{L}-\widetilde{U}, \end{aligned}$$

where the notation $\varvec{O}$ is used to denote the zero matrix.

By [30], the PAGSOR method for $\tilde{A}u=\tilde{b}$ is established as follows.

Algorithm 1

The PAGSOR method 

The definition of $\widetilde{W}$, $\widetilde{T}$, $\widetilde{p}$, $\widetilde{q}$ are the same as those in (11), where $\alpha$, $\beta$ are two real parameters and $\omega > 0$.

Furthermore, the iterative method (12) can be equivalently rewritten as follows:

$$\begin{aligned} \left( \begin{array}{cc} x_{k+1}\\ y_{k+1} \end{array}\right) =Q_\omega (\alpha ,\beta )\left( \begin{array}{cc} x_{k}\\ y_{k} \end{array}\right) +G_\omega (\alpha ,\beta )\left( \begin{array}{cc} \widetilde{p}\\ \widetilde{q} \end{array}\right) , \end{aligned}$$

or

$$\begin{aligned} \left( \begin{array}{cc} x_{k+1}\\ y_{k+1} \end{array}\right) =Q_\omega (\alpha ,\beta )^{k+1}\left( \begin{array}{cc} x_{0}\\ y_{0} \end{array}\right) +\sum _{j=0}^{k}Q_\omega (\alpha ,\beta )^jG_\omega (\alpha ,\beta ) \left( \begin{array}{cc} \widetilde{p}\\ \widetilde{q} \end{array}\right) ,\ k=0,1,\cdots , \end{aligned}$$

(13)

where

$$\begin{aligned}&Q_\omega (\alpha ,\beta )=\left( \begin{array}{cc} \widetilde{W}&{}\varvec{O}\\ \beta \widetilde{T}&{}\widetilde{W} \end{array}\right) ^{-1}\left( \begin{array}{cc} (1-\alpha )\widetilde{W}&{}\alpha \widetilde{T}\\ \varvec{O}&{}(1-\beta )\widetilde{W} \end{array}\right) , \end{aligned}$$

(14)

$$\begin{aligned}&G_\omega (\alpha ,\beta )= \left( \begin{array}{cc} \widetilde{W}&{}\varvec{O}\\ \beta \widetilde{T}&{}\widetilde{W} \end{array}\right) ^{-1}\left( \begin{array}{cc} \alpha I&{}\varvec{O}\\ \varvec{O}&{}\beta I \end{array}\right) . \end{aligned}$$

(15)

Obviously, the matrix $Q_\omega (\alpha ,\beta )$ is referred to as the iteration matrix of the PAGSOR method. Now, let us consider another decomposition of matrix $\widetilde{A}$,

$$\begin{aligned} \widetilde{A}=B_\omega (\alpha ,\beta )-C_\omega (\alpha ,\beta ) \end{aligned}$$

(16)

with

$$\begin{aligned}&B_\omega (\alpha ,\beta )=\left( \begin{array}{cc} \alpha I&{}\varvec{O}\\ \varvec{O}&{}\beta I \end{array}\right) ^{-1}\left( \begin{array}{cc} \widetilde{W}&{}\varvec{O}\\ \beta \widetilde{T}&{}\widetilde{W} \end{array}\right) =\left( \begin{array}{cc} \frac{1}{\alpha } I&{}\varvec{O}\\ \varvec{O}&{}\frac{1}{\beta } I \end{array}\right) \left( \begin{array}{cc} \widetilde{W}&{}\varvec{O}\\ \beta \widetilde{T}&{}\widetilde{W} \end{array}\right) , \end{aligned}$$

(17)

$$\begin{aligned}&C_\omega (\alpha ,\beta )= \left( \begin{array}{cc} \frac{1}{\alpha } I&{}\varvec{O}\\ \varvec{O}&{}\frac{1}{\beta } I \end{array}\right) \left( \begin{array}{cc} (1-\alpha )\widetilde{W}&{}\alpha \widetilde{T}\\ \varvec{O}&{}(1-\beta )\widetilde{W} \end{array}\right) . \end{aligned}$$

(18)

Evidently, we get

$$\begin{aligned} Q_\omega (\alpha ,\beta )=B_\omega (\alpha ,\beta )^{-1} \ C_\omega (\alpha ,\beta ),\quad G_\omega (\alpha ,\beta ) =B_\omega (\alpha ,\beta )^{-1}. \end{aligned}$$

(19)

Specifically, the AGSOR method, as outlined in [23], represents a particular form of the PAGSOR iterative method when $\omega =1$.

2.2 The Modified Newton-PAGSOR Method

For convenience, we introduce the following notation:

$$\begin{aligned} \hat{u}=\left( \begin{array}{cc} \textrm{Re}(u)\\ \textrm{Im}(u) \end{array}\right) , \end{aligned}$$

where $\textrm{Re}(u)$ and $\textrm{Im}(u)$ represent the real and imaginary parts of any complex vector or matrix u, respectively. Naturally, F(u) has the form $F(u)=P(u)+\textrm{i} Q(u)$, where $P(u)=\textrm{Re}(F(u))$, $Q(u)=\textrm{Im}(F(u))$. We assume that the Jacobian matrix $F'(u)$ can be expressed in the form

$$\begin{aligned} F'(u)=W(u)+\textrm{i}T(u), \end{aligned}$$

where $W(u)=\textrm{Re}(F'(u))\in \mathbb {R}^{n\times n}$, $T(u)=\textrm{Im}(F'(u))\in \mathbb {R}^{n\times n}$ are real symmetric matrices, with W(u) being positive definite and T(u) positive semi-definite.

Our MN-PAGSOR iteration method is developed to solve the complex nonlinear system, with which the PAGSOR method applied to solve the following Newton equations:

$$\begin{aligned} \left\{ \begin{array}{l} A(u_k)d_k=-H(u_k),\quad u_{k+\frac{1}{2}}=u_k+d_k,\\ A(u_k)h_k=-H(u_{k+\frac{1}{2}}),\quad u_{k+1} =u_{k+\frac{1}{2}}+ h_k ,\quad k=0,1,2,\cdots , \end{array}\right. \end{aligned}$$

(20)

where

$$\begin{aligned} A(u)=\left( \begin{array}{cc} W(u) &{}-T(u)\\ T(u)&{}W(u) \end{array}\right) , \end{aligned}$$

and

$$\begin{aligned} H(u)=\left( \begin{array}{cc} P(u)\\ Q(u) \end{array}\right) . \end{aligned}$$

(21)

Hence, we can use the following expression for the MN-PAGSOR method:

$$\begin{aligned} \widetilde{A}u_k=\left( \begin{array}{cc} \widetilde{W}(u_k) &{}-\widetilde{T}(u_k)\\ \widetilde{T}(u_k)&{}\widetilde{W}(u_k) \end{array}\right) \left( \begin{array}{cc} x_k\\ y_k \end{array}\right) =\left( \begin{array}{cc} \widetilde{P}(u_k)\\ \widetilde{Q}(u_k) \end{array}\right) =\widetilde{H}(u_k) \end{aligned}$$

(22)

with $\widetilde{W}(u_k)=\omega W(u_k)+T(u_k)$, $\widetilde{T}(u_k)=\omega T(u_k)-W(u_k)$, $u_k=x_k+\textrm{i}y_k$, $\widetilde{P}(u_k)=\omega P(u_k)+Q(u_k)$, $\widetilde{Q}(u_k)=\omega Q(u_k)-P(u_k)$.

Same as (16), (17), and (18), we need to simplify (22) and provide an approximate method to generate the next iterate, say, namely $u_{k+1}$,

$$\begin{aligned} B_\omega (\alpha ,\beta )\left( \begin{array}{cc} x_{k+1}\\ y_{k+1} \end{array}\right) =C_\omega (\alpha ,\beta )\left( \begin{array}{cc} x_k\\ y_k \end{array}\right) +\left( \begin{array}{cc} \widetilde{P}(u_k)\\ \widetilde{Q}(u_k) \end{array}\right) . \end{aligned}$$

(23)

Thus, we can construct the MN-PAGSOR method. The algorithm process is as follows.

Algorithm 2

The modified Newton-PAGSOR (MN-PAGSOR) method

According to (13) and (20), the calculating leads the expressions for $d_{k,l_k}$, $h_{k,m_k}$,

$$\begin{aligned} d_{k, l_k}= & {} -\sum _{j=0}^{l_k-1}Q_\omega (\alpha ,\beta , u_k)^{j} G_\omega (\alpha ,\beta ,u_k)\widetilde{H}(u_k), \\ h_{k, m_k}= & {} -\sum _{j=0}^{m_k-1}Q_\omega (\alpha ,\beta ,u _k)^{j} G_\omega (\alpha ,\beta ,u_k)\widetilde{H}(u_{k+\frac{1}{2}}), \end{aligned}$$

which are in the formula mentioned above and

$$\begin{aligned} Q_\omega (\alpha ,\beta ,u)= & {} \left( \begin{array}{cc} \widetilde{W}(u)&{}\varvec{O}\\ \beta \widetilde{T}(u)&{}\widetilde{W}(u) \end{array}\right) ^{-1}\left( \begin{array}{cc} (1-\alpha )\widetilde{W}(u)&{}\alpha \widetilde{T}(u)\\ \varvec{O}&{}(1-\beta )\widetilde{W}(u) \end{array}\right) , \\ G_\omega (\alpha ,\beta ,u)= & {} \left( \begin{array}{cc} \widetilde{W}(u)&{}\varvec{O}\\ \beta \widetilde{T}(u)&{}\widetilde{W}(u) \end{array}\right) ^{-1}\left( \begin{array}{cc} \alpha I&{}\varvec{O}\\ \varvec{O}&{}\beta I \end{array}\right) . \end{aligned}$$

Therefore, the MN-PAGSOR method can be expressed as

$$\begin{aligned} \left\{ \begin{array}{l} u_{k+\frac{1}{2}}=u_k-\sum \limits _{j=0}^{l_k-1}Q_\omega (\alpha ,\beta ,u_k)^{j} G_\omega (\alpha ,\beta ,u_k) \widetilde{H}(u_k),\\ u_{k+1}=u_{k+\frac{1}{2}}-\sum \limits _{j=0}^{m_k-1} Q_\omega (\alpha ,\beta ,u_k)^{j}G_\omega (\alpha ,\beta ,u_k) \widetilde{H}(u_{k+\frac{1}{2}}),\quad k=0,1,\cdots \ . \end{array}\right. \end{aligned}$$

(24)

Here, the matrix is split into

$$\begin{aligned} \widetilde{A}(u)=B_\omega (\alpha ,\beta ,u)-C_\omega (\alpha ,\beta ,u) \end{aligned}$$

(25)

with

$$\begin{aligned} B_\omega (\alpha ,\beta ,u)= & {} \left( \begin{array}{cc} \frac{1}{\alpha } I&{}\varvec{O}\\ \varvec{O}&{}\frac{1}{\beta } I \end{array}\right) \left( \begin{array}{cc} \widetilde{W}(u)&{}\varvec{O}\\ \beta \widetilde{T}(u)&{}\widetilde{W}(u) \end{array}\right) , \\ C_\omega (\alpha ,\beta )= & {} \left( \begin{array}{cc} \frac{1}{\alpha } I&{}\varvec{O}\\ \varvec{O}&{}\frac{1}{\beta } I \end{array}\right) \left( \begin{array}{cc} (1-\alpha )\widetilde{W}(u)&{}\alpha \widetilde{T}(u)\\ \varvec{O}&{}(1-\beta )\widetilde{W}(u) \end{array}\right) . \end{aligned}$$

Since these matrices have the following relationship with the iterative matrix $Q_\omega (\alpha ,\beta , u)$:

$$\begin{aligned}&Q_\omega (\alpha ,\beta , u)=B_\omega (\alpha ,\beta , u)^{-1} \ C_\omega (\alpha ,\beta , u),\quad G_\omega (\alpha ,\beta , u) =B_\omega (\alpha ,\beta , u)^{-1},\nonumber \\&\widetilde{A}(u)^{-1}=(I-Q_\omega (\alpha ,\beta , u))^{-1} G_\omega (\alpha ,\beta , u), \end{aligned}$$

(26)

we obtain finally an equivalent form of the MN-PAGSOR method,

$$\begin{aligned} \left\{ \begin{array}{l} u_{k+\frac{1}{2}}=u_k-(I-Q_\omega (\alpha ,\beta , u_k)^{l_k})\ \widetilde{A}(u_k)^{-1} \ \widetilde{H}(u_k),\\ u_{k+1}=u_{k+\frac{1}{2}}-(I-Q_\omega (\alpha ,\beta , u_k)^{m_k})\ \widetilde{A}(u_k)^{-1} \ \widetilde{H}(u_{k+\frac{1}{2}}),\quad k=0,1,\cdots \ . \end{array}\right. \end{aligned}$$

(27)

3 Local Convergence of MN-PAGSOR Method

In this section, we derive the local convergence of the MN-PAGSOR method, i.e., the iterates $u_k$ generated by the MN-PAGSOR method converge to $u_*$ for any sufficiently good initial guess $u_0$. Our analysis is based on the H$\ddot{\textrm{o}}$lder condition, which is weaker than the Lipschitz one.

Definition 1

A mapping $F{:}\,\,\mathbb {D}\subseteq \mathbb {C}^n\rightarrow \mathbb {C}^n$ is nonlinear, if there exists a linear operator $A\in \mathbb {L}(\mathbb {R}^n,\mathbb {R}^n)$ that satisfies

$$\begin{aligned} \lim _{t\rightarrow 0}\frac{1}{t}\Vert F(u+t h)-F(u)-tAh\Vert =0 \end{aligned}$$

for any $h\in \mathbb {C}^n$, then F is Gateaux differentiable (or G-differentiable) at an interior point $u\in \mathbb {D}$. Additionally, for an open set $\mathbb {D}_0\subset \mathbb {D}$, if the mapping $F{:}\,\mathbb {D}\subseteq \mathbb {C}^n\rightarrow \mathbb {C}^n$ is G-differentiable at every point in $\mathbb {D}_0$, it is said to be G-differentiable on the open set $\mathbb {D}_0$.

Lemma 1

(Perturbation Lemma [36]) Let $A,C\in \mathbb {C}^{n\times n}$, and assume that A is nonsingular satisfying $\Vert A^{-1}\Vert \leqslant p$. If $\Vert A-C\Vert \leqslant q$ and $pq< 1$, then B is also nonsingular and

$$\begin{aligned} \Vert B^{-1}\Vert \leqslant \frac{p}{1-pq}{.} \end{aligned}$$

We further require that $F{:}\,\mathbb {D}\subset \mathbb {C}^n\rightarrow \mathbb {C}^n$ is G-differentiable on an open neighborhood $\mathbb {D}_0\subset \mathbb {D}$ centered on $u_*\in \mathbb {D}$ with $F(u_*)=0$, and that the Jacobian matrix $F'(u)$ is continuous and symmetric. Let $\mathbb {N}(u_*, r)$ denote an open ball centered at $u_*$ with radius r. We find that the perturbation lemma plays a crucial role in the proofs of Lemma 2 and Theorem 1.

Assumption 1

For all $u\in \mathbb {N}(u_*,r)\subset \mathbb {D}_0$, the following conditions are established.

(A1):

(The bounded condition) There exist positive constants $\delta$ and $\gamma$ such that

$$\begin{aligned} \max \left\{ \Vert W(u_*)\Vert ,\Vert T(u_*)\Vert \right\} \leqslant \delta ,\quad \Vert A(u_*)^{-1}\Vert \leqslant \gamma . \end{aligned}$$

(A2):

(The Hölder condition) There exist nonnegative constants $K_w$ and $K_t$ such that

$$\begin{aligned}{} & {} \Vert W(u)-W(u_*)\Vert \leqslant K_w\Vert u-u_*\Vert ^p,\\{} & {} \Vert T(u)-T(u_*)\Vert \leqslant K_t\Vert u-u_*\Vert ^p \end{aligned}$$

with the exponential $p\in (0,1]$.

Lemma 2

Under Assumption 1, if $r\in (0,(\frac{1}{\gamma K})^{\frac{1}{p}})$, then $A(u)^{-1}$ exists for $u\in \mathbb {N}(u_*,r)$. Besides, the following inequalities hold with $K{:}=K_t+K_w$ for all $u,y\in \mathbb {N}(u_*,r)\subset \mathbb {D}_0$:

• (i) $\Vert A(u)-A(u_*)\Vert \leqslant K\Vert u-u_*\Vert ^{p},$

• (ii) $\Vert A(u)^{-1}\Vert \leqslant \frac{\gamma }{1-\gamma K\Vert u-u_*\Vert ^{p}},$

• (iii) $\Vert H(y)\Vert \leqslant \frac{K}{p+1}\Vert y-u_*\Vert ^{p+1}+2\delta \Vert y-u_*\Vert ,$

• (iv) $\Vert y - u _*-A( u )^{-1} H ( y )\Vert \leqslant \frac{\gamma }{1-\gamma K\Vert u - u_*\Vert ^{p}} \left( \frac{K}{p+1}\Vert y - u _*\Vert ^p +K\Vert u - u_*\Vert ^p \right) \Vert y-u_*\Vert .$

Proof

(i) The Hölder condition directly implies

$$\begin{aligned}&\qquad \quad \Vert A(u)-A(u_*)\Vert \\&\quad =\bigg \Vert \left( \begin{array}{cc} W(u)-W(u_*)&{}T(u_*)-T(u)\\ T(u)-T(u_*)&{}W(u)-W(u_*) \end{array}\right) \bigg \Vert \\&\quad \leqslant \bigg \Vert \left( \begin{array}{cc} W(u)-W(u_*)&{}\varvec{O}\\ \varvec{O}&{} W(u)-W(u_*) \end{array}\right) \bigg \Vert +\bigg \Vert \left( \begin{array}{cc} \varvec{O}&{}T(u_*)-T(u)\\ T(u)-T(u_*)&{}\varvec{O} \end{array}\right) \bigg \Vert \\&\quad =\Vert W(u)-W(u_*)\Vert +\Vert T(u)-T(u_*)\Vert \\&\quad \leqslant K_w\Vert u-u_*\Vert ^p+ K_t\Vert u-u_*\Vert ^p= K\Vert u-u_*\Vert ^p. \end{aligned}$$

(ii) Making use of this inequality

$$\begin{aligned} \Vert A(u_*)^{-1}( A(u_*)- A(u))\Vert \leqslant \Vert A(u_*)^{-1} \Vert \Vert A(u_*)- A(u)\Vert \leqslant \gamma K\Vert u - u_*\Vert ^p <1, \end{aligned}$$

and the perturbation lemma, we know that $A(u)^{-1}$ exists and satisfies

$$\begin{aligned} \Vert A(u)^{-1}\Vert \leqslant \frac{\Vert A(u_*)^{-1}\Vert }{1-\Vert A(u_*)^{-1}( A(u_*)- A(u))\Vert } \leqslant \frac{\gamma }{1-\gamma K\Vert u-u_*\Vert ^p}. \end{aligned}$$

(iii) Furthermore, the known bounded condition leads to

$$\begin{aligned} \Vert A(u_*)\Vert&\leqslant \bigg \Vert \left( \begin{array}{cc} W(u_*)&{}\varvec{O}\\ \varvec{O}&{}W(u_*) \end{array}\right) \bigg \Vert +\bigg \Vert \left( \begin{array}{cc} \varvec{O}&{}-T(u_*)\\ T(u_*)&{}\varvec{O}\end{array}\right) \bigg \Vert \\&=\Vert W(u_*)\Vert +\Vert T(u_*)\Vert \leqslant 2\delta , \end{aligned}$$

and

$$\begin{aligned} H(y)&=H(y)-H(u_*)-A(u_*)(y-u_*)+ A(u_*)(y-u_*)\\&=\int _0^1 (A(u_*+t(y-u_*))-A(u_*))\textrm{d}t(y-u_*)+A(u_*)(y-u_*). \end{aligned}$$

Consequently, we find

$$\begin{aligned} \Vert H(y)\Vert&\leqslant \Big \Vert \int _0^1 (A(u_*+t(y-u_*)) -A(u_*))\textrm{d}t(y-u_*)\Big \Vert +\Vert A(u_*)(y-u_*)\Vert \\&\leqslant \frac{K}{p+1}\Vert y-u_*\Vert ^{p+1}+2\delta \Vert y-u_*\Vert . \end{aligned}$$

(iv) Due to the following facts:

$$\begin{aligned}&\qquad \quad y-u_*-A(u)^{-1}H(y)\\&\quad =- A(u)^{-1}\Bigl ( H( y )- H(u_*)- A( u_*)(y - u_*) \Bigr ) + A(u)^{-1}\Bigl ( A( u )- A(u_*)\Bigr )( y - u_*) \\&\quad =- A( u )^{-1}\int _0^1 \Bigl ( A(u_*+ t(y - u_*))- A( u_*) \Bigr )\textrm{d}t (y - u_*) \\&\quad \quad \,\, + A( u )^{-1}\Bigl ( A( u )- A( u_*)\Bigr )( y - u_*), \end{aligned}$$

we have finally,

$$\begin{aligned}&\qquad \quad \Vert y-u_*-A_\lambda (u)^{-1}H(y)\Vert \\&\,\quad \leqslant \Vert - A(u )^{-1}\int _0^1 \Bigl (A( u_*+ t ( y - u_*))-A(u_*)\Bigr ) \textrm{d}t( y - u_*) \Vert \\&\,\quad \qquad +\Vert A( u )^{-1} \Bigl ( A( u )- A( u_*)\Bigr )( y - u_*)\Vert \\&\,\quad \leqslant \Vert A(u)^{-1}\Vert \Bigl (\int _0^1\Vert (A(u_*+t(y-u_*))-A(u_*)\Vert \textrm{d}t+\Vert (A(u)- A(u_*)\Vert \Bigr ) \Vert y-u_* \Vert \\&\quad \leqslant \frac{\gamma }{1-\gamma K\Vert u-u_*\Vert ^p} \left( \frac{K}{p+1}\Vert y-u_*\Vert ^p+K\Vert u-u_* \Vert ^p\right) \Vert y-u_*\Vert . \end{aligned}$$

The proof of Lemma 2 is completed.

Theorem 1

Under the assumptions of Lemma 2, denote $\Delta =\min \left\{ \alpha ,\beta \right\}$ and $\Lambda =\max \left\{ \vert 1-\alpha \vert ,\vert 1-\beta \vert \right\}$, suppose $r\in (0,r_0)$, define $r_0:=\min \left\{ r_1,r_2, r_3\right\}$, where

$$\begin{aligned}&r_1=\left( \frac{(1+\omega ^2)\Delta }{2\gamma (1+\omega )[(\omega +\beta ) K_w+(\beta \omega +1)K_t]}\right) ^{\frac{1}{p}},\\&r_2=\\&\left( \frac{\tau \theta (1+\omega ^2)\Delta }{2\gamma (1+\omega ) \Bigl ([(\Lambda \omega +1)+(1+\tau \theta )(\omega +\beta )] K_w +[(\alpha \omega +\Lambda )+(1+\tau \theta )(\beta \omega +1)] K_t \Bigr )}\right) ^{\frac{1}{p}},\\&r_3=\left( \frac{1-2\delta \gamma \left[ (\tau +1) \theta \right] ^{\nu _*}}{4K\gamma }\right) ^{\frac{1}{p}} \end{aligned}$$

with $\nu _*=\min \left\{ l_*, m_*\right\} , l_*=\lim \inf _{k\rightarrow \infty }l_k,\ m_*=\lim \inf _{k\rightarrow \infty }m_k$, and the quantity $\nu _*$ satisfies

$$\begin{aligned} \nu _*>-\left\lfloor \frac{ln(2\delta \gamma )}{ln((\tau +1) \theta )}\right\rfloor {,} \end{aligned}$$

where the symbol $\lfloor \cdot \rfloor$ is used to denote the smallest integer no less than the corresponding real number $\tau \in (0,\frac{1-\theta }{\theta })$ a predetermined positive constant and

$$\begin{aligned} \theta \equiv \theta (\alpha ,\beta ,u_*) =\Vert Q(\alpha ,\beta , u_*)\Vert < 1 \end{aligned}$$

with $\alpha , \beta$ satisfying $0<\alpha \beta<\alpha +1<\alpha \beta \frac{1-\rho (\widetilde{W}(u_*)^{-1}\widetilde{T}(u_*))}{2}+2$. Then, for any $u\in \mathbb {N}(u_*,r)$ and any sequences $\left\{ l_k\right\} _{k=0}^{\infty }$, $\left\{ m_k\right\} _{k=0}^{\infty }$ of positive integers, the iteration sequence $\left\{ u_k\right\} _{k=0}^{\infty }$ generated by the MN-PAGSOR method is well-defined, and hence converges to $u_*$. In addition, the following inequality holds:

$$\begin{aligned} \lim \sup _{k\rightarrow \infty }\Vert u_k-u_*\Vert ^{\frac{1}{k}} \leqslant g(r_0^p; \nu _*)^2, \end{aligned}$$

where, when $z\in (0, r)$ and $\iota > \nu _*$, then

$$\begin{aligned}{} & {} g(z^p, \iota )=\frac{\gamma }{1-\gamma Kz^p}\left( 3Kz^p +2\delta [(\tau +1)\theta ]^{\iota }\right) ,\\{} & {} \Vert Q_\omega (\alpha ,\beta ,u)\Vert \leqslant (\tau +1)\theta <1. \end{aligned}$$

Proof

First of all, by making use of the inverse matrix

$$\begin{aligned} {\mathcal {Z}}_\omega ^{-1}=\left( \begin{array}{cc} \omega I &{} I\\ -I&{}\omega I \end{array}\right) ^{-1}=\left( \begin{array}{cc} \frac{\omega }{1+\omega ^2} I &{} -\frac{1}{1+\omega ^2}I\\ \frac{1}{1+\omega ^2} I&{} \frac{\omega }{1+\omega ^2} I \end{array}\right) , \end{aligned}$$

we have

$$\begin{aligned} \Vert \widetilde{A}(u_*)^{-1}\Vert&=\Vert (\mathcal {Z}A(u_*))^{-1}\Vert \leqslant \Vert A(u_*)\Vert ^{-1}\Vert \mathcal {Z}\Vert ^{-1}\\&\leqslant \gamma \bigg \Vert \left( \begin{array}{cc} \frac{\omega }{1+\omega ^2} I &{} -\frac{1}{1+\omega ^2}I\\ \frac{1}{1+\omega ^2} I&{} \frac{\omega }{1+\omega ^2} I \end{array}\right) \bigg \Vert \\&\leqslant \gamma \Big (\bigg \Vert \left( \begin{array}{cc} \frac{\omega }{1+\omega ^2} I &{} \varvec{O}\\ \varvec{O}&{} \frac{\omega }{1+\omega ^2} I \end{array}\right) \bigg \Vert +\bigg \Vert \left( \begin{array}{cc} \varvec{O}&{} -\frac{1}{1+\omega ^2}I\\ \frac{1}{1+\omega ^2} I&{} \varvec{O} \end{array}\right) \bigg \Vert \Big )\\&\leqslant \gamma \left( \frac{\omega }{1+\omega ^2} +\frac{1}{1+\omega ^2}\right) = \gamma \ \frac{1+\omega }{1+\omega ^2}. \end{aligned}$$

Based on (26) and the inequality $\Vert Q_\omega (\alpha , \beta , u_*)\Vert \leqslant \vartheta (\alpha ,\beta ,u_*)< 1$ [30], the boundedness condition implies

$$\begin{aligned} \Vert B_{\omega }(\alpha ,\beta , u_*)^{-1} \Vert&=\Vert (I-Q_{\omega }(\alpha ,\beta , u_*))\widetilde{A}(u_*)^{-1}\Vert \\&\leqslant \Vert I-Q_\omega (\alpha ,\beta , u_*)\Vert \Vert \widetilde{A}(u_*)^{-1}\Vert \\&\leqslant (1+ \Vert Q_\omega (\alpha ,\beta , u_*)\Vert ) \Vert \widetilde{A}(u_*)^{-1} \Vert \leqslant 2\gamma \ \frac{1+\omega }{1+\omega ^2}. \end{aligned}$$

From the Hölder condition, we obtain

$$\begin{aligned} \Vert \widetilde{W}(u) -\widetilde{W}(u_*)\Vert&=\Vert \omega W(u) +T(u)-\omega W(u_*)-T(u_*)\Vert \\&\leqslant \omega \Vert W(u)-W(u_*)\Vert +\Vert T(u)-T(u_*)\Vert \\&\leqslant \omega K_w\Vert u-u_*\Vert ^p +K_t\Vert u-u_*\Vert ^p, \\ \Vert \widetilde{T}(u) -\widetilde{T}(u_*)\Vert&=\Vert \omega T(u) -W(u)-\omega T(u_*)+W(u_*)\Vert \\&\leqslant \omega \Vert T(u)-T(u_*)\Vert +\Vert W(u)-W(u_*)\Vert \\&\leqslant \omega K_t\Vert u-u_*\Vert ^p+K_w\Vert u-u_*\Vert ^p. \end{aligned}$$

Furthermore, according to Assumptions (A2), two estimates are produced as follows:

$$\begin{aligned}&\,\,\,\quad \quad \Vert B_\omega (\alpha ,\beta ,u)-B_\omega (\alpha ,\beta ,u_*)\Vert \\&\quad =\bigg \Vert \left( \begin{array}{cc} \frac{1}{\alpha } I&{} \varvec{O}\\ \varvec{O}&{}\frac{1}{\beta } I \end{array}\right) \left( \begin{array}{cc} \widetilde{W}(u) &{} \varvec{O}\\ \beta \widetilde{T}(u)&{}\widetilde{W}(u) \end{array}\right) -\left( \begin{array}{cc} \frac{1}{\alpha } I&{} \varvec{O}\\ \varvec{O}&{}\frac{1}{\beta } I \end{array}\right) \left( \begin{array}{cc} \widetilde{W}(u_*) &{} \varvec{O}\\ \beta \widetilde{T}(u_*)&{}\widetilde{W}(u_*) \end{array}\right) \bigg \Vert \\&\quad \leqslant \bigg \Vert \left( \begin{array}{cc} \frac{1}{\alpha } I&{} \varvec{O}\\ \varvec{O}&{}\frac{1}{\beta } I \end{array}\right) \bigg \Vert \bigg \Vert \left( \begin{array}{cc} \widetilde{W}(u) -\widetilde{W}(u_*)&{} \varvec{O}\\ \beta (\widetilde{T}(u)-\widetilde{T}(u_*))&{} \widetilde{W}(u)-\widetilde{W}(u_*) \end{array}\right) \bigg \Vert \\&\quad \leqslant \bigg \Vert \left( \begin{array}{cc} \frac{1}{\alpha } I&{} \varvec{O}\\ \varvec{O}&{}\frac{1}{\beta } I \end{array} \right) \bigg \Vert \left[ \bigg \Vert \left( \begin{array}{cc} \widetilde{W}(u) -\widetilde{W}(u_*)&{} \varvec{O}\\ \varvec{O}&{}\widetilde{W}(u)-\widetilde{W}(u_*) \end{array}\right) \bigg \Vert +\bigg \Vert \left( \begin{array}{cc} \varvec{O}&{} \varvec{O}\\ \beta (\widetilde{T}(u)-\widetilde{T}(u_*))&{}\varvec{O} \end{array}\right) \bigg \Vert \right] \\&\quad \leqslant \max \left\{ \frac{1}{\alpha },\frac{1}{\beta }\right\} \left[ \Vert \widetilde{W}(u)-\widetilde{W}(u_*)\Vert +\beta \Vert \widetilde{T}(u)-\widetilde{T}(u_*)\Vert \right] \\&\quad \leqslant \frac{1}{\Delta }\left( \omega K_w\Vert u-u_* \Vert ^p+K_t\Vert u-u_*\Vert ^p+\beta \omega K_t\Vert u-u_*\Vert ^p +\beta K_w\Vert u-u_*\Vert ^p\right) \\&\quad =\left( \frac{\omega +\beta }{\Delta }K_w +\frac{\beta \omega +1}{\Delta }K_t\right) \Vert u-u_*\Vert ^p, \\&\qquad \quad \Vert C_\omega (\alpha ,\beta ,u)-C_\omega (\alpha ,\beta ,u_*)\Vert \\&\quad =\bigg \Vert \left( \begin{array}{cc} \frac{1}{\alpha } I&{} \varvec{O}\\ \varvec{O}&{}\frac{1}{\beta } I \end{array}\right) \left( \begin{array}{cc} (1-\alpha ) \widetilde{W}(u) &{} \alpha \widetilde{T}(u)\\ \varvec{O}&{}(1-\beta )\widetilde{W}(u) \end{array}\right) -\left( \begin{array}{cc} \frac{1}{\alpha } I&{} \varvec{O}\\ \varvec{O}&{}\frac{1}{\beta } I \end{array}\right) \left( \begin{array}{cc} (1-\alpha )\widetilde{W}(u_*) &{}\alpha \widetilde{T}(u_*)\\ \varvec{O}&{}(1-\beta )\widetilde{W}(u_*) \end{array}\right) \bigg \Vert \\&\quad \leqslant \bigg \Vert \left( \begin{array}{cc} \frac{1}{\alpha } I&{} \varvec{O}\\ \varvec{O}&{} \frac{1}{\beta } I \end{array}\right) \bigg \Vert \left[ \bigg \Vert \left( \begin{array}{cc} (1-\alpha ) (\widetilde{W}(u) -\widetilde{W}(u_*))&{} \varvec{O}\\ \varvec{O}&{}(1-\beta )(\widetilde{W}(u)-\widetilde{W}(u_*))\end{array}\right) \bigg \Vert \right. \\&\qquad \qquad \left. +\bigg \Vert \left( \begin{array}{cc} \varvec{O}&{} \alpha (\widetilde{T}(u)-\widetilde{T}(u_*))\\ \varvec{O} &{}\varvec{O} \end{array}\right) \bigg \Vert \right] \\&\quad \leqslant \max \left\{ \frac{1}{\alpha }, \frac{1}{\beta }\right\} \left[ \max \left\{ \vert 1-\alpha \vert ,\vert 1-\beta \vert \right\} \Vert \widetilde{W}(u) -\widetilde{W}(u_*)\Vert +\alpha \Vert \widetilde{T}(u) -\widetilde{T}(u_*)\Vert \right] \\&\quad \leqslant \frac{1}{\Delta }\left( \Lambda \omega K_w \Vert u-u_*\Vert ^p+\Lambda K_t\Vert u-u_*\Vert ^p +\alpha \omega K_t\Vert u-u_*\Vert ^p+ K_w\Vert u-u_*\Vert ^p\right) \\&\quad = \left( \frac{\Lambda \omega +1}{\Delta }K_w+\frac{\alpha \omega +\Lambda }{\Delta }K_t\right) \Vert u-u_*\Vert ^p. \end{aligned}$$

If r satisfies

$$\begin{aligned} 2\gamma \frac{1+\omega }{1+\omega ^2} \left[ \left( \frac{\omega +\beta }{\Delta }K_w +\frac{\beta \omega +1}{\Delta }K_t\right) \Vert u -u_*\Vert ^p \right] < 1, \end{aligned}$$

then, by Lemma 1, we can further obtain

$$\begin{aligned} \Vert B_\omega (\alpha ,\beta ,u)^{-1}\Vert&=\frac{\Vert B_\omega (\alpha ,\beta , u_*)^{-1}\Vert }{1-\Vert B_\omega (\alpha ,\beta , u_*)^{-1}\Vert \Vert B_\omega (\alpha ,\beta , u_*)- B_\omega (\alpha ,\beta , u)\Vert } \\&\leqslant \frac{2\gamma \frac{1+\omega }{1+\omega ^2}}{1-2\gamma \frac{1+\omega }{1+\omega ^2}\left[ \left( \frac{\omega +\beta }{\Delta } K_w+\frac{\beta \omega +1}{\Delta } K_t\right) \Vert u-u_*\Vert ^p\right] }\\&=\frac{2\gamma (1+\omega )}{1+\omega ^2-2\gamma (1+\omega )\left[ \left( \frac{\omega +\beta }{\Delta }K_w+\frac{\beta \omega +1}{\Delta }K_t\right) \Vert u-u_*\Vert ^p\right] }. \end{aligned}$$

Since $r< r_1$, the following inequality holds:

$$\begin{aligned} \Vert u-u_*\Vert ^p&<\frac{(1+\omega ^2)\Delta }{2\gamma (1+\omega ) \left[ \left( \omega +\beta \right) K_w+\left( \beta \omega +1\right) K_t\right] }. \end{aligned}$$

Therefore,

$$\begin{aligned}&\qquad \quad \Vert Q_\omega (\alpha ,\beta ,u)-Q_\omega (\alpha ,\beta ,u_*)\Vert \\&\,\quad =\Vert B _\omega (\alpha ,\beta , u )^{-1} (C_\omega (\alpha ,\beta , u )- C _\omega (\alpha ,\beta , u _*))\\&\qquad \quad +( B_\omega (\alpha ,\beta , u)^{-1} -B_\omega (\alpha ,\beta , u_*)^{-1}) C _\omega (\alpha ,\beta ,u _*)\Vert \\&\,\quad \leqslant \Vert B_\omega (\alpha ,\beta , u )^{-1}\Vert \\&\qquad \quad \cdot \Bigl ( \Vert C _\omega (\alpha ,\beta , u ) -C_\omega (\alpha ,\beta , u_*)\Vert +\Vert B_\omega (\alpha ,\beta , u )- B_\omega (\alpha ,\beta , u_*) \Vert \Vert Q_\omega (\alpha ,\beta , u_*)\Vert \Bigr ) \\&\quad \leqslant \frac{2\gamma \frac{1+\omega }{1+\omega ^2}\left[ \left( \frac{\Lambda \omega +1}{\Delta }K_w+\frac{\Lambda +\alpha \omega }{\Delta }K_t\right) \Vert u-u_*\Vert ^p+\left( \frac{\omega +\beta }{\Delta }K_w+\frac{\beta \omega +1}{\Delta }K_t\right) \Vert u-u_*\Vert ^p\right] }{1-2\gamma \frac{1+\omega }{1+\omega ^2}\left[ \left( \frac{\omega +\beta }{\Delta }K_w+\frac{\beta \omega +1}{\Delta }K_t\right) \Vert u-u_*\Vert ^p\right] }\\&\quad = \frac{2\gamma \frac{1+\omega }{1+\omega ^2}\left( \frac{(\Lambda +1)\omega +\beta +1}{\Delta }K_w+\frac{(\alpha +\beta )\omega +\Lambda +1}{\Delta }K_t\right) \Vert u-u_*\Vert ^p}{1-2\gamma \frac{1+\omega }{1+\omega ^2}\left[ \left( \frac{\omega +\beta }{\Delta }K_w+\frac{\beta \omega +1}{\Delta }K_t\right) \Vert u-u_*\Vert ^p\right] }. \end{aligned}$$

Moreover, to establish the inequality $\Vert Q_\omega (\alpha ,\beta ,u)-Q_\omega (\alpha ,\beta ,u_*)\Vert \leqslant \tau \theta$, the following inequality holds:

$$\begin{aligned} \frac{2\gamma \frac{1+\omega }{1+\omega ^2} \left( \frac{(\Lambda +1)\omega +\beta +1}{\Delta }K_w +\frac{(\alpha +\beta )\omega +\Lambda +1}{\Delta }K_t\right) \Vert u-u_*\Vert ^p}{1-2\gamma \frac{1+\omega }{1+\omega ^2} \left[ \left( \frac{\omega +\beta }{\Delta }K_w +\frac{\beta \omega +1}{\Delta }K_t\right) \Vert u -u_*\Vert ^p\right] }\leqslant \tau \theta , \end{aligned}$$

so it follows that

$$\begin{aligned}&\Vert u - u_*\Vert ^p \\&\leqslant \frac{\tau \theta (1+\omega ^2) (1+\omega )^{-1}\Delta }{2\gamma \left[ (\Lambda \omega +1) +(1+\tau \theta )(\omega +\beta )\right] K_w +\left[ (\alpha \omega +\Lambda )+(1+\tau \theta ) (\beta \omega +1)\right] K_t}. \end{aligned}$$

Thus, when $r< \min \left\{ r_1, r_2\right\}$, for any $u\in \mathbb {N}(u_*,r)$, we have

$$\begin{aligned} \Vert Q_\omega (\alpha ,\beta ,u)\Vert \leqslant \Vert Q_\omega (\alpha ,\beta , u)-Q_\omega (\alpha ,\beta , u_*) \Vert +\Vert Q_\omega (\alpha ,\beta , u_*)\Vert \leqslant \tau \theta +\theta =(\tau +1)\theta <1. \end{aligned}$$

Next, the error of the iterative sequence$\left\{ u_k\right\} _{k=0}^\infty$ generated by the MN-PAGSOR method can be estimated using (27) and Lemma 2, yielding

$$\begin{aligned} \Vert u_{k+\frac{1}{2}}-u_*\Vert&=\Vert u_k-u_*-(I-Q_\omega (\alpha ,\beta , u_k)^{l_k})A(u_k)^{-1}H(u_k)\Vert \\&\leqslant \Vert u_k-u_*-A(u_k)^{-1}H(u_k)\Vert +\Vert Q_{\omega } (\alpha ,\beta , u_k)^{l_k}\Vert \Vert A(u_k)^{-1}H(u_k)\Vert \\&\leqslant \frac{\gamma }{1-\gamma K\Vert u_k-u_*\Vert ^p} \Bigl (\frac{K}{p+1}\Vert u_k-u_*\Vert ^{p+1}+K\Vert u_k-u_* \Vert ^{p+1}\Bigr )\\&\quad +\frac{\gamma [(\tau +1)\theta ]^{l_k}}{1-\gamma K \Vert u_k-u_*\Vert ^p}\left( \frac{K}{p+1}\Vert u_k-u_*\Vert ^{p+1} +2\delta \Vert u_k-u_*\Vert \right) \\&\leqslant \frac{\gamma K(p+2)}{(p+1)(1-\gamma K\Vert u_k-u_*\Vert ^p)} \Vert u_k-u_*\Vert ^{p+1}\\&\quad +\frac{\gamma [(\tau +1)\theta ]^{l_k}}{1-\gamma K\Vert u_k - u_*\Vert ^p}\Bigl (\frac{K}{p+1}\Vert u_k-u_*\Vert ^{p+1} +2\delta \Vert u_k - u_*\Vert \Bigr )\\&\leqslant \frac{\gamma K(p+2)+\gamma K [(\tau +1)\theta ]^{l_k}}{(p+1)(1-\gamma K\Vert u_k-u_*\Vert ^p)}\Vert u_k-u_* \Vert ^{p+1}\\&\quad +\frac{2\delta \gamma [(\tau +1)\theta ]^{l_k}}{1-\gamma K\Vert u_k-u_*\Vert ^p}\Vert u_k-u_*\Vert \\&=\frac{\gamma }{1-\gamma K\Vert u_k-u_*\Vert ^p}\\&\quad \cdot \left\{ \frac{K(p+2+[(\tau +1)\theta ]^{l_k})}{p+1}\Vert u_k-u_* \Vert ^p+2\delta [(\tau +1)\theta ]^{l_k}\right\} \Vert u_k-u_*\Vert \\&:=g(\Vert u_k-u_*\Vert ^p, l_k)\Vert u_k-u_*\Vert < \Vert u_k-u_*\Vert . \end{aligned}$$

Here, we use the notation

$$\begin{aligned} g(z^p, \iota )=\frac{\gamma }{1-\gamma Kz^p} \{3Kz^p+2\delta [(\tau +1)\theta ]^{\iota }\}. \end{aligned}$$

Considering the assumption that

$$\begin{aligned} \gamma {\{3Kr_0^p+2\delta [(\tau +1)\theta ]^{\nu _*}\}}<1-\gamma Kr_0^p, \end{aligned}$$

which is equivalent to

$$\begin{aligned} r_0<\left\{ \frac{1-2\delta \gamma [(\tau +1)\theta ]^{\nu _*}}{4K\gamma }\right\} ^{\frac{1}{p}}:=r_3. \end{aligned}$$

From the fact that $u_k\in \mathbb {N}(u_*, r)$, we can conclude that the following inequality holds:

$$\begin{aligned} g(\Vert u_k-u_*\Vert ^p, l_k)&\leqslant \frac{\gamma }{1-\gamma K r_0^{p}}\Bigl \{3Kr_0^{p} +2\delta [(\tau +1)\theta ]^{\nu _*} \Bigr \}=g(r_0^{p},\nu _*)< 1. \end{aligned}$$

Therefore, when $r< r_3$

$$\begin{aligned} \Vert u_{k+\frac{1}{2}}-u_*\Vert <\Vert u_k-u_*\Vert . \end{aligned}$$

Similarly,

$$\begin{aligned}&\qquad \,\,\,\Vert u_{k+1}-u_*\Vert \\&\quad =\Big \Vert u_{k+\frac{1}{2}}-u_*-(I-Q_{\omega }(\alpha ,\beta , u_k)^{m_k})A(u_k)^{-1}H(u_{k+\frac{1}{2}})\Big \Vert \\&\quad \leqslant \Big \Vert u_{k+\frac{1}{2}}-u_*-A(u_k)^{-1}H \left( u_{k+\frac{1}{2}}\right) \Vert +\Vert A(u_k)^{-1}H(u_{k+\frac{1}{2}})\Big \Vert \\&\quad \leqslant \frac{\gamma }{1-\gamma K\Vert u_k-u_*\Vert ^p} \Bigl (\frac{K}{p+1}\Vert u_{k+\frac{1}{2}}-u_*\Vert ^{p+1} +K\Vert u_k-u_*\Vert ^{p}\Bigr )\Vert u_{k+\frac{1}{2}}-u_*\Vert \\&\qquad +\frac{[(\tau +1)\theta ]^{m_k}\gamma }{1-\gamma K\Vert u_k-u_*\Vert ^p}\left( \frac{K}{p+1}\Vert u_{k+\frac{1}{2}}-u_*\Vert ^{p+1}+2\delta \Vert u_{k+\frac{1}{2}}-u_*\Vert \right) \\&\quad \leqslant \frac{\gamma K}{1-\gamma K\Vert u_k-u_*\Vert ^P}\left\{ \frac{1+[(\tau +1)\theta ]^{m_k}}{p+1}\Vert u_{k+\frac{1}{2}}-u_*\Vert ^{p+1}\right\} \\&\qquad +\frac{\gamma }{1-\gamma K\Vert u_k-u_*\Vert ^P}\Bigl \{K\Vert u_k-u_*\Vert ^p+2\delta [(\tau +1)\theta ]^{m_k}\Bigr \}\Vert u_{k+\frac{1}{2}}-u_*\Vert \\&\quad \leqslant \frac{\gamma g(\Vert u_k-u_*\Vert ^p, l_k)}{1-\gamma K\Vert u_k-u_*\Vert ^p}\Vert u_k-u_*\Vert \Bigl \{\frac{g(\Vert u_k-u_* \Vert ^p, l_{k})^{p}(1+[(\tau +1)\theta ]^{m_k})+p+1}{p+1}\\&\qquad \cdot K \Vert u_k-u_*\Vert ^{p} +2\delta [(\tau +1)\theta ]^{m_k} \Bigr \}\\&\quad \leqslant \frac{\gamma g(\Vert u_k-u_*\Vert ^p, l_k)}{1-\gamma K\Vert u_k-u_*\Vert ^p}\Vert u_k-u_*\Vert \Bigl \{[(2g(\Vert u_k-u_*\Vert ^p, l_k)^{p}+1)]K\Vert u_k-u_*\Vert ^p\\&\qquad +2\delta [(\tau +1)\theta ]^{m_k}\Bigr \}\\&\quad \leqslant \frac{\gamma g(\Vert u_k-u_*\Vert ^p, l_k)}{1-\gamma K\Vert u_k-u_*\Vert ^p} \Bigl \{3 K\Vert u_k-u_*\Vert ^p +2\delta [(\tau +1)\theta ]^{m_k} \Bigr \}\Vert u_k-u_*\Vert \\&\quad \leqslant g(\Vert u_k-u_*\Vert ^p, l_k) g(\Vert u_k-u_*\Vert ^p, m_k)\Vert u_k-u_*\Vert \\&\quad< g(r_0^{p}, \nu _*)^2\Vert u_k-u_*\Vert <\Vert u_k-u_*\Vert . \end{aligned}$$

That is

$$\begin{aligned} \Vert u_{k+1}-u_*\Vert <\Vert u_k-u_*\Vert . \end{aligned}$$

For arbitrary $u_0\in \mathbb {N}(u_*, r)\subset \mathbb {D}_0$, the following inequality holds:

$$\begin{aligned} 0\leqslant \dots<\Vert u_{k+1}-u_*\Vert<\Vert u_k-u_* \Vert<\dots<\Vert u_0-u_*\Vert < r. \end{aligned}$$

Consequently, the iterative sequence $\left\{ u_k\right\} _{k=0}^{\infty }$ is well-posed and converges to $u_*$. Additionally, from $\Vert u _{k+1}-u_*\Vert < g(r_0^{p}, \nu _*)^2\Vert u_k-u_*\Vert$, it follows that $\Vert u_k-u_*\Vert < g(r_0^{p}, \nu _*)^{2k}\Vert u_0-u_*\Vert$, the following inequality is correct:

$$\begin{aligned} \Vert u_k-u_*\Vert ^{\frac{1}{k}}< g(r_0^{p},\nu _*)^{2} \Vert u_0-u_*\Vert ^{\frac{1}{k}}, \end{aligned}$$

as $k\rightarrow \infty$, ${\lim \sup }_{k \rightarrow \infty }\Vert u_k-u_*\Vert ^{\frac{1}{k}}\leqslant g(r_0^{p}, \nu _*)^2$.

Table 1 The optimal parameters of Newton methods for Example 1

Table 2 Numerical results of the modified Newton methods for $\sigma =0.1, \rho =1$

Table 3 Numerical results of the modified Newton methods for $\sigma =0.2, \rho =1$

Table 4 Numerical results of the modified Newton methods for $\sigma =0.4, \rho =1$

Table 5 Numerical results of the modified Newton methods for $\sigma =0.1, \rho =10$

Table 6 Numerical results of the modified Newton methods for $\sigma =0.2, \rho =10$

Table 7 Numerical results of the modified Newton methods for $\sigma =0.4, \rho =10$

Table 8 Numerical results of the modified Newton methods for $\sigma =0.1,\rho =200$

Table 9 Numerical results of the modified Newton methods for $\sigma =0.2,\rho =200$

Table 10 Numerical results of the modified Newton methods for $\sigma =0.4, \rho =200$

4 Numerical Results

In this section, we list two frequently encountered complex nonlinear systems and compute their numerical solutions by using the respective methods. The experimental results are then compared to verify the effectiveness and feasibility of our approach. The known methods we have experimented with are MN-GSOR, MN-DGPMHSS, and MN-AGSOR methods which utilize the modified Newton method as the external iteration and GSOR, DGPMHSS, and AGSOR as the internal iterations. To ensure the reliability of the results, we have compared not only the CPU time consumption of the algorithms, but also their inner and outer iteration steps. The optimal parameters of each method and detailed information on computational results are listed below for comparison. In the tables below, the error estimation is denoted as Error, CPU time in seconds is referred to as CPU time (s), outer iteration steps are indicated as Outer IT, and inner iteration steps as Inner IT. The numerical experiments demonstrate that our method outperforms the MN-GSOR, MN-DGPMHSS, and MN-AGSOR methods. All experiments are implemented on MATLAB [version 9.12.0.2039608 (R2022a)] and run on a personal computer with a configuration of 8-core Central Processing Unit [Apple M2] and 16.00 GB memory.

Example 1

Consider the following nonlinear equations:

$$\begin{aligned} \left\{ \begin{array}{ll} u_t-(\alpha _1+\textrm{i}\beta _1)(u_{xx}+u_{y y})+\rho u =-(\alpha _2+\textrm{i}\beta _2)u^{\frac{4}{3}}, &{} \textrm{in} \ (0,1]\times \Omega ,\\ u(0, x, y)=u_{0}(x, y), &{} \textrm{in} \ \Omega ,\\ u(t, x, y)= 0, &{} \textrm{on} \ (0, 1] \times \partial \Omega , \end{array}\right. \end{aligned}$$

Table 11 The optimal parameters of Newton methods for Example 2

Table 12 Numerical results of the modified Newton methods for $\sigma =0.1, \rho =10$

Table 13 Numerical results of the modified Newton methods for $\sigma =0.2, \rho =10$

Table 14 Numerical results of the modified Newton methods for $\sigma =0.4, \rho =10$

Table 15 Numerical results of the modified Newton methods for $\sigma =0.1, \rho =200$

Table 16 Numerical results of the modified Newton methods for $\sigma =0.2, \rho =200$

Table 17 Numerical results of the modified Newton methods for $\sigma =0.4, \rho =200$

where $\Omega = (0, 1)\times (0, 1)$, and $\partial \Omega$ is its boundary. The coefficients $\alpha _1=\alpha _2=1,\ \beta _1 =\beta _2=0.5$, and $\rho$ is a positive constant used to control the reaction term. By discretizing the above problem on equidistant grids $\Delta t=h=\frac{1}{N+1}$ (N is a given positive constant), at each temporal step of the implicit scheme, we should consider a system of nonlinear equations (1) of the form

$$\begin{aligned} F(u)=Mu+(\alpha _2+\textrm{i} \beta _2)h\Delta t\Psi (u)=0, \end{aligned}$$

where

$$\begin{aligned}{} & {} M=h(1+\rho \Delta t)I_n+(\alpha _1+\textrm{i}\beta _1) \frac{\Delta t}{h} (A_N\otimes I_N+I_N\otimes A_N), \\{} & {} \Psi (u)=\left( u_1^{\frac{4}{3}}, u_2^{\frac{4}{3}}, \cdots , u_n^{\frac{4}{3}}\right) ^\textrm{T}, \end{aligned}$$

and $A_N$ is a tridiagonal matrix of the following form:

$$\begin{aligned} A_N=\textrm{tridiag}(-1, 2, -1)\in \mathbb {R}^{N\times N}. \end{aligned}$$

Here, the vector $u=(u_1, u_2,\cdots ,u_n)^\textrm{T}$, $n=N^2$, and $\otimes$ represents the Kronecker product.

We choose $u_0=1$ to start the numerical computation and use the following stopping criterion for the outer iteration:

$$\begin{aligned} \frac{\Vert H(u_k)\Vert _2}{\Vert H(u_0)\Vert _2}\leqslant 10^{-10}. \end{aligned}$$

To control the accuracy of the inner iteration, both $\sigma _k$ and $\widetilde{\sigma _k}$ are set to be $\sigma$. As a result, we need the following inequalities:

$$\begin{aligned}{} & {} \frac{\Vert \widetilde{H}(u_k)+\widetilde{A}(u_k) d_{k,l_k}\Vert }{\Vert \widetilde{H}(u_k) \Vert }\leqslant \sigma ,\\{} & {} \frac{\Bigg \Vert \widetilde{H}\left( u_{k+\frac{1}{2}}\right) +\widetilde{A} (u_k)h_{k,m_k}\Bigg \Vert }{\Bigg \Vert \widetilde{H}\left( u_{k+\frac{1}{2}}\right) \Bigg \Vert } \leqslant \sigma . \end{aligned}$$

In Table 1, we have listed the optimal parameter $\alpha$ for the MN-GSOR method, ($\alpha , \beta$) for MN-DGPMHSS and MN-AGSOR methods, and ($\alpha , \beta , \omega$) for the MN-PAGSOR method. These optimal parameters obtained from each of the methods in the numerical experiments listed here are used to compare their performance. As for a one-parameter method, there is conducted theoretical analysis for the optimal parameter; see, for example, [6, 7, 9] and references therein. But for any kind of multi-parameter method, there is either theoretical analysis for optimal parameters which is too complicated to be available, or actually no such theoretical analysis. So, we directly use numerical experimentation to determine the choice of optimal parameters. Furthermore, the numerical results show us that, as the size of the nonlinear system problem increases, the optimal parameters of the MN-PAGSOR method remain relatively stable.

In our numerical experiments, the size of the discretization N, the control parameter $\rho$, and the inner tolerance $\sigma$ are chosen unified as: $N=30, 40, 50, 100,$ $\rho =1, 10, 200,$ and $\sigma =0.1, 0.2, 0.4.$

In Tables 2–10, the four methods MN-GSOR, MN-DGPMHSS, MN-AGSOR, and MN-PAGSOR are compared for efficiency. Our numerical results in these tables demonstrate that the proposed MN-PAGSOR method has a smaller computation time than that of the other three methods. Additionally, the MN-PAGSOR method requires fewer inner and outer iteration steps. It can also be observed that the iteration steps of the MN-PAGSOR method remain relatively stable as the problem size increases. In other words, the MN-PAGSOR method converges more quickly compared to other methods. It is an effective improvement and one gets a promising approach.

Example 2

Consider the following two-dimensional complex nonlinear convection-diffusion equation:

$$\begin{aligned} \left\{ \begin{array}{ll} -(\alpha _1+\textrm{i}\beta _1)(u_{xx}+u_{y y})+\rho u =-(\alpha _2+\textrm{i}\beta _2)u \textrm{e}^u, &{} (x,y) \ \textrm{in} \ \Omega ,\\ u(x, y)= 0, &{} (x,y) \ \textrm{on} \ \partial \Omega , \end{array}\right. \end{aligned}$$

where $\Omega = (0, 1)\times (0, 1)$, and $\partial \Omega$ is its boundary. The coefficients $\alpha _1=1, \alpha _2=-1,\ \beta _1 =\beta _2=0.5$, and $\rho$ is a positive constant used to control the reaction term. By discretizing above problem on equidistant grids $h=\frac{1}{N+1}$ (N is a given positive constant), we should consider a system of nonlinear equations (1) of the form

$$\begin{aligned} F(u)=Mu+(\alpha _2+\textrm{i}\beta _2)h^2\phi (u)=0, \end{aligned}$$

where

$$\begin{aligned}{} & {} M=\rho h^2 I_n+(\alpha _1+\textrm{i}\beta _1)(A_N\otimes I_N+I_N\otimes A_N), \\{} & {} \phi (u)=(u_1\textrm{e}^{u_1}, u_2\textrm{e}^{u_2}, \dots , u_n\textrm{e}^{u_n})^\textrm{T} \end{aligned}$$

with the vector $u=(u_1, u_2,\cdots , u_n)^\textrm{T},$ $n= N^2$. The symbols $A_N,$ N, and $\otimes$ are consistent with Example 1.

Table 11 lists the optimal parameters for the four methods we mentioned before.

In our numerical experiments, the size of the discretization N, the control parameter $\rho$, and the inner tolerance $\sigma$ are chosen unified as: $N=120, 130$, $\rho =10, 200$, and $\sigma =0.1, 0.2, 0.4$.

In Tables 12–17, the four methods MN-GSOR, MN-DGPMHSS, MN-AGSOR, and MN-PAGSOR are compared for efficiency. We observe that our MN-PAGSOR method consistently outperforms the MN-GSOR, MN-DGPMHSS, and MN-AGSOR methods in terms of inner iteration steps, outer iteration steps, and CPU time under the same problem size. This highlights the superior performance of our proposed MN-PAGSOR algorithm in solving a class of complex nonlinear systems with complex symmetric Jacobians. Furthermore, the numerical results indicate that the iteration steps of the MN-PAGSOR method remain relatively stable as the problem size varies, demonstrating its robust stability. These findings reinforce the effectiveness and promising potential of the MN-PAGSOR method.

5 Conclusion

In this study, we propose the modified Newton-PAGSOR method for a class of large sparse systems of nonlinear equations with complex symmetric Jacobian matrices. Additionally, we investigate the local convergence of the MN-PAGSOR method under the Hölder continuity conditions. Numerical results demonstrate the feasibility and effectiveness of the new method, showing that MN-PAGSOR outperforms other methods in terms of computational time and number of iterations. Moreover, our numerical experiments reveal that the optimal parameters selected for MN-PAGSOR are more stable compared to other methods. However, further research is still needed to investigate the semi-local convergence analysis and optimal selection of multiple parameters, which remains an interesting problem for future study.