Conforming P₃ Divergence-Free Finite Elements for the Stokes Equations on Subquadrilateral Triangular Meshes

Abstract

The continuous $P_3$ and discontinuous $P_2$ finite element pair is stable on subquadrilateral triangular meshes for solving 2D stationary Stokes equations. By putting two diagonal lines into every quadrilateral of a quadrilateral mesh, we get a subquadrilateral triangular mesh. Such a velocity solution is divergence-free point wise and viscosity robust in the sense the solution and the error are independent of the viscosity. Numerical examples show an advantage of such a method over the Taylor-Hood $P_3$-$P_2$ method, where the latter deteriorates when the viscosity becomes small.

1 Introduction

We solve a model Stokes problem,

$$\begin{aligned} -\mu \Delta \textbf{u} + \nabla p&=\textbf{f} \quad \hbox \mathrm{{in }} \ \varOmega , \\ \textbf{u}&=\textbf{0} \quad \hbox \mathrm{{on }} \ \partial \varOmega , \end{aligned}$$

where $\mu >0$ is the viscosity and $\varOmega$ is bounded polygonal domain in 2D. The weak form is: find $(\textbf{u}, p)\in H^1_0(\varOmega )\times L^2_0(\varOmega )$ such that

$$\begin{aligned} (\mu \nabla \textbf{u}, \nabla \textbf{v}) - (p, {\text {div}}\,\textbf{v})&= (\textbf{f}, \textbf{v}), \quad \forall \textbf{v} \in H^1_0(\varOmega ), \end{aligned}$$

(1)

$$\begin{aligned} (q, {\text {div}}\,\textbf{u})&=0, \quad \forall q \in L^2_0(\varOmega ). \end{aligned}$$

(2)

A natural finite element method for the Stokes equations would be the $P_k$-$P_{k-1}$ element on triangular and tetrahedral grids which approximates the velocity in an $H^1$-subspace $\textbf{V}_h$ of continuous $P_k$ functions (referred as $C^0$-$P_k$), and approximates the pressure in an $L^2$-subspace $P_h$ of discontinuous $P_{k-1}$ functions (referred as $C^{-1}$-$P_{k-1}$). In this case, the finite element problem reads: find $(\textbf{u}_h, p_h)\in \textbf{V}_h\times P_h \subset H^1_0(\varOmega )\times L^2_0(\varOmega )$ such that

$$\begin{aligned} (\mu \nabla \textbf{u}_h, \nabla \textbf{v}_h) - (p_h, {\text {div}}\,\textbf{v}_h)&= (\textbf{f}, \textbf{v}_h), \quad \forall \textbf{v}_h \in \textbf{V}_h, \end{aligned}$$

(3)

$$\begin{aligned} (q_h, {\text {div}}\,\textbf{u}_h)&=0, \quad \forall q_h \in P_h. \end{aligned}$$

(4)

In this case the divergence-free condition is satisfied point wise and the discrete solution for the velocity is the Galerkin projection within the space of divergence-free functions. Therefore the numerical solution $\textbf{u}_h$ is independent of p and its error is independent of the viscosity $\mu$. But other methods, for example, the Taylor-Hood finite element, would deteriorate when $\mu$ is small. However, the $P_k$-$P_{k-1}$ method is not stable in general. Scott and Vogelius showed in [16, 17] that the method is stable and consequently of the optimal order on 2D triangular grids for polynomial degree $k\geqslant 4$, provided the grids have no nearly-singular vertex. Many works on the divergence-free $P_k$-$P_{k-1}$ finite element method have been done, mostly on macro-type meshes or with bubble stabilization, cf. [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15, 19,20,21,22,23,24,25,26].

The $P_3$-$P_2$ finite element is not stable. In [4], it is stabilized by enriching $P_3$ space with some rational, divergence-free bubbles. In Zhang-P₃, it is stabilized by enriching $P_3$ space with some $P_4$ divergence-free bubbles. Computationally, these methods solved the problem. Mathematically, one would like to know if the method can be stable without adding bubbles in some cases. If so, the method would be more efficient in computation without bubbles.

Fig. 1

a Two triangles in a triangular mesh form a quadrilateral. b A subquadrilateral triangular mesh. c A subquadrilateral triangular mesh without any singular vertex

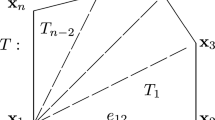
The $P_3$-$P_2$ finite element is not stable on general triangular meshes. In this work, we show the element is stable on subquadrilateral triangular meshes. What is a subquadrilateral triangular mesh? After we put two diagonal lines into every quadrilateral in a quadrilateral mesh, we get a subquadrilateral triangular mesh. We can also obtain such a mesh from a quasi-uniform triangular mesh of even number of triangles, see Fig. 1. We simply connect the two opposite points on two sides of an edge which is shared by a pair of triangles, see Fig. 1b. In both cases, the intersection point is a singular vertex, in terms of finite element analysis. At a singular vertex, the discrete pressure function is not a totally discontinuous $P_2$ function. The four values of a discrete pressure $p_2(\textbf{x})$ are subject to a continuity condition that $\sum _{i=1}^4 (-1)^i p_2|_{T_i}(\textbf{n}_0)=0$, where $\textbf{n}_0$ is the intersection point. A singular vertex would cause some extra work in computer coding. To avoid a singular vertex in this case, one can move the center point to any point of distance Ch away for some fixed $C>0$, see Fig. 1c. If it is moved a way by a distance, say $h^2$, we would have a nearly singular vertex. Then the method is no longer stable. Though a singular vertex creates more coding work, the method would be more accurate and be more efficient with less degrees of freedom. We limit this work on the case with a singular vertex. Numerical tests are presented confirming the theory. Numerical comparison also shows the robustness of the method when $\mu<<1$, and its advantage over the Taylor-Hood $P_3$-$P_2$ method.

Because the method is divergence-free, its pressure error is usually 100 times larger than that of the $P_3$-$P_2$ Taylor-Hood element. However, for large Reynolds number flows, this method would be a Reynolds number times better, e.g., both pressure and velocity errors are $10^6$ times less than that of the other method, cf. Tables 2 and 4. One would expect that it is more efficient numerically if one subdivides a quadrilateral into two triangles instead of four. But if we view the grid at a $45^{\text{o}}$ rotation, we would realize this 4-triangle subdivision is exactly a 2-triangle subdivision on size $h/\sqrt{2}$ quadrilaterals. Thus the two subdivisions are equally efficient.

2 Inf-sup Stability

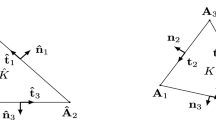
Let $\mathcal {Q}_h=\{Q\}$ be a quasi-uniform quadrilateral mesh on the domain $\varOmega$, where $h=\max \{ \hbox \mathrm{{diameter}} (Q) \}$. Connecting two pairs of points on each quadrilateral $Q(=\cup _{i=1}^4 T_i)$, we obtain a quasi-uniform triangular mesh $\mathcal {T}_h=\{T_i\}$, see Fig. 2.

The velocity finite element space is defined by

$$\begin{aligned} \textbf{V}_h&=\left\{ \textbf{v}_h\in H^1_0(\varOmega )^2 {:} \; \textbf{v}_h|_{T_i}\in P_3(T_i)^2, \ T_i\in \mathcal {T}_h \right\} . \end{aligned}$$

(5)

The pressure finite element space is defined by

$$\begin{aligned} P_h&=\left\{ p_h\in L_0^2(\varOmega ) {:} \; p_h|_{T_i}\in P_2, \ \sum _{i=1}^4 (-1)^i p_h|_{T_i}(\textbf{n}_0)=0 \right\} , \end{aligned}$$

(6)

where $\textbf{n}_0$ is the intersection point of two diagonals of quadrilateral $Q=\cup _{i=1}^4 T_i$.

Lemma 1

Let $p_2\in P_h$ defined in (6). There is a $\textbf{u}_h\in \textbf{V}_h$, defined in (5), such that

$$\begin{aligned} { {\text {div}}\,\textbf{u}_h = p_2 \quad {{ and }} \quad|\textbf{u}_h|_1 \leqslant C \Vert p_2\Vert _0. } \end{aligned}$$

(7)

Consequently,

$$\begin{aligned} \beta \leqslant \inf _{p_h\in P_h} \sup _{\textbf{v}_h\in \textbf{V}_h} \frac{ ({\text {div}}\,\textbf{v}_h, p_h) }{|\textbf{v}_h|_{1} \Vert p_h\Vert _0}, \end{aligned}$$

(8)

where $\beta >0$ is independent of the mesh size h.

Proof

Let $p_2\in P_h$. There is a smooth function $\textbf{u}\in H^1_0(\varOmega )^2\cap H^2(\varOmega )^2$ such that

$$\begin{aligned}{ {\text {div}}\,\textbf{u} = p_2 \quad \hbox \mathrm{{ and \ }} |\textbf{u}|_1 \leqslant C \Vert p_2\Vert _0. } \end{aligned}$$

We do a modified Lagrange interpolation $\textbf{u}_{h,1}$ of $\textbf{u}$. Except one node each edge, we interpolate $\textbf{u}_{h,1}(\textbf{n}_i)=\textbf{u}(\textbf{n}_i)$ at the rest nodes. At the special mid-edge nodes, $\textbf{u}_{h,1}(\textbf{n}_i)$ are chosen such that

$$\begin{aligned} \int _{\textbf{x}_1\textbf{n}_0} (\textbf{u}_{h,1} -\textbf{u})\cdot \textbf{n} {\text{d}}s =0, \end{aligned}$$

where $\textbf{n}$ is a normal vector on edge $\textbf{x}_1\textbf{n}_0$, see Fig. 2. Let

$$\begin{aligned} p_{2,1} = p_2 -{\text {div}}\,\textbf{u}_{h,1} \in P_h. \end{aligned}$$

(9)

Then we have, for all $T_i\in \mathcal {T}_h$,

$$\begin{aligned} \begin{aligned} \int _{T_i} p_{2,1} {\text{d}} \textbf{x} = \int _{T_i} ({\text {div}}\,\textbf{u} -{\text {div}}\,\textbf{u}_{h,1}) {\text{d}} \textbf{x}= \int _{\partial T_i} ( \textbf{u} - \textbf{u}_{h,1})\cdot \textbf{m}_i {\text{d}} s = 0, \end{aligned} \end{aligned}$$

(10)

where $\textbf{m}_i$ is the outward normal vector of $T_i$.

Fig. 2

Lagrange nodes on $T_1$

We will match $p_{2,1}$ separately by constructing a $\textbf{u}_h\in H^1_0(Q)^2\cap \textbf{V}_h$, on each patch of four triangles $Q=\cup _{i=1}^4 T_i$, cf. Fig. 2.

Such a $\textbf{u}_h$, as $\textbf{u}_h|_{\textbf{x}_1\textbf{x}_2}=\textbf{0}$, has the following expansion under the Lagrange basis that

$$\begin{aligned} \textbf{u}_h|_{T_1} = \sum _{i=0}^5 \textbf{u}_h(\textbf{n}_i)\phi _i(\textbf{x}). \end{aligned}$$

(11)

We replace the degree of freedom (DOF) of $P_3$ basis function of nodal value at $\textbf{n}_1$, cf. Fig. 2, by the tangential derivative basis function at point $\textbf{x}_1$. We do same replacement for Lagrange $\textbf{n}_3$ node. That is,

$$\left\{ {\begin{array}{*{20}l} \partial _{\textbf{x}_1\textbf{n}_0}\phi _1(\textbf{x}_1)&= 1,&\partial _{\textbf{x}_2\textbf{n}_0}\phi _1(\textbf{x}_2)&= 0, \\ \partial _{\textbf{x}_1\textbf{n}_0}\phi _3(\textbf{x}_1)&= 0,&\partial _{\textbf{x}_2\textbf{n}_0}\phi _3(\textbf{x}_2)&= 1, \\ \partial _{\textbf{x}_1\textbf{n}_0}\phi _2(\textbf{x}_1)&= 0,&\partial _{\textbf{x}_2\textbf{n}_0}\phi _2(\textbf{x}_2)&= 0. \hfill \\ \end{array} } \right. $$

(12)

Let

$$\begin{aligned} B = \begin{pmatrix}\textbf{x}_2-\textbf{x}_1&\textbf{n}_0 - \textbf{x}_1\end{pmatrix}, \quad \begin{pmatrix}b_{11} &{} b_{12}\\ b_{21}&{} b _{22}\end{pmatrix} = B^{-\intercal }. \end{aligned}$$

Then

$$\begin{aligned} {\text {div}}\,\textbf{u}_h|_{T_1}(\textbf{x}_1)&= \partial _x(\textbf{u}_h)_1 + \partial _y(\textbf{u}_h)_2 \\&= b_{11} \partial _{\textbf{x}_1\textbf{x}_2} (\textbf{u}_h)_1 + b_{12} \partial _{\textbf{x}_1\textbf{n}_0} (\textbf{u}_h)_1 \\ {}&\quad \ + b_{21} \partial _{\textbf{x}_1\textbf{x}_2} (\textbf{u}_h)_2 + b_{22} \partial _{\textbf{x}_1\textbf{n}_0} (\textbf{u}_h)_2 \\&= b_{12} \partial _{\textbf{x}_1\textbf{n}_0} (\textbf{u}_h)_1 + b_{22} \partial _{\textbf{x}_1\textbf{n}_0} (\textbf{u}_h)_2 \\&= \textbf{b}_2 \cdot \partial _{\textbf{x}_1\textbf{n}_0} \textbf{u}_h |_{T_1}(\textbf{x}_1) , \end{aligned}$$

where $\textbf{b}_2=\langle b_{12}, b_{22}\rangle$. Similarly, on $T_4$,

$$\begin{aligned}{\text {div}}\,\textbf{u}_h|_{T_4}(\textbf{x}_1)&= \partial _x(\textbf{u}_h)_1 + \partial _y(\textbf{u}_h)_2 \\&= c_{11} \partial _{\textbf{x}_1\textbf{x}_2} (\textbf{u}_h)_1 + c_{12} \partial _{\textbf{x}_1\textbf{n}_0} (\textbf{u}_h)_1 \\ {}&\quad \ + c_{21} \partial _{\textbf{x}_1\textbf{x}_2} (\textbf{u}_h)_2 + c_{22} \partial _{\textbf{x}_1\textbf{n}_0} (\textbf{u}_h)_2 \\&= c_{12} \partial _{\textbf{x}_1\textbf{n}_0} (\textbf{u}_h)_1 + c_{22} \partial _{\textbf{x}_1\textbf{n}_0} (\textbf{u}_h)_2 \\&= \textbf{c}_2 \cdot \partial _{\textbf{x}_1\textbf{n}_0} \textbf{u}_h |_{T_4}(\textbf{x}_1) , \end{aligned}$$

where $\textbf{c}_2=\langle c_{12}, c_{22}\rangle$, and

$$\begin{aligned} C = \begin{pmatrix}\textbf{x}_4-\textbf{x}_1&\textbf{n}_0 - \textbf{x}_1\end{pmatrix}, \quad \begin{pmatrix}c_{11} &{} c_{12}\\ c_{21}&{} c _{22}\end{pmatrix} = C^{-\intercal }. \end{aligned}$$

Together, we have a linear system of two equations,

$$\left\{ {\begin{array}{*{20}l} \textbf{b}_2 \cdot \partial _{\textbf{x}_1\textbf{n}_0} \textbf{u}_h (\textbf{x}_1)&=p_2|_{T_1}(\textbf{x}_1),\\ \textbf{c}_2 \cdot \partial _{\textbf{x}_1\textbf{n}_0} \textbf{u}_h (\textbf{x}_1)&=p_2|_{T_4}(\textbf{x}_1).\hfill \\ \end{array} } \right. $$

(13)

Because $\textbf{b}_2\perp \textbf{x}_1\textbf{x}_2$, $\textbf{c}_2\perp \textbf{x}_1\textbf{x}_4$, $\textbf{x}_1\textbf{x}_2$ and $\textbf{x}_1\textbf{x}_4$ are not on a same line, and $\textbf{b}_2\nparallel \textbf{c}_2$, (13) has a unique solution $\partial _{\textbf{x}_1\textbf{n}_0} \textbf{u}_h (\textbf{x}_1)$. Similarly we can find $\partial _{\textbf{x}_i\textbf{n}_0} \textbf{u}_h (\textbf{x}_i)$, $i=1,\cdots ,4$, to match the two $p_2$ values on two sides of the vertex.

Let $\textbf{u}_{h,2}$ be the $\textbf{V}_h$ function which has only the terms with $\partial _{\textbf{x}_i\textbf{n}_0} \textbf{u}_h (\textbf{x}_i)$ (while the rest coefficients are zero under its modified Lagrange basis expansion (11).) Then we add it the other mid-edge nodal value functions ($\textbf{u}_h(\textbf{n}_2)\phi _2$ and $\textbf{u}_h(\textbf{n}_4)\phi _4$ on $T_1$), which cancel the non-zero flux so that the new $\textbf{u}_{h,2}$ satisfies

$$\begin{aligned}{ \int _{\textbf{x}_i\textbf{n}_0} \textbf{u}_{h,2}\cdot \textbf{m}_i {\text{d}}s =0 } \end{aligned}$$

on the four internal edges. Let

$$\begin{aligned}{ p_{2,2} = p_{2,1} -{\text {div}}\,\textbf{u}_{h,2} \in L_0^2(Q) \cap \prod _{i=1}^4 P_2(T_i). } \end{aligned}$$

Then, $p_{2,2}$ also satisfies (10) and vanishes at the corner vertexes,

$$\begin{aligned} { p_{2,2}|_{T_i}(\textbf{x}_j) = 0, \quad j=1,\cdots , 4 } \end{aligned}$$

(14)

for appropriate triangles.

We continue to match $p_{2,2}$ by ${\text {div}}\,\textbf{u}_{h,3}$ and more functions without destroying earlier matches. Such a ${\text {div}}\,\textbf{u}_{h,3}$ must have the following expansion ($\phi _i$ is no longer the standard Lagrange basis function but the modified one satisfying (12)):

$$\begin{aligned} \textbf{u}_h|_{T_1}&=\textbf{u}_h(\textbf{n}_0) \phi _0 + \textbf{u}_h(\textbf{n}_2) \phi _2 + \textbf{u}_h(\textbf{n}_4) \phi _4 + \partial _{\textbf{x}_{12} \textbf{n}_0} \textbf{u}_h(\textbf{x}_{12}) \phi _5, \end{aligned}$$

(15)

where $\textbf{x}_{12}$ is the middle point on the edge $\textbf{x}_1\textbf{x}_2$, cf. Fig. 2. In particular, we select only one term to construct $\textbf{u}_{h,3}$,

$$\begin{aligned} \textbf{u}_h|_{T_1}&= \partial _{\textbf{x}_{12} \textbf{n}_0} \textbf{u}_h(\textbf{x}_{12}) \phi _5, \end{aligned}$$

where $\partial _{\textbf{x}_{12} \textbf{n}_0}\phi _5(\textbf{x}_{12})=1$. On $T_1$, we have

$$\begin{aligned} {\text {div}}\,\textbf{u}_h(\textbf{x}_{12})&= \partial _x(\textbf{u}_h)_1 + \partial _y(\textbf{u}_h)_2 \\&= d_{11} \partial _{\textbf{x}_{12}\textbf{x}_2} (\textbf{u}_h)_1 + d_{12} \partial _{\textbf{x}_{12}\textbf{n}_0} (\textbf{u}_h)_1 \\ {}&\quad \ + d_{21} \partial _{\textbf{x}_{12}\textbf{x}_2} (\textbf{u}_h)_2 + d_{22} \partial _{\textbf{x}_{12}\textbf{n}_0} (\textbf{u}_h)_2 \\&= d_{12} \partial _{\textbf{x}_{12}\textbf{n}_0} (\textbf{u}_h)_1 + d_{22} \partial _{\textbf{x}_{12}\textbf{n}_0} (\textbf{u}_h)_2 \\&= \textbf{d}_2 \cdot \partial _{\textbf{x}_{12}\textbf{n}_0} \textbf{u}_h (\textbf{x}_{12}) , \end{aligned}$$

where $\textbf{d}_2=\langle d_{12}, d_{22}\rangle$, and

$$\begin{aligned} D = \begin{pmatrix}\textbf{x}_2-\textbf{x}_{12}&\textbf{n}_0 - \textbf{x}_{12} \end{pmatrix}, \quad \begin{pmatrix}d_{11} &{} d_{12}\\ d_{21}&{} d _{22}\end{pmatrix} = D^{-\intercal }. \end{aligned}$$

The second equation matches the divergence at another mid-edge point of $T_1$,

$$\begin{aligned} {\text {div}}\,\textbf{u}_h(\textbf{x}_{10})&= \partial _x(\textbf{u}_h)_1 + \partial _y(\textbf{u}_h)_2 \\&= c_{11} \partial _{\textbf{x}_{10}\textbf{x}_{20}} (\textbf{u}_h)_1 + c_{12} \partial _{\textbf{x}_{10}\textbf{n}_0} (\textbf{u}_h)_1 \\ {}&\quad \ + c_{21} \partial _{\textbf{x}_{10}\textbf{x}_{20}} (\textbf{u}_h)_2 + c_{22} \partial _{\textbf{x}_{10}\textbf{n}_0} (\textbf{u}_h)_2 \\&= c_{12} \partial _{\textbf{x}_{10}\textbf{n}_0} (\textbf{u}_h)_1 + c_{22} \partial _{\textbf{x}_{10}\textbf{n}_0} (\textbf{u}_h)_2 \\&= c_0 \textbf{c}_2 \cdot \partial _{\textbf{x}_{12}\textbf{n}_0} \textbf{u}_h (\textbf{x}_{12}) , \end{aligned}$$

where $\textbf{x}_{10}=(\textbf{x}_1+\textbf{n}_0)/2$ is the mid-point, $\textbf{x}_{20}=(\textbf{x}_2+\textbf{n}_0)/2$, $c_0=\partial _{\textbf{x}_{10}\textbf{x}_{20}}\phi _5 > 0$, $\textbf{c}_2=\langle c_{12}, c_{22}\rangle$, and

$$\begin{aligned} C = \begin{pmatrix}\textbf{x}_{20}-\textbf{x}_{10}&\textbf{n}_0 - \textbf{x}_{10}\end{pmatrix}, \quad \begin{pmatrix}c_{11} &{}c_{12}\\ c_{21}&{} c_{22}\end{pmatrix} = C^{-\intercal }. \end{aligned}$$

We have following two equations:

$$\left\{ {\begin{array}{*{20}l} \textbf{d}_2 \cdot \partial _{\textbf{x}_{12}\textbf{n}_0} \textbf{u}_h (\textbf{x}_{12})&=p_{2,2} (\textbf{x}_{12}) ,\\ c_0 \textbf{c}_2 \cdot \partial _{\textbf{x}_{12}\textbf{n}_0} \textbf{u}_h (\textbf{x}_{12})&=\frac{1}{2}(p_{2,2} (\textbf{x}_{10})-p_{2,2} (\textbf{x}_{20})).\hfill \\ \end{array} } \right. $$

(16)

Because $\textbf{d}_2\perp \textbf{x}_{12}\textbf{x}_2$, $\textbf{c}_2 \perp \textbf{x}_{1}\textbf{x}_2$, and $\textbf{d}_2\nparallel \textbf{c}_2$, (16) has a unique solution $\partial _{\textbf{x}_{12}\textbf{n}_0} \textbf{u}_h (\textbf{x}_{12})$. Let $\textbf{u}_{h,3}|_{T_1}= \partial _{\textbf{x}_{12}\textbf{n}_0} \textbf{u}_h (\textbf{x}_{12})\phi _5$ and

$$\begin{aligned} p_{2,3}|_{T_1} = p_{2,2} -{\text {div}}\,\textbf{u}_{h,3}. \end{aligned}$$

Then

$$\begin{aligned} p_{2,3}|_{T_1} = p_{2,3}(\textbf{n}_0) l_{\textbf{n}_0} + p_{2,3}(\textbf{x}_{10}) ( l_{\textbf{x}_{10}} + l_{\textbf{x}_{20}} ), \end{aligned}$$

where $l_{*}$ is the Lagrange basis function at a $P_2$ node, and

$$\begin{aligned} p_{2,3}(\textbf{x}_{10}) = p_{2,3}(\textbf{x}_{20} ) = \frac{1}{2} ( p_{2,2}(\textbf{x}_{10}) + p_{2,2}(\textbf{x}_{20})) \end{aligned}$$

by the construction (16) and a symmetric divergence of $\textbf{c} \phi _5$. $p_{2,3}|_{T_1}$ has three non-zero nodal values. We will show it in fact has only one non-zero coefficient by the zero integral condition (10). That is,

$$\begin{aligned} 0&=\int _{T_1} p_{2,3} {\text{d}}\textbf{x} \\&=p_{2,3}(\textbf{n}_0) \int _{T_1} l_{\textbf{n}_0} {\text{d}}\textbf{x} + p_{2,3}(\textbf{x}_{10}) \left( \int _{T_1} l_{\textbf{x}_{10}}{\text{d}}\textbf{x} + \int _{T_1} l_{\textbf{x}_{20}} {\text{d}}\textbf{x}\right) \\&=0 + p_{2,3}(\textbf{x}_{10}) \left( \frac{1}{6} |T_1| + \frac{1}{6} |T_1| \right) . \end{aligned}$$

Thus $p_{2,3}(\textbf{x}_{10})=0$ and

$$\begin{aligned} p_{2,3}|_{T_1} = p_{2,3}(\textbf{n}_0) l_{\textbf{n}_0}. \end{aligned}$$

Defining $\textbf{u}_{h,3}$ on the other three triangles as we did on $T_1$, we let

$$\begin{aligned} p_{2,3} = p_{2,2} -{\text {div}}\,\textbf{u}_{h,3} \in L_0^2(Q) \cap P_h \end{aligned}.$$

(17)

Then, $p_{2,3}$ also satisfies (10) and (14), and vanishes at 4 outside mid-edge points and 8 mid-edge points,

$$\begin{aligned} p_{2,3}|_{T_i}(\textbf{x}_{i,i+1}) = 0, \quad i=1,\cdots , 4, \end{aligned}$$

(18)

$$\begin{aligned} p_{2,3}|_{T_i}(\textbf{x}_{i,0}) = p _{2,3}|_{T_{i+1}}(\textbf{x}_{i,0}) = 0, \quad i=1,\cdots , 4, \end{aligned}$$

(19)

where we use a notation convention that $\textbf{x}_5=\textbf{x}_1$ and $T_5=T_1$. We note that to get (19), we do not use/limit the DOF of $\partial _{\textbf{x}_i\textbf{n}_0}\phi _1(\textbf{x}_{10})$ and $\partial _{\textbf{x}_{10} \textbf{x}_{20}}\phi _i(\textbf{x}_{10})$ there. Thus in future construction, (19) is not preserved automatically, but (14) and (18) are.

The $p_{2,3}$ in (17) has only 4 nodal values at the central point to be matched. We match $p_{2,3}|_{T_1}(\textbf{n}_0)$ next by a ${\text {div}}\,\textbf{u}_h$. On $T_1$ and $T_2$, let

$$\begin{aligned}\textbf{u}_h = {\left\{ \begin{array}{ll} \textbf{d}_1 \phi _4 \quad &{}\hbox \mathrm{{on }}\ T_1, \\ \textbf{d}_1 \phi _2 \quad &{}\hbox \mathrm{{on }}\ T_2, \end{array}\right. } \end{aligned}$$

where $\phi _i$ on different triangles are defined as in (15) and $\textbf{d}_1$ is determined by these two equations,

$$\begin{aligned} {\text {div}}\,\textbf{u}_h|_{T_1} (\textbf{n}_0)&= 1, \quad \int _{\textbf{x}_2\textbf{n}_0} \textbf{u}_h \cdot \textbf{n} {\text{d}} s =0. \end{aligned}$$

(20)

For the first equation, we have

$$\begin{aligned} {\text {div}}\,\textbf{u}_h|_{T_1}(\textbf{n}_{0})&= \partial _x(\textbf{u}_h)_1 + \partial _y(\textbf{u}_h)_2 \\&= c_{11} \partial _{\textbf{n}_0\textbf{x}_{1}} (\textbf{u}_h)_1 + c_{12} \partial _{\textbf{n}_0\textbf{x}_2} (\textbf{u}_h)_1 \\ {}&\quad \ + c_{21} \partial _{\textbf{n}_0\textbf{x}_{1}} (\textbf{u}_h)_2 + c_{22} \partial _{\textbf{n}_0\textbf{x}_2} (\textbf{u}_h)_2 \\&= c_{12} (\textbf{d}_1)_1/(-4) + c_{22} (\textbf{d}_1)_2/(-4)\\ {}&=-\frac{1}{4} \textbf{c}_2 \cdot \textbf{d}_1, \end{aligned}$$

where $\textbf{c}_2=\langle c_{12}, c_{22}\rangle$, and

$$\begin{aligned} C = \begin{pmatrix}\textbf{x}_1-\textbf{n}_0&\textbf{x}_2-\textbf{n}_0 \end{pmatrix}, \quad \begin{pmatrix}c_{11} &{}c_{12}\\ c_{21}&{} c_{22} \end{pmatrix}= C^{-\intercal }. \end{aligned}$$

For the second equation, we have

$$\begin{aligned} \int _{\textbf{x}_2\textbf{n}_0} \textbf{u}_h \cdot \textbf{n} {\text{d}} s = \left( \frac{2}{15}|\textbf{x}_2\textbf{n}_0|\right) \textbf{n}\cdot \textbf{d}_1. \end{aligned}$$

As $\textbf{c}_2 \perp \textbf{x}_1\textbf{n}_0$, $\textbf{n} \perp \textbf{x}_2\textbf{n}_0,$ and $\textbf{c}_2\nparallel \textbf{n}$, (20) has a unique solution $\textbf{d}_1$. With it, we define

$$\begin{aligned} \textbf{u}_{h,4} = {\left\{ \begin{array}{ll} \textbf{d}_1 \phi _4 +\frac{1}{4} \textbf{u}_1 \quad &{}\hbox \mathrm{{on }}\ T_1, \\ \\ \textbf{d}_1 \phi _2 - \frac{1}{4} \textbf{u}_2 \quad &{}\hbox \mathrm{{on }}\ T_2, \end{array}\right. } \end{aligned}$$

(21)

where $\textbf{d}_1$ is defined by (13) and $\textbf{u}_i$ is defined to be the solution of (16) with the right-hand side vector $\langle 0, 1\rangle$,

$$\begin{aligned} \textbf{u}_i|_{T_i}=\textbf{c}_i \phi _5, \quad i=1,\cdots ,4. \end{aligned}$$

Here the function $\textbf{u}_1$ corrects ${\text {div}}(\textbf{d}_1\phi _4)$ at the two mid-edge points $\textbf{x}_{10}$ and $\textbf{x}_{20}$. Define

$$\begin{aligned} p_{2,4} = p_{2,3} -{\text {div}}\,\textbf{u}_{h,4} \in L_0^2(Q) \cap P_h. \end{aligned}$$

We have

$$\begin{aligned}p_{2,4}|_{T_1}(\textbf{y})&=0, \quad \textbf{y}=\textbf{x}_1, \textbf{x}_{12}, \textbf{x}_2, \textbf{x}_{20}, \textbf{n}_0, \textbf{x}_{10},\\ p_{2,4}|_{T_2}(\textbf{n}_0)&=p_{2,3}|_{T_2}(\textbf{n}_0)-p_{2,3}|_{T_1}(\textbf{n}_0) , \\ p_{2,4}|_{T_2}(\textbf{y})&=0, \quad \textbf{y}=\textbf{x}_2, \textbf{x}_{23}, \textbf{x}_3, \textbf{x}_{30}, \textbf{x}_{20}. \end{aligned}$$

To match the above one non-zero value, similar to (21), we can get a $\textbf{u}_{h,5}$ supported on $T_2$ and $T_3$. Define

$$\begin{aligned} p_{2,5} = p_{2,4} -{\text {div}}\,\textbf{u}_{h,5} \in L_0^2(Q) \cap P_h. \end{aligned}$$

We have

$$\begin{aligned} p_{2,5}|_{T_2}&=0, \\ p_{2,5}|_{T_3}(\textbf{n}_0)&=p_{2,3}|_{T_3}(\textbf{n}_0) -p_{2,3}|_{T_2}(\textbf{n}_0)+p_{2,3}|_{T_1}(\textbf{n}_0) , \\ p_{2,5}|_{T_3}(\textbf{y})&=0, \quad \textbf{y}=\textbf{x}_3, \textbf{x}_{34}, \textbf{x}_4, \textbf{x}_{40}, \textbf{x}_{30}. \end{aligned}$$

Repeating (21) one more time, we can get a $\textbf{u}_{h,6}$ supported on $T_3$ and $T_4$. Define

$$\begin{aligned} p_{2,6} = p_{2,5} -{\text {div}}\,\textbf{u}_{h,6} \in L_0^2(Q) \cap P_h. \end{aligned}$$

We have

$$\left\{ {\begin{aligned} & p_{2,6}|_{T_3}=0, \\& p_{2,6}|_{T_4}(\textbf{n}_0)a=p_{2,3}|_{T_4}(\textbf{n}_0)-p_{2,3}|_{T_3}(\textbf{n}_0) +p_{2,3}|_{T_2}(\textbf{n}_0)-p_{2,3}|_{T_1}(\textbf{n}_0) , \\ &p_{2,6}|_{T_4}(\textbf{y})=0, \quad \textbf{y}=\textbf{x}_4, \textbf{x}_{41}, \textbf{x}_1, \textbf{x}_{10}, \textbf{x}_{40}.\hfill \\ \end{aligned} } \right. $$

(22)

Because $p_{2,3}\in P_h$, we do have

$$\begin{aligned} \sum _{i=1}^4 (-1)^i p_{2,3}|_{T_i}(\textbf{n}_0) = 0. \end{aligned}$$

By (22)

$$\begin{aligned} p_{2,6} =0 \ \hbox \mathrm{{on }} \ T_i, \ i=1,2,3,4. \end{aligned}$$

Let $\textbf{u}_{h,i}$ be defined on all quadrilaterals as it is defined on this Q. Let

$$\begin{aligned} \textbf{u}_{h} = \textbf{u}_{h,1} +\textbf{u}_{h,2}+\textbf{u}_{h,3}+\textbf{u}_{h,4}+\textbf{u}_{h,5}+\textbf{u}_{h,6}. \end{aligned}$$

Then

$$\begin{aligned} {\text {div}}\,\textbf{u}_{h} = p_2. \end{aligned}$$

As all the construction of late $\textbf{u}_{h,i}$ ($i>1$) is local, we have a uniform stability under corresponding norms. Thus

$$\begin{aligned} |\textbf{u}_h|_1 \leqslant C \Vert p_2\Vert _0. \end{aligned}$$

The lemma is proved.

3 Convergence

Lemma 2

The linear system of finite element equations (3)–(4) has a unique solution $(\textbf{u}_h,p_h)\in \textbf{V}_h \times P_h$, where $\textbf{V}_h$ and $P_h$ are defined in (5) and (6), respectively.

Proof

For a finite square system of linear equations, we only need to prove the uniqueness. Let $\textbf{f}=\textbf{0}$ in (3). Letting $\textbf{v}_h=\textbf{u}_h$ in (3) and $q_h=p_h$ in (4), we add the two equations to get

$$\begin{aligned} \Vert \nabla \textbf{u}_h \Vert _0^2 = 0. \end{aligned}$$

$\textbf{u}_h$ would be constant vectors on each T. Because $\textbf{u}_h$ is continuous and it has a zero boundary condition, $\textbf{u}_h=\textbf{0}$. By the inf-sup condition (7) and (3), we have a $\textbf{v}_h$ such that ${\text {div}}\,\textbf{v}_h =p_h$ and

$$\begin{aligned} \Vert p_h\Vert _0^2&= (\hbox \mathrm{{div}} \,\textbf{v}_h, p_h) =0, \end{aligned}$$

which shows $p_h=0$. The lemma is proved.

Theorem 1

Let $(\varvec{u},p)\in (H^{4}(\varOmega ) \cap H^1_0 (\varOmega ))^2 \times (H^3 (\varOmega )\cap L^2_0 (\varOmega ))$ be the solution of the stationary Stokes problem (1)–(2). Let $(\varvec{u}_h,p_h)\in \textbf{V}_h \times P_h$ be the solution of the finite element problem (3)–(4). It holds that

$$\begin{aligned} \Vert \varvec{u}-\varvec{u}_{h}\Vert _{1}&\leqslant C h^3 |\varvec{u} |_{4} , \end{aligned}$$

(23)

where C is independent of $\mu$.

Proof

Subtracting (3) from (1), we get

$$\begin{aligned} ( \nabla (\textbf{u}-\textbf{u}_h), \nabla \textbf{v}_h )- (p-p_h,{\text {div}}\, \textbf{v}_h)&= 0, \quad \forall \textbf{v}_h \in \textbf{V}_h, \end{aligned}$$

(24)

and

$$\begin{aligned} ( \nabla ( \textbf{u}-\textbf{u}_h), \nabla \textbf{v}_h )&= 0, \quad \forall \textbf{v}_h \in \textbf{Z}_h, \end{aligned}$$

(25)

where

$$\begin{aligned}\textbf{Z}_h =\{ \textbf{z}_h \in \textbf{V}_h {:}\, {\text {div}}\,\textbf{z}_h=0 \}. \end{aligned}$$

By (25),

$$\begin{aligned} |\textbf{u}-\textbf{u}_h|_1^2&= ( \nabla ( \textbf{u}-\textbf{u}_h), \nabla ( \textbf{u}-\textbf{z}_h) ) \leqslant |\textbf{u}-\textbf{u}_h|_1 |\textbf{u}-\textbf{z}_h|_1. \end{aligned}$$

That is,

$$\begin{aligned} |\textbf{u}-\textbf{u}_h|_1 = \inf _{\textbf{z}_h \in \textbf{Z}_h} |\textbf{u}-\textbf{z}_h|_1. \end{aligned}$$

(26)

Let

$$\begin{aligned}\textbf{Z}^\perp _h = \{ \textbf{v}_h \in V_h {:}\, \,(\nabla \textbf{v}_h, \nabla \textbf{z}_h) = 0, \ \forall \textbf{z}_h\in \textbf{Z}_h\}. \end{aligned}$$

For any $\textbf{v}_h\in \textbf{V}_h$, let $\textbf{y}_h\in \textbf{Z}^\perp _h$ be the unique solution of

$$\begin{aligned} ({\text {div}}\,\textbf{y}_h, q_h)&=({\text {div}}\,(\textbf{u}-\textbf{v}_h), q_h) = ( -{\text {div}}\,\textbf{v}_h, q_h), \quad \forall q_h \in P_h. \end{aligned}$$

(27)

By the on-to condition (7) and the inf-sup condition (8), we have ${\text {div}}\,\textbf{V}_h = P_h$ and (27) has solutions. All such solutions are projected to the unique solution in $\textbf{Z}^\perp _h$. Letting $q_h=-{\text {div}}\,\textbf{v}_h$ in (27), we get

$$\begin{aligned} \Vert {\text {div}}\,\textbf{v}_h\Vert _0^2 = ({\text {div}}\,\textbf{y}_h, q_h) \geqslant \beta |\textbf{y}_h|_1 \Vert q_h\Vert _0. \end{aligned}$$

Thus

$$\begin{aligned}|\textbf{y}_h|_1 \leqslant \beta ^{-1} \Vert q_h\Vert _0 = \beta ^{-1} \Vert {\text {div}}(\textbf{u}-\textbf{v}_h)\Vert _0 \leqslant \beta ^{-1} |\textbf{u}-\textbf{v}_h|_1, \end{aligned}$$

and

$$\begin{aligned} {\text {div}}(\textbf{v}_h+\textbf{y}_h) =0, \ \hbox \mathrm{{i.e., }} \ \textbf{v}_h+\textbf{y}_h\in \textbf{Z}_h. \end{aligned}$$

By (26), we have

$$\begin{aligned}|\textbf{u}-\textbf{u}_h|_1&= \inf _{\textbf{z}_h \in \textbf{Z}_h} |\textbf{u}- \textbf{z}_h |_1 \leqslant \inf _{\textbf{v}_h \in \textbf{V}_h} |\textbf{u}-(\textbf{v}_h+\textbf{y}_h)|_1 \\&\leqslant \inf _{\textbf{v}_h \in \textbf{V}_h} |\textbf{u}- \textbf{v}_h|_1 + |\textbf{y}_h |_1 \\&\leqslant (1+\beta ^{-1}) \inf _{\textbf{v}_h \in \textbf{V}_h} |\textbf{u}- \textbf{v}_h|_1 \\&\leqslant (1+\beta ^{-1}) |\textbf{u}- \textbf{I}_h \textbf{u}|_1 \\&\leqslant C h^3 |\textbf{u}|_{4}, \end{aligned}$$

where $\textbf{I}_h$ is the nodal interpolation operator defined by DOF of (5). As $\textbf{V}_h$ includes all $P_3$ polynomials, such an $\textbf{I}_h$ can be proved $H^1$-stable and quasi-optimal up to order 3 in $H^1$-norm, cf. [18]. The proof is complete.

Theorem 2

Let $(\varvec{u},p)\in (H^{4}(\varOmega ) \cap H^1_0 (\varOmega ))^2 \times (H^3 (\varOmega )\cap L^2_0 (\varOmega ))$ be the solution of the stationary Stokes problem (1)–(2). Let $(\varvec{u}_h,p_h)\in \textbf{V}_h \times P_h$ be the solution of the finite element problem (3)–(4). It holds that

$$\begin{aligned} \Vert p-p_{h}\Vert _{0}&\leqslant C h^3 ( \mu |\varvec{u} |_{4}+|p|_{3} ). \end{aligned}$$

(28)

Proof

By (24) and (8), we get

$$\begin{aligned} \beta |\textbf{v}_h| \Vert \Pi _h p-p_h\Vert&\leqslant |({\text {div}}\,\textbf{v}_h, \Pi _h p-p_h)| \\&= |({\text {div}}\,\textbf{v}_h, p-p_h)| = | ( \mu \nabla (\textbf{u}-\textbf{u}_h), \nabla \textbf{v}_h )| \\&\leqslant \mu |\textbf{u}-\textbf{u}_h|_1 |\textbf{v}_h|_1 , \end{aligned}$$

where $\Pi _h$ is the $L^2$ projection operator onto $P_h$. Hence,

$$\begin{aligned} \Vert p-p_h\Vert _0&\leqslant \Vert p-\Pi _h p \Vert _0 + \beta ^{-1} |\textbf{u}-\textbf{u}_h|_1 \\&\leqslant C h^3(|p|_3 + \mu |\textbf{u}|_{4} ). \end{aligned}$$

Thus, (28) is proved.

Theorem 3

Let $(\varvec{u},p)\in (H^{4}(\varOmega ) \cap H^1_0 (\varOmega ))^2 \times (H^3 (\varOmega )\cap L^2_0 (\varOmega ))$ be the solution of the stationary Stokes problem (1)–(2). Let $(\varvec{u}_h,p_h)\in \textbf{V}_h \times P_h$ be the solution of the finite element problem (3)–(4). It holds that

$$\begin{aligned} \Vert \textbf{u} -\textbf{u}_{h}\Vert _{0}&\leqslant C h^{4} |\varvec{u} |_{4} , \end{aligned}$$

(29)

where C is independent of $\mu$.

Proof

We will use the duality argument. Let $\textbf{w} \in H^1_0(\varOmega )^2$ and $r \in L^2_0(\varOmega )$ such that

$$\begin{aligned}{} & {} - \hbox \mathrm{{div}}(\mu \nabla \textbf{w}) + \nabla r= \textbf{u}-\textbf{u}_h{} &{} \hbox {\,}{\text{in }} \, \varOmega ,{} & {} \end{aligned}$$

(30)

$$\begin{aligned}{} & {} \hbox \mathrm{{div}}\,\textbf{w} = 0{} & {} \hbox {\,} {\text{in }} \, \varOmega . \end{aligned}$$

(31)

We assume the following regularity:

$$\begin{aligned} \mu |\textbf{w}|_2 + |r|_1 \leqslant C \Vert \textbf{u}-\textbf{u}_h\Vert _0. \end{aligned}$$

(32)

Multiplying (30) by $(\textbf{u}-\textbf{u}_h)$ and doing integration by parts, we get

$$\begin{aligned} (\mu \textbf{u}-\textbf{u}_h,\textbf{u}-\textbf{u}_h)&= (\mu \nabla \textbf{w} , \nabla (\textbf{u}-\textbf{u}_h))-(\hbox \mathrm{{div}}(\textbf{u}-\textbf{u}_h), r). \end{aligned}$$

(33)

Let $\textbf{w}_h\in \textbf{V}_h$ and $r_h\in P_h$ be the finite element solution for problem (30)–(31), satisfying

$$\begin{aligned}{} & {} (\mu \nabla \textbf{w}_h , \nabla \textbf{v}_h ) - ({\text {div}}\,\textbf{v}_h,r_h) =(\textbf{u}-\textbf{u}_h,\textbf{v}_h),\quad \forall \textbf{v}_h \,\in \textbf{V}_h,{} & {} \end{aligned}$$

(34)

$$\begin{aligned}{} & {} ({\text {div}}\,\textbf{w}_h, q_h) =0,\quad \forall q_h\,\in P_h. \end{aligned}$$

(35)

Letting $\textbf{v}_h=\textbf{w}_h$ in (24), we get

$$\begin{aligned} (\mu \nabla (\textbf{u}-\textbf{u}_h), \nabla \textbf{w}_h)&= (\hbox \mathrm{{div}}\,\textbf{w}_h, \Pi _h p-p_h) =0. \end{aligned}$$

(36)

Subtracting (36) from (33), we get

$$\begin{aligned} \mu \Vert \textbf{u}-\textbf{u}_h\Vert _0^2&= (\mu \nabla (\textbf{w}-\textbf{w}_h), \nabla (\textbf{u}-\textbf{u}_h))-({\text {div}}(\textbf{u}-\textbf{u}_h), r-\Pi _h r). \end{aligned}$$

(37)

We have, by the quasi-optimal error bound (23) and the assumed elliptic regularity (32), from (37),

$$\begin{aligned} \Vert \textbf{u}-\textbf{u}_h\Vert _0^2&\leqslant \mu \Vert \nabla (\textbf{w}-\textbf{w}_h)\Vert _0\; \Vert \nabla (\textbf{u}-\textbf{u}_h)\Vert _0 + \Vert \textbf{u}-\textbf{u}_h\Vert _1 \Vert r-\Pi _h r\Vert _0 \nonumber \\&\leqslant C h^{4} |\textbf{u}|_{4} ( \mu |\textbf{w}|_2 + |r|_1)\nonumber \\&\leqslant C h^{4} |\textbf{u}|_{4} \Vert \textbf{u}-\textbf{u}_h\Vert _0. \end{aligned}$$

(38)

Thus, (29) follows (38).

4 Numerical Experiments

In the numerical computation, the domain is $\varOmega =(0,1)\times (0,1)$. We choose an $\textbf{f}$ in (1) so that the exact solution is

$$\begin{aligned} \left\{ \begin{aligned} \textbf{u}&=\begin{pmatrix} -2^7 (x-x^2)^2(y-y^2)(1-2y) \\ 2^7 (x-x^2)(1-2x)(y-y^2)^2 \end{pmatrix}, \\ p&= x-\frac{1}{2} . \end{aligned} \right. \end{aligned}$$

(39)

Fig. 3

The first three levels of grids for the computation in Tables 1 and 2

We compute the solution (39) on the uniform triangular grids shown in Fig. 3, by the divergence-free $P_3$-$P_2$ finite element and the Taylor-Hood $P_3$-$P_2$ finite element. The results are listed in Tables 1 and 2. We can see that the optimal order of convergence is achieved in all cases for the two finite elements in Tables 1 and 2. Both methods have the same numbers of unknowns for the velocity. The divergence-free $P_3$-$P_2$ method has more pressure unknowns than the Taylor-Hood $P_3$-$P_2$ method. However, from Table 1, all errors of the Taylor-Hood $P_3$-$P_2$ method are smaller, when $\mu =1$.

Table 1 Error profile on the triangular meshes shown as in Fig. 3 for the solution (39), $\mu =1$

We can see, from Table 1, that the divergence-free $P_3$-$P_2$ method performs worse than the Taylor-Hood $P_3$-$P_2$ method, when $\mu =1$. But it shows the opposite in Table 2 when $\mu =10^{-8}$. Both the velocity error and the pressure error of the Taylor-Hood $P_{3}$-$P_{2}$ element are about $10^{6}$ times larger than the corresponding error of the divergence-free $P_{3}$-$P_{2}$ element. In fact, the discrete velocity ${\textbf{u}}_{h}$ remains same, from Tables 1 and 2, when $\mu$ changes, verifying our theory that the $\textbf{u}_h$ convergence is independent of $\mu$.

Table 2 Error profile on the triangular meshes shown as in Fig. 3 for the solution (39), $\mu =10^{-8}$

Next, we compute the above example again, but on perturbed meshes, shown in Fig. 4, by the divergence-free $P_{3}$-$P_{2}$ element and the Taylor-Hood $P_{3}$-$P_{2}$ element. All comments made above on Tables 1 and 2 remain same for Tables 3 and 4. Between the errors on Fig. 3 meshes and on Fig. 4 meshes, the latter ones are about double the earlier ones. It is always true that it works better on meshes with the singular vertex.

Fig. 4

The first three levels of grids for the computation in Tables 3 and 4

Table 3 Error profile on the triangular meshes shown as in Fig. 4 for the solution (39), $\mu =1$

Table 4 Error profile on the triangular meshes shown as in Fig. 4 for the solution (39), $\mu =10^{-8}$