Abstract
The present study regards the numerical approximation of solutions of systems of Korteweg-de Vries type, coupled through their nonlinear terms. In our previous work [9], we constructed conservative and dissipative finite element methods for these systems and presented a priori error estimates for the semidiscrete schemes. In this sequel, we present a posteriori error estimates for the semidiscrete and fully discrete approximations introduced in [9]. The key tool employed to effect our analysis is the dispersive reconstruction developed by Karakashian and Makridakis [20] for related discontinuous Galerkin methods. We conclude by providing a set of numerical experiments designed to validate the a posteriori theory and explore the effectivity of the resulting error indicators.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We consider the initial-boundary value problem (IBVP) for a coupled system of Korteweg-de Vries (KdV) type equations, namely,
with periodic boundary conditions on the interval [0, 1]. Here, the dependent variables \(u=u(x,t)\) and \(v=v(x,t)\) are real-valued functions and subscripts connote partial differentiation. The nonlinearities are taken to be homogeneous quadratic polynomials in u and v, viz. \(P(u,v)=Au^2+Buv+Cv^2\) and \(Q(u,v)=Du^2+Euv+Fv^2\) for given real coefficients \(A, B, \cdots\), and F.
The system (1) and other related couplings of nonlinear, dispersive equations appear in the literature in models for a wide variety of physical phenomena. Indeed, several asymptotic models developed by Majda and Biello to study the Madden-Julian Oscillation are relatives of the system above. These models employed coupled systems of two (see [5, 21]) and three equations of KdV type (see [22]) to study the nonlinear interaction of equatorial baroclinic and barotropic Rossby waves. In fact, in [5], Biello derived and experimentally studied a system that is a special case of (1). In addition, a plethora of physical models exist that utilize different, yet still closely related couplings of equations combining nonlinear and dispersive effects. An excellent example is the Gear-Grimshaw system used to study the propagation of internal waves. In [19], Hakkaev considered a system quite similar to (1) with dispersion of Benjamin-Bona-Mahony type. Finally, specializations of the surface water wave models of Bona et al. (see [11, 12]) also feature a coupled KdV structure like that of the system (1).
From a mathematical perspective, the system (1) is a paradigm class for the theoretical study of systems combining nonlinearity and dispersion. Indeed, it has provided a testbed for recent work developing new theory for PDEs of this kind. See, for example, [7, 8, 13].
1.1 Local and Global Well-Posedness
We review a few results crucial to the theory developed herein. We highlight results regarding local and global well-posedness of IBVPs for the system (1). In this discussion, we introduce several important invariants of the system (1), one of which plays a key role in the analysis that follows. For a more in-depth discussion of these matters, we refer the reader to our previous work [9, Section 1.1].
The pure initial-value problem for these systems was studied in [3] and [13]. Indeed, the system (1) is always locally well posed in the \(L^2({\mathbb {R}})\)-based Sobolev spaces \(H^s({\mathbb {R}})\times H^s({\mathbb {R}})\) given \(s>-\frac{3}{4}.\) This result follows the general lines of development available already for the single Korteweg-de Vries equation
(see [13, 18]). It was also shown that for solutions of the system (1) corresponding to \(s \geqslant 0\) the integral
is independent of time. The constants a, b, and c comprise any nontrivial solution of the system
of two linear equations in three unknowns. If \(s \geqslant 1\), the integral
with
is also time-independent for u, v that solve the system (1). Here, the real constants \(\alpha , \beta , \gamma\), and \(\delta\) depend upon the original coefficients, \(A, B,\cdots ,F\). For their explicit form, see [7, Equation (2.6)].
When the quadratic form \(\varUpsilon (x,y) = ax^2 + bxy + cy^2\) is positive-definite, which is to say, \(4ac - b^2 > 0,\) these invariants allow the local theory to be extended to global well-posedness if \(s \geqslant 0\). Via an additional energy-type argument as in [18] and an observation from [7], this result can be improved so that (1) is globally well posed for arbitrarily sized data in \(H^s({\mathbb {R}}) \times H^s({\mathbb {R}})\) for any \(s > -\frac{3}{4}\) if \(4ac - b^2 \geqslant 0\).
However, for the system (1), the well-posedness in \(H^s({\mathbb {T}})\), meaning the periodic IBVP, is not as well-studied. Yet, an argument like that of Bona and Smith [14] taken with the a priori \(H^1({\mathbb {T}})\)-bound provided by the invariants (3) and (5) when \(4ac - b^2 > 0\) indeed yields global well-posedness for \(s \geqslant 1\). While this result is ripe for improvement, global well-posedness in \(H^s({\mathbb {T}}) \times H^s({\mathbb {T}})\) for \(s \geqslant 1\) suffices for the error estimates of the present essay.
1.2 Background for the A Posteriori Analysis
Due to their wide-ranging use in application and theory, the efficient and accurate numerical approximation of nonlinear, dispersive systems is of great interest. In [9] we introduced conservative and dissipative finite element schemes for the IBVP above and provided a priori error estimates for the semidiscrete approximations. In this work, we develop error estimates for the semidiscrete and fully discrete schemes from an a posteriori perspective. Indeed, our principal result bounds the \(L^2\)-norm of the error, i.e., the difference at a particular moment in time between the solution of the IBVP and the fully discrete approximation thereof, by a computable quantity.
In extending the a priori estimates of [9] this work finds inspiration in the work of Karakashian and Makridakis [20], which developed a posteriori error estimates for semidiscrete and fully discrete discontinuous Galerkin (DG) schemes for the single generalized Korteweg-de Vries (GKdV) equation. As in [20] the fundamental paradigm that is employed consists of constructing a computable quantity that has sufficient regularity (is twice continuously differentiable in space) to satisfy the system (1) pointwise but with a computable forcing term. Thus, a priori error estimation techniques can be used to bound the error by a computable quantity. Furthermore, we are not limited to using test functions that are in the finite element spaces. The critical tool to effect our analysis is the dispersive reconstruction operator \({\mathscr {R}}\) introduced in [20]. Given a discontinuous piecewise polynomial function \(w_h\) of degree \(q\geqslant 2\), the dispersive reconstruction \({\mathscr {R}} w_h\) of \(w_h\) is a piecewise polynomial of degree \(q+3\) that is twice continuously differentiable. Another characteristic feature of our approach is that in addition to the (base) time-stepping scheme generating the fully discrete approximations, a second, auxiliary, scheme is used in a way that is reminiscent of adaptive codes for systems of ordinary differential equations (e.g., the well-known Runge-Kutta-Fehlberg scheme) that have been in use for decades now. While this introduces a small amount of inefficiency, we must add that the approach herein is distinguished by being supported by rigorous error estimates. As mentioned above, our results extend those of [9] to the a posteriori domain. They also extend and improve upon those of [20]. For one, they apply to the single KdV equation since the latter can be viewed as a special case of the system. Furthermore, in [20] we had used the implicit Euler and midpoint timestepping schemes for the base and auxiliary schemes, respectively. Here, the roles of these two schemes are reversed leading to the following three improvements. The fully discrete schemes are second order in time and thus, more accurate, the fully discrete reconstruction is continuous in time requiring one fewer error indicator. More significantly, due to the special nature of the midpoint scheme, the fully discrete approximations are conservative in both space and time (in a sense that will be described in full below). Finally, in the spirit of full disclosure, we must admit that, technically speaking, our approach can be described more as a non-conforming one rather than DG since the piecewise polynomial approximations are continuous in space. However, it must be also said that we use the full machinery of DG and also this choice was dictated by a desire for simplifying the technicalities, which are already formidable.
Remark 1
We mentioned above that the global well-posedness of the IBVP (1) had been established under the assumption that the quadratic form \(\varUpsilon (x,y) = ax^2+bxy+cy^2\) was positive-definite or equivalently that \(4ac-b^2\) was positive. It should, therefore, not be surprising that the a priori results of [9] were established using the same assumption. The same is true of the results of this paper. Indeed, we shall operate under the slightly stronger assumption that there exists a constant \(\alpha >0\) such that \(4ac - b^2 \geqslant \alpha >0\). This implies the existence of a positive constant \(\sigma _{a, b, c}\) such that
This paper is organized as follows. In Sect. 2, we provide essential preliminaries and a summary of key results from [9] upon which this work is based. In Sect. 3, we quote the definition of the (spatial) dispersive reconstruction operator \({\mathscr {R}}\) and summarize the results from [20] that will be useful in the analysis. In Sect. 4, we develop a posteriori error estimates for the semidiscrete formulation introduced in Sect. 3 of [9]. In Sect. 5, we develop a posteriori error estimates for the fully discrete schemes from [9] that rely on the single-stage implicit Runge-Kutta method of Gauss-Legendre type (midpoint rule; henceforth, RK1) for their temporal discretization. In Sect. 6, we provide numerical experiments that illustrate the behavior of the various indicators. In particular, we provide evidence that the upper bounds supplied by the a posteriori error estimates appear to converge to zero, as a function of the temporal discretization parameter, at the same quadratic rate of the underlying temporal discretization method, RK1. We also provide evidence that the upper bounds supplied by the a posteriori error estimates appear to converge to zero for polynomial degree \(q>2\), albeit suboptimally. The suboptimality is to be expected due to the nonlinearities and the dispersive operators that arise in the estimators. We also study the effectiveness of the estimators for a wide variety of temporal and spatial discretization parameters, investigating how this spatial suboptimality can impact practical use of these estimators. Finally, we provide heuristic factors to correct this suboptimality, yielding heuristic estimators with \({\mathscr {O}}(1)\) effectivity indices for all polynomial degrees \(q \geqslant 2\).
2 Preliminaries
2.1 The Meshes
Let \({\mathscr {T}}_h\) denote a partition of the real interval [0, 1] of the form \({ 0=x_0< x_1< \cdots < x_M = 1}\). We will also say that \({\mathscr {T}}_h\) is a mesh on [0, 1]. The points \(x_m\) are called nodes while the intervals \(I_m = [x_m,x_{m+1}]\) will be referred to as cells. The subscript h will connote the maximum length of the cells \(I_m\), \(m = 0, 1, \cdots , M-1\). The notation \(x_m^-=x_m^+=x_m\) will be useful in taking account, respectively, of left- and right-hand limits of discontinuous functions. The caveat followed throughout is that \(x_0^-=x_M^-\) and \(x_M^+=x_0^+\) corresponding to the underlying spatial periodicity of the solutions being approximated.
2.2 The Function Spaces
For a real interval \(I = [a_1,a_2]\), the Sobolev spaces \(W^{s,p} = W^{s,p}(I)\), equipped with their usual norms will appear frequently. When \(p=2\), we also use \(H^s = H^s(I)\) to denote \(W^{s,2}(I)\). An unadorned norm \(\Vert \cdot \Vert\) will always indicate the \(L^2(0, 1)\)-norm. Use will also be made of the so-called broken Sobolev spaces \(W^{s,p}({\mathscr {T}}_h)\) that are defined as the finite Cartesian products \(\prod _{I \in {\mathscr {T}}_h} W^{s,p}(I)\). Note that when \(sp>1\), the elements of \(W^{s,p}({\mathscr {T}}_h)\) are uniformly continuous when restricted to a given cell but may be discontinuous across nodes. For the purpose of indicating these potential discontinuities, the following notation is used: for \(v \in H^k({\mathscr {T}}_h) = W^{k,2}({\mathscr {T}}_h)\) with \(k \geqslant 1\), let \(v_m^+\) and \(v_m^-\) denote the right-hand and left-hand limits, respectively, of v at the node \(x_m\). The jump \([v]_m\) of v at \(x_m\) is \(v_m^+-v_m^-\), whereas the average \(\{v\}_m\) of v at \(x_m\) is \(\frac{1}{2} (v_m^+ + v_m^-)\). These are standard notations in the context of DG-methods. In all cases, the definitions are meant to adhere to the convention that \(v_0^- = v_M^-\) and \(v_M^+ = v_0^+\), which is tantamount to identifying \(x_0\) and \(x_M\).
For integer \(m \geqslant 0\), \(C^m([0,1])\) is the space of functions that are, together with classical derivatives of order up to m, continuous on [0, 1]. The periodic versions of these spaces, namely,
will also arise. For \(m \geqslant 1\), set \(H_{\text{per}}^{m}({\mathscr {T}}_h) = C_{\text{per}}^{0}([0,1]) \cap H^m({\mathscr {T}}_h)\).
The following, basic embedding inequality (see [2]) will find frequent use. For a mesh \({\mathscr {T}}_h\), \(v \in H^1({\mathscr {T}}_h)\) and any cell \(I \in {\mathscr {T}}_h\), there is a constant c that is independent of the cell I such that
where \(h_I\) is the length of I. Indeed, the dependence of (8) on the value of \(h_I\) is easily ascertained by a simple scaling argument. Note that (8) may also be viewed as a trace inequality.
2.3 The Finite Element Spaces
The spatial approximations will be sought in the space of continuous and periodic piecewise polynomial functions \(V_h^q\) subordinate to the mesh \({\mathscr {T}}_h\), viz.,
where \({\mathscr {P}}_q\) is the space of polynomials of degree q. The spaces \(V_h^q\) are subspaces of \(H_{\text{per}}^m({\mathscr {T}}_h)\) for any \(m\geqslant 1\) and have well known, local approximation and inverse properties that are spelled out here for convenience (cf. [15]). Let \(q \geqslant 2\) be fixed and let i, j be such that \(0 \leqslant j \leqslant i \leqslant q+1\). Then, for any cell I and any function v in \(W^{j,p}(I)\), there exists a function \(\chi \in {\mathscr {P}}_q(I)\) such that
where \(|v|_{W^{j,p}(I)}\) denotes the seminorm of order j on the Sobolev space \(W^{j,p}(I)\) and the constant c is independent of \(h_I\). The equally well known inverse inequalities
for all \(\chi \in {\mathscr {P}}_q(I)\) (see, again, [15]) will also find frequent use. By \(V_h^{q, \mathrm {DG}}\), we denote the space of discontinuous piecewise polynomials subordinate to the mesh \({\mathscr {T}}_h\), i.e.,
2.4 The Weak Formulation
In this section, we present the weak formulations that form the basis for the semidiscrete and fully discrete methods developed in [9]. We begin by recalling the weak formulations developed for the nonlinear terms in (1), each of which are of the form \((uv)_x\). Keeping in mind that we will be working with continuous periodic functions, it is natural to define the form \({\mathscr {N}}\) via integration by parts, viz.,
where \((\cdot ,\cdot )_I\) denotes the inner product in \(L^2\) over the cell I. The form \({\mathscr {N}}\) is actually a trilinear form and is well defined since \(H^1({\mathscr {T}}_h)\) is a Banach Algebra. This trilinear form is also obviously symmetric in its first two arguments. By virtue of the Riesz Representation Theorem, this form defines the associated nonlinear operator \({\mathscr {N}}: H^1({\mathscr {T}}_h) \times H^1({\mathscr {T}}_h) \rightarrow V_h^q\) whose \(L^2([0,1])\)-inner product with any \(\chi \in V_h^q\) is
We recall the pertinent properties of \({\mathscr {N}}\) by quoting the following lemma [9, Lemma 1].
Lemma 1
-
(i)
The nonlinear form \({\mathscr {N}}\) defined by (11) is consistent in the sense that
$$\begin{aligned} {\mathscr {N}}(u,v;\chi ) = \left( (uv)_x,\chi \right) , \quad u,v, \chi \in H_{\text{per}}^{1}({\mathscr {T}}_h). \end{aligned}$$(13) -
(ii)
For \(u,v \in H_{\text{per}}^1({\mathscr {T}}_h)\),
$$\begin{aligned} {\mathscr {N}}(u,v;v) = \frac{1}{2} \sum _{I \in {\mathscr {T}}_h} (v^2,u_x)_I. \end{aligned}$$(14)
A simple but important consequence of periodicity is that the integral \(\int _0^1 (u^2)_xu\,\mathrm {d}x\) vanishes for \(u \in C_{\text{per}}^{1}([0,1])\). We quote a direct consequence [9, Corollary 1] of the above lemma, in which we see that the form \({\mathscr {N}}\) preserves this property on \(H_{\text{per}}^{1}({\mathscr {T}}_h)\) and in particular on \(V_h^q\).
Corollary 1
The form \({\mathscr {N}}\) is conservative in the sense that
We now consider development of a bilinear form for the dispersive (third derivative) terms. It is similar in spirit to the form \({\mathscr {D}}\) introduced in [10] with the difference being that the prevailing spaces are globally continuous. For \(u, \chi \in H^2({\mathscr {T}}_h)\), define \({\mathscr {D}}\) by
The next lemma [9, Lemma 2] delineates properties of \({\mathscr {D}}\) that justify the particular form chosen in (16).
Lemma 2
-
(i)
The bilinear form \({\mathscr {D}}\) defined by (16) is consistent in the sense that
$$\begin{aligned} {\mathscr {D}}(u,\chi ) = (u_{xxx},\chi ), \quad u\in H^3({\mathscr {T}}_h) \cap C_{\text{per}}^{2}([0,1]),\ \chi \in H_{\text{per}}({\mathscr {T}}_h). \end{aligned}$$(17) -
(ii)
The form \({\mathscr {D}}\) is skew-adjoint so that
$$\begin{aligned} {\mathscr {D}}(v,v) = 0,\quad \forall v \in H^2({\mathscr {T}}_h). \end{aligned}$$(18)
It is also convenient to define the operator counterpart \({\mathscr {D}}: H^2({\mathscr {T}}_h) \rightarrow V_h^q\) of the bilinear form \({\mathscr {D}}(\cdot ,\cdot )\) via the requirement
The dissipative version
of the bilinear form \({\mathscr {D}}\) may also be used to represent the third derivative terms. The following lemma [9, Lemma 3] summarizes the properties of \(\tilde{{\mathscr {D}}}\) that are the counterparts of those of \({\mathscr {D}}\) shown in Lemmas 1 and 2.
Lemma 3
-
(i)
The bilinear form \(\tilde{{\mathscr {D}}}\) defined in (19) is consistent in the sense that
$$\begin{aligned} \tilde{{\mathscr {D}}}(u,\chi )=(u_{xxx},\chi ), \quad u\in H^3({\mathscr {T}}_h) \cap C_{\text{per}}^2([0,1]),\ \chi \in H_{\text{per}}^2({\mathscr {T}}_h). \end{aligned}$$(20) -
(ii)
The form \(\tilde{{\mathscr {D}}}\) is dissipative, which is to say,
$$\begin{aligned} \tilde{{\mathscr {D}}}(v,v) = \frac{1}{2} \sum _{m=0}^{M-1} [v_x]_m^2, \quad v \in H^2({\mathscr {T}}_h). \end{aligned}$$(21)
We introduce the dispersive operators developed for the DG method of [10, 20], as they will be used in the definition of the dispersive reconstruction in the next section. The operators \({\mathscr {D}}^\mathrm {DG}:H^{3}({\mathscr {T}}_h)\rightarrow V_h^{q,\mathrm {DG}}\) and \(\tilde{{\mathscr {D}}}^\mathrm {DG}:H^{3}({\mathscr {T}}_h)\rightarrow V_h^{q,\mathrm {DG}}\) are defined in [10, 20] in a similar way to the operators \({\mathscr {D}}\) and \(\tilde{{\mathscr {D}}}\) so that for any \(\chi \in V_h^{q, \mathrm {DG}}\),
and
Note that since \(V_h^q\subset V_h^{q,\mathrm {DG}}\), the operators \({\mathscr {D}}\) (similarly, \(\tilde{{\mathscr {D}}}\)) and \({\mathscr {D}}^{\mathrm {DG}}\) (similarly, \(\tilde{{\mathscr {D}}}^{\mathrm {DG}}\)) coincide on \(V_h^q\). In addition, while the consistency and skew-adjointness properties listed in Lemma 2 for \({\mathscr {D}}\) hold for \({\mathscr {D}}^{\mathrm {DG}}\), they also hold given the more relaxed condition that \(\chi \in H^3({\mathscr {T}}_h)\) (see [10, 20, Lemma 2.2]). Similarly, consistency and dissipation results analogous to those shown for \(\tilde{{\mathscr {D}}}\) in Lemma 3 also hold for \(\tilde{{\mathscr {D}}}^{\mathrm {DG}}\) with the relaxed condition that \(\chi \in H^3({\mathscr {T}}_h)\).
We quote the following bound [20, Lemma 2.3], which is useful in understanding the error estimators that feature the operator \({\mathscr {D}}\).
Lemma 4
Let \(u\in H^3({\mathscr {T}}_h)\). For each cell \(I=[x_m, x_{m+1}]\), \(j=0,\cdots , M-1\), the following local bound holds:
3 The Dispersive Reconstruction Operator
The main tool used to develop the a posteriori error estimates is a (spatial) dispersive reconstruction operator \({\mathscr {R}}\) corresponding to the third order differential operators in (1) as well as to the discrete variant \({\mathscr {D}}\) defined above. We highlight the considerations that motivated the definition of the dispersive reconstruction operator in [20, Section 3].
-
(i)
For \(u\in H^3({\mathscr {T}}_h)\), the dispersive reconstruction \({\mathscr {R}}u\) should be (efficiently) computable. Indeed, it was shown in [20] that \({\mathscr {R}}u\) can be computed locally on each cell.
-
(ii)
\({\mathscr {R}}u\) should be globally smooth so that \(({\mathscr {R}}u)_{xxx}\) belongs to \(L^2(0,1)\). This will allow the reconstruction of the approximations \(u_h, v_h\) to satisfy the original system in the strong sense, up to a computable forcing term.
-
(iii)
Finally, it is useful for a reconstruction operator to be a right inverse of the corresponding dispersive projection (see [9, (2.15)] and [20, (20)]). For details, we refer the reader to [20].
We now quote the definition of the dispersive reconstruction of Karakashian and Makridakis [20, Theorem 3.1].
Theorem 1
For each \(u\in H^3({\mathscr {T}}_h)\), there corresponds a unique \(\sigma :={\mathscr {R}}u \in C^2([0,1])\cap V_h^{q+3,\mathrm {DG}}\) such that for each cell \(I=[x_m, x_{m+1}]\), \(m=0,\cdots , M-1\) in \({\mathscr {T}}_h\) there holds
Karakashian and Makridakis showed several approximation results for this reconstruction that will prove useful in the development below. Consequently, we quote these results here [20, Theorem 3.2 and Remark 3.2].
Theorem 2
(Approximation properties of \({\mathscr {R}}\))
-
(i)
Suppose that \(u\in C^2([0,1])\cap H^{q+4}({\mathscr {T}}_h)\). For each \(I\in {\mathscr {T}}_h\),
$$\begin{aligned} |u-{\mathscr {R}}u|_{j, I}\leqslant ch_I^{q+4-j}|u|_{q+4, I},\quad j = 0, 1,\cdots ,q+4. \end{aligned}$$(26) -
(ii)
Suppose \(u\in H^{q+4}({\mathscr {T}}_h)\). For \(j=0,1, \cdots , 3\) and \(I=[x_m, x_{m+1}]\in {\mathscr {T}}_h\),
$$\begin{aligned} \begin{aligned} |u-{\mathscr {R}}u|_{j, I}&\leqslant c\left( h^{q+4-j}_I|u|_{q+4,I}+h_m^{\frac{1}{2}-j}|[u]_m|+h_m^{\frac{3}{2}-j} \left( |[u_x]_m|+|[u_{x}]_{m+1}| \right) +h_m^{\frac{5}{2}-j}|[u_{xx}]_{m+1}|\right). \end{aligned} \end{aligned}$$(27)
Indeed, if \(w_h\in V_h^{q, \mathrm {DG}}\) is an \({\mathscr {O}}(h^\mu )\) approximation to a smooth function w in the sense that
the \(H^j(I)\) seminorm of the reconstruction error is bounded as follows:
4 A Posteriori Error Estimates for the Semidiscrete Approximations
We now construct a posteriori error estimates for the semidiscrete approximations. For brevity, we present the argument for the conservative semidiscrete scheme of [9]. Nearly identical arguments effect a posteriori error estimates for the dissipative scheme of [9]. We relegate the discussion of this matter to Sect. 6.
In our previous work [9, (3.1)], we defined the (conservative) semidiscrete approximation to the solution (u, v) of the IBVP for (1) as the solutions \(u_h,v_h\) in \(V_h^q\times [0,T]\) of the system of coupled operator equations
where \({\mathscr {A}}\) denotes the matrix \(\left[ \begin{array}{ccc}A &{} B &{} C\\ D &{} E &{} F\end{array}\right]\). The initial data \(u_h^0, v_h^0 \in V_h^q\) are any suitable (i.e., at least \({\mathscr {O}}(h^q)\)) approximation of the initial data \(u_0, v_0\) for the IBVP (see [9, (Theorem 3.2)]). Indeed, the \(L^2\) projection into \(V_h^q\) or the Lagrange interpolant more than satisfy this condition.
We observe that the existence and uniqueness of the approximations \(u_h, v_h\) were established under the assumption that the quadratic form \(\varUpsilon\) is positive definite; in particular that (7) holds. The same condition was used to establish the a priori error estimate
where (for the conservative scheme) \(\mu =q-1\) in general and \(\mu =q\) if the underlying mesh \({\mathscr {T}}_h\) is uniform. We note that, for the dissipative scheme, the result holds for \(\mu =q\) with no additional mesh conditions necessary.
The following lemma (which is but a smooth analog of Lemma 5 of [9]) is useful to the a posteriori analysis to come.
Lemma 5
Let (a, b, c) be a nontrivial solution of the system (4). If \(u,v \in C_{\text{per}}^{1}([0,1])\), the following identity holds:
Proof
Since the nonlinear form \({\mathscr {N}}(\cdot \,,\,\,\cdot \,;\,\, \cdot )\) is consistent for arguments in \(H_{\text{per}}^{1}({\mathscr {T}}_h)\) and u, v are in \(C_{\text{per}}^{1}([0,1])\subset H^1_{\text{per}}({\mathscr {T}}_h)\), the result follows from the proof of Lemma 5 of [9].
The next result provides a posteriori error control of \(u-u_h\) and \(v-v_h\) in terms of reconstruction errors \(u_h-{\mathscr {R}}u_h\) and \(v_h-{\mathscr {R}}v_h\). It is crucial to note that \({\mathscr {R}}u_h\) and \({\mathscr {R}}v_h\) can be explicitly constructed from \(u_h, v_h\), so that each term in the right-hand side of inequality (31) of Theorem 3 is computable. This, of course, assumes that \(u_h, v_h\) have been computed via some means, e.g., the Method of Lines.
Theorem 3
Let \(u_h, v_h:[0,T]\rightarrow V_h^q\times V_h^q\) be the solutions of the scheme (29) and let \({\mathscr {R}}u_h, {\mathscr {R}}v_h\) denote the respective dispersive reconstructions of \(u_h, v_h\) as defined in Theorem 1. Assume also that (7) holds. Then, for any \(t\geqslant 0\),
where the constant C in \({\text{e}}^{Ct}\) depends on \(\sigma _{a, b, c}\) as well as the \(W^{1,\infty }\)-semi-norms of the reconstructions \({\mathscr {R}}u_h\) and \({\mathscr {R}}v_h\). The computable quantities \(\eta _{\text{recon}}\), \(\eta _{\text{initial}}\), \(\eta _{\text{time}}\), and \(\eta _{\text{nonlin}}\) are given by
Proof
Recall that \({\mathscr {R}}u_h, {\mathscr {R}}v_h\) belong to \(C^2([0,1])\cap V_h^{q+3}\) and that \(({\mathscr {R}}u_h)_{xxx}={\mathscr {D}}u_h\) and \(({\mathscr {R}}v_h)_{xxx} = {\mathscr {D}}v_h\) in the strong sense. Therefore, from the semidiscrete system in (29), we have
Letting \(e^{(u)} = u - {\mathscr {R}}u_h\), \(e^{(v)} = v - {\mathscr {R}}v_h\), \(r^{(u)} = u_h-{\mathscr {R}}u_h\), and \(r^{(v)}=v_h-{\mathscr {R}}v_h\), where u, v form a solution to the IBVP for (1), we get
For convenience, we write this system as \(Q_t + Q_1 + Q_2 = Q_3 + Q_4\).
Multiply this system from the left by the vector \(\tilde{Q}(t) = [2ae^{(u)} + be^{(v)}\quad be^{(u)}+2ce^{(v)}]\) and integrate over [0, 1] to obtain
Computing the first term, we see that
Noting that
and
allows the conclusion
Invoking Lemma 5, \({\mathscr {I}}(e^{(u)}, e^{(v)})=0\). Let \(Q_{1,1}\) denote the first four of the last eight terms in (40). Integrating each term by parts (or by application of (14), as each function here is smooth and periodic and the form \({\mathscr {N}}(\cdot \,,\,\,\cdot \,;\,\,\cdot )\) is consistent), we obtain
In view of (7) it follows from the above that
Here, the constant \(c_{{\mathscr {R}}u_h, {\mathscr {R}}v_h, {\mathscr {A}}}\) depends on the constants in the expression for \(Q_{1,1}\) and \(|{\mathscr {R}}u_h|_{W^{1,\infty }([0,1])}\) and \(|{\mathscr {R}}v_h|_{W^{1,\infty }([0,1])}\). We denote the next two terms of (40) by \(Q_{1,2}\). From the definition of (a, b, c) given in (4), we know that \(2Ba+Eb=2Ab+4Dc\). Hence, integrating each term by parts reveals that
As a result and using (7) again, we obtain
where \(C_{{\mathscr {R}}u_h, {\mathscr {A}}}\) depends on \(|{\mathscr {R}}u_h|_{W^{1,\infty }([0,1])}\) and the constant \(2Ba+Eb\). We denote the final two terms of (40) by \(Q_{1,3}\). The fact \(4Ca+2Fb = Bb+2Ec\) allows a nearly identical argument to that conducted for \(Q_{1,2}\) yielding the bound
Combining the bounds (41), (42), and (43) shows that
where \(C_{{\mathscr {R}}u_h,{\mathscr {R}}v_h,{\mathscr {A}}}\) is the sum of the constants in (41), (42), and (43).
Next, note that for sufficiently smooth \(\phi , \psi\) periodic on [0, 1] it is the case that \((\phi _{xxx}, \psi ) = - (\psi _{xxx}, \phi ).\) Consequently,
It remains to compute the terms on the right side of (38). Note that
As a result,
where the constant \(C_{{\mathscr {A}}, \sigma _{a, b, c}}\) depends on \({\mathscr {A}}\) and \(\sigma _{a, b, c}\) from the positive definiteness condition. It remains to bound \(\int _0^1\tilde{Q}Q_4\). Let \(n_0 = {\mathscr {N}}(u_h,u_h)-({\mathscr {R}}u_h^2)_x\), \(n_1 = {\mathscr {N}}(u_h,v_h)-({\mathscr {R}}u_h{\mathscr {R}}v_h)_x\), and \(n_2 = {\mathscr {N}}(v_h,v_h)-({\mathscr {R}}v_h^2)_x\). Note that
so that
Combining (39), (44), (45), (46), and (47), shows that
This is a first-order, linear differential inequality in t. Integrating it yields
Note that \(\varOmega \big (e^{(u)}(0), e^{(v)}(0)\big )\) is computable. Furthermore, given that \(u-u_h = e^{(u)} - r^{(u)}, \, v-v_h=e^{(v)} - r^{(v)}\), application of the triangle inequality to (49) completes the proof.
Remark 2
The dependence of the constant C in (3) on the \(W^{1,\infty }\)-semi-norms of the reconstructions \({\mathscr {R}}u_h\) and \({\mathscr {R}}v_h\) is due to the nonlinear terms in the IBVP. Such dependences seem to be unavoidable for nonlinear problems. Nevertheless, C can be computed if such a need arises.
5 A Posteriori Error Estimates for the Fully Discrete Schemes
To develop a posteriori error estimates for the fully discrete scheme, we adopt the same general approach as that used by Karakashian and Makridakis [20] for the single GKdV equation in that we form a pair of two time-stepping schemes. The first, or main scheme is used to generate the fully discrete approximations and the second is used at each timestep to develop an estimation. Indeed, the goal is to use these two schemes to construct a vector-valued function with components that are spatially smooth, temporally continuous, and satisfy the system (1) in the strong sense up to a computable forcing term.
The analysis presented here has several advantages over the work of [20] even for the single GKdV equation.
-
i)
The analysis is simpler mainly due to the fact that the space-time reconstructions of \(u_h\) and \(v_h\) are continuous in time, as opposed to discontinuous across the temporal nodes. In particular, and as a consequence, the number of resulting error indicators (estimators) is reduced to three. For the setup presented in [20] an additional fourth indicator arose as a result of the discontinuous nature of the space-time reconstruction used there.
-
ii)
In [20] the implicit Euler scheme was used to produce the actual fully discrete approximations whereas the midpoint rule played an auxiliary role to produce the a posteriori error estimation. Here, the main scheme is the midpoint rule, which, in addition to being more accurate (second order in time versus first order) is conservative in time in the sense that \(\Vert u_h^{n+1}\Vert =\Vert u_h^n\Vert\) and \(\Vert v_h^{n+1} \Vert = \Vert v_h^n\Vert\) for all n.
5.1 The Fully Discrete Schemes
Let \(0=t^0<t^1<\cdots <t^N=T\) be a partition of the temporal interval [0, T] and \(\kappa _n = t^{n+1}-t^n\) for \(n=0,1,\cdots , N-1\). Herein, we generate the fully discrete approximations \(u^n_M, v^n_M\) to \(u(\cdot , t^n), v(\cdot , t^n)\) using the midpoint rule, which can be viewed as the one-stage implicit Runge-Kutta method of Gauss-Legendre type (RK1). The identification is significant in the sense that the conservative and dissipative fully discrete approximations can be constructed for the entire family of s-stage Runge-Kutta methods of Gauss-Legendre type, which are of high order (2s) and are conservative (see [9]).
For the midpoint rule the approximations \(u_M^{{n+1}}, v_M^{{n+1}}\) are given by
where the values \(u_M^{n,1}\) and \(v_M^{n,1}\) are given by \(u_M^{n,1} = (u_M^{n}+u_M^{n+1})/2\) and \(v_M^{n,1} = (v_M^n + v_M^{n+1})/2\). The initial conditions \(u_M^0\) and \(v_M^0\) are defined via \(u_M^0:=u_h(0)\) and \(v_M^0:=v_h(0)\).
At each timestep \(t^n\), we employ a step of the implicit Euler method to supply an estimation for the error generated by the RK1 method. These values \(u^{n+1}_E\) and \(v^{n+1}_E\), obtained from a single application of implicit Euler at timestep \(t^n\), are given via
We stress that, at each timestep \(t^n\), the initial values for the implicit Euler scheme are the approximations \(u_M^n, v_M^n\) at \(t^n\) as generated by the RK1 method.
The well-definedness of these schemes can be shown via a variant of Brouwer’s fixed point theorem in a manner similar to [4]. Further, the uniqueness and convergence can also be shown under appropriate CFL conditions.
5.2 The Fully Discrete Reconstruction
The semidiscrete reconstructions \({\mathscr {R}} u_h\) and \({\mathscr {R}} v_h\) are not of use in this context for the simple reason that \(u_h, v_h\) are not computable, as they are merely semidiscrete. What is needed here are space-time reconstructions that are computable in terms of the fully discrete approximations \(u^n_M, v^n_M\) as well as the auxiliary quantities \(u^n_E, v^n_E\). These are defined as the functions \(\hat{u},\hat{v}:[0,T]\rightarrow C^2([0,1])\cap V_h^{q+3}\) given on each interval \(I_n=[t^n, t^{n+1}]\) by
and
where
Here, \(\ell _{\frac{1}{2}}(t) = \frac{2}{\kappa _n}(t^{n+1}-t)\) and \(\ell _1(t)=\frac{2}{\kappa _n}(t-t^{n,1})\) are the basis functions of the space of functions affine in t that correspond to the nodes \(t^{n,1}:= (t^n+t^{n+1})/2\) and \(t^{n+1}\), respectively. As a result, \(\hat{u},\hat{v}\) are each computable and piecewise polynomial in space and time.
Remark 3
On a basic level, the definitions (52) and (53) are those of a collocation method. They are also designed to produce (55). Note that \(\left[ \begin{array}{c}U(t)\\ V(t)\end{array}\right]\) is exactly the affine function of t corresponding to the midpoint rule. The term \(\frac{1}{4}\left[ \begin{array}{c}u_M^{n+1} - u_E^{n+1}\\ v_M^{n+1} - v_E^{n+1}\end{array}\right] \hat{\ell }_{\frac{1}{2}}(t)\) is a quadratic perturbation thereof containing information from the backward Euler method.
5.2.1 A Key Property of the Fully Discrete Reconstruction
The next lemma elucidates the relationship of the fully discrete reconstructions \(\hat{u}, \hat{v}\) to the piecewise affine interpolants of \(u^n_M, v^n_M\) on each interval \(I_n\). Specifically, let
We commit a small abuse of notation below: the application of \({\mathscr {R}}\) and \({\mathscr {D}}\) to a vector is used to denote the application of \({\mathscr {R}}\) and \({\mathscr {D}}\) to each argument thereof.
Lemma 6
Let U(t), V(t) denote the piecewise affine in time interpolant of the fully discrete approximations \(u^n_M, v^n_M\). On each interval \(I_n=[t^n, t^{n+1}]\), for any \(t\in I_n\),
where \(\hat{\ell }_{\frac{1}{2}}(t)=\frac{4}{\kappa _n^2} (t-t^n)(t^{n+1}-t)\) is the basis function corresponding to the node \(t^{n,1}=\frac{t^n+t^{n+1}}{2}\) in the space of functions quadratic in t on the interval \(I_n\).
Proof
The proof comprises evaluation of \(\hat{u}(t)\) and \(\hat{v}(t)\) at \(t^n\), \(t^{n,1}\), and \(t^{n+1}\). It is clear from the definitions of \(\hat{u}\) and \(\hat{v}\) that \(\hat{u}(t^n) = {\mathscr {R}}u^n_M = {\mathscr {R}}U(t^n)\) and \(\hat{v}(t^n) = {\mathscr {R}}v^n_M = {\mathscr {R}}V(t^n)\).
Next, employ the trapezoidal rule, which is exact for affine functions, to compute \(\hat{u}(t^{n,1})\),
Since \(u_M^{n,1} = U(t^{n,1})\), it follows that \({\hat{u}}(t^{n,1})= {\mathscr {R}} \left( U(t^{n,1}) + \frac{1}{4} \left( u_M^{n+1}-u_E^{n+1}\right) \right)\). An identical argument shows \(\hat{v}(t^{n,1})={\mathscr {R}}\left( V(t^{n,1}) + \frac{1}{4}\left( v_M^{n+1}-v_E^{n+1}\right) \right)\).
Furthermore, application of the midpoint rule of integration (also exact for affine functions) yields the desired result for \(\hat{u}(t^{n+1}),\)
By similar means, \(\hat{v}(t^{n+1})={\mathscr {R}}v^{n+1}_M\).
As a result, the (piecewise quadratic in time) function \(\hat{u}(t)\) (similarly, \(\hat{v}(t)\)) is given by the sum of the (piecewise linear in time) function \({\mathscr {R}}U(t)\) (similarly, \({\mathscr {R}}V(t)\)) and the (piecewise quadratic in time) function \(\frac{1}{4}(u_M^{n+1}-u_E^{n+1})\hat{\ell }_{\frac{1}{2}}(t)\) (similarly, \(\frac{1}{4}(v_M^{n+1}-v_E^{n+1})\hat{\ell }_{\frac{1}{2}}(t)\)), yielding the desired result.
5.3 The Error Estimates
Having related the reconstructions \(\hat{u}, \hat{v}\) to the fully discrete approximations \(u^n_M, v^n_M\), the crucial result now is to show that the errors \(u-\hat{u}\) and \(v-\hat{v}\) satisfy the IBVP (1) up to a computable forcing term.
Lemma 7
The errors \(\zeta ^{(u)}:=u-\hat{u}\) and \(\zeta ^{(v)}:=v-\hat{v}\) satisfy the following system:
where \({\mathscr {E}}=\sum _{i=0}^2{{\mathscr {E}}_i}\) and the computable terms \({\mathscr {E}}_0, {\mathscr {E}}_1, {\mathscr {E}}_2\) are given according to
where \({\mathscr {I}}\) denotes the identity operator.
Proof
To obtain the error equation (58), we add the quantity
to both sides of the system (1) and show the resulting right-hand side (namely, (62)) is equivalent to \({\mathscr {E}}\). We compute the first term of (62) by recalling the definitions (52) and (53) of \(\hat{u}\) and \(\hat{v}\), respectively. Indeed, via (50) and (51) we obtain
Here in the last step we used the linearity of the operator \({\mathscr {D}}\). Now, recalling that \(\left( {\mathscr {R}} \phi \right) _{xxx} = {\mathscr {D}} \phi\) for \(\phi\) in \(V_h^q\), in view of Lemma 6 for the last term of (62) we obtain
Combining (63) and (64) and introducing the middle term of (62) yields the desired result.
The next result provides an a posteriori bound for the error generated by the fully discrete scheme (50).
Theorem 4
Let \(u^n_M, v^n_M\) denote the solutions of the fully discrete scheme (50) and let \(\hat{u}, \hat{v}\) denote their respective fully discrete reconstructions as defined in (52) and (53). The following a posteriori estimate holds:
Here, the constant C depends on \(\sigma _{a, b, c}\) and the \(W^{1,\infty }\) seminorms of \(\hat{u}\) and \(\hat{v}\) and \(\Vert {\mathscr {E}}(t)\cdot {\mathscr {E}}(t)\Vert ^2\) stand for \(\sum _{i=0}^2 \Big ( \Vert {\mathscr {E}}^{(u)}_i(t) \Vert ^2 + \Vert {\mathscr {E}}^{(v)}_i(t) \Vert ^2 \Big )\).
Proof
The remarkable similarity between the fully discrete and semidiscrete error Eqs. (58) and (37) allows the almost verbatim use of the proof of Theorem 3 with the following identifications:
Indeed, left-multiply the error Eq. (58) by the row vector \(\tilde{Q} = [2a\zeta ^{(u)}+ b\zeta ^{(v)} \quad b\zeta ^{(u)}+2c\zeta ^{(v)}]\). After lengthy computations we arrive at the differential inequality
where the constant C depends on \(\sigma _{a,b,c}\) as well as the \(W^{1,\infty }\) seminorms of \({\hat{u}}\) and \({\hat{v}}\). A Gronwall type argument can now be used to yield
Note that this inequality holds for all \(t \geqslant 0\). However we specialize it to the temporal nodes \(t^n\). We observed in the proof of Lemma 6 that \({\hat{u}}(t^n) = {\mathscr {R}} u^n_M\) and \({\hat{v}}(t^n) = {\mathscr {R}}v^n_M\). Hence applying the triangle inequality to (67), the result of the Theorem follows at once.
Remark 4
While the bound given above in terms of \(\int _0^{t^n}{{\mathscr {E}}(t)\cdot {\mathscr {E}}(t)\,\mathrm {d}t}\) is reliable, it is also useful to study a coarser bound involving the individual contributions based on each term \({\mathscr {E}}_i\) of \({\mathscr {E}}\), i.e., a bound that replaces \(\int _0^{t^n}{{\mathscr {E}}(t)\cdot {\mathscr {E}}(t)\,\mathrm {d}t}\) in (65) by \(\sum _{i=0}^2\int _0^{t^n}{{\mathscr {E}}_i(t)\cdot {\mathscr {E}}_i(t)\,\mathrm {d}t}\). This allows the separate consideration of some estimators which are expected to depend on h and others that are expected to depend on the timestep size \(\kappa\). Indeed, for \(u^n_M, v^n_M\), which behave optimally with respect to \(\kappa\), it is expected that \({\mathscr {E}}_0\) and \({\mathscr {E}}_1\) should also behave optimally with respect to \(\kappa\). Yet, it stands to reason that \({\mathscr {E}}_2\) should exhibit little, if any, dependence on \(\kappa\), as \({\mathscr {E}}_2\) appears to be a measure of the spatial reconstruction error. To consider the behavior of the terms \({\mathscr {E}}_i\) from a spatial perspective, suppose for the moment that \(u^n_M, v^n_M\) are known to be \({\mathscr {O}}(h^{\mu })\) approximations to solutions u, v of (1). Based on the single spatial derivative presented in \({\mathscr {E}}_0\), one expects the estimator \({\mathscr {E}}_0\) to suffer by one power of h, behaving as \({\mathscr {O}}(h^{\mu -1})\). Furthermore, in light of (24) and (28), one expects the term \({\mathscr {E}}_2\) to suffer by three powers of h due to the presence of the operator \({\mathscr {D}}\) in this estimator. The temporal nature of the differences in \({\mathscr {E}}_1\) suggests only cursory, if any, dependence on h. Each of these intuitions will be studied experimentally below.
6 A Posteriori Error Estimates for the Dissipative Schemes
All techniques utilized above to develop a posteriori error estimates for the conservative semidiscrete and fully discrete schemes can be easily adapted to develop estimates for the dissipative analogs discussed in [9]. Indeed, identical versions of Theorems 3 and 4 hold should the dissipative variant \(\tilde{{\mathscr {D}}}\) (defined in (19)) of the dispersive operator be utilized in lieu of the conservative operator \({\mathscr {D}}\). The only meaningful difference in the analysis is that the spatial reconstruction utilized must reflect the choice of dispersive operator, whether that be our conservative operator, our dispersive operator, or some different variant altogether. The dispersive reconstruction \(\tilde{{\mathscr {R}}}\) that is suitable for this analysis was first defined in [20, Section 6] to develop a posteriori bounds for the Cheng-Shu Formulation for IBVPs for a single GKdV equation (see [17]). We quote their result [20, Theorem 6.1] here.
Theorem 5
For each \(u\in H^3({\mathscr {T}}_h)\), there corresponds a unique \({\tilde{\sigma }}:=\tilde{{\mathscr {R}}}u \in C^2([0,1])\cap V_h^{q+3,\mathrm{DG}}\) such that for each cell \(I=[x_m, x_{m+1}]\), \(m=0,\cdots , M-1\) in \({\mathscr {T}}_h\) there holds
Naturally, only two differences of note exist between this definition and that of \({\mathscr {R}}\) in Theorem 1. The first is that the operator \(\tilde{{\mathscr {D}}}^\mathrm {DG}\) is used in place of \({\mathscr {D}}^{\mathrm {DG}}\) in the first condition of (68); the second is that \(u_x(x_m^+)\) is used in the third condition in place of \(\{u_x\}_m\). Thus, as before, we have a dispersive reconstruction \(\tilde{{\mathscr {R}}}u\) corresponding to the dispersive operator \(\tilde{{\mathscr {D}}}\) that is a locally computable, globally smooth function. Therefore, arguments essentially identical to those conducted above, merely replacing \({\mathscr {D}}\) with \(\tilde{{\mathscr {D}}}\) and \({\mathscr {R}}\) with \(\tilde{{\mathscr {R}}}\), yield Theorems 3 and 4 for the dissipative schemes.
7 Numerical Experiments
We now present numerical experiments designed to gauge the performance of the a posteriori error estimates developed above. We highlight a few important issues.
-
(i)
We provide validation of the theoretical results, including a study of the effectiveness of the error indicators \({\mathscr {E}}_i\), \(i=0,1,2\), both individually and in combination as a gauge of the error \(\Vert u(t^n)-u^n_M\Vert +\Vert v(t^n)-v^n_M\Vert\). To do this, we compute several quantities emanating from the bound in Theorem 4, namely,
$$\begin{aligned} \eta _i&:= \left( \int _0^{t^n}{{\mathscr {E}}_i(t)\cdot {\mathscr {E}}_i(t)\,\mathrm {d}t}\right) ^{\frac{1}{2}}\, \text {, for }i=0,1,2\end{aligned},$$(69)$$\begin{aligned} \eta&:= \left( \int _0^{t^n}{{\mathscr {E}}(t)\cdot {\mathscr {E}}(t)}\,\mathrm {d}t \right) ^{\frac{1}{2}}\, \text {, and}\end{aligned}$$(70)$$\begin{aligned} \eta _\varSigma&:= \left( \sum _{i = 0}^{2}\eta _i^2\right) ^{\frac{1}{2}}. \end{aligned}$$(71)In what follows, effectiveness of the various indicators is quantified via the effectivity index. The effectivity \(\mathrm {Eff}(\phi )\) of some indicator \(\phi\) is defined via
$$\begin{aligned} \mathrm {Eff}(\phi ) := \frac{\phi }{\Vert u(t^n)-u^n_M\Vert +\Vert v(t^n)-v^n_M\Vert }. \end{aligned}$$We note that in the experiments to follow, we do not show the reconstruction errors \(\Vert u^n_M - {\mathscr {R}}u^n_M\Vert\), \(\Vert v^n_M - {\mathscr {R}}v^n_M\Vert\) as these quantities are negligible (smaller by several orders of magnitude) when compared with the approximation errors and the various indicators we study below.
-
(ii)
We highlight experimentally that the a posteriori upper bounds obtained via Theorem 4 (see Remark 4) decrease with the same \({\mathscr {O}}(\kappa ^2)\) rate of the underlying fully discrete method. In this sense, these estimates can be qualified as being of optimal temporal order of accuracy.
-
(iii)
In addition, we confirm experimentally that, in general, the a posteriori upper bound obtained in Theorem 4 decays suboptimally in terms of the spatial discretization parameter h. Recalling Remark 4, we study the degree of suboptimality exhibited by the various error indicators \({\mathscr {E}}_i\), both individually and in combination.
-
(iv)
Finally, we experimentally explore consequences of this spatial suboptimality with regard to effectivity indices. We provide plots illustrating that effectivity indices remain small for reasonable choices of the spatial and temporal discretization parameters. Nevertheless, after we clearly identify a class of cases for which effectivity indices of the indicators grow too large to be practical, we provide heuristic correction factors depending on the polynomial degree of the spatial discretization by which the underlying suboptimality of the indicators can be corrected. We conclude by illustrating experimentally that this correction yields \({\mathscr {O}}(1)\) effectivity indices for essentially all choices of \(\kappa\) and h.
In what follows, we present experiments utilizing the conservative fully discrete scheme alone solely for sake of concision, as the experiments conducted for the dissipative fully discrete scheme are not dissimilar.
As in [9], we adapt the experiments to the interval [0, 1], by multiplying the third derivative terms in (1) by a small parameter \(\epsilon\), specified below. The parameters \(A,B,\cdots ,F\) are taken to be
These choices result in \(a = \frac{118}{17}, \ b = -\frac{28}{17}\), and \(\ c=1\), which in turn yield the negative discriminant \(b^2-4ac = -\frac{7\,240}{289}\).
For the various experiments, two types of solutions of (1) were used. These are both proportional traveling waves of the form \((u,v) = (u,2u)\). The first is adapted from the well known cnoidal-wave solution of the KdV equation,
where \(\mathrm {cn}(z) = \mathrm {cn}(z\!:\!m)\) is the Jacobi elliptic function with modulus \(m \in (0,1)\) (see [1]) and the parameters have the values \(m = 0.9, \lambda = 192m\epsilon K(m)^2\), \(\omega =64\epsilon (2m-1)K(m)^2\), \(\epsilon = \frac{1}{5\,760}\). Since our experiments are conducted on [0, 1], shifting by \(x_0 =\frac{1}{2}\) centers the initial value in the middle of the interval. Here, the function \(K=K(m)\) is the complete elliptic integral of the first kind and the parameters are so organized that u and v have spatial period 1.
The second class of solutions is an approximation of the proportional solitary-wave solutions that were discussed in [9, Section 1.2]. The parameters \(A, B, \cdots , F\) are the same as for the cnoidal-wave type solutions, and it is still the case that \((u,v) = (u,2u)\), but now
with \(\varLambda = 1\), \(\omega = \varLambda /3\), \(\epsilon = \frac{1}{5\,760}\), \(K= \frac{1}{2}\sqrt{\frac{\varLambda }{3\epsilon }}\), again shifting by \(x_0= \frac{1}{2}\) to center the initial wave profile. With \(v = 2u\), this is an exact solution of the system that is not truly periodic in space. Yet, the initial data can be rendered periodic by simply restricting the above solution at \(t = 0\) to the computational domain [0, 1] and imposing periodic boundary conditions across \(x = 0\) and \(x = 1\). The resulting periodicized initial data yields a periodic solution of the system. Indeed, from the previous theory, the resulting solution is approximated to within order \(\epsilon\) by the restriction of (u, 2u) to the period domain [0, 1] over a time interval of order \(\frac{1}{\epsilon }\) (c.f. [6] and [16]). The small value of \(\epsilon\) used in the experiments with proportional solitary waves thus yields a solution, the accuracy of whose numerical approximation can be determined by comparison with the exact solution (u, 2u) with u as in (74). Much of the numerical work on the KdV equation has made use of this small trick to check for accuracy and convergence, especially when issues surrounding solitary waves are under consideration.
Recall that calculation of \(u_M^{n+1}, v_M^{n+1}\) and \(u_E^{n+1}, v_E^{n+1}\) requires solving the nonlinear systems of equations given by (50) and (51), respectively. At each timestep, the nonlinear systems are solved iteratively in an explicit-implicit fashion for the nonlinear-linear terms respectively, with the starting values supplied by extrapolation.
7.1 Temporal Rates of Decrease
We begin our numerical experiments with a study of the temporal rates of decrease of the indicators \(\eta , \eta _\varSigma ,\) and \(\eta _i\) for \(i=0,1,2\). Recalling Remark 4, we would like to show that each of \(\eta _0\), \(\eta _1,\) \(\eta\), and \(\eta _\varSigma\) decrease at the rate of \({\mathscr {O}}(\kappa ^2)\) in accord with the predicted rate of decrease for the RK1 temporal discretization. In addition, we would like to show that \(\eta _2\) is independent of \(\kappa\), as it appears to be a measure of spatial reconstruction errors. In these experiments, we utilized uniform temporal grids, varying the number of timesteps N. To render the spatial errors very small and highlight the temporal errors, we utilized a uniform spatial mesh with \(M=500\) cells and polynomial degree \(q=5\). Each rate presented in Tables 1 and 2 represents the slope of the line of best fit for the natural logarithm of the respective column, where the independent variable is the natural logarithm of the stepsize \(\kappa =1/N\). These rates align quite closely with the behavior desired in each case. We remark that these experiments feature quite reasonable effectivity indices with values between 3 and 5 for the temporally dependent estimators. Indeed, this is reasonable since the parameters were selected so that temporal error is the major contributor to the errors and the estimators behave optimally with respect to the timestep size \(\kappa\).
7.2 Spatial Rates of Decrease
We continue our numerical experiments with a study of spatial rates of decrease for the various estimators. Recall from [9] that the spatial rates of decrease for the conservative fully discrete schemes are experimentally observed to be \({\mathscr {O}}(h^\mu )\) where \(\mu =q+1\) for odd polynomial degree and \(\mu =q\) for even polynomial degree. We stress that this is due to experimental observation alone, as the available theory is less generous. Nevertheless, reflecting upon Remark 4 with this observation in mind, we would like to see the estimator \(\eta _0\) behave as \({\mathscr {O}}(h^{\mu -1})\) and \(\eta _2\) and, consequently, \(\eta\) and \(\eta _\varSigma\) behave as \({\mathscr {O}}(h^{\mu -3})\). Furthermore, we expect \(\eta _1\) to exhibit little to no dependence on h.
In these experiments, we utilize uniform spatial and temporal grids. To allow the spatial errors to dominate by several orders of magnitude (a difficult task due to the high spatial order observed for (50), cf. [9] when compared with fixed second-order temporal rate), we use an extremely small timestep size \(\kappa =10^{-7}\). We utilize a range of very small numbers of cells M and polynomial degrees \(q=2,3,4\). In Tables 3, 4, and 5, we exhibit results for final time \(T=1\) computed using a cnoidal-wave solution. For sake of brevity, we omit all but every fifth entry in each of these tables. However, the estimated rates presented at the end of each table were calculated using all entries for the range \(M=15,16,17,\cdots , 60\). The unabridged tables can be provided upon request.
Despite the issues affecting experiments of this kind, Tables 3, 4, and 5 exhibit spatial rates of decrease for the estimators that are quite in line with those expected. In several cases, the \(L^2\) errors converge at a higher rate than expected, an issue that seems to be tied to the extremely small number of cells used. Nevertheless, the estimators consistently behave at rates similar to those suggested in Remark 4 based on the well-observed spatial convergence rates of the fully discrete scheme (50) from [9]. Finally, \(\eta _1\) appears to exhibit the salutary property of being independent of h, so that \(\eta _1\) and \(\eta _2\) together seem to provide independent indicators for the temporal and spatial errors.
Nevertheless, in contrast to the temporal experiments of the previous section, the effectivity indices in Tables 3, 4, and 5 suffer greatly due to the spatial suboptimality of several indicators. We stress that the parameters chosen for the experiments in Tables 3, 4, and 5 were chosen to highlight the spatial suboptimality. Indeed, it is then natural that significant growth in the effectivity indices of the various indicators occurs as the number of cells increases. Due to the computational efficiency with which the fully discrete scheme and a posteriori estimators can be computed even for high numbers of cells and high polynomial degree, it is highly unlikely that such a low degree of spatial accuracy as is considered here would ever actually be used in practice. Instead, spatial errors can be made negligible with computational ease by selecting either a reasonable number of cells or an even slightly higher polynomial degree. Once this is done, effectivity indices remain very reasonable when the temporal error is the primary contributor to the total approximation error.
Finally, though the \(L^2\) errors decay as expected, these errors seem to oscillate when M varies over such small values, causing pronounced oscillations in the effectivity indices. These oscillations in the \(L^2\) error trace back to the error in approximating the initial data of the periodic IBVP and vanish for more reasonable spatial accuracy, i.e., larger values of M. While this behavior is curious and its effects are seen again in Fig. 5 it is not a byproduct of the schemes considered here.
7.3 Effectivity of the Various Indicators
In this section, we examine the temporal behavior of the estimators \(\eta\), \(\eta _\varSigma\), and \(\eta _i\) for \(i=0,1,2\). Each plot records how the values of the \(L^2\) errors and the various estimators vary with time when the solutions to (1) are approximated up to a final time T via the scheme (50). We have not recorded the values of the terms \(\Vert u^n_M-\hat{u}(t^n)\Vert +\Vert v^n_M-\hat{v}(t^n)\Vert\) that appear in Theorem 4 as they are negligible when compared with those we have recorded.
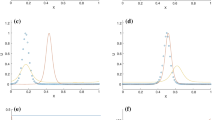
Figure 1 records the behavior of the \(L^2\) error and the estimators with the uniform timestep \(\kappa =1/16\) chosen to effect a low temporal accuracy. Figure 1a–d treat increasing levels of spatial accuracy given a fixed uniform mesh of \(M=200\) cells. Indeed, these subplots report the error and estimator values for polynomial degree \(q=2,3,4,5\), respectively. Figure 2 records similar behavior, yet with the uniform timestep \(\kappa =1/100\) chosen to effect a higher degree of temporal accuracy. Finally, two longer time experiments with high spatial accuracy (\(q=6, M=200\)) are shown in Figs. 3 (final time \(T=5\), \(\kappa =1/100\), solitary wave) and 4 (final time \(T=10\), \(\kappa =1/16\), cnoidal wave). We remark that the values considered here for the discretization parameters are more than reasonable for use in applications, especially those values that afforded higher temporal accuracy.
In each of the experiments, we consistently see reasonable \({\mathscr {O}}(1)\) effectivity indices for the various indicators. We highlight several relevant observations as follows.
-
i)
Recall that, in the previous sections, \(\eta _2\) was observed to be solely dependent on h, albeit with a rate of decrease that was suboptimal by three powers of h. This, of course, results in an extremely coarse bound for the spatial errors. Nevertheless, this (suboptimal) dependence on h comes into view again in Figs. 1 and 2. As spatial accuracy increases with the choice of polynomial degree, \(\eta _2\) becomes much smaller than the error by several orders of magnitude. In addition, we note that the plots of \(\eta _2\) and the \(L^2\) error for \(q=3\) and \(q=4\) are essentially the same, while the plots for \(q=5\) and \(q=6\) are essentially the same, which is reasonable since the convergence rates for (50) are observed to be \({\mathscr {O}}(h^4)\) for both \(q=3\) and \(q=4\) and \({\mathscr {O}}(h^6)\) for \(q=5\) and \(q=6\).
-
ii)
Even in the cases of lower spatial accuracy, \(\eta _2\), which may be viewed as an estimator of the spatial error that is suboptimal by several orders of magnitude, is around the same order of magnitude as the error. This suggests that the primary contributor to the error in each of these experiments is the temporal error. Recall that \(\eta _1\) was observed to be solely dependent on time, with optimal rate of decrease. In light of the behavior of \(\eta _2\), we expect \(\eta _1\) to be a good estimator of the error. In each figure presented here, this is indeed the case, with the curve for \(\eta _1\) closely mimicing that of the error itself.
-
iii)
Indeed, the curves for each of the estimators \(\eta _0, \eta _1, \eta ,\) and \(\eta _\varSigma\) closely mimic that of the \(L^2\) error. Indeed, though the \(L^2\) error appears to increase at a rate linear in \(t^n\) and the various estimators appear to increase at a rate proportional to \(\sqrt{t^n}\), for the majority of each plot, the curves are nearly parallel to each other. Note that this \(\sqrt{t^n}\) rate is reasonable for the various indicators as we did not plot the exponential factor entering from the estimate in Theorem 4.
-
iv)
We observe that the estimator \(\eta _\varSigma\) consistently bounds the error. Naturally, \(\eta\) provides a sharper bound, however.
-
v)
Finally, recall that the estimator \(\eta _0\) was expected and observed to behave optimally with respect to \(\kappa\) and suboptimally with respect to h. Yet, \(\eta _0\) was only suboptimal by a factor of h, as opposed to the suboptimality by a factor of \(h^3\) that affects \(\eta _2, \eta\), and \(\eta _\varSigma\). Combining this fact with the observation that in each of the figures the graph of \(\eta _0\) closely mimics the error, we suggest that it might be useful to develop a heuristic of using only \(\eta _0\) in practice.
7.4 Suboptimality and Heuristic Correction
Finally, we conduct additional experiments to gain a deeper understanding of how the observed spatial suboptimality affects the effectiveness/practical usefulness of these estimators. We remind the reader, that, in most practical cases, effectivity indices of the various indicators remain small. This is possible due to the computational ease with which the fully discrete scheme (50) can be computed. High spatial accuracy can be effected with ease by simply using a higher number of cells M or larger polynomial degree q, causing the temporal error to be the main contributor to the total error. In these cases, the temporal optimality of the indicators keeps the effectivity indices small, as the spatial errors can be made several orders of magnitude smaller than the temporal errors and, consequently, do not affect the size of the effectivity indices.
Nevertheless, for indicators to be useful in practice, it is essential to understand how the spatial suboptimality affects the effectivity indices for different temporal and spatial mesh parameters. As a result, in Fig. 5, we record the base-10 logarithms of the effectivity indices of the indicator \(\eta\) after computing the proportional cnoidal wave solution up to final time \(T=1\) for varying numbers of cells (horizontal axis) and timesteps (vertical axis). The base-10 logarithmic scale allows for a summary view of the spatial suboptimality. Moreover, it highlights the dependence of the effectivity indices on not only the number of cells but also the number of timesteps.
Of course, it is desirable that effectivity indices remain \({\mathscr {O}}(1)\) regardless of the choice of discretization parameters. As a result, we seek a heuristic correction factor by which we can multiply the spatially suboptimal indicators to correct their behavior. Based on the analysis, the natural inclination would be to correct by merely offsetting the three powers of h we have lost. This is excessive in general, since the effectivity indices already remain reasonable if the temporal error is the main contributor to the total approximation error of the fully discrete scheme. In view of this fact, the appropriate heuristic correction factor was \(C_\star :=(M/N)^p = (\kappa /h)^p\), where naturally the power p depends on the polynomial degree q used in the spatial discretization. For \(q=5\), \(p=2\), this was well supported by experimental data collected. Indeed, correction by the resulting \(C_\star\) results in a much more effective estimator \(\eta _\star :=C_\star \eta\). Figure 6 depicts the base-10 logarithm of the heuristic estimator \(\eta _{\star }\) for the same choices of M and N taken in Fig. 5. Similar results can be obtained even for low polynomial degree, e.g., for \(q=2\), a useful estimator is obtained by taking \(p=3\). Furthermore, other corrections could be proposed by harnessing the temporal indicator \(\eta _1\) and the spatial indicator \(\eta _2\) to the same end. For high polynomial degree, spatial errors are usually negligible when compared with temporal errors so that no correction is needed in practice.
8 Summary and Future Work
We have constructed a posteriori error estimates for semidiscrete and fully discrete finite element methods for a paradigm class of coupled systems of nonlinear, dispersive equations. To the best of our knowledge, these were the first results of their kind for numerical methods for this class of PDEs. Our estimate for the fully discrete methods provide several useful indicators of the error in \(L^2([0,1])\). One of these indicators, \(\eta _1\), was experimentally verified to be an indicator of the temporal error alone (i.e., independent of the spatial discretization parameter). Another, \(\eta _2\), was experimentally verified to be an indicator of the spatial error alone. Indeed, each of the temporally dependent indicators was seen to exhibit optimal temporal rates of decrease when compared to the underlying timestepping method of the fully discrete scheme.
Noting the spatial suboptimality of some of the error indicators, we provided several observations regarding their practical use. First, we noted that computational efficiency of these methods allows the spatial error to be made so small that the temporal error is the primary contributor to the total approximation error by several orders of magnitude. Under this condition, effectivity indices remain within a practical range. A second heuristic suggested was that of using the estimator \(\eta _0\) alone, which was only suboptimal by one power of h due to the nonlinear terms, as opposed to the suboptimality by three powers of h that affects \(\eta _2, \eta ,\) and \(\eta _\varSigma\). A final proposed heuristic was to multiply the suboptimal indicators by a correction factor, resulting in another error indicator with effectivity indices that were generally observed to remain \({\mathscr {O}}(1)\), independent of the choice of discretization parameters.
Many avenues exist for future exploration. From a computational perspective, a natural next step is to utilize the estimates developed herein to develop adaptive methods. From a theoretical perspective, while suboptimality of \(\eta _0\) is somewhat expected, it would be useful to obtain estimators that do not incur the suboptimality that appears to characterize \(\eta _2, \eta ,\) and \(\eta _\varSigma\) and stems from the dispersive terms. Removal or at least amelioration of this suboptimality would greatly benefit the effectiveness of the resulting indicators. Finally, extending the results obtained for fully discrete schemes to the remaining members of the family of implicit Runge-Kutta methods of Gauss-Legendre type is of interest.
References
Abramowitz, M., Stegun, I.: Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables, Applied Mathematics Series, vol. 55. National Bureau of Standards (1965)
Adams, R.: Sobolev Spaces. Academic Press, New York (1975)
Ash, J., Cohen, J., Wang, G.: On strongly interacting internal solitary waves. J. Fourier Anal. Appl. 2, 507–517 (1996)
Baker, G.A., Dougalis, V.A., Karakashian, O.A.: Convergence of Galerkin approximations for the Korteweg-de Vries equation. Math. Comput. 40(162), 419–433 (1983). http://www.ams.org/jourcgi/jour-getitem?pii=S0025-5718-1983-0689464-4
Biello, J.: Nonlinearly coupled KdV equations describing the interaction of equatorial and midlatitude Rossby waves. Chin. Ann. Math. Ser. B 30(5), 483–504 (2009)
Bona, J.L.: Convergence of periodic wavetrains in the limit of large wavelength. Appl. Sci. Res. 37(1), 21–30 (1981)
Bona, J.L., Chen, H., Karakashian, O.A.: Stability of solitary-wave solutions of systems of dispersive equations. Appl. Math. Optim. 75, 27–53 (2017)
Bona, J.L., Chen, H., Karakashian, O.A.: Instability of solitary-wave solutions of systems of coupled KdV equations: theory and numerical results (2020) (Preprint)
Bona, J.L., Chen, H., Karakashian, O.A., Wise, M.M.: Finite element methods for a system of dispersive equations. J. Sci. Comput. 77(3), 1371–1401 (2018)
Bona, J.L., Chen, H., Karakashian, O.A., Xing, Y.: Conservative, discontinuous Galerkin-methods for the generalized Korteweg-de Vries equation. Math. Comput. 82(283), 1401–1432 (2013). http://www.ams.org/jourcgi/jour-getitem?pii=S0025-5718-2013-02661-0
Bona, J.L., Chen, H., Saut, J.-C.: Boussinesq equations and other systems for small-amplitude long waves in nonlinear dispersive media. I: derivation and linear theory. J. Nonlinear Sci. 12(4), 283–318 (2002)
Bona, J.L., Chen, H., Saut, J.-C.: Boussinesq equations and other systems for small-amplitude long waves in nonlinear dispersive media. II: the nonlinear theory. Nonlinearity 17(3), 925–952 (2004)
Bona, J.L., Cohen, J., Wang, G.: Global well-posedness for a system of KdV-type equations with coupled quadratic nonlinearities. Nagoya Math. J. 215(1), 67–149 (2014)
Bona, J.L., Smith, R.: The initial-value problem for the Korteweg-de Vries equation. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. (1934–1990) 278(1287), 555–601 (1975)
Brenner, S.C., Scott, L.R.: The Mathematical Theory of Finite Element Methods, ser. Texts in Applied Mathematics, vol. 15. Springer, New York (2008)
Chen, H.: Long-period limit of nonlinear dispersive waves. Differ. Integr. Equations 19, 463–480 (2006)
Cheng, Y., Shu, C.-W.: A discontinuous Galerkin finite element method for time dependent partial differential equations with higher order derivatives. Math. Comput. 77(262), 699–730 (2008). http://www.ams.org/journal-getitem?pii=S0025-5718-07-02045-5
Colliander, J., Keel, M., Staffilani, G., Takaoka, H., Tao, T.: Sharp global well-posedness for KdV and modified KdV on \(\mathbb{R}\) and \(\mathbb{T}\). J. Am. Math. Soc. 16(3), 705–749 (2003). http://www.ams.org/jourcgi/jour-getitem?pii=S0894-0347-03-00421-1
Hakkaev, S.: Stability and instability of solitary wave solutions of a nonlinear dispersive system of Benjamin-Bona-Mahony type. Serdica Math. J. 29, 337–354 (2003)
Karakashian, O., Makridakis, C.: A posteriori error estimates for discontinuous Galerkin methods for the generalized Korteweg-de Vries equation. Math. Comput. 84(293), 1145–1167 (2015)
Majda, A., Biello, J.: The nonlinear interaction of barotropic and equatorial baroclinic Rossby waves. J. Atmos. Sci. 60(15), 1809 (2003). http://search.proquest.com/docview/236571709/
Majda, A., Biello, J.: Boundary layer dissipation and the nonlinear interaction of equatorial baroclinic and barotropic Rossby waves. Geophys. Astrophys. Fluid Dyn. 98(2), 85–127 (2004)
Acknowledgements
This work was supported in part by the National Science Foundation under grant DMS-1620288
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
On behalf of all the authors, the corresponding author states that there is no conflict of interest.
Rights and permissions
About this article
Cite this article
Karakashian, O.A., Wise, M.M. A Posteriori Error Estimates for Finite Element Methods for Systems of Nonlinear, Dispersive Equations. Commun. Appl. Math. Comput. 4, 823–854 (2022). https://doi.org/10.1007/s42967-021-00143-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s42967-021-00143-4
Keywords
- Finite element methods
- Discontinuous Galerkin methods
- Korteweg-de Vries equation
- A posteriori error estimates
- Conservation laws
- Nonlinear equations
- Dispersive equations