A Weak Galerkin Harmonic Finite Element Method for Laplace Equation

Abstract

In this article, a weak Galerkin finite element method for the Laplace equation using the harmonic polynomial space is proposed and analyzed. The idea of using the $P_k$-harmonic polynomial space instead of the full polynomial space $P_{k}$ is to use a much smaller number of basis functions to achieve the same accuracy when $k\geqslant 2$. The optimal rate of convergence is derived in both $H^1$ and $L^2$ norms. Numerical experiments have been conducted to verify the theoretical error estimates. In addition, numerical comparisons of using the $P_{2}$-harmonic polynomial space and using the standard $P_2$ polynomial space are presented.

1 Introduction

In this article, we will consider the Laplace equation with the boundary condition,

$$\begin{aligned} -\Delta u= & {} 0 \qquad \text{ in } \Omega , \end{aligned}$$

(1)

$$\begin{aligned} u= & {} g \qquad \text{ on } \partial \Omega . \end{aligned}$$

(2)

The Laplace equation is widely used in problems of electrical, magnetic, and gravitational potentials, of steady-state temperatures, and of hydrodynamics. The classical numerical method for partial differential equations is the finite difference method where the discrete problem is obtained by replacing derivatives with difference quotients involving the values of the unknown at certain points. The finite difference method may be a good method to use when the geometry is simple and not very high accuracy is required. But when the geometry becomes more complex, finite difference becomes unreasonably difficult to implement.

The finite element method is a generalization of methods in structural engineering for beams, frames, and plates, where the structure is subdivided into small parts with known simple behavior. The main difference between finite difference and finite element methods lies in the concept of approximation. Finite difference discretizes the differential operator, while the finite element method discretizes the function space. It subdivides the complicated domain into smaller, simpler parts that are called finite elements. In the classic Galerkin finite element method, the approximating functions are continuous piecewise polynomials over a prescribed finite element partition for the domain. However, allowing the use of discontinuous approximating functions on arbitrary polytopal elements is a highly demanded feature for numerical algorithms in scientific computing. Consequently, we will have a wider range of function options in applying the Galerkin formulation to partial differential equations.

Different from the classic finite element method, the weak Galerkin finite element method enables the approximating functions to take separated values in the interior and on the boundary of each element, making the method highly flexible and efficient in practical computation. The weak Galerkin method was first introduced and analyzed by Wang and Ye [11] for second-order elliptic equations. The novel idea of the method is to define weak functions and their weak derivatives as distributions. Weak functions and weak derivatives can be approximated by polynomials with various degrees. The concept of weak gradients provides a systematic framework for dealing with discontinuous functions defined on elements and their boundaries in a near classical sense.

The weak Galerkin method can be viewed as an extension of the classic Galerkin finite element method where differential operators (e.g., gradient, divergence, and curl) are substituted by weakly defined operators. The weak Galerkin method allows arbitrary shapes of finite elements in a partition by adding a parameter free stabilizer, which enforces a weak continuity and provides a convenient flexibility in mesh generation. A mixed form is developed for the second-order elliptic problems by Wang and Ye [12]. Through rigorous analysis, the optimal order of priori error estimates has been established for various weak Galerkin schemes. Numerical implementations of weak Galerkin were performed by Mu et al. [6]. The possibility of an optimal combination of polynomial spaces that minimizes the number of unknowns has been explored in several numerical experiments. Because the weak Galerkin method inherits the advantages and overcomes the weaknesses of a discontinuous Galerkin method, it has been developed to solve many equations, such as elliptic interface problems [9], second-order elliptic equations with mixed boundary conditions [2], biharmonic equations [4, 16], Helmholtz equations [5], Brinkman equations [3], Stokes equations [13], Maxwall equation [8], hyperbolic equation [15], heat equations [17], and time-dependent convection diffusion equations [14].

A harmonic polynomial is a multivariate polynomial with zero Laplacian. In two dimensions, the regular $P_k$ finite element space has $(k+1)(k+2)/2$ basis functions on each element, whereas the $P_k$-harmonic finite element space has $2k+1$ basis functions on each element. The Laplace equation (1)–(2) has been discussed by Sorokina and Zhang [10] using a conforming and nonconforming harmonic finite element method and achieved the optimal convergence in $H^1$ and $L^2$ norms. The purpose of this work is to propose a weak Galerkin method for the Laplace equation using harmonic polynomial finite elements instead of using the full polynomial space $P_k$ to achieve the same order of accuracy and convergence and thus to improve the efficiency. For the sake of simplicity, we will confine our attention to the case $k=2$ in this paper.

The paper is organized as follows. In Sect. 2, we introduce the weak Galerkin scheme on the harmonic finite element space. We discuss the weak Galerkin algorithm in Sect. 3. The error analysis for the weak Galerkin solutions in an energy norm will be investigated in Sect. 4. In Sect. 5, we will derive the $L^2$ error estimates for the weak Galerkin finite element method for solving (1)–(2). The results of some numerical experiments are reported in Sect. 6 to validate our method. In the end, some concluding remarks are given in Sect. 7.

2 The Weak Galerkin Finite Element Method

In this section, we will introduce the weak function spaces, the discrete weak gradients and the weak Galerkin scheme for (1)–(2).

2.1 Weak Function and Discrete Weak Gradients

We denote the $L^2$ norm and inner product used in this article as $|\!|\cdot |\!|_{L^{2}(\Omega )}$ and $(\cdot ,\cdot )_{\Omega }$, respectively. The vector-valued space $H({\text{div}};\Omega )$ is defined as

$$\begin{aligned} H({\text{div}};\Omega )=\left\{ \varvec{\nu } : \varvec{\nu } \in [L^{2}(\Omega )]^{2},\nabla \cdot \varvec{\nu } \in L^{2}(\Omega )\right\} . \end{aligned}$$

Let K be a polygonal domain $K\subset {\textbf{R}}^{2}$ with the interior $K^0$ and the boundary $\partial K$. A weak function $v=\{v_0,v_{\text{b}}\}$ on K is such that $v_0\in L^{2}(K^0)$ and $v_{\text{b}}\in L^{2}(\partial K)$. In this instance, the component $v_{0}$ symbolizes the interior value of v, and the component $v_{\text{b}}$ symbolizes the edge value of v on $K^{0}$ and $\partial K$, respectively. Note that $v_{\text{b}}$ is not necessarily the trace of $v_0$ on $\partial K$. Then, we define the space of weak functions in the following way:

$$\begin{aligned} \textit{W}(K)=\left\{ v=\{v_0,v_{\text{b}}\}:v_{0} \in L^{2}(K^{0}),v_{\text{b}}\in L^{2}(\partial K)\right\} . \end{aligned}$$

(3)

Definition 1

For any $v=\{v_0,v_{\text{b}}\}\in \textit{W}(K)$, the weak gradient $\nabla _{\text{w}} v$ is the linear functional on H(div, K) satisfying

$$\begin{aligned} (\nabla _{\text{w}} v,\varvec {\tau })_{K}=-\int _{K} v_{0} \nabla \cdot \varvec {\tau }\;\partial x+\int _{\partial K} v_{\text{b}}(\varvec {n}\cdot \varvec {\tau })\;\partial s,\quad \forall \varvec {\tau }\in H({\text{div}},K), \end{aligned}$$

(4)

where $\varvec {n}$ is the unit outward normal vector to $\partial K$. Note that because of trace theorem and variation theorem $\nabla _{\text{w}} v$ is well defined and $\nabla _{\text{w}} v=\nabla v$ if $v\in H^{1}(K)$.

For each $k\geqslant 0$, denote by $P_{k}(K)$ the set of polynomials defined on K with degree no more than k. Denote the vector-valued space $[P_{k}(K)]^{2}$, then for any $v \in \textit{W}(K)$, the discrete weak gradient $\nabla _{{\text{w}},k,K} v$ is defined below.

Definition 2

For any $v \in \textit{W}(K)$, the discrete weak gradient $\nabla _{{\text{w}},k,K} v\in [P_{k}(K)]^{2}$ is the unique polynomial satisfying

$$\begin{aligned} (\nabla _{{\text{w}},k,K} v,\varvec {\tau }_{k})_{K}=-\int _{K} v_{0} \nabla \cdot \varvec {\tau }_{k}\;\partial x+\int _{\partial K} v_{\text{b}}(\varvec {n}\cdot \varvec {\tau }_{k})\;\partial s,\quad \forall \varvec {\tau }_{k}\in [P_{k}(K)]^{2}; \end{aligned}$$

(5)

for simplicity, we use $\nabla _{\text{w}} v$ instead of $\nabla _{{\text{w}},k,K} v$ in the sequel.

2.2 The Weak Galerkin Scheme

Let $\mathcal{T}_{h}$ be a partition of the domain $\Omega$ with the mesh size $h=\max \limits_{T\in \mathcal{T}_{h}}h_T$ that consists of polygons in $\textbf{R}^{2}$, and let $\mathcal {E}_h$ be the set of all edges in $\mathcal{T}_{h}$. Denote by $\mathcal {E}^{0}_h=\mathcal {E}_h\backslash \partial \Omega$ the set all interior edges. Let $\mathcal{T}_{h}$ be a shape regular partition (see [7]) of $\Omega$. For each $T \in \mathcal{T}_{h}$, the $P_{k}$-harmonic polynomial space is defined as

$$\begin{aligned} P_{k,{\text{harm}}}(T)=\left\{ P| P\in P_{k}(T), \Delta P =0\right\} . \end{aligned}$$

(6)

Let $P_{k,{\text{harm}}}(T^{0})$ be the set of harmonic polynomials defined in $T^{0}$ and $P_{k}(e)$ be the set of polynomials defined on $e\in \partial T$ with degree no more than k. Then, we define two weak Galerkin finite element spaces of weak functions as follows:

$$\begin{aligned} V_{h}=\left\{ v=\left\{ v_{0},v_{\text{b}}\right\} :v_{0}|_{T}\in P_{2,{\text{harm}}}(T^{0}), \forall T\in \mathcal{T}_{h}, v_{\text{b}}|_{e}\in P_{1}(e), \forall e\in \partial T\right\} , \end{aligned}$$

(7)

and

$$\begin{aligned} V_{h}^{0}=\left\{ v \in V_{h},v_{\text{b}}=0 \text{ on } \partial \Omega \right\} . \end{aligned}$$

(8)

According to (5), for any $v \in V_{h}$, the discrete weak gradient operator $\nabla _{\text{w}} v$ of v on each element T is defined as follows.

Definition 3

For any $v=\left\{ v_{0},v_{\text{b}}\right\} \in V_{h}$, the discrete weak gradient $\nabla _{\text{w}} v|_{T}\in [P_{1}(T)]^{2}$ is a vector satisfying

$$\begin{aligned} (\nabla _{w} v,\varvec {\tau })_{T}=-\int _{T} v_{0} \nabla \cdot \varvec {\tau }\;\partial T+\int _{\partial T} v_{\text{b}}(\varvec {n}\cdot \varvec {\tau })\;\partial s,\quad \forall \varvec {\tau }\in [P_{1}(T)]^{2}. \end{aligned}$$

(9)

Next, we define four global projections $Q_{0},Q_{\text{b}},Q_{h}$, and $\mathbb {Q}_{h}$ as follows.

Definition 4

For each element $T\in \mathcal{T}_{h}$,

$$\begin{aligned} Q_{0}:&L^{2}(T)\longrightarrow P_{2,{\text{harm}}}(T),\\ Q_{\text{b}}:&L^2(e)\longrightarrow P_{1}(e),\\ \mathbb {Q}_{h}:&[L^{2}(T)]^{2}\longrightarrow [P_{1}(T)]^{2} \end{aligned}$$

are the $L^{2}$ projections onto the associated local polynomial spaces. Finally, we define a projection operator $Q_{h}v=\left\{ Q_{0}v,Q_{\text{b}}v\right\} \in V_{h}$ for $v\in H^{1}(\Omega )$.

For simplicity, we adopt the following notations:

$$\begin{aligned} (v,w)_{\mathcal{T}_h}= & {} \sum _{T\in \mathcal{T}_h}(v,w)_{T}=\sum _{T\in \mathcal{T}_h}\int _{T}v w {\text{d}}x,\\ \left\langle v,w\right\rangle _{\partial \mathcal{T}_h}= & {} \sum _{T\in \mathcal{T}_h}\left\langle v,w\right\rangle _{\partial T}=\sum _{T\in \mathcal{T}_h}\int _{\partial T}v w {\text{d}}s. \end{aligned}$$

For any $v=\left\{ v_{0},v_{\text{b}}\right\}$ and $w=\left\{ w_{0},w_{\text{b}}\right\}$ in $V_{h}$, we define the stabilization term as follows:

$$\begin{aligned} s(v,w)= \sum _{T\in \mathcal{T}_{h}}h_{T}^{-1} \left\langle Q_{\text{b}}v_{0}-v_{\text{b}},Q_{\text{b}}w_{0}-w_{\text{b}}\right\rangle _{\partial T}. \end{aligned}$$

(10)

The following bilinear forms will be needed later:

$$\begin{aligned} A(v,w)= & {} (\nabla _{\text{w}} v\cdot \nabla _{\text{w}} w)_{\mathcal{T}_{h}}, \end{aligned}$$

(11)

$$\begin{aligned} A_{s}(v,w)= & {} A(v,w)+s(v,w). \end{aligned}$$

(12)

Now, we are situated to introduce the weak Galerkin algorithm for (1)–(2).

3 Weak Galerkin Algorithm

A numerical approximation for (1)–(2) can be obtained by seeking $u_{h}=\{u_{0},u_{\text{b}}\}\in V_{h}$ satisfying $u_{\text{b}}=Q_{\text{b}}g$ on $\partial \Omega$ and

$$\begin{aligned} A_{s}(u_{h},v)=0, \quad \forall v=\left\{ v_{0},v_{\text{b}}\right\} \in V_{h}^{0}, \end{aligned}$$

(13)

where $A_{s}(\cdot ,\cdot )$ is defined in (12).

Accordingly, we define an energy norm $|\!|\!|\cdot |\!|\!|$ on $V_{h}^{0}$: for any $v\in V_{h}^{0}$,

$$\begin{aligned} |\!|\!|v|\!|\!|^{2}=\sum _{T\in \mathcal{T}_h}|\!|\nabla _w v|\!|^{2}_{T}+s(v,v)=A_{s}(v,v). \end{aligned}$$

(14)

It can be easily verified that this energy norm is a norm on $V_{h}^{0}$.

Lemma 1

The weak Galerkin algorithm has one and only one solution.

Proof

Let $u_{h}^{(1)}$ and $u_{h}^{(2)}$ be two solutions of (13). Then, $\varrho _{h} =u_{h}^{(1)}-u_{h}^{(2)}$ would satisfy the forthcoming equation

$$\begin{aligned} A_{s}(\varrho _{h},v)=0,\quad \forall v\in V_{h}^{0}. \end{aligned}$$

(15)

Note that $\varrho _{h}\in V_{h}^{0}$. Letting $v=\varrho _{h}$ in (15) yields

$$\begin{aligned} |\!|\!|\varrho _{h}|\!|\!|^{2}=A_{s}(\varrho _{h},\varrho _{h})=0,\nonumber \end{aligned}$$

which implies $\varrho _{h}\equiv 0$. Consequently, $u_{h}^{(1)}\equiv u_{h}^{(2)}$.

Next, we will show the commutative property for the $Q_{h}$ and $\mathbb {Q}_{h}$ operators.

Lemma 2

(see [11]) Let $Q_{h}$ and $\mathbb {Q}_{h}$ be the projection operators defined in previous sections and $\phi \in H^{1}(\Omega ).$ Then, for each element $T\in \mathcal{T}_{h}$, we have the following commutative property:

$$\begin{aligned} \nabla _{\text{w}}(Q_{h}\phi )=\mathbb {Q}_{h}(\nabla \phi ). \end{aligned}$$

(16)

Lemma 3

Let $\psi \in H^{1}(\Omega )$. Then, for all $v\in V_{h}$, we have

$$\begin{aligned} (\nabla \psi ,\nabla v_{0})_{T}=(\nabla _wQ_{h} \psi ,\nabla _w v)_{T}+\left\langle \mathbb {Q}_{h}\nabla \psi \cdot \varvec {n},v_{0}-v_{\text{b}}\right\rangle _{\partial T}. \end{aligned}$$

(17)

Proof

It follows from Lemma 2, using (9), and integration by parts that

$$\begin{aligned}&(\nabla _{\text{w}} Q_{h}\psi ,\nabla _{\text{w}} v)_{T}=(\mathbb {Q}_{h}\nabla \psi ,\nabla _{\text{w}} v)_{T}\\&\quad =-(v_{0},\nabla \cdot (\mathbb {Q}_{h}\nabla \psi ))_{T}+\left\langle v_{\text{b}},\mathbb {Q}_{h}\nabla \psi \cdot \varvec {n}\right\rangle _{\partial T}\\&\quad =(\nabla v_{0}, \mathbb {Q}_{h}\nabla \psi )_{T}-\left\langle v_{0}-v_{\text{b}}, \mathbb {Q}_{h}\nabla \psi \cdot \varvec {n}\right\rangle _{\partial T}\\&\quad =(\nabla \psi ,\nabla v_{0})_{T}-\left\langle \mathbb {Q}_{h}\nabla \psi \cdot \varvec {n},v_{0}-v_{\text{b}}\right\rangle _{\partial T}. \end{aligned}$$

Solving for $(a\nabla \psi ,\nabla v_{0})_{T}$ gives us the required result.

Let $u_{h}$ and u be the numerical solution of (13) and the exact solution of (1)–(2), respectively. Denote by $\varrho _{h}=Q_{h}u-u_{h}$ the error where $Q_{h}u$ is the projection of u. We will state and prove the forthcoming error equation.

Lemma 4

Let $u_{h}\in V_{h}$ be the solution to the formulation (13) and let u be the solution of (1)–(2). Then, the error $\varrho _{h}$ satisfies

$$\begin{aligned} A_{s}(\varrho _{h},v)=s(Q_{h}u,v)-\ell (u,v),\quad \forall v\in V_{h}^{0}, \end{aligned}$$

(18)

where $\ell (u,v)=\sum \limits_{T\in \mathcal{T}_{h} }\left\langle ( \mathbb {Q}_{h}\nabla u-\nabla u)\cdot \varvec {n},v_{0}-v_{\text{b}}\right\rangle _{\partial T}$.

Proof

Testing (1) by $v_{0}$ and using integration by parts, we get

$$\begin{aligned} 0= & {} -(\Delta u,v_{0})\\= & {} (\nabla u,\nabla v_{0})_{\mathcal{T}_{h}}-\sum _{T\in \mathcal{T}_{h}}\left\langle \nabla u\cdot \varvec {n},v_{0}\right\rangle _{\partial T}. \end{aligned}$$

Using the fact that $\sum \limits_{T\in \mathcal{T}_{h}}\left\langle \nabla u\cdot \varvec {n},v_{\text{b}}\right\rangle _{\partial T}=0$, we get

$$\begin{aligned} (\nabla u,\nabla v_{0})_{ \mathcal{T}_{h}}-\sum _{T\in \mathcal{T}_{h}}\left\langle \nabla u\cdot \varvec {n},v_{0}-v_{\text{b}}\right\rangle _{\partial T}=0. \end{aligned}$$

By setting $\psi =u$ in (17) and substituting it into the equation above, we obtain

$$\begin{aligned} ( \nabla _{\text{w}} Q_{h} u,\nabla _{\text{w}} v)_{ \mathcal{T}_{h}}=-\sum _{T\in \mathcal{T}_{h}}\left\langle (\mathbb {Q}_{h}\nabla u-\nabla u)\cdot \varvec {n},v_{0}-v_{\text{b}}\right\rangle _{\partial T}. \end{aligned}$$

Adding the term $s(Q_{h}u,v)$ to both sides of the above equation gives rise to

$$\begin{aligned} (\nabla _{\text{w}} Q_{h} u,\nabla _{\text{w}} v)_{ \mathcal{T}_h}+s(Q_{h}u,v)= & {} s(Q_{h}u,v)\nonumber -\sum \limits_{T\in \mathcal{T}_h }\left\langle (\mathbb {Q}_{h}\nabla u-\nabla u)\cdot \varvec {n},v_{0}-v_{\text{b}}\right\rangle _{\partial T}. \end{aligned}$$

(19)

Subtracting (13) from (19) yields

$$\begin{aligned} A_{s}( \varrho _{h},v)=s(Q_{h}u,v)-\ell (u,v). \end{aligned}$$

(20)

The proof is completed.

4 Error Estimates in Energy Norm

We will derive error estimates in this section. First, we present two essential inequalities in shape regular partitions. For further details, please see [12].

Lemma 5

(Trace inequality) On each element $T\in \mathcal{T}_h$, the following inequality holds true for some constant C:

$$\begin{aligned} |\!|\varphi |\!|_{e}^{2}\leqslant C\left( h_{T}^{-1}|\!|\varphi |\!|_{T}^{2}+h_{T}|\!|\nabla \varphi |\!|_{1,T}^{2}\right) , \quad \varphi \in H^{1}(T). \end{aligned}$$

(21)

Lemma 6

(Inverse inequality) There exists a constant C such that for any piecewise polynomial $\varphi \in P_{k}(T)$,

$$\begin{aligned} |\!|\nabla \varphi |\!|_{T}\leqslant Ch^{-1}_{T}|\!|\varphi |\!|_{T}, \quad \forall T\in \mathcal{T}_h. \end{aligned}$$

(22)

Before presenting Lemma 8, we need to prove the following lemma.

Lemma 7

Suppose that $u\in C^{m}(T)$ and $\Delta u=0$. Then, for any $0\leqslant k<m$, the degree k Taylor polynomial of u centered at $p\in T$, $P_{k}(x_{1},x_{2})$, is harmonic.

Proof

First

$$\begin{aligned} P_{k}(x)=\sum _{i=0}^{k}\sum _{|\alpha |=i}\frac{D^{\alpha }u(p)}{\alpha !}(x-p)^{\alpha }. \end{aligned}$$

Since

$$\left\{\begin{array}{lll} D^{(2,0)}u(p)+D^{(0,2)}u(p)= {} 0,\quad \forall p\in T,\\ D^{\alpha +(2,0)}u(p)+D^{\alpha +(0,2)}u(p)= {} 0,\quad \forall |\alpha |\leqslant k-2, \end{array}\right.$$

(23)

we want to show that for each $0\leqslant i\leqslant k,$

$$\begin{aligned} \Delta \sum _{|\alpha |=i}\frac{D^{\alpha }u(p)}{\alpha !}(x-p)^{\alpha }=0. \end{aligned}$$

It follows from (23) that

$$\begin{aligned} \sum _{|\alpha |=i}\frac{D^{\alpha }u(p)}{\alpha !}(x-p)^{\alpha }= & {} \sum _{0\leqslant j\leqslant \frac{i}{2}}D^{(i-2j,2j)}u(p)\frac{(x_{1}-p_{1})^{i-2j}(x_{2}-p_{2})^{2j}}{(i-2j)! (2j)!}\\&+\sum _{0\leqslant j\leqslant \frac{i-1}{2}}D^{(i-1-2j,2j+1)}u(p)\frac{(x_{1}-p_{1})^{i-1-2j}(x_{2}-p_{2})^{2j+1}}{(i-1-2j)! (2j+1)!}\\= \, & {} D^{(i,0)}u(p)\sum _{0\leqslant j\leqslant \frac{i}{2}}(-1)^{j}\frac{(x_{1}-p_{1})^{i-2j}(x_{2}-p_{2})^{2j}}{(i-2j)! (2j)!}\\&+D^{(i-1,1)}u(p)\sum _{0\leqslant j\leqslant \frac{i-1}{2}}(-1)^{j}\frac{(x_{1}-p_{1})^{i-1-2j}(x_{2}-p_{2})^{2j}}{(i-1-2j)!(2j+1)!}\\= & {} D^{(i,0)}u(p) A+D^{(i-1,1)}u(p) B. \end{aligned}$$

We need to show that $\Delta A=\Delta B=0,$

$$\begin{aligned} \Delta A= & {} \sum _{0\leqslant j\leqslant \frac{i}{2}}(-1)^{j} (i-2j)(i-2j-1)\frac{(x_{1}-p_{1})^{i-2j-2}(x_{2}-p_{2})^{2j}}{(i-2j)! (2j)!}\\&+\sum _{0\leqslant j\leqslant \frac{i}{2}}(-1)^{j}2j(2j-1)\frac{(x_{2}-p_{2})^{2(j-1)}(x_{1}-p_{1})^{i-2j}}{(i-2j)! (2j)!}\\= & {} \sum _{0\leqslant j\leqslant \frac{i}{2}-1}(-1)^{j} \frac{(x_{1}-p_{1})^{i-2j-2}(x_{2}-p_{2})^{2j}}{(i-2j-2)! (2j)!}\\&+\sum _{1\leqslant j\leqslant \frac{i}{2}}(-1)^{j}\frac{(x_{1}-p_{1})^{i-2j}(x_{2}-p_{2})^{2j-2}}{(i-2j)! (2j-2)!}\\= \, & {} 0. \end{aligned}$$

Similarly, $\Delta B=0$.

Remark 1

The proof of Lemma 7 implies that the dimension of $P_{k,{\text{harm}}}$ is $2k+1$.

The forthcoming lemma presents estimates for the projection operators $Q_{0}$ and $\mathbb {Q}_{h}$.

Lemma 8

Let $\mathcal{T}_h$ be a partition of $\Omega$ satisfying the shape regularity and u be the exact solution of the problem (1)–(2). Then, the $L^{2}$ projections $Q_{0}$ and $\mathbb {Q}_{h}$ satisfy

$$\begin{aligned}&\sum _{T\in \mathcal{T}_h }\left( |\!|u-Q_{0}u|\!|_{T}^{2}+h_{T}^{2}|\!|\nabla (u-Q_{0}u)|\!|_{T}^{2}\right) \leqslant Ch^{2(s+1)}|\!|u|\!|_{s+1}^{2}, \quad 0\leqslant s\leqslant k, \end{aligned}$$

(24)

$$\begin{aligned}&\sum _{T\in \mathcal{T}_h }\left( |\!|\nabla u-\mathbb {Q}_{h}\nabla u|\!|_{T}^{2}+h_{T}^{2}|\!|\nabla u-\mathbb {Q}_{h}\nabla u|\!|_{T}^{2}\right) \leqslant Ch^{2s}|\!|u|\!|_{s+1}^{2}, \quad 0\leqslant s\leqslant k. \end{aligned}$$

(25)

Proof

Let $u\in H^{m}(\Omega )$. For each $T\in \mathcal{T}_h$, let $B\subset T$ be a ball, and $\psi \geqslant 0$ such that $\psi \in C^{\infty }(B),\int _{B}\psi {\text{d}} x =1$, and $\psi (x)=0$ for $x\in T\backslash B$. Then, by Bramble-Hilbert Lemma [1],

$$\begin{aligned} |\!|u-v|\!|_{t,T}\leqslant C h_{T}^{m-t}|\!|u|\!|_{m,T}, \end{aligned}$$

where

$$\begin{aligned} v(x) =\int _{B}T^{m}_{y}u(x)\psi (y) \text{d} y \end{aligned}$$

and

$$\begin{aligned} T^{m}_{y}u(x)=\sum _{k=0}^{m-1}\sum _{|\alpha |=k}\frac{1}{\alpha !}D^{\alpha }u(y)(x-y)^{\alpha }. \end{aligned}$$

By Lemma 7,

$$\begin{aligned} \Delta T_{y}^{m}u(x)=0. \end{aligned}$$

Thus,

$$\begin{aligned} \Delta v(x)=\int _{B}\Delta T_{y}^{m}u(x)\psi (y) \text{d} y =0. \end{aligned}$$

Letting $m=s+1$ and $t=0,1$ yields

$$\begin{aligned} |\!|u-v|\!|_{T}^{2}\leqslant Ch_{T}^{2(s+1)}|\!|u|\!|^{2}_{T,s+1}\quad \text{ and }\quad h_{T}^{2}|\!|u-v|\!|_{T,1}^{2}\leqslant Ch_{T}^{2(s+1)}|\!|u|\!|^{2}_{T,s+1}, \end{aligned}$$

(26)

respectively. Summing up inequalities (26) over $T\in \mathcal{T}_h$ yields

$$\begin{aligned} |\!|u-v|\!|^{2}\leqslant C h^{2(s+1)}|\!|u|\!|^{2}_{s+1}\quad \text{ and }\qquad h^{2}|\!|u-v|\!|^{2}\leqslant C h^{2s}|\!|u|\!|^{2}_{s+1}. \end{aligned}$$

Since

$$\left\{\begin{aligned}& |\!|u-v|\!|^{2}\leqslant {} |\!|u-Q_{0}u|\!|^{2}+|\!|Q_{0}u-v|\!|^{2},\\ & |\!|u-Q_{0}u|\!|^{2}\leqslant {} Ch^{2(s+1)}|\!|u|\!|^{2}_{s+1} \end{aligned}\right.$$

(27)

and

$$\begin{aligned}|\!|Q_{0}u-v|\!|^{2} &\leqslant Ch^{2s+1}|\!|u|\!|^{2}_{s+1}, \\ |\!|u-Q_{0}u|\!|_{1}^{2} & =|\!|u-v|\!|_{1}^{2}+|\!|Q_{0}u-v|\!|_{1}^{2} \\ &\leqslant Ch^{2s}|\!|u|\!|^{2}_{s+1}+h^{-2}|\!|Q_{0}u-v|\!|^{2} \\&\leqslant Ch^{2s}|\!|u|\!|_{s+1}^{2}. \end{aligned}$$

(28)

(24) follows from (27) and (28). (25) follows from (24).

Lemma 9

Assume that $u_{h}\in V_{h}$ is the solution to the formulation (13). Let $u\in H^{3}(\Omega )$ be the exact solution of (1)–(2). Then, there exists a positive constant C such that for any $v\in V_{h}^{0}$, the following estimates hold true:

$$\begin{aligned} |\ell (u,v)|\leqslant & {} C h^{2}|\!|u|\!|_{3}|\!|\!|v|\!|\!|, \end{aligned}$$

(29)

$$\begin{aligned} |s(Q_{h}u,v)|\leqslant & {} C h^{2}|\!|u|\!|_{3}|\!|\!|v|\!|\!|. \end{aligned}$$

(30)

Proof

Applying the Cauchy-Schwarz inequality, we obtain

$$\begin{aligned} |\ell (u,v)|\leqslant & {} \sum _{T\in \mathcal{T}_h }|\left\langle (\nabla u-\mathbb {Q}_{h}\nabla u)\cdot \varvec {n},v_{0}-v_{\text{b}}\right\rangle _{ \partial T}|\\\leqslant & {} C \sum _{T\in \mathcal{T}_h } |\!|\nabla u-\mathbb {Q}_{h}\nabla u)|\!|_{\partial T}|\!|v_{0}-v_{\text{b}}|\!|_{\partial T}\\\leqslant & {} C \left( \sum _{T\in \mathcal{T}_h }h_{T} |\!|\nabla u-\mathbb {Q}_{h}\nabla u|\!|_{\partial T}^{2}\right) ^{\frac{1}{2}} \left( \sum _{T\in \mathcal{T}_h }h_{T}^{-1} |\!|v_{0}-v_{\text{b}}|\!|_{\partial T}^{2}\right) ^\frac{1}{2}. \end{aligned}$$

Using the trace inequality (21) and Lemma 8, we directly have

$$\begin{aligned} |\ell (u,v)|\leqslant & {} C h^{2} |\!|u|\!|_{3}\left( \sum _{T\in \mathcal{T}_h }h_{T}^{-1} |\!|v_{0}-v_{\text{b}}|\!|_{\partial T}^{2}\right) ^{\frac{1}{2}}\\\leqslant & {} Ch^{2} |\!|u|\!|_{3}|\!|\!|v|\!|\!|. \end{aligned}$$

As to inequality (30), start using the Cauchy-Schwarz inequality followed by the trace inequality (21) and Lemma 8, we find that

$$\begin{aligned} \left| s(Q_{h}u,v)\right|= & {} \sum _{T\in \mathcal{T}_h}h_{T}^{-1}\left| \left\langle Q_{\text{b}}(Q_{0}u) -Q_{\text{b}}u,Q_{\text{b}}v_{0}-v_{\text{b}}\right\rangle _{\partial T} \right| \\= & {} \sum _{T\in \mathcal{T}_h}h_{T}^{-1}\left| \left\langle Q_{0}u -u,Q_{\text{b}}v_{0}-v_{\text{b}}\right\rangle _{\partial T} \right| \\\leqslant & {} C\left( \sum _{T\in \mathcal{T}_h}h_{T}^{-1}|\!| Q_{0} u-u|\!|_{\partial T}^{2}\right) ^{\frac{1}{2}}\left( \sum _{T\in \mathcal{T}_h}h_{T}^{-1}|\!| Q_{\text{b}}v_{0}-v_{\text{b}}|\!|_{\partial T}^{2}\right) ^{\frac{1}{2}} \\\leqslant & {} C \left( \sum _{T\in \mathcal{T}_h} h_{T}^{-2} \left( |\!| Q_{0}u-u|\!|_{T}^{2}+h_{T}^{2}|\!| \nabla (Q_{0}u-u)|\!|_{T}^{2}\right) \right) ^{\frac{1}{2}} \left( \sum _{T\in \mathcal{T}}h_{T}^{-1} |\!| Q_{\text{b}}v_{0}-v_{\text{b}}|\!|_{\partial T}^{2}\right) ^{\frac{1}{2}} \\\leqslant & {} Ch^{2}|\!|u|\!|_{3}|\!|\!|v|\!|\!|. \end{aligned}$$

This completes the proof.

Theorem 1

Assume that $u_{h}\in V_{h}$ and $u\in H^{3}(\Omega )$ are the weak Galerkin solution to the formulation (13) and the exact solution of the problem (1)–(2), respectively. Then, there exists a constant $C>0$ such that

$$\begin{aligned} |\!|\!|u_{h}-Q_{h}u|\!|\!|\leqslant Ch^{2}|\!|u|\!|_{3}. \end{aligned}$$

(31)

Proof

Letting $v=\varrho _{h}$ in (18), we obtain

$$\begin{aligned} |\!|\!|\varrho _{h}|\!|\!|^{2}=-\ell (u,\varrho _{h})+s(Q_{h}u,\varrho _{h}). \end{aligned}$$

From the estimates (29) and (30), we find that

$$\begin{aligned} |\!|\!|\varrho _{h}|\!|\!|^{2}\leqslant Ch^{2}|\!|u|\!|_{3}|\!|\!|\varrho _{h}|\!|\!|, \end{aligned}$$

which gives (31).

5 Error Estimates in $L^2$ Norm

We are going to derive the $L^2$ error estimate for the weak Galerkin finite element scheme. Consider the problem that seeks $w \in H^1_0(\Omega )$ satisfying

$$\begin{aligned} -\Delta w= & {} \varrho _0 \quad \text{ in } \Omega , \end{aligned}$$

(32)

$$\begin{aligned} w= & {} 0 \quad \text{ on } \partial \Omega \end{aligned}$$

(33)

with the $H^2$-regularity assumption $\Vert w\Vert _2 \leqslant C\Vert {\varrho _0}\Vert$.

Theorem 2

Let $u\in H^{3}(\Omega )$ and $u_h\in V_h$ be the solutions of the problem (1)–(2) and (13), respectively. Then, there exists a constant C such that

$$\begin{aligned} \Vert {Q_{0}u-u_0}\Vert \leqslant Ch^{3}\Vert u\Vert _{3}. \end{aligned}$$

(34)

Proof

Testing (32) with $\varrho _0$, we get

$$\begin{aligned} \Vert {\varrho _0}\Vert ^2=-(\Delta w,\varrho _0). \end{aligned}$$

Using integration by parts, we get

$$\begin{aligned} \Vert {\varrho _0}\Vert ^2=\sum _{T\in \mathcal{T}_h}(\nabla w,\nabla \varrho _0)_T-\sum _{T\in \mathcal{T}_h}\langle \nabla w\cdot \varvec {n},\varrho _0\rangle _{\partial T}. \end{aligned}$$

Since $\sum \limits_{T\in \mathcal{T}_h}\langle \nabla w\cdot \varvec {n},\varrho _{\text{b}}\rangle _{\partial T}=0$, we can rewrite the above expression as

$$\begin{aligned} \Vert {\varrho _0}\Vert ^2=\sum _{T\in \mathcal{T}_h}(\nabla w,\nabla \varrho _0)_{T}-\sum _{{T}\in \mathcal{T}_h}\langle \nabla w\cdot \varvec {n}, \varrho _0-\varrho _{\text{b}}\rangle _{\partial T}. \end{aligned}$$

(35)

Setting $\psi =w$ and $v=\varrho _h$ in (17) gives

$$\begin{aligned} \sum _{T\in \mathcal{T}_h}(\nabla w, \nabla \varrho _0)_{T}=\sum _{T\in \mathcal{T}_h}(\nabla _wQ_hw,\nabla _w \varrho _h )_{T}+\sum _{T\in \mathcal{T}_h}\langle \varrho _0-\varrho _{\text{b}},\mathbb {Q}_{h}\nabla w \cdot \varvec {n}\rangle _{\partial T}. \end{aligned}$$

(36)

Substituting (35) into (36), we get

$$\begin{aligned} \Vert {\varrho _0}\Vert ^2=A(Q_h w,\varrho _h)+\sum _{T\in \mathcal{T}_h}\langle ( \mathbb {Q}_{h} \nabla w-\nabla w) \cdot \varvec {n},\varrho _0-\varrho _{\text{b}}\rangle _{\partial T }. \end{aligned}$$

Adding and subtracting the term $s(Q_hw,\varrho _h)$, we obtain

$$\begin{aligned} \Vert {\varrho _0}\Vert ^2=A_s(Q_h w,\varrho _h)-s(Q_hw,\varrho _h)+\sum _{T\in \mathcal{T}_h}\langle ( \mathbb {Q}_h \nabla w-\nabla w) \cdot \varvec {n},\varrho _0-\varrho _{\text{b}}\rangle _{\partial T }. \end{aligned}$$

(37)

It follows from the error Eq. (18) that

$$\begin{aligned} A_s(Q_h w,\varrho _h)=\sum _{T\in \mathcal{T}_h}\langle (\nabla u-\mathbb {Q}_h\nabla u)\cdot \varvec {n},Q_0 w-Q_{\text{b}} w\rangle _{\partial T}+s(Q_hu,Q_h w). \end{aligned}$$

(38)

By combining (37) with (38), we get

$$\begin{aligned} \Vert {\varrho _0}\Vert ^2 & = \sum _{T\in \mathcal{T}_h}\langle (\nabla u-\mathbb {Q}_{h}\nabla u)\cdot \varvec {n},Q_0 w-Q_{\text{b}} w\rangle _{\partial T}+s(Q_hu,Q_hw)-s(Q_hw,\varrho _h)\nonumber \\&\quad +\sum _{T\in \mathcal{T}_h}\langle ( \mathbb {Q}_{h} \nabla w-\nabla w) \cdot \varvec {n},\varrho _0-\varrho _{\text{b}}\rangle _{\partial T}\nonumber \\ & = \ell (u,Q_{h}w)+s(Q_hu,Q_hw)-s(Q_hw,\varrho _h)+\ell (w,\varrho _h). \end{aligned}$$

(39)

Now we are going to bound the terms on the right-hand side of (39). Using the Cauchy-Schwarz inequality and the definition of $Q_{\text{b}}$, we get

$$\begin{aligned} \left| \ell (u,Q_{h}w)\right|= & {} \left| \sum _{T\in \mathcal{T}_h}\langle (\nabla u-\mathbb {Q}_{h}\nabla u)\cdot \varvec {n},Q_0 w-Q_{\text{b}} w\rangle _{\partial T}\right| \nonumber \\\leqslant & {} \left( \sum _{T\in \mathcal{T}_h} \Vert (\nabla u-\mathbb {Q}_{h}\nabla u)\Vert ^2_{\partial T} \right) ^{1/2} \left( \sum _{T\in \mathcal{T}_h} \Vert Q_0 w-Q_{\text{b}} w \Vert ^2_{\partial T} \right) ^{1/2} \nonumber \\\leqslant & {} C \left( \sum _{T\in \mathcal{T}_h} \Vert (\nabla u-\mathbb {Q}_{h}\nabla u)\Vert ^2_{\partial T} \right) ^{1/2} \left( \sum _{T\in \mathcal{T}_h} \Vert Q_0 w-w \Vert ^2_{\partial T} \right) ^{1/2}. \end{aligned}$$

(40)

From the trace inequality (21) and the estimate (24), we have

$$\begin{aligned} \left( \sum _{T\in \mathcal{T}_h} \Vert (\nabla u-\mathbb {Q}_{h}\nabla u)\Vert ^2_{\partial T} \right) ^{1/2}\leqslant & {} C h^{\frac{3}{2}} \Vert u \Vert _{3}, \end{aligned}$$

(41)

$$\begin{aligned} \left( \sum _{T\in \mathcal{T}_h} \Vert Q_0 w-w \Vert ^2_{\partial T} \right) ^{1/2}\leqslant & {} C h^{\frac{3}{2}} \Vert w \Vert _{2}. \end{aligned}$$

(42)

Substituting (41) and (42) into (40), we get

$$\begin{aligned} \left| \ell (u,Q_{h}w)\right| \leqslant Ch^{3} \Vert u\Vert _{3} \Vert w\Vert _2. \end{aligned}$$

(43)

Similarly, it follows from the definition of $Q_{\text{b}}$, the trace inequality (21), and the estimate (24) that

$$\begin{aligned} |s(Q_hu,Q_hw)|\leqslant & {} \sum _{T\in \mathcal{T}_h}h_T^{-1} \left| Q_0u-Q_{\text{b}}u,Q_0w-Q_{\text{b}}w \right| \nonumber \\\leqslant & {} \left( \sum _{T\in \mathcal{T}_h} h_T^{-1} \Vert Q_0u-u\Vert ^2_{\partial T} \right) ^{1/2} \left( \sum _{T\in \mathcal{T}_h} h_{T}^{-1} \Vert Q_0 w- w \Vert ^2_{\partial T} \right) ^{1/2} \nonumber \\\leqslant & {} Ch^{3} \Vert u\Vert _{3} \Vert w\Vert _2. \end{aligned}$$

(44)

The estimates (30) and (31) imply that

$$\begin{aligned} |s(Q_hw,\varrho _h)| \leqslant Ch \Vert w\Vert _2 |\!|\!|\varrho _h|\!|\!|\leqslant Ch^{3} \Vert u\Vert _{3} \Vert w\Vert _2. \end{aligned}$$

(45)

For the fourth term, using the Cauchy-Schwarz inequality, the trace inequality (21), and (31), we have

$$\begin{aligned} \left| \ell (w,\varrho _h)\right|= & {} \left| \sum _{T\in \mathcal{T}_h}\langle (\mathbb {Q}_{h}\nabla w-\nabla w)\cdot \varvec {n},\varrho _0-\varrho _{\text{b}}\rangle _{\partial T }\right| \nonumber \\\leqslant & {} \left( \sum _{T\in \mathcal{T}_h}h_{T}\Vert (\mathbb {Q}_{h}\nabla w-\nabla w)\Vert ^{2}_{\partial T}\right) ^{\frac{1}{2}}\left( \sum _{{T}\in \mathcal{T}_h}h^{-1}_{T}\Vert \varrho _0-\varrho _{\text{b}}\Vert ^{2}_{\partial T}\right) ^{\frac{1}{2}}\nonumber \\\leqslant & {} Ch\Vert w\Vert _2{|||} \varrho _h{|||}\nonumber \\\leqslant & {} Ch^{3} \Vert u\Vert _{3} \Vert w\Vert _2. \end{aligned}$$

(46)

Substituting (43)–(46) into (39) yields

$$\begin{aligned} \Vert {\varrho _0}\Vert ^2\leqslant Ch^{3}\Vert u\Vert _{3}\Vert w\Vert _2. \end{aligned}$$

Using the regularity assumption $\Vert w\Vert _2 \leqslant C \Vert \varrho _0\Vert$, we arrive at

$$\begin{aligned} \Vert {\varrho _0}\Vert \leqslant Ch^{3}\Vert u\Vert _{3}, \end{aligned}$$

which concludes the proof.

6 Numerical Experiments

Fig. 1

A triangulation of a square domain in computation

Fig. 2

A triangulation of an L-shape domain

We are devoting this section to verify our theoretical results in previous sections by three numerical examples. On each triangle T, the standard $P_2$-space and $P_{2,{\text{harm}}}$-space are

$$\begin{aligned} P_{2}(T)= & {} {\text{span}}\{1,x,y,xy,x^2,y^2\},\\ P_{2,{\text{harm}}}(T)= & {} {\text{span}}\{1,x,y,xy,x^2-y^2\}. \end{aligned}$$

We apply the weak Galerkin algorithm (13) with $(P_{2}(T),P_{1}(e))$ and $(P_{2,{\text{harm}}}(T),P_{1}(e))$ finite element space on a square domain and an L-shaped domain to find the weak Galerkin solution $u_h=\{u_0,u_{\text{b}}\}$ in the computation. The first two levels of meshes are shown in Figs. 1 and 2.

6.1 Example 1

In this example, we numerically solve the problem (1)–(2) on an L-shaped domain $\Omega =[-1,1]^{2} \setminus (0,1)\times (-1,0)$ and the exact solution is

$$\begin{aligned} u(x,y)=x^{4}-6x^{2}y^{2}+y^{4}. \end{aligned}$$

The errors and convergence results are reported in Table 1. The errors measured in the $H^{1}$ norm and $L^{2}$ norm have convergence rate of $\mathcal {O}(h^{2})$ and $\mathcal {O}(h^{3})$, respectively. The numerical error and convergence rate plots are shown in Fig. 3.

Table 1 $H^{1}$ and $L^{2}$ errors and the rate of convergence of $P_{2,{\text{harm}}}$ elements and $P_{2}$ elements

Fig. 3

Example 1: plot of the errors and convergence rate for $\left( P_{2}(T),P_{1}(e),[P_{1}(T)]^{2}\right)$ and $h = 1/64$, for errors measured by $\Vert Q_{0}u-u\Vert \text{ and } {|||} Q_{h}u-u{|||}$: (a), (b) $P_{2,{\text{harm}}}$ elements; (c), (d) standard $P_{2}$ elements

6.2 Example 2

In this example, we use the $P_{2}$ WG scheme (13) to solve the problem $-\Delta u=0$ with the Dirichlet boundary condition on an L-shaped domain $\Omega =[-1,1]^{2} \setminus (0,1)\times (-1,0)$ and the analytic solution is

$$\begin{aligned} u(x, y) = {\text{e}}^{x} \cos y. \end{aligned}$$

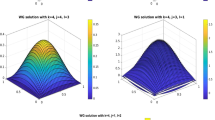
Table 2 lists errors and the convergence rates for $H^{1}$ norm and $L^{2}$ norm. The numerical results are convergent with order $\mathcal {O}(h^{2})$ in $H^{1}$ norm and $\mathcal {O}(h^{3})$ in $L^{2}$ norm. The numerical solutions and the error $Q_{h}u-u_{h}$ are plotted in Fig. 4.

Fig. 4

Example 2: plot of numerical solutions (a) and the error $Q_{h}-u_{h}$ (b) for $\left( P_{2}(T),P_{1}(e),[P_{1}(T)]^{2}\right)$ and $h = 1/64$: $P_{2,{\text{harm}}}$ elements (top); standard $P_{2}$ elements (bottom)

Table 2 $H^{1}$ and $L^{2}$ errors and the rate of convergence of $P_{2,{\text{harm}}}$ elements and $P_{2}$ elements

6.3 Example 3: a Singular Harmonic Solution

Let $\Omega =(0, 1)^{2}$ and the boundary value condition (1) is chosen such that the exact solution is

$$\begin{aligned} u(x,y)=(x^{2}+y^{2})^{1/3}\sin \left( \frac{2}{3}\arctan \left( \frac{y}{x}\right) \right) . \end{aligned}$$

The solution is in space $H^{1+2/3}(\Omega )$. The results obtained in Table 3 show the convergence rates in the $H^{1}$ norm is 0.67 and $L^{2}$ norm is 1.67. The numerical error and convergence rate plots can be found in Fig. 5.

Fig. 5

Example 3: plot of the errors and convergence rate for $\left( P_{2}(T),P_{1}(e),[P_{1}(T)]^{2}\right)$ and $h = 1/64$, for errors measured by $\Vert Q_{0}u-u\Vert \text{ and } {|||} Q_{h}u-u{|||}$: (a), (b) $P_{2,{\text{harm}}}$ elements; (c), (d) standard $P_{2}$ elements

Table 3 $H^{1}$ and $L^{2}$ errors and the rate of convergence of $P_{2,{\text{harm}}}$ elements and $P_{2}$ elements

7 Conclusion

In this work, we propose a weak Galerkin harmonic finite element method for the Laplace equation. The error estimates and rate of convergence are proved. Numerical results show that while the same order of convergence can be achieved using standard $P_2$ elements and $P_{2,{\text{harm}}}$ elements, using $P_{2,{\text{harm}}}$-space requires less degrees of freedom, which makes the numerical computation more efficient.