A Cubic H³-Nonconforming Finite Element

Abstract

The lowest degree of polynomial for a finite element to solve a 2kth-order elliptic equation is k. The Morley element is such a finite element, of polynomial degree 2, for solving a fourth-order biharmonic equation. We design a cubic $H^3$-nonconforming macro-element on two-dimensional triangular grids, solving a sixth-order tri-harmonic equation. We also write down explicitly the 12 basis functions on each macro-element. A convergence theory is established and verified by numerical tests.

1 Introduction

The Courant triangle is an $H^1$-conforming finite element, of polynomial degree one, solving second-order elliptic equations. The Crouzeix–Raviart triangle is a linear $H^1$-nonconforming finite element on triangles. The Morley element is a quadratic but $H^2$-nonconforming finite element for solving the biharmonic equation. On a macro-triangle grid, the Powell–Sabin element [11] is a quadratic $H^2$-conforming finite element. For solving a 2kth-order partial differential equation, the minimum polynomial degree is k, as the above four elements show. This is because a kth-order derivative of polynomial degree $k-1$ or less would be zero. Wang and Xu successfully extended the Morley element to a family of $P_k$ nonconforming finite elements for 2kth-order elliptic partial differential equations in $\mathbb {R}^n$ for any $n\ge k$, on simplicial grids [14]. Such minimum finite elements are very simple comparing to the conforming finite elements. For example, for $k=2,3,4$ and $n=3$, the polynomial degrees of the three-dimensional $C^1$, $C^2$ and $C^3$ spaces are 9, 17 and 25, respectively, cf. [1, 2, 16], while those of Wang–Xu’s elements are 2, 3 and 4 only, respectively. However, there is a limit, $n\ge k$, that is, Wang and Xu constructed a cubic $H^3$-nonconforming element in three dimensions, but not in two dimensions.

On rectangular grids, the above problem is relatively simple. Hu, Huang and Zhang constructed an n-dimension $C^1$-$Q_2$ element on rectangular grids [7]. Here $Q_k$ means the space of polynomials of separated degree k or less. Then the element is extended to a whole family of $C^{k-1}$-$Q_k$ elements, in any space dimension, in [8], that is, the minimum polynomial degree k is achieved in constructing $H^k$-conforming finite elements, on rectangular grids, in any space dimension. There is no limit of $n\ge k$.

In this paper, we would take the challenge of removing the limit of $n\ge k$ in Wang–Xu’s work [14], nevertheless only for the lowest order in two dimensions. That is, we construct a cubic ($P_3$) $H^3$-nonconforming finite element in two dimensions, on triangular grids. Such an element may not be constructed on a single triangle, but on a macro-triangle, as Hu–Huang–Zhang did on macro-rectangular grids in [7, 8]. Here we use the Hsieh–Clough–Tocher macro-triangle, shown in Fig. 1.

Fig. 1

A Hsieh–Clough–Tocher macro-triangle, and the finite element degrees of freedom on it

The new element is a piecewise cubic polynomial on three triangles, ${\mathbf {x}}_0{\mathbf {x}}_1{\mathbf {x}}_2$, ${\mathbf {x}}_0{\mathbf {x}}_2{\mathbf {x}}_3$ and ${\mathbf {x}}_0{\mathbf {x}}_3{\mathbf {x}}_1$, shown in Fig. 1. The 12 degrees of freedom are the function value, the first derivatives at three vertexes ${\mathbf {x}}_1$, ${\mathbf {x}}_2$ and ${\mathbf {x}}_3$, and the second normal derivative at the outer mid-edge points ${\mathbf {e}}_1$, ${\mathbf {e}}_2$ and ${\mathbf {e}}_3$. These produce $3\cdot 3\cdot 2+3=21$ equations for the $3\cdot 10$ coefficients of a piecewise cubic polynomial. In addition, we require the continuity of function and first derivatives of the finite element function at the barycentric center ${\mathbf {x}}_0$, resulting in $2\times 3=6$ equations. All three second derivatives are continuous at the three mid-points of the three internal edges, $\mathbf {m}_1$, $\mathbf {m}_2$ and $\mathbf {m}_3$. These generate $3\times 3=9$ equations, in theory. Finally, we limit the sum of three jumps of a third-order scaled directional derivative at the mid-points of the three internal edges to zero,

$$\begin{aligned} \sum _{i=1}^3 \partial _{\mathbf {l}_{i+1,1}^3} u|_{K_{i+1}}(\mathbf {m}_{i}) - \partial _{\mathbf {l}_{i+1,1}^3} u|_{K_{i+2}}(\mathbf {m}_{i}) =0, \end{aligned}$$

(1.1)

where the vector $\mathbf {l}_{i,j}={\mathbf {x}}_{i+j}-{\mathbf {x}}_{i}$, and triangles $K_i={\mathbf {x}}_0{\mathbf {x}}_{i+1}{\mathbf {x}}_{i+2}$. Here and in the rest of the paper, we use a periodic index, i.e., ${\mathbf {x}}_i={\mathbf {x}}_{i+3}$ and $K_i=K_{i+3}$. In (1.1), the scaled directional derivative is, for $\mathbf {l}_{i+1,1}= \langle l_1, l_2\rangle$,

$$\begin{aligned} \partial _{\mathbf {l}_{i+1,1}^3} u&=l_1^3 \frac{\partial ^3 u}{\partial x_1^3} + 3 l_1^2l_2 \frac{\partial ^3 u}{\partial x_1^2\partial x_2} + 3 l_1l_2^2 \frac{\partial ^3 u}{\partial x_1\partial x_2^2} + l_2^3 \frac{\partial ^3 u}{\partial x_2^3}. \end{aligned}$$

Equation (1.1) is a weird constraint, never seen in any similar construction of finite element. Any way, we will show that, together, the above 37 linear equations uniquely determine the 30 coefficients of a $P_3$ (cubic polynomial) finite element function. Using the Hermite type basis functions, we show the finite element space is well defined on a general triangular (base) grid. The standard error analysis is provided and confirmed by a numerical test. We refer interested readers to [9, 15] for $H^3$-nonconforming elements which use essentially $P_4$ polynomials.

We end this section by introducing some short-hand notations used in the paper. Given a vector $\mathbf {l}=\langle l_1, l_2\rangle$, define

$$\begin{aligned} \partial _{\mathbf {l}}u=l_1\frac{\partial u}{\partial x_1}+l_2\frac{\partial u}{\partial x_2} \end{aligned}$$

and

$$\begin{aligned} \partial _{{\mathbf {l}}^2}u=l_1^2\frac{\partial ^2 u}{\partial x_1^2}+2l_1l_2\frac{\partial ^2 u}{\partial x_1\partial x_2} +l_2^2\frac{\partial ^2 u}{\partial x_2^2}. \end{aligned}$$

We shall also use the following notation:

$$\begin{aligned} \partial _{ x_1^{\alpha _1} x_2^{\alpha _2}}u=\frac{\partial ^ \alpha u}{\partial x_1^{\alpha _1}\partial x_2^{\alpha _2}} \quad \text { for }\alpha =\langle \alpha _1, \alpha _2\rangle . \end{aligned}$$

2 The Finite Element

We solve a model tri-harmonic equation:

$$\begin{aligned} \Delta ^3 u&= f \quad \hbox {in } \Omega , \end{aligned}$$

(2.1)

$$\begin{aligned} u&=\partial _{\mathbf {n}} u=\partial _{\mathbf {n}^2} u = 0 \quad \hbox {on } \partial \Omega , \end{aligned}$$

(2.2)

where $\Omega$ is a bounded two-dimensional polygonal domain, and $\mathbf {n}$ is the unit outer normal to $\partial \Omega$. Doing integration by parts three times, the weak formulation of (2.1) is: find $u\in H^3_0(\Omega )$ such that

$$\begin{aligned} a(u,v)&=(f,v), \quad \forall v\in H^3_0(\Omega ), \end{aligned}$$

(2.3)

where $H^3_0(\Omega )=\{ v\in H^3(\Omega ) \ \mid \ v=\partial _{\mathbf {n}} v=\partial _{\mathbf {n}^2} v \ \hbox {on } \partial \Omega \}$ and $H^3(\Omega )$ is the standard Sobolev space [3]. The bilinear forms are

$$\begin{aligned} a(u,v)&= \int _\Omega D^3 u \, :\, D^3 v \mathrm{d}\mathbf {x}, \\ (f,v)&= \int _\Omega fv \mathrm{d}\mathbf {x}, \end{aligned}$$

where

$$\begin{aligned} D^3 u = \nabla ^{\text{T}} \nabla \nabla ^{\text{T}} u = \begin{pmatrix} \partial _{x_1^3} u &{} \partial _{x_1^2x_2} u \\ \partial _{x_1^2x_2} u &{} \partial _{x_1x_2^2} u \\ \partial _{x_2x_1^2} u &{} \partial _{x_2^2x_1} u \\ \partial _{x_2^2x_1} u &{} \partial _{x_2^3} u \end{pmatrix}. \end{aligned}$$

Fig. 2

A macro-grid ${\mathcal {M}}_h$ and its HCT subgrid ${\mathcal {T}}_h$

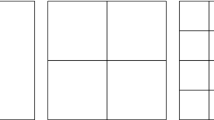
Let ${\mathcal {M}}_h=\{M\}$ be a quasi-uniform triangulation on $\Omega$, cf. [3]. Let ${\mathcal {P}}_h^0=\{\mathbf {x}_i\}$ be the set of all internal vertexes of triangles in ${\mathcal {M}}_h$. Let ${\mathcal {P}}_h^b=\{{\mathbf {x}}_i\}$ be the set of all boundary vertexes of triangles in ${\mathcal {M}}_h$, ${\mathbf {x}}_i\in \partial \Omega$. Let ${\mathcal {E}}_h^0=\{{\mathbf {e}}_j\}$ be the set of all internal mid-edge points of triangles in ${\mathcal {M}}_h$. Let ${\mathcal {E}}_h^b=\{{\mathbf {e}}_j\}$ be the set of all boundary mid-edge points of triangles in ${\mathcal {M}}_h$, ${\mathbf {e}}_j\in \partial \Omega$. Each triangle M in ${\mathcal {M}}_h$ is further subdivided into three sub-triangles, by connecting its barycentric center with three vertexes, shown in Fig. 1. The refined triangulation is denoted by ${\mathcal {T}}_h$. Such a macro-grid ${\mathcal {M}}_h$ and a grid ${\mathcal {T}}_h$ are plotted in Fig. 2.

On a macro-triangle $M={\mathbf {x}}_0{\mathbf {x}}_1{\mathbf {x}}_2\cup {\mathbf {x}}_0{\mathbf {x}}_2{\mathbf {x}}_3\cup {\mathbf {x}}_0{\mathbf {x}}_3{\mathbf {x}}_1$, cf. Fig. 1 and (1.1), we require the continuity of a finite element function $v_h$ at the vertexes of all three $K_i$ of M:

$$\begin{aligned} \partial _{x_1^{\alpha _1} x_2^{\alpha _2}} v_h \Big |_{K_{i+2}}({\mathbf {x}}_j)&= \partial _{x_1^{\alpha _1} x_2^{\alpha _2}} v_h\Big |_{K_{i+1}}({\mathbf {x}}_j), \quad i=1,2,3, \quad j=i \, \hbox { or } 0 \end{aligned}$$

(2.4)

and

$$\begin{aligned} |\alpha |=|\langle \alpha _1, \alpha _2\rangle |=0,1. \end{aligned}$$

Further, the second derivatives are continuous across the three internal edges, at the middle point, for all $|\alpha |=2$,

$$\begin{aligned} \partial _{x_1^{\alpha _1} x_2^{\alpha _2}} v_h\Big |_{K_{i+2}}(\mathbf {m}_i)&= \partial _{x_1^{\alpha _1} x_2^{\alpha _2}} v_h\Big |_{K_{i+1}}(\mathbf {m}_i), \quad i=1,2,3. \end{aligned}$$

(2.5)

On a single macro-element, the finite element space is defined by

$$\begin{aligned} V_M = \big \{ v_h \in L^2(M) \ \mid \ v_h|_{K_i}\in P_3(K_i) \ \hbox { satisfying }(2.4), (2.5)\hbox { and }(1.1) \big \}. \end{aligned}$$

(2.6)

Abstractly we define the global space of the cubic ($P_3$) $H^3$ nonconforming finite element

$$\begin{aligned} V_h&= \big \{ v_h \in L^2(\Omega ) \ \mid \ v_h|_{M}\in V_M, \nonumber \\&\quad \; \partial _{x_1^{\alpha _1} x_2^{\alpha _2}} v_h|_M(\mathbf {x}_i)=\partial _{x_1^{\alpha _1} x_2^{\alpha _2}} v_h|_{M'} ({\mathbf {x}}_i), \ \forall {\mathbf {x}}_i\in {\mathcal {P}}_h^0, \ |\alpha |=0,1, \nonumber \\&\quad \; \partial _{\mathbf {n}^2} v_h|_M({\mathbf {e}}_j)=\partial _{\mathbf {n}^2} v_h |_{M'} ({\mathbf {e}}_j), \ \forall {\mathbf {e}}_j\in {\mathcal {E}}_h^0, \ \nonumber \\&\quad \; \partial _{x_1^{\alpha _1} x_2^{\alpha _2}} v_h |_M({\mathbf {x}}_i)=0, \ \forall {\mathbf {x}}_i\in {\mathcal {P}}_h^b, \ |\alpha |=0,1, \nonumber \\&\quad \; \partial _{\mathbf {n}^2} v_h |_M({\mathbf {e}}_{j})=0, \ \forall {\mathbf {e}}_j\in {\mathcal {E}}_h^b \big \}, \end{aligned}$$

(2.7)

where $\mathbf {n}$ is a unit outer normal vector to M at a mid-point ${\mathbf {e}}_j$, and $M'$ is a macro-triangle sharing an edge with M at point ${\mathbf {e}}_j$.

The finite element discretization problem for (2.3) reads: find $u_h\in V_h$ such that

$$\begin{aligned} a_h(u_h,v_h)&=(f,v_h), \quad \forall v_h\in V_h, \end{aligned}$$

(2.8)

where

$$\begin{aligned} a_h(u_h,v_h)&= \sum _{K\in {\mathcal {T}}_h} \int _K D^3 u_h \,:\,D^3 v_h \mathrm{d}\mathbf {x}. \end{aligned}$$

3 Basis of the Finite Element Space

We find first the Hermit type basis functions for the finite element space $V_{{\hat{M}}}$ on the reference triangle ${\hat{M}}=\hat{\mathbf {x}}_1\hat{\mathbf {x}}_2\hat{\mathbf {x}}_3$, cf. Fig. 3, where

$$\begin{aligned} \hat{\mathbf {x}}_i=\left\langle \frac{1}{2\sqrt{3}}\cos \frac{4i-9}{6}\uppi , \frac{1}{2\sqrt{3}} \sin \frac{4i-9}{6}\uppi \right\rangle ,\quad i=1,2,3. \end{aligned}$$

(3.1)

Fig. 3

A reference triangle ${\hat{M}}$ and a general triangle M, where the affine mapping F preserves vectors $\hat{\mathbf {l}}_i$

We define an interpolation $v_h$, for a $C^3({\hat{M}})$ function u, to be a solution of the following linear system of equations:

(The 12 dofs:)

$$\begin{aligned} v_h|_{{\hat{K}}_2}(\hat{\mathbf {x}}_1)&= u(\hat{\mathbf {x}}_1) , \end{aligned}$$

(3.2a)

$$\begin{aligned} v_h|_{{\hat{K}}_{i+1}}(\hat{\mathbf {x}}_i)&=u (\hat{\mathbf {x}}_i) , \quad i=2,3, \end{aligned}$$

(3.2b)

$$\begin{aligned} \partial _{\hat{\mathbf {l}}_{i,j}} v_h|_{{\hat{K}}_{i+1}} (\hat{\mathbf {x}}_i)&= \partial _{\hat{\mathbf {l}}_{i,j}} u (\hat{\mathbf {x}}_i), \quad i=1,2,3,\ j=1,2, \end{aligned}$$

(3.2c)

$$\begin{aligned} \partial _{\hat{\mathbf {l}}_{i}^2} v_h|_{{\hat{K}}_i}({\hat{{\mathbf {e}}}}_i)&= \partial _{\hat{\mathbf {l}}_{i}^2} u({\hat{{\mathbf {e}}}}_i) , \quad i=1,2,3, \hbox { or } \end{aligned}$$

(3.2d)

$$\begin{aligned} \int _{\hat{\mathbf {x}}_{i+1}\hat{\mathbf {x}}_{i+2}} \partial _{\hat{\mathbf {l}}_{i}^2}&(v_h|_{\hat{K}_i} -u) \, {\text{d}}\mathbf {x} =0, \quad i=1,2,3, \end{aligned}$$

(3.2d')

(and the continuity constraints)

$$\begin{aligned} v_h|_{{\hat{K}}_{i+1}}(\hat{\mathbf {x}}_i)&= v_h|_{{\hat{K}}_{i+2}}(\hat{\mathbf {x}}_i), \quad i= 1,2,3, \end{aligned}$$

(3.2e)

$$\begin{aligned} \partial _{\hat{\mathbf {l}}_{i,j}} v_h|_{{\hat{K}}_{i+1}}(\hat{\mathbf {x}}_i)&= \partial _{\hat{\mathbf {l}}_{i,j}} v_h|_{{\hat{K}}_{i+2}}(\hat{\mathbf {x}}_i), \quad i=1,2,3,\ j=1,2, \end{aligned}$$

(3.2f)

$$\begin{aligned} v_h|_{{\hat{K}}_{i}}(\hat{\mathbf {x}}_0)&= v_h|_{{\hat{K}}_{i+1}}(\hat{\mathbf {x}}_0), \quad i= 1,2, \end{aligned}$$

(3.2g)

$$\begin{aligned} \partial _{{\hat{x}}_j} v_h|_{{\hat{K}}_{i}}(\hat{\mathbf {x}}_0)&= \partial _{{\hat{x}}_j} v_h|_{{\hat{K}}_{i+1}}(\hat{\mathbf {x}}_0), \quad i= 1,2, \ j=1,2, \end{aligned}$$

(3.2h)

$$\begin{aligned} \partial _{{\hat{x}_{1}^{{\alpha _{1} }} \hat{x}_{2}^{{\alpha _{2} }} }} v_{h} |_{{\hat{K}_{{i + 1}} }} (\widehat{{\mathbf{m}}}_{i} ) = \partial _{{\hat{x}_{1}^{{\alpha _{1} }} \hat{x}_{2}^{{\alpha _{2} }} }} v_{h} |_{{\hat{K}_{{i + 2}} }} (\widehat{{\mathbf{m}}}_{i} ),\quad i = 1,2,3,\;|\alpha | = 2, \end{aligned}$$

(3.2i)

$$\begin{aligned} \sum _{i=1}^3 \partial _{\hat{\mathbf {l}}_{i+1,1}^3} v_h|_{\hat{K}_{i+1}}(\hat{\mathbf {m}}_i) = \sum _{i=1}^3 \partial _{\hat{\mathbf {l}}_{i+1,1}^3} v_h|_{\hat{K}_{i+2}}(\hat{\mathbf {m}}_i). \end{aligned}$$

(3.2j)

Here

$$\begin{aligned} \hat{\mathbf {l}}_{i,j}&= \hat{\mathbf {x}}_{i+j} - \hat{\mathbf {x}}_i, \quad j=1,2, \\ \hat{\mathbf {l}}_i&= \frac{\hat{\mathbf {x}}_{i+1}+\hat{\mathbf {x}}_{i+2}}{2} - \hat{\mathbf {x}}_i, \quad i=1,2,3. \end{aligned}$$

For basis functions, we solve the 12 dof equations (3.2a)–(3.2d) plus 25 constraint equations ((2.4), (2.5) and (1.1)), to obtain each of the 12 basis functions on the reference element ${\hat{M}}$. For example, the basis function ${\hat{\phi }}_{1,0}$ is the solution of the system of 37 equations, where $u(\hat{\mathbf {x}}_1)=1$ and rest data are zero. These 37 equations have a unique solution, to be shown in Lemmas 3.1 and 3.2,

$$\begin{aligned} {\hat{\phi }}_{1,0} = {\left\{ \begin{array}{ll} \left( 6 {\hat{x}}_1^2+12 \sqrt{3} {\hat{x}}_1 {\hat{x}}_2-3 {\hat{x}}_1-6 {\hat{x}}_2^2-\sqrt{3} {\hat{x}}_2+1\right) \\ \times \left( -2 {\hat{x}}_1-\frac{2}{\sqrt{3}} {\hat{x}}_2+ \frac{1}{3}\right) &{} \quad \hbox {on } {\hat{K}}_1, \\ \frac{1}{3}-3 {\hat{x}}_1-\sqrt{3} {\hat{x}}_2-4 {\hat{x}}_1^2+4 \sqrt{3} {\hat{x}}_1 {\hat{x}}_2-4 {\hat{x}}_1^3 \\ +\,20 \sqrt{3} {\hat{x}}_1^2 {\hat{x}}_2+12 {\hat{x}}_1 {\hat{x}}_2^2+4 \sqrt{3} {\hat{x}}_2^3 &{} \quad \hbox {on } {\hat{K}}_2, \\ \frac{1}{3}-3 {\hat{x}}_1-\sqrt{3} {\hat{x}}_2+2 {\hat{x}}_1^2-6 {\hat{x}}_2^2+16 {\hat{x}}_1^3\\ +\,8 \sqrt{3} {\hat{x}}_1^2 {\hat{x}}_2-8 \sqrt{3} {\hat{x}}_2^3 &{}\quad \hbox {on } {\hat{K}}_3. \end{array}\right. } \end{aligned}$$

(3.3)

Before we consider the solution of the 37 equations in (3.2), we show the uniqueness of the solution to an equivalent, square, linear system of 30 equations, in Lemma 3.1. We drop 7 equations from (3.2i), equivalently three equations for the continuity of second-order tangential derivatives, three equations for the continuity of second-order mixed derivative, and one equation for the continuity of second-order normal derivative at $\hat{\mathbf {m}}_3$, to get, i.e., the nine equations in (3.2i) replaced by two equations,

$$\begin{aligned} \partial _{\mathbf{n}_{{\hat{K}}_{i+1}}^{2}} v_h \Big |_{{\hat{K}}_{i+1}} (\mathbf{m}_{i}) = - \partial _{\mathbf{n}_{{\hat{K}}_{{i+2}}}^{2}}v_h \Big |_{{\hat{K}}_{i+2}} ({\mathbf{m}}_i), \quad i=1,2. \end{aligned}$$

(3.2i')

Here and below, $\mathbf {n}_{{\hat{K}}_{i}}$ denotes the outer normal vector on $\partial {\hat{K}}_{i}$, and $\mathbf {t}_{{\hat{K}}_{i}}$ is the $90^{\circ }$ rotation of $\mathbf {n}_{{\hat{K}}_{i}}.$

Lemma 3.1

On the reference element${\hat{M}}$, defined in (3.1), there is a unique solution to the linear system of 30 equations (3.2) with (3.2i) replaced by (3.2i’), with general data for 12 degrees of freedom, in (3.2a)–(3.2d).

Proof

We will show the uniqueness of solution, which implies the existence of solution. As a piecewise cubic polynomial ($P_3$) function has 30 degrees of freedom on ${\hat{M}}$, we have a square system of linear equations. Let $v_1$ and $v_2$ be two solutions for the thirty equations. Let $v=v_1-v_2$. By equations in (3.2), v and its tangential derivatives are zero at two vertexes of edge $\hat{\mathbf {x}}_1\hat{\mathbf {x}}_2$. Then, v is identically zero on the edge. We can factor out the linear function ${\hat{\lambda }}_3$ from v:

$$\begin{aligned} v|_{{\hat{K}}_3} = {\hat{\lambda }}_3\,p_2, \quad p_2\in P_2\,({\hat{x}}_1,\, {\hat{x}}_2), \end{aligned}$$

where the linear function is uniquely defined by

$$\begin{aligned} {\hat{\lambda }}_3(\hat{\mathbf {x}}_1)=0, \ {\hat{\lambda }}_3(\hat{\mathbf {x}}_2)=0, \ {\hat{\lambda }}_3(\hat{\mathbf {x}}_0)=1. \end{aligned}$$

By the zero first normal derivative at $\hat{\mathbf {x}}_1$ and $\hat{\mathbf {x}}_2$, and the zero second normal derivative at ${\hat{{\mathbf {e}}}}_3$, of $v|_{{\hat{K}}_3}$, cf. Fig. 1, the six degrees of freedom of $p_2$ in $v={\hat{\lambda }}_3 p_2$ are restricted to three degrees of freedom.

We will select three basis functions, $\{b_{3,1}, b_{3,2}, b_{3,3}\}\subset P_3$, for expanding this quadratic function $p_2$ in $v|_{{\hat{K}}_3}$. One obvious candidate is ${\hat{\lambda }}_3^3$, which has all first and second normal derivatives equal to zero, on the whole edge ${\hat{\lambda }}_3=0$. But we will combine it with other basis functions as the first basis function. A second basis function could be $b_{3,2}={\hat{\lambda }}_3^2 {\hat{\lambda }}_{3}^\perp$ which has the first normal derivative zero on the edge, and the second normal derivative at the mid-point. Here ${\hat{\lambda }}_{3}^\perp$ is the linear function for the line orthogonal to edge $\hat{\mathbf {x}}_1\hat{\mathbf {x}}_2$ at the mid-point ${\hat{{\mathbf {e}}}}_3$, i.e.,

$$\begin{aligned} {\hat{\lambda }}_{3}^\perp ({\hat{{\mathbf {e}}}}_3)=0, \ \partial _{\hat{\mathbf {n}}_3} {\hat{\lambda }}_{3}^\perp ({\hat{{\mathbf {e}}}}_3)=0, \ {\hat{\lambda }}_{3}^\perp (\hat{\mathbf {x}}_1)=1. \end{aligned}$$

A third basis function $b_{3,3}$ is constructed using a circle function

$$\begin{aligned} {\hat{\tau }}^2 := {\hat{x}}_1^2 + {\hat{x}}_2^2 - \frac{1}{12} \end{aligned}$$

that ${\hat{\tau }}^2=0$ is the circle passing through three vertexes of ${\hat{M}}$. ${\hat{\lambda }}_3 {\hat{\tau }}^2$ has its first normal derivative zero at the two end points, but not zero second normal derivative at the mid-point ${\hat{{\mathbf {e}}}}_3$. So we correct the second normal derivative by ${\hat{\lambda }}_3^2$ (which has the normal derivative zero at the two end points) as follows:

$$\begin{aligned} b_{3,3} =24{\hat{\lambda }}_3{\hat{\tau }}^2+{\hat{\lambda }}_3^2 = {\hat{\lambda }}_3\left( 24 {\hat{\tau }}^2+{\hat{\lambda }}_3\right) . \end{aligned}$$

Let us check the second normal derivative condition (note that ${\hat{\lambda }}_3=4\sqrt{3}{\hat{x}}_2+1$ and $\hat{\mathbf {l}}_3 =\langle 0,-\sqrt{3}/4 \rangle$):

$$\begin{aligned} \partial _{ \hat{\mathbf {l}}_3^2} b_{3,3} ({\hat{{\mathbf {e}}}}_3) = (108 \sqrt{3}{\hat{x}}_2+ 27)({\hat{{\mathbf {e}}}}_3) =0. \end{aligned}$$

We expand v under three basis functions,

$$\begin{aligned} v|_{{\hat{K}}_3}&= a_{3,1} b_{3,1} + a_{3,2} b_{3,2} + a_{3,3} b_{3,3} \nonumber \\&:= a_{3,1} \left( {\hat{\lambda }}_3^3 + 24{\hat{\lambda }}_3{\hat{\tau }}^2+{\hat{\lambda }}_3^2+9 {\hat{\lambda }}_3^2{\hat{\lambda }}_{3}^\perp \right) + a_{3,2} {\hat{\lambda }}_3^2{\hat{\lambda }}_{3}^\perp + a_{3,3} \left( 24 {\hat{\lambda }}_3{\hat{\tau }}^2+{\hat{\lambda }}_3^2\right) , \end{aligned}$$

(3.4)

where we combine the first candidate ${\hat{\lambda }}_3^3$, the second and third basis functions as $b_{3,1}$.

Similar to (3.4), we find three basis functions on edge $\hat{\mathbf {x}}_2\hat{\mathbf {x}}_3$ and let

$$\begin{aligned} v|_{{\hat{K}}_1}&= a_{1,1} b_{1,1} + a_{1,2} b_{1,2} + a_{1,3} b_{1,3} \nonumber \\&:= a_{1,1} \left( {\hat{\lambda }}_1^3 +24 {\hat{\lambda }}_1{\hat{\tau }}^2+{\hat{\lambda }}_1^2 -9{\hat{\lambda }}_1^2{\hat{\lambda }}_{1}^\perp \right) + a_{1,2} {\hat{\lambda }}_1^2{\hat{\lambda }}_{1}^\perp + a_{1,3} \left( 24{\hat{\lambda }}_1{\hat{\tau }}^2+{\hat{\lambda }}_1^2\right) . \end{aligned}$$

(3.5)

Here ${\hat{\lambda }}_1^\perp (\hat{\mathbf {x}}_2)=1$. By the continuity of v at $\hat{\mathbf {x}}_0$, and by a geometric argument or by the values of basis functions:

$$\begin{aligned} \begin{pmatrix} b_{3,1} &{} b_{3,2}&{} b_{3,3} \\ b_{1,1} &{} b_{1,2}&{} b_{1,3}\end{pmatrix} (\hat{\mathbf {x}}_0)&=\begin{pmatrix}0 &{} 0 &{} -1 \\ 0 &{} 0 &{} -1\end{pmatrix}, \end{aligned}$$

we conclude that

$$\begin{aligned} a_{3,3} = a_{1,3}. \end{aligned}$$

(3.6)

By the continuity of the first derivatives at $\hat{\mathbf {x}}_0$,

$$\begin{aligned} \partial _{\hat{\mathbf {t}}_2} \begin{pmatrix} b_{3,1} &{} b_{3,2}&{} b_{3,3} \\ b_{1,1} &{} b_{1,2}&{} b_{1,3}\end{pmatrix} (\hat{\mathbf {x}}_0)&=\begin{pmatrix} 0 &{} 2 &{} 0 \\ 0 &{} 2 &{} 0\end{pmatrix}, \\ \partial _{\hat{\mathbf {n}}_2} \begin{pmatrix} b_{3,1} &{} b_{3,2}&{} b_{3,3} \\ b_{1,1} &{} b_{1,2}&{} b_{1,3}\end{pmatrix} (\hat{\mathbf {x}}_0)&= \begin{pmatrix} 24 {\sqrt{3}} &{} 2\sqrt{3} &{} 0 \\ 24 {\sqrt{3}} &{} -2\sqrt{3} &{} 0\end{pmatrix}, \end{aligned}$$

where $\hat{\mathbf {n}}_2$ is the outer unit normal vector of ${\hat{K}}_2$ on edge $\hat{\mathbf {x}}_3\hat{\mathbf {x}}_1$, and $\hat{\mathbf {t}}_2$ is the $90^{\circ }$ counter-clockwise rotation of $\hat{\mathbf {n}}_2$, we have, by (3.6),

$$\begin{aligned} a_{3,2}&= a_{1,2}, \end{aligned}$$

(3.7)

$$\begin{aligned} a_{3,1}&= a_{1,1}. \end{aligned}$$

(3.8)

Finally, by the continuity of the second normal derivatives at $\hat{\mathbf {m}}_2$, (3.2i’),

$$\begin{aligned} \partial _{\mathbf {n}_{\hat{K}_3}^2} \begin{pmatrix} b_{3,1} &{} b_{3,2}&{} b_{3,3} \\ b_{1,1} &{} b_{1,2}&{} b_{1,3}\end{pmatrix} (\hat{\mathbf {m}}_2)&= \begin{pmatrix}-336 &{} -60 &{} 96 \\ -336 &{} 60 &{} 96\end{pmatrix}, \end{aligned}$$

we have, by (3.6)–(3.8),

$$\begin{aligned} a_{3,2}&= 0 . \end{aligned}$$

(3.9)

In addition, we check the jump of the third scaled directional derivative of v:

$$\begin{aligned} \partial _{\hat{\mathbf {l}}_{3,1}^3} \begin{pmatrix} b_{3,1} &{} b_{3,2}&{} b_{3,3} \\ b_{1,1} &{} b_{1,2}&{} b_{1,3}\end{pmatrix} (\hat{\mathbf {m}}_2)&= \begin{pmatrix}216 &{} 54 &{} -108\\ -216 &{} 54 &{} 108\end{pmatrix}. \end{aligned}$$

(3.10)

On the third triangle ${\hat{K}}_2$, similar to (3.4) and (3.5),

$$\begin{aligned} v|_{{\hat{K}}_2}&= a_{2,1} b_{2,1} + a_{2,2} b_{2,2} + a_{2,3} b_{2,3} \nonumber \\&{:=}\, a_{2,1} ({\hat{\lambda }}_2^3 +24{\hat{\lambda }}_2{\hat{\tau }}^2+{\hat{\lambda }}_2^2-9 {\hat{\lambda }}_2^2{\hat{\lambda }}_{2}^\perp ) + a_{2,2} {\hat{\lambda }}_2^2{\hat{\lambda }}_{2}^\perp + a_{2,3} (24{\hat{\lambda }}_2{\hat{\tau }}^2+{\hat{\lambda }}_2^2). \end{aligned}$$

(3.11)

Here ${\hat{\lambda }}_{2}^\perp (\hat{\mathbf {x}}_3)=1$, and it is not symmetric to the ${\hat{\lambda }}_{1}^\perp$ in (3.5), where ${\hat{\lambda }}_1^\perp (\hat{\mathbf {x}}_2)=1$. By the continuity of v at $\hat{\mathbf {x}}_0$,

$$\begin{aligned} \begin{pmatrix} b_{3,1} &{} b_{3,2}&{} b_{3,3} \\ b_{2,1} &{} b_{2,2}&{} b_{2,3}\end{pmatrix} (\hat{\mathbf {x}}_0)&=\begin{pmatrix}0 &{} 0 &{} -1 \\ 0 &{} 0 &{} -1\end{pmatrix}, \end{aligned}$$

we conclude that

$$\begin{aligned} a_{3,3} = a_{2,3}. \end{aligned}$$

(3.12)

By the continuity of the first derivatives at $\hat{\mathbf {x}}_0$,

$$\begin{aligned} \partial _{\hat{\mathbf {t}}_1} \begin{pmatrix} b_{3,1} &{} b_{3,2}&{} b_{3,3} \\ b_{2,1} &{} b_{2,2}&{} b_{2,3}\end{pmatrix} (\hat{\mathbf {x}}_0)&=\begin{pmatrix} 36 &{} 2 &{} 0 \\ -36 &{} 2 &{} 0\end{pmatrix}, \\ \partial _{\hat{\mathbf {n}}_1} \begin{pmatrix} b_{3,1} &{} b_{3,2}&{} b_{3,3}\\ b_{2,1} &{} b_{2,2}&{} b_{2,3} \end{pmatrix} (\hat{\mathbf {x}}_0)&= \begin{pmatrix} 12 {\sqrt{3}} &{} 2\sqrt{3} &{} 0 \\ 12 {\sqrt{3}} &{} -2\sqrt{3} &{} 0\end{pmatrix}, \end{aligned}$$

where $\hat{\mathbf {n}}_1$ is the outer unit normal vector of ${\hat{K}}_1$ on edge $\hat{\mathbf {x}}_1\hat{\mathbf {x}}_3$, and $\hat{\mathbf {t}}_1$ is the $90^{\circ }$ counter-clockwise rotation of $\hat{\mathbf {n}}_1$, we get, by (3.9),

$$\begin{aligned} a_{3,1}&= - a_{2,1} + \frac{1}{18} a_{2,2}, \end{aligned}$$

(3.13)

$$\begin{aligned} a_{3,1}&= a_{2,1} - \frac{1}{6} a_{2,2}. \end{aligned}$$

(3.14)

Finally, by the continuity of the second normal derivatives at $\hat{\mathbf {m}}_1$, (3.2i’),

$$\begin{aligned} \partial _{\mathbf {n}_{\hat{K}_3}^2} \begin{pmatrix} b_{3,1} &{} b_{3,2}&{} b_{3,3} \\ b_{2,1} &{} b_{2,2}&{} b_{2,3}\end{pmatrix} (\hat{\mathbf {m}}_2)&= \begin{pmatrix}744 &{} 60 &{} 96 \\ 744 &{} -60 &{} 96\end{pmatrix}, \end{aligned}$$

we get, by (3.12),

$$\begin{aligned} a_{3,1}&= a_{2,1} - \frac{5}{62} a_{2,2}. \end{aligned}$$

(3.15)

Later we check the jump of the third scaled directional derivative of v:

$$\begin{aligned} \partial _{\hat{\mathbf {l}}_{2,1}^3} \begin{pmatrix} b_{3,1} &{} b_{3,2}&{} b_{3,3} \\ b_{2,1} &{} b_{2,2}&{} b_{2,3}\end{pmatrix} (\hat{\mathbf {m}}_1)&= \begin{pmatrix} 756 &{} 54 &{} 108 \\ -756 &{} 54 &{} -108\end{pmatrix}. \end{aligned}$$

(3.16)

By (3.13)–(3.15), we obtain

$$\begin{aligned} a_{3,1} = a_{2,1} = a_{2,2}=0. \end{aligned}$$

(3.17)

By (3.6)–(3.9), (3.12) and (3.17),

$$\begin{aligned} a_{1,3}&= a_{2,3}= a_{3,3}, \\ a_{1,1}&= a_{1,2}=a_{2,1}= a_{2,2}= a_{3,1}= a_{3,2}=0. \end{aligned}$$

Thus,

$$\begin{aligned} v = {\left\{ \begin{array}{ll} a_{3,3} (24{\hat{\lambda }}_1{\hat{\tau }}^2+{\hat{\lambda }}_1^2) &{}\hbox {on } \ {\hat{K}}_1, \\ a_{3,3} (24{\hat{\lambda }}_2{\hat{\tau }}^2+{\hat{\lambda }}_2^2) &{}\hbox {on } \ {\hat{K}}_2, \\ a_{3,3} (24{\hat{\lambda }}_3{\hat{\tau }}^2+{\hat{\lambda }}_3^2) &{}\hbox {on } \ {\hat{K}}_3. \end{array}\right. } \end{aligned}$$

We note that, if we apply the continuity of the second normal derivatives at $\hat{\mathbf {m}}_3$, we would get again

$$\begin{aligned} a_{1,3}=a_{2,3}. \end{aligned}$$

That is why we have an additional constraint on the third derivatives. Applying the zero-sum of jumps of the third scaled directional derivatives (1.1), by (3.10) and (3.16), we get

$$\begin{aligned} \sum _{i=1}^3 a_{3,3} (-108-108) =0, \quad a_{3,3}=0, \ v\equiv 0. \end{aligned}$$

Lemma 3.2

On the reference element${\hat{M}}$, defined in (3.1), there is a unique solution to the linear system of 37 equations (3.2) with general data for 12 degrees of freedom, in (3.2a)–(3.2d).

Proof

We showed in the previous lemma the unique solution $v_h$ of the system of 30 equations, replacing 9 equations in (3.2i) by the two equations in (3.2i’). If this solution satisfies the 9 equations in (3.2i), then the system of 37 equations (3.2) has a unique solution too. We first check the continuity of the last second normal derivative, missing in (3.2i’),

$$\begin{aligned} \partial _{\mathbf {n}_{{\hat{K}}_{1}}^2} v|_{{\hat{K}}_{1}} (\hat{\mathbf {m}}_3)&= - \partial _{\mathbf {n}_{{\hat{K}}_{2}}^2} v|_{{\hat{K}}_{2}} (\hat{\mathbf {m}}_3). \end{aligned}$$

(3.2i'')

We only need to prove that the solutions (of 30 equations) for the 12 basis functions satisfy (3.2i”). We start with the basis function ${\hat{\phi }}_{3,0}$ having nodal value 1 at $\hat{\mathbf {x}}_3$. If it fails (3.2i”), WLOG,

$$\begin{aligned} \partial _{\mathbf {n}_{{\hat{K}}_{1}}^2} {\hat{\phi }}_{3,0}|_{{\hat{K}}_{1}} (\hat{\mathbf {m}}_3) - \partial _{\mathbf {n}_{{\hat{K}}_{2}}^2} {\hat{\phi }}_{3,0}|_{{\hat{K}}_{2}} (\hat{\mathbf {m}}_3)=m_0>0 . \end{aligned}$$

(3.18)

Subtracting the reflection, we let $v_0 ({\hat{x}}_1,{\hat{x}}_2)={\hat{\phi }}_{3,0}({\hat{x}}_1,{\hat{x}}_2) - {\hat{\phi }}_{3,0}(-{\hat{x}}_1,{\hat{x}}_2)$. Then, $v_0$ has all vanishing 12 dof values but, by (3.18),

$$\begin{aligned} \partial _{\mathbf {n}_{{\hat{K}}_{1}}^2} v_0|_{{\hat{K}}_{1}} (\hat{\mathbf {m}}_3) - \partial _{\mathbf {n}_{{\hat{K}}_{2}}^2} v_0|_{{\hat{K}}_{2}} (\hat{\mathbf {m}}_3)=2m_0>0 . \end{aligned}$$

(3.19)

As $v_0$ satisfies 30 homogeneous equations (3.2) with (3.2i) replaced by (3.2i’), by the above expansion of $v_0$, we have shown that $v_0\equiv 0$, contradicting to (3.19). Thus, (3.2i”) holds for ${\hat{\phi }}_{3,0}$. Noting the special symmetry of ${\hat{\phi }}_{3,0}$, if we start with ${\hat{\phi }}_{1,0}$ or ${\hat{\phi }}_{2,0}$, no conclusion can be drawn from this argument. By rotating ${\hat{\phi }}_{3,0}$$120^{\circ }$ or $240^{\circ }$, we found the rotated function satisfies the same 30 equations for ${\hat{\phi }}_{2,0}$ or for ${\hat{\phi }}_{1,0}$, respectively. As we have shown the uniqueness of ${\hat{\phi }}_{1,0}$ and ${\hat{\phi }}_{2,0}$, we conclude that (3.2i”) holds for ${\hat{\phi }}_{1,0}$ and ${\hat{\phi }}_{2,0}$, as both are rotations of ${\hat{\phi }}_{3,0}$. Repeating the above argument on ${\hat{\phi }}_{3,0}$ for ${\hat{\phi }}_{3,m}$ (the basis function having $\partial _{\hat{\mathbf {l}}_3^2}{\hat{\phi }}_{3,\mathbb {E}}(\hat{{\mathbf {e}}}_3)=1$), we conclude that (3.2i”) holds for ${\hat{\phi }}_{3,\mathbb {E}}$, ${\hat{\phi }}_{2,\mathbb {E}}$ and ${\hat{\phi }}_{1,\mathbb {E}}$.

But such a symmetry does not exist for ${\hat{\phi }}_{3,1}$ or ${\hat{\phi }}_{3,2}$. We do a decomposition by letting $v_1=2 ({\hat{\phi }}_{3,2}-{\hat{\phi }}_{3,2})$ and $v_2=-(3/\sqrt{2}) ({\hat{\phi }}_{3,1}+{\hat{\phi }}_{3,2})$, that is, $\partial _{{\hat{x}}_1} v_1(\hat{\mathbf {x}}_3)=1$ and $\partial _{{\hat{x}}_2} v_2(\hat{\mathbf {x}}_3)=1$. By the argument like (3.18)–(3.19), (3.2i”) holds for $v_2$, as it is symmetric. Now we let

$$\begin{aligned} v ({\hat{x}}_1,{\hat{x}}_2 ) = v_1 ({\hat{x}}_1,{\hat{x}}_2 ) + v_1 (-{\hat{x}}_1,{\hat{x}}_2 ). \end{aligned}$$

Then, $\partial _{{\hat{x}}_1} v (\hat{\mathbf {x}}_3)=0$, and in fact, all values of 12 degrees of freedom of $v ({\hat{x}}_1,{\hat{x}}_2 )$ vanish. Thus, by Lemma 3.1, as $v(\hat{\mathbf {x}})$ satisfying the 30 equations there, $v(\hat{\mathbf {x}})\equiv 0$ and $v_1({\hat{x}}_1,{\hat{x}}_2 )=-v_1 (-{\hat{x}}_1,{\hat{x}}_2 )$. Therefore,

$$\begin{aligned} \partial _{\mathbf {n}_{{\hat{K}}_{1}}^2} v_1|_{{\hat{K}}_{1}} (\hat{\mathbf {m}}_3)&= \partial _{ {\hat{x}}_1^2} v_1 |_{{\hat{K}}_{1}} (\hat{\mathbf {m}}_3)=-\partial _{ {\hat{x}}_1^2} v_1 |_{{\hat{K}}_{1}} (\hat{\mathbf {m}}_3)=0. \end{aligned}$$

So the second normal derivative vanishes at $\hat{\mathbf {m}}_3$ on both sides of $\hat{\mathbf {x}}_0\hat{\mathbf {x}}_3$, and (3.2i”) holds for $v_1$. Because (3.2i”) holds for $v_1$ and $v_2$, it holds for ${\hat{\phi }}_{3,1}$ and ${\hat{\phi }}_{3,2}$. Finally, by rotations, (3.2i”) holds for all ${\hat{\phi }}_{1,2}$, ${\hat{\phi }}_{1,3}$, ${\hat{\phi }}_{2,1}$ and ${\hat{\phi }}_{2,3}$.

Next, we check the continuity of second tangential derivatives

$$\begin{aligned} \partial _{ \mathbf {t}_{{\hat{K}}_{i+1}}^2}v|_{{\hat{K}}_{i+1}} (\hat{\mathbf {m}}_i)&=\partial _{\mathbf {t}_{{\hat{K}}_{i+2}}^2} v|_{{\hat{K}}_{i+2}} (\hat{\mathbf {m}}_i), \quad i=1,2,3. \end{aligned}$$

(3.20)

Because $v(\hat{\mathbf {x}}_i)$, $v(\hat{\mathbf {x}}_0)$, $\partial _{\mathbf {t}_{{\hat{K}}_{i+1}}} v(\hat{\mathbf {x}}_i)$, and $\partial _{\mathbf {t}_{{\hat{K}}_{i+1}}} v(\hat{\mathbf {x}}_0)$ are same on the two sides of edge $\hat{\mathbf {x}}_i\hat{\mathbf {x}}_0$, the piecewise cubic polynomial v is continuous on $\hat{\mathbf {x}}_i\hat{\mathbf {x}}_0$, so is its second tangential derivative (a linear function) at the mid-point.

Lastly, we check the continuity of mixed second derivatives

$$\begin{aligned} \frac{ \partial ^2 v|_{{\hat{K}}_{i+1}}}{\partial \mathbf {t}_{{\hat{K}}_{i+1}} \partial \mathbf {n}_{{\hat{K}}_{i+1}} } (\hat{\mathbf {m}}_i)&= - \frac{ \partial ^2 v|_{{\hat{K}}_{i+2}} }{\partial \mathbf {t}_{{\hat{K}}_{i+2}} \partial \mathbf {n}_{{\hat{K}}_{i+2}} } (\hat{\mathbf {m}}_i), \quad i=1,2,3. \end{aligned}$$

(3.21)

Because $\partial \mathbf {n}_{{\hat{K}}_{i+1}} v(\hat{\mathbf {x}}_i)$ and $\partial \mathbf {n}_{{\hat{K}}_{i+1}} v(\hat{\mathbf {x}}_0)$ are same at the two sides of edge $\hat{\mathbf {x}}_0\hat{\mathbf {x}}_i$, we have

$$\begin{aligned} |\hat{\mathbf {x}}_0\hat{\mathbf {x}}_i| \frac{ \partial ^2 v|_{{\hat{K}}_{i+1}}}{\partial \mathbf {t}_{{\hat{K}}_{i+1}} \partial \mathbf {n}_{{\hat{K}}_{i+1}} } (\hat{\mathbf {m}}_i)&= \int _{\hat{\mathbf {x}}_0\hat{\mathbf {x}}_i} \frac{ \partial ^2 v|_{{\hat{K}}_{i+1}}}{\partial \mathbf {t}_{{\hat{K}}_{i+1}} \partial \mathbf {n}_{{\hat{K}}_{i+1}} } \mathrm{d}s \\&= {\partial \mathbf {n}_{{\hat{K}}_{i+1}} } v|_{{\hat{K}}_{i+1}}(\hat{\mathbf {x}}_i) - {\partial \mathbf {n}_{{\hat{K}}_{i+1}} } v|_{{\hat{K}}_{i+1}}(\hat{\mathbf {x}}_0) \\&= |\hat{\mathbf {x}}_0\hat{\mathbf {x}}_i| \frac{ \partial ^2 v|_{{\hat{K}}_{i+2}} }{\partial \mathbf {t}_{{\hat{K}}_{i+1}} \partial \mathbf {n}_{{\hat{K}}_{i+1}} } (\hat{\mathbf {m}}_i). \end{aligned}$$

For computation, in addition to ${\hat{\phi }}_{1,0}$, we need only two more precomputed basis functions. The rest basis functions, and the basis function on other triangles, can be computed by these three basis functions, as shown in the next lemma. One basis function is ${\hat{\phi }}_{1,2}$, satisfying $\partial _{\hat{\mathbf {l}}_{1,1}} {\hat{\phi }}_{1,2}(\hat{\mathbf {x}}_1) =1$,

$$\begin{aligned} {\hat{\phi }}_{1,2} = {\left\{ \begin{array}{ll} \left( -\frac{1}{2} {\hat{x}}_1^2+ \frac{7}{\sqrt{3}} {\hat{x}}_1 {\hat{x}}_2+ \frac{1}{6} {\hat{x}}_2^2-\frac{1}{6} {\hat{x}}_1 - \frac{11}{12\sqrt{3}} {\hat{x}}_2+ \frac{5}{36}\right) \\ \times\, \left( -2 {\hat{x}}_1- \frac{2}{\sqrt{3}} {\hat{x}}_2+ \frac{1}{3}\right) &{}\quad \hbox {on } {\hat{K}}_1, \\ \left( \frac{1}{2} {\hat{x}}_1^2- \frac{17}{ \sqrt{3}} {\hat{x}}_1 {\hat{x}}_2+ \frac{ 11}{6} {\hat{x}}_1 - \frac{1}{6} {\hat{x}}_2^2+\frac{11}{12\sqrt{3}} {\hat{x}}_2- \frac{5}{36}\right) \\ \times\, \left( -2 {\hat{x}}_1+ \frac{2}{\sqrt{3}} {\hat{x}}_2- \frac{1}{3}\right) &{}\quad \hbox {on } {\hat{K}}_2, \\ \frac{5}{108}- \frac{1}{3} {\hat{x}}_1- \frac{7}{12\sqrt{3}} {\hat{x}}_2- \frac{ 11}{6} {\hat{x}}_1^2+ \frac{ 13}{6} {\hat{x}}_2^2 \\ +\, 8 {\hat{x}}_1^3 + \frac{2}{\sqrt{3} } {\hat{x}}_1^2 {\hat{x}}_2-8 {\hat{x}}_1 {\hat{x}}_2^2+ \frac{26}{3\sqrt{3} } {\hat{x}}_2^3 &{}\quad \hbox {on } {\hat{K}}_3. \end{array}\right. } \end{aligned}$$

(3.22)

And the last basis function needed is $\partial _{\hat{\mathbf {l}}_{1}^2} {\hat{\phi }}_{1,\mathbb {E}}({\hat{{\mathbf {e}}}}_1) =1$, and

$$\begin{aligned} {\hat{\phi }}_{1,\mathbb {E}} = {\left\{ \begin{array}{ll} \left( -\frac{7}{3} {\hat{x}}_1^2-\frac{26}{ 3\sqrt{3}} {\hat{x}}_1 {\hat{x}}_2-\frac{1}{ 18} {\hat{x}}_1+\frac{5}{9} {\hat{x}}_2^2 -\frac{1}{ 18\sqrt{3}} {\hat{x}}_2-\frac{1}{27}\right) \\ \times\, \left( -2 {\hat{x}}_1-\frac{2}{ \sqrt{3}} {\hat{x}}_2+ \frac{1}{3}\right) &{}\quad \hbox {on } {\hat{K}}_1, \\ \left( -\frac{5}{3} {\hat{x}}_1^2-\frac{2}{ 3\sqrt{3}} {\hat{x}}_1 {\hat{x}}_2-\frac{5}{9} {\hat{x}}_2^2- \frac{7}{18} {\hat{x}}_1 +\frac{1}{ 18\sqrt{3}} {\hat{x}}_2+\frac{1}{27}\right) \\ \times\, \left( -2 {\hat{x}}_1+\frac{2}{ \sqrt{3}} {\hat{x}}_2-\frac{1}{3}\right) &{}\quad \hbox {on } {\hat{K}}_2, \\ \left( \frac{44}{ 9\sqrt{3}} {\hat{x}}_2^2+\frac{22}{27} {\hat{x}}_2-\frac{4}{ 27\sqrt{3}} +\frac{8}{3} {\hat{x}}_1 {\hat{x}}_2 +\frac{2}{ 3\sqrt{3}} {\hat{x}}_1+\frac{4}{ \sqrt{3}} {\hat{x}}_1^2\right) \\ \times\, \left( {\hat{x}}_2+\frac{1}{4\sqrt{3}} \right) &{}\quad \hbox {on } {\hat{K}}_3. \end{array}\right. } \end{aligned}$$

(3.23)

For example, for the basis function ${\hat{\phi }}_{1,3}$, satisfying $\partial _{\hat{\mathbf {l}}_{1,2}} {\hat{\phi }}_{1,3}(\hat{\mathbf {x}}_1) =1$, we use the affine transformation (linear in this case) which maps ${\hat{M}}$ to itself with $\hat{\mathbf {x}}_2$ and $\hat{\mathbf {x}}_3$ swapped:

$$\begin{aligned} \begin{pmatrix} x_1 \\ x_2\end{pmatrix} = \begin{pmatrix} \cos \frac{\pi }{3} &{} \sin \frac{\pi }{3}\\ \sin \frac{\pi }{3} &{} -\cos \frac{\pi }{3}\end{pmatrix} \begin{pmatrix}{\hat{x}}_1\\ {\hat{x}}_2\end{pmatrix}. \end{aligned}$$

Then,

$$\begin{aligned} {\hat{\phi }}_{1,3} (x_1, x_2) = {\hat{\phi }}_{1,2} \left( x_1 \cos \frac{\pi }{3} + x_2\sin \frac{\pi }{3} , x_1 \sin \frac{\pi }{3} - x_2\cos \frac{\pi }{3} \right) . \end{aligned}$$

This way, we obtain

$$\begin{aligned} {\hat{\phi }}_{1,3} ={\left\{ \begin{array}{ll} \left( - \frac{7}{4} {\hat{x}}_1^2- \frac{5}{2 \sqrt{3}} {\hat{x}}_1 {\hat{x}}_2+ \frac{13}{24} {\hat{x}}_1+ \frac{25}{12} {\hat{x}}_2^2- \frac{5}{24 \sqrt{3}} {\hat{x}}_2- \frac{5}{36}\right) \\ \times\, \left( 2 {\hat{x}}_1+ \frac{2}{\sqrt{3}} {\hat{x}}_2- \frac{1}{3}\right) &{}\quad \hbox {on } {\hat{K}}_1, \\ \frac{5}{108} - \frac{11}{24} {\hat{x}}_1- \frac{5}{24 \sqrt{3}} + \frac{7}{6} {\hat{x}}_1^2 -2 \sqrt{3} {\hat{x}}_1 {\hat{x}}_2- \frac{5}{6} {\hat{x}}_2^2+ \frac{3}{2} {\hat{x}}_1^3 \\ - \,\frac{5}{2 \sqrt{3}} {\hat{x}}_1^2 {\hat{x}}_2 + \frac{35}{2} {\hat{x}}_1 {\hat{x}}_2^2+ \frac{25}{6 \sqrt{3} } {\hat{x}}_2^3 &{}\quad \hbox {on } {\hat{K}}_2, \\ \left( - \frac{55}{3 \sqrt{3}} {\hat{x}}_2^2- \frac{55}{18} {\hat{x}}_2+ \frac{5}{9 \sqrt{3}} +10 {\hat{x}}_1 {\hat{x}}_2- \frac{11}{2 \sqrt{3}} {\hat{x}}_1+ \frac{17}{ \sqrt{3}} {\hat{x}}_1^2\right) \\ \times\, \left( {\hat{x}}_2+\frac{1}{4\sqrt{3}}\right) &{}\quad \hbox {on } {\hat{K}}_3. \end{array}\right. } \end{aligned}$$

(3.24)

Lemma 3.3

On a general triangleM, the dimension of$V_M$ (defined in (2.6)) is 12 and the function can be expanded uniquely by the 12 nodal values:

$$\begin{aligned} v_h = \sum _{i=1}^3 v_h({\mathbf {x}}_i) \phi _{i,0} + \sum _{i=1}^3 \sum _{j=1}^2 \partial _{\mathbf {l}_{i,j} } v_h({\mathbf {x}}_i) \phi _{i,j} + \sum _{i=1}^3 \partial _{\mathbf {l}_{i}^2 } v_h({\mathbf {e}}_i) \phi _{i,\mathbb {E}}, \end{aligned}$$

(3.25)

where the scaled directional derivatives are defined in (3.2), and the basis functions are affine-transformed from those reference basis functions${\hat{\phi }}_{i,j}$, defined in (3.3), (3.22), (3.23), (3.24) and (3.2),

$$\begin{aligned} \phi _{i,j} (\mathbf {x}) = \hat{\phi }_{i,j}(\hat{\mathbf {x}}_1 + B (\mathbf {x}-{\mathbf {x}}_1)), \quad B = \begin{pmatrix}{\mathbf {x}}_2-{\mathbf {x}}_1 \\ {\mathbf {x}}_3-{\mathbf {x}}_1\end{pmatrix}^{-{\rm T}}\begin{pmatrix}\hat{\mathbf {x}}_2-\hat{\mathbf {x}}_1 \\ \hat{\mathbf {x}}_3-\hat{\mathbf {x}}_1\end{pmatrix}^{\rm T}. \end{aligned}$$

(3.26)

Proof

Let $v\in V_M$ be mapped by $v = {\hat{v}}(\hat{\mathbf {x}}_1 + B (\mathbf {x}-\mathbf {x}_1))$. For an affine mapping, the function values are preserved (by the continuously change of variables), i.e., for $v\in V_M$,

$$\begin{aligned} v(\mathbf {x}) = {\hat{v}}(\hat{\mathbf {x}}), \quad \hbox { where } \ \hat{\mathbf {x}}= \hat{\mathbf {x}}_1 + B (\mathbf {x}-{\mathbf {x}}_1). \end{aligned}$$

For the scaled directional derivatives, we have

$$\begin{aligned} \partial _{\mathbf {l}_{1,2} } v({\mathbf {x}}_1)&= |{\mathbf {x}}_1{\mathbf {x}}_2|\partial _{\frac{\mathbf {l}_{1,2}}{|\mathbf {l}_{1,2}|} } v({\mathbf {x}}_1) = |{\mathbf {x}}_1{\mathbf {x}}_2|\partial _{\frac{\hat{\mathbf {l}}_{1,2}}{|\hat{\mathbf {l}}_{1,2}|} } {\hat{v}}(\hat{\mathbf {x}}_1) \frac{ |\hat{\mathbf {x}}_1\hat{\mathbf {x}}_2|}{ |{\mathbf {x}}_1{\mathbf {x}}_2|} \\&= \partial _{\hat{\mathbf {l}}_{1,2} } {\hat{v}}(\hat{\mathbf {x}}_1). \end{aligned}$$

For the scaled second directional derivatives at mid-points, we have

$$\begin{aligned} \partial _{\mathbf {l}_1^2 } v({\mathbf {e}}_1)&= |{\mathbf {x}}_1{\mathbf {e}}_1|^2\partial _{\left( \frac{\mathbf {l}_1}{|\mathbf {l}_1|} \right) ^2 } v({\mathbf {e}}_1) = |{\mathbf {x}}_1{\mathbf {e}}_1|^2\partial _{\left( \frac{\hat{\mathbf {l}}_1}{|\hat{\mathbf {l}}_1|}\right) ^2 } {\hat{v}}({\hat{{\mathbf {e}}}}_1) \frac{ |\hat{\mathbf {x}}_1{\hat{{\mathbf {e}}}}_1|^2}{ |{\mathbf {x}}_1{\mathbf {e}}_1|^2} \nonumber \\&= \partial _{\hat{\mathbf {l}}_1 ^2 } {\hat{v}}({\hat{{\mathbf {e}}}}_1). \end{aligned}$$

(3.27)

There, as function values and two scaled tangential directional derivatives are preserved at the center point ${\mathbf {x}}_0$, v satisfies (3.2g) and (3.2h). By Lemma 3.1 and (3.2i), ${\hat{v}}$ has all its second-order scaled directional derivatives continuous at all three internal mid-edge points $\hat{\mathbf {m}}_i$. By (3.27), v satisfies (3.2i) as well as its three second-order scaled directional derivatives are continuous there. Finally, for the third-order scaled directional derivative, we have also

$$\begin{aligned} \partial _{\mathbf {l}_{2,3}^3 } v(\mathbf {m}_1)&= \partial _{\hat{\mathbf {l}}_{2,3}^3 } {\hat{v}}(\hat{\mathbf {m}}_1). \end{aligned}$$

So (3.2j) holds for v. Therefore, v is the unique solution for (3.2) on a general triangle M.

4 Error Analysis

We will show the finite element equations have a unique solution. We then bound the consistent error and derive the optimal order convergence for the finite element solution.

Theorem 4.1

The system of finite element equations  (2.8) has a unique solution.

Proof

We are going to prove the bilinear form $a_h(\cdot ,\cdot )$ is coercive on space $V_h$. Let $a_h(u_h,u_h)=0$ for some $u_h\in V_h$. On each (sub)triangle $K\in {\mathcal {T}}_h$,

$$\begin{aligned} D^3 u_h \equiv 0 \quad \Rightarrow \ u_h \in P_2(K). \end{aligned}$$

Let $M\in {\mathcal {M}}_h$ be formed by three (sub)triangles $K_1, K_2, K_3$, cf. Fig. 1. The $P_2$ polynomials $u_2=u_h|_{K_2}$ and $u_3=u_h|_{K_3}$ have the same value and first derivatives at the two end points ${\mathbf {x}}_0$ and ${\mathbf {x}}_1$ of the common edge ${\mathbf {x}}_0\mathbf {x}_1$. Thus, $u_2$ and $u_3$ are $C^1$ across edge ${\mathbf {x}}_0\mathbf {x}_1$. As they are quadratic polynomials, $u_2-u_3=c \lambda _{0,1}^2$, where $\lambda _{0,1}=0$ is an equation for the line ${\mathbf {x}}_0\mathbf {x}_1$. $u_2$ and $u_3$ have the second normal derivative continuous at the middle point $\mathbf {m}_1$ of edge ${\mathbf {x}}_0\mathbf {x}_1$. This concludes $c=0$ in $u_2-u_3=c \lambda _{0,1}^2$. Hence, $u_h$ is a global $P_2$ polynomial on three triangles $\cup K_i = M$. Next, repeating the above argument, by the given continuity conditions on the edge ${\mathbf {x}}_1\mathbf {x}_2$, cf. Fig. 1, $u_h$ is a common quadratic polynomial on M and the next neighbor macro-triangle $M'$, sharing a common edge ${\mathbf {x}}_1\mathbf {x}_2$ with M. This way, $u_h$ is a global quadratic polynomial on the whole domain $\Omega$. By the boundary conditions (2.2), $u_h=0$.

Lemma 4.1

Let$u\in H^4(\Omega )\cap H^3_0(\Omega )$. For any$w_h\in V_h$,

$$\begin{aligned} \frac{|a_h(u,w_h) - (f,w_h)|}{ | w_h|_{H^3_h(\Omega )} } \le C( h |u|_{H^4(\Omega )}+h^3 \Vert f\Vert _{L^2(\Omega )}), \end{aligned}$$

(4.1)

where$| \cdot |_{H^3_h(\Omega )}$ is the piecewise$H^3$-semi norm on triangulation${\mathcal {T}}_h$.

Proof

A direct proof would be very difficult and tedious. We introduce a $C^2$-$P_9$ interpolation and use approximation argument to give a simple proof.

By Zhang [16], the following nodal values define a unique $C^2$-$P_9$ interpolation ${\tilde{u}}_h={\tilde{I}}_h u$ of u (assumed to be $C^4$, for instance, on $K_3$ of macro-element M):

$$\begin{aligned} &\partial _{x_1^{\alpha _1} x_2^{\alpha _2}} {\tilde{u}}_h({\mathbf {x}}_i)=\partial _{x_1^{\alpha _1} x_2^{\alpha _2}} u({\mathbf {x}}_i), \quad i=0,1,2, \ |\alpha |=0,1,2,3,4, \\ &\partial _{\mathbf {n}_{K_3}} {\tilde{u}}_h(\mathbf {m}_i)= \partial _{\mathbf {n}_{K_3}} u (\mathbf {m}_i), \quad i=1,2, \\ &\partial _{\mathbf {n}_{K_3}} {\tilde{u}}_h({\mathbf {e}}_3)= \partial _{\mathbf {n}_{K_3}} u ({\mathbf {e}}_3), \\ &\partial _{\mathbf {n}^2_{K_3}} {\tilde{u}}_h({\mathbf {x}}_{i,j})= \partial _{\mathbf {n}^2_{K_3}} u ({\mathbf {x}}_{i,j}), \quad i=0,1,2, \ {\mathbf {x}}_{i,j}=\frac{j{\mathbf {x}}_i+(3-j){\mathbf {x}}_{i+1}}{3}, \ j=1,2, \\ &{\tilde{u}}_h({\mathbf {x}}_{K_3})= u({\mathbf {x}}_{K_3}). \end{aligned}$$

Here ${\mathbf {x}}_{K_3}$ is the barycentric point of $K_3$. The function, 1st, 2nd, 3rd and 4th partial derivatives at three vertices provide $3(1+2+3+4+5)=45$ equations. The first normal derivative and two second normal derivatives on each edge provide $3(1+2)=9$ equations. The barycentric nodal value gives one equation. Together, we have 55 equations and $\dim P_9=(9+1)(9+2)/2=55$.

We extend this operator ${\tilde{I}}_h$ to $V_h$ functions, i.e., define ${\tilde{w}}_h ={\tilde{I}}_h w_h$ by the true values or average values of $w_h$. This stability can be proved relatively easily, though not standard. We bound interpolated coefficients in nodal expansion of ${\tilde{I}}_h w_h$ by those of $w_h$ to get

$$\begin{aligned} |{\tilde{I}}_h w_h|_{H^3(\Omega )} \le C | w_h|_{H^3_h(\Omega )}, \quad \forall w_h\in V_h. \end{aligned}$$

(4.2)

But the approximation would be proved relatively long, involving bounding local differences by the $H^3$-norm on triangles around a node. Anyway, similar to the proof in [6, 13], we do have

$$\begin{aligned} \Vert w_h-{\tilde{I}}_h w_h \Vert _{L^2(\Omega )} \le C h^3 | w_h |_{H^3_h (\Omega )}, \quad \forall w_h\in V_h. \end{aligned}$$

(4.3)

It is interesting, such an interpolant is orthogonal to $V_h$ functions, because we use (3.2d’) instead of (3.2d), for $v_h\in V_h$,

$$\begin{aligned} a_h( w_h-{\tilde{w}}_h, v_h)&= - \sum _{K\in {\mathcal {T}}_h} \int _K D^2(w_h-{\tilde{w}}_h): D^4 v_h {\rm d}\mathbf {x} \\&\quad + \sum _{K\in {\mathcal {T}}_h} \int _{\partial K} D^2(w_h-{\tilde{w}}_h): (D^3 v_h\cdot \mathbf {n}) \mathrm{d}s, \end{aligned}$$

where $D^4 v_h=0$. Hence,

$$\begin{aligned} a_h( w_h-{\tilde{w}}_h, v_h)&= \sum _{F\in {\mathcal {F}}_h} \int _F \{D^2(w_h-{\tilde{w}}_h)\}: [(D^3 v_h\cdot \mathbf {n})] \mathrm{d}s \\&\quad +\sum _{F\in {\mathcal {F}}_h} \int _F [D^2(w_h-{\tilde{w}}_h)]: \{(D^3 v_h\cdot \mathbf {n})\} \mathrm{d}s, \end{aligned}$$

where ${\mathcal {F}}_h$ is the set of edges of $\mathcal {T}_h$, $[\cdot ]$ and $\{\cdot \}$ denote the jump and average of a piecewise smooth function across edge F, respectively, which become traces on boundary edges. Since $(D^3 v_h\cdot \mathbf {n})$ is a constant on each side of edge F, $\int _F [D^2(w_h-{\tilde{w}}_h)]: \{(D^3 v_h\cdot \mathbf {n})\} \mathrm{d}s=0$. In addition, the interpolation ${\tilde{w}}_h$ can be taken such that $\int _F \{ D^2(w_h-{\tilde{w}}_h)\} \mathrm{d}s = 0$, which leads to

$$\begin{aligned} a_h( w_h-{\tilde{w}}_h, v_h)=0. \end{aligned}$$

(4.4)

For the nonconforming finite element interpolation $I_h u$, defined by (3.2), by the standard proof of, e.g., [12], the operator is stable in $H^3$-semi norm. Consequently, because the interpolation is stable in $H^3$ and preserves $P_3$ polynomials locally, $I_hu$ approximates u at the optimal order O(h) in $H^3$ norm:

$$\begin{aligned} |u-I_h u|_{H^3_h(\Omega )} \le Ch |u|_{H^4(\Omega )}. \end{aligned}$$

(4.5)

By (4.5), (4.3), (4.4) and (4.2),

$$\begin{aligned} a_h(u,w_h) - (f,w_h)&= a_h(u,w_h-{\tilde{w}}_h) - (f, w_h-{\tilde{w}}_h) \\&= a_h(u-I_hu,w_h-{\tilde{w}}_h) - (f, w_h-{\tilde{w}}_h)\\&\quad \ + a_h(I_hu,w_h-{\tilde{w}}_h)\\&\le |u-I_hu|_{H^3_h(\Omega )} |w_h-{\tilde{w}}_h|_{H^3_h(\Omega )} + \Vert f\Vert _{L^2(\Omega )} \Vert w_h-{\tilde{w}}_h\Vert _{L^2(\Omega )} + 0 \\&\le C h |u-I_hu|_{H^3_h(\Omega )} |w_h|_{H^3_h(\Omega )} + C h^3 \Vert f\Vert _{L^2(\Omega )} |w_h|_{H^3_h(\Omega )}. \end{aligned}$$

This completes the proof.

Theorem 4.2

Let$u\in H^4(\Omega )\cap H^3_0(\Omega )$ be the solution of (2.1). Let $u_h\in V_h$ be the solution of (2.8).

Then,

$$\begin{aligned} | u-u_h|_{H^3_h(\Omega )} \le C\left( h |u|_{H^4(\Omega )}+h^3 \Vert f\Vert _{L^2(\Omega )}\right) . \end{aligned}$$

(4.6)

Proof

By the second Strang lemma, cf. [3], we get, applying (4.1) and (4.5),

$$\begin{aligned} | u-u_h|_{H^3_h(\Omega )}&\le \inf _{w_h\in V_h} | u-w_h|_{H^3_h(\Omega )} + C \sup _{w_h\in V_h} \frac{|a_h(u,w_h) - (f,w_h)|}{ | w_h|_{H^3_h(\Omega )} } \\&\le |u-I_h u |_{H^3_h(\Omega )} + C h |u|_{H^4(\Omega )}+ C h^3 \Vert f\Vert _{L^2(\Omega )} \\&\le C \left( h |u|_{H^4(\Omega )}+ h^3 \Vert f\Vert _{L^2(\Omega )}\right) . \end{aligned}$$

This completes the proof.

5 Numerical Tests

We compute three examples in 2D, on the unit square domain. We cut the domain by a northeast line to get the level one triangular base-grid ${\mathcal {M}}_1$, in the computation. Then, each triangle is refined into four congruent triangles, to define the next level triangular base-grid, ${\mathcal {M}}_k$. Each base-grid ${\mathcal {M}}_k$ is refined to a HCT grid ${\mathcal {T}}_k$ by cutting each triangle into three sub-triangles, by connecting its bary-center and three vertices. The first two levels of grid are shown in Fig. 4.

Fig. 4

The level one grid ${\mathcal {T}}_1$ and level two grid ${\mathcal {T}}_2$ in computation

5.1 Example 1

We compute the finite element solutions approximating the exact solution

$$\begin{aligned} u= x^3 - y^3, \end{aligned}$$

(5.1)

of the tri-harmonic equation

$$\begin{aligned} \Delta ^3 u =0, \end{aligned}$$

with non-homogeneous boundary conditions that $u|_{\partial \Omega }$, $\partial _{\mathbf {n}} u|_{\partial \Omega }$ and $\partial _{\mathbf {n}^2} u|_{\partial \Omega }$ are given by (5.1). As expected, the finite element solution does reproduce the exact solution, a polynomial of degree 3, shown in Table 1.

Table 1 Example 1. The error $e_h=I_h u- u_h$ and the order of convergence, for (5.1)

5.2 Example 2

We approximate the exact solution

$$\begin{aligned} u=2^6 \left( x- x^2\right) ^3 \left( y- y^2\right) ^3, \end{aligned}$$

(5.2)

by solving the tri-harmonic equation

$$\begin{aligned} \Delta ^3 u = f, \end{aligned}$$

with homogeneous boundary conditions that

$$\begin{aligned} u|_{\partial \Omega }=\partial _{\mathbf {n}} u|_{\partial \Omega }= \partial _{\mathbf {n}^2} u|_{\partial \Omega }=0. \end{aligned}$$

As shown by the theorem, the finite element solution does converge at the optimal order, shown in Table 2.

Table 2 Example 2. The error $e_h=I_h u- u_h$ and the order of convergence, for (5.2)

Typically, for solving problems like (5.2), nonconforming finite element solutions are bigger than the exact solution while conforming finite element solutions are smaller. To see how conforming the new $H^3$$P_3$ finite element is, we plot its error in Fig. 5. As expected, the nonconforming finite element solution is bigger (negative error).

Fig. 5

The solution $u_h$ of (5.2) and the error $e_h=I_hu-u_h$ (bottom graph), on the fourth-level grid

5.3 Example 3

We solve the problem of Example 2 again, by the $P_4$-bubble enriched $P_3$$H^3$-nonconforming finite element method. This finite element is designed by [9], and extended to a full-$P_4$ element by [8]. On one triangle $K=\triangle {\mathbf {x}}_1{\mathbf {x}}_2{\mathbf {x}}_3$ with barycentric coordinates $(\lambda _1, \lambda _2, \lambda _3)$, where $\lambda _i$ is a linear function assuming 1 at a vertex ${\mathbf {x}}_i$ and 0 on the opposite edge, the shape-function space is

$$\begin{aligned} V_K =\mathrm{span} \left\{ P_3(K), \lambda _1^2\lambda _2\lambda _3 , \lambda _1\lambda _2^2\lambda _3 \right\} . \end{aligned}$$

(5.3)

Note that $\lambda _1\lambda _2\lambda _3^2=\lambda _1\lambda _2\lambda _3-\lambda _1^2\lambda _2\lambda _3- \lambda _1\lambda _2^2\lambda _3$ is already in the above linear space. The local degrees of freedom are exactly the same as our macro-element:

$$\begin{aligned} v_h({\mathbf {x}}_i), \partial _x v_h({\mathbf {x}}_i), \partial _y v_h({\mathbf {x}}_i), \int _{e_i} \partial _{{\mathbf {n}}_i{\mathbf {n}}_i} v_h \mathrm{d}s, i=1,2,3, \end{aligned}$$

that is, ${\rm dof}=3\times 4=12=\dim V_K$. Here $e_i$ is the edge opposite to vertex ${\mathbf {x}}_i$ with the normal vector ${\mathbf {n}}_i$.

The error and the order of convergence are listed in Table 3. Though the order of convergence, in various norms, is same for the two finite elements, the errors of the $P_4$-enriched $P_3$ element are much less than those by the HCT $P_3$ elements. The total number of unknowns in the two linear systems is same. But the condition number of the linear system of $P_4$-enriched $P_3$ element seems much bigger, as the number of conjugate-gradient iterations (without any preconditioning) is about ten times as many as that for the HCT $P_3$ element.

Table 3 Example 3. The error $e_h=I_h u- u_h$ and the order of convergence, for (5.2), by $P_4{\text{-}}$ bubble enriched $P_3$ element (5.3)

5.4 Example 4

We solve the tri-harmonic equation

$$\begin{aligned} \Delta ^3 u = -2^6 \mathrm{e}^{x+y}, \end{aligned}$$

with appropriate boundary conditions so that the exact solution is

$$\begin{aligned} u=2^3\mathrm{e}^{x+y}. \end{aligned}$$

(5.4)

We apply the $P_3$-$H^3$-nonconforming finite element method, on the HCT grids described above. The finite element solution converges at the optimal order, shown in Table 4.

Table 4 Example 4. The error $e_h=I_h u- u_h$ and the order of convergence, for (5.4)