New type of gamma kernel density estimator

Abstract

We discuss a new kernel type estimator for density function $f_X(x)$ with nonnegative support. Here, we use a type of gamma density as a kernel function and modify it with expansions of exponential and logarithmic functions. Our modified gamma kernel density estimator is not only free of the boundary bias, but the variance is also in smaller orders, which are $O(n^{-1}h^{-1/4})$ in the interior and $O(n^{-1}h^{-3/4})$ in the boundary region. Furthermore, the optimal orders of its mean squared error are $O(n^{-8/9})$ in the interior and $O(n^{-8/11})$ in the boundary region. Simulation results that demonstrate the proposed method’s performances are also presented.

1 Introduction

Nonparametric methods are gradually becoming popular in statistical analysis for analyzing problems in many fields, such as economics, biology, and actuarial science. In most cases, this is because of a lack of information on the variables being analyzed. Smoothing concerning functions, such as density or cumulative distribution, plays a special role in nonparametric analysis. Knowledge on a density function, or its estimate, allows one to characterize the data more completely. We can derive other characteristics of a random variable from an estimate of its density function, such as the probability itself, hazard rate, mean, and variance value.

Let $X_1,X_2,...,X_n$ be independently and identically distributed random variables with an absolutely continuous distribution function $F_X$ and a density $f_X$. Parzen (1962) and Rosenblatt (1956) introduced the kernel density estimator (we will call it the standard one) as a smooth and continuous estimator for density functions. It is defined as

$$\begin{aligned} {\widehat{f}}_X(x)=\frac{1}{nh}\sum _{i=1}^n K\left( \frac{x-X_i}{h}\right) , \; \; \; x\in {\mathbb {R}}, \end{aligned}$$

(1)

where K is a function called a “kernel”, and $h>0$ is the bandwidth, which is a parameter that controls the smoothness of ${\widehat{f}}_X$. It is usually assumed that K is a symmetric (about 0) continuous nonnegative function with $\int _{-\infty }^\infty K(v)\mathrm {d}v=1$, as well as $h\rightarrow 0$ and $nh\rightarrow \infty$ when $n\rightarrow \infty$. It is easy to prove that the standard kernel density estimator is continuous and satisfies all the properties of a density function.

A typical general measure of the accuracy of ${\widehat{f}}_X(x)$ is the mean integrated squared error, defined as

$$\begin{aligned} MISE({\widehat{f}}_X)=E\left[ \int _{-\infty }^\infty \{{\widehat{f}}_X(x)-f_X(x)\}^2 w(x)\mathrm {d}x\right] , \end{aligned}$$

(2)

where w is a weight function. In this article, we consider only $w(x)=1$. For point-wise measures of accuracy, we will use bias, variance, and the mean squared error $MSE[{\widehat{f}}_X(x)]=E[\{{\widehat{f}}_X(x)-f_X(x)\}^2]$. It is well known that the MISE and the MSE can be computed with

$$\begin{aligned} MISE({\widehat{f}}_X)= & {} \int _{-\infty }^\infty MSE[{\widehat{f}}_X(x)]\mathrm {d}x, \end{aligned}$$

(3)

$$\begin{aligned} MSE[{\widehat{f}}_X(x)]= & {} Bias^2[{\widehat{f}}_X(x)]+Var[{\widehat{f}}_X(x)]. \end{aligned}$$

(4)

Under the condition that $f_X$ has a continuous second order derivative $f_X''$, it has been proved by the above-mentioned authors that, as $n\rightarrow \infty$,

$$\begin{aligned} Bias[{\widehat{f}}_X(x)]= & {} \frac{h^2}{2}f_X''(x)\int u^2 K(u)\mathrm {d}u+o(h^2),\\ Var[{\widehat{f}}_X(x)]= & {} \frac{f_X(x)}{nh}\int K^2(u)\mathrm {d}u+o\left( \frac{1}{nh}\right) . \end{aligned}$$

There have been many proposals in the literature for improving the bias property of the standard kernel density estimator. Typically, under sufficient smoothness conditions placed on the underlying density $f_X$, the bias is reduced from $O(h^2)$ to $O(h^4)$, and the variance remains in the order of $n^{-1}h^{-1}$. Those methods that could potentially have greater impact include bias reduction by geometric extrapolation by Terrel and Scott (1980), variable bandwidth kernel estimators by Abramson (1982), variable location estimators by Samiuddin and El-Sayyad (1990), nonparametric transformation estimators by Ruppert and Cline (1994), and multiplicative bias correction estimators by Jones et al. (1995). One also could use, of course, the so-called higher order kernel functions, but this method has a disadvantage in that negative values might appear in the density estimates and distribution function estimates.

All of the previous explanations implicitly assume that the true density is supported on the entire real line. If we deal with a nonnegative supported distribution, for instance, the standard kernel density estimator will suffer the so-called boundary bias problem, and this is the main problem that we are going to overcome. Throughout this paper, the interval [0, h] is called a “boundary region”, and points greater than h are called “interior points”.

In the boundary region, the standard kernel density estimator ${\widehat{f}}_X(x)$ usually underestimates $f_X(x)$. This is because it does not “feel” the boundary, and it puts weights for the lack of data on the negative axis. To be more precise, if we use a symmetric kernel supported on $[-1,1]$, we have

$$\begin{aligned} Bias[{\widehat{f}}_X(x)]=\left[ \int _{-1}^c K(u)\mathrm {d}u-1\right] f_X(x)-hf_X'(x)\int _{-1}^c uK(u)\mathrm {d}u+O(h^2) \end{aligned}$$

when $x\le h$, $c=\frac{x}{h}$. This means that this estimator is not consistent at $x=0$ because

$$\begin{aligned} \lim _{n\rightarrow \infty }Bias[{\widehat{f}}_X(0)]=\left[ \int _{-1}^c K(u)\mathrm {d}u-1\right] f_X(0)\ne 0, \end{aligned}$$

unless $f_X(0)=0$.

Several ways of removing the boundary bias problem, each with their own advantages and disadvantages, are data reflection (Schuster 1985) simple nonnegative boundary correction (Jones and Foster 1996), boundary kernels (Muller 1991, 1993; Muller and Wang 1994), pseudodata generation (Cowling and Hall 1996), a hybrid method (Hall and Wehrly 1991), empirical transformation (Marron and Ruppert 1994), a local linear estimator (Lejeune and Sarda 1992; Jones 1993), data binning and a local polynomial fitting on the bin counts (Cheng et al. 1997), and others. Most of them use symmetric kernel functions as usual, and then modify their forms or transform the data.

Chen (2000) proposed a simple way to circumvent the boundary bias that appears in the standard kernel density estimation. The remedy consists in replacing symmetric kernels with asymmetric gamma kernels, which never assign a weight outside of the support. In addition to satisfactory asymptotic features, Chen (2000) reported good finite sample performances of this cure through a simulation study.

Let K(y; x, h) be an asymmetric function parameterized by x and h, called an “asymmetric kernel”. Then, the definition of the asymmetric kernel density estimator is

$$\begin{aligned} {\widehat{f}}(x)=\frac{1}{n}\sum _{i=1}^n K(X_i;x,h). \end{aligned}$$

(5)

Since the density of $Gamma(xh^{-1}+1,h)$,

$$\begin{aligned} \frac{y^{\frac{x}{h}}e^{-\frac{y}{h}}}{\Gamma \left( \frac{x}{h}+1\right) h^{\frac{x}{h}+1}}, \end{aligned}$$

(6)

is an asymmetric function parameterized by x and h, it is natural to use it as an asymmetric kernel. Hence, Chen (2000) defined his first gamma kernel density estimator as

$$\begin{aligned} {\widehat{f}}_C(x)=\frac{1}{n}\sum _{i=1}^{n} \frac{X_i^{\frac{x}{h}}e^{-\frac{X_i}{h}}}{\Gamma \left( \frac{x}{h} +1\right) h^{\frac{x}{h}+1}}. \end{aligned}$$

(7)

The intuitive approach to seeing how Eq. (7) can be used as a consistent estimator is as follows. Let Y be a $Gamma(xh^{-1}+1,h)$ random variable with the pdf stated in Eq. (6); then,

$$\begin{aligned} E[{\widehat{f}}_C(x)]=\int _0^\infty f_X(y)K(y;x,h)\mathrm {d}y=E[f_X(Y)]. \end{aligned}$$

By Taylor expansion,

$$\begin{aligned} E[f_X(Y)]=f_X(x)+h\left[ f_X'(x)+\frac{1}{2}xf_X''(x)\right] +o(h), \end{aligned}$$

which will converge to $f_X(x)$ as $n\rightarrow \infty$. For a detailed theoretical explanation regarding the consistency of asymmetric kernels, see Bouezmarni and Scaillet (2005).

The bias and variance of Chen’s first gamma kernel density estimator are

$$\begin{aligned} Bias[{\widehat{f}}_C(x)]= & {} \left[ f_X'(x)+\frac{1}{2}xf_X''(x)\right] h+o(h),\end{aligned}$$

(8)

$$\begin{aligned} Var[{\widehat{f}}_C(x)]= & {} {\left\{ \begin{array}{ll} \frac{f_X(x)}{2\sqrt{\pi x}n\sqrt{h}}, &{} \frac{x}{h}\rightarrow \infty , \\ \frac{\Gamma (2\kappa +1)f_X(x)}{2^{2\kappa +1}\Gamma ^2(\kappa +1)nh}, &{} \frac{x}{h}\rightarrow c, \end{array}\right. } \end{aligned}$$

(9)

for some $c>0$. Since the result is quite similar, we do not discuss Chen’s second gamma kernel density estimator in this article; see Chen (2000) for reference.

Chen’s gamma kernel density estimator obviously solved the boundary bias problem because the gamma pdf is a nonnegative supported function, so no weight will be put on the negative axis. However, it also has some problems; they are:

• The variance depends on a factor $x^{-1/2}$ in the interior, which means the variance becomes much larger quickly when x is small,

• Zhang (2010) showed that the MSE is $O(n^{-2/3})$ when x is close to the boundary (worse than the standard kernel density estimator).

In this article, we try to improve Chen’s estimator. Using a similar idea but with different parameters of gamma density as a kernel function, we intend to reduce the variance. Then, we strive to reduce the bias by modifying it with expansions of exponential and logarithmic functions. Hence, our modified gamma kernel density estimator is not only free of the boundary bias, but the variance also has smaller orders both in the interior and near the boundary, compared with Chen’s method. As a result, the optimal orders of the MSE and the MISE are smaller as well. A simulation study is discussed in Section 3, and detailed proofs can be found in the appendices.

2 New type of gamma kernel density estimator formulation

Before starting our discussion, we need to impose assumptions; they are:

A1.:

The bandwidth $h>0$ satisfies $h\rightarrow 0$ and $nh\rightarrow \infty$ when $n\rightarrow \infty$,

A2.:

The density $f_X$ is three times continuously differentiable, and $f_X^{(4)}$ exists,

A3.:

The integrals $\int \left[ \frac{f_X'(x)}{f_X(x)}\right] ^2\mathrm {d}x$, $\int x^4\left[ \frac{f_X''(x)}{f_X(x)}\right] ^2\mathrm {d}x$, $\int x^2[f_X''(x)]^2\mathrm {d}x$, and $\int x^6[f_X'''(x)]^2\mathrm {d}x$ are finite.

The first assumption is the usual assumption for the standard kernel density estimator. Since we will use exponential and logarithmic expansions, we need A2 to ensure the validity of our proofs. The last assumption is necessary to make sure we can calculate the MISE.

As we stated before, the modification of the gamma kernel, done to improve the performance of Chen’s method, is started by replacing the shape and scale parameters of the gamma density with suitable functions of x and h, and this kernel is defined as a new gamma kernel. Our purpose in doing this is to reduce the variance so that it is smaller than the variance of Chen’s method. After trying several combinations of functions, we chose the density of $Gamma(h^{-1/2},x\sqrt{h}+h)$, which is

$$\begin{aligned} K(y;x,h)=\frac{y^{\frac{1}{\sqrt{h}}-1}e^{-\frac{y}{x\sqrt{h}+h}}}{\Gamma \left( \frac{1}{\sqrt{h}}\right) (x\sqrt{h}+h)^\frac{1}{\sqrt{h}}}, \end{aligned}$$

(10)

as a kernel, and we define the new gamma kernel density “estimator” as

$$\begin{aligned} A_h(x)=\frac{\sum _{i=1}^{n}X_i^{\frac{1}{\sqrt{h}}-1}e^{-\frac{X_i}{x \sqrt{h}+h}}}{n\Gamma \left( \frac{1}{\sqrt{h}}\right) (x\sqrt{h}+h)^\frac{1}{\sqrt{h}}}, \end{aligned}$$

(11)

where n is the sample size, and h is the bandwidth.

Remark 2.1

Even though the formula in Eq. (11) can work as a density estimator properly, it is not our proposed method (that is why we put quotation marks around the word “estimator”). As we will state later, we need another modification for Eq. (11) before our proposed estimator is created.

After this, we need to derive the bias and the variance formulas of $A_h(x)$. Consult the following theorem.

Theorem 2.2

Assuming A1 and A2, for the function $A_h(x)$ in Eq. (11), its bias and variance are

$$\begin{aligned} Bias[A_h(x)]=\left[ f_X'(x)+\frac{1}{2}x^2f_X''(x)\right] \sqrt{h}+o(\sqrt{h}) \end{aligned}$$

(12)

and

$$\begin{aligned} Var[A_h(x)]= {\left\{ \begin{array}{ll} \frac{R^2\left( \frac{1}{\sqrt{h}}-1\right) f_X(x)}{2(x+\sqrt{h}) \sqrt{\pi (1-\sqrt{h})}R\left( \frac{2}{\sqrt{h}}-2\right) nh^{\frac{1}{4}}} +O\left( \frac{h^\frac{1}{4}}{n}\right) , &{} \frac{x}{h}\rightarrow \infty \\ \frac{R^2\left( \frac{1}{\sqrt{h}}-1\right) f_X(x)}{2(c\sqrt{h}+1) \sqrt{\pi (1-\sqrt{h})}R\left( \frac{2}{\sqrt{h}}-2\right) nh^{\frac{3}{4}}} +O\left( \frac{1}{nh^\frac{1}{4}}\right) , &{} \frac{x}{h}\rightarrow c, \end{array}\right. } \end{aligned}$$

(13)

for some positive number c, and

$$\begin{aligned} R(z)=\frac{\sqrt{2\pi }z^{z+\frac{1}{2}}}{e^z\Gamma (z+1)}. \end{aligned}$$

(14)

Remark 2.3

The function R(z) (Brown and Chen 1999) monotonically increases with $\lim _{z\rightarrow \infty }R(z)=1$ and $R(z)<1$, which means $\frac{R^2\left( \frac{1}{h}-1\right) }{R\left( \frac{2}{h}-2\right) }\le 1$. From these facts, we can conclude that $Var[A_h(x)]$ is $O(n^{-1}h^{-1/4})$ when x is in the interior, and it is $O(n^{-1}h^{-3/4})$ when x is near the boundary. Both of these rates of convergence are faster than the rates of the variance of Chen’s gamma kernel estimator for both cases, respectively. Furthermore, instead of $x^{-1/2}$, $Var[A_h(x)]$ depends on $(x+\sqrt{h})^{-1}$, which means the value of the variance will not speed up to infinity when x approaches 0.

Even though we have succeeded in reducing the order of the variance, we now encounter a larger bias order. To avoid this problem, we use geometric extrapolation to change the order of bias back to h.

Theorem 2.4

Let $A_h(x)$ be the function in Eq. (11). Assuming A1 and A2, if we define $J_h(x)=E[A_h(x)]$, then

$$\begin{aligned}{}[J_h(x)]^2[J_{4h}(x)]^{-1}=f_X(x)+O(h). \end{aligned}$$

(15)

Remark 2.5

The function $J_{4h}(x)$ is the expectation of the function in Eq. (11) with 4h as the bandwidth. Furthermore, the term after $f_X(x)$ in Eq. (15) is in the order h, which is the same as the order of bias for Chen’s gamma kernel density estimator. This theorem will lead us to the idea to modify $A_h(x)$. We present the explicit asymptotic formula of O(h) in the appendices.

Theorem 2.4 gives us the idea to modify $A_h(x)$ and to define our new estimator. Hence, we propose

$$\begin{aligned} {\widetilde{f}}_X(x)=[A_h(x)]^2[A_{4h}(x)]^{-1} \end{aligned}$$

(16)

as the modified gamma kernel density estimator, our proposed method. This idea is actually straightforward. It uses the fact that the expectation of the operation of two statistics is asymptotically equal (in probability) to the operation of the expectation of each statistic. Though we do not use any concept of convergence in probability in our proofs, the idea is still applicable when using Taylor expansion.

For the bias of our proposed estimator, we have the following theorem.

Theorem 2.6

Assuming A1 and A2, the bias of the modified gamma kernel density estimator is

$$\begin{aligned} Bias[{\widetilde{f}}_X(x)]=-2\left[ b(x)-\frac{a(x)}{2f_X(x)}\right] h +o(h)+O\left( \frac{1}{nh^{\frac{1}{4}}}\right) , \end{aligned}$$

(17)

where

$$\begin{aligned} a(x)= & {} f_X'(x)+\frac{1}{2}x^2f_X''(x), \end{aligned}$$

(18)

$$\begin{aligned} b(x)= & {} \left( x+\frac{1}{2}\right) f_X''(x)+x^2\left( \frac{x}{3} +\frac{1}{2}\right) f_X'''(x). \end{aligned}$$

(19)

As expected, the bias’ leading term is actually the same as the explicit form of O(h) in Theorem 2.4 (see appendices). Its order of convergence changed back to h, the same as the bias of Chen’s method. This is quite the accomplishment because if we can keep the order of the variance the same as $Var[A_h(x)]$, we can then conclude that the MSE of our modified gamma kernel density estimator is smaller than the MSE of Chen’s gamma kernel estimator. However, before jumping into the calculation of variance, we need the following theorem.

Theorem 2.7

Assuming A1 and A2, for the function in Eq. (11) with bandwidth h, $A_h(x)$, and with bandwidth 4h, $A_{4h}(x)$, the covariance of them is equal to

$$\begin{aligned} Cov[A_h(x),A_{4h}(x)]= & {} \frac{R\left( \frac{1}{\sqrt{h}}-1\right) R \left( \frac{1}{2\sqrt{h}}-1\right) }{2\sqrt{\pi }R\left( \frac{3}{2\sqrt{h}} -2\right) (3x+5\sqrt{h})}\frac{\left( \frac{3}{2}-2\sqrt{h}\right) ^{\frac{3}{2\sqrt{h}} -\frac{3}{2}}}{(2-2\sqrt{h})^{\frac{1}{\sqrt{h}}-\frac{1}{2}}(1 -2\sqrt{h})^{\frac{1}{2\sqrt{h}}-\frac{1}{2}}}\\&\times \left( \frac{x+\sqrt{h}}{3x+5\sqrt{h}}\right) ^{\frac{1}{2 \sqrt{h}}-1}\left( \frac{2x+4\sqrt{h}}{3x+5\sqrt{h}}\right) ^{\frac{1}{\sqrt{h}} -1}\frac{f_X(x)}{nh^{\frac{1}{4}}}+O\left( \frac{h^\frac{1}{4}}{n}\right) , \end{aligned}$$

when $xh^{-1}\rightarrow \infty$, and

$$\begin{aligned} Cov[A_h(x),A_{4h}(x)]=\frac{R\left( \frac{1}{\sqrt{h}}-1\right) R \left( \frac{1}{2\sqrt{h}}-1\right) }{2\sqrt{\pi }R\left( \frac{3}{2\sqrt{h}} -2\right) (3c\sqrt{h}+5)}\frac{\left( \frac{3}{2}-2\sqrt{h}\right) ^{\frac{3}{2 \sqrt{h}}-\frac{3}{2}}}{(2-2\sqrt{h})^{\frac{1}{\sqrt{h}} -\frac{1}{2}}(1-2\sqrt{h})^{\frac{1}{2\sqrt{h}}-\frac{1}{2}}}\\ \times \left( \frac{c\sqrt{h}+1}{3c\sqrt{h}+5}\right) ^{\frac{1}{2\sqrt{h}}-1} \left( \frac{2c\sqrt{h}+4}{3c\sqrt{h}+5}\right) ^{\frac{1}{\sqrt{h}}-1} \frac{f_X(x)}{nh^{\frac{3}{4}}}+O\left( \frac{1}{nh^\frac{1}{4}}\right) , \end{aligned}$$

when $xh^{-1}\rightarrow c>0$.

Theorem 2.8

Assuming A1 and A2, the variance of the modified gamma kernel density estimator is

$$\begin{aligned} Var[{\widetilde{f}}_X(x)]=4Var[A_h(x)]+Var[A_{4h}(x)]-4Cov[A_h(x),A_{4h}(x)] +o\left( \frac{1}{nh^{\frac{1}{4}}}\right) ,\nonumber \\ \end{aligned}$$

(20)

where its orders of convergence are $O(n^{-1}h^{-1/4})$ in the interior and $O(n^{-1}h^{-3/4})$ in the boundary region.

As a conclusion to Theorems 2.6 and 2.8 , with the identity of MSE, we have

$$\begin{aligned} MSE[{\widetilde{f}}_X(x)]= {\left\{ \begin{array}{ll} O(h^2)+O\left( \frac{1}{nh^{\frac{1}{4}}}\right) , &{} \frac{x}{h}\rightarrow \infty ,\\ O(h^2)+O\left( \frac{1}{nh^{\frac{3}{4}}}\right) , &{} \frac{x}{h}\rightarrow c. \end{array}\right. } \end{aligned}$$

(21)

The theoretical optimum bandwidths are $h=O(n^{-4/9})$ in the interior and $h=O(n^{-4/11})$ in the boundary region. As a result, the optimum orders of convergence are $O(n^{-8/9})$ and $O(n^{-8/11})$, respectively. Both of them are smaller than the optimum orders of Chen’s estimator, which are $O(n^{-4/5})$ in the interior and $O(n^{-2/3})$ in the boundary region. Furthermore, since the MISE is just the integration of MSE, it is clear that the orders of convergence of the MISE are the same as of the MSE.

Calculating the explicit formula of $MISE({\widetilde{f}}_X)$ is nearly impossible because of the complexity of the formulas of $Bias[{\widetilde{f}}_X(x)]$ and $Var[{\widetilde{f}}_X(x)]$. However, there is one thing we would like to discuss regarding this matter. Using a similar argument stated by Chen (2000), the boundary region part of $Var[{\widetilde{f}}_X(x)]$ is negligible while integrating the variance. Thus, instead of computing $\int _{boundary}Var[{\widetilde{f}}_X(x)]+\int _{interior}Var[{\widetilde{f}}_X(x)]$, it is sufficient to just calculate $\int _0^\infty Var[{\widetilde{f}}_X(x)]\mathrm {d}x$ using the formula of the variance in the interior. With that, computing

$$\begin{aligned} MISE({\widetilde{f}}_X)=\int _0^\infty Bias^2[{\widetilde{f}}_X(x)]\mathrm {d}x+\int _0^\infty Var[{\widetilde{f}}_X(x)]\mathrm {d}x \end{aligned}$$

can be approximated by using numerical methods (assuming $f_X$ is known).

3 Simulation study

In this section, we provide the results of a simulation study we did to show the performances of our proposed method and compare them with other estimators’ results. The measures of error we use in this article are the MISE, the MSE, bias, and variance. Since we are working under assumptions A1, A2, and A3, the MISE of our proposed estimator is finite. We calculated the average integrated squared error (AISE), the average squared error (ASE), simulated bias, and simulated variance, with a sample size of $n=50$ and 10000 repetitions for each case.

We compared four gamma kernel density estimators: Chen’s gamma kernel density estimator ${\widehat{f}}_C(x)$ in Chen (2000), two nonnegative bias-reduced Chen’s gamma estimators ${\widehat{f}}_{KI1}(x)$ and ${\widehat{f}}_{KI2}(x)$ (Igarashi and Kakizawa 2015, Eq. 10 and 11), and our modified gamma kernel density estimator ${\widetilde{f}}_X(x)$. We generated several distributions for this study; they are exponential distribution exp(1 / 2), gamma distribution Gamma(2, 3), log-normal distribution log.N(0, 1), inverse Gaussian distribution IG(1, 2), Weibull distribution Weibull(3, 2), and absolute normal distribution abs.N(0, 1). The least squares cross-validation technique was used to determine the value of the bandwidths.

Table 1 Comparison of the average integrated squared error ($\times 10^5$)

Table 2 Comparison of the average squared error ($\times 10^5$) when $x=0.01$

Table 3 Comparison of the bias ($\times 10^4$) when $x=0.01$

Table 4 Comparison of the variance ($\times 10^5$) when $x=0.01$

Fig. 1

Comparison of point-wise bias, variance, and ASE of ${\widetilde{f}}_X(x)$, ${\widehat{f}}_C(x)$, ${\widehat{f}}_{KI1}(x)$, and ${\widehat{f}}_{KI2}(x)$ for estimating density of exp(1 / 2) with sample size $n=150$

Table 1 compares AISEs, representing the general measure of error. As we can see, the proposed method outperformed the other estimators by giving us the smallest errors (numbers in bold). Since one of our main concerns is eliminating the boundary bias problem, it is necessary to take our attention to the values of the measures of error in the boundary region. Tables 2, 3, and 4 show the ASE, bias, and variance of those four estimators when $x=0.01$. Once again, our estimator had the best results (bold numbers). Though the differences among the values of bias were relatively not big (Table 3), from Table 4, we can witness how our variance reduction has an effect.

Fig. 2

Comparison of the point-wise bias, variance, and ASE of ${\widetilde{f}}_X(x)$, ${\widehat{f}}_C(x)$, ${\widehat{f}}_{KI1}(x)$, and ${\widehat{f}}_{KI2}(x)$ for estimating density of Gamma(2, 3) with sample size $n=150$

Fig. 3

Comparison of the point-wise bias, variance, and ASE of ${\widetilde{f}}_X(x)$, ${\widehat{f}}_C(x)$, ${\widehat{f}}_{KI1}(x)$, and ${\widehat{f}}_{KI2}(x)$ for estimating density of abs.N(0, 1) with sample size $n=150$

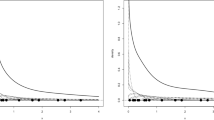
As further illustrations, we also provide graphs of point-wise ASE, bias, squared bias, and variance to compare our estimator’s performances with those of the others. We generated exponential, gamma, and absolute normal distributions 1000 times to produce Figs. 1, 2, and 3 .

In some cases, we found that the bias value of our proposed estimator was away from 0 more than the other estimators (e.g., Fig. 1a around $x=1$, Fig. 2a around $x=4$, and Fig. 3a around $x=0.2$). Though this could reflect poorly on the proposed estimator, from the variance parts (Figs. 1b, 2b, and 3b), we see that our estimator never failed to give the smallest value of variance, confirming that we succeeded in reducing variance with our method. Moreover, the result of the variance reduction is the reduction of point-wise ASE itself, shown in Figs. 1d, 2d, and 3d. One may take note of Fig. 2d when $x\in [1,4]$ because the estimators of Igarashi and Kakizawa (2015) slightly outperformed the proposed method. However, as x got larger, $ASE[{\widehat{f}}_{KI1}(x)]$ and $ASE[{\widehat{f}}_{KI2}(x)]$ failed to get closer to 0 (they will when x is large enough), while $ASE[{\widetilde{f}}_X(x)]$ approached 0 immediately.

4 Conclusion

We proposed a new estimator for the density function of nonnegative data. First, we defined a function as a “pre-estimator” by choosing suitable parameters to reduce the order of variance and then using geometric extrapolation to reduce the order of convergence of the bias from $O(\sqrt{h})$ to O(h). As a result, the MISE of the proposed method is smaller than Chen’s gamma kernel estimator. Moreover, the results of a simulation study revealed the superior performances of our proposed method. Establishing new estimators using this kernel for other functions such as the distribution function or the hazard rate function would be a promising study to consider.

Appendices

Proof of Theorem 2.2

First, by usual reasoning of i.i.d. random variables, we have

$$\begin{aligned} E[A_h(x)]=\int _{0}^\infty \frac{w^{\frac{1}{\sqrt{h}}-1}e^{-\frac{w}{x \sqrt{h}+h}}}{\Gamma \left( \frac{1}{\sqrt{h}}\right) (x\sqrt{h}+h)^\frac{1}{ \sqrt{h}}}f_X(w)\mathrm {d}w. \end{aligned}$$

If we define a random variable $W\sim Gamma(h^{-1/2},x\sqrt{h}+h)$ with mean

$$\begin{aligned} \mu _W=h^{-1/2}(x\sqrt{h}+h), \end{aligned}$$

$Var(W)=h^{-1/2}(x\sqrt{h}+h)^2$, and $E[(W-\mu _W)^3]=2h^{-1/2}(x\sqrt{h}+h)^3$, we can see the integral as an expectation of $f_X(W)$, and we are then able to use Taylor expansion twice, first around $\mu _W$, and next around x. This results in

$$\begin{aligned} E[f_X(W)]= & {} E\left[ f_X(\mu _W)+f_X'(\mu _W)(W-\mu _W) +\frac{f_X''(\mu _W)}{2}(W-\mu _W)^2+...\right] \\= & {} f_X(x+\sqrt{h})+\frac{1}{2}f_X''(x+\sqrt{h})\frac{1}{\sqrt{h}}(x\sqrt{h}+h)^2+...\\= & {} f_X(x)+\left[ f_X'(x)+\frac{1}{2}x^2f_X''(x)\right] \sqrt{h}+o(\sqrt{h}). \end{aligned}$$

Hence, we have

$$\begin{aligned} Bias[A_h(x)]=\left[ f_X'(x)+\frac{1}{2}x^2f_X''(x)\right] \sqrt{h}+o(\sqrt{h}), \end{aligned}$$

which is in the order of $\sqrt{h}$.

Next, we derive the formula of the variance, which is

$$\begin{aligned} Var[A_h(x)]=n^{-1}E[K^2(X_1;x,h)]+O(n^{-1}). \end{aligned}$$

First, we take a look at the expectation part,

$$\begin{aligned} E[K^2(X_1;x,h)]= & {} \int _{0}^\infty \frac{v^{\frac{2}{\sqrt{h}}-2} e^{-\frac{2v}{x\sqrt{h}+h}}}{\Gamma ^2\left( \frac{1}{\sqrt{h}}\right) (x\sqrt{h}+h)^\frac{2}{\sqrt{h}}}f_X(v)\mathrm {d}v\\= & {} \frac{\Gamma \left( \frac{2}{\sqrt{h}}-1\right) \left( \frac{x\sqrt{h} +h}{2}\right) ^{\frac{2}{\sqrt{h}}-1}}{\Gamma ^2\left( \frac{1}{\sqrt{h}}\right) (x\sqrt{h}+h)^\frac{2}{\sqrt{h}}}\int _{0}^\infty \frac{v^{\left( \frac{2}{\sqrt{h}} -1\right) -1}e^{-\frac{2v}{x\sqrt{h}+h}}}{\Gamma \left( \frac{2}{\sqrt{h}}-1\right) \left( \frac{x\sqrt{h}+h}{2}\right) ^{\frac{2}{\sqrt{h}}-1}}f_X(v)\mathrm {d}v\\= & {} B(x,h)E[f_X(V)], \end{aligned}$$

where V is a $Gamma(2h^{-1/2}-1,(x\sqrt{h}+h)/2)$ random variable, B(x, h) is a factor outside the integral, and the integral itself can be considered as $E[f_X(V)]$. Similar as before, the random variable V has mean $\mu _V=(2h^{-1/2}-1)(x\sqrt{h}+h/2)$ and

$$\begin{aligned} Var(V)=(2h^{-1/2}-1)(x\sqrt{h}+h)^2/4. \end{aligned}$$

In the same fashion as in $E[f_X(W)]$ before, we have

$$\begin{aligned} E[f_X(V)]= & {} f_X\left( x+\sqrt{h}-\frac{x\sqrt{h}+h}{2}\right) +\frac{1}{2}f_X''\left( x+\sqrt{h}-\frac{x\sqrt{h}+h}{2}\right) \\&\; \; \; \times \left( \frac{2}{\sqrt{h}}-1\right) \left( \frac{x\sqrt{h}+h}{2}\right) ^2+...\\= & {} f_X(x)+O(\sqrt{h}). \end{aligned}$$

Now, let $R(z)=\frac{\sqrt{2\pi }z^{z+\frac{1}{2}}}{e^z\Gamma (z+1)}$; then, B(x, h) can be rewritten to become

$$\begin{aligned} B(x,h)= & {} \frac{\sqrt{2\pi }\left( \frac{2}{\sqrt{h}}-2\right) ^{\frac{2}{\sqrt{h}}-\frac{3}{2}}}{e^{\frac{2}{\sqrt{h}}-2}R\left( \frac{2}{\sqrt{h}}-2\right) }\frac{e^{\frac{2}{\sqrt{h}}-2}R^2\left( \frac{1}{\sqrt{h}}-1\right) }{2\pi \left( \frac{1}{\sqrt{h}}-1\right) ^{\frac{2}{\sqrt{h}}-1}} \frac{1}{2^{\frac{2}{\sqrt{h}}-1}(x\sqrt{h}+h)}\\= & {} \frac{R^2\left( \frac{1}{\sqrt{h}}-1\right) }{2(x+\sqrt{h}) \sqrt{\pi (1-\sqrt{h})}R\left( \frac{2}{\sqrt{h}}-2\right) h^{\frac{1}{4}}}. \end{aligned}$$

Thus, we obtain Eq. 13, and the proof is completed.

Proof of Theorem 2.4

We have already expanded $J_h(x)$ until the $\sqrt{h}$ term. Now, extending it until the h term results in

$$\begin{aligned} J_h(x)= & {} f_X(x)+\sqrt{h}f_X'(x)+o(\sqrt{h})+\frac{1}{2}(x^2\sqrt{h}+2xh+h\sqrt{h})\\&\; \; \; \times [f_X''(x)+\sqrt{h}f_X'''(x)+o(\sqrt{h})]+...\\= & {} f_X(x)\bigg [1+\left\{ f_X'(x)+\frac{1}{2}x^2f_X''(x)\right\} \frac{\sqrt{h}}{f_X(x)}\\&\; \; \; +\left\{ \left( x+\frac{1}{2}\right) f_X''(x)+x^2\left( \frac{x}{3} +\frac{1}{2}\right) f_X'''(x)\right\} \frac{h}{f_X(x)}+o(h)\bigg ]\\= & {} f_X(x)\left[ 1+\frac{a(x)}{f_X(x)}\sqrt{h}+\frac{b(x)}{f_X(x)}h+o(h)\right] , \end{aligned}$$

where $a(x)=f_X'(x)+\frac{1}{2}x^2f_X''(x)$, and $b(x)=\left( x+\frac{1}{2}\right) f_X''(x)+x^2\left( \frac{x}{3}+\frac{1}{2} \right) f_X'''(x)$. By taking the natural logarithm and using its expansion, we have

$$\begin{aligned} \log J_h(x)= & {} \log f_X(x)+\sum _{k=1}^{\infty }\frac{(-1)^{k-1}}{k} \left[ \frac{a(x)}{f_X(x)}\sqrt{h}+\frac{b(x)}{f_X(x)}h+o(h)\right] ^k\\= & {} \log f_X(x)+\frac{a(x)}{f_X(x)}\sqrt{h}+\frac{b(x)}{f_X(x)}h+o(h) -\frac{1}{2}\left[ \frac{a(x)}{f_X(x)}\sqrt{h}+\frac{b(x)}{f_X(x)}h+o(h)\right] ^2\\&\; \; \; +\frac{1}{3}\left[ \frac{a(x)}{f_X(x)}\sqrt{h}+\frac{b(x)}{f_X(x)}h+o(h)\right] ^3-...\\= & {} \log f_X(x)+\frac{a(x)}{f_X(x)}\sqrt{h}+\left[ b(x)-\frac{a^2(x)}{2f_X(x)} \right] \frac{h}{f_X(x)}+o(h). \end{aligned}$$

Next, if we define $J_{4h}(x)=E[A_{4h}(x)]$ (using quadrupled bandwidth), i.e.,

$$\begin{aligned} \ln J_{4h}(x)=\ln f_X(x)+\frac{2a(x)}{f_X(x)}\sqrt{h}+\frac{4}{f_X(x)}\left[ b(x) -\frac{a^2(x)}{2f_X(x)}\right] h+o(h), \end{aligned}$$

we can set up conditions to eliminate the term $\sqrt{h}$ while keeping the term $\ln f_X(x)$. Now, since $\ln [J_h(x)]^{t_1}[J_{4h}(x)]^{t_2}$ equals

$$\begin{aligned} (t_1+t_2)\ln f_X(x)+(t_1+2t_2)\frac{a(x)}{f_X(x)}\sqrt{h}+(t_1+4t_2)\left[ b(x) -\frac{a^2(x)}{2f_X(x)}\right] \frac{h}{f_X(x)}+o(h), \end{aligned}$$

the conditions we need are $t_1+t_2=1$ and $t_1+2t_2=0$. It is obvious that the solution is $t_1=2$ and $t_2=-1$, and we get

$$\begin{aligned} \ln [J_h(x)]^2[J_{4h}(x)]^{-1}=\ln f_X(x)-\frac{2}{f_X(x)}\left[ b(x)-\frac{a^2(x)}{2f_X(x)}\right] h+o(h). \end{aligned}$$

If we take the exponential function and use its expansion, we have

$$\begin{aligned}{}[J_h(x)]^2[J_{4h}(x)]^{-1}= & {} f_X(x)\sum _{k=0}^{\infty }\frac{(-1)^k}{k!} \left[ \frac{2}{f_X(x)}\left\{ b(x)-\frac{a^2(x)}{2f_X(x)}\right\} h+o(h)\right] ^k\\= & {} f_X(x)\left[ 1-\frac{2}{f_X(x)}\left\{ b(x)-\frac{a^2(x)}{2f_X(x)}\right\} h +o(h)\right] \\= & {} f_X(x)-2\left[ b(x)-\frac{a^2(x)}{2f_X(x)}\right] h+o(h)\\= & {} f_X(x)+O(h). \end{aligned}$$

Proof of Theorem 2.6

Because of the definition of $J_h(x)$ and $J_{4h}(x)$, we can rewrite $A_h(x)=J_h(x)+Y$ and $A_{4h}(x)=J_{4h}(x)+Z$, where Y and Z are random variables with E(Y) and E(Z) are both 0, $Var(Y)=Var[A_h(x)]$, and $Var(Z)=Var[A_{4h}(x)]$. Then, by the expansion $(1+p)^q=1+pq+O(p^2)$, we get

$$\begin{aligned} {\widetilde{f}}_X(x)= & {} [J_h(x)]^2[J_{4h}(x)]^{-1}\left[ 1+\frac{Y}{J_h(x)} \right] ^2\left[ 1+\frac{Z}{J_{4h}(x)}\right] ^{-1}\\= & {} [J_h(x)]^2[J_{4h}(x)]^{-1}\left[ 1+\frac{2Y}{J_h(x)} +O\left\{ \frac{Y^2}{J_h^2(x)}\right\} \right] \left[ 1 -\frac{Z}{J_{4h}(x)}+O\left\{ \frac{Z^2}{J_{4h}^2(x)}\right\} \right] \\= & {} [J_h(x)]^2[J_{4h}(x)]^{-1}+\frac{2J_h(x)}{J_{4h}(x)}Y -\left[ \frac{J_h(x)}{J_{4h}(x)}\right] ^2Z+O[(Y+Z)^2]. \end{aligned}$$

Hence,

$$\begin{aligned} E[{\widetilde{f}}_X(x)]= & {} [J_h(x)]^2[J_{4h}(x)]^{-1}+\frac{2J_h(x)}{J_{4h}(x)}E(Y)-\left[ \frac{J_h(x)}{J_{4h}(x)}\right] ^2E(Z)+O[E\{(Y+Z)^2\}]\\= & {} f_X(x)-2\left[ b(x)-\frac{a(x)}{2f_X(x)}\right] h+o(h) +O\left( \frac{1}{nh^{\frac{1}{4}}}\right) , \end{aligned}$$

and its bias is

$$\begin{aligned} Bias[{\widetilde{f}}_X(x)]=-2\left[ b(x)-\frac{a(x)}{2f_X(x)}\right] h +o(h)+O\left( \frac{1}{nh^{\frac{1}{4}}}\right) . \end{aligned}$$

Proof of Theorem 2.7

By usual calculation of i.i.d. random variables, we have

$$\begin{aligned} Cov[A_h(x),A_{4h}(x)]=\frac{1}{n}E[K(X_1;x,h)K(X_1;x,4h)]+O\left( \frac{1}{n}\right) . \end{aligned}$$

Now, for the expectation,

$$\begin{aligned} E[K(X_1;x,h)K(X_1;x,4h)]= & {} \int _{0}^{\infty }\frac{t^{\frac{1}{\sqrt{h}} -1}e^{-\frac{t}{x\sqrt{h}+h}}}{\Gamma \left( \frac{1}{\sqrt{h}}\right) (x\sqrt{h} +h)^\frac{1}{\sqrt{h}}}\frac{t^{\frac{1}{2\sqrt{h}}-1}e^{-\frac{t}{2x\sqrt{h} +4h}}}{\Gamma \left( \frac{1}{2\sqrt{h}}\right) (2x\sqrt{h} +4h)^\frac{1}{2\sqrt{h}}}f_X(t)\mathrm {d}t\\= & {} \frac{\Gamma \left( \frac{3}{2\sqrt{h}}-1\right) \left[ \frac{2\sqrt{h}(x +\sqrt{h})(x+2\sqrt{h})}{3x+5\sqrt{h}}\right] ^{\frac{3}{2\sqrt{h}}-1}}{\Gamma \left( \frac{1}{\sqrt{h}}\right) \Gamma \left( \frac{1}{2\sqrt{h}}\right) (x\sqrt{h}+h)^\frac{1}{\sqrt{h}}(2x\sqrt{h}+4h)^{\frac{1}{2\sqrt{h}}}}\\&\; \; \; \times \int _{0}^\infty \frac{t^{\left( \frac{3}{2\sqrt{h}}-1\right) -1}e^{-t\left[ \frac{3x+5\sqrt{h}}{2\sqrt{h}(x+\sqrt{h})(x+2\sqrt{h})}\right] }}{\Gamma \left( \frac{3}{2\sqrt{h}}-1\right) \left[ \frac{2\sqrt{h}(x+\sqrt{h})(x +2\sqrt{h})}{3x+5\sqrt{h}}\right] ^{\frac{3}{2\sqrt{h}}-1}}f_X(t)\mathrm {d}t\\= & {} C(x,h)E[f_X(T)], \end{aligned}$$

where C(x, h) is the factor outside the integral, and T is a random variable with mean

$$\begin{aligned} \mu _T=\frac{3(x+\sqrt{h})(x+2\sqrt{h})}{3x+5\sqrt{h}}+O(\sqrt{h}) \end{aligned}$$

and variance $Var(T)=O(\sqrt{h})$. Utilizing Taylor expansion results in

$$\begin{aligned} E[f_X(T)]= & {} f_X(x)+\left[ \frac{3(x+\sqrt{h})(x+2\sqrt{h})}{3x+5\sqrt{h}} -x+O(\sqrt{h})\right] f_X'(x)+o(\sqrt{h})\\&\; \; \; +\frac{1}{2}f_X''\left[ \frac{3(x+\sqrt{h})(x+2\sqrt{h})}{3x +5\sqrt{h}}+O(\sqrt{h})\right] O(\sqrt{h})\\= & {} f_X(x)+O(\sqrt{h}). \end{aligned}$$

Using the definition of R(z) as before, we get

$$\begin{aligned} C(x,h)= & {} \frac{[2\sqrt{h}(x+\sqrt{h})(x+2\sqrt{h})]^{\frac{3}{2\sqrt{h}}-1}}{(x\sqrt{h}+h)^\frac{1}{\sqrt{h}}(2x\sqrt{h}+4h)^\frac{1}{2\sqrt{h}}(3x +5\sqrt{h})^{\frac{3}{2\sqrt{h}}-1}}\\&\times \frac{\sqrt{2\pi }\left( \frac{3}{2\sqrt{h}}-2\right) ^{\frac{3}{2\sqrt{h}} -\frac{3}{2}}}{e^{\frac{3}{2\sqrt{h}}-2}R\left( \frac{3}{2\sqrt{h}}-2\right) } \frac{e^{\frac{1}{\sqrt{h}}-1}R\left( \frac{1}{\sqrt{h}}-1\right) }{\sqrt{2\pi } \left( \frac{1}{\sqrt{h}}-1\right) ^{\frac{1}{\sqrt{h}}-\frac{1}{2}}} \frac{e^{\frac{1}{2\sqrt{h}}-1}R\left( \frac{1}{2\sqrt{h}}-1\right) }{\sqrt{2\pi }\left( \frac{1}{2\sqrt{h}}-1\right) ^{\frac{1}{2\sqrt{h}}-\frac{1}{2}}} \\= & {} \frac{R\left( \frac{1}{\sqrt{h}}-1\right) R\left( \frac{1}{2\sqrt{h}}-1\right) }{2h^{\frac{1}{4}}\sqrt{\pi }R\left( \frac{3}{2\sqrt{h}}-2\right) (3x+5\sqrt{h})}\frac{\left( \frac{3}{2}-2\sqrt{h}\right) ^{\frac{3}{2\sqrt{h}} -\frac{3}{2}}}{(2-2\sqrt{h})^{\frac{1}{\sqrt{h}}-\frac{1}{2}}(1 -2\sqrt{h})^{\frac{1}{2\sqrt{h}}-\frac{1}{2}}}\\&\times \left( \frac{x+\sqrt{h}}{3x+5\sqrt{h}}\right) ^{\frac{1}{2\sqrt{h}} -1}\left( \frac{2x+4\sqrt{h}}{3x+5\sqrt{h}}\right) ^{\frac{1}{\sqrt{h}}-1}, \end{aligned}$$

when $x>h$ (for $x\le h$, the calculation is similar). Hence, the covariance term is

$$\begin{aligned} Cov[A_h(x),A_{4h}(x)]=\frac{R\left( \frac{1}{\sqrt{h}}-1\right) R \left( \frac{1}{2\sqrt{h}}-1\right) }{2\sqrt{\pi }R\left( \frac{3}{2\sqrt{h}} -2\right) (3x+5\sqrt{h})}\frac{\left( \frac{3}{2}-2\sqrt{h}\right) ^{\frac{3}{2\sqrt{h}} -\frac{3}{2}}}{(2-2\sqrt{h})^{\frac{1}{\sqrt{h}}-\frac{1}{2}} (1-2\sqrt{h})^{\frac{1}{2\sqrt{h}}-\frac{1}{2}}}\\ \times \left( \frac{x+\sqrt{h}}{3x+5\sqrt{h}}\right) ^{\frac{1}{2\sqrt{h}} -1}\left( \frac{2x+4\sqrt{h}}{3x+5\sqrt{h}}\right) ^{\frac{1}{\sqrt{h}} -1}\frac{f_X(x)}{nh^{\frac{1}{4}}}+O\left( \frac{h^\frac{1}{4}}{n}\right) , \end{aligned}$$

when $xh^{-1}\rightarrow \infty$, and

$$\begin{aligned} Cov[A_h(x),A_{4h}(x)]=\frac{R\left( \frac{1}{\sqrt{h}}-1\right) R \left( \frac{1}{2\sqrt{h}}-1\right) }{2\sqrt{\pi }R\left( \frac{3}{2\sqrt{h}} -2\right) (3c\sqrt{h}+5)}\frac{\left( \frac{3}{2}-2\sqrt{h}\right) ^{\frac{3}{2 \sqrt{h}}-\frac{3}{2}}}{(2-2\sqrt{h})^{\frac{1}{\sqrt{h}}-\frac{1}{2}}(1-2 \sqrt{h})^{\frac{1}{2\sqrt{h}}-\frac{1}{2}}}\\ \times \left( \frac{c\sqrt{h}+1}{3c\sqrt{h}+5}\right) ^{\frac{1}{2\sqrt{h}} -1}\left( \frac{2c\sqrt{h}+4}{3c\sqrt{h}+5}\right) ^{\frac{1}{\sqrt{h}}-1} \frac{f_X(x)}{nh^{\frac{3}{4}}}+O\left( \frac{1}{nh^\frac{1}{4}}\right) , \end{aligned}$$

when $xh^{-1}\rightarrow c>0$.

Proof of Theorem 2.8

It is easy to prove that $[J_h(x)][J_{4h}(x)]^{-1}=1+O(\sqrt{h})$ by using the expansion of $(1+p)^q$. This fact brings us to

$$\begin{aligned} Var[{\widetilde{f}}_X(x)]= & {} Var[2\{1+O(\sqrt{h})\}Y-\{1+O(\sqrt{h})\}^2Z] +Var[O\{(Y+Z)^2\}]\\= & {} Var[2A_h(x)-A_{4h}(x)]+o\left( \frac{1}{nh^{\frac{1}{4}}}\right) \\= & {} 4Var[A_h(x)]+Var[A_{4h}(x)]-4Cov[A_h(x),A_{4h}(x)]+o\left( \frac{1}{nh^{\frac{1}{4}}}\right) . \end{aligned}$$

Last, since the equation above is just a linear combination of two variance formulas, the orders of the variance do not change, which are $n^{-1}h^{-1/4}$ in the interior and $n^{-1}h^{-3/4}$ in the boundary region.