1 Introduction

Switched Reluctance Machine (SRM) is a new type of motor that has attracted much attention in recent years. Due to its low cost, firm and simple structure, and wide speed range, it has broad development prospects [1]. With the continuous development of multi-electric aircraft, there is a need for more built-in starters/generators that can be used in the complex and harsh environments of the aircraft. The excellent characteristics of SRM make it an important alternative. However, due to the non-linear characteristics of the SRM, it still has a lot of problems to be solved urgently in terms of power converter design, motor design, high-performance control, and position senseless technology.

Because SRM relies on position closed-loop to drive, an accurate rotor position is required for effective control. Traditional mechanical position sensors require a large enough area for installation, which increases the volume, cost, and complexity of the motor. The photoelectric position sensor is susceptible to interference from complex conditions such as dust, which causes its accuracy to drop drastically. In this context, the position sensorless control of SRM has become an important direction of SRM research. In [2], a new method to detect the initial rotor position of SRM is presented, which doesn’t need any extra premeasurement. The method of sensorless control of SRM can be classified into the following categories: observer-based methods [3, 4], magnetic characteristics-based methods [5, 6] artificial intelligence-based methods [7, 8], inductance gradient-based methods [9], and back-emf-based estimation [10]. Among these methods, observer-based methods can estimate the rotor position and speed from the known inputs. These kinds of methods are simple and robust, which are very popular in the field of machine control.

The SMO is a simple and intolerant method. There are many research advances for SMO [11]. In [12], a hybrid model is proposed, which employs two-running algorithms of both current-based and flux-based SMO for wide-range operation. In [13], a sliding-mode observer control scheme is used to promote the UPQC’s performance. The scheme considers more model uncertainties such as inductor and phase resistance. In [14], a four-quadrant operation with an SMO-based algorithm is presented. Over time, SMO has become more closely linked to other technologies. In [15], Back-propagation (BP) neural network with a phase-locked loop (PLL) is used in an SMO to estimate the speed and position of permanent magnet synchronous motors (PMSMs). The accuracy is greatly improved. Ningning Ren’s study shows that SMO based on sigmoid function has high precision and avoids chattering under different conditions [16]. The features of both the exponential reaching law (ERL) and the power rate reaching law (PRL) also can be integrated into the design of the SMO to optimize the result of estimation [17]. The flux-model-based SMO is presented in [18], and this model uses magnetizing curves and assumes the monotonically increasing function for flux-linkage. In [19], a flux-model-based SMO is used and flux-excitation-position data is adopted to develop a Fourier expression for flux-linkage. Therefore, the error in the flux measurement might influence the error in rotor position estimation.

Various studies have been carried out to reduce errors in flux estimation for sensorless control of the SRM [20]. An automated winding resistance correction method is used to correct a circuit-based flux-linkage measurement method. Although this can reduce and eliminate errors, it requires additional circuit components [21]. An inductance model based on the SMO is used to reduce the requirement of additional functions for flux-linkage calculation and the model only uses operating signals [22]. To reduce the complexity of the analytical expression, a transformed saturated inductance characteristics-based method is proposed [23]. In [24], an integral flux error correction technique is designed to reduce phase resistance error caused by temperature variation. A third-order phase-licked loop is applied to reduce the effect of SRM terminal measurement noise and numerical measurement residual error caused by a numerical method of flux estimation [25].

This paper presents an accurate sensorless control method based on the calibrated flux-linkage characteristics and the SMO which has more appropriate gains. The contributions of this paper can be concluded as follows.

  1. (1)

    The proposed method only requires the flux-linkage of the SRM at aligned and unaligned rotor positions from the experiment, which takes a low-measurement effort to get the rotor position. The calibration method can improve the accuracy of the flux-linkage characteristics significantly. Meantime, the selection of the SMO parameters also improves the dynamic performance of the estimation.

  2. (2)

    Using better flux-linkage characteristics, can get better current results through the look-up table. The estimation of the speed and position is extremely relevant to the precision of the flux-linkage characteristics. Compared to the FEM simulations, the proposed method is robust to parameter variations and has better accuracy in position and speed estimation.

  3. (3)

    The experiment shows the estimated results of the speed and position. The proposed method demonstrates a high degree of accuracy and dynamic response. In a wide variable speed range, the proposed method can still maintain high accuracy and good tracking performance.

2 Reluctance Calibration Strategy

The reluctance calibration strategy is based on the flux-linkage characteristics obtained by the indirect method and FEM. Using the reluctance calibration strategy can effectively boost the precision of the flux-linkage characteristics. In this section, a reluctance calibration strategy is introduced to calibrate the results from FEM simulation and the indirect method without a rotor clamping device [26].

2.1 Measurement of Flux-Linkage Characteristics

Among all the flux-linkage characteristics, flux characteristics at aligned and unaligned positions are the most important. To obtain the flux-linkage characteristics of SRM, the first step is to measure the flux-linkage at aligned and unaligned positions.

According to [27], an indirect method to measure flux-linkage at aligned positions is presented. The flux-linkage at an unaligned position can be obtained by calculating the unaligned inductance from the dynamic current waveform.

The phase voltage equation of an SRM can be written as

$$u = Ri + L\frac{di}{{dt}} + i\omega \frac{dL}{{d\theta }}$$
(1)

where i is the phase current, L is the phase inductance and ω and θ are the machine rotor angular speed and position, respectively.

The back electromotive (iωdL/dθ) can be eliminated at an unaligned position and low speed. Hence, the inductance at an unaligned position can be deducted as

$$L = \frac{u - Ri}{{di/dt}}$$
(2)

The current change rate can be estimated with the least-squares method (LSM) as

$$\frac{di}{{dt}} = \frac{{\sum\nolimits_{k = 1}^{n} {\left( {t_{{\text{k}}} - \frac{1}{n}\sum\nolimits_{k = 1}^{n} {t_{{\text{k}}} } } \right)\left( {i_{{\text{k}}} - \frac{1}{n}\sum\nolimits_{k = 1}^{n} {i_{{\text{k}}} } } \right)} }}{{\sum\nolimits_{k = 1}^{n} {\left( {t_{{\text{k}}} - \frac{1}{n}\sum\nolimits_{k = 1}^{n} {t_{{\text{k}}} } } \right)^{2} } }}$$
(3)

where tk and ik are the instantaneous time and current, respectively, and n is the number of samples.

Based on the curve-fitting result with the LSM, the flux-linkage trajectory at the unaligned position can be calculated.

2.2 Reluctance Calibration Strategy

According to MEC, the reluctance can be obtained from flux-linkage characteristics, which is given as

$$R = \frac{\theta }{\phi } = \frac{{N^{{2}} I}}{\psi }$$
(4)

where N is the number of turns, ϕ is magnetic flux, and ψ is the phase flux linkage, respectively.

The reluctance of the SRM consists of airgap reluctance and iron core reluctance. The airgap reluctance Rg can be calculated from the airgap inductance Lg as

$$R_{{\text{g}}} = \frac{{N^{{2}} }}{{L_{{\text{g}}} }} = \frac{{l_{{\text{g}}} }}{{\mu_{0} S}}$$
(5)

where lg, μ0, and S are the mean effective length of airgap, the air magnetic permeability, and the cross-sectional area of airgap, respectively.

In Fig. 1, θu is the unaligned position, θa is the aligned position, θ1 is the position where the rotor pole and the stator pole begin to overlap, θ2 is the position where the back edge of the rotor pole and stator pole begin to overlap.

Fig.1
figure 1

Airgap inductance and reluctance with the function of rotor position

Full size image

The air gap inductance is a nonlinear function of rotor position θ. The measured airgap reluctance at unaligned and aligned positions are used to calibrate the reluctance in these two regions.

$$R_{{{\text{g,Cali}}{.}}} (\theta ) = \frac{{R_{{{\text{ug,Mea}}{.}}} }}{{R_{{{\text{ug,Sim}}{.}}} }}R_{{{\text{g,Sim}}{.}}} ,\theta_{{\text{u}}} \le \theta \le \theta_{{1}}$$
(6)
$$R_{{{\text{g,Cali}}{.}}} (\theta ) = \frac{{R_{{{\text{ag,Mea}}{.}}} }}{{R_{{{\text{ag,Sim}}{.}}} }}R_{{{\text{g,Sim}}{.}}} ,\theta_{2} \le \theta \le \theta_{{\text{a}}}$$
(7)

where Rg, Sim., Rg, Mea., and Rg, Cali. are FEM simulated, measured, and calibrated reluctance, respectively. Rug,Mea., Rug,Sim., Rag,Mea. and Rag,Sim. are the corresponding values at θu and θa, respectively.

Iron core reluctance Ri can be calculated as

$$R_{{\text{i}}} = \frac{{l_{{\text{i}}} }}{{\mu_{0} \mu_{{\text{r}}} S}}$$
(8)

where li andμr are average flux paths in the ferromagnetic material and relative permeability of ferromagnetic material, respectively.

At first, μr is assumed to be independent with the rotor position, and it only depends on the phase current, it is calibrated as

$$\mu_{{\text{r,Cali}}} = \frac{{R_{{\text{ai,Sim}}} }}{{R_{{\text{ai,Mea}}} }}\mu_{{\text{r}}}$$
(9)

The simulated iron reluctance can be calibrated

$$R_{{\text{i,Cali}}} (\theta ) = \frac{{\mu_{{\text{r}}} }}{{\mu_{{\text{r,Cali}}} }}R_{{\text{i,Sim}}} (\theta ) = \frac{{R_{{\text{ai,Mea}}} }}{{R_{{\text{ai,Sim}}} }}R_{{\text{i,Sim}}} (\theta )$$
(10)

The total calibrated reluctance is the sum of the calibrated airgap and iron core reluctance, which is shown as

$$R_{{{\text{Cali}}}} = R_{{\text{g,Cali}}} + R{}_{{\text{i,Cali}}}$$
(11)

The final calibrated flux linkage can be calculated by

$$\psi_{{{\text{Cali}}}} = R_{{\text{g,Cali}}} + R_{{\text{i,Cali}}}$$
(12)

3 Sliding-Mode Observer

3.1 1Modeling of SRM

The nonlinear model of SRM can be described by

$$\frac{{d\psi_{{\text{n}}} }}{dx} = v_{{\text{n}}} \left( t \right) - i_{{\text{n}}} \left( t \right)R_{{\text{n}}} ,n = 1,2, \ldots ,N_{{{\text{ph}}}}$$
(13)

where vn and in are the phase voltage and current respectively, Rn is the winding resistance of active phase n, and Nph is the number of phases. ψn is the flux-linkage, which is a nonlinear function of current and position.

The movement equations are presented in (14) and (15).

$$\frac{d\theta \left( t \right)}{{dt}} = \omega \left( t \right)$$
(14)
$$\frac{d\omega \left( t \right)}{{dt}} = \alpha \left( t \right)$$
(15)

where θ and ω are the rotor position and speed, respectively, and α is the angular speed acceleration.

3.2 SMO for SRM

The flux-linkage estimation error en can be defined as

$$e_{{\text{n}}} = \psi_{{\text{n}}} \left( t \right) - \psi ^{\prime}_{\text{n}} \left( t \right),n = 1,2,3$$
(16)

where ψn(t) and ψˈn(t) are measured flux-linkage and estimated flux-linkage, respectively.

Flux-linkage measurements and estimates are obtained by

$$\psi_{{\text{n}}} \left( t \right) = \mathop \int \nolimits_{0}^{t} \left( {v_{{\text{n}}} \left( \varepsilon \right) - i_{{\text{n}}} \left( \varepsilon \right)R_{{\text{n}}} } \right)d\varepsilon$$
(17)
$$\psi ^{\prime}_{{\text{n}}} \left( t \right) = \psi ^{\prime}_{{\text{n}}} \left( {i_{{\text{n}}} \left( t \right),\theta ^{\prime}\left( t \right)} \right)$$
(18)

where vn and in are phase voltage and phase current, respectively, and θˈ(t) is the estimated rotor position.

To realize the closed-position control of SRM, the sliding-mode observer is required to observe and obtain the estimated rotor position and speed of the SRM. The following equations are the design principles of the sliding-mode observer

$$\left\{ {\begin{array}{*{20}l} {\frac{d\theta ^{\prime}}{{dt}} = \omega ^{\prime} + k_{{\uptheta }} {\text{sgn}}\left( {e_{{\uptheta }} } \right)} \hfill \\ {\frac{d\omega ^{\prime}}{{dt}} = - \frac{B}{J}\omega ^{\prime} + \frac{1}{J}\left( {T_{{\text{e}}}^{^{\prime}} - T_{{\text{L}}} } \right) + k_{{\upomega }} {\text{sgn}}\left( {e_{{\upomega }} } \right)} \hfill \\ {T_{{\text{e}}} = \mathop \sum \limits_{j = 1}^{{N_{{{\text{ph}}}} }} \frac{1}{2}\frac{{\partial L_{{\text{ph,j}}} }}{\partial \theta }i_{{\text{ph,j}}}^{2} } \hfill \\ \end{array} } \right.$$
(19)

where sgn() is the sign function, eθ and eω are the angle error function and speed error function, respectively. kθ and kω are SMO gains. ωˈ is the estimated result of speed, B is the coefficient of viscosity, J is the rotary inertia, Te and Tˈe are the electromagnetic torque and the estimated electromagnetic torque, respectively. TL is the load torque, Nph is the phase number, j is the serial number from 1 to Nph, Lph,j is the phase inductance at phase j, and iph,j is the phase current at phase j.

Sliding-mode surface is defined as

$$s_{{\uptheta }} = e_{{\uptheta }} = \theta - \theta ^{\prime}$$
(20)
$$s_{{\upomega }} = e_{{\upomega }} = \omega - \omega ^{\prime}$$
(21)

SMO can be designed by

$$\left\{ {\begin{array}{*{20}l} {\dot{\theta }^{\prime} = \omega ^{\prime} + k_{{\uptheta }} {\text{sgn}}\left( s \right)} \hfill \\ {\omega ^{\prime} = \dot{\alpha }^{\prime}\left( t \right) + k_{{\upomega }} {\text{sgn}}\left( s \right)} \hfill \\ {\dot{\alpha }^{\prime}\left( t \right) = k_{{\upalpha }} {\text{sgn}}\left( s \right)} \hfill \\ \end{array} } \right.$$
(22)

where α is acceleration.

While SMO is working, the actual rotor position and speed in real-time cannot be entered directly into the SMO. The above equations cannot be calculated without the data of rotor position and speed. According to the electromagnetic torque equation, this paper chooses a new error function ef

$$e_{{\text{f}}} = T_{{\text{e}}} - T_{{\text{e}}}^{^{\prime}} = \mathop \sum \limits_{j = 1}^{{N_{{{\text{ph}}}} }} \left( {\frac{1}{2}\frac{{\partial L_{{\text{j}}} }}{\partial \theta }i_{{\text{j}}}^{2} - \frac{1}{2}\frac{{\partial L_{{\text{j}}} }}{\partial \theta ^{\prime}}i_{{\text{j}}}^{^{\prime}2} } \right)$$
(23)

In this equation, can consider \(\frac{{\partial L_{{\text{j}}} }}{\partial \theta } \approx \frac{{\partial L_{{\text{j}}} }}{\partial \theta ^{\prime}}\), and the value of the sign function is determined by the positive and negative of the error function. So (17) can be simplified, which is given as

$$e_{{\text{f}}} = \mathop \sum \limits_{j = 1}^{{N_{{{\text{ph}}}} }} \frac{1}{2}\frac{{\partial L_{{\text{j}}} }}{\partial \theta ^{\prime}}(i_{{\text{j}}}^{2} - i_{{\text{j}}}^{^{\prime}2} )$$
(24)
$$H_{{\text{j}}} \left( \theta \right) = {\text{sin}}\left( {N_{{\text{r}}} \theta - \left( {j - 1} \right) \times \left( {2\pi /N_{{{\text{ph}}}} } \right)} \right)$$
(25)

3.3 Design Gains of SMO

When SMO works, jitter is inevitable. To reduce the impact of jitter, this paper uses the following two methods.

  1. (a)

    The switching surface of SMO is improved. Assuming that the linear region in the switching surface is μ, then (22) can be improved, which is given as

    $$\left\{ {\begin{array}{*{20}l} {\dot{\theta }^{^{\prime}} = \omega^{^{\prime}} + k_{{\uptheta }} {\text{sat}}\left( s \right)} \hfill \\ {\omega^{^{\prime}} = \dot{\alpha }^{^{\prime}} \left( t \right) + k_{{\upomega }} {\text{sat}}\left( s \right)} \hfill \\ {\dot{\alpha }^{^{\prime}} \left( t \right) = k_{{\upalpha }} {\text{sat}}\left( s \right)} \hfill \\ \end{array} } \right.$$
    (26)

where sat() is

$${\text{sat}}\left( s \right) = \left\{ {\begin{array}{*{20}l} {{\text{sgn}}\left( s \right),\left| s \right| > \mu } \hfill \\ {s/\mu ,\left| s \right| \le \mu } \hfill \\ \end{array} } \right.$$
(27)

By adjusting the switching surface, the accuracy and robustness of SMO can be effectively improved.

  1. (b)

    To improve the performance of the SMO, it is necessary to select an appropriate gain during design.

The estimation error of SMO is defined as follows

$$\left\{ {\begin{array}{*{20}c} {e_{{\uptheta }} \left( t \right) = \theta \left( t \right) - \theta ^{\prime}\left( t \right)} \\ {e_{{\upomega }} \left( t \right) = \omega \left( t \right) - \omega ^{\prime}\left( t \right)} \\ {e_{{\upalpha }} \left( t \right) = \alpha \left( t \right) - \alpha ^{\prime}\left( t \right)} \\ \end{array} } \right.$$
(28)

The dynamic process of error can be obtained by differentiation

$$\begin{array}{*{20}c} {\dot{e}_{{\uptheta }} = \dot{\theta } - \dot{\theta }^{\prime} = e_{{\upomega }} - k_{{\uptheta }} {\text{sgn}} \left( s \right)} \\ {\dot{e}_{{\upomega }} = \dot{\omega } - \dot{\omega }^{\prime} = e_{{\upalpha }} - k_{{\upomega }} {\text{sgn}} \left( s \right)} \\ {\dot{e}_{{\upalpha }} = \dot{\alpha } - \dot{\alpha }^{\prime} = \dot{\alpha } - e_{{\upalpha }} {\text{sgn}} \left( s \right)} \\ \end{array}$$
(29)

Based on Lyapunov function

$$V = \frac{{e_{{\uptheta }}^{2} }}{2}$$
(30)

Further derivation can be obtained

$$\dot{V} = e_{{\uptheta }} e_{{\upomega }} - e_{{\uptheta }} k_{{\uptheta }} {\text{sgn}} \left( s \right)$$
(31)

To ensure that the Lyapunov dynamic function is negative at all times, it needs to satisfy

$$k_{{\uptheta }} > \left| {e_{{\upomega }} } \right|$$
(32)
$$k_{{\uptheta }} > \left| {e_{{\upomega }} } \right|_{\max }$$
(33)

In the case that the rotor speed cannot be measured directly, it is necessary to assume a maximum rotor speed error to ensure that the Lyapunov function meets the above conditions at any moment when the SRM is running. Therefore, the following formulas need to be met.

$$\left\{ {\begin{array}{*{20}l} {k_{{\uptheta }} > \left| {e_{{\upomega }} } \right|_{{{\text{max}}}} } \hfill \\ {k_{{\upomega }} \ge k_{{\uptheta }} \frac{{\left| {e_{{\upalpha }} } \right|_{\max } }}{{\left| {e_{{\upomega }} } \right|_{\max } }}} \hfill \\ {k_{{\upalpha }} \ge k_{{\upomega }} \frac{{\left| {\dot{\alpha }} \right|_{\max } }}{{\left| {e_{{\upalpha }} } \right|_{\max } }}} \hfill \\ \end{array} } \right.$$
(34)

Through all the above calculations, this paper gets the minimum gains when designing SMO and the relationship between them. By reasonably setting the maximum speed estimation error, the maximum acceleration estimation error, and the maximum acceleration change rate over time, the minimum gain can be obtained.

4 Simulation Verification

4.1 The Structure of the Control System

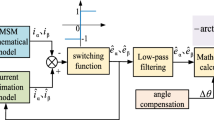
The proposed SMO method to estimate rotor position and speed is applied on a 12/8 three-phase SRM in MATLAB/Simulink environment. Figure 2 shows the structure of the control system based on SMO. In the simulation, the load can be adjusted to control the speed of the SRM (Fig. 3, Table 1).

Fig.2
figure 2

The control structure of SRM is based on SMO

Full size image
Fig.3
figure 3

The simulation model of SRD

Full size image
Table 1 Observer gains
Full size table

4.2 Build the Simulation Model

The main parameters of the prototype are shown in Table 2.

Table 2 The main parameters of the prototype
Full size table

Based on the principles introduced before, the SMO simulation model is built.

To control the SRM in a wide range of speeds, and ensure the rapid response of the motor at different rated speeds. A look-up table in the first integral part is added. The look-up table reflects the difference of the initial value in the integral part at different speed ranges.

4.3 Simulation Results

The simulations are performed at 1000–1500 rpm at 5 Nm to verify the effectiveness and accuracy of the proposed method (Fig. 4). The simulation results are shown in Figs. 5, 6 and 7.

Fig.4
figure 4

Simulation results of the rotor position estimation at 1000 rpm

Full size image
Fig.5
figure 5

Simulation results of the rotor speed estimation

Full size image
Fig.6
figure 6

Simulation results of the rotor speed estimation from 1000 to 1500 rpm

Full size image
Fig.7
figure 7

Experimental setup

Full size image

To prove that the flux-linkage characteristics obtained after the reluctance calibration method are applied in the sliding-mode observer, the estimation accuracy can be significantly improved, this paper also simulates by using the flux-linkage characteristics obtained by FEM (Table 3).

Table3 The position estimation error
Full size table

Figure 4 shows the estimated position and actual position at steady-state and Fig. 5 shows the comparison of the reluctance calibration method and finite element method. Figure 6 shows the comparison of the reluctance calibration method and finite element method when rotor speed from 1000 to 1500 rpm.

Simulation results demonstrate the effectiveness of the SMO method to estimate the position and speed at high-speed operation. The speed errors are calculated and shown in Table 4.

Table 4 The speed errors
Full size table

The estimated error of speed and position is mainly caused by the errors generated when estimating the flux linkage. As shown in Figs. 5 and 6, using the FEM to obtain the flux linkage cannot always get a good result in position and speed estimation. Using calibration method to calibrate the FEM results, can further validate the effectiveness and applicability.

From the error calculation and comparison of the table above, it can be seen that

  1. (a)

    The estimation error of the SMO in the wide speed range is very small and fully conforms to the design requirements, and the flux-linkage characteristics obtained by the reluctance calibration method are more accurate.

  2. (b)

    The estimation error of the slide observer decrease in multiples and the fluctuation decreases significantly.

5 Experimental Verification

A semi-physical simulation development platform consisting of an SRM peripheral hardware platform and a dSPACE system was built. Due to the limitation of the experimental test bench, the experiments are performed when the load torque is set to 2Nm in Figs. 8, 9 and 11. In the case of load change, the torque varies from 2 to 1 Nm in Fig. 10 (Table 5).

Fig.8
figure 8

Experimental results of the rotor position estimation at 1500 rpm

Full size image
Fig.9
figure 9

Experimental results of the rotor speed estimation at 1000 rpm

Full size image
Fig.10
figure 10

Experimental results of the rotor speed estimation at 1000 rpm when torque is changing from 2 to 1 Nm

Full size image
Table 5 The position estimation error
Full size table

The experiment result of rotor position estimation is shown in Fig. 8. The actual position measured by the resolver is recorded for comparison. Figure 9 shows the experimental result of the estimated rotor speed. Figure 10 shows that the estimated rotor speed can track the actual rotor speed perfectly when torque is changing. Figure 11 shows the calibration method can work in a wide speed arrange and has a high dynamic response. When the speed varies from 500 to 1000 rpm, the estimated position and speed can track the actual position and speed precisely. The speed error is between 0.5 and 4%. The SMO is usually performing better in high speed, so the error is large at low speed. However, the proposed method can work in a wide speed range and show good precision and track performance. The reluctance calibration method can calibrate the FEM simulation results and apply them in the experiment. The result shows that this calibration method has certain robustness and precision to the variation of experiment parameters.

Fig.11
figure 11

Experimental results of the rotor speed estimation from 500 to 1000 rpm

Full size image

During the experiment, the motor working conditions under different speeds and load conditions were verified, the motor runs smoothly, and realizes the sensorless control of the motor very well.

The experimental results are different from the previous simulation results, which is mainly due to the vibration, electromagnetic interference, and other interference factors in the experimental process. These factors have a greater impact on the actual operation of the SRM. However, from the overall law of the experiment, it is still consistent with the previous theoretical simulation.

From the experimental results, this paper proves that the rotor position and speed can be precisely estimated with an acceptable error. It demonstrates that the proposed method can be applied for SRM sensorless control.

6 Conclusion

This paper proposes a new sensorless control method for SRM drives based on SMO. A reluctance calibration method is introduced to improve the finite element simulation results. It can effectively obtain the flux linkage characteristics of the SRM on the standard test bench and has a certain degree of robustness to parameter variations. In addition to geometric characteristics, only the rotor positions at aligned and non-aligned positions that are convenient for measurement need to be obtained. Compared to traditional methods, such as the FEM method, the method is simple, fast, and accurate, does not require a special test bench, reduces the cost and complexity, is convenient, and is suitable for practical applications. This paper estimates the current based on the flux linkage and rotor position of SRM. Based on the estimated and actual current, the sliding-mode surface in the SMO design is formed. To ensure the accuracy and stability of the SMO work, this paper completes the SMO design by the calculation and selection of the optimal gain values. Through simulation and experiment, this paper proves that the calibration strategy can be used in the current estimation for the SMO to improve the dynamic response and estimation accuracy.