Multi-objective Optimal Allocation of TCSC for Power Systems with Wind Power Considering Load Randomness

Abstract

Optimum allocation of flexible AC transmission system (FACTS) can improve the power grids performances such as available transmission capacity (ATC) and voltage stability. Optimal allocation of FACTS with multiple optimization objectives for power systems comprise multiple random variables is still a challenging task to be solved. This paper derives a scenario generation method for systems containing multiple random variables first. Then, a thyristor-controlled series capacitor (TCSC) multi-objective optimal allocation model with ATC and voltage stability L index as an objective function is established. By adding the chaos initialization and the variable inertia weight setting, an improved multi-objective particle swarm optimization (MOPSO) algorithm is also proposed to easily solve the established model. Finally, based on the improved IEEE-30 bus system, the non-inferior solutions of multiple system scenarios are compared and analyzed. Simulation results show that the proposed scenario processing method, the TCSC multi-objective optimal allocation model and the improved MOPSO algorithm are effective in solving related problems.

1 Introduction

1.1 Research Motivation

The large-scale operation of new energy facilitates power system transform from a deterministic system into a strongly uncertain one. For power system containing wind farm, the changes and uncertainties of operational situation are mainly determined by the random uncertainty of wind power and load. This new operation mode puts forward new requirement for the available transmission capacity (ATC) between power system regions, and its impact on system voltage stability cannot be ignored. Since the maturity of power grid development is much higher than the development of new energy, it is difficult to solve the transmission bottleneck and voltage stability problems caused by new energy connection through expanding the power grid [1].

In order to improve the interregional available transmission capacity without changing the existing grid structure and ensuring a better voltage stability index (L) simultaneously, this paper seeks to optimize the allocation of flexible AC transmission system (FACTS) for power grids under wind power and load randomness.

1.2 Literature Review

Some literatures have studied the problems related to this issue. For instance, [1] discussed the complexity of grid connection of wind power, and analyzed the relationship between various solutions by delineating three stages for the future power systems to move towards a high penetration level of renewable energy. The basis of research on power systems containing renewable energy is the random and uncertain output of the renewable energy. References [2,3,4,5] proposed methods to obtain renewable energy output scenarios. In [2], a method based on Monte Carlo simulation is proposed to obtain wind power output scenarios using the Weibull distribution probability density function. However, consideration for the correlation of different renewable energy sources has not been considered. Reference [3] generates wind power scenarios based on the Weibull distribution probability density function by Monte Carlo sampling, and reduces the scenarios by backward reduction technology. In [4], a scenario matrix is generated using the heuristic moment matching technique that captures the stochastic moments and correlation between historical wind and photovoltaic power. Reference [5] also uses Monte Carlo sampling method based on the probability density function of wind speed to obtain wind power output scenarios, and then solves the allocation problem of energy storage capacity. Because several random variable scenarios complicate the analysis and calculation, they need to be reduced to typical representative scenarios. References [6,7,8] present different reduction techniques for renewable energy scenarios. Reference [6] proposes a scenario reduction method for wind power based on the combination of the improved k-means clustering and the backward reduction. In [7], the Latin hypercube sampling is used to get initial scenarios, and the k-means clustering algorithm is used to get the typical scenarios. Reference [8] describes the random variable prediction error by approximating the normally distributed probability density to seven segments, then generates the random variable initial scenarios, and uses scenario reduction techniques based on the repetition and low likelihood scenarios cancellation to obtain the typical representative scenarios. Based on the reduced typical representative scenarios, References [9,10,11] defined ATC and L index, presented calculation methods, and established optimization models for them. Using only a single-objective of ATC, Reference [9] proposes a novel probabilistic approach to evaluate ATC incorporating the uncertainties of load, wind power and transmission line outages. Reference [10] proposes an interval optimization-based algorithm for ATC calculation. However, it is still an optimization in a single-goal framework. Reference [11] defines the voltage stability L index, and establishes a multi-objective reactive power optimization scheduling model with the L index and active power network loss as targets. It is difficult to solve complex mixed integer and real number nonlinear optimization model by traditional mathematical methods. Modern intelligent optimization algorithms show great advantages in this regard. For example, References [12,13,14,15] have solved multiple complex optimization problems using particle swarm or improved particle swarm algorithm. In [12], a multi-objective chaos particle swarm optimization (PSO) cooperated with an interior point method is used to solve the economic-environmental dispatching with node voltage deviation as the third objective function. Reference [13] improves the particle swarm algorithm for coordinated and optimized scheduling of cross-region interconnected systems. Reference [14] proposes a modified hybrid PSO and Gravitational Search Algorithm (PSOGSA) with chaotic maps approach to solve the optimal power flow problem when including wind power and FACTS. Reference [15] solves the problem of power grid voltage imbalance compensation by single target PSO algorithm.

Overall, several related studies have been published in the literatures. However, there are still some problems to be solved. For example: other uncertainties and random factors such as load dynamics are seldomly considered simultaneously with the existence of wind power. Much attention was given to optimize a single objective function, or transform multiple objectives into a single one, with few attempts to solve multi-objective optimization by considering the correlation and restriction of multiple objective parameters. While much research can be found on extreme scenarios, few analyses have been conducted on scenarios which the system is most likely to face.

1.3 Contributions and Organization of this Paper

This section mainly describes the contributions and the structure of the paper.

The contributions of this paper are summaried as follows:

• 1. A scenario generation method based on the combination of the probability distribution of random variables, k-means clustering and Monte Carlo sampling is derived. It helps to solve the scenario generation problem of power systems with multiple random variables.

• 2. A TCSC multi-objective optimal allocation model is established with ATC and L index as objectives. It provides a new idea of improving ATC without changing the power grid structure and maintaining voltage stability.

• 3. An improved multi-objective particle swarm optimization algorithm (IMOPSO) algorithm is derived by adding chaos initialization and inertial weight coefficient linear decreasing setting. This helps to better solve the nonlinear multi-objective optimization problem.

Moreover, through experiments, the validity of these contributions have been verified.

The remaining sections of this paper are organized as follows: In Sect. 2, the method for dividing system scenarios is presented. In Sect. 3, a multi-objective optimal allocation model of TCSC is established with ATC and L index as objectives. In Sect. 4, an improved MOPSO algorithm and design solution flow are explained. In Sect. 5, the model is solved based on a modified IEEE-30 bus power system, and the optimization results are analyzed to verify the proposed methods. Key conclusions are drawn in Sect. 6.

2 System scenario Generation Method

In order to get the typical system scenarios, random factors in power systems as presented in Sects. 2.1 and 2.2 must be considered.

2.1 Wind Power randomness Model, Generation and Reduction Methods of Wind Power Scenarios

• (1) Wind speed model

Wind speed v conforms to two-parameter Weibull distribution [16], and its probability density function is given by (1).

$$f(v) = \frac{k}{c}\left( \frac{v}{c} \right)^{k - 1} \exp \left[ { - \left( \frac{v}{c} \right)^{k} } \right]$$

(1)

where k is the shape coefficient that is in a typical range 1.5–2.5. c is the scale coefficient, which represents the average wind speed, and its typical range is 5–10 m/s. v is the wind speed in m/s.

• (2) Model of wind turbine output

The output power of a single wind turbine is usually estimated by its power-wind speed characteristics [17]. The relationship between the output power P(v) and wind speed v is expressed as (2).

$$P(v) = \left\{ {\begin{array}{*{20}l} {0,0 \le v < v_{{{\text{ci}}}} ,v \ge v_{{{\text{co}}}} } \hfill \\ {P_{{\text{R}}} \frac{{v - v_{{{\text{ci}}}} }}{{v_{{\text{R}}} - v_{{{\text{ci}}}} }},v_{{{\text{ci}}}} \le v < v_{{\text{R}}} } \hfill \\ {P_{{\text{R}}} ,v_{{\text{R}}} \le v < v_{{{\text{co}}}} } \hfill \\ \end{array} } \right.$$

(2)

where P_R is the rated output power of a single wind turbine. v_ci, v_R and v_co are the cut-in, rated and cut-out wind speeds of the turbine, respectively. When wind speed v is higher than v_ci , the wind turbine starts operation. When v is greater than v_R, wind turbine maintains rated power output. When v is lower than v_ci or higher than v_co, wind turbine is down and is disconnected from the grid.

• (3) Generation and reduction methods of wind power scenarios.

Based on (1), annual wind speed is generated in hours by the Weibull random number generator in matlab. Then the generation method of annual duration load curve is referred to generate annual duration wind speed curve. Combined with (2), wind power is divided into zero output scenario, under-output scenario and rated output scenario. The under-output scenario can be further divided into multiple small scenarios. That is, first the annual duration wind speed curve is divided into four scenarios: [v_co, + ∞), [0, v_ci), [v_ci, v_R) and [v_R, v_co). Then, k-means clustering is conducted for the middle under-output part [v_ci, v_R) to obtain multiple small scenarios [18]. Combining all wind speed scenarios of the first step and the second step we can obtain the total annual step wind speed curve. Each level represents a wind power scenario. The occurrence probability of variable can be replaced by its occurrence frequency [6], so the ratio of the covering time length of each level to the total time can be approximated as the probability of the corresponding wind power scenario.

2.2 Load Randomness Model, Generation and Reduction Methods of Load Scenarios

• (1) Load model

The uncertainty of load D is modeled by normal probability density function with mean μ_D and standard deviation σ_D [19]. The load probability density function is given by (3).

$$f(D) = \frac{1}{{\sqrt {2\pi } \sigma_{D} }}exp\left[ { - \frac{{(D - \mu_{D} )^{2} }}{{2\sigma_{D}^{{2}} }}} \right]$$

(3)

• (2) Generation and reduction of load scenarios

According to (3), the annual load curve is generated in hours by the normally distributed random number generator in matlab. Then the annual duration load curve is generated according to the annual load curve, and the annual duration load curves are clustered by k-means clustering method to obtain the annual hierarchical load curve [7,8,9, 20,21,22]. The value of each cluster center represents a load scenario. Using the frequency of variable occurrence to approximately replace probability of occurrence [6], the ratio of time covered by each load scenario to the total hours is the occurrence probability of the corresponding load scenario.

2.3 Generation Methods of System Scenarios

The power system considered in this paper contains two random variables: wind power and load, so the system scenarios are determined by these two variables. System scenarios are obtained by Monte Carlo sampling [3]. It contains three steps: The first step is to form a system scenario by sampling wind power and load scenarios. The second step is to repeat the sampling multiple times to generate multiple system scenarios. Since the system scenarios obtained from step 2 may have repetition, the third step is to count the total number of every system scenario occurrence and calculate its occurrence probability.

For the sampling of wind power and load scenarios in step 1, suppose that wind power has three scenarios (the probabilities are P₁, P₂ and P₃), and load has four scenarios (the probabilities are P₁′, P₂′, P₃′ and P₄′). The scenario divisions, probabilities and cumulative probabilities can be illustrated by Fig. 1. Generating two uniformly distributed random numbers r₁ and r₂ between 0 and 1. Then comparing r₁ with the cumulative probability of wind power scenarios to judge which interval r₁ falls in. Meanwhile, comparing r₂ with the cumulative probability of load scenarios to judge which interval r₂ falls in. If P₁ < r₁ ≤ P₁ + P₂ and P₁^’ + P₂′ < r₂ ≤ P₁′ + P₂′ + P₃^’, it means r₁ falls in the second interval and r₂ falls in the third interval. For this sampling, wind power is in the second wind power scenario w₂ and load is in the third load scenario d₃. The system scenario obtained from this sampling is a system scenario composed of w₂ and d₃.

Fig. 1

Sampling component status based on component cumulative probability

Then, the sampling is repeated N times in step 2 and the occurrences of all system scenarios are counted in step 3. If system scenario s₁, a system composed of wind power scenario w₂ and load scenario d₃, appears M times, the frequency of occurrence of this system scenario is M/N. When the sampling number N is large enough, the probability of occurrence of the system scenario can be approximately replaced by frequency [6].

3 TCSC Multi-objective Optimization Allocation Model

This section mainly describes the method for building a multi-objective optimization model through three aspects: objective functions, constraints and the constraint processing technique.

Take the minimization of multiple objectives as an example to illustrate the model of multi-objective optimization, as given by (4).

$$\left\{ {\begin{array}{*{20}l} {F(x) = \min f_{\alpha } (x),\alpha = 1,2, \ldots } \hfill \\ {s.t.\left\{ {\begin{array}{*{20}c} {g_{\beta } (x) \le 0,\beta = 1,2, \ldots } \\ {h_{\gamma } (x) = 0,\gamma = 1,2, \ldots } \\ \end{array} } \right.} \hfill \\ \end{array} } \right.$$

(4)

where F(x) is objective function, the decision variable x is (x₁, x₂, …, x_n), f_α(x) is the αth objective function, g_β(x) is the βth inequality constraint, h_γ(x) is the γth equality constraint. The solving process of multi-objective optimization algorithm is to obtain the optimal pareto front (set of nondominated solutions) for the above mathematical model.

3.1 Objective Functions

In this paper, a multi-objective optimization model is established with inter-regional available transmission capacity (ATC) and static voltage stability L index as objectives.

• (1) Inter-regional available transmission capacity

As shown in Fig. 2, the system has three areas A, B and C with each region indicated by generator and load. If ATC between areas A and C is to be calculated, keeping the generator output and load of area B unchanged, keeping the generator output of area C and load of area A unchanged, increasing generator output of area A and load of area C until reaching the line transmission capacity limit T_AC, then the sum of increasing generator output of zone A is the ATC from area A to area C [20], as given by (5).

$$ATC = \sum {(\lambda_{i} P_{Gi} )} ,i \in N_{GS}$$

(5)

where P_Gi, λ_i and N_GS are the ground state active output of the generator connected to node i, the increase proportion of P_Gi and the set of nodes connected by generators in the sending region, respectively.

Fig. 2

Schematic of inter-regional available transmission capacity

• (2) Static voltage stability index

There are many indicators to evaluate the stability of static voltage. The static voltage stability L index is based on solutions of power flow, and it represents the distance between actual state and the limit stability state of the system [21]. Because the L index has a clear physical concept and can be calculated quickly, it is widely used in the online static voltage stability evaluation [22, 23].

First, divide all nodes into set of generator nodes and set of load nodes, then establish a network matrix as in (6).

$$\left[ {\begin{array}{*{20}c} {{\mathbf{I}}_{G} } \\ {{\mathbf{I}}_{D} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\mathbf{Y}}_{GG} } & {{\mathbf{Y}}_{GD} } \\ {{\mathbf{Y}}_{DG} } & {{\mathbf{Y}}_{DD} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\mathbf{U}}_{G} } \\ {{\mathbf{U}}_{D} } \\ \end{array} } \right]$$

(6)

where U_G and I_G are the voltage and current vector matrix of the generator node. U_D and I_D are the voltage and current vector matrix of the load node. Y_GG, Y_DD, Y_GD and Y_DG are self-admittance submatrices and mutually admittance submatrices of the corresponding nodes.

Take local inverse for (6) and set Z_DD =Y_DD ^-1 to get (7).

$$\left[ {\begin{array}{*{20}c} {{\mathbf{I}}_{G} } \\ {{\mathbf{U}}_{D} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\mathbf{Y}}_{GG} - {\mathbf{Y}}_{GD} {\mathbf{Z}}_{DD} {\mathbf{Y}}_{DG} } & {{\mathbf{Y}}_{GD} {\mathbf{Z}}_{DD} } \\ { - {\mathbf{\rm Z}}_{DD} {\mathbf{Y}}_{DG} } & {{\mathbf{Z}}_{DD} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\mathbf{U}}_{G} } \\ {{\mathbf{I}}_{D} } \\ \end{array} } \right]$$

(7)

Let F = − Z_DDY_DG, the static voltage stability index L_i of load node i is calculated by (8).

$$L_{i} = \left| {1 - \sum\limits_{{j \in N_{{\text{G}}} }} {\frac{{F_{ij} U_{j} }}{{U_{i} }}} } \right|,i \in N_{D}$$

(8)

where i and j are the serial numbers of nodes. U_i and U_j are the voltage amplitude of node i and node j. F_ij is the load node participation factor, it is the ith row and jth column of matrix F. N_D and N_G are the set of load nodes and set of generator nodes.

The static voltage stability L index of system is defined as (9).

$${\text{L}} = \mathop {\max (L_{i} )}\limits_{{i \in N_{D} }}$$

(9)

The voltage stability of the system can be judged by comparing L with 1 [24]. L < 1 indicates that the system voltage is stable, L = 1 indicates that the system voltage stability is critical, while L > 1 indicates that the system voltage is instable.

3.2 Constraints

• (1) Equality constraints

The equality constraint h_γ(x) mainly refers to power balance constraints in the system, including active and reactive power balance of nodes, as given by (10).

$$\left\{ {\begin{array}{*{20}l} {(1 + \lambda_{i} )P_{Gi} + P_{Wi} - (1 + \eta_{i} )P_{Di} = U_{i} \sum\limits_{j = 1}^{q} {U_{j} (G_{ij} \cos \theta_{ij} + B_{ij} \sin \theta_{ij} )} } \hfill \\ {Q_{Gi} + Q_{Wi} - (1 + \eta_{i} )Q_{Di} = U_{i} \sum\limits_{j = 1}^{m} {U_{j} (G_{ij} \sin \theta_{ij} - B_{ij} \cos \theta_{ij} )} } \hfill \\ \end{array} } \right.$$

(10)

where θ_ij is the voltage phase angle difference between nodes i and j. G_ij and B_ij are the conductance and susceptance of the line between ith bus and jth bus. q is the total number of nodes connected to node i. P_Gi and Q_Gi are the active and reactive output of generator connected to node i. P_Di and Q_Di are the active and reactive power of load connected to node i. P_Wi and Q_Wi are the active and reactive output of wind farm connected to node i. λ_i is the growth ratio of active output of generator connected to node i. If node i does not belong to the sending region, λ_i is set to 0. η_i is the growth ration of load connected to node i. If node i does not belong to the receiving region, η_i is set to 0.

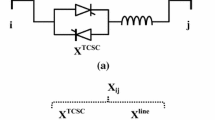
TCSC consists of a capacitor in parallel with a thyristor-controlled reactor. By adjusting the thyristor conduction angle, the reactance of TCSC changes, and the equivalent impedance of the branch becomes a controllable parameter [25]. The connection of TCSC to power system is shown in Fig. 3.

Fig. 3

Connection of TCSC to power system

The changing process of branch parameter is given by (11).

$$\left\{ {\begin{array}{*{20}l} {X_{ij}^{^{\prime}} = X_{ij} + X_{{{\text{TCSC}}}} } \hfill \\ {X_{{{\text{TCSC}}}} = - \beta_{{{\text{TCSC}}}} X_{ij} } \hfill \\ \end{array} } \right.$$

(11)

where i and j are the serial numbers of nodes. X_ij and X_ij^' are reactance of the branch before and after compensation, respectively. β_TCSC is the compensation degree. In the steady-state analysis of the power system, only relevant impedance value of the branch containing TCSC needs to be changed.

If a branch is allocated with TCSC, the reactance of this branch needs to be changed to (1 − β_TCSC)*X_ij, the G_ij and B_ij of corresponding branch in the power balance equation (10) need to be changed also.

• (2) Inequality constraints

The inequality constraint g(x) includes both decision variable constraints and state variable constraints.

The decision variable constraints mainly include: the constraint of TCSC allocation position, the range constraint of TCSC compensation degree, and the active power range constraints of generators in the sending area, as given by (12).

$$\left\{ {\begin{array}{*{20}l} {B \in N_{b} } \hfill \\ {\beta_{{{\text{TCSC}}}}^{\min } \le \beta_{{{\text{TCSC}}}} \le \beta_{{{\text{TCSC}}}}^{\max } } \hfill \\ {P_{Gi}^{\min } \le (1 + \lambda_{i} )P_{Gi} \le P_{Gi}^{\max } ,i \in N_{GS} } \hfill \\ \end{array} } \right.$$

(12)

where β ^max_TCSC and β ^min_TCSC are the upper and lower limits of TCSC compensation degree. P_Gi, λ_i and N_GS are the same as the corresponding symbols in (5), which indicate the ground state active output of generator connected to node i in the sending region, the increase proportion of P_Gi and the set of nodes connected by generators in the sending region.

The state variable constraints mainly include: voltage amplitude constraints of nodes connected by load, reactive power constraints of generators and transmission upper limit constraints of branches, as given by (13).

$$\left\{ {\begin{array}{*{20}l} {U_{i}^{\min } \le U_{i} \le U_{i}^{\max } ,i \in N_{{\text{D}}} } \hfill \\ {{\text{Q}}_{j}^{\min } \le Q_{j} \le {\text{Q}}_{j}^{\max } ,j \in N_{{\text{G}}} } \hfill \\ {\left| {S_{{{\text{b}}r}} } \right| \le S_{{{\text{b}}r}}^{\max } ,br \in N_{{\text{b}}} } \hfill \\ \end{array} } \right.$$

(13)

where N_D and N_G are the same as the corresponding symbols in (8), which indicate the set of nodes connected by loads and the set of nodes connected by generators. U_i^max and U_i^min are the upper and lower limits of voltage amplitudes of nodes connected by loads. Q_j^max and Q_j^min are the upper and lower limits of the reactive power of generators. S_br and S_br^max are capacity and the upper limit of capacity of branch br. N_b represents the set of branches in the system.

3.3 Constraint Processing Technique

The decision variables are set artificially to satisfy constraints. The state variables change because of the decision variables and cannot satisfy constraints by themselves. If a state variable exceeds its limit, the off-limit quantity is added to the original objective function in form of a penalty term to construct an objective function considering inequality constraints. This will force the control variable to gradually optimize in the direction of satisfying the constraints, as given by (14).

$$f_{\alpha } (x) = f_{\alpha } (x) + p(t)*H(x,u),\alpha = 1,2, \ldots$$

(14)

where x, u and t are decision variable, state variable and iteration number, respectively. p(t) and H(x, u) are penalty coefficient and penalty term. The penalty term H(x, u) is determined by penalty intensity r(ξ) and penalty coefficient θ(ξ) [26]. Each part can be calculated by (15).

$$\left\{ {\begin{array}{*{20}l} {p(t) = (t)^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} } \hfill \\ {H(x,u) = \theta (\xi ) * \xi^{r(\xi )} } \hfill \\ {r(\xi ) = \left\{ {\begin{array}{*{20}c} {1,\xi \le 1} \\ {2,\xi > 1} \\ \end{array} } \right.} \hfill \\ {\theta (\xi ) = \left\{ {\begin{array}{*{20}l} {10,\xi \le 0.001} \hfill \\ {20,0.001 < \xi \le 0.1} \hfill \\ {100,0.1 < \xi \le 1} \hfill \\ {300,\xi > 1} \hfill \\ \end{array} } \right.} \hfill \\ \end{array} } \right.$$

(15)

The value of intermediate variable ξ in (15) is affected by inequality constraint off-limit function h(x,u) of the state variable, as shown by (16).

$$\left\{ {\begin{array}{*{20}l} {\xi = \max \{ 0,h(x,u)\} } \hfill \\ {h(x,u) = \left\{ {\begin{array}{*{20}c} {u - u_{\max } ,u > u_{\max } } \\ {0,u_{\min } \le u \le u_{\max } } \\ {u_{\min } - u,u < u_{\min } } \\ \end{array} } \right.} \hfill \\ \end{array} } \right.$$

(16)

4 Algorithm and Fuzzy Optimal Solution Selection

In order to solve the model established in Sect. 3, this section presents improved MOPSO algorithm and design solution process. In addition, since in real-world decision makers often face the situation of choosing a solution from multiple non-inferior solutions, a method to obtain a fuzzy optimal solution from multiple non-inferior solutions is proposed.

4.1 Improved MOPSO Algorithm and the Computational Flowchart

Since the power increase ratios of generators in sending area and TCSC compensation degree are continuous variables while the compensation branch is discrete variable, the model in this paper belongs to a mixed real, integer nonlinear multi-objective optimization problem. The MOPSO algorithm with few parameters, fast searching speed and strong searching ability is used to solve it [27].

• (1) Encoding

The decision variable x is encoded by real number as [B, β_TCSC, λ₁,…, λ_NGS]. Where, B and β_TCSC are the installation branch and compensation degree of TCSC, respectively. “λ₁,…,λ_NGS” are the active power growth ratios of generators in the sending area.

• (2) Chaos initialization and variable inertia weight setting

Considering that the initial population uniformity of the conventional MOPSO algorithm is poor, and chaos can implement the traversal which is conducive to improving the population uniformity and diversity, chaotic initialized population is generated by the Logistic sequence [28] as per (17).

$$x_{m + 1} = 4x_{m} \left( {1 - x_{m} } \right)$$

(17)

where m represents the serial number of particles. The specific steps are as follows: n-dimensional chaotic variable x₀ is generated first, each dimensional of x₀ is between 0 and 1. Then, multiple chaotic vectors are generated by multiple iterations based on (17). Finally, the generated multiple chaotic vectors are reflected to the value intervals of the decision variables one by one to generate the initial particle population.

In addition, in order to increase global optimization speed in early stage and local optimization ability in later stage, and to get rid of the limitation of accurately setting the speed change range, the inertial weight is set as a variable which decreases linearly with the number of iteration within a certain value interval. Particle velocity and position update rules are given by (18).

$$\left\{ {\begin{array}{*{20}l} {v_{md}^{t + 1} = wv_{md}^{t} + c_{1} r_{1} (p_{md} - x_{md}^{t} ) + c_{2} r_{2} (g_{d}^{t} - x_{md}^{t} )} \hfill \\ {x_{md}^{t + 1} = x_{md}^{t} + v_{md}^{t + 1} } \hfill \\ {w = w_{\max } - (w_{\max } - w_{\min } )\frac{t}{{t_{\max } }}} \hfill \\ \end{array} } \right.$$

(18)

where x^t_md and v^t_md represent the position and speed of the dth dimensional variable of the mth particle at the tth iteration. t_max is the maximum number of iterations. c₁ and c₂ are the individual and social learning parameters, both are set as 2. w, w_max and w_min are the inertial weight and its limits. r₁ and r₂ represent random numbers in the interval of 0–1. p_md represents the optimal position of the dth dimensional variable of the mth particle in the historical search. g^t_d represents the group optimal position of the dth dimensional variable in the tth iteration.

• (3) Computational flowchart

The computational flowchart for solving the model of this paper by the improved MOPSO algorithm is shown in Fig. 4.

Fig. 4

Flowchart based on the improved MOPSO algorithm

4.2 Fuzzy Optimal Solution Selection

After solving the multi-objective optimization model based on Fig. 4, multiple non-inferior solutions can be obtained by the output of the first layer of MOPSO memorizer. Since there are two objective functions, each non-inferior solution is a two-dimensional point, multiple non-inferior solutions constitute a pareto graph. The non-inferior solution set is usually visually displayed in the form of a pareto graph rather than directly listing the coordinate values of all the non-inferior solutions. In order to choose the best one from multiple non-inferior solutions, fuzzy satisfaction function S is employed. The fuzzy satisfaction function is used to evaluate every non-inferior solution. The non-inferior solution with the maximum comprehensive satisfaction can be selected as the fuzzy optimal solution [29]. Comprehensive satisfaction S is defined as (19).

$$\left\{ {\begin{array}{*{20}l} {S = \frac{1}{2}\sum\limits_{\alpha = 1}^{2} {s_{\alpha } } } \hfill \\ {s_{\alpha } = \left\{ {\begin{array}{*{20}l} {1,f_{\alpha } \le f_{\alpha }^{\min } } \hfill \\ {\frac{{f_{\alpha }^{\max } - f_{\alpha } }}{{f_{\alpha }^{\max } - f_{\alpha }^{\min } }},f_{\alpha }^{\min } < f_{\alpha } < f_{\alpha }^{\max } } \hfill \\ {0,f_{\alpha } \ge f_{\alpha }^{\max } } \hfill \\ \end{array} } \right.} \hfill \\ \end{array} } \right.$$

(19)

where f_α^max and f_α^minare the maximum and minimum values of the αth objective function f_α, respectively.

5 Simulation Case Studies

To assess the robustness of the proposed methods in Sects. 2 Through 4, case studies based on IEEE-30 bus system are presented in this section.

As shown in Fig. 5, the modified IEEE-30 system comprises a wind farm (including 20 turbines) connected to bus 15. The rated output power of each wind turbine is 1.5 MW with a unity power factor during normal operation [30]. The cut-in, cut-out and rated wind speed are 3 m/s, 20 m/s and 11 m/s, respectively.

Fig. 5

Modified IEEE-30 system

One hundred initial particles are produced. The memorizer is capable of storing 100 particles. The maximum number of iteration is set as 100. The changing range of inertia weight is 0.9–0.4. All branches are chosen as suitable locations to connect the TCSC. The range of TCSC compensation degree is − 0.2–0.8. The available transmission capacity from area 3 to area 2 is taken as an example to calculate the ATC.

5.1 Scenario Results

The shape and scale coefficients of local wind speed are 2 and 10, respectively. According the method presented in Sect. 2.1, the wind power scenarios are generated first. The annual wind speed curve is shown in Fig. 6.

Fig. 6

Annual wind speed curve

Based on Fig. 6, wind power scenarios w₁–w₆ are generated by the method presented in Sect. 2.1. w₁ and w₆ are zero output scenarios, w₂ is the rated output scenario, w₃–w₅ are under-output scenarios, as shown in Fig. 7.

Fig. 7

Annual duration wind speed curve and discrete step wind speed curve

The equivalent wind speed, equivalent power, scenario probability and cumulative probability of each wind power scenario are listed in Table 1.

Table 1 Scenarios of wind power

For load, its mean value is set as its rated value P_N, the standard deviation is set as 10% of P_N. The annual load curve is shown in Fig. 8.

Fig. 8

Annual load curve

Load scenarios are generated by the method presented in Sect. 2.2. According to the equivalent load values, load scenarios are sorted into scenarios d₁–d_5, as shown in Fig. 9. To simplify the analysis, each load is assumed to have the same scenario distribution.

Fig. 9

Annual duration load curve and discrete step load curve

The equivalent load value, scenario probability and cumulative probability for each load scenario are listed in Table 2.

Table 2 Scenarios of load

According to the cumulative probabilities of wind power scenarios and load scenarios, Monte Carlo sampling is conducted for 87,600 times based on the method in Sect. 2.3. The system scenario information is counted and ranked according to the scenario probabilities in descending order, as shown in Table 3.

Table 3 Scenarios of the system

As can be seen from Table 3: System scenario s₁ has the largest occurrence probability (8.32%) and belongs to the scenario that the system is most likely to face. The system scenario s₁₄ corresponds to wind power scenario w₂ and load scenario d₁. For s₁₄, wind power and load have the largest values, therefore the requirement for network transmission capacity is the highest one, so it belongs to the most severe scenario. However, the occurrence probability of s₁₄ is 2.76%, which only accounts for 31.25% of the occurrence probability of s₁.

5.2 Non-inferior Solution Sets and Comparison of Fuzzy Optimal Solutions

Multi-objective optimization is conducted for the system scenario with maximum occurrence probability (system scenario s₁). The optimization results before and after the allocation of TCSC are shown in Fig. 10.

Fig. 10

Comparison of optimization results before and after TCSC allocation in s₁ scenario

The calculation results of Fig. 10 show that, after TCSC allocation, a better pareto frontier can be obtained compared with the ground state. The ATC increases by nearly 20% (from 34.37MW to 41.16MW) while the L index is basically the same (0.057). It shows that, for system scenario s₁, a reasonable allocation of TCSC enables the system to obtain a larger ATC and a smaller voltage stability L index.

When wind power is large (rated output of wind turbine), the requirement for ATC is strict, so it is necessary to investigate the optimization results in this case. The optimization results after the allocation of TCSC for scenarios with the largest wind power (scenario s₁, s₂, s₃, s₁₃ and s₁₄) are shown in Fig. 11.

Fig. 11

Comparison of fuzzy optimal solutions before and after TCSC allocation in different scenarios

As can be seen from Fig. 11: When wind power is large, if loads are different, the non-inferior solution sets for the corresponding system scenarios are different. It means that load randomness can’t be ignored in the correlation analysis. ATC is below 50MW, this value is mainly determined by the power increasing upper limit of two generators in the sending area (the power increasing upper limits of generator 22 and generator 27 are 28.41MW and 28.09MW, respectively). Due to the compensation of TCSC, the upper limit of line transmission capacity is no longer a major factor restricting ATC. The L index almost never exceeds 0.07, voltage stability is good. The pareto chart tends to a better direction (L decreases under the same ATC, and ATC increases under the same L) with the load reduction (system scenario s₁₄, s₃, s₁, s₂ and s₁₃). System scenario s₁₃ corresponds to the scenario with minimum load under maximum wind power. The position of optimization result curve for s₁₃ is better than that of the other four curves. System scenario s₁₄ corresponds to the scenario with maximum load under maximum wind power. The position of optimization result curve for s₁₄ is worse than that of the other four curves, which verifies that the margin of network transmission capacity is small and the test for ATC is the most stringent. Even so, Compared with the pareto curve of s₁₄ without TCSC (the marked black curve), the solution set after TCSC allocation is still better. Records the fuzzy optimal solutions and corresponding allocation schemes for the five scenarios of Fig. 11, as listed in Table 4.

Table 4 Fuzzy optimal solutions and TCSC allocation schemes for system scenarios with maximum wind power

As can be seen from Table 4: For the modified IEEE-30 bus system, on the basis of comprehensive consideration of wind power and load randomness, the minimum ATC and maximum ATC from region 3 to region 2 are 36.7818MW and 47.0089MW by optimization allocation of TCSC, and the L indexes are not more than 0.0636 simultaneously. The fuzzy optimal solutions change in the same direction as the pareto diagrams, ATC decreased (from 47.0089 to 36.7818) and L index increased (from 0.0501 to 0.0636) under load increasing. If ATC and L index of the system scenario with the highest occurrence probability are mainly considered, TCSC is recommended to be allocated on the 25th branch,and the compensation degree should be 0.6263. If the main consideration is the scenario of highest requirement for network transmission capability,TCSC can be allocated by referring to the optimization result of system scenario s₁₄.

5.3 Superiority Verification of the Proposed Methods

To verify the superiority of the proposed methods, the system scenario s₁ is taken as an example. The experiments of TCSC optimization allocation are performed based on different algorithms, and the optimization results are compared, as shown in Fig. 12.

Fig.12

Comparison of the optimization results of different algorithms

As can be seen from Fig. 12, the optimization results obtained by the improved MOPSO algorithm cover a larger scope and have a more uniform distribution. This proves the benefit of increasing chaotic initialization. In addition, the fuzzy optimal solution of the improved MOPSO has a larger ATC while the corresponding L index is basically the same as that of the MOPSO. This proves the benefit of variable inertia weight setting.

5.4 Generality Verification of the Proposed Methods

In order to test the universality of the proposed methods and experimental conclusions, we have redone some experiments while increasing the wind power penetration. Taking the system scenario s₁ as an example, when the number of wind turbines is increased to 25, the effect of TCSC is tested, the results are shown in Fig. 13.

Fig.13

Comparison of optimization results before and after TCSC allocation in s1 scenario under increased wind power penetration

As can be seen from Fig. 13, compared with the optimization results of Fig. 10, although the value ranges of ATC and L index changed, the relative position relationship of pareto diagrams is similar. It means that even with a different wind power penetration, the reasonable allocation of TCSC can still improve ATC and ensure the voltage stability without changing the grid structure. This verifies the generality of the proposed methods in this paper.

6 Conclusion

This paper studies the TCSC multi-objective optimal allocation for power systems with wind power under load randomness. The main works are as follows:

• 1. Based on clustering and Monte Carlo sampling techniques, a system scenario generation method is derived for power system with multiple random variables and its validity is verified on a modified IEEE-30 bus system.

• 2. On the basis of comprehensive consideration of wind power and load randomness, a TCSC multi-objective optimal allocation model is established with ATC and L index as objective functions.

• 3. The MOPSO algorithm is improved by increasing chaotic initialization and linear decreasing setting of inertial weight, and then used to solve the model established in this paper.

The results show that the scenario generation method, the TCSC multi-objective optimal allocation model and the calculation process proposed in this paper can effectively solve related problems. This paper provides a new idea for the power system to improve the inter-regional available transmission capacity and promote the consumption of wind power by flexibly adjusting the grid structure.

In the next study, we will study the typical system scenario generation method which considers the load and wind power correlation, and try to conduct a multi-objective random optimization model considering multiple random factors to easily determine the acceptable maximum wind power penetration.