1 Introduction

Responding to the growing need for energy requires increasing attention to renewable resources. These resources play an important role in reducing environmental pollution and fossil fuels [1, 2]. Given the need to reduce emissions for energy in the coming years, attention to clean energy is an unstoppable approach, and this has been repeatedly reminded by [3, 4]. Overall, the development of clean energy is critical for preventing global climate change and global warming. Currently, wind energy [5, 6], solar energy [7], biomass [8], geothermal energy [9], biodiesel and hydraulic energy [10, 11] are the most important sources of renewable energy to extract clean energy.

Due to economic and environmental considerations, bioenergy production has been widely considered, and in the meantime, microbial fuel cell (MFC) is the most important tool for generating electricity using the ability of microorganisms [12]. The microbial fuel cell achieves four effective functions including electricity generation, hydrogen production, wastewater treatment and biological oxygen demand (BOD) biosensors [13]. In view of the above, the microbial fuel cell is one of the best tools for generating electrical energy along with other useful functions, and recently, numerous studies have been conducted for its analysis and control [14,15,16,17,18,19].

One of the important fields about MFC is the design of a suitable control method for achieving stability and optimal performance in different operating conditions. To date, various models have been proposed to describe the actual performance of the microbial fuel cell system [20,21,22,23,24]. It is clear that the proposed models are not able to accurately describe the MFC behavior and anyway, there are uncertainties in the models. The next issue is the need to pay attention to the nonlinear behavior of MFC in different operating conditions. Therefore, in the controller design, it is necessary to consider the nonlinear terms in the studied models away from linearization. Due to the high efficiency of the robust controller in various applications [25,26,27,28,29,30,31,32], the use of this approach is necessary to cover the mentioned effects.

So far, various control methods have been considered for MFC control including the method of backstepping [33, 34], adaptive sliding mode [35], fuzzy proportional integral derivative (PID) [36], adaptive fuzzy [37], model predictive control [38], on/off and PID [39], gain scheduling [40], sampled-time digital control [41] and so on. Each of the mentioned methods has advantages and disadvantages. In backstepping and adaptive backstepping methods, computational complexity is the most important problem and other methods also suffer from linearization, uncertainty and other problems. The most important goals pursued in this study are the achieving to the desired output, proper operation, stability guarantee and finite time control of MFC in the presence of model uncertainty and considering nonlinear effects. Finite time control makes it possible to achieve the desired output specifications in a limited time [42,43,44], not infinite, and during this limited time, which is pre-adjustable and predictable, the system state variables converge exactly to the equilibrium point. Moreover, the combination of sliding mode control method with adaptive method has been used to achieve the desired output characteristics, of course, the adaptive method is also used to determine the coefficients of the sliding mode control method. For unknown upper bound of uncertainty, applying the adaptive method can overcome the limitation and of course, the control signal obtained from the proposed method causes the non-linear system state variables follow the desired output completely after a finite time and with zero error. Accordingly, this paper is arranged as follows: In the second section, the mathematical model is presented for MFC under study. Descriptions of the actual MFC system and the model used are given in this section. The third section describes the proposed control method. This section includes the class of the MFC system providing a finite time sliding mode method by using of an adaptive method to determine its coefficients and ensure the stability of the closed-loop system. In the fourth section, the simulation results obtained by using of proposed method on the sample MFC are given. The fifth section also includes the conclusion and the direction of future studies.

2 Microbial Fuel Cell Model

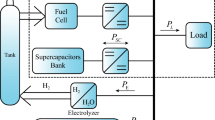
Microbial fuel cells are bio-electrochemical systems that convert chemical energy into electrical energy by catalytic reaction and the use of microorganisms as catalysts. Various models have been proposed to describe the performance of microbial fuel cells and to investigate the impact of a number of factors on their behavior [20,21,22,23,24]. Several parameters such as substrate concentration, voltage, current and output power affect the performance of microbial fuel cells. A schematic of the overall performance of a microbial fuel cell is shown in Fig. 1.

Fig. 1
figure 1

Single chamber MFC with proton-exchange membrane (PEM)

Full size image

From a control point of view, several kinds of models have been considered to explain MFC behavior. In this paper, the single chamber single population MFC control model is used to design the controller. According to [35], the state space equations of this model are as follows:

$$\dot{x}_{1} = - \theta_{1}^{ - 1} .Y^{ - 1} \frac{{x_{1} }}{{K_{s} + x_{1} }}x_{2} + u\left( {C_{so} - x_{1} } \right)$$
(1)
$$\dot{x}_{2} = \left( {\theta_{1}^{ - 1} \frac{{x_{1} }}{{K_{s} + x_{1} }} - K_{d} - u} \right)x_{2}$$
(2)

In the above equations, \(x_{1}\) represents the substrate concentration and \(x_{2}\) represents the concentration of biomass. \(\theta_{1}^{ - 1}\) defines specific bacterial growth maximum value, \(Y\) states biomass growth, \(K_{s}\) identifies half-saturation constant, \(C_{so}\) specifies the substrate concentration, \(K_{d} > 0\) states the Bacteria decay coefficient and \(u\) is the control input. The reader can refer to [33, 35] for more information about the model used.

3 Finite Time Adaptive Sliding Mode Control

In this part, a finite time adaptive sliding mode controller is designed to control the states of the microbial fuel cell system, which has the advantages of sliding mode control, finite time mechanism and adaptive algorithm. First, a terminal sliding mode controller is designed for finite time stability of the fuel cell system. It is necessary to determine the upper bound of uncertainties in problem with the terminal sliding mode design. To eliminate this shortcoming, an adaptive method has been used to estimate the upper bound of parametric uncertainty and also to determine the sliding mode control coefficients. A schematic of the proposed control method is shown in Fig. 2. Now the controller design steps are described. Let’s define the error as follows:

$$e_{1} = x_{1} - x_{1d} .$$
(3)
$$e_{2} = x_{2} - x_{2d}$$
(4)

where \(x_{1d}\) and \(x_{2d}\) are arbitrary equilibrium points. By deriving the error, it is obtained

$$\dot{e}_{1} = - \theta^{ - 1} Y^{ - 1} \frac{{x_{1} x_{2} }}{{k_{s} + x_{1} }} - x_{1} u + c_{s0} u - \dot{x}_{1d}$$
(5)
$$\dot{e}_{1} = \theta^{ - 1} \frac{{x_{1} x_{2} }}{{k_{s} + x_{1} }} - (x_{2} - 1)u - k_{d} e_{2} - k_{d} x_{2d} - \dot{x}_{2d} - u$$
(6)
Fig. 2
figure 2

Schematic of the proposed control method

Full size image

By definition

$$u = u_{1} + u_{2}$$
(7)
$$f_{1} \left( {t,x} \right) = - \theta^{ - 1} Y^{ - 1} \frac{{x_{1} x_{2} }}{{k_{s} + x_{1} }} - x_{1} u + c_{s0} u_{2} - \dot{x}_{1d}$$
(8)
$$f_{2} \left( {t,x} \right) = - \theta^{ - 1} \frac{{x_{1} x_{2} }}{{k_{s} + x_{1} }} - \left( {x_{2} - 1} \right)u - u_{1} - k_{d} e_{2} - k_{d} x_{2d} - \dot{x}_{2d}$$
(9)

System error equations are rewritten as follows:

$$\dot{e}_{1} = f_{1} \left( {t,x} \right) + c_{s0} u_{1}$$
(10)
$$\dot{e}_{2} = f_{2} \left( {t,x} \right) - u_{2}$$
(11)

By selecting the sliding lines as follows

$$s_{1} \left( t \right) = e_{1} \left( t \right)$$
(12)
$$s_{2} \left( t \right) = e_{2} \left( t \right)$$
(13)

To stabilize the error system, we select the control vectors \(u_{1}\) and \(u_{2}\) as follows:

$$u_{1} \left( t \right) = \frac{1}{{c_{so} }}\left( { - k_{1} e_{1} - k_{2} e_{1}^{v} - \hat{f}_{1} sgn\left( {s_{1} } \right)} \right)$$
(14)
$$u_{2} \left( t \right) = k_{3} e_{2} + k_{4} e_{2}^{v} + \hat{f}_{2} sgn\left( {s_{2} } \right))$$
(15)

where \(v = \frac{p}{q}, p,q > 0\), \(\hat{f}_{1}\) and \(\hat{f}_{2}\) are adaptive estimators for sliding control benefits to eliminate uncertainty and nonlinear effects of the system.

Now to prove the stability, Lyapunov function is candidate as follows.

$$V\left( {\text{t}} \right) = \frac{1}{2}s_{1}^{2} \left( t \right) + \frac{1}{2}s_{2}^{2} + \frac{1}{2}\tilde{f}_{1}^{2} + \frac{1}{2}\tilde{f}_{2}^{2}$$
(16)

where

$$\tilde{f}_{1} = f_{1} - \hat{f}_{1}$$
$$\tilde{f}_{2} = f_{2} - \hat{f}_{2}$$

It is obtained by deriving the Lyapunov function and substituting \(u_{1}\) and \(u_{2}\).

$$\begin{aligned} \dot{V}\left( t \right) = & s_{1} \left( t \right)\dot{s}_{1} \left( t \right) + s_{2} \left( t \right)\dot{s}_{2} \left( t \right) - \frac{1}{{\lambda_{1} }}\tilde{f}_{1} \mathop {\hat{f}_{1} }\limits^{ \cdot } - \frac{1}{{\lambda_{2} }}\tilde{f}_{2} \mathop {\hat{f}_{2} }\limits^{ \cdot } \\ = & - k_{1} e_{1}^{2} - k_{2} e_{1} e_{1}^{v} - k_{3} e_{2}^{2} - k_{4} e_{2} e_{2}^{v} + s_{1} \left( t \right)(f_{1} \\ - & \hat{f}_{1} {\text{sgn}} \left( {s_{1} \left( t \right)} \right) + & s_{2} \left( t \right)(f_{2} - \hat{f}_{2} {\text{sgn}} \left( {s_{2} \left( t \right)} \right) - \frac{1}{{\lambda_{1} }}\tilde{f}_{1} \mathop {\hat{f}_{1} }\limits^{ \cdot } - \frac{1}{{\lambda_{2} }}\tilde{f}_{2} \mathop {\hat{f}_{2} }\limits^{ \cdot } \\ \end{aligned}$$
(17)

By simplifying the above equation is obtained.

$$\begin{aligned} \dot{V}\left( t \right) \le - k_{1} e_{1}^{2} - & k_{2} e_{1} e_{1}^{v} - k_{3} e_{2}^{2} - k_{4} e_{2} e_{2}^{v} + \left| {s_{1} \left( t \right)} \right|\left| {f_{1} \left( {t,e} \right)} \right| \\ - & \hat{f}_{1} s_{1} \left( t \right){\text{sgn}} \left( {s_{1} \left( t \right)} \right) + \left| {s_{2} \left( t \right)} \right|\left| {f_{2} \left( {t,e} \right)} \right| - \hat{f}_{2} s_{2} \left( t \right){\text{sgn}} \left( {s_{2} \left( t \right)} \right) \\ - & \frac{1}{{\lambda_{1} }}\tilde{f}_{1} \mathop {\hat{f}_{1} }\limits^{ \cdot } - \frac{1}{{\lambda_{2} }}\tilde{f}_{2} \mathop {\hat{f}_{2} }\limits^{ \cdot } \\ \le & - k_{1} e_{1}^{2} - k_{2} e_{1} e_{1}^{v} - k_{3} e_{2}^{2} - k_{4} e_{2} e_{2}^{v} + \tilde{f}_{1} \left| {s_{1} \left( t \right)} \right| + \tilde{f}_{2} \left| {s_{2} \left( t \right)} \right| \\ - & \frac{1}{{\lambda_{1} }}\tilde{f}_{1} \mathop {\hat{f}_{1} }\limits^{ \cdot } - \frac{1}{{\lambda_{2} }}\tilde{f}_{2} \mathop {\hat{f}_{2} }\limits^{ \cdot } \\ \end{aligned}$$
(18)

̇Now by defining the adaptive laws as follows.

$$\mathop {\hat{f}_{1} }\limits^{ \cdot } = \lambda_{1} \left| {s_{1} \left( t \right)} \right|$$
(19)
$$\mathop {\hat{f}_{2} }\limits^{ \cdot } = \lambda_{2} \left| {s_{2} \left( t \right)} \right|$$
(20)

It is obtained.

$$\dot{V}\left( t \right) \le - k_{1} e_{1}^{2} - k_{2} e_{1} e_{1}^{v} - k_{3} e_{2}^{2} - k_{4} e_{2} e_{2}^{v}$$
(21)

Thus, the designed control law guarantees the stability of the MFC system under the above mentioned uncertainties.

Lemma 1 ([45]).

Assume that there exists a continuous positive definite function \(V\left( t \right)\) that satisfies the following differential inequality:

$$\dot{V} \le - \rho_{1} V - \rho_{2} V^{\varrho } , \forall t > t_{0}$$
(22)

where \(\rho _{1} > 0,~\rho _{2} > 0,\;{\text{and~}}\;0 < {\varrho } < 1,\) then \(V\left( t \right)\) converges to the equilibrium point in finite time \({ }t_{f}\) defined by

$$t_{f} \le t_{0} + \frac{1}{{\rho_{1} \left( {1 - \varrho } \right)}}\ln \frac{{\rho_{1} V^{1 - \varrho } \left( {t_{0} } \right) + \rho_{2} }}{{\rho_{2} }}$$
(23)

Lemma 2 ([45]).

Suppose \(\tau_{1} ,\tau_{2} , \ldots ,\tau_{n} {\text{and}}\) \(0 < h < 1\) are all positive constants, then the following inequality holds.

$$\left( {\tau_{1}^{2} + \tau_{2}^{2} + \ldots + \tau_{n}^{2} } \right)^{2h} \le \left( {\tau_{1}^{2h} + \tau_{2}^{2h} + \ldots + \tau_{n}^{2h} } \right)^{2}$$
(24)

Consider the following Lyapunov function candidate:

$$V = \frac{1}{2}s_{1}^{2} \left( t \right) + \frac{1}{2}s_{2}^{2}$$
(25)

The time derivative of the Lyapunov function \(V\) given by (25) results in

$$\dot{V} \le - k_{1} e_{1}^{2} - k_{2} e_{1} e_{1}^{v} - k_{3} e_{2}^{2} - k_{4} e_{2} e_{2}^{v} + \left| {e_{1} } \right|\tilde{f}_{1} + \left| {e_{2} } \right|\tilde{f}_{2}$$
(26)

where the facts that

$$\left| {e_{1} } \right|\tilde{f}_{1} \le c_{1} e_{1}^{2} + \frac{{\tilde{f}_{1}^{2} }}{{4c_{1} }}$$
(27)
$$\left| {e_{2} } \right|\tilde{f}_{2} \le c_{2} e_{2}^{2} + \frac{{\tilde{f}_{2}^{2} }}{{4c_{2} }}$$
(28)
$$\begin{aligned} - k_{1} e_{1}^{2} - k_{3} e_{2}^{2} + & \left| {e_{1} } \right|\tilde{f}_{1} + \left| {e_{2} } \right|\tilde{f}_{2} \\ = & - 2\left( {k_{1} - c_{1} } \right)\left( {\frac{1}{2}e_{1}^{2} } \right) - 2\left( {k_{3} - c_{2} } \right)\left( {\frac{1}{2}e_{2}^{2} } \right) + \frac{{\tilde{f}_{1}^{2} }}{{4c_{1} }} + \frac{{\tilde{f}_{2}^{2} }}{{4c_{2} }} \\ \le & - \gamma_{1} \left( {\frac{1}{2}e_{1}^{2} + \frac{1}{2}e_{2}^{2} } \right) + c_{3} \\ \end{aligned}$$
(29)

where

$$\gamma_{1} = 2 min\left( {k_{1} - c_{1} ,k_{3} - c_{2} } \right)$$
(30)
$$c_{3} = \frac{{\tilde{f}_{1}^{2} }}{{4c_{1} }} + \frac{{\tilde{f}_{2}^{2} }}{{4c_{2} }}$$

Using the following inequality

$$\begin{aligned} k_{2} e_{1}^{v + 1} + k_{4} e_{2}^{v + 1} \le & min\left( {k_{2} ,k_{4} } \right)\left( {e_{1}^{v + 1} + e_{2}^{v + 1} } \right) \\ \le & min\left( {k_{2} ,k_{4} } \right)\left( {e_{1}^{2} + e_{2}^{2} } \right)^{{\frac{v + 1}{2}}} \\ \le & 2 min\left( {k_{2} ,k_{4} } \right)\left( {\frac{1}{2}e_{1}^{2} + \frac{1}{2}e_{2}^{2} } \right)^{{\frac{v + 1}{2}}} \le \gamma_{2} V^{{\frac{v + 1}{2}}} \\ \end{aligned}$$
(31)

where Lemma 2 is applied and \(\gamma_{2} = 2 min\left( {k_{2} ,k_{4} } \right)\) is a positive constant, then (26) can be further expressed as

$$\dot{V} \le - \gamma_{1} V - \gamma_{2} V^{{\frac{v + 1}{2}}} + c_{3}$$
(32)

Then (32) can be reworked as the following two structures:

$$\dot{V} \le - \left( {\gamma_{1} - \frac{{c_{3} }}{V}} \right)V - \gamma_{2} V^{{\left( {v + 1} \right)/2}}$$
(33)
$$\dot{V} \le - \gamma_{1} V - \left( {\gamma_{2} - \frac{{c_{3} }}{{V^{{\left( {v + 1} \right)/2}} }}} \right)V^{{\left( {v + 1} \right)/2}}$$
(34)

From (33), if \(\left( {\gamma_{1} - \frac{{c_{3} }}{V}} \right) > 0\), then the finite-time stability is still guaranteed by using Lemma 1, which implies that \(V\) converges to the region \(V \le c_{3} /\gamma_{1}\) in finite time, and hence, the sliding manifold \(s\) will converge to the region

$$\left\| s \right\| \le \sqrt {\frac{{c_{3} }}{{2 min\left( {k_{1} - c_{1} ,k_{3} - c_{2} } \right){ }}}}$$
(35)

in finite time. From (34), if \(\left( {\gamma_{2} - \frac{{c_{3} }}{{V^{{\left( {v + 1} \right)/2}} }}} \right) > 0\), then the finite-time stability is still assured by using Lemma 2, which indicates that \(V\) converges to the region \(V \le \left( {c_{3} /\gamma_{2} } \right)^{{2/\left( {v + 1} \right)}}\) in finite time, and thus, the sliding manifold \(s\) will converge to the region

$$\left\| s \right\| \le \sqrt {\left( {\frac{{c_{3} }}{{2 min\left( {k_{2} ,k_{4} } \right)}}} \right)^{{2/\left( {v + 1} \right)}} }$$
(36)

in finite time. Therefore, the sliding manifold \(s\) will reach the region \(\left\| s \right\| \le \Delta\) in finite time.

$$\left\| s \right\| \le \Delta = min\left\{ {\sqrt {\frac{{c_{3} }}{{2 min\left( {k_{1} - c_{1} ,k_{3} - c_{2} } \right){ }}}} } \right.,\left. {\sqrt {\left( {\frac{{c_{3} }}{{2 min\left( {k_{2} ,k_{4} } \right)}}} \right)^{{2/\left( {v + 1} \right)}} } } \right\}$$
(37)

4 Simulation Results

In this section, we simulate the fuel cell system using the proposed control method. One of the control objectives in relation to the fuel cell system is to track the reference concentrations of substrate and biomass to achieve the desired output voltage. Achieving this goal has been considered by examining various control criteria. Also, to prove the performance of the designed controller, the results obtained have been compared with the adaptive backstepping and the adaptive sliding mode controllers [34, 35]. For this purpose, we consider 2 different scenarios. Also, the controller parameters presented in this paper are selected as follows.

$$k_{1} = 10,k_{2} = 1,k_{3} = 10,k_{4} = 1,\lambda_{1} = 1,\lambda_{2} = 1$$

Scenario 1

The system parameters don’t have uncertainty. In this case, the system model fully describes the behavior of the system. The simulation results in this scenario are shown in Figs. 3 - 5. Figure 3 shows the system states in tracking the reference concentrations for substrate and biomass. Figure 4 shows the control signal obtained from the three controllers, and Figs. 5 shows the output voltages of the anode, cathode, and MFC. However, as shown in Fig. 3, the finite-time adaptive sliding mode method provides faster convergence to the reference value than other methods. In Fig. 4, the control signals obtained from the three methods show that the proposed method in the paper has a high amplitude in the first moments, while over time, it tends to zero quickly, and of course the control signals obtained from the other two methods, despite the relatively large amplitude in the initial moments, move at a slower speed towards the limited values. The output obtained for the anode, cathode and MFC also indicate that the proposed method has a higher convergence speed than the other two methods. It gives a constant output voltage without overshoot and without undershoot.

Fig. 3
figure 3

Performance of a substrate concentration b biomass concentration

Full size image
Fig. 4
figure 4

Control Signal

Full size image
Fig. 5
figure 5

Voltages of single chamber a Anode, b Cathode, c MFC

Full size image

Scenario 2

In this scenario, a parametric uncertainty is considered as follows.

$$\left\{ {\begin{array}{*{20}c} {\theta^{ - 1} = 0.4} & {if t < 40} \\ {\theta^{ - 1} = 0.38} & {if t \ge 40} \\ \end{array} } \right.$$

The simulation results under the above-mentioned uncertainty are shown in Figs. 6 to 8. As can be seen from Fig. 6, the proposed method provides a higher convergence speed without overshoot-undershoot, while the backstepping method has a behavior with overshoot-undershoot and with a lower convergence speed. The control signals similar to the previous scenario are shown in Fig. 7. The anode, cathode and MFC output voltages are also shown in Fig. 8, respectively. As can be seen from the figure, the proposed method provides a stable output without any overshoot-undershoot at a high convergence rate, while the output voltages fluctuates in the adaptive backstepping method. Also, the output obtained from adaptive sliding mode method moves towards instability. In addition, the MFC has the highest output voltage under the finite time adaptive sliding mode method which is another reason for the superiority of the proposed method.

Fig. 6
figure 6

Performance of a substrate concentration b biomass concentration

Full size image
Fig. 7
figure 7

Control Signal

Full size image
Fig. 8
figure 8

Voltages of single chamber a Anode, b Cathode, c MFC

Full size image

To show the advantage of the proposed control technique in terms of transient state behavior of the system, its overshoot and undershoot is compared in Tables 1 and 2. As can be seen from the tables, under the planned controller, the states of the system experience smoother behavior without overshoot and undershoot.

Table 1 The percentage of overshoot and undershoot values of all responses for both the controllers in Scenario 1
Full size table
Table 2 The percentage of overshoot and undershoot values of all responses for both the controllers in Scenario 2
Full size table

5 Conclusion

In this paper, a new robust finite time control method is presented based on adaptive algorithm and terminal sliding mode control approach. The proposed method offers the following advantages simultaneously:

(1) Covering the effects of uncertainties (2) Covering nonlinear terms without removing or linearizing (3) Ensuring finite time stability (4) Achieving the desired MFC operating points without overshoot and undershoot in the system response (5) Eliminate the chattering effects of the sliding mode method using the adaptive method to determine its coefficients (6) No need to know the upper bound of uncertainties in the system. The simulation results show that the proposed method offers higher convergence speed, lower chattering, and response without overshoot and undershoot as well as better stability than the other two methods. Also, the error of tracking the reference values in this method is less and the simulation results show the robustness of the proposed method against the uncertainties in the system. Considering the effects of noise and disturbance as well as limitations on actuators and states can be a good path for future studies in this field.