1 Introduction

With the development of new energy technology, grid-connected inverters have received considerable research attention [1]. However, the output current of the inverter contains a large number of switching frequency harmonics, because of which an L-type or LCL-type filter needs to be added between the inverter and the grid to satisfy the requirements of grid connection. Compared with the L-type filter, the LCL-type filter is used more commonly owing to its small volume, low cost and strong attenuation of high-frequency switching ripples [2,3,4]. However, the LCL-type filter suffers from resonance problem, so effective damping becomes necessary to ensure the stability of the system. Two methods, including passive damping and active damping, are employed to damp the resonance of LCL-type filter [5,6,7,8,9,10,11]. Compared with passive damping solutions, active damping methods are more efficient and flexible, and thus are more commonly used [12,13,14,15,16,17]. It is usually realized by current loop control and this paper chooses grid-side current feedback for its simplicity.

In addition to the LCL-type filter resonance, the grid background harmonics caused by nonlinear loads can distort the grid-side current and degrade the quality of the output power of the inverter, which makes the grid-side current difficult to meet the grid standards, such as IEEE 519-1992 and IEEE 929-1988.

Many researches have been done to suppress the negative effects on the grid connected LCL-filtered inverter of grid background harmonics [18,19,20,21,22,23,24,25,26,27,28]. The methods to mitigate distortion of the output current are mainly divided into inverter-side current feedback control, grid-side current feedback control.

Inverter-side current feedback was used to suppress the distortion of the output current caused by grid background harmonics [18,19,20]. However, this strategy failed to obtain the harmonic information because the harmonic currents flew through the filter capacitor. The current/voltage of the partial capacitor, or grid voltage needs to be sampled to acquire the harmonic information of the grid-side current, which increases invest cost and system complexity.

The grid-side current feedback is an effective strategy to suppress the distortion of the output current [19, 21,22,23,24,25,26,27,28]. Twining and Holmes proposed a dual loop control strategy with the grid current outer loop using proportional-integral controller and the inner capacitance current loop using proportional controller [21]. But the authors did not point out the physical significance of the inner controller. Liu et al. [22] gave a parameter design process of the dual loop controller using pole placement and pole-zero cancellation, but it was too difficult to calculate and realize based on the work of Twining and Holmes [21]. A dual-sequence adaptive-gain variable-structure voltage control scheme was applied for effective mitigation of random and aperiodic grid disturbances [19]. However, this method required designing an appropriate sliding surface. Furthermore, the sliding-mode control exhibited jitter problem. A capacitor-current-feedback active damping and a proportional resonant regulator with harmonic compensation were adopted to achieve strong robustness of stability and high harmonic-rejection ability [23, 24]. When many kinds of harmonics need to be suppressed, it is necessary to design more resonance controllers, which will increase complexity of the control and degrade stability of the system. Using a double closed-loop control strategy based on inductor voltage difference and grid current feedback [25], can suppress the grid background harmonics effectively. However, inductor voltage difference will amplify the effect of noise and is difficult to be implemented in the experimental system. A feedforward scheme based on the band-pass-filter (BPF) was used to compensate the grid harmonics at the selected frequencies [26]. To realize high rejection of grid current low-order harmonics, the band-pass filters at the harmonic frequencies were used to detect the variation of the grid impedance as well as to facilitate the adaptive PCC voltage feedforward [27]. A Kalman filter was used by employing output current and grid voltage to remove the effect of grid voltage disturbances on the output current [28]. This method depends on the accurate model of the plant. Unified Power Quality Controller (UPQC) was utilized to compensate voltage and current distortions simultaneously in multi-feeder system [29].

The grid-side current feedback methods mentioned above used active damping with feedback of capacitor current, capacitor voltage, inductor voltage or feedforward of grid voltage to ensure stability of the control system. In this way, additional sensors are required to sample the capacitance current, capacitance voltage, inductor voltage and grid side voltage, which will increase the hardware cost.

This paper investigates the impact of the grid background harmonics on the output current of grid-connected LCL filtered inverter from the perspective of grid impedance. PI + HC is used to suppress the harmonics of the grid-side current in dq synchronous frame which can reduce complexity of the control system with fewer resonant controllers. However, the single-loop grid-side current feedback control system suffers from stability problem, so improved HPF is proposed by employing the grid-side current. The proposed method can suppress the distortion of the output current effectively and reduce hardware invest compared with other active damping.

The remainder of this paper is organized as follows: Section 2 presents the grid-connected LCL-filtered inverter with PI + HC and analyzes stability of the grid-side current feedback control system. Section 3 is devoted to designing an improved HPF and choosing the optimized feedback coefficient. Section 4 presents the results of simulation and experiments. Finally, Sect. 5 gives the conclusions of this study.

2 System Model and Stability Analysis of GCF

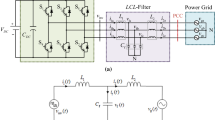
Figure 1 shows the topology of a three-phase grid-connected LCL-filtered inverter with the GCF control strategy, where the filter consists of an inverter inductor L1, capacitor C and grid inductor L2.

Fig. 1
figure 1

Topology of three-phase grid-connected LCL-filtered inverter with GCF

Full size image

The derivative resistances of the inductors are negligible to denote the most extreme case. The inverter is supplied with input DC voltage Vdc, while vgf and vgh represent the grid voltage and grid background harmonics, respectively. i2* is the reference of the grid-side current.

2.1 Current Controller Based on PI + HC

The grid background harmonics arise from the nonlinear load connected in the power grid, which will affect the waveform quality of the grid-side current.

The equivalent block diagram of the grid-side current feedback control is shown in Fig. 2.

Fig. 2
figure 2

Equivalent block diagram of the grid-side current feedback control

Full size image

According to Fig. 2, the grid-side current i2 can be calculated from the reference current \(i_{2}^{ * }\) and the grid voltage vg based on (1):

$$i_{2} = \frac{{G_{c} \left( s \right)G_{d} \left( s \right)G_{1} \left( s \right)G_{2} \left( s \right)}}{{1 + G_{c} \left( s \right)G_{d} \left( s \right)G_{1} \left( s \right)}}i_{2}^{ * } - \left( {\frac{{G_{1} \left( s \right)G_{2}^{2} \left( s \right)}}{{1 + G_{c} \left( s \right)G_{d} \left( s \right)G_{1} \left( s \right)}} + sCG_{2} \left( s \right)} \right)v_{g}$$
(1)

where \(G_{c} \left( s \right)\) represents the current controller,\(G_{d} (s) = e^{{ - 1.5sT_{s} }}\),\(G_{1} \left( s \right) = \frac{{s^{2} L_{2} C + 1}}{{s^{3} L_{1} L_{2} C + s\left( {L_{1} + L_{2} } \right)}}\),\(G_{2} \left( s \right) = \frac{1}{{s^{2} L_{2} C + 1}}\) and \(\omega_{res} = \sqrt {\left( {L_{1} { + }L_{2} } \right)/L_{1} L_{2} C}\).

Then (1) can be transformed to (2):

$$i_{2} = \frac{{T\left( s \right)G_{2} \left( s \right)}}{1 + T\left( s \right)}i_{2}^{ * } - \frac{{G_{1} \left( s \right)G_{2}^{2} \left( s \right) + sCG_{2} \left( s \right)T\left( s \right)}}{1 + T\left( s \right)}v_{g}$$
(2)

where \(T\left( s \right) = G_{c} \left( s \right)G_{d} \left( s \right)G_{1} \left( s \right)\), \(G_{c} \left( s \right){ = }\,G_{PI} (s) + G_{R} (s)\).

It can be seen from (2) that when T(s) tends to be infinite, the grid-side current can track \(i_{2}^{ * }\) and is almost independent of the grid voltage. That is to say, the gain of GR(s) at the grid background harmonics is required to be large enough.

Therefore, this paper adopts resonance controller to suppress the current harmonics caused by grid background harmonics and the ideal resonance controller is given as (3):

$$G_{R}(s) = \frac{{k_{ir} s }}{{s^2+w_{h}^2 }}$$
(3)

where kir is the coefficient of the controller’s integral and wh is the resonant frequency.

The gain at grid background harmonic frequency is

$$\left| {G_{R} \left( s \right)} \right|_{{s = jw_{h} }} = \sqrt {\left( {\frac{{k_{ir} w_{h} }}{{ - \left( {w_{h} } \right)^{2} + \left( {w_{h} } \right)^{2} }}} \right)^{2} } \to \infty$$
(4)

It is clear from (4) that the gain of GR(s) at grid background harmonic frequency is infinite, so it can suppress the grid-side current harmonics.

However, in practice, the ideal resonant controller is challenging to implement in digital systems due to the accuracy of the components and discrete control. Furthermore, when the frequency of the grid fluctuates, the harmonic mitigation capability of the controller significantly decreases because the gain in the ideal resonance controller sharply declines outside the resonance frequency. Therefore, a quasi-resonant controller is expressed in (5):

$$G_{R} \left( s \right) = \frac{{k_{ir} s}}{{s^{2} + 2w_{c} s + w_{h}^{2} }}$$
(5)

where wc is the cutoff frequency and its value ranges from 5 ~ 20 rad/s.

The gain at the harmonic frequency is

$$\left| {G_{R} \left( s \right)} \right|_{{s = jw_{h} }} = \sqrt {\left( {\frac{{k_{ir} *jw_{h} }}{{ - \left( {w_{h} } \right)^{2} + 2w_{c} *\left( {jw_{h} } \right) + \left( {w_{h} } \right)^{2} }}} \right)^{2} } { = }\,\frac{{k_{ir} }}{{2w_{c} }}$$
(6)

According to (6), the greater kir is, the higher the gain at the resonant frequency is. However, if kir is too great, the stability and convergence of the system will be affected. A too small wc can reduce the bandwidth of the controller. Therefore, wc = 5 and kir = 800, 400 are selected as the cut-off frequency and integral coefficient of resonant controller to suppress the 5th, 7th and 11th harmonics.

Both proportional resonant (PR) regulator and proportional integrator (PI) regulator can track the output current reference accurately. However, PR controller regulates the output current in \(\alpha \beta\) stationary frame. When the grid current contains 5th, 7th, 11th, and 13th harmonics, four resonant controllers need to be designed, which increases complexity of the controller design and degrades system stability. PI controller regulates the output current in dq synchronous frame and harmonics with the same orders, which can be suppressed by two resonant controllers with resonant frequencies (6w0 and 12w0) [30], thus reducing complexity of the control system. Hence, this paper adopts PI + HC to control the grid-side current.

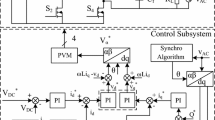
The block diagram of the proportional integral and quasi-resonant controller is shown in Fig. 3, where vd_ref and vq_ref are the outputs of the controller and the controller is expressed in (7):

$$G_{c} \left( s \right) = k_{p} + \frac{{k_{i} }}{s} + \frac{{2k_{ir} w_{c} s}}{{s^{2} + 2w_{c} s + \left( {6nw_{0} } \right)}}$$
(7)
Fig. 3
figure 3

Block diagram of proportional integral resonance control

Full size image

2.2 Stability Analysis of the System

Ignoring the effects of component-derived resistors, the open loop transfer function of the control system is expressed as (8):

$$T_{i} = G_{c} \left( s \right)G_{d} \left( s \right)k_{PWM} G_{1} \left( s \right)G_{2} \left( s \right)$$
(8)

The stability analysis is carried out using the Logarithmic frequency stability criterion. The Bode diagram is drawn based on the open loop transfer function of the control system and parameters in Table 1. In the open-loop Bode diagram, only the frequency ranges with magnitudes above 0 dB are considered. For the phase plot in these ranges, a ± (2 k + 1)π crossing in the direction of phase rising is defined as a positive crossing, while a crossing in the direction of phase falling is defined as a negative crossing. N + and N– denote the numbers of the positive and negative crossings, respectively. According to the Logarithmic frequency stability criterion, the number of the open-loop unstable poles P must meet P = 2(N + – N–) to ensure system stability. As can be seen from (5), (7), (8) and (9), P = 0, so N + – N– = 0 is required for the control systems.

Table 1 Parameters of LCL grid-connected inverter
Full size table

Figure 4 is the open-loop Bode diagrams of GCF with different delays.

Fig. 4
figure 4

Bode diagrams of GCF loop gain with different delays (PI + HC)

Full size image

It can be seen that with Td = 0, there is only a negative crossing, i.e. N– = 1, so the control system is unstable. By increasing time delays, the control system becomes stable. For instance, when Td = π/ωres, N +  = N– = 0, the system keeps stable. Therefore, increasing time delays to a certain extent can improve system stability [31]. However, making the system stable only by adjusting time delay has certain limitations in engineering applications. So an improved active damping is needed.

3 Grid-Side Current Feedback Control System Based on Improved HPF

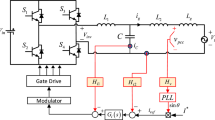
Grid background harmonics can cause current distortion and affect the quality of the output power of the grid-connected LCL-filtered inverter. The GCF can control the grid-side current directly and mitigate harmonics of the grid-side current. Moreover, it does not require extra high-accuracy sensors to obtain harmonic information of the grid-side current. However, as discussed in Section II, GCF control system is unstable so it requires an active damping strategy. In this paper, improved HPF active damping with delay feedback is used by employing output current. Figure 5 shows the equivalent control block diagram of the improved HPF in the s-domain.

Fig. 5
figure 5

Active damping control diagram of GCF based on improved HPF

Full size image

Where \(W\left( s \right) = \frac{1}{{1{ + }e^{{ - \lambda sT_{s} }} }}G_{H} \left( s \right)\), \(G_{H} (s) = - \frac{{k_{H} }}{{s + w_{d} }}\).

Figure 5 can be equivalently transformed into Fig. 6: the output of W(s) is moved to the output of 1/(sL1), and the input of W(s) is moved to the output of 1/(sC). The equivalent control block diagram is shown in Fig. 6, where the active damping strategy can be regarded as virtual impedance in reverse parallel with the capacitor C.

Fig. 6
figure 6

Active damping control diagram of GCF based on improved HPF

Full size image

zeq is obtained as (9):

$$z_{eq} = \frac{{sL_{1} L_{2} }}{{k_{PWM} G_{d} \left( s \right)W\left( s \right)}}$$
(9)

By substituting W(s) and GH(s) into (8), zeq can be obtained as (10):

$$z_{eq} \left( {s,\lambda } \right) = \frac{{ - s\left( {s + w_{d} } \right)L_{1} L_{2} \left( {e^{{1.5sT_{s} }} + e^{{\left( {1.5 - \lambda } \right)sT_{s} }} } \right)}}{{k_{PWM} k_{H} }}$$
(10)

Substituting s = jw into (10) obtains the equivalent virtual resistance and inductance in parallel, as shown in Fig. 7, where Req and Xeq are expressed in (11):

$$\left\{ \begin{gathered} R_{eq} \left( {w,\lambda } \right) = \frac{{wL_{1} \left( {L_{2} + L_{g} } \right)\left( {w^{2} + w_{d}^{2} } \right)g\left( {w,\lambda } \right)}}{{k_{PWM} k_{H} g_{R} \left( {w,\lambda } \right)}} \hfill \\ X_{eq} \left( {w,\lambda } \right) = \frac{{wL_{1} \left( {L_{2} + L_{g} } \right)\left( {w^{2} + w_{d}^{2} } \right)g\left( {w,\lambda } \right)}}{{k_{PWM} k_{H} g_{X} \left( {w,\lambda } \right)}} \hfill \\ \end{gathered} \right.$$
(11)
Fig. 7
figure 7

The circuit of equivalent virtual impedance

Full size image

\(g\left( {w,\lambda } \right)\),\(g_{R} \left( {w,\lambda } \right)\) and \(g_{X} \left( {w,\lambda } \right)\) in (11) are expressed in (12):

$$\left\{ \begin{gathered} g\left( {w,\lambda } \right) = \cos \left( {\frac{\lambda }{2}wT_{s} } \right) \hfill \\ g_{R} \left( {w,\lambda } \right) = \sqrt {w^{2} + w_{d}^{2} } \sin \left( {\frac{3 - \lambda }{2}wT_{s} + \theta } \right) \hfill \\ g_{X} \left( {w,\lambda } \right) = - \sqrt {w^{2} + w_{d}^{2} } \cos \left( {\frac{3 - \lambda }{2}wT_{s} + \theta } \right) \hfill \\ \end{gathered} \right.$$
(12)

Equations (11) and (12) show that the equivalent virtual resistance is not always positive in the effective damping range (0, fs/4) when λ = 0 or λ ≥ 3. Therefore, λ can only take 1 or 2 as value.

Tables 2 and 3 show the equivalent impedance at different ranges of frequency with λ = 1 and λ = 2, respectively. It can be derived that the effective damping region of the system is (0, f1R) for λ = 1, while λ = 2 is (0, fs/4), where \(f_{1R} \in (f_{s} /4, f_{s} /2)\).

Table 2 Equivalent impedance analysis when λ = 1
Full size table
Table 3 Equivalent impedance analysis when λ = 2
Full size table

Figure 8 shows Bode diagram of the control system using HPF and the improved HPF with different delay feedbacks. The system becomes stable at fres with HPF regardless of the value of λ. It is worth noting that the magnitude and phase exhibit new peaks at 3800 Hz and 7800 Hz with λ = 1 and λ = 2, respectively. However, the stability of system cannot be affected by the new peak of negative magnitude. Finally, an improved HPF with unit delay feedback (λ = 1) is chosen owing to its larger damping region than HPF and improved HPF with λ = 2.

Fig. 8
figure 8

Bode diagrams of control system using HPF with different delay feedbacks

Full size image

4 Simulation and Experimental Results

Simulations and experiments were conducted to assess effectiveness and correctness of the proposed method. The parameters of the grid-connected LCL-filtered inverter control system were shown in Table 1.

4.1 Simulation Results

The GCF control system using the improved HPF was built in MATLAB/PLEC with Td = 1.5 Ts and 5% of the seventh harmonic to simulate the grid background harmonics. The current reference of the grid is 5 A and the improved HPF is employed at 0.01 s.

Figure 9 showed the dynamic process of employing HPF. The grid-side current feedback control system was unstable without HPF. By introducing the improved HPF at 0.01 s, the inverter-side current and grid-side current reached their reference values after a transient transition of 0.01 s, demonstrating that the system became stable.

Fig. 9
figure 9

Waveforms of inverter-side current and grid-side current based on the improved HPF

Full size image

According to previous works [7,8,9,10], grid background harmonics caused a distortion in the grid-side current and degraded quality of the output power of the LCL-filtered inverter. This paper thus controlled the grid-side current directly by adopting PI + HC to mitigate the seventh harmonic. Figure 10 illustrates waveforms of the inverter-side current and grid-side current with HC employed at 0.08 s.

Fig. 10
figure 10

Waveforms of inverter-side current and grid-side current before and after HC

Full size image

The control system is controlled by PI before 0.08 s and the output current tracked the reference value of 5 A. However, the PI controller could not reduce the grid-side current harmonics caused by the grid background harmonics, which degrades the quality of the output power of the inverter. By introducing HC at 0.08 s, as displayed in Fig. 10, the seventh harmonic of the grid-side current reduces after about half a period of the transient process, which showed the effectiveness of the resonance controller.

To further illustrate the effectiveness of the PI + HC, the total harmonic distortion (THD) of the grid-side current i2 was compared in Figs. 11 and 12. Figures 11 and 12 show the waveform and harmonic spectrum of i2 with the PI controller and PI + HC, respectively.

Fig. 11
figure 11

The waveform and harmonic spectrum of grid-side current without the proposed strategy

Full size image
Fig. 12
figure 12

The waveform and harmonic spectrum of grid-side current with the proposed strategy

Full size image

As shown in Fig. 11, the grid-side current i2 presents significant distortion, with a THD of 11.58%, mainly centering on 350 Hz. The THD does not satisfy grid standards such as the IEEE Std 929-2000.

By contrast, the grid-side current is effectively improved by HC and the harmonics at 350 Hz significantly reduces in Fig. 12. The THD is 2.82%, which meets the IEEE Std 929-2000, whereby the THD of the current should be < 5%.

Figure 13 shows the dynamic process of the system when the grid-side current i2 increases from 5 to 10 A with PI + HC. The grid current tracks the changed value in less than a period and reduces the grid-side current harmonics, which indicates that the control system could operate stably and perform well during the dynamic process.

Fig. 13
figure 13

Transient waveforms of inverter current i1 and grid current i2 with the proposed strategy

Full size image

To further illustrate the stability of the control system, a total of 5% of the 5th, 7th, and 11th harmonics are injected. The simulation results are shown in Fig. 14.

Fig. 14
figure 14

Waveforms of inverter-side current and grid-side current before and after HC

Full size image

4.2 Experimental Results

To further test the effectiveness of the proposed strategy, experiments were carried out on the dSPACE DS1104 platform and its output signals were transformed to the IGBT on the inverter’s bridge. The non-ideal grid and DC power supply were implemented using Chroma 61511 and HAP60-600, respectively. LV28-P and LEM LT208-S7/SP1 were employed to sense the PCC voltage and the grid-side current, respectively. The switching devices were Infineon K75T60 and series IGBT. The input DC voltage and Root-Mean-Square (RMS) value of grid voltage were 150 V and 40 V, respectively. The other parameters were shown in Table 1.

Figure 15 shows waveforms of the grid voltage vg and i2 with seventh harmonic during the dynamic process. Before the improved HPF was employed, the control system was unstable and featured significant resonance in the grid-side current i2, which rendered the PI + HC to be invalid. When the improved HPF is used, resonance in the grid-side current i2 reduces, which shows the effectiveness of the improved HPF.

Fig. 15
figure 15

Waveforms of i2 with seventh harmonic before and after HPF

Full size image

Under the premise of ensuring the stability of the GCF system, PI + HC were employed to mitigate the harmonics of the grid-side current i2. Figures 16 and 17 show waveforms of the grid-side current i2 with PI controller and PI + HC, respectively.

Fig. 16
figure 16

Waveforms of i2 with seventh harmonic using PI

Full size image
Fig. 17
figure 17

Waveforms of i2 with seventh harmonic using PI + HC

Full size image

Figure 16 shows that when the grid voltage contains the seventh harmonic, it distorts the grid-side current and affects the quality of the output power of the LCL-filtered inverter.

Comparatively, Fig. 17 shows the grid-side current i2 with PI + HC. The added resonant controller effectively reduces distortion in the grid-side current caused by the grid harmonic, thus demonstrating the effectiveness of the HC resonant control design.

To further confirm the reduction in harmonics using HC, a spectrum analysis of the grid-side current i2 is carried out, shown in Fig. 18. The single-phase waveforms and spectrum analysis of grid-side current i2 before HC were employed and Fig. 18 shows the waveforms and spectrum analysis of i2 using HC. As shown in Fig. 18, the distortion in the grid-side current is severe and large volume of harmonics is observed at 350 Hz.

Fig. 18
figure 18

Waveforms and spectrum of i2 with seventh harmonic using PI

Full size image

By contrast, Fig. 19 shows the single-phase waveforms of the grid-side current i2 using HC, where the harmonics at 350 Hz significantly reduces. This verifies the correctness of parameters of the HC.

Fig. 19
figure 19

Waveforms and spectrum analysis of i2 with seventh harmonic using PI + HC

Full size image

Figure 20 shows the dynamic response of the reference value of the grid-side current from 1 to 3 A. When the reference value changes, the grid-side current i2 quickly tracks the given value and runs stably, which shows that the control system manifests perfect dynamic performance and stability.

Fig. 20
figure 20

Transient waveform of i2 with seventh harmonic after HC

Full size image

Figures 21 and 22 show the waveform of grid-side current before and after HC (with a total of 5% of the 5th, 7thand 11th harmonics injected), respectively. It can be seen that the proposed method can suppress the distortion caused by grid background harmonics and maintain stability when other orders harmonics are injected.

Fig. 21
figure 21

Waveforms of grid-side current before HC with 5th, 7th and 11th harmonics injected

Full size image
Fig. 22
figure 22

Waveforms of grid-side current after HC with 5th, 7th and 11th harmonics injected

Full size image

5 Conclusions

This paper proposed a method for mitigating distortion of grid-side current for the grid-connected LCL-filtered inverter. The proposed strategy could reduce cost and system complexity by controlling the grid-side current directly. The PI + HC control algorithm reduced the distortion in grid-side current caused by grid background harmonics. To ensure the stability of the system and effectiveness of the proposed algorithm, an improved HPF with active damping based on unit delay feedback was used. Simulation and experimental results show that the control strategy can improve the quality of grid-side current under non-ideal grid condition, thereby guaranteeing the output power quality of grid-connected inverter.