1 Introduction

Robots have been developed widely in the last two decades. Starting from a simple mobile robot that can be easily driven by using two motorized wheels [1] to new structures where four wheels are utilized to drive the motion of a mobile robot [2]. When four motorized wheels are in use, four controllers are needed at least to control the movement of such mobile robots.

On sloppy, rough or irregular terrains, wheeled robots may lose their ability to move whereas, legged robots have the ability to move on complex types of terrains [3, 4]. In some tasks such as climbing upstairs or crossing over ditches, legged robots are more suitable to perform those types of missions rather than wheeled robots. Therefore, significant efforts have been devoted to designing legged robots that imitate a gait of animals such as horses or dogs [5,6,7,8,9,10].

From the early 70 s of the last century, researchers simulated a gait of human beings. The authors in Refs. [11, 12] used the inverted pendulum structure to study some characteristics of human motion. The authors in Ref. [13] suggested a three-link legged robot structure to simulate human gaits and to study more characteristics of human locomotion.

In recent years, more complex architectures of robotics systems have been introduced based on quadruped robots [14,15,16,17,18]. This type of robotics can be applied in new applications that require complex motions where quadruped robots can perform jumping and traverse barriers. In other words, it can exhibit feasible performance over irregular terrains. As illustrated in the literature, the most utilized types are two links per leg. In complex applications, quadruped robots are mostly used instead of human beings such as military applications, space exploration, dangerous sites, harmful sites, and repeated tasks.

Quadruped robots demonstrate great advantages in the movement which can reach a high degree of freedom. Uncertainties and high nonlinearity inherently exist in the mathematical model of quadruped robots; therefore, the design of stable and robust controllers for the quadruped robot is a considerable challenge. In the state of the art, researchers have conducted different approaches to control the motion of quadruped robots. In Ref. [19], a controller is designed using slide mode to drive a quadruped robot. In that method, tracking error was improved regardless of the presence of disturbances. In Ref. [20], a novel control scheme was presented for quadruped locomotion control. The control scheme was based on a proportional-integral (PI) controller and the Jacobean to drive legs’ joints based on applied torques. Another controller was proposed based on neural networks [21] in which fuzzy neural networks were applied to control joints’ motion to follow the desired trajectory. In addition, a robust controller [22] was designed to control and stabilize a legged robot system. The robustness was investigated based on parametric uncertainty for a constant bound and unstructured bound of a position-velocity.

The authors in Ref. [23] presented a novel approach for controlling the hopping height of a monopod instantaneously, i.e., during the flight phase, the controller computes the required action to achieve the demanded height of the next step. In Ref. [24], the authors presented a learning approach to quadruped robot galloping control. The control function is obtained through directly approximating real gait data by a learning algorithm, without consideration of the robot’s model and the environment where the robot is located.

Although some attempts were provided in the survey to control the motion of legged robots, those controllers were only applied for two links per leg. Additionally, the modeling analysis was mainly dedicated to the same rather than three links per leg. Therefore, in this paper, we extend the scope of work to three links per leg and this can exhibit a higher degree of freedom and flexibility while moving. However, such an extension will increase the complexity of designing a robust controller in which 12 controllers will be required. Three controllers are applied per leg to control the servo motors over the three links per leg. The designed controllers are firstly based on a proportional, integral and derivative (PID) controllers and secondly, based on a Fuzzy controller. The novelty of this paper can be understood by designing a stable and robust controller for quadruped robots where uncertainties and high nonlinearity inherently exist in the mathematical model of a quadruped robot. Moreover, an ACO algorithm is used to find the optimal parameters of the 12 PID controller and the 12 Fuzzy controllers. Furthermore, the mathematical model has been analyzed for three links per leg quadruped robot which new modelling has been proposed in this work. When the proposed Fuzzy controllers are compared with the PID controllers, it has been observed significant improvements in terms of the stability and time response.

The rest of the paper is organized as follows: The modelling of a quadruped robot is described in Sect. 2. The explanation of the control system design is detailed in Sect. 3. Particle swarm optimization is demonstrated in Sect. 4. The Lyapunov stability test for the Fuzzy system has been performed in Sect. 4. The simulation results are conducted and analyzed in Sect. 5. In Sect. 6, comparisons have been provided and discussed. Finally, the conclusion has been highlighted in Sect. 7.

2 Modelling of a Quadruped Robot

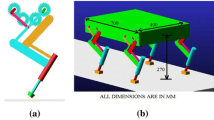
A quadruped robot with multiple degrees of freedom will exhibit highly nonlinear behavior. The modelling of a quadruped robot can be derived based on both kinematic and dynamic characteristics [25,26,27]. Figure 1 below demonstrates the 3D structure of the quadruped robot. As shown, there are four legs, in any of which, three links are given to provide a high range of flexibility during the motion. This structure is implemented using the Multibody Simscape package. The front and rear of the right-handed side legs are utilized in deriving the mathematical models of kinematic and dynamic characteristics that govern the motion of the quadruped robot in a given workspace. The other two legs behave similarly to the front and the rear of the right-handed side legs.

Fig. 1
figure 1

The 3D structure of the quadruped robot

Full size image

The inspiration to derive the mathematic model is based on two links per leg which extend to three links per leg taking into consideration a new structure of the movement. The systematic diagram of the quadruped robot is depicted in Fig. 2 which also shows the distribution of masses the elements that comprise the body of the quadruped robot. The front and the rear of right-handed side legs are shown in Fig. 3 which illustrates the kinematic analysis of the body’s links. These two legs will be only used in deriving the kinematic and dynamic models as the other two legs are likewise. The parameters utilized in this structure are identified as follows:

Fig. 2
figure 2

Systematic diagram of the quadruped robot

Full size image
Fig. 3
figure 3

The three kinematic analysis of the quadruped robot

Full size image

\(m:\) mass of the body of a quadruped robot.

\(L:\) length of the body of the quadruped robot.

\(m_{i} :\) mass of \(ith\) link.

\(L_{i} :\) length of \(ith\) link.

\(L_{ci} :\) the distance between the center of mass and the lower joint of \(ith\) link.

\(\theta_{i} :\) angle of \(ith\) link with respect to the horizontal axis.

\(\left( {x_{ci} ,y_{ci} } \right):\) are the coordinates of the center of mass of \(ith\) link.

The modelling of the quadruped robot can be analyzed based on both kinematic and dynamic characteristics as follows:

  1. (a)

    Kinematic Model

This section deals with the derivation of the center positions of each link of the two legs shown in Fig. 3 with respect to the ground plane. For the first three links of the rear right-handed side, the center positions can be determined using the following equations:

$$x_{c1} = - L_{c1} \cos \theta_{1}$$
(1)
$$y_{c1} = L_{c1} sin\theta_{1}$$
(2)
$$x_{c2} = - L_{1} \cos \theta_{1} + L_{c2} cos\theta_{2}$$
(3)
$$y_{c2} = L_{1} sin\theta_{1} + L_{c2} sin\theta_{2}$$
(4)
$$x_{c3} = - L_{1} \cos \theta_{1} + L_{2} cos\theta_{2} + L_{c3} cos\theta_{3}$$
(5)
$$y_{c3} = L_{1} sin\theta_{1} + L_{2} sin\theta_{2} + L_{c3} sin\theta_{3}$$
(6)

Similarly, for the first three links of the rear left-handed side, the center positions can be determined using the following equations:

$$x_{c4} = - L_{1} \cos \theta_{1} + L_{2} cos\theta_{2} + L_{3} cos\theta_{3} + L + L_{4} \cos \theta_{4} - L_{c4} \cos \theta_{4}$$
(7)
$$y_{c4} = L_{1} sin\theta_{1} + L_{2} sin\theta_{2} + L_{3} sin\theta_{3} - L_{4} sin\theta_{4} + L_{c4} sin\theta_{4}$$
(8)
$$x_{c5} = - L_{1} \cos \theta_{1} + L_{2} cos\theta_{2} + L_{3} cos\theta_{3} + L + L_{4} \cos \theta_{4} + L_{5} cos\theta_{5} - L_{c5} \cos \theta_{5}$$
(9)
$$y_{c5} = L_{1} sin\theta_{1} + L_{2} sin\theta_{2} + L_{3} sin\theta_{3} - L_{4} sin\theta_{4} - L_{5} sin\theta_{5} + L_{c5} sin\theta_{5}$$
(10)
$$x_{c6} = - L_{1} \cos \theta_{1} + L_{2} cos\theta_{2} + L_{3} cos\theta_{3} + L + L_{4} \cos \theta_{4} + L_{5} cos\theta_{5} - L_{c6} \cos \theta_{6}$$
(11)
$$y_{c6} = L_{1} sin\theta_{1} + L_{2} sin\theta_{2} + L_{3} sin\theta_{3} - L_{4} sin\theta_{4} - L_{5} sin\theta_{5} + L_{c6} sin\theta_{6}$$
(12)
  1. (b)

    Dynamic Model

The dynamic model of a quadruped robot can be analyzed based on its overall structure which is composed of different bodies, joints, and links. The elements if the quadruped robot’s body are acting based on applied forces in addition to internal and external characteristics such as the moment of inertia, friction, gravity and body’s constraints. In this paper, the Lagrange dynamic equation is utilized to model the motion of a quadruped robot as in the following equation:

$$D\left( \theta \right)\ddot{\theta } + H\left( {\theta ,\dot{\theta }} \right)\dot{\theta } + G\left( \theta \right) = T$$
(13)

where \(\theta = \left[ {\begin{array}{*{20}c} {\theta_{1} } & {\theta_{2} } & {\begin{array}{*{20}c} {\theta_{3} } & {\theta_{4} } & {\begin{array}{*{20}c} {\theta_{5} } & {\theta_{6} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]\) is the vector angle of \(i{th}\) link with respect to the vertical ground plane.

\(D\left( \theta \right) = \left[ {d_{ij} \left( \theta \right)} \right] \left( {i,j = 1, \ldots ,6} \right)\) is the inertia matrix; \(H\left( {\theta ,\dot{\theta }} \right) = col\left[ {\mathop \sum \nolimits_{{j = 1\left( {j \ne i} \right)}}^{6} \left( {h_{ij} \left( {\dot{\theta }_{j} } \right)^{2} } \right)} \right]\) is the centrifugal matrix; \(G\left( \theta \right) = col\left[ {G_{i} \left( \theta \right)} \right]\) is the gravity vector;

\(T = \left[ {\begin{array}{*{20}c} {T_{1} } & {T_{2} } & {\begin{array}{*{20}c} {T_{3} } & {T_{4} } & {\begin{array}{*{20}c} {T_{5} } & {T_{6} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]^{\varvec{T}}\) is the vector of external torque applied at joints.

The \(D\left( \theta \right)\) is a 6 × 6 inertia matrix and can be given as follows:

$$D\left( \theta \right) = \left[ {\begin{array}{*{20}c} {d_{11} } & {d_{12} } & {\begin{array}{*{20}c} {d_{13} } & {\begin{array}{*{20}c} {d_{14} } & {\begin{array}{*{20}c} {d_{15} } & {d_{16} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ {d_{21} } & {d_{22} } & {\begin{array}{*{20}c} {d_{23} } & {\begin{array}{*{20}c} {d_{24} } & {\begin{array}{*{20}c} {d_{25} } & {d_{26} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} {d_{31} } \\ {d_{41} } \\ {\begin{array}{*{20}c} {d_{51} } \\ {d_{61} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {d_{32} } \\ {d_{42} } \\ {\begin{array}{*{20}c} {d_{52} } \\ {d_{62} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {d_{33} } \\ {d_{43} } \\ {\begin{array}{*{20}c} {d_{53} } \\ {d_{63} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {d_{34} } \\ {d_{44} } \\ {\begin{array}{*{20}c} {d_{54} } \\ {d_{64} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {d_{35} } \\ {d_{45} } \\ {\begin{array}{*{20}c} {d_{55} } \\ {d_{65} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {d_{36} } \\ {d_{46} } \\ {\begin{array}{*{20}c} {d_{56} } \\ {d_{66} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]$$
(14)

The parameters of the inertia matrix \(D\left( \theta \right)\) can be determined as in below:

$$d_{11} = I_{1} + m_{1} L_{1c}^{2} + \left( {m_{2} + m_{3} + m_{4} + m_{5} + m_{6} + m} \right)L_{1}^{2}$$
$$d_{12} = p_{12} \cos \left( {\theta_{1} + \theta_{2} } \right), d_{13} = p_{13} \cos \left( {\theta_{1} + \theta_{3} } \right)$$
$$d_{14} = p_{14} \cos \left( {\theta_{1} - \theta_{4} } \right),\quad d_{15} = p_{15} \cos \left( {\theta_{1} - \theta_{5} } \right)$$
$$d_{16} = p_{16} \cos \left( {\theta_{1} + \theta_{6} } \right),\quad d_{21} = d_{12} ,$$
$$d_{22} = I_{2} + m_{2} L_{2c}^{2} + \left( {m_{3} + m_{4} + m_{5} + m_{6} + m} \right)L_{2}^{2}$$
$$d_{23} = p_{23} \cos \left( {\theta_{2} - \theta_{3} } \right),\quad d_{24} = p_{24} \cos \left( {\theta_{2} + \theta_{4} } \right)$$
$$d_{25} = p_{25} \cos \left( {\theta_{2} + \theta_{5} } \right),\quad d_{26} = p_{26} \cos \left( {\theta_{2} - \theta_{6} } \right)$$
$$d_{31} = d_{13} ,\quad d_{32} = d_{23} ,$$
$$d_{33} = I_{3} + m_{3} L_{3c}^{2} + \left( {m_{3} + m_{4} + m_{5} + m_{6} + m} \right)L_{3}^{2}$$
$$d_{34} = p_{34} \cos \left( {\theta_{3} + \theta_{4} } \right),\quad d_{35} = p_{35} \cos \left( {\theta_{3} + \theta_{5} } \right)$$
$$d_{36} = p_{36} \cos \left( {\theta_{3} - \theta_{6} } \right)$$
$$d_{41} = d_{14} ,\quad d_{42} = d_{24} ,\quad d_{43} = d_{34}$$
$$d_{44} = I_{4} + m_{4} L_{4c}^{2} - 2m_{4} L_{4} L_{4c} + \left( {m_{5} + m_{6} } \right)L_{4}^{2}$$
$$d_{45} = p_{45} \cos \left( {\theta_{4} - \theta_{5} } \right),\quad d_{46} = p_{46} \cos \left( {\theta_{4} + \theta_{6} } \right)$$
$$d_{51} = d_{15} ,\quad d_{52} = d_{25} ,\quad d_{53} = d_{35} ,\quad d_{54} = d_{45} ,$$
$$d_{55} = I_{5} + m_{5} L_{5c}^{2} - 2m_{5} L_{5} L_{5c} + \left( {m_{5} + m_{6} } \right)L_{5}^{2}$$
$$d_{56} = p_{56} \cos \left( {\theta_{5} + \theta_{6} } \right)$$
$$d_{61} = d_{16} ,\quad d_{62} = d_{26} , \quad d_{63} = d_{36} ,\quad d_{64} = d_{46}$$
$$d_{65} = d_{56} ,\quad d_{66} = I_{6} + m_{6} L_{6c}^{2}$$

\(I_{i}\) is the moment of inertia with respect to an axis that passes through the mass center of \(ith\) link and it is perpendicular to the motion plane.

The centrifugal matrix \(H\left( {\theta ,\dot{\theta }} \right)\) is also a 6 × 6 matrix and its parameters can be calculated as in the following equations:

$$H\left( \theta \right) = \left[ {\begin{array}{*{20}c} {h_{11} } & {h_{12} } & {\begin{array}{*{20}c} {h_{13} } & {\begin{array}{*{20}c} {h_{14} } & {\begin{array}{*{20}c} {h_{15} } & {h_{16} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ {h_{21} } & {h_{22} } & {\begin{array}{*{20}c} {h_{23} } & {\begin{array}{*{20}c} {h_{24} } & {\begin{array}{*{20}c} {h_{25} } & {h_{26} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} {h_{31} } \\ {h_{41} } \\ {\begin{array}{*{20}c} {h_{51} } \\ {h_{61} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {h_{32} } \\ {h_{42} } \\ {\begin{array}{*{20}c} {h_{52} } \\ {h_{62} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {h_{33} } \\ {h_{43} } \\ {\begin{array}{*{20}c} {h_{53} } \\ {h_{63} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {h_{34} } \\ {h_{44} } \\ {\begin{array}{*{20}c} {h_{54} } \\ {h_{64} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {h_{35} } \\ {h_{45} } \\ {\begin{array}{*{20}c} {h_{55} } \\ {h_{65} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {h_{36} } \\ {h_{46} } \\ {\begin{array}{*{20}c} {h_{56} } \\ {h_{66} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]$$
(15)
$$h_{11} = 0,\quad h_{12} = - p_{12} \sin \left( {\theta_{1} + \theta_{2} } \right),\quad h_{13} = - p_{13} \sin \left( {\theta_{1} + \theta_{3} } \right),$$
$$h_{14} = p_{14} \sin \left( {\theta_{1} - \theta_{4} } \right),\quad h_{15} = p_{15} \sin \left( {\theta_{1} - \theta_{5} } \right),$$
$$h_{16} = - p_{16} \sin \left( {\theta_{1} + \theta_{6} } \right),$$
$$h_{21} = h_{12} , \quad h_{22} = 0,\quad h_{23} = p_{23 } { \sin }\left( {\theta_{2} - \theta_{3} } \right)$$
$$h_{24} = p_{24 } { \sin }\left( {\theta_{2} + \theta_{4} } \right),\quad h_{25} = p_{25 } { \sin }\left( {\theta_{2} + \theta_{5} } \right)$$
$$h_{26} = p_{26 } { \sin }\left( {\theta_{2} - \theta_{6} } \right)$$
$$h_{31} = h_{13} , h_{32} = - h_{23} , h_{33} = 0,\quad h_{34} = - p_{34 } { \sin }\left( {\theta_{3} + \theta_{4} } \right)$$
$$h_{35} = p_{35 } { \sin }\left( {\theta_{3} - \theta_{5} } \right),\quad h_{36} = p_{36 } { \sin }\left( {\theta_{3} - \theta_{6} } \right)$$
$$h_{41} = - h_{14} , \quad h_{42} = h_{24} , \quad h_{43} = h_{34} ,\quad h_{44} = 0$$
$$h_{45} = - p_{45 } { \sin }\left( {\theta_{4} - \theta_{5} } \right),\quad h_{46} = - p_{46 } { \sin }\left( {\theta_{4} + \theta_{6} } \right)$$
$$h_{51} = - h_{15} , \quad h_{52} = h_{25} , \quad h_{53} = h_{35} ,\quad h_{56} = - h_{45} ,\quad h_{55} = 0$$
$$h_{56} = - p_{56 } { \sin }\left( {\theta_{5} + \theta_{6} } \right)$$
$$h_{61} = h_{16} ,\quad h_{62} = - h_{26} ,\quad h_{63} = - h_{36} ,\quad h_{64} = h_{46} ,$$
$$h_{65} = h_{56} ,\quad h_{66} = 0.$$

where

$$p_{12} = m_{2} L_{2c} L_{1} + \left( {m_{3} + m_{4} + m_{5} + m_{6} + m} \right)L_{1} L_{2}$$
$$p_{13} = m_{3} L_{1} L_{3c} + \left( {m_{4} + m_{5} + m_{6} + m} \right)L_{1} L_{3}$$
$$p_{14} = m_{4} L_{1} L_{4c} - \left( {m_{4} + m_{5} + m_{6} } \right)L_{1} L_{4}$$
$$p_{15} = m_{5} L_{1} L_{5c} - \left( {m_{5} + m_{6} } \right)L_{1} L_{5}$$
$$p_{16} = m_{6} L_{1} L_{6c}$$
$$p_{23} = m_{3} L_{2} L_{3c} + \left( {m_{4} + m_{5} + m_{6} + m} \right)L_{2} L_{3}$$
$$p_{24} = m_{4} L_{2} L_{4c} - \left( {m_{4} + m_{5} + m_{6} } \right)L_{2} L_{4}$$
$$p_{25} = m_{5} L_{2} L_{5c} - \left( {m_{5} + m_{6} } \right)L_{2} L_{5}$$
$$p_{26} = m_{6} L_{2} L_{6c}$$
$$p_{34} = m_{4} L_{3} L_{4c} - \left( {m_{4} + m_{5} + m_{6} } \right)L_{3} L_{4}$$
$$p_{35} = m_{5} L_{3} L_{5c} - \left( {m_{5} + m_{6} } \right)L_{3} L_{5}$$
$$p_{36} = m_{6} L_{3} L_{6c}$$
$$p_{45} = - m_{5} L_{4} L_{5c} + \left( {m_{5} + m_{6} } \right)L_{4} L_{5}$$
$$p_{46} = - m_{6} L_{4} L_{6c}$$
$$p_{56} = - m_{6} L_{5} L_{6c}$$

The parameters of gravity vector \(G\left( \theta \right)\) can be computed as follows:

$$G_{1} = \left[ {m_{1} L_{1c} + \left( {m_{2} + m_{3} + m_{4} + m_{5} + m_{6} + m} \right)L_{1} } \right]gcos\left( {\theta_{1} } \right)$$
$$G_{2} = \left[ {m_{2} L_{2c} + \left( {m_{3} + m_{4} + m_{5} + m_{6} + m} \right)L_{2} } \right]gcos\left( {\theta_{2} } \right)$$
$$G_{3} = \left[ {m_{3} L_{3c} + \left( {m_{4} + m_{5} + m_{6} + m} \right)L_{3} } \right]gcos\left( {\theta_{3} } \right)$$
$$G_{4} = - \left[ {m_{4} \left( {L_{4} - L_{4c} } \right) + \left( {m_{5} + m_{6} } \right)L_{4} } \right]gcos\left( {\theta_{4} } \right)$$
$$G_{5} = - \left[ {m_{5} \left( {L_{5} - L_{5c} } \right) + m_{6} L_{5} } \right]gsin\left( {\theta_{5} } \right)$$
$$G_{6} = \left( {L_{6c} + L_{6} } \right)m_{6} gsin\left( {\theta_{6} } \right)$$

\(g\) is acceleration of gravity.

It is assumed that \(U = \left[ {\begin{array}{*{20}c} {u_{1} } & {u_{2} } & {u_{3} } & {u_{4} } & {u_{5} } & {u_{6} } \\ \end{array} } \right]\) is the vector of the driving torques of the six rotating joints of quadruped robot which are generated from the servo motors, thus, the following equation can be written as:

$$T = SU^{T}$$
(16)

where \(S \in {\mathbb{R}}^{6 \times 6}\) is a transformation matrix which can be given as:

$$S = \left[ {\begin{array}{*{20}c} { - 1} & 0 & 0 & 0 & 0 & 0 \\ { - 1} & { - 1} & 0 & 0 & 0 & 0 \\ 0 & 0 & { - 1} & 0 & 0 & 0 \\ 0 & 0 & 0 & { - 1} & 0 & 0 \\ 0 & 0 & 0 & { - 1} & { - 1} & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 \\ \end{array} } \right]$$

3 Control System Design

In this section, control systems are designed and implemented as will be discussed in the following subsections. These two controlling systems are the PID controller and the Fuzzy logic controller. In the designed system, there are four legs in which each leg has three links. Therefore, there will be twelve links in total. Each link is driven from a separate servo motor. The structure of each group of links is identical to others. Hence, we will only introduce the control system for one link and the others are exactly the same architecture. The block diagram of each link has two inputs and three outputs. The inputs are the ‘B’ which represents the port that connects the current link with the previous one. The second input is ‘t’ which represents the control signal supplied to the torque of a servo motor. The outputs are F, q and w, F is the connection point between the current link and the next one. The q and w are the angle and speed of a current link, respectively. Figure 4 below shows the block diagram of a link in a leg.

Fig. 4
figure 4

Block diagram of a link in a leg

Full size image

Based on the operation of the DC servo motor, the speed and torque of the DC servo motor can be controlled by sending electrical pulses of variable width. For each servo motor, there is a minimum pulse and a maximum pulse and any of which has a repetition rate. The width of the sent electrical pulses changes the value of the applied voltage accordingly where the speed of a servo is dependent. Furthermore, as the voltage changes, the flowing current will be changed which leads to the torque being changed as well.

Overall, there will be three block diagrams in our design for each leg, thus, twelve block diagrams in the entire system. Consequently, this requires twelve controllers to achieve feasible movement of a quadruped robot.

3.1 PID Controller

The PID controller is widely used in many industrial applications [28]. The structure of the PID controller consists of three parameters, i.e., proportional gain (\({\text{k}}_{\text{P}}\)), integral gain (\({\text{k}}_{\text{I}}\)) and derivative gain (\({\text{k}}_{\text{D}}\)), any of which can be tuned to obtain an optimal value based on specifications of a given system. The main equation that governors the operation of such a controller is illustrated below.

$$u_{PID} \left( t \right) = k_{P} e\left( t \right) + k_{I} \int e\left( t \right)dt + k_{D} \dot{e}\left( t \right)$$
(17)

where \(e\left( t \right)\) is an error signal between two signals, i.e., reference and actual values. The reference value is supplied signal based on the desired input of a plant and the actual value is the real output response of that plant.

The parameters of the PID controller play a crucial role in changing an overall performance and a time response of the system and it can significantly influence the operation conditions either positively or negatively. In order to reach the best response possible, the kp, ki and kd need to be tuned optimally. The architecture of a PID controller in connection with only one link in a leg is given in Fig. 5 below.

Fig. 5
figure 5

PID controller for one link in a leg

Full size image

To obtain optimal performance of PID controllers, we need to optimize their parameters using optimization algorithms. Recently, many optimization algorithms are developed such as Genetic Algorithm (GA) [29], Particle Swarm Optimization (PSO) algorithm [30], Artificial Bee Colony (ABC) algorithm [31] and Ant Colony Optimization (ACO) [32, 33], any of which has its own structure and method in order to approach an optimal solution for a given optimization algorithm. The ACO algorithm has been developed as a meta-heuristic algorithm that can address high combinational optimization problems. It has unique advantages such as the construction graph used in the ACO algorithm that can make the search space represented less redundant. In addition, it has fewer parameters and strong robustness [34]. The principle operation of ACO is based on the behavior of ants which can be represented by individuals that can find a suitable solution for an optimization problem. The best solution can be determined globally by the cooperation of all ants together.

In this paper, the ACO algorithm will be utilized to tune the parameters of the twelve PID controllers in the offline mode. Therefore, a parameter matrix (PM) can be created which has three columns and \(N\) rows as shown below:

$$PM = \left[ {\begin{array}{*{20}c} {P_{11} } & {P_{12} } & {P_{13} } \\ {P_{21} } & {P_{22} } & {P_{23} } \\ . & . & . \\ . & . & . \\ . & . & . \\ {P_{N1} } & {P_{N2} } & {P_{N3} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {k_{P1} } & {k_{I1} } & {k_{D1} } \\ {k_{P2} } & {k_{I2} } & {k_{D2} } \\ . & . & . \\ . & . & . \\ . & . & . \\ {k_{PN} } & {k_{IN} } & {k_{DN} } \\ \end{array} } \right]$$
(18)

where each row of \(PM\) matrix represents the candidates of \(k_{P} ,\, k_{I} \,{\text{and}}\,k_{D}\), respectively; \(N\) is the total number of candidates for any parameters. For reducing the time of optimization search, the maximum and minimum values are assumed known. The values of candidates’ elements of \(k_{P} ,\,k_{I} \,and\,k_{D}\) are equally distributed between these values (maximum and minimum values). The problem is to find the optimal value for each parameter that minimizes the cost function.

Figure 6 illustrates the graphical representation for selecting the best parameters of the PID controller using the ACO algorithm. The three columns represent the tunable parameters of a PID controller. The selection of the node in any column “by ant” is based on pheromone trails between nodes of each parameter. The connection matrix between the columns is called the pheromone matrix \(\tau \in {\mathbb{R}}^{3 \times N}\). Each element of the pheromone matrix is denoted by \(\tau_{ij} \,for\,i = 1,2,3\,and\,j = 1,2, \ldots ,N\). The selection of the specific node from any column “by ant” is achieved according to the state transition rule as illustrated in algorithm no. 1.

Fig. 6
figure 6

Graphical representation of ACO for selection process

Full size image

Algorithm no.1 given below, summaries the tuning procedures of ant colony optimization algorithm to select optimal parameters for a PID. The algorithm starts by defining the inputs and outputs and then providing tuning processing based on the behavior of the ACO algorithm to obtain optimal parameters of PID controller. The numbers of iterations that are needed to find the best parameters of the PID controller can be reduced by introducing knowledge in the range of parameters of the PID controller (maximum and minimum values). The learning tours of the ACO algorithm are stopped when the cost function is equal to or less than a small value \(\varepsilon\).

figure a

In other words, we firstly initialized the elements of the parameter matrix (PM) where \(\tau_{ij} \left( 0 \right) = \tau_{0}\), secondly, the selection of the values of candidates for each control parameter has been accomplished by using Step no. 4 in the Algorithm no. 1 above. Thirdly, the choice of the PID controller’s parameters has been achieved by using Step no. 9 in the same algorithm. Fourthly, the control signal of the PID controller is computed by using Eq. (17) given earlier which is applied to the plant. Then, the value of the cost function needs to be calculated by Step no. 12 as in the above algorithm. Finally, the value of the cost function is compared with the set value \(\varepsilon\), consequently, if the cost function (\(CF\)) \(\le \varepsilon\), then the optimal values are reached, otherwise, another set of PID controller’s parameters will be chosen based on Step no. 9 and the following will re-occurring until the main condition of the cost function is satisfied. It seen that, the cost function is based on a mean squared error.

3.2 Fuzzy Controller

Fuzzy control has successfully proved its suitability and effectiveness to solve complex problems [35,36,37,38]. The principle operation of Fuzzy control systems is based on multiple stages, i.e., fuzzification, inference engine, and defuzzification. The implementation of those stages is based on selecting appropriate membership functions and inference engine rules which are specifically designed to a particular problem. In this work, twelve fuzzy controllers are designed (one for each joint) to control the gait of a quadruped robot. Each fuzzy control system has two inputs (an error and a change of error) and one output (control signal). The input membership functions are assumed symmetrical about the y-axis. For each input variable, five equally spaced triangular membership functions are selected. Other types of membership functions have been tested such as Gaussian functions and Bell functions. However, it is found that the triangular membership functions are more suitable than the others. It is assumed that the parameters of the input membership functions are inadaptable. The universe of discourse of error membership functions is ranged from ‘− 20’ to ‘20’, while the universe of discourse of change of error membership functions is ranged from ‘− 5’ to ‘5’. The input membership functions are labelled as Negative Big (NB), Negative Small (NS), Zero (ZE), Positive Small (PS), and Positive Big (PB). While the distribution of seven output triangular membership functions on the output universe of discourse is initialized randomly. Table 1 shows the rules relationships between error and change of error from one side and the output ‘q’ from the other side. The centres of output membership functions are assumed adaptable. Figure 7 below shows the block diagram of a Fuzzy controller for one link in a leg.

Table 1 The rules inference for each fuzzy controller
Full size table
Fig. 7
figure 7

Fuzzy controller for one link in a leg

Full size image

As explained earlier regarding the tuning of PID controllers using the ACO algorithm, the latter is used to tune the parameters of the centres of membership functions the fuzzy controllers. The algorithm no. 2 demonstrates the steps to reach optimal values of centres of output membership functions. Likewise, the algorithm starts by identifying the inputs and the outputs, ranging boundaries of the minimum and maximum values. The control signal generated from the fuzzy controller is computed from the equation below:

$$u\left( \varvec{x} \right) = \frac{{\mathop \sum \nolimits_{i} u_{i} \left( \varvec{x} \right) \times \delta_{{{\text{premise}}\left( {i } \right)}} \left( \varvec{x} \right)}}{{\mathop \sum \nolimits_{i} \delta_{{{\text{premise}}\left( {i } \right)}} \left( \varvec{x} \right)}}$$
(19)

where \(u_{i} \left( x \right)\) is the output value of \(ith\) rule, \(\delta_{{{\text{premise}}\left( {i } \right)}} \left( \varvec{x} \right)\) is the value of the premise. It is computed from the following equation.

$$\delta_{{{\text{premise}}\left( {i } \right)}} \left( \varvec{x} \right) = min\left\{ {\delta_{{A_{i1} }} \left( {x_{1} } \right),\delta_{{A_{i2} }} \left( {x_{2} } \right), \ldots ,\delta_{{A_{in} }} \left( {x_{n} } \right) } \right\} \in \left[ {0,1} \right],\quad \forall x_{i} \in X,\quad where\,i = 1, \ldots ,R$$
(20)

where: \(\delta_{{A_{ik} }}\) (\(x_{k} )\) is the input membership function of \(kth\) linguistic value; and \(X\) is the universe of discourse of the input linguistic variables.

figure b

4 Lyapunov Stability Test for Fuzzy System

To prove that the controlled system stays stable and has an acceptable response, the testing of the stability of the proposed controller should be achieved to confirm the effectiveness and suitability of the proposed controller even different significant disturbances are applied to the controlled system. Therefore, in this section, the Lyapunov stability criterion [39] is used to test the stability of the fuzzy control system. The Lyapunov stability criterion states that the nonlinear system is stable if the following conditions are satisfied [40]:

  1. 1.

    \(\mu \left( \varvec{x} \right) > 0\) for all values of states \(\varvec{x} \ne 0\).

  2. 2.

    \(\dot{\mu }\left( \varvec{x} \right) \le 0\) for all values of states \(\varvec{x}\).

where \(\mu \left( \varvec{x} \right)\) is a Lyapunov function which is assumed as:

$$\mu \left( \varvec{x} \right) = \varvec{x}^{T} \rho \varvec{x}$$
(21)

where \(\rho \in {\mathbb{R}}^{n \times n}\) is assumed as a symmetric positive definite matrix. Depending on this assumption, the first condition of the Lyapunov stability criterion is satisfied. The first derivative of the Lyapunov function is written as:

$$\dot{\mu }\left( \varvec{x} \right) = \dot{\varvec{x}}^{T} \rho \varvec{x} + \varvec{x}^{T} \rho \dot{\varvec{x}}$$
(22)

The state-space equations of any nonlinear system can be written as [1]:

$$\dot{\varvec{x}} = A\left( \varvec{x} \right) + B\left( \varvec{x} \right)u\left( \varvec{x} \right)$$
(23)

where: \(\varvec{x} \in {\mathbb{R}}^{n \times 1}\) is the state variable; \(A\left( \varvec{x} \right) \in {\mathbb{R}}^{n \times 1}\) is nonlinear function vector; \(B\left( \varvec{x} \right) \in {\mathbb{R}}^{n \times 1}\) is nonlinear function vector; \(u\left( \varvec{x} \right)\) is the control signal and \(n\) is the number of the state variables.

If the fuzzy system is proposed as a controller for a nonlinear system, the control signal is given by Eq. (18).

Therefore, Eq. (21) can be rewritten as:

$$\therefore \dot{\mu }\left( \varvec{x} \right) = \varGamma \left( \varvec{x} \right) + \varPhi \left( \varvec{x} \right)u\left( \varvec{x} \right)$$
(24)

where the terms of the equation above are given by: \(\varGamma \left( \varvec{x} \right) = A\left( \varvec{x} \right)^{T} \rho \varvec{x} + \varvec{x}^{T} \rho A\left( \varvec{x} \right)\) and \(\varPhi \left( \varvec{x} \right) = B\left( \varvec{x} \right)^{T} \rho \varvec{x} + \varvec{x}^{T} \rho B\left( \varvec{x} \right)\)

The vector \(\varPhi \left( \varvec{x} \right)\) is defined into three regions:

  1. 1.

    Positive region: \(\varPhi \left( \varvec{x} \right) > 0\) or it is described as the following set: \(\varPhi_{ + ve} = \left\{ {x \in X\left| {\varPhi \left( \varvec{x} \right)} \right\rangle 0} \right\}\).

  2. 2.

    Negative region: \(\varPhi \left( \varvec{x} \right) < 0\) or it is described as the following set: \(\varPhi_{ - ve} = \left\{ {x \in X|\varPhi \left( \varvec{x} \right) < 0} \right\}\).

  3. 3.

    Zero region: \(\varPhi \left( \varvec{x} \right) = 0\) or it is as the following set: \(\varPhi_{ze} = \left\{ {x \in X|\varPhi \left( \varvec{x} \right) = 0} \right\}\).

If the Lyapunov function exists, then the following points should be satisfied:

  1. 1.

    \(\varGamma \left( \varvec{x} \right) \le 0,\quad \forall \varvec{x} \in \varPhi_{ze}\).

  2. 2.

    \(u_{i} \left( \varvec{x} \right) \le - \frac{{\varGamma \left( \varvec{x} \right)}}{{\varPhi \left( \varvec{x} \right)}}\,\,for\,\varvec{x} \in X_{i}^{a} \cap \varPhi_{ + ve} \,and\,u_{i} \left( \varvec{x} \right) \ge - \frac{{\varGamma \left( \varvec{x} \right)}}{{\varPhi \left( \varvec{x} \right)}}\,for\,\varvec{x} \in X_{i}^{a} \cap \varPhi_{ - ve} \quad for\,i = 1, \ldots ,R\).

  3. 3.

    For any initial state \(\varvec{ x}_{0} \in X\), the set \(\left\{ {\varvec{x} \in X|\dot{\mu }\left( \varvec{x} \right) = 0} \right\}\).

Now, the second condition of the Lyapunov stability criterion should be satisfied for all regions of vector \(\varPhi \left( \varvec{x} \right)\).

  1. 1.

    If \(\varPhi \left( \varvec{x} \right)\) is positive, for any arbitrary initial state \(\varvec{ x}_{0} \in X\), then:

    $$u_{i} \left( { \varvec{x}_{0} } \right) \le - \frac{{\varGamma \left( { \varvec{x}_{0} } \right)}}{{\varPhi \left( { \varvec{x}_{0} } \right)}} \Rightarrow u\left( { \varvec{x}_{0} } \right) = \frac{{\mathop \sum \nolimits_{i} u_{i} \left( {\varvec{x}_{0} } \right) \times \delta_{{premise\left( {i } \right)}} \left( {\varvec{x}_{0} } \right)}}{{\mathop \sum \nolimits_{i} \delta_{{premise\left( {i } \right)}} \left( {\varvec{x}_{0} } \right)}} \le \frac{{\frac{{ - \varGamma \left( { \varvec{x}_{0} } \right)}}{{\varPhi \left( { \varvec{x}_{0} } \right)}}\mathop \sum \nolimits_{i} \delta_{{premise\left( {i } \right)}} \left( {\varvec{x}_{0} } \right)}}{{\mathop \sum \nolimits_{i} \delta_{{premise\left( {i } \right)}} \left( {\varvec{x}_{0} } \right)}} = - \frac{{\varGamma \left( { \varvec{x}_{0} } \right)}}{{\varPhi \left( { \varvec{x}_{0} } \right)}}$$
    $$\therefore \dot{\mu }\left( {x_{0} } \right) = \varGamma \left( {x_{0} } \right) + \varPhi \left( {x_{0} } \right)u\left( {x_{0} } \right) \le \varGamma \left( {x_{0} } \right) + \varPhi \left( {x_{0} } \right)\left( { - \frac{{\varGamma \left( { \varvec{x}_{0} } \right)}}{{\varPhi \left( { \varvec{x}_{0} } \right)}}} \right) = 0$$

    \(\therefore \dot{\mu }\left( x \right) \le 0 \Rightarrow\) the second condition of the Lyapunov stability criterion is satisfied.

  2. 2.

    If \(\varPhi \left( \varvec{x} \right)\) is negative, for any arbitrary initial state \(\varvec{ x}_{0} \in X\), then:

    $$u_{i} \left( { \varvec{x}_{0} } \right) \ge - \frac{{\varGamma \left( { \varvec{x}_{0} } \right)}}{{\varPhi \left( { \varvec{x}_{0} } \right)}} \Rightarrow u\left( { \varvec{x}_{0} } \right) = \frac{{\mathop \sum \nolimits_{i} u_{i} \left( {\varvec{x}_{0} } \right) \times \delta_{{premise\left( {i } \right)}} \left( {\varvec{x}_{0} } \right)}}{{\mathop \sum \nolimits_{i} \delta_{{premise\left( {i } \right)}} \left( {\varvec{x}_{0} } \right)}} \ge \frac{{\frac{{ - \varGamma \left( { \varvec{x}_{0} } \right)}}{{\varPhi \left( { \varvec{x}_{0} } \right)}}\mathop \sum \nolimits_{i} \delta_{{premise\left( {i } \right)}} \left( {\varvec{x}_{0} } \right)}}{{\mathop \sum \nolimits_{i} \delta_{{premise\left( {i } \right)}} \left( {\varvec{x}_{0} } \right)}} = - \frac{{\varGamma \left( { \varvec{x}_{0} } \right)}}{{\varPhi \left( { \varvec{x}_{0} } \right)}}$$
    $$\therefore \dot{\mu }\left( {x_{0} } \right) = \varGamma \left( {x_{0} } \right) + \varPhi \left( {x_{0} } \right)u\left( {x_{0} } \right) \le \varGamma \left( {x_{0} } \right) + \varPhi \left( {x_{0} } \right)\left( { - \frac{{\varGamma \left( { \varvec{x}_{0} } \right)}}{{\varPhi \left( { \varvec{x}_{0} } \right)}}} \right) = 0$$

    \(\therefore \dot{\mu }\left( x \right) \le 0 \Rightarrow\) the second condition of the Lyapunov stability criterion is satisfied.

  3. 3.

    If \(\varPhi \left( \varvec{x} \right)\) is zero, for any arbitrary initial state \(\varvec{ x}_{0} \in X\), then:

    $$\dot{\mu }\left( {x_{0} } \right) = \varGamma \left( {x_{0} } \right) + \varPhi \left( {x_{0} } \right)u\left( {x_{0} } \right) = \varPhi \left( {x_{0} } \right) \le 0$$

    \(\therefore \dot{\mu }\left( x \right) \le 0 \Rightarrow\) the second condition of the Lyapunov stability criterion is satisfied.

It can be seen that, the Lyapunov condition for the stability requirement is satisfied. Therefore, the proposed fuzzy controller is globally asymptotically stable.

5 Simulation Results

The simulation results are conducted to investigate the performance of the designed controllers and validate their effectiveness in guiding a quadruped robot to reach a given destination without interruptions. Three case studies are considered, i.e., firstly, an open-loop system where no controllers are used in the robot movement. Secondly, a closed-loop system using PID controllers and thirdly, a closed-loop system using fuzzy controllers as demonstrated in the following subsections.

  1. 1.

    Case study 1: open-loop system

In this case, no controllers are used in the looping system and it is required by the quadruped robot to achieve a feasible movement linearly on a road. The reference movement in the input is based on chosen angles. The robot should be able to complete its motion stably with being collapsed. However, this could not be approachable as the robot has lost its stability and collapsed immediately after the simulation starts. Figure 8a shows the quadruped robot standing at the initial position before running the simulation. When the operation is activated, the robot is collapsed without elapsing any distance as depicted in Fig. 8b.

Fig. 8
figure 8

Case study 1 a quadruped robot stands at its initial posture, b quadruped robot has just attempted to move but collapsed immediately at the same position, this is without any controller

Full size image
  1. 2.

    Case study 2: closed loop using PID controller

From the previous results, it was observed that there is a need to design a more efficient controller to stabilize the movement of the quadruped robot and move it smoothly and feasibly to its destination without breakdown. In response to such a situation, we endeavor to introduce PID controllers. As there are twelve servomotors in the robotic mechanism, therefore, twelve PID controllers are needed to control the movement of the quadruped robot parallelly across all the three links in the four legs. In order to achieve the design of the twelve PID controllers, an ACO algorithm is utilized to tune the parameters of each PID controller to reach optimal performance. The required data for the ACO algorithm is provided as in Table 2 below, which illustrates the number of iterations, ants, and nodes. After completing the tuning process, the optimal parameters of each PID controller are obtained as given in Table 3.

Table 2 The parameter of the ACO algorithm for PID controllers
Full size table
Table 3 Optimal parameters of PID controllers
Full size table

The simulation results using PID controllers have demonstrated some improvements over the previous case study as shown in Fig. 9 below. The quadruped robot commences his movement successfully starting from Fig. 9a and has reached a selected position after a few meters as shown in Fig. 9b. However, the quadruped robot has not been able to reach the expected target as it is halted at the middle distance as can be noted in Fig. 9c.

Fig. 9
figure 9

Case study 2 a quadruped robot stands at its initial posture, b quadruped robot has moved a few metres and c when the quadruped robot has proceeded further but this is the final reached position based on PID controllers

Full size image

The control efforts for the proposed PID controller are provided to demonstrate its effectiveness. Figure 10 shows the control efforts of the front left leg for three links, i.e., ankle, hip, and knee. The time responses of the control efforts illustrate that their values reach high magnitudes about 350 Nm. Such values mean that the PID control exerts high efforts to drive the quadruped robot. In Figs. 11, 12 and 13 demonstrate the control efforts for the other three legs. The simulation results show that the control efforts are quite high.

Fig. 10
figure 10

Control efforts of PID controller for front left leg

Full size image
Fig. 11
figure 11

Control efforts of PID controller for front right leg

Full size image
Fig. 12
figure 12

Control efforts of PID controller for rear right leg

Full size image
Fig. 13
figure 13

Control efforts of PID controller for rear left leg

Full size image
  1. 3.

    Case study 3: closed loop using fuzzy controller

As provided earlier, there are still some drawbacks in the overall operation of the quadruped robot. In order to obtain the best performance possible, we propose novel Fuzzy controllers to control the motion of the quadruped robot and stabilize its movement until it reaches the required position. The best-chosen parameters for the ACO algorithm are provided in Table 4. These parameters are the number of iterations, ants and nodes which represent the main elements in implementing the ACO algorithm. Accordingly, the five centres of areas are obtained as given in Table 5 for all the twelve Fuzzy controllers. From Fig. 14a–c, it is observable that the quadruped robot has stably and feasibly managed to travel along the given distance without being halted at any position in its route while moving. Based on the obtained results, it has been confirmed that all the aforementioned implications have been successfully eliminated and the proposed Fuzzy controllers have improved the overall performance significantly.

Table 4 The parameter of the ACO algorithm for Fuzzy controllers
Full size table
Table 5 Optimal centres of area for Fuzzy controllers
Full size table
Fig. 14
figure 14

Case study 3 a quadruped robot stands at its initial posture, b quadruped robot reaches approximately the middle distance and c when the quadruped robot has successfully reached the target based on Fuzzy controllers

Full size image

Similarly, the control efforts for the proposed Fuzzy controllers are obtained to demonstrate its performance as shown in Figs. 15, 16, 17 and 18. The control efforts are provided for every three links per leg which means twelve control signals are delivered to the system. It is noticeable that the control efforts for Fuzzy controllers have been decreased significantly in comparison with the PID controllers. This, in turn, provides a Fuzzy controller with great advantage as this is a key improvement in addition to the stabilized movement along the given path.

Fig. 15
figure 15

Control signal of Fuzzy controller for front left leg

Full size image
Fig. 16
figure 16

Control signal of Fuzzy controller for rear left leg

Full size image
Fig. 17
figure 17

Control signal of Fuzzy controller for rear right leg

Full size image
Fig. 18
figure 18

Control signal of Fuzzy controller for front right leg

Full size image

6 Comparison of the Proposed Controllers

In this section, we introduce some comparisons to investigate the suitability and effectiveness of the proposed controllers, i.e., PID and Fuzzy controllers in controlling the quadruped robot to move stability over the given path and reach its destination. The comparisons are based on the total travelled distances in relationship to the elapsed time for the whole path and the values of the control effort applied in the designed controllers. As can be clearly seen in Fig. 19, the Fuzzy controllers have led the quadruped robot to reach its final destination. Therefore, the total distance is higher compared to the other two case studies. In the case of no controller is applied, the distance is zero as the quadruped robot has not travelled any noticeable distance. Only, a few meters have been travelled when the PID controllers are utilized. However, this is not the target as the quadruped robot is unable to reach the final required position.

Fig. 19
figure 19

Travelled distance for the three case-studies

Full size image

The execution time is made to be fixed in all conducted case studies and it equals to 35 s. Regarding the scalability of the proposed algorithms, it has been observed that the performance of the Fuzzy controller presents significant adaptability of the designed system in comparison with the performance of the PID controller.

Furthermore, control efforts have been compared between Fuzzy and PID controllers to evaluate the significance of improvements between both types of controllers. The comparisons are only conducted for the front right leg; thus, three comparisons are needed for each link. In Fig. 20, the control efforts for the ankle joint of both Fuzzy and PID controllers are provided. They clearly demonstrate the effectiveness of the Fuzzy controller in achieving the target while minimizing the control efforts remarkably. Likewise, in Fig. 21, it is observable that the control effort of the Fuzzy controller for the hip joint is reduced. Finally, the last comparison is obtained as depicted in Fig. 22 for the knee joint which also shows a feasible response of the control efforts for the Fuzzy controller over the PID controller. These simulation results demonstrate and validate the privileges of the designed Fuzzy controller over the PID controller.

Fig. 20
figure 20

Control efforts of the ankle joint

Full size image
Fig. 21
figure 21

Control efforts of the hip joint

Full size image
Fig. 22
figure 22

Control efforts of the knee joint

Full size image

7 Conclusion

In this paper, we proposed the modelling of the quadruped robot based on three movable links per leg. This will introduce the robot with great advantages to move feasibly and smoothly. The architecture of this design has been implemented for each individual link and combined together to obtain the whole system. The latter has been tested without applying any controller and it is noticed that the robot is not capable of performing any movement. Hence, we proposed two novel controllers, i.e., PID and Fuzzy controllers which there are twelve controllers for each servomotor in each link. The PID controller has demonstrated a relatively practical start but has not been able to take the quadruped robot to the final position. Instead, the Fuzzy controller is capable of achieving the required of our design and has shown effectiveness and suitability after the performance has been validated. The parameters of both PID and Fuzzy controllers have been tuned using an ant colony optimization algorithm which has optimized the performance of each designed controller by obtaining its optimal parameters.

To investigate the overall performance of the proposed controllers and the whole designed system, two main comparisons are introduced based on the travelled distance against the elapsed time and the control efforts. The simulation results have shown high effectiveness and robustness of the proposed Fuzzy controllers in comparison to PID controllers. Moreover, the stability of the Fuzzy controllers has been approved by using the Lyapunov stability method.

In future work, the proposed three links per leg architecture will be constructed using a 3D printer. Hence, real-time experiments will be conducted to validate the proposed control systems practical and then some comparisons will be done between the theoretical and practical experiments thoroughly.