1 Introduction

Dynamical systems are frequently applied in modeling artificial and natural systems of various fields such as neuroscience, astronomy, physics, electronics, and ecology [1,2,3,4,5]. When the time of a dynamical system is described in the discrete domain, the dynamical system is called a discrete-time dynamical system (DTDS). A number of studies have also addressed the discrete-time chaotic system (DTCS) [6], a subclass of the DTDS. For example, DTCSs are proven useful in the processing of climate-related data including prediction of weather and sea surface temperatures [7, 8]. More recently, DTCSs are hired in the implementation of pseudo random number generators and cryptosystems in addition to applications in sustainable energy systems, e.g. [9, 10]. Among the important issues in the applications of DTCSs are the identification and generation of DTCSs.

Some of the representative models suggested for the identification of dynamical systems include the recurrent neural networks (RNNs), information theoretic models, and wavelet-based models [11, 12]. Among these models, the RNNs have been exploited most frequently [13,14,15,16] since their structures can be chosen adequately in quite a flexible way, and appropriate parameter optimization (training) algorithms for them can be selected from an abundance of existing algorithms. In the studies of DTCSs also, the RNNs have been used diversely. For instance, in the early studies [13, 17], DTCSs have been identified with RNNs trained by the steepest descent algorithm. The identification of DTCSs has been considered also with enhanced algorithms such as the Levenberg–Marquardt (LM), hybrid algorithms, and fuzzy neural networks [18,19,20]. In the meantime, the generation of DTCSs has been investigated in several studies including those of [21, 22].

In this paper, we apply two-layered RNNs in the identification and generation of the DTCS. The proposed method of identification allows the RNN to have only two layers, less than in the conventional identification procedures, and thus results in lower computational complexity. The proposed generation procedure of one-dimensional DTCSs is based on the Li–Yorke theorem [6]: The proposed generation procedure therefore enables us to generate a DTCS with a range of chaotic behavior specified in advance. Simulation results indicate that the proposed procedure for the identification of DTCSs using the two-layered RNN, employing the LM algorithm in the training stage, exhibits comparable performance compared to conventional identification procedures.

2 Discrete-Time Chaotic Systems

Consider an \(n\)-dimensional DTDS of which the state \(\varvec{X}\left[ t \right]\) is expressed as

$$\begin{aligned} \varvec{X}[t] & = \left[ {X_{1} [t]\;\;\;X_{2} [t]\;\;\; \cdots \;\;X_{n} [t]} \right]^{T} \\ & = \varvec{F}\left( {\varvec{X}[t - 1]} \right), \\ \end{aligned}$$
(1)

at time \(t = 1,2, \cdots\) with the initial state \(\varvec{X}[0] = \varvec{X}_{0}\). Here, the next-state function

$$\varvec{F}\left( \cdot \right) = \;\left[ {F_{1} \left( \cdot \right)\;\;\;F_{2} \left( \cdot \right)\;\;\; \cdots \;\;\;F_{n} \left( \cdot \right)} \right]^{T} ,$$
(2)

is of size \(n \times 1\), with \(F_{i}\) a scalar function on the \(n\)-dimensional space. We define \(\varvec{F}^{m} (\varvec{X}) = \varvec{F}\left( {\varvec{F}^{m - 1} (\varvec{X})} \right)\) for \(m = 1,2, \cdots\) with \(\varvec{F}^{0} (\varvec{X}) = \varvec{X}\). When \(\varvec{X} = \varvec{F}^{p} (\varvec{X})\) for a number \(p \in {\mathbb{Z}}^{ + } = \{ 1,2, \cdots \}\), the point \(\varvec{X}\) is called a periodic point of \(\varvec{F}\) and the function \(\varvec{F}\) is said to have a point of period \(p\). For example, the function \(F(X) = 4X(1 - X)\) has a point of period \(3\) and \(X = \frac{1}{2}\left( {1 + \cos \frac{\pi }{9}} \right)\) is a periodic point of \(F\) since \(\frac{1}{2}\left( {1 + \cos \frac{\pi }{9}} \right) = F^{3} \left( {\frac{1}{2}\left( {1 + \cos \frac{\pi }{9}} \right)} \right)\).

An \(n\)-dimensional DTDS with a next-state function \(\varvec{F}\) is called an \(n\)-dimensional DTCS if there exist

  1. C1.

    A number \(\tilde{p} \in {\mathbb{Z}}^{ + }\) such that \(\varvec{F}\) has a point of period \(p\) for every integer \(p \ge \tilde{p}\),

  2. C2.

    A scrambled set \(S\) (i.e., an uncountable set containing no periodic point of \(\varvec{F}\)) such that

    1. (a)

      \(\varvec{F}(\varvec{X}) \in S\) for all \(\varvec{X} \in S\), and

    2. (b)

      When \(\mathop {\varvec{X}_{0} }\limits^{ \vee }\) is a periodic point of \(\varvec{F}\) or is an element of \(S\),

    $$\mathop {\lim \sup }\limits_{m \to \infty } \left\| {\varvec{F}^{m} (\varvec{X}_{0} ) - \varvec{F}^{m} \left( {\mathop {\varvec{X}_{0} }\limits^{ \vee } } \right)} \right\|\; > \;0,$$
    (3)

    for all \(\varvec{X}_{0} \in S\) such that \(\varvec{X}_{0} \ne \mathop {\varvec{X}_{0} }\limits^{ \vee },\)

    and

  3. C3.

    An uncountable subset \(\mathop S\limits^{ \vee }\) of \(S\) such that

$$\mathop {\lim \inf }\limits_{m \to \infty } \left\| {\varvec{F}^{m} (\varvec{X}_{0} ) - \varvec{F}^{m} \left( {\mathop {\varvec{X}_{0} }\limits^{ \vee } } \right)} \right\|\; = \;0,$$
(4)

  for all \(\varvec{X}_{0} \in \mathop S\limits^{ \vee }\) and \(\mathop {\varvec{X}_{0} }\limits^{ \vee } \in \mathop S\limits^{ \vee }.\)

3 Identification of DTCS

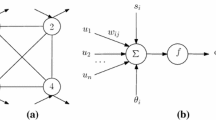
The structure of the two-layered RNN, which we will consider in the identification and generation of the DTCS, is depicted in Fig. 1. In Fig. 1, \(\varvec{w}_{2}\) denotes the \(n_{2} \times n_{1}\) weight matrix of the links from layer 1 to 2, \(\varvec{w}_{r}\) denotes the \(n_{1} \times n_{2}\) weight matrix of the links from layer 2 to 1, \(\varvec{b}_{i}\) denotes the \(n_{i} \times 1\) bias vector of layer \(i\), and \(\varphi_{i}\) denotes the transfer function of the \(n_{i}\) neurons in layer \(i\) with \(n_{i}\) denoting the number of neurons in layer \(i\). Then, the state \(\varvec{x}[t] = \left[ {x_{1} [t]\;\;\;x_{2} [t]\;\;\; \cdots \;\;\;x_{{n_{2} }} [t]} \right]^{T}\) of the two-layered RNN can be expressed as

Fig. 1
figure 1

Structure of the RNN employed in the proposed procedures of identification and generation of the DTCS

Full size image
$$\begin{aligned} \varvec{x}[t]\; & = \;\varvec{f}\left( {\varvec{x}[t - 1]} \right) \\ & = \;\underline{{\varphi_{2} }} \left( {\varvec{w}_{2} \underline{{\varphi_{1} }} (\varvec{w}_{r} \varvec{x}[t - 1] + \varvec{b}_{1} ) + \varvec{b}_{2} } \right), \\ \end{aligned}$$
(5)

with the initial state \(\varvec{x}[0] = \varvec{x}_{0}\). In (6), the matrix of an element-wise function is denoted by an underline: For example, we have

$$\underline{{\varphi_{1} }} ( \varvec x)\; = \left[ {\begin{array}{*{20}c} {\varphi_{1} (x_{1,1} )} & {\varphi_{1} (x_{1,2} )} & \cdots & {\varphi_{1} (x_{1,n} )} \\ {\varphi_{1} (x_{2,1} )} & {\varphi_{1} (x_{2,2} )} & \cdots & {\varphi_{1} (x_{2,n} )} \\ \vdots & \vdots & \ddots & \vdots \\ {\varphi_{1} (x_{m,1} )} & {\varphi_{1} (x_{m,2} )} & \cdots & {\varphi_{1} (x_{m,n} )} \\ \end{array} } \right],$$
(6)

where \(\varvec{x}\) is an \(m \times n\) matrix with the entry \(x_{m,n}\) in the \(m\)-th row and \(n\)-th column, and \(\varphi_{1}\) is a scalar function whose domain is one-dimensional. It should be mentioned that, by the universal approximation theorem [23], the RNN shown in Fig. 1 can approximate any bounded and continuous function. Consequently, the next state function of any DTCS, a bounded and continuous function, can be represented by the function \(\varvec{f}\) shown in (5) if the parameters are chosen properly.

Let us now describe the proposed identification procedure of a DTCS employing the two-layered RNN.

  1. (i)

    Given a state sequence \(\left\{ {\varvec{X}[t]} \right\}_{t = 0}^{{\tilde{t}}}\), observe the dimension of the DTCS. Set \(n_{2}\) to the value of the dimension observed. Let \(\varvec{x}[0] = \varvec{X}[0]\) and \(\varphi_{2} (x) = x\), and select \(n_{1}\) and \(\varphi_{1}\) from \({\mathbb{Z}}^{ + }\) and \(\varPhi\), respectively. Set the training goal \(\bar{E}_{I}\) to a sufficiently small value and the maximum number \(\tau_{I}\) of iterations to a sufficiently large value.

  2. (ii)

    Randomly select the elements of the weights and biases \(\varvec{w}_{r}\), \(\varvec{w}_{2}\), \(\varvec{b}_{1}\), and \(\varvec{b}_{2}\) in the interval \([ - 0.05, \, 0.05]\), in which the elements of weights and biases of an RNN are usually initialized [24]. Define the \(n_{I} \times 1\) vector

    $$\varvec{w}_{I} = \left[ {{\text{vec}}^{T} \left( {\varvec{w}_{r} } \right)\;\;\;\varvec{b}_{1}^{T} \;\;\;{\text{vec}}^{T} \left( {\varvec{w}_{2} } \right)\;\;\;\varvec{b}_{2}^{T} } \right]^{T} ,$$

    where \(n_{I} = 2n_{1} n_{2} + n_{1} + n_{2}\) and \({\text{vec}}\left( \varvec{A} \right)\) is the vectorization of a matrix \(\varvec{A}\): That is, all columns in \(\varvec{A}\) are listed one by one vertically to form \({\text{vec}}\left( \varvec{A} \right)\). Set \(\tau\) to \(0\) and \(\varvec{w}_{I}^{(\tau )}\) to \(\varvec{w}_{I}\), and choose a very small value \(\lambda_{I0}\) for the damping factor \(\lambda\). Evaluate the value \(E_{I,\tau } = E_{I} \left( {\varvec{w}_{I}^{(\tau )} } \right)\) of the cost function

    $$E_{I} (\varvec{w}_{I} )\; = \frac{1}{{\tilde{t}}}\sum\limits_{t = 1}^{{\tilde{t}}} {\left\| {\varvec{X}[t] - \varvec{x}[t]} \right\|^{2} } ,$$
    (7)

    where \(\varvec{x}[t]\) is obtained from (5).Update the weights and biases as follows: Obtain \(\varvec{w}_{I}^{(\tau + 1)}\) as

    $$\begin{aligned} \varvec{w}_{I}^{(\tau + 1)} \, & = \, \varvec{w}_{I}^{(\tau )} - \left\{ {\varvec{J}_{I}^{T} \left( {\varvec{w}_{I}^{(\tau )} } \right)\varvec{J}_{I} \left( {\varvec{w}_{I}^{(\tau )} } \right) + \lambda \varvec{I}_{{n_{I} }} } \right\}^{ - 1} \\ & \quad \, \varvec{J}_{I}^{T} \left( {\varvec{w}_{I}^{(\tau )} } \right)\varvec{ \in }_{I} \left( {\varvec{w}_{I}^{(\tau )} } \right), \\ \end{aligned}$$
    (8)

    and evaluate \(E_{I,\tau + 1}\), where

    $$\varvec{ \in }_{I} (\varvec{w}_{I} ) \, = \, \left[ {\begin{array}{*{20}c} {X_{1} [1] - x_{1} [1]} \\ {X_{2} [1] - x_{2} [1]} \\ \vdots \\ {X_{{n_{2} }} [\widetilde{t}] - x_{{n_{2} }} [\widetilde{t}]} \\ \end{array} } \right],$$
    (9)

    is the \(n_{2} \tilde{t} \times 1\) error vector and the \(n_{2} \tilde{t} \times n_{I}\) matrix

    $$\begin{aligned} J_{I} (w_{I} )\; & = \;\frac{{\partial \in_{I} \left( {w_{I} } \right)}}{{\partial w_{I} }} \\ & = \left[ {\begin{array}{*{20}c} {\frac{{\partial \in_{I,1} }}{{\partial w_{I,1} }}} & {\frac{{\partial \smallint_{I,1} }}{{\partial w_{I,2} }}} & \cdots & {\frac{{\partial \in_{I,1} }}{{\partial w_{{I,n_{I} }} }}} \\ {\frac{{\partial \in_{I,2} }}{{\partial w_{I,1} }}} & {\frac{{\partial \in_{I,2} }}{{\partial w_{I,2} }}} & \cdots & {\frac{{\partial \in_{I,2} }}{{\partial w_{{I,n_{I} }} }}} \\ \vdots & \vdots & \ddots & \vdots \\ {\frac{{\partial \in_{{I,n_{2} \tilde{t}}} }}{{\partial w_{I,1} }}} & {\frac{{\partial \in_{{I,n_{2} \tilde{t}}} }}{{\partial w_{I,2} }}} & \cdots & {\frac{{\partial \in_{{I,n_{2} \tilde{t}}} }}{{\partial w_{{I,n_{I} }} }}} \\ \end{array} } \right], \\ \end{aligned}$$
    (10)

    is the Jacobian of \(\varvec{ \in }_{I} (\varvec{w}_{I} )\) with \(\varvec{ \in }_{I,i}\) and \(w_{I,i}\) denoting the \(i\)-th elements of \(\varvec{ \in }_{I}\) and \(\varvec{w}_{I}\), respectively. If \(E_{I,\tau + 1} \le E_{I,\tau } \left( {E_{I,\tau + 1} > E_{I,\tau } } \right)\), store \(\varvec{w}_{I}^{(\tau + 1)} \left( {\varvec{w}_{I}^{(\tau )} } \right)\), divide (multiply) \(\lambda\) by a pre-fixed value \(\lambda_{I1}\) larger than one, and increase \(\tau\) by one (zero). If \(\tau = \tau_{I}\) go to step (iii); on the other hand, if \(\tau < \tau_{I}\), repeat from (8).

  3. (iii)

    If \(E_{{I,\tau_{I} }} \le \bar{E}_{I}\), stop the procedure, and the identification is considered to be successful: Reset \(\varvec{w}_{r}\) and \(\varvec{w}_{2}\) to matrices whose elements in the \(i\)-th row and \(j\)-th column are the \(\left( {i + (j - 1)n_{1} } \right)\)-th and \(\left( {n_{1} (n_{2} + 1) + i + (j - 1)n_{2} } \right)\)-th elements of \(\varvec{w}_{I}^{{(\tau_{I} )}}\), respectively, and \(\varvec{b}_{1}\) and \(\varvec{b}_{2}\) to vectors whose \(i\)-th elements are the \(\left( {n_{1} n_{2} + i} \right)\)-th and \(\left( {2n_{1} n_{2} + n_{1} + i} \right)\)-th elements of \(\varvec{w}_{I}^{{(\tau_{I} )}}\), respectively. On the other hand, if \(E_{{I,\tau_{I} }} > \bar{E}_{I}\), increase \(n_{1}\) by one and repeat (ii).

The proposed procedure of identification of the DTCS is depicted in Fig. 2.

Fig. 2
figure 2

Block diagram of the proposed identification procedure

Full size image

4 Generation of One-Dimensional DTCS

Theorem 1 [6]

If a one-dimensional DTDS with a next-state function\(F\)has a point\(X[0]\)such that

$$\begin{aligned} X[3]\; \le \;X[0]\; < \;X[1]\; < \;X[2] \, or \, \hfill \\ \, X[3]\; \ge \;X[0]\; > \;X[1]\; > \;X[2], \hfill \\ \end{aligned}$$
(11)

then the DTDS is a one-dimensional DTCS and the interval\(\left[ {\hbox{min} \left( {X[2],X[3]} \right),\hbox{max} \left( {X[2],X[3]} \right)} \right]\)includes a point of period\(p\)for every\(p \in {\mathbb{Z}}^{ + }\), and a scrambled set\(S\)and a set\(\mathop S\limits^{ \vee }\)specified in\({\text{C2}}\)and\({\text{C3}}\).

Based on Theorem 1, let us now propose a procedure to generate one-dimensional DTCSs with the RNN shown in Fig. 1.

  1. (i)

    Create a sequence \(\left\{ {X[t]} \right\}_{t = 0}^{3}\) such that

    $$\begin{aligned} X[3]\; < \;X[0]\; < \;X[1]\; < \;X[2]{\text{ or }} \hfill \\ \, X[3]\; > \;X[0]\; > \;X[1]\; > \;X[2]. \hfill \\ \end{aligned}$$
    (12)

    In the RNN of Fig. 1, let \(n_{2} = 1\), \(x[0] = X[0]\), and \(\varphi_{2} (x) = x\), and select \(n_{1}\) and \(\varphi_{1}\) from \({\mathbb{Z}}^{ + }\) and \(\varPhi\), respectively. Set the training goal \(\bar{E}_{G}\) to a value sufficiently smaller than \(\hbox{min} \left( {\left| {X[3] - X[0]} \right|,\left| {X[0] - X[1]} \right|,\left| {X[1] - X[2]} \right|} \right)\) and maximum number \(\tau_{G}\) of iterations to a sufficiently large value. Note that the two equalities in (11) have been removed in (12) to avoid the impractical case of \(\bar{E}_{G} = 0\).

  2. (ii)

    Randomly select the elements of the weights and biases \(\varvec{w}_{r}\), \(\varvec{w}_{2}\), \(\varvec{b}_{1}\), and \(b_{2}\) in the interval \([ - 0.05, \, 0.05]\): Note that the bias \(b_{2}\) is a scalar in the one-dimensional DTCS. Define the \((3n_{1} + 1) \times 1\) vector \(\varvec{w}_{G} = \left[ {\varvec{w}_{r}^{T} \;\;\;\varvec{b}_{1}^{T} \;\;\;\varvec{w}_{2} \;\;\;b_{2} } \right]^{T}\). Set \(\tau\) to \(0\) and \(\varvec{w}_{G}^{(\tau )}\) to \(\varvec{w}_{G}\), and choose a very small value \(\lambda_{G0}\) for the damping factor \(\lambda\). Evaluate the value \(E_{G,\tau } = E_{G} \left( {\varvec{w}_{G}^{(\tau )} } \right)\) of the cost function

    $$E_{G} (\varvec{w}_{G} )\; = \;\sqrt {\frac{1}{3}\sum\limits_{t = 1}^{3} {\left| {X[t] - x[t]} \right|^{2} } } ,$$
    (13)

    where \(\varvec{x}[t]\) is obtained from (5) with the selected \(\varvec{w}_{r}\), \(\varvec{w}_{2}\), \(\varvec{b}_{1}\), and \(b_{2}\). Update the weights and biases as follows: Obtain \(\varvec{w}_{G}^{(\tau + 1)}\) as

    $$\begin{aligned} w_{G}^{{(\tau + 1)}} {\mkern 1mu} = & {\mkern 1mu} w_{G}^{{(\tau )}} - {\mkern 1mu} \left\{ {J_{G}^{T} \left( {w_{G}^{{(\tau )}} } \right)J_{G} \left( {w_{G}^{{(\tau )}} } \right) + \lambda I_{{3n_{1} + 1}} } \right\}^{{ - 1}} {\mkern 1mu} \\ & \times J_{G}^{T} \left( {w_{G}^{{(\tau )}} } \right) \in _{G} \left( {w_{G}^{{(\tau )}} } \right) \\ \end{aligned}$$
    (14)

    and evaluate \(E_{G,\tau + 1}\), where

    $$\varvec{ \in }_{G} (\varvec{w}_{G} ) = \left[ {\begin{array}{*{20}c} {X[1] - x[1]} \\ {X[2] - x[2]} \\ {X[3] - x[3]} \\ \end{array} } \right],$$
    (15)

    is the \(3 \times 1\) error vector and the \(3 \times (3n_{1} + 1)\) matrix

    $$\begin{aligned} \varvec{J}_{G} (\varvec{w}_{G} ) \,& = \, \frac{{\partial \varvec{ \in }_{G} \left( {\varvec{w}_{G} } \right)}}{{\partial \varvec{w}_{G} }} \\& = \left[ {\begin{array}{*{20}c} {\frac{{\partial \in_{G,1} }}{{\partial w_{G,1} }}} & {\frac{{\partial \in_{G,1} }}{{\partial w_{G,2} }}} & \cdots & {\frac{{\partial \in_{G,1} }}{{\partial w_{{G,3n_{1} + 1}} }}} \\ {\frac{{\partial \in_{G,2} }}{{\partial w_{G,1} }}} & {\frac{{\partial \in_{G,2} }}{{\partial w_{G,2} }}} & \cdots & {\frac{{\partial \in_{G,2} }}{{\partial w_{{G,3n_{1} + 1}} }}} \\ {\frac{{\partial \in_{G,3} }}{{\partial w_{G,1} }}} & {\frac{{\partial \in_{G,3} }}{{\partial w_{G,2} }}} & \cdots & {\frac{{\partial \in_{G,3} }}{{\partial w_{{G,3n_{1} + 1}} }}} \\ \end{array} } \right], \\ \end{aligned}$$
    (16)

    is the Jacobian of \(\in_{G} (\varvec{w}_{G} )\) with \(\in_{G,i}\) and \(w_{G,i}\) denoting the \(i\)-th elements of \(\in_{G}\) and \(\varvec{w}_{G}\), respectively. If \(E_{G,\tau + 1} \le E_{G,\tau } \left( {E_{G,\tau + 1} > E_{G,\tau } } \right)\), store \(\varvec{w}_{G}^{(\tau + 1)} \left( {\varvec{w}_{G}^{(\tau )} } \right)\), divide (multiply) \(\lambda\) by a pre-fixed value \(\lambda_{G1}\) larger than one, and increase \(\tau\) by one (zero). If \(\tau = \tau_{G}\) go to step (iii); on the other hand, if \(\tau < \tau_{G}\), repeat from (14).

  3. (iii)

    If \(E_{{G,\tau_{G} }} \le \bar{E}_{G}\), stop the procedure: We now have a one-dimensional DTCS whose next-state function is described by (5). Reset \(\varvec{w}_{r}\), \(\varvec{b}_{1}\), and \(\varvec{w}_{2}\) to vectors whose \(i\)-th elements are the \(i\)-th, \((n_{1} + i)\)-th, and \((2n_{1} + i)\)-th elements of \(\varvec{w}_{G}^{{(\tau_{G} )}}\), respectively, and \(b_{2}\) to the last element of \(\varvec{w}_{G}^{{(\tau_{G} )}}\). If \(E_{{G,\tau_{G} }} > \bar{E}_{G}\), on the other hand, increase \(n_{1}\) by one and repeat ii).

The proposed generation procedure of a one-dimensional DTCS is summarized in Fig. 3.

Fig. 3
figure 3

Block diagram of the proposed generation procedure

Full size image

It is obvious that a DTCS generated by the proposed procedure has a range of chaotic behavior predictable in advance: In other words, we can specify a range of chaotic behavior in advance if we employ the proposed procedure when generating a DTCS. This is a noticeably important advantage of the proposed procedure over the conventional ones. In addition, the required length of the training state sequence is only three, and consequently, the additional burden in computation incurred by the proposed procedure is negligible: Specifically, since the dimension of the error vector (15) is relatively small, the proposed procedure requires low computational power for the training stage (e.g. in terms of obtaining (14) and evaluating \(E_{G,\tau + 1} )\).

5 Simulation Results

In this section, we investigate the performance of the proposed identification procedure. Since the generation of DTCSs is rather obvious, we consider mainly the identification of DTCSs.

5.1 Identification

Consider two of the most well-known DTCSs; the logistic and Hénon systems of which the states at time instant \(t\) are given as

$$X[t]\; = \;4X[t - 1]\left( {1 - X[t - 1]} \right)$$
(17)

and

$$\begin{aligned} \varvec{X}[t] & = \left[ {X_{1} [t]\;X_{2} [t]} \right]^{T} \\ & = \left[ {\begin{array}{*{20}c} {1 + X_{2} [t - 1] - 1.4X_{1}^{2} [t - 1]} \\ {0.3X_{1} [t - 1]} \\ \end{array} } \right], \\ \end{aligned}$$
(18)

respectively. We have obtained state sequences \(\left\{ {X[t]} \right\}_{t = 0}^{199}\) and \(\left\{ {\varvec{X}[t]} \right\}_{t = 0}^{199}\) from the logistic and Hénon systems with \(X[0] = 0.2\) and \(\varvec{X}[0] = \left[ {1\; \, \;0} \right]^{T}\), respectively, and used the sequences in the identification.

For each of the two DTCSs, the identification has been repeated \(100\) times with the corresponding state sequence employing the transfer function

$$\varphi_{1} (x)\; = \;\frac{1}{{1 + e^{ - x} }}.$$
(19)

We have selected \(n_{1} = 8\), \(\tau_{I} = 1000\), \(\bar{E}_{I} = 10^{ - 8}\), \(\lambda_{I0} = 10^{ - 3}\), and \(\lambda_{I1} = 10\). From the state sequences, we have then observed that the dimensions of the logistic and Hénon systems are one and two, respectively: We have therefore let \(n_{2}\) be one and two for the logistic and Hénon systems, respectively. Because the value \(\tau_{I}\) is sufficiently large so that the RNNs can be trained to their best, all of the \(200\) repetitions of the identification with the initial value \(8\) of \(n_{1}\) has been observed to be successful.

5.2 Generalization Performance

To investigate the generalization performance, we have generated state sequences \(\left\{ {X[t]} \right\}_{t = 0}^{49}\) and \(\left\{ {\varvec{X}[t]} \right\}_{t = 0}^{49}\) from the logistic and Hénon systems with \(X[0] = 0.7\) and \(\varvec{X}[0] = \left[ {0.5 \, \;\;0} \right]^{T}\), respectively. For each of the \(100\) RNNs obtained by the \(100\) repetitions in the identification of the logistic system, we have obtained a state sequence \(\left\{ {x[t]} \right\}_{t = 0}^{49}\) with \(x[0] = 0.7\). Similarly, we have obtained a state sequence \(\left\{ {\varvec{x}[t]} \right\}_{t = 0}^{49}\) with \(\varvec{x}[0] = \left[ {0.5\;\;\;0} \right]^{T}\) for each of the \(100\) RNNs obtained by the \(100\) repetitions in the identification of the Hénon system. We have next calculated the mean squared error (MSE), \(\frac{1}{50}\sum\nolimits_{t = 0}^{49} {\left( {X[t] - x[t]} \right)^{2} }\) for the logistic system and \(\frac{1}{50}\sum\nolimits_{t = 0}^{49} {\left\| {\varvec{X}[t] - \varvec{x}[t]} \right\|^{2} }\) for the Hénon system, between the state sequence from the RNN and the target state sequence.

Table 1 shows the average of the \(100\) MSEs. Included also in the table are the results from the procedures in [18] and [19]. It is observed that the generalization performance of the proposed identification procedure is similar to that of the procedure in [19] and is slightly worse than that of the procedure in [18]. Nonetheless, we would like to note that, unlike the procedure in [18] which employs a global optimization algorithm, the proposed identification procedure and the procedure in [19] hire the LM algorithm, a local optimization algorithm: In general, local optimization algorithms consume less time than global optimization algorithms. It should also be noted that the RNNs employed in the proposed identification procedure, procedure in [18], and procedure in [19] hire two, three, and four layers, not counting layer \(0\) which is a delayed duplicate of the last layer: A smaller number of layers generally implies a smaller number of parameters, and as a result, lower requirement for computation.

Table 1 Comparison of the proposed and conventional procedures for the logistic and Hénon systems: Generalization performance in MSE, optimization algorithm required, and number of layers employed
Full size table

We have next considered the generalization performance of the proposed procedure in comparison with that of the procedure in [20] for a discretized version of Lorenz system of which the state at time instant \(t\) is given as

$$\begin{aligned} \frac{d}{dt}\varvec{X}(t) =& \left[ {\frac{{dX_{1} (t)}}{dt}\;\;\frac{{dX_{2} (t)}}{dt}\;\;\frac{{dX_{3} (t)}}{dt}} \right]^{T} \\ = &\left[ {\begin{array}{*{20}c} {q_{1} \left( {X_{2} (t) - X_{1} (t)} \right)} \\ {q_{2} X_{1} (t) - X_{2} (t) - X_{3} (t)X_{1} (t)} \\ {X_{2} (t)X_{3} (t) - q_{3} X_{3} (t)} \\ \end{array} } \right], \\ \end{aligned}$$
(20)

with \(q_{1} = 1\), \(q_{2} = 5.46\), \(q_{3} = \, 20,\) and initial value \(\varvec{X}(t) = [- 0.3\; \, 0.3\; \, 0.2]\). We have chosen other parameters the same as those adopted for the logistics and Hénon systems. From the results shown in Table 2, it is observed that the generalization performance of the proposed identification procedure, even with less number of layers, is better than that of the procedure in [20] for the Lorenz system.

Table 2 Comparison of the proposed and conventional procedures for Lorenz system: Generalization performance in MSE, optimization algorithm required, and number of layers employed
Full size table

In essence, the proposed identification procedure (A) exhibits generalization performance comparable to those of the conventional procedures, (B) employs a local optimization algorithm and requires less layers in the RNN than the conventional procedures, and as a result, (C) requires less consumption of computation time than the conventional procedures.

6 Conclusion

Employing two-layered recurrent neural networks, we have addressed the identification and generation of discrete-time chaotic systems. The proposed identification procedure requires a smaller number of layers in the recurrent neural network than the conventional procedures. Unlike the conventional generation procedures, the generation procedure proposed in this paper allows us to predict the range of chaotic behavior in advance when generating discrete-time chaotic systems. Simulation results have indicated that the proposed identification procedure of discrete-time chaotic systems shows comparable performance compared to other conventional identification procedures at reduced complexity. The proposed procedure can be hired, for example, in the implementation of pseudo random number generators and cryptosystems in addition to various applications including sustainable energy systems.