Abstract
A continuum model for lung parenchyma is constructed. The model describes the thermomechanical response over a range of loading rates—from static to dynamic to shock waves—and a range of stress states, including isotropic expansion, triaxial extension, simple shear, and plane wave compression. Nonlinear elasticity, viscoelasticity, and damage are included, with the latter associated with changes of biological function as well as mechanical stiffness. A Gram–Schmidt decomposition of the deformation gradient leads to strain attributes that enter the thermodynamic potentials as state variables. A free energy function is designed for loading at low to moderate rates and tensile pressures, whereby the tissue response, with surface tension, is preeminent. An internal energy function is designed for wave propagation analysis, including shock waves, whereby compressibility of the air inside the alveoli is addressed via a composite stiffness based on a closed-cell assumption. The model accurately represents the response to triaxial loading, pressure relaxation, and dynamic torsion with relatively few parameters. Longitudinal wave speeds are reasonable for ranges of internal airway pressure and transpulmonary pressure. Airway pressure strongly affects the response to plane wave compression. Criteria for local injury and damage progression depend on a normalized energy density and its gradient, where the latter is paramount for impact problems involving fast pressure rises. Results suggest that local damage associated with edema is induced at load intensities much lower than those that would cause significant stiffness changes due to rupture, major tearing, or local collapse.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
An increased understanding of behavior of soft biological tissues is afforded by constitutive models for static and dynamic loading. Deformations are often large, necessitating nonlinear elastic models. Viscoelasticity becomes important to account for rate dependence, hysteresis, and stress relaxation. For traumatic events, models linking degradation of mechanical properties to loss of biological function are sought. For overviews of the subject, refer to, e.g., [1,2,3,4]. Concurrent work by the authors [5,6,7] seeks to develop a general theoretical framework enabling modeling of the abovementioned physical phenomena. The framework should be applicable to a host of soft biological tissues, e.g., muscle, skin, internal organs, as well as other viscoelastic solids.
The focus of the present work is application of such a theory to the lung, which is the largest vital organ in the human thorax by volume. Sought eventually are modeling and numerical simulation capabilities of large deformation, stress wave propagation, damage, and injury mechanisms when the thorax is subjected to traumatic insult by blunt impact at various rates [8,9,10], or by rapidly rising high-pressure (i.e., blast) waves [11,12,13,14,15]. Pulmonary contusion is the the most common thoracic soft tissue injury for blunt trauma, with a mortality rate of 10–25% [16]. Damage to the lungs with resultant respiratory insufficiency and arterial embolization of air from alveolar pulmonary venous fistulae is the main cause of morbidity and mortality from blast exposure [17]. Lung laceration is also debilitating [18].
Perhaps the most popular nonlinear constitutive model for lung mechanics is based on work of Fung, Vawter, and colleagues [19,20,21,22]. Notably, an exponential term in an isotropic strain energy function accounts for elasticity of the microstructure of connective tissues in the lung, such as septal walls, assumed to behave similarly to the skin [19] and other compliant elastic tissues [23]. A second term in the energy function accounts for energy of surface tension of the alveolar membranes [24]. Both terms are constructed from usual invariants of the Lagrangian Green strain tensor. A simplification invoked in this theory is the use of a pseudo-hyperelastic strain energy function giving a different response in loading and unloading paths [20, 21], rather than use of a more general viscoelastic treatment [25]. Calibration of the model is cumbersome, for example, requiring sophisticated optimization algorithms [21, 26, 27].
Modern finite element simulations [10, 26, 27] adopt pseudo-hyperelastic theory, with minor variations to account for a different bulk modulus than that derived from hyperelasticity [10], a viscoelastic deviatoric response [28], or an equation-of-state for the bulk response under blast loading [15, 29] where immobility and compressibility of the gas within become important [30, 31]. Mild anisotropy is likely and may provide better parameterization to data [21], but it is usually neglected [20, 22, 28] to keep calculations and calibrations tractable.
The present approach seeks a constitutive framework with more physically descriptive, fewer, and easier calibrated parameters for a given soft solid than existing models. In this approach, the parenchyma—including alveoli, connective tissues, and internal fluids (gas and liquid)—is treated as a homogeneous isotropic continuum, following other models [4, 10, 15, 22, 27, 28, 32]. Details of the microstructure [33, 34] and fluid-structure interactions [35,36,37] are not resolved to maintain tractable computations. Cyclic response is also outside the present scope.
This paper is organized as follows. Elements of the general theory of [5, 7, 38] are reviewed in Section 2. Nonlinear elasticity, viscoelasticity, damage, and injury mechanisms are considered in the context of both static and dynamic loading. A free energy function is detailed in Section 3. Evaluation of this function and its derivatives entering the governing equations are described in the context of experiments in Section 4. An internal energy function for problems involving wave motion is given in Section 5. Features are evaluated in the context of elastic wave velocities and planar shock compression in Section 6. Conclusions follow in Section 7. Vectors and tensors of higher order are written in boldface type, scalars, and scalar components in italics. When index notation is used, summation is implied over repeated indices.
2 General continuum mechanical theory
General governing equations of the present theory in Section 2 closely follow those of a nonlinear viscoelastic-damage framework based on QR kinematics [5, 7]. Specialization of model features to the lung follows in Sections 3 and 5.
2.1 Kinematics of finite deformation
Denoted by X and x are Lagrangian and Eulerian position vectors of a material particle in respective reference and spatial configurations, each referred to a global Cartesian system with fixed origin. Let t denote time. Motions are as follows:
Space-time derivatives are presently presumed sufficiently smooth; shocks are addressed later in Section 6. The material time derivative, material gradient, and spatial gradient of a generic quantity f are the respective operations as follows:
Particle velocity and acceleration are as follows:
Arguments, e.g., (X,t) in the Lagrangian description, are dropped hereafter unless needed for clarity. The deformation gradient and its inverse are as follows:
Referential and spatial velocity gradients are as follows:
Then with \(J = \det \boldsymbol {F} >0\), the local ratio of spatial to referential volume and tr(⋅), the trace, \( \dot {J} = J \nabla \cdot \boldsymbol {\upsilon } = J \text {tr} (\dot {\boldsymbol {F}} \boldsymbol {F}^{-1}) \).
A fixed global Cartesian frame with basis vectors {ei}, i = 1,2,3 is used, to which vector and tensor components are referred unless noted otherwise. Let capital Roman indices J = 1,2,3 denote Lagrangian components. Then, \(\boldsymbol {e}_{i} = \boldsymbol {e}^{i} = {\delta ^{i}_{J}} \boldsymbol {e}^{J} = {\delta ^{i}_{J}} \boldsymbol {e}_{J}\). The deformation gradient in this coordinate frame is \(\boldsymbol {F} = {F^{i}_{J}} \boldsymbol {e}_{i} \otimes \boldsymbol {e}^{J} = F_{\mathit {ij}} \boldsymbol {e}_{i} \otimes \boldsymbol {e}_{j}\). This can be decomposed uniquely into the product of a rotation Q and upper triangular matrix T, where the latter is known as the Laplace stretch [39]:
Greek indices α = 1,2,3 correspond to an intermediate configuration whose tangent vectors are pulled back from the spatial configuration by Q− 1 or pushed forward from the reference configuration by T. The same global Cartesian basis is used for this configuration, called the “physical configuration” in [40]:
In matrix form, with all components referred to the global Cartesian bases of Eq. 2.7,
Physically descriptive deformation measures are the three positive elongation ratios a,b,c that enter the extension matrix Λ and the three shear magnitudes α,β,γ that enter the simple shear matrix Γ. Volume change is measured by \(J = \det \boldsymbol {T} = \det \boldsymbol {\varLambda } = abc\). Parameters a,b,c,α,β,γ are physical attributes because they can be measured directly by an experimentalist in the physical coordinate system of later (2.12), without post analysis [38, 40, 41].
Let
denote the symmetric right Cauchy–Green deformation tensor. Nonzero components of \(\boldsymbol {T} = T_{\text {IJ}} \boldsymbol {e}^{I} \otimes \boldsymbol {e}^{J}\) are as follows [42]:
Elongations and shears are as follows:
Index numbers 1,2,3 to the {ei} should be assigned carefully when the QR decomposition is used. Let the {ei} be rotated by Q. Then, there is an ideal choice among coordinate bases for which the direction aligned with the rotated 1-axis and the direction normal to the rotated 1-2-plane remain invariant under a transformation by T [43]. A pivoting algorithm to achieve the corresponding upper triangular dominance of T is given in [40]. The physical basis of [40], denoted here by {gα}, corresponds to the following:
The {gα} comprise a local Cartesian frame at each X. If Q is not spatially homogeneous, then {gα} do not comprise a global frame. The mixed-variant velocity gradient in the second of Eq. 2.5 obeys the following, where Ω is skew is as follows:
2.2 Strain attributes
Let a0,b0,c0 and α0,β0,γ0 denote values of a,b,c and α,β,γ in a reference state corresponding to time instant t = t0. A vector consisting of seven strain attributes 𝜖i, i = 0,…,6 is defined as follows:
Only six of the seven strain attributes in Eq. 2.14 are independent kinematic variables since
A measure of the dilatation is 𝜖0. When a0 = b0 = c0 = 1 is chosen for the datum state, \(\epsilon _{0} = \ln J\). This choice is used henceforth, as are α0 = β0 = γ0 = 0. Logarithmic squeeze modes are 𝜖1,𝜖2,𝜖3. Simple shears are 𝜖4,𝜖5,𝜖6.
2.3 Stresses and stress power
Denote by σ, k, s, and P the Cauchy, Kirchhoff, rotated Kirchhoff, and first Piola–Kirchhoff stress tensors, respectively. In the Cartesian frame \(\{ \boldsymbol {e}_{i} \} = \{ \boldsymbol {e}_{J} {\delta ^{J}_{i}} \}\), these stress tensors are related by the following:
Tensor s is also referred to as a physical stress. Stress power is as follows:
where \(\{ \hat {\tau }_{i} \}\), i = 0,…,6 in terms of sαβ, are defined as follows [40]:
Negative pressure per unit reference volume is \(\hat {\tau }_{0} = -J p\), where Cauchy pressure is \(p = -\frac {1}{3} \text {tr} \boldsymbol {\sigma }\). Normal stress differences are \(\hat {\tau }_{1},\hat {\tau }_{2},\hat {\tau }_{3}\). Shear stresses are \(\hat {\tau }_{4},\hat {\tau }_{5},\hat {\tau }_{6}\). Stress differences conjugate to squeeze modes of strain obey the following:
2.4 Conservation laws and entropy production
Let ρ and ρ0 be spatial and initial mass densities of the material. Body force per unit initial volume is b. Local balance equations for mass, linear momentum, and angular momentum are the usual forms from continuum mechanics:
Thermodynamic potentials, measured per unit initial volume, include internal energy density U, Helmholtz free energy density Ψ, and entropy density η, related by the following:
Absolute temperature is T > 0. The heat flux vector in the reference configuration is q, and a scalar point heat source per unit volume is r. The local balance of energy is as follows:
Local entropy production inequalities, the latter following from Eqs. 2.21 and 2.22, include the following:
2.5 Thermodynamic potentials
Thermodynamic potentials Ψ or U depend on temperature (T) or entropy (η), internal state variables, and strain attributes. Let {χi} be a set of dimensionless, strain-like scalar variables associated with viscoelasticity, where i = 0,…,6. A single relaxation time is considered here; generalization to a larger discrete number of relaxation times is presented in [5, 7]. Denote by D ∈ [0,1], an internal state variable linked to damage processes to be assigned a physical interpretation later. Strain attributes and viscoelastic state variables comprise the column vectors as follows:
Free and internal energy densities are assigned, respectively, the functional forms below for homogeneous solids are as follows:
2.6 Constitutive laws
Using Eq. 2.25 in the second of Eq. 2.23 gives the following dissipation inequality:
Stress power can be written, using Eqs. 2.15 and 2.19, in terms of components of \(\dot {\boldsymbol {\epsilon }}\) as follows:
The following thermoelastic constitutive equations are inferred from Eq. 2.26 to maintain admissibility for stresses:
and entropy:
The first of Eq. 2.28 corresponds to \(p = - J^{-1}\hat {\tau }_{0} = - \frac {\partial \varPsi }{ \partial J}\). Constraints (2.15) and (2.19) have not been imposed in the derivation of Eq. 2.28. Thus, for Eq. 2.28 to always apply, Ψ must be specified consistently with the following:
Partial differentiation with respect to 𝜖i is performed with 𝜖j fixed for all i≠j, regardless of Eq. 2.15. The residual dissipation inequality is as follows:
The seven-element column vector of stress variables conjugate to strain attributes is as follows;
Concisely, this is related to strain derivatives of free energy according to the following:
If seven components in Eq. 2.28 are known, then the physical stress tensor s is, from Eq. 2.18, as follows:
Other stress tensors can be obtained from s using Eq. 2.16. Thermoelastic constitutive equations in terms of internal energy are derived similarly [5, 7]:
Constraints analogous to Eq. 2.30 are imposed on the internal energy U: \({\sum }_{i=1,2,3} \partial U / \partial \epsilon _{i} = 0\).
2.7 Thermoelasticity and dissipation
Let c(𝜖,T,χ,D) denote specific heat per unit reference volume at constant deformation, where
The following temperature evolution equation can be derived from the local balance of energy:
Thermal stress coefficients κ and Grüneisen coefficients g are defined as follows:
Isothermal and isentropic second-order thermodynamic elastic coefficients (not necessarily constants) are as follows:
Denote thermal expansion coefficients by A = ∂𝜖/∂T, with partial differentiation taken at constant stress and constant internal state. Denote specific heat at constant stress by cs. The following relationships can be derived as follows [44]:
Define conjugate thermodynamic forces to internal state variables as the negative derivatives as follows:
Substitution of Eqs. 2.38 and 2.41 into Eq. 2.37 gives the energy balance in a more compact form as follows:
Assume that dissipation from conduction is always non-negative in Eqs. 2.23 and 2.31. Then,
3 Free energy formulation for lung tissue mechanics
A constitutive formulation for static and dynamic loading of the lung based on Helmholtz free energy Ψ is developed. This model is preferred for tensile stress states, and it is ideal for isothermal problems. It can be used for dynamic problems wherein viscoelasticity affects isolated tissue stiffness but air compressibility does not, for example, dynamic torsion and inflation/deflation. Since it does not account for compressibility of air trapped inside the lung, it is not an appropriate model of the composite lung (tissue + gas) for dynamic compression including high-frequency wave propagation and shock loading. The internal energy-based model developed in Section 5 addresses the latter scenarios.
3.1 General form
The following form of Ψ in Eq. 2.25 is invoked:
Equilibrium thermoelastic free energy is \(\varPsi ^{\infty }_{0}\). Configurational energy associated with viscoelasticity is Υ0. The damage degradation function is f. The purely thermal free energy accounting for specific heat and unaffected by damage is ψ.
3.2 Thermoelastic strain energy
A material element is considered to occupy a stress-free reference state when undeformed and in the absence of surface tension at the air-liquid interface, wherein its mass density is ρ0 and temperature is T0. This definition of reference state is consistent with those in [19, 20]. Surface tension can be effectively eliminated by washing the tissue in saline; naturally moist lung, when expanded to the same volume as a saline-rinsed lung, will require a tensile pressure in the reference state to offset the effect of surface tension and prevent the tissue from contracting.
Equilibrium thermoelastic free energy depends explicitly on three functions of the strain attributes of Eq. 2.14, denoted by ξi, i = 1,2,3. The first accounts for volume changes and is equal to the first attribute itself, the second accounts for squeeze deformations, and the third accounts for simple shears:
This is a three-mode isotropic theory in the sense of [5, 7, 40, 41], where the material may respond differently under pure shear (squeeze) and simple shear. As such, the material is not isotropic in the conventional sense of invariants or group theory; its linearization is reminiscent of a classical linear elastic solid with cubic symmetry [5, 7]. It will be demonstrated later how this model effectively represents the more compliant response of the lung in simple shear, i.e., torsion, relative to pure shear under biaxial or triaxial extension. A useful property of \({\varPsi }_{0}^{\infty }(\xi _{1},\xi _{2},\xi _{3},T)\) is that the thermoelastic free energy analog of Eq. 2.30 is identically satisfied via Eq. 2.15.
Thermoelastic strain energy density per unit reference volume is prescribed as follows:
Denoted by \({B_{0}^{T}}\) is the isothermal bulk modulus, μ0 the shear modulus for pure shear, and G0 the shear modulus for simple shear, all at the undeformed reference state for equilibrium quasi-static deformation (no viscoelasticity), in the absence of damage. Isothermal pressure derivatives of the shear moduli at the reference state are \(\mu ^{\prime }_{0}\) and \(G^{\prime }_{0}\):
Dimensionless higher order elastic constants corresponding to dilatation, squeeze, and simple shear are c1, c2, and c3. The associated exponential stiffening is reminiscent of Fung’s formulation soft biological tissues [23]. The equilibrium tangent isothermal bulk modulus corresponding to Eq. 3.3 is as follows:
with pressure derivative at the ambient state computed as follows [5, 7]:
The volumetric coefficient of thermal expansion is A0, and the nonzero coefficient in Eq. 2.40 is κ0 = A0B0. Lagrangian surface tension in the reference state is K0. Thermal free energy is, with c0 specific heat at constant volume, as follows:
The general formula (3.3) is valid for lung in air and saline. When saline-washed, values of the bulk thermoelastic constants \({B_{0}^{T}}\) and c1 differ [24, 33], with the saline-treated lung more compliant, and K0 = 0 by construction, since surface tension vanishes. In the limit that \(c_{i} \rightarrow 0\) (i = 1,2,3), the free energy in Eq. 3.3 becomes quadratic in volumetric and shear strains. When μ0 = G0, a two-mode theory [5, 40, 41] is obtained, and the equilibrium elastic compliances of the material in pure shear and simple shear are identical for small strains. In the limit that deformations (strains and rotations) are small, then the response in this two-mode case reduces to isotropic linear elasticity [5, 7].
3.3 Configurational free energy
Viscoelasticity is addressed via a configurational energy Υ0 and evolution equations for viscous stress components that ensure non-negative dissipation. The general formulation derived in [5, 7] extends [45, 46] to QR kinematics and conjugate stress–strain attributes and allows for multiple relaxation processes α = 1,…,m each with time scale tα > 0. For simplicity and sufficiency in forthcoming applications, the configurational energy accounts for only one relaxation process with α = 1 and complementary relaxation time t1. Define total configurational free energy as follows:
Denoted by Ψ0 = Ψ0(𝜖,T) is a free energy function that corresponds to relaxation process α = 1 with time scale t1 > 0. Denoted by μ1 ≥ 0 is a temperature-dependent parameter with dimensions of elastic stiffness. Viscosity is ν1 = μ1t1. Define conjugate internal stresses for the free energy Ψ0 not modified by damage function f as follows [5, 7]:
The condition imposed for thermodynamic equilibrium is that these internal stresses vanish at infinite time.
Temperature coupling addressed in more general frameworks of [5, 7, 45] is omitted, so now μ1 = constant, irrespective of T. The only independent parameters, beyond those introduced already in Section 3.2, entering this model are \(\beta _{1} = \mu _{1} / {B^{T}_{0}}\) and t1. The following quadratic form of relaxation energy is invoked [5, 7, 45]:
Then, Eq. 3.9 produces the following:
Viscoelastic kinetics obey, for the present specific formulation, wherein α = m = 1 is as follows:
Internal strains and their rates are as follows:
The rate of dissipated energy reduces to \(|\boldsymbol {\zeta }|^{2} / \nu _{1} = \nu _{1} |\dot {\boldsymbol {\chi }}|^{2} \geq 0\). At equilibrium, \(\boldsymbol {\chi }_{\infty } = \boldsymbol {\epsilon }\). The constraint below on squeeze terms of internal strain is imposed, analogously to Eq. 2.15, such that Eq. 2.30 will be obeyed:
3.4 Damage
A continuum damage mechanics model is used, following [5, 7, 47, 48]. Recall that the internal state variable representative of deleterious processes that affect mechanical and/or biological functions is denoted by the internal state variable D ∈ [0,1]. The thermodynamic driving force for damage of Eq. 2.41 is, from Eq. 3.1,
The following restrictions are imposed to ensure damage evolution is physically and thermodynamically irreversible:
The present model applies the standard linear degradation function of continuum damage mechanics [44, 47, 49, 50]:
Free energy of the undamaged material Ψ0 is thermodynamically conjugate to the rate of damage growth. A canonical constitutive assumption is that D, or its rate, should be influenced by Ψ0. A dimensionless transformation of Ψ0 is as follows:
Strictly, the argument of Z is a function of a partitioning and normalization of Ψ0, rather Ψ0 itself. Thermoelastic free energy is partitioned in contributions from volume change, squeeze, and simple shear as follows:
Analogously, configurational energy is partitioned as follows:
The maximum value of normalized free energy attained at a material point X over a time history \(s \in (-\infty ,t]\) is as follows:
The following two-parameter damage function is invoked:
Dimensionless scalar parameters are the threshold thermodynamic force for damage initiation Z0 > 0 and αD ≥ 0 that controls the extent of damage progression with force exceeding this threshold. The larger the value of αD, the greater the reduction in mechanical stiffness with increasing normalized strain energy exceeding the initiation threshold. Constitutive Eq. 3.26 obeys D ∈ [0,1] with \(D \rightarrow 1\) as \(Z_{m} \rightarrow \infty \). The material time derivative of Eq. 3.26 is as follows:
Since Zm can only remain constant or increase with time according definition (3.25) and since αD is non-negative, \(\dot {D} \geq 0\). Furthermore, \(\dot {Z}_{m} > 0\) only in the domain Ψ0 ≥ 0 according to the definition of Z in Eq. 3.20. Thus, \({{\varPsi }}_{0} \dot {D} \geq 0\).
3.5 Stresses, entropy, and temperature
Derivatives of the free energy function comprised of terms for thermoelasticity, viscoelasticity, and damage set forth in Sections 3.2, 3.3, and 3.4, respectively, produce stress components and entropy according to Eqs. 2.28 and 2.29. Equilibrium free energy \({{\varPsi }}_{0}^{\infty }\) of Eq. 3.3, thermal energy ψ of Eq. 3.8, configurational energy of Υ0 of Eq. 3.12, and damage degradation function f of Eq. 3.19 are substituted into Eq. 3.1 to yield the following total free energy function:
Stress components conjugate to strain attributes obtained from Eqs. 2.28 and 3.28 are as follows:
Three dimensionless stiffness ratios βi (i = 1,2,3) have been introduced in Eq. 3.29:
Prescription of any one of the βi constrains the other two along with μ1. Instantaneous dynamic moduli at the reference state (ξi = 0, D = 0, χ = 0) are \({B^{T}_{0}} \times (1+\beta _{1})\), μ0 × (1 + β2), and G0 × (1 + β3). Cauchy stress σ can be obtained from \(\hat {\tau }_{i}\) via Eqs. 2.34 and 2.16. Verification is straightforward that constraints Eqs. 2.19 and 2.30 hold.
Entropy density per unit reference volume is found from Eq. 2.29, noting that Υ0 does not depend on T:
Total dissipation in Eq. 2.43 becomes the following:
where the (in)equality is verified by Eq. 3.18 with \(\nu _{1} = \beta _{1} {B^{T}_{0}} t_{1} > 0\). The energy balance (2.42) reduces to the following:
4 Static and dynamic loading
The constitutive model of Section 3 is applied to describe several experimental datasets from different loading protocols. Most calculations are applied toward describing the response of dog lung, for which data appear most abundant [1, 19,20,21, 32, 51,52,53]. Available data or observations on sheep, rabbit, and pig (i.e., porcine data) are substituted when the need arises, in the absence of data on dog. Differences among certain lung tissue properties, e.g., linearized elastic moduli valid for small deformations, for many mammals are not excessive [1, 33, 53,54,55,56,57,58], perhaps because alveolar dimensions, including thickness of septal walls and membranes, are comparable for animals of similar mass. Humans, however, tend to exhibit a stiffer mechanical response [59].
Under small deformation, lung tissue responds reasonably isotropically, as indicated by static and wave propagation experiments [30, 31, 33, 53, 58, 60, 61]. However, anisotropy may arise under large deformations due to rearrangement (e.g., rotation) of microstructure features [21, 61]. In the present model, which invokes a three-mode response [40, 41] in the QR kinematic framework consisting of dilatation, squeeze, and simple shear, isotropy under small strains is achieved by G0 = μ0 [5, 7]. However, different stress–strain responses are possible under finite pure shear and simple shear; accordingly, c2≠c3 in the present thermoelastic theory. The pressure derivative of the squeeze modulus is assumed equal to that of the shear modulus (\(\mu ^{\prime }_{0} = G^{\prime }_{0}\)) since only the latter appears to have been measured directly from shear wave propagation tests. Values are \(G^{\prime }_{0} \approx -0.7\) [33, 55,56,57, 60], where the negative sign indicates that shear stiffness increases with increasing tension. This value is listed in Table 1 along with others.
4.1 Triaxial extension
Cauchy pressure is defined as positive for compressive loading. The definition of the bulk modulus in Eq. 3.6 is consistent with this sign convention. Following [1, 19, 20, 22], pressure p supported by a material element is presumed equal to the negative of the transpulmonary pressure ptp, where the latter is positive under tensile loading. By definition [1, 19, 20, 22], transpulmonary pressure is the difference between the internal airway pressure in the lung (or inside an internally pressurized element of lung tissue) denoted by pa and the pleural pressure ppl, which is the external pressure acting on the outer surface of the lung or an element of it:
Effects of tension and curvature in the pleural membrane [19, 20] are embedded in ppl and not are resolved explicitly here. Both pa and ppl are positive in compression. In vivo, pressure in the intrapleural space is less than airway pressure (i.e., negative relative to atmosphere), in order to keep the lung from collapsing due to its intrinsic surface tension. Under normal breathing cycles, tissue remains perpetually in a tensile state [62], whereby the tissue pressure (elastic + surface tension contributions) p < 0 and ptp > 0. Typically pa ≈ 1 atm = 101.3 kPa = 1.033 × 103 cm H2O.
The low strain rate response is considered here, consistent with experimental data analyzed, and for which a hyperelastic or pseudoelastic model suffices [19, 20, 52]. In air, hysteresis may be evident leading to differences in loading and unloading branches of the pressure–volume cycle [51]. Such hysteresis is minimal in saline-filled specimens, demonstrating that much of the viscoelastic response is linked to changes in surface tension. In the forthcoming analysis, test data and model results correspond to the more compliant unloading branch.
4.1.1 Spherical extension
When the deformation state is spherical, F = J1/31, the stress state is hydrostatic according to Eq. 3.29: \(\boldsymbol {\sigma } = (\hat {\tau }_{0} / J) \textbf {1} = - p \textbf {1}\). Notably, \(\epsilon _{0} = \xi _{1} = \ln J\), ξ2 = ξ3 = 0, and 𝜖i = 0 for i ≥ 1. Pressure is related to volume change J and damage D under isothermal (T = T0) static deformations as follows from the first of Eq. 3.29 in the infinite time limit (\(\chi _{0} \rightarrow \epsilon _{0}\)):
The tangent bulk modulus is, extending Eq. 3.6,
Damage obeys (3.26) in terms of \(Z_{m}(\boldsymbol {X},t) = \max \limits _{s \in (-\infty ,t]} Z(\boldsymbol {X},s)\); for D ∈ (0,1),
The instantaneous potential driving force for \({{\varPsi }}_{0} = {{\varPsi }}_{0}^{V \infty } \geq 0\) is, with J = J(X,t) ≥ 1,
Five parameters affect the spherical isothermal static response: the isothermal bulk modulus \({B^{T}_{0}}\), the dimensionless nonlinear elastic constant c1 that controls bulk stiffening for volume changes, the surface tension K0 in the undeformed state from air-tissue interfaces, the threshold normalized energy for damage initiation Z0, and the damage growth parameter αD. For lung tissue in saline, K0 = 0 and four parameters suffice. For volumetric cycling in regimes within the damage threshold, as in normal breathing activities, Z < Z0 and αD is not needed.
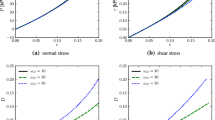
Shown in Fig. 1 are model results for pressure and tangent bulk modulus obtained using parameters given in Table 1. Experimental data for dog lung in saline are extracted from figures in [51, 52], and for dog lung in air from [33, 51, 60]. Data only address the tensile regime, for which J ≥ 1. The compressive response is an extrapolation.
Note that the tangent bulk modulus is minimal near zero pressure. Air-filled lung has a stiffer pressure–volume response due to a higher bulk modulus and surface tension [62]. Surface tension is represented by K0. Lung in saline is stress-free at the reference state J = 1. Lung in air at J = 1 is under tension (p < 0) due to K0. The stress-free state for lung in air according to the present model corresponds to J = 0.9245, meaning surface tension causes some contraction in the absence of tensile pleural pressure relative to airway pressure.
4.1.2 Damage criteria
Little quantitative experimental data relating stress-strain state to visibly observable damage mechanisms exist. Cyclic expansion of lung by ventilator at airway pressures exceeding those witnessed in normal breathing causes injury (functional degradation), reduction in shear modulus [63], and changes in bulk modulus [64, 65]. Bulk modulus may increase or decrease for cycling in air, where decrease is associated with edema as the air-liquid interface responsible for surface tension is compromised. Longer term changes in stiffness due to biological adaptation (e.g., stiffness increase due to scarring or inflammation [66]) are not addressed herein.
The static damage model is calibrated following experiments on saline-ventilated rabbit lung [1, 67]. In these experiments, alveolar edema and commensurate weight increase due to fluid accumulation occurred in lung stretched beyond a critical magnitude. The rate of edema increased with increasing stretch beyond this threshold. It was concluded in [67] that permeability of tissue membranes was compromised at such stretch levels, which were below those necessary to impart observable local tearing or fracture of blood vessels and other structures. Threshold transpulmonary pressures for edema were recorded as 20 to 25 cm H2O, or ≈ 2 kPa. This value was used to obtain Z0 = 0.64 entering (4.4). In saline, J at this tensile pressure is 1.73. The same value used for air, whereby J is 1.62 at Z = 0.64.
Available data do not enable a precise determination of damage kinetic parameter αD. Strain softening commensurate with extreme damage (\(D \rightarrow 1\)) is not evident in experimental data on saline-treated dog lung for J ≤ 3.5 [51, 52]. Nor is any marked reduction in stiffness evident at lower strain levels upon unloading from triaxial stretch ratios exceeding 1.4 in any or all directions [52]. However, stiffening associated with elastic nonlinearity (manifested by positive c1,c2,c3 in the present model) might mask any decremental contributions from local tearing or damage incurred under large stretch. Eventually, the lung will rupture when stretched beyond an extreme value of J, which should exceed 3.5 according to experimental observations. In the present model, it is assumed that rupture corresponding to D = 1 will occur in air-filled lung when J ≥ 5, i.e., expansion to five times or more of the nominal volume. This assumption furnishes the value of αD = 0.0167 listed in Table 1. The same value is used for saline-treated lung.
Predictions of Eq. 4.4 are given in Fig. 2. Damage initiates at a slightly lower volume ratio but slightly higher transpulmonary pressure in air than saline. Damage accumulates more rapidly with increasing volume in air, and more rapidly with increasing tensile pressure in saline, where the different trends manifest from different bulk moduli in the two environments. Pressure-volume curves for lung in air and saline under the extreme loading range 0.5 ≤ J ≤ 5 are reported in Fig. 2c. Peak tensile pressure in air-filled lung is attained at J ≈ 4.57. At larger expansions, tensile pressure decreases with increasing volume as damage accumulates, softening the tangent bulk modulus.
Shown in Fig. 3a are experimental pressure-volume data extracted from Fig. 2 (“fig. data”) and Table II (“tab. data”) of [52] on saline-treated dog lung. Model results with and without damage enabled are compared. Differences due to damage are minimal for Lagrangian tensile pressures \(\hat {\tau }_{0} \leq 20\) kPa. At larger extensions, the model with damage enabled provides slightly better agreement with test data. Under compressive loading, damage initiates at \(J \lesssim 0.58\), which is thought to be physically realistic. Collapse and air trapping followed by reopening and air release have been observed during cyclic loading to very large compression (\(J \lesssim 0.5\)) [68].
Response for triaxial loading: a pressure-volume results of lung model under spherical extension in air and saline, with (D ≥ 0) and without (D = 0) damage, versus experimental data [52]. Curves with and without damage are nearly coincident. b Squeeze mode stress–strain results under triaxial extension in saline versus experimental data [51, 52]. c Damage D for five lateral traction values
4.1.3 Biaxial and triaxial loading
A coordinate system is chosen with basis vectors {eK} aligned parallel to the principal directions of deformation. In complementary experiments [21, 51], cube-shaped samples of lung tissue are sequentially stretched and unloaded parallel to each direction, whereby cube faces are orthogonal to directions of stretch. In the experiments of [51], further analyzed in [52, 61], the X1-direction is that of primary stretch ratio λ1 corresponding to Lagrangian traction component t1. Stretches in orthogonal directions are nearly equal (λ2 ≈ λ3), as are tractions t2 ≈ t3. The latter orthogonal tractions are held constant in a particular experiment while t1 is varied. In practice, equality of lateral tractions is enforced mechanically, while all three stretch ratios are measured, confirming that λ2 ≈ λ3.
Let the origin of the coordinate frame be located at the center of the undeformed cube of material. Then, the motion is xk = λkXk (no sum on k = 1,2,3). The deformation gradient is diagonal, and hence upper triangular by default is as follows:
Strain attributes are as follows:
Combinations entering the free energy function are ξ1 = 𝜖0 and ξ2 = (𝜖1)2 + (𝜖3)2, noting ξ3 = 0 in the absence of simple shearing modes. The first Piola–Kirchhoff stress tensor (force per unit reference area) is P = diag(t1,t2,t3) where t2 = t3 for symmetric lateral loading. Cauchy stress σ = J− 1s, with the physical stress tensor s equal to the Kirchhoff stress since Q = 1, is as follows:
Denoted by p is the Cauchy pressure. The stress attribute vector is as follows:
Nonzero components are obtained from strain attributes, without temperature changes or viscous effects, as follows:
Free energy of Eq. 3.28 reduces to the following:
Contributions, not reduced by damage, from dilatation and squeeze are, respectively,
The driving force for damage, whose evolution again obeys Eq. 4.4, is as follows:
Parameters μ0 and c2 are obtained via calibration to experimental data for saline-treated dog lung of [51, 52], wherein K0 = 0 is irrelevant. In these calculations, λ1 is imposed and t1 is the model output. Transverse stretch components λ2 = λ3 are adjusted until Lagrangian tractions t2 = t3 match discrete experimental values.
Shown in Fig. 3b are results and data for all five values of imposed lateral traction \(\sqrt {t_{2} t_{3}} \approx t_{2}\). The squeeze strain is 𝜖3 and its conjugate shear stress is \(\hat {\tau }_{3}\). The sigmoidal response curve is a result of the exponential stiffening of the tangent shear modulus via c2 > 0. Damage is enabled in these results, though it has a near negligible effect on the mechanical response. The model appears insensitive to lateral traction since results are nearly continuous in \(\hat {\tau }_{3} - \epsilon _{3}\) space, but different values of lateral traction are required to probe the entire domain. Test data show great scatter, but the model produces the correct order of magnitude and reveals an apparent trend of steeply increasing squeeze modulus with large variations in axial stretch ratio.
Shown in Fig. 4 are Lagrangian traction t1 versus stretch λ1 for each discrete value of transverse traction. Effects of D on mechanical response are very small, but thresholds for affecting biological function (Zm > Z0) are attained at sufficient stretch levels. Evolution of damage versus extension λ1 for all five cases is shown in Fig. 3c. Damage is most severe for larger lateral tensile loads, as physically expected. For large lateral stress levels, increasing λ1 above unity does not notably increase D, since the deviatoric strain energy is reduced as dilatational energy increases. The model provides excellent fits to the data at small transverse tractions in Fig. 4a, b. Quality of data matching degrades in Fig. 4c at larger values of \(\sqrt {t_{2} t_{3}}\) for \(\lambda _{1} \lesssim 1.4\). Omission of descriptions of microstructure affecting the nonlinear response may account for discrepancies in Fig. 4c. Predictability for high triaxiality could likely be improved by adding term(s) to the strain energy potential to account for higher than first-order coupling between dilatation and squeeze, i.e., between pressure and pure shear stress. This would require calibration of more parameter(s) beyond \(\mu ^{\prime }_{0}\) so is not undertaken here, such that simplicity of the model and its calibration are not compromised. The current exponential model requires calibration of only 4 elastic parameters for lung in saline, compared to a polynomial strain energy function with 9 distinct parameters [52].
Principal traction versus stretch for saline-treated dog lung under static isothermal triaxial deformation at different lateral traction values in (a–c), with data from [52]. Model curves for t1 with and without (D = 0) damage enabled are nearly indistinguishable since \(D \lesssim 0.03\) over the prescribed ranges of λ1 and λ2 = λ3
4.2 Dynamic pressure relaxation
Viscoelastic response parameters are obtained by calibration of the model to pressure relaxation experiments on rabbit lung in air [69]. The two parameters of interest in Table 1 are β1 and t1. A simple model with only a single relaxation time is implemented to demonstrate basic features and calibrate the instantaneous dynamic response; more viscous modes must be included to address more sophisticated loading protocols (e.g., cycling at disparate frequencies) and the nonlinear viscoelastic response [25, 66, 70,71,72]. The ratio of instantaneous dynamic modulus to equilibrium modulus observed in rabbit lung for spherical deflation [69] is comparable in magnitude to values observed in pig lung under indentation [73] and human lung under tensile relaxation [59].
Viscous stress component ζ0 associated with non-equilibrium pressure is generally nonzero. All six other components of ζ vanish by construction, so ζi = 0 ⇒ χi = 𝜖i for i ≥ 1. The homogeneous deformation state is spherical: F = J1/31. The stress state is hydrostatic: \(\boldsymbol {\sigma } = (\hat {\tau }_{0} / J) \textbf {1} = - p \textbf {1}\). Elastic strain variables are \(\epsilon _{0} = \xi _{1} = \ln J\), ξ2 = ξ3 = 0, and 𝜖i = 0 for i ≥ 1, leading to χi = 0 for i ≥ 1. The tensile deformation state under which relaxation is measured is not severe enough to induce damage: D(t) = 0∀t ≥ 0. Viscous heating is omitted under the time scales involved.
Pressure is related to J and D under isothermal (T = T0) deformations from the first of Eq. 3.29 (D = 0):
Free energy is as follows:
Under pressure relaxation at fixed volume, J = J0 = constant. At equilibrium, as \(t \rightarrow \infty \), \(\chi _{0} \rightarrow \epsilon _{0} = \ln J = \ln J_{0}\). The value of J0 was prescribed such that \(p (t \rightarrow \infty )\) matches the experimental value [69]: J0 = 1.313. For J = 1.313, the maximum driving force at t = 0 is Zm = 0.414 < Z0 = 1 at ptp = −p = 1.11 kPa, so damage never ensues. The internal strain χ0 evolves according to the viscoelastic kinetic law for ζ0. From Eqs. 3.14 and 3.15 with J = J0 = constant,
Substituting Eq. 4.16 into Eq. 4.14 at J = J0 produces the relaxation function as follows:
Viscoelastic parameters β1 and t1 are obtained by matching the relaxation response of p from Eq. 4.17 versus decay time t to experimental data from [69]. Results are reported in Fig. 5, demonstrating suitability of this two-parameter fit.
Pressure versus relaxation time for constant volume stress relaxation in air: model calibration versus experimental data on rabbit lung [69]
4.3 Simple shear
Dynamic shear is studied, where results are compared to torsion data on porcine lung [74] and simple shear data on human lung [75]. The lone material parameter to be identified in Table 1 is c3. A coordinate system is chosen with basis vector e2 aligned normal to the plane of shear and e1 parallel to the direction of shear. In a torsion test, e2 would be parallel to the axis of twist along a cylindrical specimen, and e1 would be aligned in an orthogonal circumferential direction. In the latter case, a material element of study would be located near the outer radius of the specimen, where shear stress is maximal. The local deformation gradient at a material element, in these coordinates, is presumed as follows:
The only non-vanishing strain attribute, strain combination, and viscous state variable entering the free energy are as follows:
Nonzero stress attributes in terms of Cauchy pressure p and shear stress τ conjugate to γ are as follows:
Nonzero pressure may result from nonlinear coupling with shear, temperature change, and surface tension. Free energy, not including the damage prefactor, is as follows:
The lone scalar viscous stress component is \(\zeta = \zeta _{4} = - \partial _{\chi } {{\varPsi }}_{0} = -\partial _{\chi } {{\Upsilon }^{G}_{0}}\). Viscoelastic kinetics of Eq. 3.14 produce the following:
For constant strain rate loading, \(\gamma = \dot {\gamma } t \) where \(\frac {\mathrm {d}}{\mathrm {d}t} \gamma = \dot {\gamma } =\) constant, this reduces to the following:
The internal strain is, from Eq. 3.15,
The minimum strain rate considered in what follows is \(\dot {\gamma } = 550\) s− 1, for which \({\min \limits } [\exp (-t/t_{1})] = 0.9964\) at γ = 1 and \(t = \frac {1}{550}\) s. Therefore, for such rapid loading, viscous relaxation is insignificant, and χ(t) = 0∀t ≥ 0 is a very accurate approximation. Damage accrues according to Eq. 3.26, where \(Z_{m} = \max \limits _{s \in [0,t]} Z(s)\) with
Results of the model for an imposed strain rate of \(\dot {\gamma } = 550\) s− 1 are shown in Fig. 6, with and without damage enabled. Viscous effects are omitted in the static results, which correspond to γ = χ or β3 = 0. Rate dependence is evident by the stiffer response of the viscoelastic relative to the static results. Damage only ensues for \(\gamma \gtrsim 0.4\), and even then, its effect on τ is minimal for γ ≤ 1. Damage increases with shear strain as indicated in Fig. 6b. Damage evolves more severely with γ in the dynamic case due to contributions from viscous configurational energy to the driving force Z. Although loss of biological function may arise at the onset of nonzero D at relatively low stress (Z > Z0 for \(\tau \gtrsim 1.05\) kPa), the lung can sustain very large simple shear deformations before total rupture: \(D \rightarrow 1\) only when \(\gamma \gtrsim 3.4\). This prediction is consistent with experimental data for spherical expansion [67] discussed in Section 4.1.2.
Model response in dynamic simple shear: a shear stress τ versus simple shear strain γ, compared to experimental max/min data on porcine lung [74] tested at \(\dot {\gamma } = 550\) s− 1; b damage variable D versus shear γ for dynamic (with viscosity); and static (without viscosity) loading
Shear stress τ is compared with data obtained at the same strain rate from dynamic torsion experiments [74]. Data presented in that work demonstrate significant test-to-test variability; only their maximum stress–strain curve is reproduced here in Fig. 6a. Not shown are experimental data obtained from direct, dynamic simple shear experiments on human lung at two higher strain rates [75], which demonstrate a notably stiffer response. The present viscoelastic model, with c3 = 0.5, produces τ-γ response curves close to the maximal porcine data for \(\gamma \gtrsim 0.4\). Dog data are expected to more closely match porcine than human data, as also suggested by [59] where human lung tissue was reported to be stiffer than dog lung tissue in biaxial tension.
5 Internal energy formulation for air-tissue response
A constitutive formulation for static and dynamic loading of the lung based on the internal energy potential U is now developed. This model is preferred for compressive stress states and very high strain rates. It can be used to model adiabatic shock loading processes in which air does not have time to redistribute among or escape from the alveoli.
5.1 General form
The following form of U in the second of Eq. 2.25 is invoked:
This function mirrors that of free energy (3.1), where temperature T is replaced with entropy density η. Equilibrium internal energy, including strain energy and coupling from thermal expansion, is \(U^{\infty }_{0} = U^{V \infty }_{0} + U^{\mu \infty }_{0} +U^{G \infty }_{0} \), partitioned into contributions from dilatation, squeeze, and simple shear. Configurational internal energy associated with viscoelasticity, partitioned similarly, is \({\Upsilon }_{0} = {{\Upsilon }^{V}_{0}} + {\Upsilon }^{\mu }_{0} + {{\Upsilon }^{G}_{0}}\). Thermoelastic and viscous contributions sum:
Functions entering Υ0 will be assigned identical forms to those in Section 3. Two damage degradation functions are \(\bar {f}\) and f, where the latter will be prescribed identically to that in Eq. 3.1. Function f degrades the stiffness in pure and simple shear. Function \(\bar {f}\) degrades the bulk stiffness, and \(\bar {f}(D) \geq f(D)\) is imposed conditionally later such that under rapid compression, the tangent bulk modulus cannot fall below that of air alone in the initial state.
5.2 Thermoelastic strain energy
A material element consists of dense lung tissue, surface liquid, and air inside alveoli. Under slow deformation processes, air has time to move throughout the microstructure—or when the entire lung is considered, enter and exit through open trachea—and only the tissue network and surface liquid affect the stiffness. Under very rapid loading (or if the trachea is artificially sealed), air does not have time to redistribute or escape, and compressibility of the air affects the response in conjunction with the dense tissue and liquid phase [30]. Effects of trapped air on stiffness measured during wave propagation have been widely documented [1, 30, 31, 58, 67]. The loading rate or frequency at which a transition from open tissue-dominated to air-dominated stiffness affects wave speeds is not known precisely; an intermediate region between the two regimes likely exists [31].
For the open-cell model, the reference state is identical to that of the free energy-based theory of Section 3.2. The stress supported by the continuum material element is that sustained by the tissue and its surface air-liquid interface, if not saline-washed. A material element is considered to occupy a stress-free reference state when undeformed (F = 1 and J = 1) and in the absence of surface tension at the air-liquid interface, wherein its mass density is ρ0 and entropy is η0. Surface tension will produce tensile pressure at J = 1. Transpulmonary pressure ptp is equal to the negative of pressure supported by continuum element, related to internal airway pressure pa and pleural/external pressure ppl via Eq. 4.1. Neither pa nor ppl need be known explicitly to use the open-cell model or the framework of Sections 3 and 4. When one is given (e.g., pa = 1 atm), then the other (e.g., ppl) can be computed a posteriori once p is obtained from the constitutive model. All pressures entering Eq. 4.1 are referred in this work to a datum of absolute zero (vacuum). Accordingly, pa ≥ 0 since air cannot sustain tensile pressure under conventional models such as ideal gases [76].
The closed-cell model is more complicated. A continuum material element consists of the dense tissue phase (solid + liquid) as well as the internal air phase (gas). Volume fractions occupied by each phase in the reference state are denoted by vt and va for dense tissue and air, respectively, related by vt + va = 1. The reference state of the effective continuum element for which F = 1, J = 1, ρ = ρ0, and η = η0 is defined as follows. The continuum stress vanishes, and thus p = 0, for this element at the reference state in the absence of surface tension. The internal airway pressure at the reference state is imposed a priori as pa = pa0 > 0, where a vacuum airway state is not considered to avoid singularities. Thus, from Eq. 4.1, the pleural pressure, positive in compression, at the reference state at J = 1 is ppl = p + pa = −K0 + pa0, where K0 is the surface tension. In the absence of surface tension, pleural pressure and internal airway pressure balance to ensure the reference state is stress-free. Material coefficients entering the internal energy function depend on vt and pa0, which are regarded as fixed initial values during solution of any boundary value problem. This does not imply that internal airway pressure pa remains constant during the time history of deformation.
Equilibrium thermoelastic internal energy depends explicitly on three functions of the strain attributes of Eq. 2.14, denoted by ξi, i = 1,2,3, defined identically to Eq. 3.2. The thermoelastic internal energy analog of Eq. 2.30 is identically satisfied through Eq. 2.15. Thermoelastic strain energy density per unit reference volume is prescribed as follows:
Energy is partitioned into contributions from dilatation, squeeze, and simple shear analogously to Eqs. 3.21 and 3.22:
Denoted by \(\bar {B}_{0}^{\eta }\) is the effective isentropic bulk modulus, μ0 the shear modulus for pure shear, and G0 the shear modulus for simple shear, all at the undeformed reference state for equilibrium quasi-static deformation (no viscoelasticity), in the absence of damage. The latter two are identical in value and definition to μ0 and G0 introduced in Eq. 3.3. The datum value of entropy at the reference state is chosen as η0 = 0 for simplicity. Temperature at the reference state is the constant T0. The isentropic pressure derivatives of the shear moduli at the reference state are \(\mu ^{\prime }_{0}\) and \(G^{\prime }_{0}\). The isothermal bulk modulus is \({B^{T}_{0}}\), identical to that in Section 3.2; c1, c2, c3, and K0 also match those in Eq. 3.3 and Table 1.
The first term in Eq. 5.3 accounts for the isentropic pressure-volume response and contains the isentropic bulk modulus at the reference state, \(\bar {B}^{\eta }_{0}\). The second term in Eq. 5.3 accounts for thermoelastic coupling and contains the Grüneisen parameter at the reference state, g0. The purely entropic contribution to internal energy is as follows:
denoted by ρt, the constant mass density of the condensed tissue phase at the reference state; denoted by ρa0, the mass density of the internal air at the reference state. Treating air as an ideal gas, ρa0 = (pa0/p1)ρa1, where ρa1 = 1.2 × 10− 3 g/cm3 is its mass density at room temperature T0 and p1 = 1 atm. The reference mass density of the composite lung is
In practice, the mass density of the composite lung ρ00 is measured in air at a given internal pressure pa0 = ppl, i.e., at zero transpulmonary pressure. The reference state mass density ρ0 is then found from mass conservation as ρ0J0 = ρ00J00, where J00 is the calculated contraction due to surface tension K0 computed using the static spherical response of Section 4.1.1. For properties given in Table 1, J00 = 0.9245 is obtained from implicit solution of Eq. 4.2 with D = 0. Note that J0 = 1 in the undeformed reference state. Finally, vt is obtained by an implicit solution of Eq. 5.7. In subsequent analysis, ρ0 and vt are then treated as constants for a given lung sample and set of initial conditions.
Mixture theory estimates the coefficient of thermal expansion for the composite, A0, and the specific heat per unit reference volume at constant volume, c0: denoted by subscripts (⋅)t and (⋅)a quantities for dense tissue and air phases at the reference state at temperature T0, and denoted by C the specific heat per unit mass at constant volume. Then
For an ideal gas, Aa = 1/T0, and specific heat per unit mass is reasonably approximated as constant at moderate excursions from room temperature [76], here Ca = 718 J/kg×K. Equation 5.8 can be formally derived under the condition that temperature T is equal in each phase; otherwise, these relations are viewed as basic modeling assumptions.
The definition of the effective isentropic bulk modulus at the undeformed reference state depends on the loading regime, where an open-cell model is used for static to moderate volumetric strain rates, and a closed-cell model for high rates, wherein air does not have time to flow through or exit the alveolar microstructure. Specifically [30, 31],
The closed-cell equation for \(\bar {B}^{\eta }_{0}\) can be formally derived under the condition that pressure changes in each phase are identical for small average volume changes from the reference state, or it can be treated as a basic modeling assumption. The latter is more amenable to the present application since pressures and volume changes presumably both vary heterogeneously among phases during passage of a stress wave through the material. The isentropic bulk modulus of the dense phase at the reference state is \(B^{\eta }_{t}\). The isentropic bulk modulus of air under the ideal gas model is \(B^{\eta }_{a} = \varGamma {B^{T}_{a}} = \varGamma p_{a0}\), with Γ = 1.4 the ratio of specific heat at constant pressure to that at constant volume of air.
The Grüneisen parameter is obtained from the thermodynamic identity as follows [76, 77]:
where A0 and c0 are found from Eq. 5.8. The effective isothermal bulk modulus \(\bar {B}^{T}_{0}\) at the reference state is as follows:
5.3 Viscoelasticity and damage
Viscoelasticity is addressed as in Section 3.3. The viscoelastic response is the same for closed- and open-cell models because air in the closed-cell model is treated as an inviscid compressible fluid (e.g., ideal gas) that does not contribute to dynamic viscosity. The specific relaxation internal energy U0 is equal to the free energy function of Eq. 3.11:
The thermodynamic driving force for damage in Eq. 2.41 is found in terms of thermoelastic strain, viscous internal strain, and entropy by equating partial derivatives of free and internal energies with respect to D:
This derivation is analogous to that followed for obtaining stress components as partial strain derivatives of internal energy in Eq. 2.35 [5, 7]. The thermodynamic driving force for damage of Eq. 5.13 is then, from differentiation of Eq. 5.1,
The linear degradation function of classical damage mechanics introduced in Section 3.4 is retained for f:
This function is contrasted with quadratic functions used in phase field and other generalized continuum theories [78,79,80,81], which are all admissible in the generic thermodynamic framework of [5, 7]. The degradation function \(\bar {f}\) is as follows:
denoted by \(\bar {\gamma } \leq 1\) is the ratio of the bulk modulus of the gas phase to that of the composite material. As \(D \rightarrow 1\), \(\bar {f} \rightarrow \bar {\gamma }\), and the bulk stiffness of the composite at null applied strain reduces to that of the air contained within: \(\bar {B}^{\eta }_{0} \rightarrow B^{\eta }_{a0} = \varGamma p_{a0}\). From Eq. 5.16,
It follows from insertion of Eqs. 5.15, 5.16, and 5.17 into Eq. 5.13 that, in order to ensure damage evolution is physically and thermodynamically irreversible,
Conditional internal energy density per unit reference volume \(\bar {U}_{0} = \bar {F}\) is defined as follows:
The following dimensionless transformation of U0 is defined as a driving force or indicator of damage:
This function matches that of the free energy-based damage model of Eq. 3.20, intended for low to moderate strain rates in Section 3.4, with two exceptions. First, internal energy density normalized by the isentropic bulk modulus in Eq. 5.20 replaces free energy density normalized by the isothermal bulk modulus in Eq. 3.20. Second, the factor 1 + ω appears only in the present internal energy-based model intended for moderate to high strain rates, most notably those involving wave propagation. Arguments of Z are indicated only implicitly by those in parenthesis on the left of Eq. 5.20.
The function ω is defined as follows, with ωD a dimensionless non-negative scalar constant and l a length parameter later associated with alveolar diameter and used for normalization along with the open-cell bulk modulus \(B^{\eta }_{0}\):
The function ω is included in the driving force Z to account for deleterious effects of pressure gradients on the lung when subjected to blast loading [9, 12, 13]: steep pressure rises have been experimentally and numerically associated with more severe injuries than those incurred by gradual loading to similar overall stress and strain magnitudes.
The damage evolution law makes use of the maximum value of instantaneous driving force Z defined in Eq. 5.20 over the time history of deformation at material point X, analogously to Eq. 3.25: \(Z_{m}(\boldsymbol {X},t) = \max \limits _{s \in (-\infty ,t]} Z(\boldsymbol {X},s)\). Damage then obeys Eq. 3.26, where now Zm accounts for normalized energy and its material gradient. Since Zm can only remain constant or increase with time via Eq. 3.25, and because αD ≥ 0 and Z0 > 0, \(\dot {D} \geq 0\). Furthermore, \(\dot {Z}_{m} > 0\) only in the domain \(\bar {U}_{0} \geq 0\) according to Eq. 5.20. Therefore, \(\bar {U}_{0} \dot {D} = \bar {F} \dot {D} \geq 0 \), ensuring positive dissipation according to Eq. 5.18.
5.4 Stresses, entropy, and temperature
Equilibrium internal energy \(U_{0}^{\infty }\) of Eq. 5.3, thermal energy u of Eq. 5.6, configurational energy of Υ0 of Eq. 3.12, and damage degradation functions f of Eq. 5.15 and \(\bar {f}\) of Eq. 5.16 are substituted into Eq. 5.1 to yield the total internal energy function:
Stress components conjugate to strain attributes obtained from Eqs. 2.35 and 5.22 are as follows:
Ratios βi (i = 1,2,3) are identical to Eq. 3.30. From Eq. 2.35, since Υ0, \(U^{\mu }_{0}\), and \({U^{G}_{0}}\) do not depend on η,
Temperature tends to increase with decreasing volume and increasing entropy. Total dissipation in Eq. 2.43 is as follows:
6 Low-amplitude waves and shock waves
The constitutive model of Section 5 is applied to problems of wave propagation in the lung.
6.1 Composite properties and wave speeds
Addressed first is the response of lung tissue under low-amplitude isentropic wave propagation. The initial state be statically pressurized and finitely spherically deformed from an unstressed state, but wave motion is restricted to small deformations and small deformation gradients superposed on the initial state as in linear elastodynamics [82, 83].
An upper triangular deformation matrix is sufficient for this application. A global coordinate system is chosen such that Q = 1, following [84]. In this context, F = T cannot be arbitrary, but rather Laplace stretch must be integrable to a vector potential [5, 7]. Let u(X,t) denote the displacement field. Then, measured relative to the initial state is as follows:
Components of the linear strain tensor are \(e_{\text {ij}} = \frac {1}{2}(\partial u_{i}/ \partial X_{j} + \partial u_{j} / \partial X_{i})\), and eα (α = 1,2,…,6) are components of strain in Voigt notation. Under the condition that |eα|≪ 1, the following relationships to strain attributes of Eq. 2.14 are derived:
Next, the stress–strain equations of Eq. 5.23 are linearized about a reference state at pressure p0 under isentropic conditions pertinent to elastic wave propagation, in the absence of damage (D = 0). For instantaneous response applicable to high-frequency waves, no viscoelastic relaxation occurs, and thus χi = 0. Truncation at O(|e|2) gives the following:
Letting \(\bar {\beta }_{1} = \beta _{1} \times {B^{T}_{0}} / \bar {B}^{\eta }_{0}\), dynamic thermoelastic moduli are \(\bar {B}^{\eta }_{D} = \bar {B}^{\eta }_{0} \times (1 + \bar {\beta }_{1}) =\bar {B}^{\eta }_{0} + \beta _{1} {B^{T}_{0}}\), μD = (1 + β2) × μ0, and GD = (1 + β3) × G0. Then, from Eq. 2.18, linearized constitutive equations for Kirchhoff stress components sij = kij are as follows:
These equations are identical to those of linear anisotropic elasticity for cubic symmetry and an initial homogeneous pressure p0. When μD = GD, they reduce to linear isotropic elasticity. For low-frequency waves (χi = 𝜖i), or in the absence of viscoelasticity (e.g., saline-washed lung, βi = 0), the linearized stress–strain equations are of identical form, but with static moduli replacing dynamic moduli. Strain components eα are those measured relative to the initial state wherein \(\boldsymbol {F} = J_{0}^{1/3} \textbf {1}\). Surface tension, − K0, is assumed included in p0, and thus is not explicitly written in Eq. 6.3 or Eq. 6.4.
Under the foregoing small deformation assumptions, equations of motion in the absence of body forces are as follows [82, 83]:
where ρ0 is the mass density in the initial state upon which wave motion is superposed. Addition of a homogeneous initial stress field, e.g., p0, does not affect the left side of Eq. 6.5.
For the rectilinear Cartesian coordinate system associated with Eq. 6.1, each of the three coordinate axes is a pure mode direction for plane wave motion. Each axis permits a longitudinal plane wave (displacement parallel to propagation direction) propagating at velocity cL and two shear plane waves (polarization orthogonal to propagation direction) propagating at velocity cS. Considering Eqs. 6.4 and 6.5, wave speeds are deduced to be of the standard form [85, 86]
where in general, now admitting a homogeneous initial damage field D0, the tangent moduli in the initial state are as follows:
Properties of each of the two phases are listed below the horizontal demarcation line in Table 2. Mass density of the dense tissue phase ρt and its isentropic bulk modulus \(B^{\eta }_{t}\) are obtained from [30]. These two values are unaffected by any initial static (transpulmonary) pressure p0 and any corresponding static volume change J0 of a composite material element. Specific heats and thermal expansion coefficients for the dense phase are estimated from [87,88,89,90].
Composite properties above the demarcation line correspond to dog lung. Composite mass density ρ0 is obtained from the stress-free mass density ρ00 = 3.65 g/cm3 reported in [22] using the analysis procedure described in Section 5.2. Densities of each phase then enter Eq. 5.7, which is solved iteratively for the value of vt listed in Table 2. The composite bulk modulus \(\bar {B}^{\eta }_{0}\), composite specific heat c0, composite thermal expansion coefficient A0, and composite Grüneisen parameter g0 are obtained using relations in Eqs. 5.8, 5.9, and 5.10, where the closed-cell model equations are invoked. The value listed for ΩD will be justified in Section 6.2, wherein the alveolar diameter l (dog lung [1]) is introduced.
The closed-cell bulk modulus \(\bar {B}^{\eta }_{0}\) is on the order of 200 kPa for an internal airway pressure of 1 atm, compared to the value of static isothermal bulk modulus \({B^{T}_{0}}\) in Table 1 of 2.5 kPa in air and 2.0 kPa in saline. The open-cell isentropic bulk modulus computed from Eq. 5.9 is nearly indistinguishable, essentially also 2.5 kPa in air and 2.0 kPa in saline. Effects of viscoelasticity on \(\bar {B}^{\eta }_{D}\) are effectively negligible since β1 = 0.6 from Table 1 and \(\bar {\beta }_{1} = \beta _{1} {B^{T}_{0}} / \bar {B}^{\eta }_{0} \approx 0.007 \). Also, \(\mu _{D} \approx G_{D} \ll \bar {B}^{\eta }_{D}\). Therefore, for pa0 ≈ 1 atm, longitudinal wave propagation is effectively isotropic with a velocity essentially equal to the bulk sound speed: \( c_{L} \approx \sqrt { \bar {B}^{\eta }_{D} / {\rho }_{0} } \approx \sqrt { \bar {B}^{\eta }_{0} / {\rho }_{0} }\).
Results of Eqs. 5.9 and 6.6 for the closed-cell model are reported in Fig. 7. Shown in Fig. 7a versus pa0 are this closed-cell dynamic bulk modulus normalized by the open-cell modulus \(B^{\eta }_{0} \simeq {B^{T}_{0}}\) for lung in air and saline, with respective values of 2.5 and 2.0 kPa. The condition J0 = 1 is imposed for Fig. 7a: initial transpulmonary pressures are p0 = −K0 = 0.2 kPa in air and p0 = 0 in saline. As internal air pressure increases from 0.1 to 10 atm, the ratio of dynamic to static, i.e., closed to open cell, bulk modulus increases from around 10 to around 1000. Shown in Fig. 7b versus initial airway pressure are longitudinal wave speeds computed from the first of Eq. 6.6, normalized by wave speed cL1 = 27.1 m/s, where the latter is computed at pa1 = 1 atm. Here, transpulmonary pressure is fixed at ptp0 = −p0 = 5 cm H2O = 0.49 kPa. Complementary experimental ratios of wave velocity versus internal airway pressure, measured at the same fixed transpulmonary pressure of 5 cm H2O in horse lung [30], are shown for comparison.
Predictions for isentropic bulk modulus and longitudinal wave speed versus initial airway pressure normalized by pa1 = 1 atm, with data for horse lung in air from [30]: a bulk modulus \(\bar {B}^{\eta }_{D}\) computed from Eq. 5.9 and Eq. 6.7 at reference state with J0 = 1 and D0 = 0; b wave speed cL computed from Eq. 6.6 at reference state of ptp0 = 5 cm H2O
Shown in Fig. 8 are predictions of cL for dog lung from Eq. 6.6 for a fixed external (pleural) pressure of ppl = 1 atm and a variable initial transpulmonary pressure ptp0 = −p0 up to approximately 2 kPa. According to Eq. 4.1, initial airway pressure pa0 is close to atmospheric since \(|p_{0}| \lesssim 2~\text {kPa} \ll 101\) kPa= 1 atm. Since \(B^{\eta }_{t}\) and \(B^{\eta }_{a} = \varGamma p_{a0}\) do not depend on transpulmonary pressure, effects of ptp0 on cL in the present model emerge primarily from effects of transpulmonary pressure on J0, and thus on initial mass densities ρt, ρa0, and finally ρ0 according to Eq. 5.7. Specifically, \(\rho _{t} \rightarrow \rho _{t} / J_{0}\), where the reference value at J0 = 1 is given in Table 2. Shear moduli are affected by initial transpulmonary pressure associated with expansion J0, e.g., \(\mu _{0} \rightarrow \mu _{0} - \mu ^{\prime }_{0} {B^{T}_{0}} \ln J_{0} \), where values of μ0 = G0 = 1 kPa and \(\mu ^{\prime }_{0}=G^{\prime }_{0} = -~0.7\) are listed in Table 1. However, the shear modulus trivially affects cL since \(\bar {B}^{\eta }_{D}\) exceeds μD by two orders of magnitude. As ptp0 increases, the lung expands and mass density ρ0 decreases, leading to an increase in wave speed. A change in \(\bar {B}^{\eta }_{D}\) might be expected with initial expansion J0 > 1, but this effect is deemed secondary relative to density changes [58].
Predictions are compared in Fig. 8 with high-frequency response data on horse lung [30] as well as data on rabbit lung measured under sealed trachea conditions [58]. Maximum initial transpulmonary pressures probed in the model and these experiments are on the order of 2 kPa or 20 cm H2O, just beneath those required to cause edema in saline-treated rabbit lung [67]. At the upper end of this pressure range, according to the present theory, minimal damage D0 and stiffness reduction incurred in the initial state due to tensile transpulmonary pressure ptp0 do not significantly affect tangent moduli or wave speeds. Model predictions of wave speed cL in dog lung reasonably match those for rabbit lung [58]. Agreement with data on horse lung is reasonable at null transpulmonary pressure.
6.2 Shock compression
Propagation of a planar compressive shock wave through the lung is analyzed. The present treatment is of much greater scope than [6] that did not address damage, injury, or distinctions between normal and saline-infused lung.
The shock is analyzed in the framework of the Rankine–Hugoniot jump conditions [76, 77, 85, 91]. Material in the vicinity of the shock, both upstream and downstream, is treated as a homogeneous continuum with effective properties such as mass density, internal energy, and bulk stiffness. The shock front, i.e., the region across which density, pressure, and particle velocity rapidly increase, is not resolved explicitly. Validity of application of the Rankine–Hugoniot jump conditions for mass, momentum, and energy requires that either the thickness of this front, called the “shock width,” be infinitesimal (i.e., a limiting singular surface), or that the entire waveform analyzed, even if the front is of finite width, moves at constant Lagrangian velocity [76, 77]. The latter interpretation is more physically valid in the present context, as the minimum width w of the shock front should be constrained by the microstructure, here the diameter l of an alveolus. In other words, \(w \gtrsim l\) is presumed, since the entire pressure rise cannot be contained within a single alveolus as it would only sample material of the gas phase, rather than the effective continuum. The shock is initiated by a step loading (impact) in particle velocity or pressure on the lung surface. Presumably, after a transit period, a steady shock structure will be attained beyond some distance from the impact surface, where w is ultimately dictated by the microstructure as well as dissipation that tends to spread the front. Even though the lung is a two-phase material with gas and relatively stiff dense tissue, a continuum treatment is deemed valid. Similar equations are widely used to analyze highly porous solids [76] including metallic foams, particulates, and powders, wherein, like the lung, a large volume fraction of the medium consists of trapped air.
6.2.1 Governing equations
The planar shock problem is idealized via standard protocols of shock physics [50, 76, 77, 85, 91, 92]. An infinitely column of lung material consisting of dense tissue and air phases is subjected to a planar longitudinal compressive shock wave traveling at constant Lagrangian velocity υs in the X = X1-direction in material coordinates. States of the material on either side of the wavefront, which may be of small but finite width w, are uniform. Let superscripts (⋅)+ and (⋅)− denote quantities or conditions measured ahead of and behind the shock front, respectively, corresponding to respective un-shocked (upstream) and shocked (downstream) states.
Material ahead of the shock is undeformed (J+ = 1) and at rest. The upstream airway pressure is \(p^{+}_{a} = p_{a0}\), which varies among calculations later. The upstream stress in the lung tissue is hydrostatic. The transpulmonary pressure in the tissue upstream is the initial surface tension \(p^{+} = -p^{+}_{\text {tp}} = -K_{0}\) for standard lung, and \(p^{+} = - p^{+}_{\text {tp}} = 0\) for saline-treated lung. The external (e.g., pleural) pressure necessary to impose both conditions is then found via Eq. 4.1 as \(p_{\text {pl}}^{+} = p^{+} + p^{+}_{a}\). The upstream entropy density is taken as the zero datum, η+ = 0, and the upstream temperature is chosen as T0 = 310 K. The following abbreviated notations are then used:
The downstream pressure p− is defined relative to the datum initial state in the absence of surface tension. In other words, p− = p+ in the limit of zero imposed compression in the shock wave. A total downstream pressure can be defined as ptot = p− + pa0, which thus is defined relative to a datum state close to vacuum because initial surface tension is much smaller in magnitude than atmospheric pressure. Thus, ptot includes the initial airway pressure, initial surface tension, and the pressure rise due to the shock, while p−≤ ptot does not include initial airway pressure. The same solutions apply regardless of which datum is used for pressure since only the jumps in stress and energy are used.
The downstream Cauchy stress state σ− in the composite lung material is determined from simultaneous solution of the Rankine–Hugoniot jump conditions and closed-cell constitutive model of Section 5 for the homogenized effective medium. This stress tensor is diagonal due to symmetries of the material and loading mode, but it is not necessarily spherical. The downstream pressure is \(p^{-} = -\frac {1}{3}\text {tr} \boldsymbol {\sigma }^{-}\). The shock stress is defined as the longitudinal component of Cauchy stress, positive in compression: \(P = -\sigma _{11}^{-}\). Lateral stress components are \(\sigma _{22}^{-} = \sigma _{33}^{-}\), and a measure of Cauchy shear (squeeze) stress is the difference \(\tau = -\frac {1}{2}(\sigma _{11}^{-} - \sigma _{22}^{-})\). When the shocked state is perfectly spherical, then τ = 0 and P = p−. A total downstream stress tensor that also includes initial airway pressure is defined consistently as \(\boldsymbol {\sigma }_{\text {tot}} = \boldsymbol {\sigma }^{-} - p_{a0} \textbf {1}\). Neither the downstream airway pressure nor the isolated pressure in the dense tissue phase are individually calculable in the shocked state using this composite material model.
Summarizing the above textual definitions, downstream and upstream deformation gradients are, respectively,
Cauchy stresses in the shocked and initial states are the following:
Upstream pressure p+ has been relabeled as p0. Composite mass densities are, from Eqs. 5.7 and 6.9,
where the value of vt in Table 2 is maintained. Since J+ = 1 and ρt = constant, ρ+ is nearly constant in forthcoming calculations, with only a slight variation incurred from ρa0 as initial airway pressure changes.
As was the case in Section 6.1, the deformation process is deemed too rapid for viscoelastic stress relaxation to commence. As justification, consider a shock front of maximum width w = 10l ≈ 600μ m and minimum propagation velocity υs = cL ≈ 20 m/s, giving a maximum rise time of tR = w/υs ≈ 30μ s. Considering the relaxation time scale t1 = 5 × 105μ s from Table 1, tR/t1 ≪ 1, viscous relaxation is negligible, and thus internal strain vanishes, i.e., χ = 0.
According to Eq. 6.9, all strain attributes of Eq. 2.14 vanish identically in the upstream state, i.e., \(\epsilon ^{+}_{i} = 0\) and 𝜖+ = 0. Furthermore, the initial condition D+ = D0 = 0 is imposed, consistent with the low initial transpulmonary pressure due only to surface tension at J+ = 1, which does not impart sufficient driving force Z+ ≥ Z0 according to Eqs. 3.20 and 3.26 to instigate any damage in the reference state. Since η+ = 0 by construction, the internal energy density of Eq. 5.22 in the upstream state also vanishes: U+ = 0. Notation 𝜖− = 𝜖, U− = U, and D− = D is thus adopted.
Define the jump and average of a quantity across the shock front as follows:
denoted by υp = υ1(X,t), the uniaxial particle velocity field. Since the upstream material is quiescent, \(\upsilon _{p}^{+} = 0\), and the abbreviated notation \(\upsilon _{p}^{-} = \upsilon _{p}\) is invoked. Recall that υs is defined as the steady Lagrangian shock velocity; this is equal to the Eulerian shock velocity since \(\upsilon _{p}^{+} = 0\) and J+ = 1. Rankine–Hugoniot jump conditions for mass, linear momentum, and energy conservation across the shock front are expressed in Lagrangian form as follows [76, 77]:
For compressive shocks, 0 < a < 1 and υs > υp > 0. Under the trivial case of null deformation, a = 1, P = p0, and υs = υp = 0. Assume that the deformation induced by the shock, a, is imposed as the loading parameter. Assume that the upstream pressure and density are known according to Eqs. 6.10 and 6.11. Then, Eqs. 6.13– 6.15 are three scalar equations with five unknowns in the set (υp,υs,P,U,η). The system becomes closed when augmented by constitutive equations for stress and internal energy that both depend on a and η. The jump form of the entropy production inequality in the present adiabatic case requires that η ≥ 0, i.e., entropy must not decrease across the shock front.
From Eq. 6.9, strain attributes of Eq. 2.14 in the downstream state are as follows:
State variables of strain in Eq. 3.2 are as follows:
Damage D− = D may be nonzero due to driving force Z induced by shock compression that may exceed Z0 for shock stresses of sufficient magnitude [1, 93]. Stress components conjugate to rates of Eq. 6.16 are, from Eq. 5.23, dropping the (⋅)− superscript for brevity on the left and with 𝜖0 = 𝜖0(a) on the right,
Nonzero Cauchy stress components \(\sigma _{\text {ij}} = \frac {1}{J} s_{\text {ij}}\) are, from Eq. 2.34,
Shock stress, pressure, and shear stress of Eq. 6.10 are then
Normally, P ≥ p−≥ 0 and τ ≥ 0, so \(\hat {\tau }_{0} \leq 0\) and \(\hat {\tau }_{1} = -\hat {\tau }_{3} \leq 0\). Internal energy in the shocked state is, from Eq. 5.22,
Downstream temperature is, from Eq. 5.24,
Damage obeys Eq. 3.26, where for non-trivial evolution in regime \(\frac {Z_{m}}{Z_{0}} \in \left [ 1,1 + \frac {\ln 2}{\alpha _{D}} \right ]\),
Internal energy density of Eq. 6.21 is partitioned according to Eqs. 5.4 and 3.23 as follows:
Substitution into Eqs. 5.20 and 5.21 gives the driving force for damage kinetics for non-negative energy density \(\bar {U}_{0} = (1-\bar {\gamma }) (U^{V \infty }_{0} + {{\Upsilon }^{V}_{0}}) + U^{\mu \infty }_{0} + {\Upsilon }^{\mu }_{0} \geq 0\) with \(B^{\eta }_{0} \simeq {B^{T}_{0}}\):
The internal energy gradient across the shock front is estimated by assuming a linear profile over the shock width w [94], recalling that \(U^{+}_{0} = 0\) in the initial upstream state and \(U_{0} = U_{0}^{-}\):
6.2.2 Results: shock wave mechanics
Hugoniot response curves are generated for lung in air and treated with saline, at initial airway pressures ranging from pa0 = 0.5 atm to pa0 = 3 atm. The dense tissue phase has initial volume fraction vt given in Table 2, regarded as a fixed material property for dog lung. Governing equations in Section 6.2.1 are solved using an iterative numerical procedure. Results for an initial internal airway pressure of pa0 = 1 atm are discussed first. These are given in Fig. 9 for both normal lung tissue in air and saline-treated lung tissue. Mass density in the shocked state is ρ− = ρ and in the initial state is ρ+ = ρ0. Calculations span 0.6 ≤ ρ0/ρ ≤ 1, where the maximum compressive strain is 40%.
Predicted Hugoniot response for air or saline-treated lung under planar shock compression at initial air pressure pa0 = 1 atm with mass density in the shocked state denoted by ρ = ρ− and that of the undeformed lung in the upstream state by ρ+ = ρ0: a axial stress, i.e., shock pressure, P b shear stress τ c shock velocity υs versus particle velocity υp,, d entropy η normalized by composite specific heat at constant volume c0
Shown in Fig. 9a is longitudinal shock stress \(P = -\sigma ^{-}_{11}\) of Eq. 6.20. Axial stress is very similar in both air and saline up to moderate compression ratios, with the former becoming larger than the latter for \(\rho _{0} / \rho \lesssim 0.75\). At low shock stress magnitudes, the stiffening effect of surface tension on the bulk modulus is offset by the initial tensile transpulmonary pressure K0. An inflection occurs for ρ0/ρ ≈ 0.75 as damage affects the tangent bulk modulus. Strong stiffening resumes for \(\rho _{0} / \rho \lesssim 0.68\) as the highly compressed material behaves like a densified compressible fluid. Even at 40% compression, the mass density of lung in air is ρ = 0.561 g/cm3, compared to ρt = 1.003 g/cm3 for the tissue phase. Thus, a significant amount of compressed air remains in the composite material even for the strongest shocks considered here. At much larger compressive pressures, effects of air would lessen relative to stiffness of the dense phase, and the curves should approach each other as surface tension effects become negligible.
Reported in Fig. 9b is Cauchy shear stress τ of Eq. 6.20, proportional to squeeze stress component \(\hat {\tau }_{1}\). Initially, for low compressive strain, the shear stress in air exceeds that of saline because of viscoelastic stiffening of the tangent shear modulus. At larger compressions \(\rho _{0} / \rho \lesssim 0.8\), the shear stress for saline-treated lung becomes larger than standard lung tissue in air. The distinction will later be attributed to damage-induced softening of the tangent squeeze modulus. Presented in Fig. 9c is the steady Lagrangian shock velocity υs versus downstream particle velocity υp, related via Eq. 6.13. The inflection in the saline curve corresponds to a change in curvature of the P − ρ Hugoniot in Fig. 9a. This implies a small range of instability (\( 0.663 \lesssim \rho _{0} / \rho \lesssim 0.688 \)) wherein spreading of the shock structure, unaccounted for in the present calculations, would be expected for the saline-treated lung, though the predicted stress-volume and damage responses should remain accurate regardless due to the low entropy produced. Computed results yield \(\upsilon _{s} \rightarrow c_{L}\) in the limit of small deformations, as \(\upsilon _{p} \rightarrow 0\), providing cross-validation of model predictions for longitudinal sound speed and shock velocity. Shown in Fig. 9d is downstream entropy density per unit reference volume η normalized by specific heat c0 of Eq. 5.8. Entropy is always positive, as required by thermodynamics.
Discussed next are model predictions for standard (i.e., not saline-washed) lung at initial air pressures from 0.5 to 3 atm. In each case, the initial transpulmonary pressure due to surface tension is fixed at ptp0 = −p0 = K0 = 0.2 kPa. Mass density in the shocked state is ρ− = ρ. In the initial state at 1 atm airway pressure, density is ρ0. Reported in Fig. 10a are shock stress, normalized by \({B^{T}_{0}} = 2.5\) kPa, versus density ratio at different initial airway pressures. Shock stress P increases substantially with increasing airway pressure since pa0 dominates the closed-cell bulk modulus of Eq. 5.9. Given in Fig. 10b are shear stress, normalized by G0 = μ0 = 1 kPa, versus density ratio for the same internal pressure range. Origins of each curve at the bottom right are offset slightly since ρ increases with increasing initial air pressure. Increased damage leads to a reduction in tangent shear modulus that causes lower shear strength. Shown in Fig. 10c are shock velocity versus particle velocity profiles. Shock velocity increases substantially with increasing pa0, consistent with increasing longitudinal elastic wave speeds reported in Fig. 7b. Finally, Fig. 10d presents entropy normalized by specific heat, for pa0 ∈ [0.5,3] kPa. Dissipation increases with P and pa0.
Predicted Hugoniot response of lung in air at four different values of initial air pressure pa0, with mass density in the shocked state denoted by ρ = ρ− and that of the undeformed lung at pa0 = 1 atm by ρ0: a axial stress P normalized by isothermal bulk modulus \({B^{T}_{0}}\), b shear stress τ normalized by static shear modulus G0 = μ0, c shock velocity υs versus particle velocity υp, d entropy η normalized by composite specific heat at constant volume c0
6.2.3 Results: injury and damage criteria
Numerical results predicted by Eq. 3.26 are reported first, followed by a more thorough discussion relating D to physics of trauma and local material failure. Results for compressive shocks on lung at pa0 = 1 atm are shown in Fig. 11. Differences between the tissue types arise from surface tension and viscous stiffening omitted for saline-washed lung.
Shown in Fig. 11a are damage variable D versus density ratio for the usual, realistic case where ΩD = 8 from Table 2 is invoked as well as for the case when the gradient amplification is omitted via ΩD = 0. The value of D is magnified by a factor of 10 in the latter case to enable visualization. Mass density in the shocked state is ρ− = ρ and in the initial state is ρ+ = ρ0. The value of ΩD = 8 is chosen such that, in saline-treated lung, the threshold shock stress P for the onset of injury is P = 15 kPa. This corresponds to the threshold pressure for injury imparted by a shock tube to exposed, saline-treated rabbit lung in experiments described in [1, 93]. In these experiments, \(P \lesssim 14\) kPa produced no evidence of injury, while \(P \gtrsim 16.5\) kPa produced edema as evidenced by increased lung weight with time after the impact event. Initial transpulmonary pressure (tension) was 10 cm H2O (ptp0 = −p0 ≈ 1 kPa) in these experiments. Damage increases slightly more rapidly in air than in saline-treated lung. Also, when the deleterious effect of energy gradients, i.e., steepness of the pressure rise, is omitted via ΩD = 0, damage criterion Eq. 3.26 requires compressive strains exceeding 30% and shock stresses exceeding 110 kPa to impart the onset of injury via Z > Z0 ⇒ D > 0.
Presented in Fig. 11b is D versus shock stress P of Eq. 6.20, where only results with ΩD = 8 are reported here and subsequently in Fig. 12. Initially with increasing P, damage accumulates more quickly in air than saline. The threshold pressure P for D > 0 is 15.3 kPa in saline and 14.4 kPa in air. After a cross-over at P ≈ 100 kPa, damage accumulates more rapidly in saline-treated lung. Threshold impact pressures for mild injury are low, on the order of 15 kPa or 2 psi, in accordance with experimental observations on edema in bare exposed lung tissue [1, 93], which is very delicate. Local lung over-pressures required for hemorrhage and contusion are thought to be in the 70 to 100 kPa range [10, 95]. According to Fig. 11b, this level of injury correlates to damage variable values in the range of \(0.25 \lesssim D \lesssim 0.5\), which is physically realistic. For lung tissue in air, according to the present results, local damage reaches its maximum possible value of D = 1 for shock pressures P exceeding 135 kPa. Lethal global over-pressures can be on the order several hundred kPa [11, 14, 29] depending on pulse shape and duration; however, in vivo, the lung is encased by the ribcage, skin, muscle, and other soft tissue. Transmission and reflection affect injury in such cases.
Damage and local injury predictions for lung in air (no saline treatment) at pa0 = 0.5, 1, 2, and 3 atm are given in Fig. 12. The density range probed is 0.8 ≤ ρ0/ρ ≤ 1, i.e., a maximum compressive strain of 20%. Shown in Fig. 12a and b are damage state variable D versus density ratio ρ0/ρ and versus shock stress P, respectively, with ρ0 a constant from Eq. 5.7 at 1 atm. Damage increases more rapidly with increasing compressive strain, i.e., with decreasing ρ0/ρ, as pa0 increases since more energy is imparted by a shock wave of corresponding strain as airway pressure increases. The threshold for onset of injury in terms of compressive strain attained in the shock front decreases with increasing initial air pressure. However, as seen in Fig. 12b, the shock stress P required to impart a given level of damage D increases with increasing pa0 since bulk stiffness increases significantly with increasing airway pressure. The threshold shock stress P = P0 for initiation of injury (edema) increases accordingly with pa0.
A physical description of the micro-mechanical and biological changes associated with ranges of D ∈ [0,1] is afforded by Fig. 13. The horizontal axis corresponds to driving force Z0, which essentially depends on normalized internal energy U0 and its gradient ∇0U0 through Eqs. 5.20, 5.21, and 3.26. The energy gradient, in turn, is related to the jump in internal energy across the shock front as indicated in Eq. 6.28. The power of \(\frac {1}{2}\) in the driving force effectively leads to a dependence of damage on axial strain or shock pressure. The amplification of injury due to the rate of pressure rise, or the magnitude of pressure jump, is discussed in [12], wherein the correlation of thoracic wall acceleration to injury severity is quantified experimentally. As explained in [9, 12, 96], as a longitudinal wave pulse propagates through the lung, pressure differentials emerge in the microstructure across capillary–alveolar interfaces, where larger local differentials are linked to shorter rise times of the pulse. Failure of the interfaces and hemorrhages will occur above a threshold that depends, in macroscopic experiments and models, on both the total normalized work or energy [95] and its rate of deposition. A similar local injury criterion reported in [15] is found to correlate with contusion in sheep subjected to blast loading. Overextension, bulging, and ultimately tearing and rupture of alveolar membranes have been observed in histology studies on blast lung in human cadavers [97].
Physical processes related to injury and microstructure degradation in lung tissue in conjunction with evolution of damage variable D. Exponential growth versus driving force is consistent with Eq. 3.26
Summarizing static and dynamic experiments in [1, 67, 93], permeability changes to tissue membranes are induced at relatively low thresholds of imparted pressure, strain, or energy. These result in edema, i.e., pooling of liquid, after sufficient time for fluid transport to occur. Threshold stresses and strains for the onset of injury are exceeded, by substantial margins in some cases, in static and dynamic experiments [1, 19, 21, 51, 52, 59], but these experiments show no significant reduction of elastic stiffness upon unloading. compressive loading.
Assume now as in Eq. 6.28 that, to first order, internal energy and other state variables change relative to their initial or upstream values linearly within a steady shock wave of width w, Lagrangian velocity υs, and rise time tR. The latter three are simply related, leading to several expressions for the material energy gradient ∇0U0:
The next-to-rightmost approximation in terms of internal energy jump is used in Eq. 6.28 and the present calculations. However, in numerical simulations involving finite elements [10, 15, 28], calculation of energy gradients may be cumbersome, so the ratio of material time derivative to wave speed may be a pragmatic choice as a driving force for injury, as also suggested in [96]. In that case, to avoid damage magnification during rapid unloading, \(| \dot {U}_{0} | \rightarrow \langle \dot {U}_{0} \rangle \) could be used such that only positive energy rates are applied to ω. The approximation υs ≈ cL can further be invoked in the weak shock regime. According to the model of Eq. 3.26 and experimental evidence quoted in [9, 12, 96], likelihood and severity of injury increases with increasing |∇0U0|. According to Eq. 6.29, for a fixed amount of energy density U0 supplied by the wave pulse at a fixed wave speed υs ≥ cL, injury severity increases with decreasing rise time tR.
Calculations conducted here invoke a value of \({\Omega }_{D} = \omega _{D} \sqrt {l/w}\) of 8 as calibrated to match experimental data of [93]. The alveolar size is known a priori (l = 60.1μ m in dog lung from Table 2 and [1]), but neither the material constant ωD nor the variable shock width w is known or obtainable from presently available data. Assume for illustration that w = w1 in the experiments of [93], leading to \({\Omega }_{D1} = \omega _{D} \sqrt {l/w_{1}}\). Then, when the lung is subjected to shock pulses of different width or rise time propagating at the same speed \(\upsilon _{S} \gtrsim c_{L}\), the value of ΩD would vary as follows:
Thus, as intended, ΩD decreases as rise time of the shock front tR increases relative to tR1. This in turn results in less damage accrued through Eq. 3.26 for the same imparted internal energy U0. Shown in Fig. 14 are predicted effects of rise time of the shock pulse on damage progression and the onset of injury corresponding to edema. Damage accrues more slowly in Fig. 14a with increasing shock stress as the rise time increases, wherein trauma to standard lung in air is depicted. The threshold shock stress for initiation of damage also increases with rise time as shown in Fig. 14b.
Predicted damage response and injury threshold for exposed lung at different pulse rise times tR, where tR1 is the minimum rise time for shock compression corresponding to experimental data [93]: a damage variable D versus shock stress P for lung in air; b threshold stress for injury P0 versus normalized pulse rise time tR/tR1
7 Conclusions
A geometrically and materially nonlinear model of lung mechanics has been presented. The model accounts for thermoelasticity, viscoelasticity, and damage phenomena, where the latter encompasses both injury and mechanical stiffness degradation. Kinematics and thermodynamics are based on a QR decomposition of the deformation gradient, strain attributes, and conjugate scalar stress measures. Viscoelasticity and damage are treated by internal state variables in a thermodynamically consistent manner, leading to non-negative dissipation. Two variations of the model have been developed: a free energy-based theory pragmatic for static and isothermal loading, and an internal energy-based theory more amenable to dynamic problems involving wave propagation, including shock compression analyzed here. The latter theory accounts for effects of enclosed air on the overall thermodynamic properties, most importantly the dynamic bulk modulus that becomes two orders of magnitude larger than the static tensile modulus when air compressibility is included. The present work is thought to represent the most complete continuum theory for lung mechanics in terms of loading regimes and physical mechanisms encompassed.
Damage and injury have been addressed to the extent afforded by existing data relating mechanics to biology. The model incorporates realistic thresholds for the onset of injury, corresponding to local membrane permeability changes and edema. Threshold stresses, strains, or deposited energies for such injury are far below those that impart noticeable stiffness deterioration, e.g., substantial tears or rupturing of alveolar membranes and/or septal chords comprising the microstructure. Importance of inclusion of the gradient or rate of applied energy/pressure on injury criteria has been verified. Moderate values of the damage variable correlate well with local pressures for hemorrhage and lung contusion reported elsewhere for blunt impact and blast loading. However, a more quantitative linkage of damage progression to observed injury mechanisms above known threshold levels should be sought in the future. Accuracy of the model would also benefit from consistent data from single source, including a fixed species and means of specimen preparation.
References
Fung, Y. -C.: Biomechanics: Motion, Flow, Stress, and Growth. Springer, New York (1990)
Fung, Y. -C.: Biomechanics: Mechanical Properties of Living Tissues, 2nd edn. Springer, New York (1993)
Humphrey, J. D.: Continuum biomechanics of soft biological tissues. Proc. R. Soc. Lond. A 459, 3–46 (2003)
Freed, A. D.: Soft Solids. Birkhauser, Cham (2016)
Clayton, J. D., Freed, A.D.: Viscoelastic-damage theory based on a QR decomposition of deformation gradient. Technical Report ARL-8840, Army Research Laboratory, Aberdeen Proving Ground, MD (2019)
Clayton, J.D., Banton, R.J., Freed, A.D.: A nonlinear thermoelastic-viscoelastic continuum model of lung mechanics for shock wave analysis. AIP Conference Proceedings, in press (2019)
Clayton, J. D., Freed, A. D.: A constitutive framework for finite viscoelasticity and damage based on the Gram-Schmidt decomposition. Acta Mechanica submitted (2019)
Grimal, Q., Gama, B. A., Naili, S., Watzky, A. l., Gillespie, J. W.: Finite element study of high-speed blunt impact on thorax: linear elastic considerations. International Journal of Impact Engineering 30, 665–683 (2004)
Grimal, Q., Naili, S., Watzky, A.: A high-frequency lung injury mechanism in blunt thoracic impact. J. Biomech. 38, 1247–1254 (2005)
Shen, W., Niu, Y., Mattrey, R. F., Fournier, A., Corbeil, J., Kono, Y., Stuhmiller, J. H.: Development and validation of subject-specific finite element models for blunt trauma study. J. Biomech. Eng. 130, 021022 (2008)
Bowen, I. G., Fletcher, E. R., Richmond, D.R.: Estimate of man’s tolerance to the direct effects of air blast. Technical report, Lovelace Foundation for Medical Education and Research, Albuquerque NM (1968)
Cooper, G. J., Pearce, B. P., Sedman, A. J., Bush, I. S., Oakley, C.W.: Experimental evaluation of a rig to simulate the response of the thorax to blast loading. Journal of Trauma and Acute Care Surgery 40, 38S–41S (1996)
Cooper, G.J., Jonsson, A.: Protection against blast injury. In: Cooper, G.J., Dudley, H.A.F., Gann, D.S., Little, R.A., Maynard, R.L. (eds.) Scientific Foundations of Trauma, pp 258–283. Butterworth Heinemann, Oxford (1997)
Rafaels, K. A., Cameron, R., Panzer, M. B., Salzar, R. S.: Pulmonary injury risk assessment for long-duration blasts: a meta-analysis. Journal of Trauma and Acute Care Surgery 69, 368–374 (2010)
Gibbons, M. M., Dang, X., Adkins, M., Powell, B., Chan, P.: Finite element modeling of blast lung injury in sheep. J. Biomech. Eng. 137, 041002 (2015)
Stitzel, J. D., Gayzik, F. S., Hoth, J. J., Mercier, J., Gage, H. D., Morton, K. A., Duma, S. M., Payne, R. M.: Development of a finite element-based injury metric for pulmonary contusion part I: model development and validation. Stapp Car Crash J. 49, 271–289 (2005)
Stuhmiller, J. H., Chuong, C. J., Phillips, Y. Y., Dodd, K. T.: Computer modeling of thoracic response to blast. Journal of Trauma 28, S132–S139 (1988)
Vlessis, A.A., Trunkey, D.D.: Non-penetrating injury of the thorax. In: Cooper, G.J., Dudley, H.A.F., Gann, D.S., Little, R.A., Maynard, R.L. (eds.) Scientific Foundations of Trauma, pp 127–143. Butterworth Heinemann, Oxford (1997)
Fung, Y. -C.: Stress, deformation, and atelectasis of the lung. Circ. Res. 37, 481–496 (1975)
Fung, Y. -C., Patitucci, P., Tong, P.: Stress and strain in the lung. ASCE Journal of Engineering Mechanics 104, 201–223 (1978)
Vawter, D. L., Fung, Y. -C., West, J. B.: Constitutive equation of lung tissue elasticity. J. Biomech. Eng. 101, 38–45 (1979)
Vawter, D. L.: A finite element model for macroscopic deformation of the lung. J. Biomech. Eng. 102, 1–7 (1980)
Fung, Y. -C.: Elasticity of soft tissues in simple elongation. Am J Physiol 213, 1532–1544 (1967)
Bachofen, H., Hildebrandt, J., Bachofen, M.: Pressure-volume curves of air-and liquid-filled excised lungs-surface tension in situ. J. Appl. Physiol. 29, 422–431 (1970)
Suki, B., Bates, J. H.: A nonlinear viscoelastic model of lung tissue mechanics. J. Appl. Physiol. 71, 826–833 (1991)
Gayzik, F. S., Hoth, J. J., Daly, M., Meredith, J. W., Stitzel, J. D.: A finite element-based injury metric for pulmonary contusion: investigation of candidate metrics through correlation with computed tomography. Stapp Car Crash J. 51, 189–209 (2007)
Gayzik, F. S., Hoth, J. J., Stitzel, J. D.: Finite element–based injury metrics for pulmonary contusion via concurrent model optimization. Biomech. Model. Mechanobiol. 10, 505–520 (2011)
Hallquist, J. O.: LS-DYNA Theory Manual. Livermore Software Technology Corporation (2006)
Cronin, D. S.: Model for pulmonary response resulting from high deformation rate loading. In: Proceedings of the 2011 International Research Council on Biomechanics of Injury (IRCOBI) Conference, pp 181–192 (2011)
Rice, D. A.: Sound speed in pulmonary parenchyma. J. Appl. Physiol. 54, 304–308 (1983)
Butler, J. P., Lehr, J. L., Drazen, J. M.: Longitudinal elastic wave propagation in pulmonary parenchyma. J. Appl. Physiol. 62, 1349–1355 (1987)
Freed, A. D., Einstein, D. R.: An implicit elastic theory for lung parenchyma. Int. J. Eng. Sci. 62, 31–47 (2013)
Stamenovic, D.: Micromechanical foundations of pulmonary elasticity. Physiol. Rev. 70, 1117–1134 (1990)
Freed, A. D., Einstein, D. R., Carson, J. P., Jacob, R. E.: Viscoelastic model for lung parenchyma for multi-scale modeling of respiratory system, phase II: Dodecahedral micro-model. Technical report, Pacific Northwest National Laboratory (PNNL), Richland, WA (US) (2012)
D’yachenko, A. I., Manyuhina, O. V.: Modeling of weak blast wave propagation in the lung. J. Biomech. 39, 2113–2122 (2006)
Regueiro, R. A., Zhang, B., Wozniak, S. L.: Large deformation dynamic three-dimensional coupled finite element analysis of soft biological tissues treated as biphasic porous media. Computer Modeling in Engineering and Sciences (CMES) 98, 1–39 (2014)
Fankell, D. P., Regueiro, R. A., Kramer, E. A., Ferguson, V. L., Rentschler, M. E.: A small deformation thermoporomechanics finite element model and its application to arterial tissue fusion. J. Biomech. Eng. 140, 031007 (2018)
Freed, A. D., Zamani, S.: On the use of convected coordinate systems in the mechanics of continuous media derived from a QR factorization of F. Int. J. Eng. Sci. 127, 145–161 (2018)
Freed, A. D., Graverend, J. B., Rajagopal, K. R.: A decomposition of Laplace stretch with applications in inelasticity. Acta Mech. 230, 3423–3429 (2019)
Freed, A. D., Zamani, S.: Elastic Kelvin-Poisson-Poynting solids described through scalar conjugate stress/strain pairs derived from a QR factorization of F. Journal of the Mechanics and Physics of Solids 129, 278–293 (2019)
Freed, A. D.: A note on stress/strain conjugate pairs: explicit and implicit theories of thermoelasticity for anisotropic materials. Int. J. Eng. Sci. 120, 155–171 (2017)
Srinivasa, A. R.: On the use of the upper triangular (or QR) decomposition for developing constitutive equations for Green-elastic materials. Int. J. Eng. Sci. 60, 1–12 (2012)
McLellan, A. G.: The Classical Thermodynamics of Deformable Materials. Cambridge University Press, Cambridge (1980)
Clayton, J. D.: Nonlinear Mechanics of Crystals. Springer, Dordrecht (2011)
Holzapfel, G. A., Simo, J. C.: A new viscoelastic constitutive model for continuous media at finite thermomechanical changes. Int. J. Solids Struct. 33, 3019–3034 (1996)
Holzapfel, G. A.: On large strain viscoelasticity: continuum formulation and finite element applications to elastomeric structures. Int. J. Numer. Methods Eng. 39, 3903–3926 (1996)
Simo, J. C.: On a fully three-dimensional finite-strain viscoelastic damage model: formulation and computational aspects. Comput. Methods Appl. Mech. Eng. 60, 153–173 (1987)
Balzani, D., Brinkhues, S., Holzapfel, G. A.: Constitutive framework for the modeling of damage in collagenous soft tissues with application to arterial walls. Comput. Methods Appl. Mech. Eng. 213, 139–151 (2012)
Krajcinovic, D.: Damage Mechanics. North-Holland, Amsterdam (1996)
Clayton, J. D., Tonge, A.: A nonlinear anisotropic elastic-inelastic constitutive model for polycrystalline ceramics and minerals with application to boron carbide. Int J Solids Struct 64–65, 191–207 (2015)
Hoppin, F. G., Lee, G. C., Dawson, S. V.: Properties of lung parenchyma in distortion. J. Appl. Physiol. 39, 742–751 (1975)
Lee, G. C., Frankus, A.: Elasticity properties of lung parenchyma derived from experimental distortion data. Biophys. J. 15, 481–493 (1975)
Lai-Fook, S. J., Wilson, T. A., Hyatt, R. E., Rodarte, J. R.: Elastic constants of inflated lobes of dog lungs. J. Appl. Physiol. 40, 508–513 (1976)
Hajji, M. A., Wilson, T. A., Lai-Fook, S. J.: Improved measurements of shear modulus and pleural membrane tension of the lung. J. Appl. Physiol. 47, 175–181 (1979)
Jahed, M., Lai-Fook, S. J., Bhagat, P. K., Kraman, S. S.: Propagation of stress waves in inflated sheep lungs. J. Appl. Physiol. 66, 2675–2680 (1989)
Jahed, M., Lai-Fook, S. J., Bhagat, P. K.: Effect of vascular volume and edema on wave propagation in canine lungs. J. Appl. Physiol. 68, 2171–2176 (1990)
Jahed, M., Lai-Fook, S. J.: Stress wave velocity measured in intact pig lungs with cross-spectral analysis. J. Appl. Physiol. 76, 565–571 (1994)
Yen, R. T., Fung, Y. C., Ho, H. H., Butterman, G.: Speed of stress wave propagation in lung. J. Appl. Physiol. 61, 701–705 (1986)
Zeng, Y. J., Yager, D., Fung, Y. C.: Measurement of the mechanical properties of the human lung tissue. J. Biomech. Eng. 109, 169–174 (1987)
Lai-Fook, S. J.: The elastic constants of lung parenchyma: the effect of pressure-volume hysteresis on the behavior of blood vessels. J. Biomech. 12, 757–764 (1979)
Denny, E., Schroter, R. C.: A model of non-uniform lung parenchyma distortion. J. Biomech. 39, 652–663 (2006)
Hoppin, F. G., Stothert, J. C., Greaves, I. A., Lai, Y. -L., Hildebrandt, J.: Lung recoil: elastic and rheological properties. In: Handook of Physiology. The Respiratory System. Mechanics of Breathing, pp 195–216. American Physiological Society, Bethesda (1986)
McGee, K. P., Mariappan, Y. K., Hubmayr, R. D., Carter, R. E., Bao, Z., Levin, D. L., Manduca, A., Ehman, R. L.: Magnetic resonance assessment of parenchymal elasticity in normal and edematous, ventilator-injured lung. J. Appl. Physiol. 113, 666–676 (2012)
Carney, D., DiRocco, J., Nieman, G.: Dynamic alveolar mechanics and ventilator-induced lung injury. Crit. Care Med. 33, S122–S128 (2005)
Perlman, C. E., Lederer, D. J., Bhattacharya, J.: Micromechanics of alveolar edema. Am. J. Respir. Cell Mol. Biol. 44, 34–39 (2011)
Ingenito, E. P., Mark, L., Davison, B.: Effects of acute lung injury on dynamic tissue properties. J. Appl. Physiol. 77, 2689–2697 (1994)
Fung, Y. -C., Yen, R. T., Tao, Z. L., Liu, S. Q.: A hypothesis on the mechanism of trauma of lung tissue subjected to impact load. J. Biomech. Eng. 110, 50–56 (1988)
Tao, Z. L., Fung, Y. C.: Lungs under cyclic compression and expansion. J. Biomech. Eng. 109, 160–162 (1987)
Hughes, R., May, A. J., Widdicombe, J. G.: Stress relaxation in rabbits’ lungs. J Physiol 146, 85–97 (1959)
Fredberg, J. J., Stamenovic, D.: On the imperfect elasticity of lung tissue. J. Appl. Physiol. 67, 2408–2419 (1989)
Suki, B., Barabasi, A. L., Lutchen, K. R.: Lung tissue viscoelasticity: a mathematical framework and its molecular basis. J. Appl. Physiol. 76, 2749–2759 (1994)
Navajas, D., Maksym, G. N., Bates, J. H.: Dynamic viscoelastic nonlinearity of lung parenchymal tissue. J. Appl. Physiol. 79, 348–356 (1995)
Dai, Z., Peng, Y., Mansy, H. A., Sandler, R. H., Royston, T. J.: A model of lung parenchyma stress relaxation using fractional viscoelasticity. Medical Engineering and Physics 37, 752–758 (2015)
Sanborn, B., Nie, X., Chen, W., Weerasooriya, T.: High strain rate pure shear and axial compressive response of porcine lung tissue. J. Appl. Mech. 80, 011029 (2013)
Saraf, H., Ramesh, K. T., Lennon, A. M., Merkle, A. C., Roberts, J. C.: Mechanical properties of soft human tissues under dynamic loading. J. Biomech. 40, 1960–1967 (2007)
Davison, L.: Fundamentals of Shock Wave Propagation in Solids. Springer, Berlin (2008)
Clayton, J.D.: Nonlinear Elastic and Inelastic Models for Shock Compression of Crystalline Solids. Springer, Cham (2019)
Clayton, J. D., Knap, J.: A geometrically nonlinear phase field theory of brittle fracture. Int. J. Fract. 189, 139–148 (2014)
Clayton, J. D., Knap, J.: Phase field modeling of coupled fracture and twinning in single crystals and polycrystals. Comput. Methods Appl. Mech. Eng. 312, 447–467 (2016)
Clayton, J. D.: Finsler geometry of nonlinear elastic solids with internal structure. J. Geom. Phys. 112, 118–146 (2017)
Clayton, J. D.: Generalized finsler geometric continuum physics with applications in fracture and phase transformations. Zeitschrift fur Angewandte Mathematik und Physik (ZAMP) 68, 9 (2017)
Malvern, L. E.: Introduction to the Mechanics of a Continuous Medium. Prentice-Hall, Englewood Cliffs (1969)
Graff, K. F.: Wave Motion in Elastic Solids. Oxford University Press London, Oxford (1975)
McLellan, A. G.: Finite strain coordinates and the stability of solid phases. Journal of Physics C: Solid State Physics 9, 4083–4094 (1976)
Thurston, R.N.: Waves in solids. In: Truesdell, C. (ed.) Handbuch der Physik, vol. VI, pp 109–308. Springer, Berlin (1974)
Clayton, J. D., Lloyd, J. T.: Analysis of nonlinear elastic aspects of precursor attenuation in shock-compressed metallic crystals. Journal of Physics Communications 2, 045032 (2018)
Weir, C. E.: Effect of temperature on the volume of leather and collagen in water. J. Res. Natl. Bur. Stand. 41, 279–285 (1948)
Kanagy, J. R.: Specific heats of collagen and leather. J. Res. Natl. Bur. Stand. 55, 191–195 (1955)
Kakivaya, S. R., Hoeve, C. A.: The glass point of elastin. Proc. Natl. Acad. Sci. 72, 3505–3507 (1975)
Lillie, M. A., Gosline, J. M.: Unusual swelling of elastin. Biopolymers: Original Research on Biomolecules 64, 115–126 (2002)
McQueen, R.G., Marsh, S.P., Taylor, J.W., Fritz, J.N., Carter, W.J.: The equation of state of solids from shock wave studies. In: Kinslow, R. (ed.) High-Velocity Impact Phenomena, pp 294–417. Academic Press, New York (1970)
Clayton, J. D.: Analysis of shock compression of strong single crystals with logarithmic thermoelastic-plastic theory. Int. J. Eng. Sci. 79, 1–20 (2014)
Yen, R. T., Fung, Y. C., Liu, S. Q.: Trauma of lung due to impact load. J. Biomech. 21, 745–753 (1988)
Clayton, J. D.: Finsler-geometric continuum dynamics and shock compression. Int. J. Fract. 208, 53–78 (2017)
Stuhmiller, J. H., Ho, K., Vander Vorst, M. J., Dodd, K. T., Fitzpatrick, T., Mayorga, M.: A model of blast overpressure injury to the lung. J. Biomech. 29, 227–234 (1996)
Grimal, Q., Watzky, A., Naili, S.: A one-dimensional model for the propagation of transient pressure waves through the lung. J. Biomech. 35, 1081–1089 (2002)
Tsokos, M., Paulsen, F., Petri, S., Madea, B., Puschel, K., Turk, E. E.: Histologic, immunohistochemical, and ultrastructural findings in human blast lung injury. Am. J. Respir. Crit. Care Med. 168, 549–555 (2003)
Acknowledgments
J.D.C. acknowledges support of the CCDC Army Research Laboratory. A.D.F. acknowledges support of a Joint Faculty Appointment with the CCDC Army Research Laboratory.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Clayton, J.D., Freed, A.D. A constitutive model for lung mechanics and injury applicable to static, dynamic, and shock loading. Mech Soft Mater 2, 3 (2020). https://doi.org/10.1007/s42558-020-0018-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s42558-020-0018-9