Model-based arbitrage in multi-exchange models for Bitcoin price dynamics

Abstract

Bitcoin is a digital currency started in early 2009 by its inventor under the pseudonym of Satoshi Nakamoto. In the last few years, Bitcoin has received much attention and has shown a surprising price increase. Bitcoin is currently traded on many web-exchanges making it a rare example of a good for which different prices are readily available; this feature implies important issues about arbitrage opportunities since prices on different exchanges are shown to be driven by the same risk factor. In this paper, we show that simple strategies of strong arbitrage arise by trading across different Bitcoin exchanges taking advantage of the common risk factor. The suggested arbitrage strategies are based on two alternative model specifications. Precisely, we consider the multivariate versions of Black and Scholes model and of an attention-based dynamics recently introduced in the literature.

1 Introduction

The white paper on Bitcoin appeared in November 2008, see Nakamoto (2008), written by a computer programmer(s) using the pseudonym Satoshi Nakamoto. His/her invention is an open-source, peer-to-peer network where transactions in the digital currency do not require a third party and are secured by rules based on cryptography and on the blockchain technology, a distributed ledger. The motivation underlying Bitcoin inception was to have a deflationary currency, independent of financial intermediaries and of central authorities.

After 10 years of its inception, the “state-of-art” of Bitcoin is quite far from the ideology which has given it birth. Indeed, most transactions are realized within web exchanges, which act essentially as brokers for retail investors registering as a user on the exchange platform rather than directly as a node in the peer-to-peer network. Some of the transactions are also finalized on the exchange without even being recorded in the blockchain¹; in addition, the huge returns that Bitcoin was able to pay to its initial users, have increased media attention on the cryptocurrency and attracted market speculators. At the time of writing, Bitcoin is seldom used as a payment system between peers but rather as an investment opportunity; it is evened out with volatile financial assets and also affected by sentiment/eagerness factors, see Yermack (2015), Kristoufek (2015), Cretarola et al. (2018). Bitcoin is traded on dozens of online platforms, so-called exchanges, where Bitcoins and other cryptocurrencies are traded at different bid and ask prices; this feature leads to the possibility of strong arbitrage by minimizing the price for the long positions and maximizing that for the short positions across exchanges. Since short-selling is not possible on exchanges, the long position should always be executed before. Until recently, these strong arbitrages were possible only in theory, due to latency in the system, both related to the time confirmation of transactions in the blockchain and to time needed to transfer a fiat currency from the bank account of the investor to his digital account on the web exchange. Currently, instant trades are possible and instant wire transfer has been made available for some exchanges² To achieve a profitable arbitrage, transaction fees should be added to the long–short positions: these were optional at inception of Bitcoin but they are compulsory and non-negligible across all the exchanges.

In this paper, extending preliminary results in Bistarelli et al. (2019), we show, by applying classical statistical techniques, that Bitcoin returns, computed daily by considering the different prices across major exchanges, are essentially perfectly correlated and that the risk (variability) of the overall system is mostly explained by a single source of randomness, as it is intuitively expected.

We take advantage of this preliminary outcome to consider two model specifications for the dynamics of Bitcoin price on multiple exchanges. The first example is the multivariate version of the Black and Scholes model (see Black and Scholes 1973) which is a natural benchmark for similar studies to ours. The second example is the analogous generalization of the dynamics suggested in Cretarola and Figà-Talamanca (2018) which was related to a non-tradeable second source of risk, measuring market attention; motivations for the choice of this specific model dynamics will be detailed in due time.

The rest of the paper is organized as follows: in Sect. 2, we illustrate the data and report the outcomes of the preliminary statistical analysis; in Sect. 3 we describe two alternative models, while in Sect. 4 we define the strong arbitrage strategies corresponding to the different models specifications. Section 5 briefly addresses how the two models are estimated on market data and finally Sect. 6 reports the achievements of the model-based arbitrage strategies when applied for trading on the different exchanges considered in our sample. Concluding remarks are summed up in Sect. 7.

2 Preliminary analysis and motivation

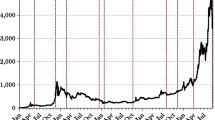
Bitcoin is traded on multiple online exchanges, where different exchange rates are applied against the same fiat currency; with a little abuse, we refer to Bitcoin prices rather than exchange rates, by considering the US Dollar (USD) as the fiat currency with respect to which Bitcoin is priced. The analyzed data sample, retrieved from the website https://bitcoincharts.com/, consists of daily closing prices³ for Bitcoin across 5 major exchanges, namely Bitstamp, Gdax, Kraken, Cex.IO and BitKonan, observed from January 2015 to December 2017; we ignore for the moment the bid/ask spreads.

In Fig. 1, we plot the above Bitcoin prices in USD over the whole time span and also focus on two shorter periods; pictures are almost indistinguishable across the exchanges but the difference is better appreciated by looking at the shorter periods where only CEX.IO and BitKonan exchanges prices are plotted. It is beyond the aim of this paper to understand deeply the motivation for different prices on different exchanges. Nevertheless, it is important to remark⁴ that these difference may be partially due to a different trustworthiness of involved exchanges as argued in Moore and Christin (2013).

Fig. 1

The Bitcoin price in USD according to 5 different exchanges (top) and two sub-samples with only two exchange rates (bottom)

From the above picture, it may be conjectured that price across exchanges, though slightly different, are driven by the same source/sources of randomness. For what concerns the returns, it is straightforward to check that the correlation parameters of returns across different exchanges are very close to one; hence, Bitcoin returns are almost perfectly positively correlated. To formally test that prices are also driven by the same risk factor/s computing correlation parameter is not of any help being the price time series non-stationary. In fact, we can apply a cointegration test to this purpose⁵; in Table 1 we sum up the outcomes of the Johansen cointegration test, see Johansen 1991, applied to the logarithmic prices across considered exchanges.⁶

As we can see from the table, the test fails to reject the null of cointegration rank $r=4$; hence, we cannot reject that the logarithmic prices of Bitcoin on the analyzed exchanges are cointegrated, supporting the argument of a single stochastic factor driving the different price time series.

Table 1 Johansen cointegration test between Bitcoin log-prices across five major exchanges: data are from January 1st 2015 to December 31, 2017

As a further check, we also perform a Principal Component Analysis (in short PCA) on the matrix composed by the vectors time series of the five exchanges under investigation, see Jolliffe (2011).

The outcomes⁷ are summed up in Tables 2 and  3.

Table 2 Percentage of the total variance explained by each principal component

According to the numbers in Table 2, the first component PC1 accounts for more than $83\%$ of the variability of the overall system and can be viewed as the level of Bitcoin returns within the considered exchanges. Indeed, it is a weighted sum of the 5 time series, where weights are all positive and very similar in value as it is evidenced in Table 3.

Table 3 PCA Coefficients for Bitcoin returns across five major exchanges observed daily from January 1st 2015 to December 31, 2017

2.1 Risk factors: a further look

To motivate, at least partially, the choice of model in Eq. (3), which assumes that Bitcoin returns and volatility depend on an exogenous attention factor, we introduce in advance a PCA analysis where a time series, measuring market attention, is added to the Bitcoin return matrix defined above. Specifically, the Bitcoin trading volume and the SVI Google index for the word “bitcoin” are taken as such proxies, as suggested in Cretarola et al. (2018), Figà-Talamanca and Patacca (2018).

In Tables 4 and 5, we report the outcomes of the PCA applied to the matrix including the time series of Bitcoin returns on the 5 exchanges and a time series for the attention factor, measured by the trading volume and the SVI Google index, respectively.

Table 4 Percentage of the total variance explained by each principal component

Table 5 Percentage of the total variance explained by each principal component

The outcomes show that two principal components are needed to explain about $86\%$ of the system variability, for both attention measures; besides, while the first component is still a nearly equally weighted average of Bitcoin returns on different exchanges and no weight on the attention factor, the second component is essentially the attention factor itself and contributes to about $16\%$ of the system variability, see Tables 6 and 7.

Table 6 PCA Coefficients for Bitcoin returns across five major exchanges and A = trading volume observed daily from January 1st 2015 to December 31, 2017

Table 7 PCA Coefficients for Bitcoin returns across five major exchanges and A = Google SVI observed daily from January 1st 2015 to December 31, 2017

3 Modeling the Bitcoin price dynamics and arbitrage opportunities

From the above analysis, it is quite clear that prices are all based on a common risk factor: the time series for the different exchanges are interchangeable in terms of their macroscopic informational content. Still, prices can be slightly different across exchanges for some periods allowing for arbitrage opportunities.

In this paper, we assume that there are I exchanges trading Bitcoin in the same fiat currency (i.e., USD) and denote by $S_t^{(i)}$ the price of one Bitcoin quoted on exchange i at time t. To account for a single price risk factor, we consider multivariate models to describe the dynamics of Bitcoin price on different exchanges, depending on a single source of randomness.

Precisely, we assume that the price process $S^{(i)}=\{S_t^{(i)},\ t\in [0,T]\}$ in exchange number i, is described, for a finite horizon $T>0$, by the following equation:

$$\begin{aligned} \mathrm dS^{(i)}_t = \mu _i(t,S^{(i)}_t,Y_t) \mathrm dt + \sigma _i(t,S^{(i)}_t,Y_t)\mathrm dW_t, \quad S_0^i =s_0^i\in \mathbb {R}^+, \end{aligned}$$

(1)

for every $i = 1, \ldots , I$, where $W=\{W_t,\ t\in [0,T]\}$ is a standard Brownian motion and $Y=\{Y_t,\ t\in [0,T]\}$ is an exogenous stochastic process, both defined on a complete probability space $(\varOmega ,\mathcal {F},\mathbf {P})$ endowed with a filtration $\mathbb {F}= \{\mathcal {F}_t,\ t\in [0,T]\}$ that satisfies the usual conditions of right continuity and completeness, see, e.g., (Protter 2005). Furthermore, we assume that $\mathcal {F}_0$ coincides with the trivial sigma-algebra.

The functions $\mu _i: [0,T] \times \mathbb {R}^+ \times \mathbb {R}\rightarrow \mathbb {R}$ and $\sigma _i: \mathbb {R}^+ \times [0,T] \times \mathbb {R}\rightarrow \mathbb {R}^+$, with $i = 1, \ldots , I$, are the so-called drift and diffusion terms, respectively, which are assumed to satisfy suitable regularity conditions to guarantee the existence of a unique strong solution of Eq. (1). In this general setting, arbitrage opportunities are ruled out under specific assumptions on the drift and diffusion functions and the market is said to be complete if the number of traded securities is equal to that of the randomness sources. It is worth to remark that, in the model described by Eq. (1), prices available on different exchanges are perfectly correlated and the market has the same “degree of incompleteness”, regardless the number of considered exchanges. Indeed, as soon as Y does not represent the price of a tradeable asset and it is an exogenous stochastic factor, i.e., it is a process driven by some additional risk factors, for example, another Brownian motion, the corresponding market model is generally incomplete. To ensure the completeness of the market, an investment possibility covering the risk arising from Y should be introduced.

In what follows, we take two special cases of the dynamics in Eq. (1) into account: the first one based on the pioneering model of Black and Scholes (1973) and the other one building on the model recently proposed in Cretarola et al. (2018), where Bitcoin price dynamics depends on an attention factor, which is assumed to be exogenous. We obtain no-arbitrage conditions based on the market price of risk (also known as Sharpe ratio) computed in each of the two model specifications.

3.1 The Black and Scholes model

Assume that the price dynamics of Bitcoin is described, in every exchange, by the well-known Black and Scholes model (Black and Scholes 1973). Precisely, $S^{i}$, with $i = 1,\ldots , I$, satisfies

$$\begin{aligned} \mathrm dS^{(i)}_t = \mu _i S_t^{(i)} \mathrm dt+\sigma _i S_t^{(i)}\mathrm dW_t,\quad S_0^{(i)}=s_0^{(i)}\in \mathbb {R}^+. \end{aligned}$$

(2)

Here, for every $i=1,2,\ldots ,I$, the constants $\mu _{i} \in \mathbb {R}$, $\sigma _{i} \in \mathbb {R}^+$, represent model parameters, This is a very special case of the model given in Eq. (1), where the drift and the diffusion functions are linear with respect to the stock price $S_t^{(i)}$ and do not depend on any exogenous factor. Note that different exchanges are characterized by (possibly) different parameters values in the dynamics. In Fig. 2, we plot one possible path for 3 months of daily prices simulated according to model given in Eq. (2) for two different set of parameters where $\mu _1=\mu _2=1.5$ and $\sigma _1=0.75,\sigma _2=0.5$. The picture exhibits a similar pattern to the one observed in Fig. 1.

Fig. 2

An example with simulated paths for 3 months of daily prices according to different parameters: $\mu _1=1.5$ and $\sigma _1=0.75$ (solid blue), $\mu _2=1.5$$\sigma _2=0.5$ (dotted red), respectively (color figure online)

3.2 An attention-based multi-exchange modeling

In Cretarola et al. (2018) the authors propose a model in continuous time to describe the behavior of the Bitcoin price and of the investors attention on the overall network. The model assumes that both the returns level and their variance depend on an exogenous factor representing investor attention; this feature is mainly motivated by previous research where market attention and sentiment were proven to affect Bitcoin returns and volatility significantly, see, among others, Kristoufek (2013, 2015), Figà-Talamanca and Patacca (2018). In addition, the analysis carried out in Sect. 2.1, further evidences the relevance of attention measures on the overall variability of the system, when measured either by the trading volume in Bitcoins or by the search volume index on the topic. It is worth to remark, as noticed in Cretarola et al. (2018), that the specification in Eqs. (3, 4) below makes possible to build an approximation of the exact likelihood of the returns process which can be maximized to estimate model parameters on historical data. This is briefly recalled in Sect. 5.2 and will be applied below in our multivariate setting. Moreover, another point in favour of such model choice is that it provides a closed formula for European style plain vanilla and binary options on Bitcoin.

However, in Cretarola et al. (2018), it is assumed that Bitcoin has a unique price, given by the average price provided by the website https://blockchain.info; hence, price variability across exchanges is not taken into account.

In a multi-exchange setting, we assume that the price dynamics of $S^{(i)}$, with $i = 1,\ldots , I$, is described by the equation

$$\begin{aligned} \mathrm{d}S^{(i)}_t = \mu _i A_{t-\tau _i} S_t^{(i)} \mathrm{d}t+\sigma _i \sqrt{A_{t-\tau _i}}S_t^{(i)}\mathrm{d}W_t,\quad S_0^{(i)}=s_0^{(i)}\in \mathbb {R}^+, \end{aligned}$$

(3)

where, for every $i=1,2,\ldots ,I$, the constants $\mu _{i} \in \mathbb {R}$, $\sigma _{i} \in \mathbb {R}^+$, $\tau _i \in \mathbb {R}^+$ (delays) represent model parameters; moreover, $A=\{A_t,\ t \in [0,T]\}$ describes the attention factor for the Bitcoin system.

The behavior of A is described, as in Cretarola et al. (2018), by the equation

$$\begin{aligned} \mathrm{d}A_t =\mu _A A_t\mathrm{d}t+\sigma _A A_t\mathrm{d}Z_t, \quad A_t = \phi (t),\ t \in [-L,0], \end{aligned}$$

(4)

where $\mu _A \in \mathbb {R}$, $\sigma _A \in \mathbb {R}^+$, $L \in \mathbb {R}^+$ are constant parameters and $Z = \{Z_t,\ t \in [0,T]\}$ is a standard Brownian motion on $(\varOmega ,\mathcal {F},\mathbf{P}; \mathbb {F})$, which is independent of W. Notice that the process A affects Bitcoin prices $S^{i}$ through a dependence of both the drift and the diffusion terms up to a certain preceding time $t - \tau _i$, therefore accounting for the effect of the past. The introduction of a delay parameter may enlarge the possible mutual behavior for prices on different exchanges. Further, $\phi :[-L,0]\rightarrow R_0^+$, with $L > \max \{\tau _1,\ldots ,\tau _I\}$, is a non-random function which is introduced to make the dynamics well defined for $t\in [0,\tau _i]$ for $i=1,2,\ldots ,I$. The model given in Eqs. (3, 4) is in fact a special case of Eq. (1), where the exogenous factor is given by $Y_t=A_{t-\tau _i}$, for each $t \in [0,T]$. In particular, $Y_t = \phi (t-\tau _i)$, for $t \in [0,\tau _i]$. It is worth noticing that the function $\phi$ might be defined, in principle, by any non-negative function. In the empirical application, it will be replaced by a suitable discrete sample for the attention factor observed up to the theoretical initial date $t=0$.

In this setting, different exchanges are characterized not only by (possibly) different parameters values in the dynamics but also by (possibly) different delays with respect to the attention factor. Moreover, two sources of randomness are present in the above model specification, one driving the price changes and another driving the attention factor; this is not in contradiction with the findings of a single market risk factor in Sect. 2, since only the Brownian motion W affects directly the Bitcoin price dynamics and, as evidenced in Sect. 2.1, market attention may also explain the variability of Bitcoin prices across exchanges.

In Fig. 3 we plot a possible path for 2 months of daily prices simulated according to model in Eqs. (3)–(4) for two sets of parameters: $\mu _A=0.5$, $\sigma _A=1.0$, $\mu _{S_1}=\mu _{S_2}=0.04$, $\sigma _{S_1}=\sigma _{S_2}=0.1$, and $\tau _{1}=1$ day (solid blue), $\tau _{2}=5$ days (dotted red); we just change the value of the parameter $\tau$, to better appreciate its contribution to the dynamics. The picture exhibits both a vertical movement and an horizontal shift.

Fig. 3

An example with two simulated paths for 3 months of daily prices: parameters are set to $\mu _A=0.5$, $\sigma _A=1.0$, $\mu _{S_1}=\mu _{S_2}=0.04$, $\sigma _{S_1}=\sigma _{S_2}=0.1$, and $\tau _{1}=1$ day (solid blue), $\tau _{2}=5$ days (dotted red), respectively (color figure online)

4 Arbitrage opportunities

When dealing with multivariate models in continuous time, it is important to ensure the absence of arbitrage opportunities in the underlying financial market. An arbitrage strategy consists of a dynamical family of transactions in which no money can be lost and some can be earned in certain states of nature; it does not require an initial investment and leads to a positive value with positive probability. A strong arbitrage is a free lunch, i.e., it costs nothing to set up and is achieved when the positive gain is made without taking any risks (with probability one).

When there are no frictions, such opportunities should not arise, which motivates the investigation of financial markets under the assumption of absence of arbitrage opportunities. The latter assumption allows to get some relations between the prices of securities and their payoffs that are easily expressed in terms of state prices.

From a mathematical point of view, arbitrage-free markets are characterized by the existence of an equivalent martingale measure associated with a market price of risk, which determines a risk-neutral price for derivatives. In arbitrage-free and also complete markets, every derivative is hedge-able and there exists a unique risk-neutral price, which coincides with the value of the replicating self-financing strategy. On the contrary, in arbitrage-free and incomplete markets, not every derivative can be replicated and there exist infinitely many risk-neutral prices, corresponding to infinitely many equivalent martingale measures. Note that, it may be that the market is complete, but there exists no equivalent martingale measure; so, arbitrage opportunities arise.

For the sake of simplicity, we assume that we have $I=2$ exchanges. We show that the Black and Scholes (BS henceforth) multivariate model given in Eq. (2) is arbitrage free, if all the assets have the same market price of risk, see Sect. 4.1. Analogous results are obtained and the existence of arbitrage opportunities is discussed within the model given in Eqs. (3, 4) (CFTP henceforth), see Sect. 4.2.

4.1 Multi-exhange BS model

It is well known and easy to prove that the Black and Scholes multivariate specification in Eq. (2) is free from arbitrage opportunities if the market price of risk, also called the Sharpe ratio, is equal across the different assets (exchanges). We assume a constant risk-free interest rate $r \in \mathbb {R}_0^+$. The Sharpe ratios of both exchanges are constant over time and are given by

$$\begin{aligned} {\mathrm{Sharpe\,ratio}}_i&= \frac{{\mathrm{Risk\,premium}}_i}{\sigma _i} =\frac{\mu _i - r}{\sigma _i},\quad i =1,2. \end{aligned}$$

Then, the risk premium is the return in excess of the risk-free rate of return an investment in Bitcoin is expected to yield. Now, assume that under the multivariate Black and Scholes framework, we have

$$\begin{aligned} {{\mathrm{Sharpe\,ratio}}}_1 > {{\mathrm{Sharpe\,ratio}}}_2. \end{aligned}$$

Define the self-financing portfolio $(\alpha ^1, \alpha ^2, \beta )$, where:

• we buy the amount $\alpha ^1=C\left( S^{(1)}\sigma _1\right) ^{-1}$ of Bitcoin with price $S^{(1)}$ on exchange 1;

• we short-sell the quantity $\alpha ^2=C\left( S^{(2)}\sigma _2\right) ^{-1}$ of Bitcoin with price $S^{(2)}$ on exchange 2;

• we invest/borrow the risk-free bond in the amount of the cost difference given by $\displaystyle C\left( \frac{1}{\sigma _1}-\frac{1}{\sigma _2}\right)$, where C is an arbitrary positive constant.

Precisely, we choose

$$\begin{aligned} \alpha _t^1=C\frac{1}{S_t^{(1)}\sigma _1}, \quad \alpha _t^2=C\frac{1}{S_t^{(2)}\sigma _2},\quad t \in [0,T], \end{aligned}$$

and

$$\begin{aligned} \beta _t=e^{- rt}C\left( \frac{1}{\sigma _1}-\frac{1}{\sigma _2}\right) , \quad t \in [0,T]. \end{aligned}$$

If $V_t$ denotes the corresponding portfolio value at time t, then $(\alpha ^1,\alpha ^2,\beta )$ is a strategy with null initial value, since

$$\begin{aligned} V_0&= -\alpha _0^1 S_0^{(1)} + \alpha _0^2 S_0^{(2)} + \beta _0 = C\left( -\frac{1}{\sigma _1} + \frac{1}{\sigma _2} + \frac{1}{\sigma _1} - \frac{1}{\sigma _2}\right) = 0. \end{aligned}$$

Moreover, the return of the above strategy is

$$\begin{aligned} \mathrm dV_t&= \alpha _t^1 \mathrm dS_t^{(1)} - \alpha _t^2 \mathrm dS_t^{(2)} - r \beta _t e^{rt} \mathrm dt \\&= \frac{C}{S_t^{(1)}\sigma _1}\mathrm dS_t^{(1)} - \frac{C}{S_t^{(2)}\sigma _2 } \mathrm dS_t^{(2)} - r C\left( \frac{1}{\sigma _1 }-\frac{1}{\sigma _2}\right) \mathrm dt\\&= C\left( \frac{\mu _1- r}{\sigma _1 } - \frac{\mu _2 - r}{\sigma _2}\right) \mathrm dt = C\left( \mathrm{Sharpe\,ratio}_1 - \mathrm{Sharpe\,ratio}_2 \right) \mathrm dt > 0. \end{aligned}$$

The total gain of the strategy in the time interval [0, s], for an investment horizon $s>0$, is given by

$$\begin{aligned} C\left( \frac{\mu _1- r}{\sigma _1 } - \frac{\mu _2 - r}{\sigma _2}\right) s > 0. \end{aligned}$$

Here, C represents a scale factor which leverages the total gain. Therefore, the above investment strategy is a strong arbitrage opportunity, since it produces a positive profit with probability 1 (free-lunch). Note that the above arbitrage strategy exists because of perfect correlation between the returns model dynamics on the two exchanges. While perfect correlation has been evidenced on Bitcoin exchanges, this is not the case in traditional financial markets: though some common risk factors may be identified to describe the systematic fraction of the variance of each asset, the idiosyncratic part of the variance is non-negligible.

4.2 Multi-exchange CFTP model

In this setting, a second source of randomness is introduced, related to the dynamics of the market attention factor. It is worth noticing that the price of risk relative to the second source of uncertainty (price of attention risk) does not vary across assets/exchanges; hence, arbitrage opportunities are only related to the market Sharpe ratio as we will show below.

The risk premia for the the Bitcoins quoted on exchanges 1 and 2, respectively, are defined in this setting as

$$\begin{aligned} {{\mathrm{Risk\,premium}}}_1 = \mu _1 A_{t-\tau _1} - r,\quad {{\mathrm{Risk\,premium}}}_2 = \mu _2 A_{t-\tau _2} - r, \end{aligned}$$

for every $t \in [0,T]$. Again, the risk-free rate is assumed as a non-negative constant r. The corresponding Sharpe ratios, that is, the average returns earned in excess of the risk-free rate per unit of volatility or total risk, are defined as

$$\begin{aligned} {{\mathrm{Sharpe\,ratio}}}_1&= \frac{{{\mathrm{Risk\,premium}}}_1}{\sigma _1 \sqrt{A_{t-\tau _1}}}=\frac{\mu _1 A_{t-\tau _1} - r}{\sigma _1 \sqrt{A_{t-\tau _1}}} \\ {{\mathrm{Sharpe\,ratio}}}_2&= \frac{{{\mathrm{Risk\,premium}}}_2}{\sigma _2 \sqrt{A_{t-\tau _2}}}=\frac{\mu _2 A_{t-\tau _2} - r}{\sigma _2 \sqrt{A_{t-\tau _2}}}, \end{aligned}$$

for every $t \in [0,T]$. Indeed, if $\tau _1 \ne \tau _2$, equality

$$\begin{aligned} \frac{\mu _1 A_{t-\tau _1} - r}{\sigma _1 \sqrt{A_{t-\tau _1}}} = \frac{\mu _2 A_{t-\tau _2} - r}{\sigma _2 \sqrt{A_{t-\tau _2}}} \end{aligned}$$

is in general not satisfied, for every $t \in [0,T]$, even when $\mu _1=\mu _2$ and $\sigma _1=\sigma _2$.

As in the BS example, it is easy to prove that, if the following (or the opposite inequality) holds for some $t\in [0,T]$

$$\begin{aligned} \frac{\mu _1 A_{t-\tau _1} - r}{\sigma _1 \sqrt{A_{t-\tau _1}}} > \frac{\mu _2 A_{t-\tau _2} - r}{\sigma _2 \sqrt{A_{t-\tau _2}}}, \end{aligned}$$

(5)

then the market is not arbitrage free. Indeed, suppose that (5) holds and set

$$\begin{aligned} k_t:= \frac{\mu _1 A_{t-\tau _1} - r}{\sigma _1 \sqrt{A_{t-\tau _1}}} - \frac{\mu _2 A_{t-\tau _2} - r}{\sigma _2 \sqrt{A_{t-\tau _2}}}. \end{aligned}$$

Then, if $k_t>0$, let us consider the self-financing portfolio $(\alpha ^1, \alpha ^2, \beta )$, defined by

$$\begin{aligned} \alpha _t^1=\frac{1}{S_t^{(1)}\sigma _1 \sqrt{A_{t-\tau _1}}}, \quad \alpha _t^2=\frac{1}{S_t^{(2)}\sigma _2 \sqrt{A_{t-\tau _2}}},\quad t \in [0,T], \end{aligned}$$

and

$$\begin{aligned} \beta _t=e^{-rt}\left( \frac{1}{\sigma _1 \sqrt{A_{t-\tau _1}}}-\frac{1}{\sigma _2 \sqrt{A_{t-\tau _2}}}\right) , \quad t \in [0,T]. \end{aligned}$$

Precisely,

• we buy the amount $\alpha ^1$ of Bitcoin with price $S^{(1)}$ on exchange 1;

• we short-sell the quantity $\alpha ^2$ of Bitcoin with price $S^{(2)}$ on exchange 2;

• we invest/borrow the amount $\beta$ in the risk-free bond.

If $V_t$ denotes the corresponding portfolio value at time t, we get that $(\alpha ^1, \alpha ^2, \beta )$ is a strategy with null initial value, since

$$\begin{aligned} V_0&= -\alpha _0^1 S_0^{(1)} + \alpha _0^2 S_0^{(2)} + \beta _0 \\&= -\frac{1}{\sigma _1 \phi (-\tau _1)} + \frac{1}{\sigma _2 \phi (-\tau _2)} + \frac{1}{\sigma _1 \phi (-\tau _1)} - \frac{1}{\sigma _2 \phi (-\tau _2)} = 0. \end{aligned}$$

Moreover, the return of the above strategy is

$$\begin{aligned}&\alpha _t^1 \mathrm dS_t^{(1)} - \alpha _t^2 \mathrm dS_t^{(2)} - r \beta _t e^{rt} \mathrm dt \\&\quad = \frac{1}{S_t^{(1)}\sigma _1 \sqrt{A_{t-\tau _1}}}\mathrm dS_t^{(1)} - \frac{1}{S_t^{(2)}\sigma _2 \sqrt{A_{t-\tau _2}}} \mathrm dS_t^{(2)} - r \left( \frac{1}{\sigma _1 \sqrt{A_{t-\tau _1}}}-\frac{1}{\sigma _2 \sqrt{P_{t-\tau _2}}}\right) \mathrm dt\\&\quad = \left( \frac{\mu _1 A_{t-\tau _1} - r}{\sigma _1 \sqrt{A_{t-\tau _1}}} - \frac{\mu _2 A_{t-\tau _2} - r}{\sigma _2 \sqrt{A_{t-\tau _2}}}\right) \mathrm dt > 0. \end{aligned}$$

On the contrary, whenever $k_t<0$, we apply the opposite of the above strategy by inverting log and short positions.

The total gain of the above strategy in the time interval [0, s], for an investment horizon $s>0$, is given by

$$\begin{aligned} C\int _0^s|k_t| \mathrm dt > 0. \end{aligned}$$

Therefore, it gives rise to a strong arbitrage opportunity since, at no initial cost, it produces a sure profit that is strictly greater than 0. Note that the total gain is a positive value but it is not known at time 0 because it depends on the attention process; precisely, it is a random variable with support in $\mathbb {R}^+$.

Again, C represents a scale factor, which leverages the total gain, and investment quotes should be revised in continuous time to keep the profit riskless.

5 Model fitting

Now, we estimate the above multivariate models on daily prices from 01/01/2015 to 12/31/2017 available on Bitstamp, Gdax, Kraken, Cex.IO and BitKonan.

5.1 BS parameters estimation

In the Black and Scholes framework, parameter estimation is straightforward. Indeed, considering discrete time observations for each exchange i, with observation step $\varDelta$, the logarithmic returns $R_t^{(i)}:=\ln \left( \frac{S^{(i)}_t}{S^{(i)}_{t-1}}\right)$, according to the dynamics in Eq. (2), for $t=1,2,3,\ldots ,T$ are given by

$$\begin{aligned} R_t^{(i)}=\left( \mu _i-\frac{\sigma ^2_i}{2}\right) \varDelta + \sigma _i \sqrt{\varDelta } \epsilon _t, \quad i=1,\dots ,I, \end{aligned}$$

where $\lbrace \epsilon _t\rbrace _{t=1,2,\ldots ,T}$ is a Gaussian white noise with unit variance.

The parameter of interest may be estimated by computing the sample mean and variance of observed logarithmic returns using the following formulas:

$$\begin{aligned} \mu _i=\frac{\bar{R}^{(i)}}{\varDelta } + \frac{\sigma ^2_i}{2}; \qquad \sigma _i^2=\frac{\mathbb {V}ar\left[ R^{(i)}\right] }{\varDelta }; \qquad i=1,\dots ,I, \quad t=1,\dots , T. \end{aligned}$$

The results of the estimation can be found in Table 8. The standard deviation of the estimates is also reported (in brackets) as well as significance of the parameters, obtained by means of a classical t test for the drift and diffusion parameters. All estimates are strongly significant.

Table 8 Parameters estimates with corresponding standard error (in brackets) of BS model for the considered exchanges on daily data from January 1, 2015 to December 31, 2017

The Sharpe ratio, which is the strategic value to build the arbitrage strategy, is computed for each exchange and is also reported in Table 8. Again, the standard deviation is added (in brackets) as well as the significance level, obtained by applying Bootstrap techniques⁸, see Tibshirani and Efron (1993).

In our empirical exercise, the arbitrage will be achieved by investing on the two exchanges which show the largest difference in the Sharpe ratio values, i.e., Cex.IO and Gdax.

5.2 CFTP parameters estimation

A simple estimation procedure for the model specification given in Eqs. (3, 4), when considering a single exchange, is introduced in Cretarola et al. (2018). For the sake of brevity, we report here the main steps for the estimation procedure which is based on the maximization of the approximated likelihood of the returns. The interested reader is referred to the quoted paper for further details.

Given a discrete sample for both Bitcoin prices and a market attention proxy, the following procedure is repeated for several values of the delay parameter $\tau$:

• 1. the cumulative attention measure is computed for each time interval within the discrete sample, assuming that the underlying attention process can be observed at a finer grid than the Bitcoin price;

• 2. the distribution of the cumulative attention is approximated by applying the outcomes in Levy (1992);

• 3. the joint approximate likelihood of the market cumulative attention and Bitcoin returns is computed by applying the Bayes rule, the conditional normality of returns (given the cumulative attention) and the approximated distribution of the attention obtained in step 3;

• 4. parameters other than the delay are estimated by maximizing the approximate likelihood obtained in the previous step.

Finally, $\tau$ is chosen so to maximize the value of the approximate likelihood.

The overall procedure can be referred to as profile quasi maximum likelihood method and it is applied separately to each exchange; the attention factor is measured for all exchanges either via the daily trading volume or the Google Search Volume Index (SVI) retrieved from www.blockchain.info and www.googletrends.com, respectively.

In Tables 9, 10, we report estimated values as well as standard deviations (in brackets) for model parameters of the five major exchanges when attention is measured by the total trading volume and by the SVI, respectively. Estimates are all strongly significant with the only exception of the attention drift parameter, when attention is measured by trading volume.

For the above model specification, the Sharpe ratio of each exchange is a random process which is a function of the attention process itself; so it is not reported in the table. Again, in the empirical application, the arbitrage is built by investing in Cex.IO and Gdax to compare the outcomes with those of the BS-based strategy.

Table 9 Parameter estimates with corresponding standard error (in brackets) for Bitstamp, Gdax, Kraken, Cex.IO and BitKonan exchanges, attention measured by trading volume: from 01/01/2015 to 12/31/2017

Table 10 Parameter estimates with corresponding standard error (in brackets) for GDAX, Bitstamp, Kraken, Cex.IO and BitKonan trading exchanges, attention measured by Google SVI: from 01/01/2015 to 12/31/2017

It is worth noticing that for both the trading volume of transactions and the SVI, the Bitcoin price is affected by market attention with the same delay for different exchanges but in all cases $\widehat{\tau }\ne 0$.

6 Arbitrage strategies in discrete time

It is evident that it is in-feasible in practice to update trading strategies in continuous time as it is requested in continuous time model-based arbitrages. If trading strategies are revised at discrete points in time, their non-riskiness property as defined in Sect. 4 is not guaranteed anymore; in fact, there is a readjustment cost depending on the discrete time step from one revision to the other; so, the suggested strategies do not necessarily lead to strong arbitrage opportunities.

Though, it is still interesting to investigate the performance of these model-based strategies as special investment opportunities where no capital is initially allocated.

In what follows, we apply the trading strategies defined in Sects. 4.1 and 4.2 with a daily-based revision scheme. We consider several investment horizons, namely $s=1,7,15,30,$ 45, 60, 90 days.

To measure the overall performance of the strategies, we compute the mean daily gain as well as the deviation from the mean value across all the different investment horizons.

For the sake of comparison between the strategies based on the multi-exchange BS and CFTP models, respectively, we also compute a profit to risk ratio of the trading schemes based on the different model specifications and for different investment horizons. The suggested index, named Gain Sharpe ratio ($\mathrm{GSR}$ in the tables), shares the same underlying idea with the traditional Sharpe ratio; though it is computed on gains rather than returns since the trading strategies defined above have zero initial cost which makes it impossible to compute returns, neither expected nor realized. More precisely, if the value of a strategy at time k is denoted by V(k), and we have daily observations, then the daily gain is $G(k):=V(k)-V(k-1)$. For an investment horizon $s>1$ day, the mean daily gain EG, its deviation GDEV and the Gain Sharpe ratio $\mathrm{GSR}$ are defined, respectively, as

$$\begin{aligned} \mathrm{EG}(s)&:= \frac{\sum _{k=1}^s G(k)}{s},\\ \mathrm{GDEV}^2(s)&:= \frac{\sum _{k=1}^s [G(k)-EG(s)]^2}{s-1},\\ \mathrm{GSR}(s)&:= \frac{\mathrm{EG}(s)}{\mathrm{GDEV}(s)}. \end{aligned}$$

Clearly, for $s=1$ we have $\mathrm{EG}(1)=G(1)$ and neither GDEV nor GSR may be defined.

Note that the selection of the two exchanges on which to invest is chosen on the first day of investment by maximizing the difference in the market price of risk. In our example, the selection is towards Gdax and CEX.IO exchanges. The outcomes are summed up in Tables 11 and 12.

It is worth noticing that the trading strategies are computed from January 1, 2018 to March 31, 2018 based on parameters estimated on a time series ending December 2017 and the selection of the exchanges is not updated through time. If such a strategy was automatized by updating parameters estimates and by reviewing the selection of exchanges showing maximal difference for their relative market price of risk, then the overall profit of the strategy would certainly improve further.

Table 11 Comparison between the mean gain EG, the deviation GDEV and the Gain Sharpe ratio GSR for BS-based strategy and CFTP-based strategy where market attention is measured by trading volume: several investment horizons from 1 to 90 days

Table 12 Comparison between the mean gain EG, the deviation GDEV and the Sharpe ratio GSR for BS-based strategy and CFTP-based strategy where market attention is measured by The Google SVI: several investment horizons from 1 to 90 days

From the table, it is quite clear that all the strategies, though implemented in a discretized way, lead to a positive profit with positive probability starting from an initial 0 capital allocation, i.e., they are indeed weak arbitrages. In terms of pure profit, the best performance in the short term ($s\le 30$) is achieved by the CFTP model-based strategy where attention is measured by the total trading volume while for $s\ge 45$ the best profit is obtained by the BS-based strategy. Of course, it is important to measure also the variability of the profit so we introduce the Gain Sharpe ratio, defined as the ratio between mean profit and deviation from that mean, as a single index to measure the performance of the strategies. By looking at this single value, the CFTP model-based strategy provides the best performance for all the investment horizons.

Fig. 4

Expected gain for CFTP model-based strategy where market attention is measured by trading volume (left) or The Google SVI (right): comparison between CFTP model-based strategy (solid blue) and CFTP model-based strategy with fees (dotted red) (color figure online)

We also consider the analogous trading strategies where fees are payed according to the rules established by the exchanges: Gdax fees are in the range of 0.10–0.30% on the trades⁹ while CEX.IO fees are in the range¹⁰ of 0.10–0.25%. In both exchanges, the exact amount of fees is based on 30-day trade volume. As expected, when fees are included, the cumulative gain reduces but it is still positive, hence defining an arbitrage. In Fig. 4, we plot the cumulative gain for the arbitrage strategies based on the CFTP model with and without fees and with the trading volume and the Google SVI, respectively, as attention measures. Fees are fixed to $0.25\%$ of the trade for both exchanges, to make things easier; it is likely that this choice reduces the gain with respect to the application of precise (lower for most trades in our example) fees for CEX.IO trade positions.

Since the profit distribution is asymmetric, the mean and the deviation of the profit may not be enough to describe and compare profits across the different strategies and it would be necessary to take into account the whole distribution function of the profits. To this aim we estimate the density of the profit distribution by using kernel methods¹¹, see for instance (Bowman and Azzalini 1997).

In Fig. 5 we plot the estimated distributions across different investment horizons, namely $s=15,30,60,90$ days. The distributions tend to become similar when the investment horizon increases. For each time horizon, the CFTP model-based strategy gives better result in terms of variability since the distributions are always tighter around their mean value; for short-term investment (e.g., for $s=15$ days), it also delivers higher profit values. On the other hand, when attention is measured by the Google SVI, the distribution of realized profits is tighter around its mean (leading to almost sure profit) but of very limited value.

The overall message of our investigation is that the above model-based strategies do lead to arbitrage opportunities and that the best performance is achieved by the strategy based on model (Cretarola et al. 2018) with the trading volume as a measure of attention. It is worth to remark that all the above strategies might be further optimized by adjusting parameter estimates at a fixed frequency within the longer horizon or by properly revising the selection of exchanges.

Fig. 5

Comparison between the Ksdensity plot for BS-based strategy (red) and CFTP-based strategy (blue) where market attention is measured by trading volume: several investment horizons from 15 to 90 days (color figure online)

7 Concluding remarks

In this paper, we have shown that simple model-based arbitrage strategies can be constructed by long–short trading on different Bitcoin exchanges. This can be done by taking advantage of the evidence that the Bitcoin prices across the analyzed exchanges depend on a single market risk factor, pointed out in our preliminary statistical analysis. We consider two alternative multi-exchange frameworks, based on Black and Scholes model (Black and Scholes 1973) and on Cretarola et al. (2018), respectively, to model the Bitcoin price dynamics across exchanges. By applying established results in mathematical finance, we show that the models are arbitrage free under usual assumptions, if the market prices of risk (or Sharpe ratios) computed on different exchanges are equal. Once the two models are estimated on daily closing prices for five major exchanges available on https://bitcoincharts.com/ (see Cretarola et al. 2018), we show that the no arbitrage constraint is violated and that arbitrage opportunities exist in the real market. Though, a strong arbitrage may not be designed since continuous trading is infeasible and also non-profitable when transactions fees are taken into account. The discretized real-market versions of the model-based arbitrage strategies are finally implemented by assuming a daily revision on the long-short positions in the two exchanges where the difference is maximized of the corresponding market price of risks. The expected gain, as well as the standard deviation of the gain, is computed for each strategy relative to several investment horizons from 1 day to 3 months. Notably, the CFTP model-based strategy provides a better performance than the BS model-based alternative. This outcome is persistent across all investment horizons when market attention is measured by the trading volume. In addition, the result also holds when transaction fees are included in the strategies. To increase the profit from these strategies, one may either update parameter estimates during the investment period or allow for a switch in the two chosen exchanges when this proves to be profitable. Further research will be devoted to this optimized investing rules and to their possible automation.