1 Introduction

Mediation analysis plays a significant role in the exploration of a causal relationship between two variables. A mediation model effect focuses on how two variables are related directly or indirectly: for example, consider the presence or absence of coronary heart disease (CHD) in high-risk men given as the independent variable (X), death due to myocardial infarction given as the dependent variable (Y), mediated by smoking where the smoking variable is the mediator (M).

Mediation analysis, which was first developed in the psychological sciences, is now instrumental in other disease development mechanisms for identifying intermediate factors useful for treatments and clinical trials. Methodological applications have increased over the past years, and more progress has also been made in understanding and applying mediation analysis in various research fields. Wright [1] proposed the mechanism of mediation by using “Wright's path analysis.” His model demonstrates the mathematical equations and diagrammatical representation in understanding the causal relationship between two variables such that the equations included the coefficients. In contrast, the diagrammatic representation included arrows to illustrate the relation's direction. These path coefficients were useful in defining the mediation effect. Wright [2] showed that although path analysis can be useful in quantifying causal relationships, it was extremely challenging to determine a causal effect between two variables. Several studies criticize path analysis and suggest more knowledge is still needed in identifying causal relations. The use of mediation analysis for research purposes also requires more in-depth information [3].

However, the first mediation hypothetically used was in stimulus-organism-response (S–O–R) [4]. The mediation analysis concept has been applied in various areas, including psychology, medical sciences, epidemiology, and clinical trials [5]. Fisher [6] introduced the use of covariate as a third variable. Later on, Lazarsfeld and his colleague Kendall [7] worked on the expansion method to explain the relationship between the two variables to the third variable. According to Wright's path analysis model, economists and sociologists could generalize the covariance model [8,9,10,11]. Hence, this model was called the structural equation model, which improved the estimated mediated effects' accuracy. Sobel [12] used the structural equation model to reduce the direct and indirect effects of standard errors and then used the standard errors in computing the mediated effects’ confidence interval. More studies and research to identify the complexity of the causal effect in mediation analysis have been made [13], [14], [3].

The simplest mediation model, which consists of one mediator, is known as the single mediator model. In this model, in addition to the direct effect, the independent variable X affects the dependent variable Y through a mediator M. The variables in a mediation model can either be continuous or categorical. The ordinary regression model is used to analyze continuous variables, while logistic regression is used to analyze categorical variables.

Missing data are a challenge affecting datasets and medical records in many areas of research. It can also occur in mediation analysis, and improperly handling this missingness may introduce biased mediation effects. The majority of statistical modeling approaches are designed for complete observations for the variables included in the data. It is crucial to deal with missing data using various methods to have valid inferences. Rubin [15] introduced the taxonomy of missing data mechanisms, widely used in the statistical literature. The methods of handling data with missing observations depend on the underlying assumption of the missing data mechanisms, which are Missing Completely at Random (MCAR), Missing at Random (MAR), Missing Not at Random (MNAR).

Categorical mediation data for simple analyses can also be presented in terms of contingency tables. Missing counts in contingency tables are important in missing data analysis, and there exist various methods for dealing with missingness in contingency tables. We can use Model-based procedures such as the Baker, Rosenberger, and Dersimonian (BRD) Models [16]. These models were proposed by Baker, Rosenberger, and Dersimonian (BRD) for analyzing missing counts in a two-way contingency table with three supplementary margins, using log-linear and maximum likelihood estimates [16]. In two-way contingency tables, the cell counts adjustments for log-linear factorization of likelihood methods have been used in several research papers. Hocking and Oxspring [17] also explained the use of maximum likelihood estimation in factoring partially classified contingency tables. Several publications recommend using log-linear models for partially classified contingency tables using conditional probabilities [18]. This paper focuses on the application of estimation of the mediation effect under the non-ignorable missing data mechanism (MNAR) using the extension of Baker, Rosenberger, and Dersimonian (BRD) models proposed by Rochani et al. [19] for a three-way contingency table. Estimation of mediation effect by BRD model approach has two main advantages over other available methods for non-ignorable data. First, the BRD approach explicitly models the missing mechanism, which will result in a full likelihood specification of the models with unique interpretations. Second, the estimation method will not be affected by the proportion of missing information which can affect the rate of convergence of methods like the Expected maximum (EM) algorithm.

Section 2 will focus on an overview of existing methods used for mediation analysis for categorical variables under non-ignorable missing data mechanisms. New models derived using the BRD model approach used for at least two non-missing categorical variables in the mediation analysis will be discussed in Sect. 3. Simulations are presented in Sect. 4. We will include the application of proposed models using the Multiple Risk Factor Intervention Trial (MRFIT) data for the Prevention of Coronary Heart Disease in Sect. 5, followed by a discussion in Sect. 6.

2 Mediation Analysis under Non-Ignorable Missing Data Mechanisms

Several methods exist in analyzing the mediation effect of continuous and categorical variables under non-ignorable missing data mechanisms. However, the purpose of this paper focuses on the non-ignorable missing data mechanism (MNAR) using the Baker, Rosenberger, and Dersimonian (BRD) model approach in analyzing the mediation models using categorical mediation variables.

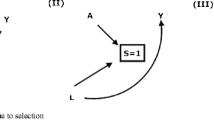
Given a mediation model, the relationship between smoking and coronary heart disease can be denoted by the regression coefficient parameter, “a.” On the other hand, the regression coefficient, which explains the relationship between the presence or absence of coronary heart disease in high-risk men and death due to myocardial infraction when controlling for smoking, can be denoted as “\(c^{\prime}\),” which is also called the direct effect. The coefficient parameter used to describe the relationship between smoking and death due to myocardial infarction can be denoted as “b.” Given these coefficients', the product value of “a” and “b" is called the indirect effect. Both the direct effect and the indirect effect make up the total effect c. Figure 1 represents the path diagram and equations for the mediation model.

Fig. 1
figure 1

Path diagram and equations for the mediation model

Full size image

Researchers used mediation analysis to test the difference between the total effect c and direct effect c'. As a rule of thumb, a mediator is considered significant in the model if the value of (c- c') is greater than 20% [3]. Moreover, this is interpreted that X's independent variable affects the dependent variable Y indirectly via a mediator M. In general, for any mediation model with categorical or continuous variables, the model population coefficient a can be calculated as:

$$\widehat{a}=\frac{Cov[X,M]}{Var[X]},$$
(1)

where \(Cov[X,M\)] is the covariance between variables X and M, and Var[X] is the variance of X. The model population coefficient of b and c' are given, respectively, as:

$$\widehat{b}=\frac{Var\left[X\right]Cov\left[X,Y\right]-Cov\left[X,M\right]Cov\left[X,Y\right]}{Var\left[X\right]Var\left[M\right]-{Cov\left[X,M\right]}^{2}}$$
(2)
$$\widehat{{c}^{\mathrm{^{\prime}}}}=\frac{Var\left[M\right]Cov\left[X,Y\right]-Cov\left[X,M\right]Cov\left[M,Y\right]}{Var\left[X\right]Var\left[M\right]-{Cov\left[X,M\right]}^{2}},$$
(3)

In the mediation analysis for categorical variables, logistic regression analysis is recommended when at least the dependent variable Y is categorical. Logistic regression has become well known in numerous fields, one of which is its easy transformation to the odds ratio. The equivalence (\(\hat{a}\hat{b} = \hat{c} - \hat{c^{\prime}}\)) is true when the dependent variable Y is continuous in calculating the mediated effect. However, this is not true when the dependent variable Y is categorical. The standard error is more complicated because the covariance between \(\hat{c}{\text{ and }}\hat{c^{\prime}}\) for ordinary regression does not directly apply to logistic regression. Hence, this makes the mediation effect estimation also complicated in terms of computing. Samawi et al. [20] developed a more straightforward method of analyzing the mediated effect among three variables when the dependent and mediator variables were dichotomous using a new approach called the latent variable technique to adjust for \(ab = c - c^{\prime}\).

Although the logistic regression can analyze the categorical variables, the categorical dependent variable's scale \(Y^{ * }\) cannot be observed directly. The residual variance and error terms are not the same as in terms of ordinary linear regression as explained by MacKinnon, and Dwyer [21]. This is because in ordinary linear regression, the dependent variance is observed and constant across the models while in logistic regression, the residual variance is fixed across the models. Winship and Mare [22] recommended setting the residual variance to \(\frac{{\pi^{2} }}{3}\) to fix the scale of the unobserved dependent \(Y^{ * }\) variable and hence the variance of \(Y^{ * }\) becomes

$$\sigma_{{Y^{ * } }}^{2} = \hat{c}^{2} \sigma_{X}^{2} + \frac{{\pi^{2} }}{3}$$
(4)

where Eq. (4) is the scale of the unobserved dependent \(Y^{ * }\) for the model of the independent variable X predicting the dependent variable Y.

By applying this recommendation, MacKinnon, and Dwyer [21] showed using a simulation study that the mediation effect estimation of \(\hat{c} - \hat{c^{\prime}}\) and \(\hat{a}\hat{b}\) were approximately equal either in the logistic or probit regression. However, in probit regression analysis, \(\frac{{\pi^{2} }}{3}\) it will be replaced with 1.

There are several methods considered for modeling missingness in mediation models with categorical variables. The commonly used method for dealing with missingness in categorical data is to substitute the missing values of each observation with the most common observation value. Although this method has been proven a common approach, its challenge is that it does not consider dependencies among the observation values. Other widely used methods include complete case analysis, multiple imputation, and Model-based analysis. This paper focuses on the extension of the model-based analysis method called Baker, Rosenberger, and Dersimonian (BRD) Models to a three-way contingency table proposed by Rochani et al. [19] for estimation of the mediation effect under the non-ignorable missing data mechanism (MNAR).

3 Estimation of Models

As mentioned earlier, a contingency table can represent categorical variables for mediation analysis, especially a three-way table for a simple medication model. An illustration of a three-way contingency table with supplementary margins for analyzing the association between two binary variables I, J while controlling for a third variable K in a 2 \(\times 2\times 2\) contingency table is given in Table 1.

Table 1 Three-way table with supplementary margins
Full size table

These three-way tables with supplementary margins are used to apply log-linear models in the analysis for contingency tables with missing counts, where the missing data indicator \(\mathrm{for }{\mathrm{variable} I \mathrm{is denoted as} {R}_{I} (R}_{I}=1\) represents observed values for I and \({R}_{I}=2\) represents missing values for I). Similarly, \({R}_{J}\) is an indicator for J's missing data such that \({R}_{J}=1\) represents observed values for J and \({R}_{J}=2\) represents missing values for J. The same approach applies for \({R}_{K} \mathrm{where } {R}_{K}=1\) indicates that K is observed. The cell counts are denoted as {\({n}_{ijkab1}\)}, where i, j, and k are the levels for variables I, J, and K. The subscript a and b, when equal to 1, shows that I and J have been observed for the comparable cell and vice versa. The cell count \(n_{ + jk211}\) shows where \(j\) and \(k\) and both are observed but \(i\) is missing. The cell count \(n_{i + k121}\) shows where \(i\) and \(k\) and both are observed but \(j\) is missing. Furthermore, cell count \(n_{ + + k221}\) shows where \(i\) and \(j\) and both are missing but \(k\) is fully observed.

Rochani et al. [19] identified sixteen BRD models using the log-linear model to an incomplete three-way table to correct for missingness in two variables with the third variable fully observed (Fig. 2).

Fig. 2
figure 2

Schematic presentation of BRD models [23]

Full size image

The Fig. 2 gives a general representation of the BRD models for the I × J two-way table with three supplementary margins. In these models, α is the missing data indicator for variable I, and β is the missing data indicator for J. The first and second subscript for parameters α and β corresponds to the variables I and J, respectively. The subscript '.' indicates that the parameter is constant over the corresponding index [16]. For example, (\({\alpha }_{i..}\),\({\beta }_{...}\))can be interpreted as missingness in a variable I depends on its own realization, while the missingness in variable J is constant across variables I and J.

This paper identifies four special case BRD models that can be used to correct for missingness in one categorical variable with the other two categorical variables fully observed. These models are model (\({\alpha }_{\dots }\)), Model (\({\alpha }_{i}\)), model (\({\alpha }_{.j.}\)), and Model (\({\alpha }_{..k}\)). Model (\({\alpha }_{\dots }\)) is under the ignorable missing mechanism assumption, while the other three are under the non-ignorable missing data mechanisms.

In deriving the proposed models for this paper, the first procedure requires deriving the models' likelihood functions and afterward solving the system of equations for each model’s maximum likelihood estimates. For illustrative purposes, we will use model (\({\alpha }_{i..}\)) to show the parameter estimates \(\widehat{\alpha }\) and \({\widehat{M}}_{ijk}\). The joint probability distribution and the log-likelihood function is given in Eq. 1 and 2, respectively.

$$\begin{gathered} L = \left\{ {\prod\limits_{i,j,k} {\frac{{e^{{ - \mu_{{_{ijk111} }} }} (\mu_{{_{ijk111} }} )^{{n_{{_{ijk111} }} }} }}{{^{{n_{{_{ijk111} }} }} }}} \times \prod\limits_{j,k} {\frac{{e^{{ - \mu_{{_{ + jk211} }} }} (\mu_{{_{ + jk211} }} )^{{n_{ + jk211} }} }}{{n_{ + jk211} }}} } \right\} - \mu_{ + + + 111} \hfill \\ \hfill \\ \end{gathered}$$
(5)
$$L = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{k} {n_{{_{ijk111} }} \log (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{m}_{{_{ijk} }} )} } } + \sum\limits_{j} {\sum\limits_{k} {n_{ + jk211} \log \left( {\sum\limits_{i} {(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{m}_{{_{ijk} }} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\alpha }_{{_{i..} }} )} } \right)} } - \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{k} {\left\{ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{m}_{{_{ijk} }} (1 + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\alpha }_{{_{i..} }} )} \right\}} } } + \Delta$$
(6)

Further simplification of the model gives the parameter estimates \(\sum_{i}{\widehat{m}}_{ijk}{\widehat{\alpha }}_{i..}\) = \({n}_{+jk211}\) \(\forall\) \({\widehat{\alpha }}_{i..}\) and.

\({\widehat{m}}_{ijk}= {n}_{ijk111}\). (For a detailed derivation of these models, refer to the appendix.)

Table 2 illustrates the estimated expected cell counts using (\({\alpha }_{i..}\)) model for complete cells and missing counts for a three-way table. Table 3 illustrates the collapsed expected cell counts for the three-way table into a 2 × 2 × 2 cross-classified table, obtained by adding the cells for the estimated cell counts of the complete cells and missing cells. Based on this estimated expected count, it can be expanded into a long-form of the data and used for the analysis of fitting the mediation models and estimating the coefficients \(\widehat{a}\widehat{, b}, \widehat{c},{c}{\prime}\), and the mediation effect estimate (\(\widehat{a}\widehat{b}\)) using logistic regressions.

Table 2 Estimated cell counts under model (\({\alpha }_{\mathrm{i}..}\))
Full size table
Table 3 2 × 2 × 2 cross classified table of the estimated expected counts under model (\({\alpha }_{\mathrm{i}..}\))
Full size table

We can find ad hoc boundary estimates if any solution is negative, as discussed by Baker et al. [16]. Rochani et al. [19] proposed that the ML estimates can still be computed by maximizing the likelihood function using the limited memory algorithm for constrained optimization (Byrd et al., 1995).

4 Simulations

A simulation study was conducted to evaluate the performance of estimating the mediation effect under the non-ignorable missing mechanism by the BRD model approach compared to the complete case method and commonly used Multiple imputation method under MAR assumption. We will use the proposed model for handling missingness in one categorical variable with the other two variables are fully observed. Then under model (\({\alpha }_{.j.}\)), the missing values were created for different percent missing in such a way that missingness in the independent variable X depends on the dependent variable Y. To model the missing probability for variable X, the following logistic regression model was considered as follows:

$$\mathrm{Pr }(X =\mathrm{missing}| Y) = \frac{\mathrm{exp}\left({\gamma }_{0}+{\beta }_{1}Y\right)}{1+\mathrm{exp}\left({\gamma }_{0}+{\beta }_{1}Y\right)},$$
(7)

where \({\beta }_{1}=1\) and the choice of \({\gamma }_{0}\), which was selected by simulation, depends on the percent missing. For each iteration, sample sizes of 300, 500, and 1000 with mean (\(\mu\)) = \(\left[\begin{array}{ccc}0& 0& 0\end{array}\right]\) and correlation matrix (\(\rho\)) =\(\left[\begin{array}{ccc}1.000& 0.612& 0.125\\ 0.612& 1.000& 0.612\\ 0.125& 0.612& 1.000\end{array}\right]\) were used. This correlation matrix will give a 75% mediation effect [24]. Using a 75% mediation, the population correlations \({\rho }_{XM}=0.612\), \({\rho }_{MY}=0.612\) and \({\rho }_{XY}=0.612\) produce 0.612 \(\times\) 0.612 = 0.3745, which is a 3:1 ratio to 0.125. These correlations produce path coefficients of a = 0.612, b = 0.856 with the product of ab = 0.524. One thousand iterations were performed for each simulation scenario for various sample sizes and varying percentages of missingness. The multiple imputation (MI) method and the BRD model (\({\alpha }_{.j.}\)) were used for illustrative purposes to generate expected cell counts for complete cells and missing counts. These expected counts were expanded into a long-form and used to fit the mediation models using logistic regression. Table 2 shows the biases and mean squared errors (MSEs) of the mediation effect for the complete case (CC) method, multiple imputation (MI) method, and the BRD models.

By examining the overall trend and performance in Table 4, as the percent missing in the data increases, so does the bias and MSE of the mediated effect for complete case method, model-based method, and MI method, which uses the Markov Chain Monte Carlo (MCMC) method for imputation. In general, the mediated effect estimates (\(\widehat{a}\widehat{b}\)) for the proposed model under the non-ignorable missing mechanism shows decreased relative biases and reduced MSE for different percent missing in the data compared to the complete case method and multiple imputation method. This shows that the application of this simulation to a simulated dataset using any of the proposed models shown in this paper will at least fit that particular simulated model as shown in this section.

Table 4 Bias and MSE comparison between complete case data, model case, and MI method data for the model (\({\mathrm{\alpha }}_{.\mathrm{j}.}\))
Full size table

5 Application to Multiple Risk Factor Intervention Trial (MRFIT) data

This section demonstrates the application of estimating the mediation effect by applying the BRD models using the Multiple Risk Factor Intervention Trial (MRFIT) data. The MRFIT dataset was available by request from the Biologic Specimen and Data Repository Information Coordinating Center (BioLINCC), which serves as the National Heart, Lung, and Blood Institute (NHLBI) biospecimens and data under the Identifier no: NCT00000487. This dataset consisted of 12,866 men equally randomized to either an intervention or usual care group after the first two screenings. The primary endpoint in the study was death due to coronary heart disease. A total of 12,866 men were assessed to be in the upper 10–15% of CHD risk based on high serum cholesterol levels, diastolic blood pressure (BP), and cigarette use and were randomized into the study. After randomization, participants were screened annually and assessed for changes in the risk factor. The usual care group (n = 6438) was referred to their regular source of medical care and was examined annually. Participants in the particular intervention group (n = 6428) participated in an in-depth sustained multifactor intervention program to lower serum cholesterol and blood pressure and promoting smoking cessation. Participants were followed up till February 1982. Each participant was followed up for a minimum of 6 years, and the average follow-up was seven years. During follow-up, deaths were ascertained by clinical center staff, and the cause of death was determined by a committee blinded to the intervention group. The primary endpoint was CHD death and included death from MI, sudden death, Congestive heart failure (CHF), and coronary artery surgery. Other deaths from cardiovascular diseases (CVD) were from stroke, hypertension with left ventricular failure, pulmonary embolus, and unclassified CVD deaths.

Based on this MRFIT dataset, the variables of interest for this paper are the presence of coronary heart disease, which will be the independent variable, smoking which will be used as the mediating variable, and death due to myocardial infarction as the dependent variable. We will use these variables to analyze the mediation models in estimating the mediation effect using the MRFIT dataset, i.e., how smoking status mediates the relationship between coronary heart disease in high-risk men and the outcome of death due to myocardial infarction. Given the three variables of interest, missingness is present in two (Smoking and presence of coronary heart disease) while the third variable is completely observed. This is shown in Table 5.

Table 5 Three-way table data representation of the MRFIT dataset with missing
Full size table

For illustrative purposes, by focusing on one of the sixteen BRD models, say model (\({\alpha }_{i..}\),\({\beta }_{...}\)), where α represents the missing data parameter for the smoking variable and β represents the missing data parameter for the presence of coronary heart disease variable. Hence this model implies that the participant's nonresponse on smoking depends on their smoking status and implies that the probability of missingness in the presence of coronary heart disease is independent of either presence of coronary heart disease or smoking status. This model was chosen as a more probable model under the assumption that smokers are more likely not to respond to their smoking status while missing in CHD is completely at random. However, it is always important to evaluate our conclusion's robustness by conducting a sensitivity analysis based on other non-ignorable models.

Table 6 shows the model comparison and parameter estimates for the sixteen BRD models discussed in earlier chapters using the MRFIT dataset. It is important to note that conducting a sensitivity analysis aids in the confidence of the initial assumption chosen and the conclusion made. Examining the other models will give the researcher more confidence about their hypothetical level of confidence in sticking to the initial conclusion if the conclusion does not change. Hence, from this table, there is no mediation effect based on the BRD models' p values. This implies that smoking status is not a mediating factor in the relationship between coronary heart disease in high-risk men and the outcome of death due to myocardial infarction. However, it is essential to note that in practice, decisions about having a mediation effect are often based on if the indirect effect is more than 20% of the total effect or not and not solely on a significant p-value (as shown in Table 6). Therefore, by considering this method for conclusion purposes, it is left at the discretion of the researcher to decide on which models with mediation effect is plausible for use or not.

Table 6 Model comparison and parameter estimates for the MRFIT dataset
Full size table

6 Conclusion

In this paper, we have shown the application of estimation of the mediation effect under the non-ignorable missing data mechanism (MNAR) using the extension of Baker, Rosenberger, and Dersimonian (BRD) models. Generally, mediation analysis is becoming very popular in several research areas. Investigators are interested in simply knowing the cause-effect relationship between two variables; they want to understand how and why a third variable mediates this relationship. This paper illustrated how well the mediation effect's estimation under the non-ignorable missing mechanism of the BRD model approach produces accurate inference compared to either the complete case method or the MI method. Performing a sensitivity analysis based on the non-ignorable BRD models was used in evaluating the robustness of the initial assumption chosen and the conclusion made. While this paper developed a sufficient method to evaluate the performance of the estimation of the single mediation effect under the non-ignorable missing mechanism by the BRD model approach, it is recommended that further research be conducted for scenarios of multiple mediation effects. In addition, although this paper considered only categorical variables for the simple mediation model, there is also a need for future research to accommodate the mediation model variables to be a combination of continuous and categorical variables.