1 Introduction

Separation of anomalies from background values is crucial in exploration geochemistry. Various methods have been used to separated geochemical anomalies. Obviously, each method has its own characteristics with respect to mathematical, statistical, geometric problems, and type of mineralization. Statistical methods are employed in order to determine anomaly thresholds. Various statistical quantities such as median, standard deviation, \( \overline{X}+S \), and \( \overline{X}+2S \) could be used to define thresholds [1]. In addition, the statistical parameters and the graphics such as box plots, cumulative probability plots, Q–Q plots, coefficient of variation, and median + 2MAD (median absolute deviation) could be applied in combination for identification of anomalous regions [1]. The median–standard deviation method is a traditional and common method to determine the threshold. In geochemical evaluation, \( \overline{X}+2S \) determine the threshold. In other words, values larger than this limit will be considered as anomalies. Lepeltier suggested that, after drawing data into the probability paper, the percentiles of 50, 84, and 97.5 are equal to median, background, and threshold values. In all of the above methods, weak anomalies have not been demonstrated. Therefore, different fractal methods have been considered to separate weak anomalies. Fractal/multifractal method of geochemical data is an attractive research topic in the field of applied geochemistry and has been a powerful tool to identify geochemical anomalies or to determine environmental baselines [2,3,4]. Several fractal/multifractal methods have been developed and effectively applied to geochemical data for defining and mapping anomalies, for example, concentration–area (C–A) model [5,6,7], spectrum–area (S–A) model [8,9,10], and singularity index [11,12,13]. The C–A model has been demonstrated to be a powerful tool for identifying geochemical anomalies and has been become a fundamental technique for modeling of geochemical anomalies [14]. The singularity technique represents the important progress of fractal/multifractal modeling of geochemical data. The concept of singularity is to characterize anomalous behaviors of singular physical processes that often result in anomalous amounts of energy release or material accumulation within a narrow spatial–temporal interval. For point interpolation, various methods could be classified into exact and approximate. There exist numerous exact methods such as most distance-weighting methods, kriging, spline interpolation, interpolating polynomials, and finite difference methods [15, 16]. The purpose of this paper is to use finite difference method in drawing maps, to compare different methods of C–A, S–A, and singularity techniques determining geochemical anomalies, and to select the best method in introducing Pb and Zn anomalies as well as to adapt geochemical maps to mineralization.

2 Material and Methods

2.1 Geological Setting

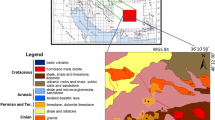
The studied area was situated in the Malayer-Esfahan Pb–Zn metallogenic belt. From the regional tectonic point of view, Pb–Zn deposits are arranged on the margins of a rift-generated sedimentary basin. The deposit is situated about 25 km SW of Khomein and SE of Arak city in Sannanaj-Sirjan zone (Fig. 1). Based on the geological map of Haft-Savaran area, sandstone and shale of the lower Jurassic are the main rocks in the deposit (Fig. 1). In this area, geological formations are comprised Jurassic (Liassic coal–bearing shale and sandstone) and Cretaceous (limestone). The Pb + Zn, Pb/Pb + Zn, Cu + Pb + Zn, and Cu ratios in the shales and sandstone show that mineralization is Sedex deposit in the Haft-Savaran region [17]. Lead–zinc mineralization has occurred in shales and sandstones and along the normal fault with a NE to SW trend. Mineralization is in the form of strata-bound ore deposits. Haft-Savaran deposit is classified into three facies as stockwork, massive sulfide, and stratiform according to geometry, texture, and grade. Mineralization includes quartz, iron-rich dolomite, sericite, pyrite, sphalerite, gallon, and chalcopyrite, and the grade of Pb–Zn is 5% in the stockwork facies. Mineralization is strata-bound in the massive sulfide deposit and includes dolomite and quartz minerals with sulfides such as pyrite, sphalerite, gallon, and chalcopyrite [17]. The Pb–Zn grade varies from 10 to 18%. Stratiform facies includes silt particles, organic matter, and sulfide minerals. Sulfides are pyrite, sphalerite, and chalcopyrite, and the grade of Pb–Zn ore is very low (0.5%). The shale and sandstone host rock are subjected to silica, dolomite, and sericite hydrothermal alteration and are mainly found around the stockwork facies. Stockwork sulfide facies and alterations related to the hydrothermal processes and mineralizations have been induced by passing fluids through normal faults in the Haft-Savaran region [17].

Fig. 1
figure 1

Haft-Savaran Pb–Zn deposit in Sannandaj-Sirjan zone

Full size image

2.2 Sampling and Analysis Methods

From 33 boreholes in Haft-Savaran area, 170 samples were selected (Fig. 2). The average depth of boreholes and the average distance between boreholes was 50 m and 100 m, respectively. As shown in Fig. 3, samples were illustrated in vertical sections (Fig. 3). The number of samples is 63, 48, and 59 in the first, second, and third sections, respectively. Samples were analyzed by inductively coupled plasma-mass spectrometry (ICP-MS) for Pb and Zn. Measurement of Pb and Zn in ICP-MS was performed by digestion of four acids including HF, HCl, HClO4, and HNO3. The detection limits for Pb and Zn is 1 mg/kg.

Fig. 2
figure 2

Simplified geologic map of Haft-Savaran area

Full size image
Fig. 3
figure 3

The used samples were illustrated on the three vertical sections in Haft-Savaran area

Full size image

2.3 Finite Difference Interpolation Method

The finite difference method (FDM) is one of the numerical methods used to solve the approximate differential equations. In this work, FDM is applied to interpolate the vertical sections, shown in Fig. 3, using samples information. In fact, the FDM is a completely mathematical method and application of this estimation method is investigated along with fractal models. The basis of FDM is to use the Taylor method approximation function for solving equations [18]. The method is relatively simple, and the advantages of this method can be estimated in its simple application, the relative accuracy of the obtained results. In this way, if the distances of each network are smaller, the more accurate the work. The theory of this method is investigated by the Laplace equation and boundary conditions (Eqs. (1) and (2)).

$$ {f}_{xx}+{f}_{yy}=0\kern0.5em $$
(1)
$$ {f}_{xx}+{f}_{yy}=F\left(x,y\right) $$
(2)

Laplace equation and boundary conditions were used to work with finite difference interpolation. Here f (i,j) is the concentration of elements in a point with specific coordinates (i,j). Finally, the value of each point in the cross section was calculated by averaging the four points around it.

FDM needs to grid the computational field, the vertical sections (Fig. 4a). Here we assume that scales along x- and y-axes are the same in the computational field. The size of the network in each direction is ΔX and ΔY (Fig. 4b). Consider Eqs. (3)–(5) as contractually:

Fig. 4
figure 4

a Gridding of the basin in a FDM problem. b The graphical calculation of the FDM

Full size image

In general, the second-order central approximation is obtained from Eq. (6) at points i, j for the second derivative of the function.

$$ {f}_{\left\langle xx|i,j\right\rangle }=\frac{f_{i+1,j}-2{f}_{i,j}+{f}_{i-1,j}}{\Delta {x}^2} $$
(3)

For the second derivative in the y direction, we can write Eq. (7).

$$ {f}_{\left\langle yy|i,j\right\rangle }=\frac{f_{i,j+1}-2{f}_{i,j}+{f}_{i,j-1}}{\Delta {y}^2} $$
(4)

By replacing the calculated values of the finite difference approximation in the Laplace Eq. (1), the relations are as Eq. (5).

$$ \frac{f_{i+1,j}-2{f}_{i,j}+{f}_{i-1,j}}{\Delta {x}^2}+\frac{f_{i,j+1}-2{f}_{i,j}+{f}_{i,j-1}}{\Delta {y}^2}=0 $$
(5)

And taking into account \( \frac{\Delta {x}^2}{\Delta {y}^2}={\beta}^2 \): Eq. (6).

$$ \frac{f_{i+1,j}-2{f}_{i,j}+{f}_{i-1,j}}{\Delta {x}^2}+\frac{f_{i,j+1}-2{f}_{i,j}+{f}_{i,j-1}}{\Delta {y}^2}=0 $$
(6)

If we arrange the equations in terms of the function in points i, j, we have Eq. (7):

$$ \frac{f_{i+1,j}-2{f}_{i,j}+{f}_{i-1,j}}{\Delta {x}^2}+\frac{f_{i,j+1}-2{f}_{i,j}+{f}_{i,j-1}}{\Delta {y}^2}=0 $$
(7)

In a particular case, the size of the computational network is equal in two directions (Δx = Δy) (Eqs. (8) and (9)).

$$ {f}_{i+1,j}+{f}_{i,j+1}+{f}_{i-1,j}+{f}_{i,j-1}-4{f}_{i,j}=0 $$
(8)
$$ \frac{f_{i+1,j}-2{f}_{i,j}+{f}_{i-1,j}}{\Delta {x}^2}+\frac{f_{i,j+1}-2{f}_{i,j}+{f}_{i,j-1}}{\Delta {y}^2}=0 $$
(9)

In Eq. (9), the value of the function at the point i, j with its mean in the points around it is equal, and the estimate of each point in this method is done by averaging the points around it. These calculations are repeated after being performed for all networks. The basis of this method is based on the iteration, and the iteration continues until the answers converge to some degree or the difference in the two values obtained in two consecutive steps is less than the error. In some studies, the difference between adjacent networks is less than a certain value of about 0.1 as the end of the calculation. FDM algorithm was developed in a MATLAB code, and its pseudocode is presented below:

figure a

2.4 The Lepeltier Method

For detecting the concentration of elements, we use Lepeltier method [19]. The values of X + 2S (X is mean and S is standard deviation) for each elements were calculated, and 3D models of concentrations was created with Rock Works software. Distribution 3D models for elements were prepared based on the kriging method [20]. The objective of the kriging is to provide a probability based on estimate of trace and heavy element distribution and their spatial continuity.

2.5 Concentration–Area Method

In concentration–area (C–A) method, the relationship between co-concentration lines and area could be established from Eq. (10).

$$ A\left(\mu \ge {X}_0\right)=F{X}_0^{-\alpha } $$
(10)

in which A(μ ≥ X0) is the cumulative area enclosed by co-concentration lines whose size is larger than X0. Threshold is obtained in the graph of the total logarithm of the area. α is the dimension of the co-concentration line [15]. If A(ρ) is the area of concentration values larger than ρ in a contour map, then A(ρ) must be an incremental distribution of ρ. If θ represents the threshold values, Eqs. (11) and (12) are employed.

$$ \left(\rho \le \vartheta \right)\propto {\rho}^{\frac{1}{\beta }} $$
(11)
$$ A\left(\rho >\vartheta \right)\propto {\rho}^{\frac{\beta }{3}} $$
(12)

If a graph of A (≥ ρ) versus ρ (in logarithmic coordinates) is linear, then the data belongs to a population and distribution is simple fractal. However, the diagrams could be straightforward in several sections, so multifractal distribution will occur, and breakpoints between the straight-line sections are the thresholds that separate the populations [15]. The biggest difference between fractal dimensions is the resolution of segregation of population.

2.6 Spectrum–Area Method

In spectrum method, the input data are transformed to frequency field using Fourier transforms. This means that the variations of the standard for all the positions of the input map (raw data) are converted to the frequency domain [21]. To execute, input data is prepared using an interpolation method in the form of a co-concentration line map. The next step is to calculate the two-dimensional function of the frequency spectrum, which must be applied to the output matrix of the two-dimensional Fourier transform. To calculate this function, there are several methods that most of them yield the same answer. Here, the frequency spectrum was calculated with Eq. (13).

$$ E\left({W}_X,{W}_y\right)={F}_r^2\left({W}_x,{W}_y\right)+{F}_i^2\left({W}_x,{W}_y\right) $$
(13)

where Wx, Wy is equal to the wave number for the X- and Y-axes, Fr is equal to the real part of the two-dimensional Fourier, and Fi is equal to the two-dimensional Fourier episode. The power spectrum was mapped and divided into different groups. The area of each group is measured, and the logarithmic diagram of the power spectrum is plotted to the area. Using the least squares method, the best line is fitted to them. Due to the intersection of the lines, area boundary and threshold values are determined and according to the slope of the obtained line, the fractal dimension could be calculated [9, 22].

2.7 Singularity Index

According to multifractal theory, singularity index is related to the distribution of self-similarity [16]. In modern nonlinear theory, the concept of multifractal is characterized by the law–power model. The window-based method is used to estimate singularity. Different types of windows such as square, circle, and polygon could be applied to measure concentration around a point. The singularity index is estimated in a small neighborhood according to Eq. (14).

$$ C=c.{\upvarepsilon}^{\alpha -E} $$
(14)

where C represents the mean concentration of the element, c the constant, α the index of singularity, Ɛ the normalized distance, and E the Euclidean geometry. The singularity index is evaluated on a straight line with a pair of data C and Ɛ. Each point of the field is considered using the variables A(r) (circle) with variable windows with sizes rmin = r1 < r2 < … < rn = rmax. The mean value of the concentration is calculated for each window and shows linear relationship in the logarithmic diagram (Eq. (15)).

$$ \log C\left[A(r)\right]=c+\left(\alpha -2\right)\log (r) $$
(15)

The estimated slope of the linear relation is introduced as α − 2. The values of the singularity index are typically 2 in the two-dimensional maps which are defined as non-singular points.

2.8 Coefficient of Areal Association

The coefficient of areal association (CAA) is used to determine the similarity and matching of the results of different methods. In this study, CAA was applied based on Eq. (16).

$$ \mathrm{CAA}=\frac{S_{\mathrm{AA}}+{S}_{\mathrm{BB}}}{S_{\mathrm{AB}}+{S}_{\mathrm{BA}}+{S}_{\mathrm{AA}}+{S}_{\mathrm{BB}}} $$
(16)

where S represents area, indexes are the geochemical communities, A is the anomaly, and B indicates the background. SAA is area in the first and second methods of anomaly estimation, and SBAis area in the first method as background and in the second method as anomaly [23].

3 Results and Discussion

3.1 The Lepeltier Method

The Lepeltier method is a traditional and common method for estimating threshold and shows some disadvantages compared to other methods. The main disadvantage is that only numerical values are considered in the calculations and does not attend the spatial continuity of the data [1]. Also, this method can only detect strong anomalies in a strong background and does not have the power to detect weak anomalies. Three-dimensional maps of background, threshold, and anomaly values were provided for Pb and Zn in the studied area (Fig. 5). Pb–Zn anomalies are mainly in the center of the mineralization body turned to an NE–SW trend. It is likely that the significant Zn–Pb enrichments are found on the SW portion of the block near the fault-controlled shale contact, though the enrichment in Zn ores occurs both on the NE–SW of the block [17]. Therefore, the ore is replaced epigenetically in hydrothermally altered shale as well as the faulted–fractured shale contact. Mineralization includes dolomite and quartz minerals with sulfides such as pyrite, sphalerite, gallon, and chalcopyrite. It is interesting that the concentration of the elements and ore values increase consistently toward the hydrothermally shale rocks with depth. Multiplicative composite rock-geochemical halos of multielement data have been successfully used to delineate the possible exploration target for concealed mineralization [17]. Accordingly, Zn/(Pb + Zn), Zn/Pb, SiO2/Zn, and V/(Ni + V) of the composite halos demonstrate an increase above the main zone of the Haft-Savaran Zn–Pb mineralization in trend of NE–SW. The rocks of the area have hydrothermal alteration. The Hashimoto index distribution showed input of K and Mg and exit of Ca and Na confirm possible locations specified by mineralization ((MgO + K2O)/(MgO + K2O + CaO + Na2O)). This index is widely spread in the east and west regions with the enrichment in the west and indicates that there is further potential of these areas for mineralization. The index distribution of silicification has a high-grade area in trend of NE–SW [17].

Fig. 5
figure 5

Three-dimensional diagram of background, threshold, and anomaly regions for Pb and Zn using median–standard deviation method; a, b, c: 3D illustration of ore deposit with three level of background, threshold and anomaly for Pb element. d, e, f: 3D illustration of ore deposit with three level of background, threshold and anomaly for Zn element

Full size image

3.2 Concentration–Area Method

Based on the concentration–area (C–A) approach, the first step is to grid study area. According to the sampling scale and minimum distance between the boreholes, the optimum size of the grid network was selected 2 m by 2 m. The gridded vertical sections, shown in Fig. 4, were interpolated by FDM and C–A log–log plots consisting of the concentrations of Pb and Zn versus the area of pixels with concentrations of Pb and Zn greater than ρ (Fig. 6). As illustrated in Fig. 6, there are two geochemical populations for Pb (Fig. 6a) and three for Zn (Fig. 6b). First and second populations in log–log plot of Zn show low and medium anomalies. Such a classification was provided for rare earth elements in the Nanling belt of China [24]. Based on C–A method, it was found high, medium, and low anomaly zones for rare earth elements [24]. The third population indicates high concentration and also called high intensive anomalous regions. Based on the outputs, the anomaly maps of three vertical sections were generated as depicted in Fig. 7. In the first vertical section, high anomalous Pb is in the eastern boundary at a height of 1210 m (Fig. 7a). The Pb is centered in the second section (Fig. 7b) and in the third section is in the western boundary at a height of 1160 m (Fig. 7c). In addition, the extent of the anomaly has increased from east to west. The trend of Zn is similar to Pb (Fig. 7d–f). But extent of the Zn anomaly is more than Pb. Trend of Pb–Zn anomalies is consistent with local faults (Fig. 8). Therefore, there is a good agreement between the geochemical concentration of the Pb–Zn calculated by the C–A method with other methods such sulfide mineralization, Lepeltier method, halos index, and alteration index.

Fig. 6
figure 6

C–A log–log plot of (a) for Pb element and (b) for Zn element in the first vertical section

Full size image
Fig. 7
figure 7

Concentration–area model for Pb and Zn in three vertical sections; a, b, c: 2D illustration of ore deposit in three different vertical sections for Pb element. d, e, f: 2D illustration of ore deposit in three different vertical sections for Zn element. 

Full size image
Fig. 8
figure 8

The faults with trend of NE–SW of the studied area

Full size image

3.3 Spectrum–Area Method

In spectrum fractal model, the cumulative sum of area was performed on the corresponding values of the power spectral map. In terms of spectrum–power as well as including areas, all values were calculated logarithmically. Finally, straight lines were used to separate the various communities using the least squares law on them in the MATLAB software package. It determined three to four distinct populations for all data (Fig. 9). In Fig. 9, end of lines were considered as boundary of separation of frequency populations. The obtained threshold values of the elements were used for the design of the digital filter. In addition, by applying it over the frequency data derived from the two-dimensional Fourier, the distribution map of elements was obtained for the anomalous areas. Eventually, data were returned to the concentration–spatial space by the inverse Fourier transformation. Similar to this method, it determined local anomalies of As, Au, Ag, and Hg due to Au mineralization in Yunnan province, South China [25]. High Pb anomaly is concentrated in the eastern part of the first vertical section (Fig. 10a), in the center of the second section (Fig. 10b), and in the western part of the third vertical section (Fig. 10c). The extent of Pb anomaly has also decreased from east to west. Also, comparison of three different vertical sections shows that Pb mineralization zone was expanded from NE to SW of the studied area and corresponded to local fault. Zn unlike Pb does not follow a particular trend in the three vertical sections (Fig. 10d–f). Therefore, there is a good agreement between Pb anomaly calculated by this method with other methods such sulfide mineralization, Lepeltier method, halos index, and alteration index. Research in the Kahang area of Iran showed that the anomalies obtained from spectrum–area model correlated with the geological features of the deposit, including alterations, faults, and lithological units [9]. There is a strong correlation between high elemental anomalies in the fault zone.

Fig. 9
figure 9

Log Pb (a) and Zn (b) power spectrum values versus log area in the first vertical section

Full size image
Fig. 10
figure 10

Power spectrum–area model for Pb and Zn in the three vertical sections; a, b, c: 2D illustration of ore deposit in three different sections for Pb element. d, e, f: 2D illustration of ore deposit in three different sections for Zn element.

Full size image

3.4 Singularity Index Method

In the singularity method for any point in the region, a value is determined as α which is singularity index. To obtain α in the plotted graph, the fitted line slope is added with 2 (Fig. 11a, b). Finally, the areas with α less than 2 represent enriched areas with positive singularity and the areas with α greater than 2 represent negative singularities. Areas with α equal to 2 are non-singular regions. The singularity method was used in the Nanling belt of China and produced good results. The singularity method showed well rich and depleted areas for rare earth elements [24]. Environments with positive singularities correspond to environments where elements have increased as a result of mineralization or other local geochemical processes, whereas environments with normal singularity values are associated with areas of geochemical background [11]. The Pb has high anomalies in several areas of the east in the first vertical section (Fig. 12a). The Pb anomaly is concentrated in the center (depth) and west (surface) in the second section (Fig. 12b), and Pb anomaly is in the west of third section (Fig. 12c). The Pb anomaly has increased from east to west. The Zn anomaly trend is similar to that of Pb anomaly and is from east to west (Fig. 12d–f). The dispersion of Zn anomaly is more than Pb anomaly in three sections. On the other hand, the distribution of Zn anomaly is almost similar to that of Pb anomaly in the three sections. The Pb–Zn anomaly in the singularity method such as the Lepeltier method, the C–A method, and S–A method is consistent with the local fault trends in the region.

Fig. 11
figure 11

Log Pb (a) and Zn (b) singularity value versus log area in the first vertical section

Full size image
Fig. 12
figure 12

Singularity index model for Pb and Zn in the three vertical sections; a, b, c: 2D illustration of ore deposit in three different sections for Pb element. d, e, f: 2D illustration of ore deposit in three different sections for Zn element

Full size image

3.5 Coefficient of Areal Association

In the first vertical section of Pb element, the overlapping is 92% between spectrum–area and concentration–area methods (Table 1). Singularity index method shows 95% overlapping with spectrum–area method in the second section, and overlapping is decreased to 93% with concentration–area in the third section (Table 1). Therefore, the used methods could highlight the same area as anomalous region and are suitable to separate Pb anomalies. But for Zn, the highest overlapping is about 61% for two methods of concentration–area and singularity index in the first section. In the second section, the highest matching is 97% between singularity index and the concentration–area methods. Also, the results of the concentration–area and the singularity index methods show 76% overlapping in the third section (Table 2). Then, according to Table 2, it is obvious that both concentration–area method and singularity index method are suitable for the separation of Zn anomalies in the region. In summary, it can be said that singularity method is better in separation of Pb–Zn anomalies than the C–A method and spectrum-arS-Aea method. The importance of the singularity method in separating weak anomalies has been highlighted in other research such as Zou et al. [26], Wang and Zuo [27, 28], Liu et al. [29], and Ersoy and Yunsel [30].

Table 1 Coefficient of areal association for different fractal models in Pb
Full size table
Table 2 Coefficient of areal association between different fractal models in Zn
Full size table

4 Conclusions

Finite difference interpolation method and multifractal models were integrated to provide anomalous regions of Pb–Zn in Haft-Savaran area. Finite difference interpolation interpolated concentration of Pb and Zn in three vertical sections to satisfy the requirements of multifractal models. Determination of Pb and Zn anomaly by Lepeltier method, fractal method (C–A and S–A method), and singularity methods showed that singularity method was more suitable than other methods in separating weak Pb–Zn anomalies. The singularity method can provide a powerful tool to extract significant anomalies for spatial distribution of mineralization using original geochemical element concentration values and can quantify the properties of enrichment and depletion caused by mineralization. Producing maps of singularities can help to identify relatively weak metal concentration anomalies in complex geological regions. In our case study, these local anomalies of Pb–Zn are directly associated with the NE–SW orientations faults. In addition, the anomalies are consistent with sulfide mineralization, halos zone, and alteration indices.