1 Introduction

The ball mill grinding (BMG) system is one of the most significant processes in the mining industry, having considerable influence on the worth of recovering valuable minerals. Therefore, applying control algorithms which lead to reducing the energy and increasing the performance of sub-processes can be an appropriate solution for mining processes. On the other hand, the grinding system outputs cannot be separately controlled due to their multi-input–multi-output (MIMO) structure and the great interactions between the system inputs and outputs. Variations of the system parameters over time and existing large external disturbances which cause poor performance of the controller can be considered as the other challenge of the grinding systems [1]. However, the existence of disturbance in industrial processes is inevitable and cannot be removed from the system. The effects of disturbances on control loop performance can be mitigated by the accurate estimation of disturbances. Also, the delay phenomenon exists in many physical and engineering systems, causing poor performance and possibly even leading to instability in the system [1,2,3,4].

Based on the above-mentioned statements, the control of BMG systems has attracted a lot of attention from researchers in recent years. Multi-loop control of PID is a traditional control approach applied for BMG systems due to its simplicity of computation and implementation [5]. However, the PID controller does not have good performance and there is no robustness against the variation in system parameters and delay. Also, if the system parameters change, the controller terms must be tuned again [1, 6,7,8]. Another applicable control method that is widely used for grinding systems is model predictive control (MPC). MPC is robust against delay, instability, and change in the parameters of the system. However, due to the dependency of this control approach on the precise model of the industrial processes, which is usually not accessible, this control algorithm is not efficient [1, 9,10,11]. Furthermore, other methods such as robust control [12], adaptive control [13], neuro-control [14], and intelligent control [15, 16] are used on grinding systems. In [17], a linear optimal control method based on fuzzy logic is proposed for controlling the product size in the BMG system, while increasing performance, reducing losses, and optimizing the product quality are the purposes of an optimal algorithm. Intelligent control is one of the effective methods for industrial processes due to the unnecessity of this approach to the process model [18].

As previously mentioned, in most industrial processes, the presence of disturbance and uncertainty is an inevitable problem. For example, in the grinding system, the performance of this process is affected by various disturbances, including external and internal disturbances, variation in the ore degree of hardness and its size, interaction effects, model mismatches, and uncertainties. The mentioned factors have a huge influence on the performance of the closed-loop system. Many advanced control approaches do not have satisfactory performance in multivariable systems with time delay in the presence of strong external disturbances and uncertainties. Additionally, control approaches based on feedback cannot appropriately reject the disturbances and compensate for the uncertainties of the process. Although the control system can minimize the influence of these factors to almost slow speeds by adjusting feedback, it may cause a decrease in system performance in the presence of strong disturbances and uncertainties [5, 11].

In order to improve the disturbance rejection in these cases, sensors can be used to gather information about the disturbance, albeit this will increase the production cost as well as system complexity. An appropriate approach to the disturbance rejection problem is employing a feed-forward compensation part for the disturbances alongside the feedback part. A direct approach for this purpose is the extraction of the disturbance model; however, this is very difficult in real systems. A more effective approach is estimating the disturbance through an observer and eliminating its effects on the system without altering the input–output behavior [1, 3,4,5, 10, 19, 20]. The disturbance observer (DOB) technique has the ability to eliminate strong external disturbances since it does not depend on the exact mode of disturbance [21, 22]. The DOB technique is widely used because of its simple structure and great ability to reject disturbances and compensate for the uncertainties of the process [23,24,25]. Although DOBs are usually suitable for minimum phase systems with time delay, they do not perform well for time-delayed non-minimum phase systems. Therefore, to deal with such systems, an improved disturbance observer (IDOB) is introduced in [4]. Also, the multivariable disturbance observer (MDOB) based on inverse multivariable system approximation is provided for advanced feedback control techniques to improve the disturbance rejection performance [4].

To overcome the challenges of BMG systems, i.e., high interaction, strong external disturbance, time delay, and time-variable parameters, the proposed structure of this paper is presented as follows. The proposed approach is composed of two terms. A fuzzy logic self-tuning PID (FLST-PID) controller is employed for model mismatch and parameter variations of the BMG system. Due to its robust and adaptive structure, this controller can perform in the uncertain condition of the system with zero steady-state error. The most important feature of the proposed control algorithm is that the controller is designed based on the IDOB algorithm, which can eliminate the influence of interaction in such an MIMO system, as well as internal and external disturbances in the output, and overcome the delay problem of the system without the necessity for separate compensators. Hence, the MIMO structure can be divided into two sections, in which the FLST-PID controller is employed for every section. The first part is related to the control of product particle size and the second part is associated with the control of circulating load. Consequently, the proposed FLST-PID controller of this paper based on the IDOB algorithm is able to resolve all of the mentioned challenges of BMG circuits, such as delay, parameter variation, and MIMO structure.

The rest of this paper is organized as follows. The BMG system and its problems are introduced and investigated in Section 2. The FLST-PID controller is presented and incorporated with the IDOB algorithm to increase the controller’s ability and reject strong external disturbances in Section 3. The simulation results and comparison to PI-IDOB are offered in Section 4. Finally, the conclusions are given in Section 5.

2 The BMG System

The BMG system is a size reduction process that is used in the mining industry to increase useable minerals in mineral stones. The BMG circuit, which includes a ball mill, pump sump, hydro-cyclones, and solids feed conveyors, is shown in Fig. 1 [3]. The size of the product particles is the most important output in this system. The fresh coarse ore is fed to a mill through a vibratory conveyor. Afterwards, the tumbling action of the balls within the revolving mill crushes the feed to finer sizes. Then, the slurry, together with the finer particles, is discharged from the ball mill to a pump sump. Finally, the material obtained by adding dilution water in the pump sump is pumped to hydro-cyclones for classification. After the classification phase, they are separated into two streams, consisting of the desired size and larger particles that should be returned to the process as circulating load. Strong external disturbances, such as changes in grain size and hardness of the ore, can lead to continuous fluctuations in the size of the final product. Therefore, regulating and maintaining the degree of ore hardness and the size of the grains according to the stability of the dilution water and the feed rate of the new minerals are the control goals of BMG circuits [1].

Fig. 1
figure 1

Process diagram of the ball mill grinding (BMG) circuit [1]

Full size image

The relationship between the outputs and inputs is shown in Fig. 2. The fresh ore feed rate (u1) affects the output particle size (y1) with the P11 transfer function. However, output y1 is affected additionally by the dilution water flow rate (u2) with the P12 transfer function and the disturbance with the H1 transfer function. The output of y2 (circulating load) is also affected by the input u2 (dilution water flow rate) with the P22 transfer function, the input u1 with the P21 transfer function, and the disturbance with the H2 transfer function. For regulating the outputs, the factors influencing them should be controlled. Disturbances are not at our discretion; hence, we must reject their influence on the output.

Fig. 2
figure 2

The relationships between the variables in the ball mill grinding (BMG) system [1]

Full size image

It should be noted that the interaction in this process is clearly observed and the separation is used to design an efficient controller. Also, due to the disturbance input being uncontrollable, the controller must be designed in such a way that its influence on the system output is minimized. In addition to the several existing disturbances, the MIMO structure of the BMG circuit, the variations of the system parameters, and delay are the other challenges faced by this system.

3 Controller Design for the BMG System

In industrial applications such as BMG systems, the designed controller should be effective and simple, so that its implementation is cost-effective [16, 26]. Therefore, a multi-loop PID controller has been utilized in this study due to advantages such as the simplicity in computation and implementation and the ability in reducing the interaction effects between the inputs and outputs. On the other hand, fuzzy logic is one of the artificial intelligence methods that has the ability to formulate human knowledge in a systematic manner and improve the dynamic response in different conditions of system operation [27].

Therefore, in order to manage the mentioned system challenges, a fuzzy logic PID controller is proposed in this research. Moreover, the robust structure of the fuzzy logic controller is incorporated into the adaptive specification of a self-tuning controller to handle uncertain conditions and is named as FLST-PID. This controller tunes itself according to changes in the process coefficients. This structure is based on estimating the disturbance through an IDOB for reducing the effect of disturbance on system performance. Hence, the approach of this paper for controlling the BMG circuit is applying the proposed technique of the FLST-PID controller based on an IDOB.

3.1 PID Controller

The PID controller is one of the most effective controllers in the industry. Today, in process control, more than 95% of controllers are of the PID type. As shown in Fig. 3, each PID controller has three terms, consisting of proportional (P), integral (I), and derivative (D). The traditional PID controller is as follows:

$$ u(t)={k}_pe(t)+{k}_i\underset{0}{\overset{t}{\int }}e(t) dt+{k}_d\frac{de(t)}{dt} $$
(1)

where u(t) is the control signal and e(t) is the control error (e(t) = r(t) − y(t)). The reference value, r(t), is called the set-point [27].

Fig. 3
figure 3

PID controller

Full size image

The parameters of the PID controller are the proportional gain (kp), integral gain (ki), and derivative gain (kd). The proportional controller (kp) decreases the rise time and also reduces the steady-state error. The integral controller (ki) can eliminate the steady-state error; however, it may reduce the transient response of the system. The derivative controller (kd) improves system stability and reduces the maximum overshoot and also improves transient response.

3.2 Fuzzy Controller

Fuzzy control is one of the intelligent methods widely used for automatic control of industrial plants due to its independence from needing to know the exact model of the system. A fuzzy inference system (FIS) is composed of several main parts, consisting of a fuzzifier, rule base, inference engine, and defuzzifier. The main part of a fuzzy system is a knowledge base that follows the fuzzy if-then rules [28, 29].

3.3 FLST-PID Controller

When the conditions and parameters of a system change, the designed controller does not necessarily work well. Using an FLST-PID controller is a good solution for overcoming these conditions. In contrast to PID controllers, in the FLST-PID controller, the values of the PID parameters during the control of the system will be changed and they are set in fuzzy logic. Applying Mamdani’s minimum for the fuzzy implication and center mean for the defuzzification state, the fuzzy control law is considered as:

$$ {u}_1=\frac{\sum_{i,j}\left[\left({\mu}_{E_i}\left({e}_1\right)\cap {\mu}_{E_j}\left({e}_2\right)\right).{U}_{n\left(i,j\right)}\right]}{\sum_{i,j}\left({\mu}_{E_i}\left({e}_1\right)\cap {\mu}_{E_j}\left({e}_2\right)\right)} $$
(2)

where \( {\mu}_{E_i}\left({e}_1\right)\cap {\mu}_{E_j}\left({e}_2\right) \) depicts the intersection of two fuzzy sets and is defined as the “min” operation:

$$ {\mu}_{E_i}\left({e}_1\right)\cap {\mu}_{E_j}\left({e}_2\right)=\min \left[{\mu}_{E_i}\left({e}_1\right),{\mu}_{E_j}\left({e}_2\right)\right] $$
(3)

The fuzzy if-then rule which builds the fuzzy control rule in a fuzzy logic controller can be shown as:

$$ R: if\ {e}_1\ is\ {E}_i\ and\ {e}_2\ is\ {E}_j\ Then\ {u}_1\ is\ {U}_{n\left(i,j\right)} $$
(4)

In Eq. (4), e1 and e2 make up the error e(k) and its change Δe(k). Furthermore, Ei, Ej, and Un(i, j) denote the linguistic changes of e1, e2, and u1, respectively. n(i, j) is presumed to be a function whose value at i and j is an integer [30, 31]. For mismatch dynamics, uncertainty on system parameters, and compensating the disturbance effects, a self-tuning structure is embedded into the fuzzy controller, resulting in a change to [32]:

$$ R: if\ {e}_1\ is\ {E}_i\ and\ {e}_2\ is\ {E}_j\ Then\ C\ is\ {C}_{m\left(i,j\right)} $$
(5)

In the above equation, C and Cm(i, j) are the changes in the center of the output membership function (MF) and its linguistic variable. Similar to n(i, j), presume that m(i, j) shows any function with integer value [30, 31]. Applying Mamdani’s minimum and center mean for fuzzy implication and defuzzification, the center of the MF output for the self-tuning fuzzy controller is defined as:

$$ {U}_{n\left(i,j\right)}={U}_{n\left(i,j\right)}+\frac{\sum_{i,j}\left[\left({\mu}_{E_i}\left({e}_1\right)\cap {\mu}_{E_j}\left({e}_2\right)\right).{C}_{m\left(i,j\right)}\right]}{\sum_{i,j}\left({\mu}_{E_i}\left({e}_1\right)\cap {\mu}_{E_j}\left({e}_2\right)\right)} $$
(6)

Therefore, the performance of the system is improved by tuning the control signal according to the changes in the center of MFs.

3.4 Improved Disturbance Observer (IDOB)

Disturbance and model uncertainty are two of the most important challenges that have a great influence on the control performance of the closed-loop system. The DOB technique is one of the most effective approaches applied to overcoming disturbances. In this approach, without any changes in the input–output behavior, the disturbance can be estimated and its effects on the system performance can be eliminated [1, 3,4,5]. Due to this method not relying on an explicit model of disturbance, the strong external disturbances of the model can be rejected.

In time-delay systems, in order to maintain the system performance, using the DOB method is suggested [3,4,5]. In the BMG system, time delay exists in the model of the system. However, due to the presence of the inverse of the nominal model with time delay (G−1(s)), this part cannot physically be realized and the conventional DOB cannot be used [1]. This problem can be solved by designing the IDOB. The main differences between the IDOB and the conventional DOBs are as follows:

  • In previous studies, the system is considered as single-input–single-output (SISO), while in this study, the MIMO structure is assumed for the system.

  • In previous investigations, the internal disturbance is not considered. But in this research, all of the internal disturbances are also estimated.

  • In previous structures, the disturbance is directly coupled to the input, while in this approach, external disturbances influence the output through disturbance channels.

Consider a two-input–two-output process given by Eq. (7):

$$ \left[\begin{array}{c}{Y}_1(s)\\ {}{Y}_2(s)\end{array}\right]=\left[\begin{array}{cc}{P}_{11}(s)& {P}_{12}(s)\\ {}{P}_{21}(s)& {P}_{22}(s)\end{array}\right]\left[\begin{array}{c}{U}_1(s)\\ {}{U}_2(s)\end{array}\right]+\left[\begin{array}{c}{D}_{ex1}(s)\\ {}{D}_{ex2}(s)\end{array}\right] $$
(7)

where:

$$ {P}_{ij}(s)={p}_{ij}(s){e}^{-{\tau}_{ij}s}\left(i=1,2;j=1,2\right) $$
$$ {D}_{ex i}(s)={H}_i(s){D}_{ex}(s)\left(i=1,2\right) $$

In the above structure, Ui(s) are input variables that can be changed for control purposes; Yi(s) are controlled outputs that should follow the desired input values; Dex(s) is the external disturbance; Dexi(s) is the effect of external disturbances on the output of Yi(s); Pij(s) is defined as the process channel models; pij(s) represents the minimum phase of each process channel; and Hi(s) is the disturbance model. Assume that the control variable U1 is paired with the output Y1(s). This means control output 1 by input 1 and use input 2 to control output 2; the IDOB structure is designed for loop 1 between input and output 1, as shown in Fig. 4. A similar condition is established for loop 2 between input and output 2. Due to the non-minimum phase models being difficult to control, the structure of the IDOB has been divided into minimum phase and non-minimum phase parts [1].

Fig. 4
figure 4

Block diagram of the improved disturbance observer (IDOB) [1]

Full size image

Time delay is considered in non-minimum phase form:

$$ {P}_{11}(s)={p}_{11}(s){e}^{-{\tau}_{11}s} $$
(8)
$$ {G}_{11}(s)={g}_{11}(s){e}^{-{\tau}_{11a}s} $$
(9)

where:

$$ {D}_{m1}(s)=\left[{p}_{11}(s){e}^{-{\tau}_{11}s}-{g}_{11}(s){e}^{-{\tau}_{11n}s}\right]{U}_1(s) $$
(10)
$$ {D}_{c1}(s)={p}_{12}(s){e}^{-{\tau}_{12}s}{U}_2(s) $$
(11)

From Fig. 4c, Eq. (12) can be derived:

$$ {Y}_1(s)={g}_{11}(s){e}^{-{\tau}_{11n}s}{U}_1(s)+{D}_{m1}(s)+{D}_{ex1}(s)+{D}_{c1}(s) $$
(12)

Inserting Eq. (10) into Eq. (12), Eq. (13) is obtained:

$$ {Y}_1(s)={g}_{11}(s){e}^{-{\tau}_{11n}s}{U}_1(s)+{D}_1(s) $$
(13)

If the measurement noise is assumed to be equal to zero, the following will be derived from Fig. 4c:

$$ {\hat{D}}_{f1}(s)=Q(s){g}_{11}^{-1}(s){Y}_1(s)-Q(s){e}^{-{\tau}_{11n}s}{U}_1(s) $$
(14)

By substituting Eq. (13) into Eq. (14), this equation can be rewritten as:

$$ {\hat{D}}_{f1}(s)=Q(s){g}_{11}^{-1}(s){D}_1(s) $$
(15)

\( \overset{\sim }{D}(s) \) is defined as a disturbance estimation error (error between the real and estimated values):

$$ {\overset{\sim }{D}}_1(s)={D}_1(s)-{g}_{11}(s){e}^{-{\tau}_{11n}s}{\hat{D}}_{f1}(s) $$
(16)

By entering Eq. (15) in Eq. (16), Eq. (17) is obtained:

$$ {\overset{\sim }{D}}_1(s)=\left[1-Q(s){e}^{-{\tau}_{11n}s}\right]{D}_1(s) $$
(17)

Using the final-value theorem, the following equation is deduced:

$$ {\displaystyle \begin{array}{c}{\overset{\sim }{d}}_1\left(\infty \right)=\underset{t\to \infty }{\lim }{\overset{\sim }{d}}_1(t)=\underset{s\to 0\ }{\lim }{\overset{\sim }{D}}_1(s)s=\underset{s\to 0\ }{\lim}\left[1-Q(s){e}^{-{\tau}_{11n}s}\right]\underset{s\to 0\ }{\lim }{D}_1(s)s\\ {}=\underset{s\to 0\ }{\lim}\left[1-Q(s){e}^{-{\tau}_{11n}s}\right]\underset{t\to \infty }{\lim }{d}_1(t)=\underset{s\to 0\ }{\lim}\left[1-Q(s){e}^{-{\tau}_{11n}s}\right]{d}_1\left(\infty \right)\end{array}} $$
(18)

It is well known from Eq. (18) that, if the Q(s) filter is selected in such a way that the steady-state gain is equal to one, the steady-state estimation error will be zero and the disturbance can be completely rejected. Therefore, the IDOB performed well for systems with time delay. Note that, in this section, the IDOB design is explained for loop 1, though the IDOB can be designed for the u2 − y2 loop in a similar fashion [1].

3.5 Proposed Controller

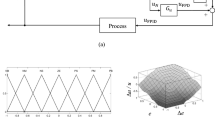
As previously mentioned, an FLST-PID controller is designed in this study. In the proposed controller, the error and its integral are considered as the inputs and Kp, Ki, and Kd are considered as the outputs. Fuzzy inference is made through fuzzy rules. The fuzzy rules are the most important part of a controller and proper design of the fuzzy rules will lead to desirable performance. Therefore, the tuning accuracy of the rules is very important. For inputs, five levels are considered, including: the negative large (NL), the negative small (NS), the zero (ZE), the positive small (PS), and the positive large (PL), and for outputs, seven levels are considered: the positive very small (PVS), the positive small (PS), the positive mean small (PMS), the positive mean (PM), the positive mean large (PML), the positive large (PL), and the positive very large (PVL). Figures 5, 6, 7, 8, and 9 are the inputs and outputs of the fuzzy system.

Fig. 5
figure 5

The input membership function (MF) of the error variable

Full size image
Fig. 6
figure 6

The input membership function (MF) of the integral of error variable

Full size image
Fig. 7
figure 7

The variable output membership function (MF) Kp

Full size image
Fig. 8
figure 8

The variable output membership function (MF) Ki

Full size image
Fig. 9
figure 9

The variable output membership function (MF) Kd

Full size image

In the design of the fuzzy controller, membership functions are taken as triangular. The fuzzy rules for output based on the error and its variations are shown in Tables 1, 2, and 3.

Table 1 Fuzzy rules for Kp
Full size table
Table 2 Fuzzy rules for Ki
Full size table
Table 3 Fuzzy rules for Kd
Full size table

By tuning the PID controller’s coefficients according to these rules and employing Eqs. (2)–(6), the FLST-PID controller is composed. Due to the ability of fuzzy controllers to cover a wide variety of operational conditions and work well in noise and disturbance conditions, PID controllers using fuzzy logic are used for this purpose. In other words, despite the classical PID strategy, which is offline and its parameters are fixed during the system changes, the FLST-PID controller is online and its parameters tuned. Therefore, the FLST-PID controller is incorporated into the IDOB to solve all of the challenges of the BMG system in this research. Also, the input u1 with the output of y1 and the input u2 with the output y2 are paired. By this selection, the FLST-PID controller along with the IDOB schemes can be seen in Fig. 10. As shown in this figure, the controller uses two FLST-PID controllers and two IDOBs.

Fig. 10
figure 10

Block diagram of the proposed controller as the combination of the fuzzy logic self-tuning PID (FLST-PID) controller and improved disturbance observer (IDOB) applied to the multi-input–multi-output (MIMO) model of the ball mill grinding (BMG) circuit

Full size image

4 Simulation Results and Comparisons

In this section, the FLST-PID controller based on an IDOB is designed and simulations of the proposed controller on the BMG circuit are presented. Simulations are performed for three cases consisting of set-point tracking on both outputs and external disturbance rejection. In case 1, the set-point change is considered on particle size, while the variation of set-point on circulating load is investigated in case 2. Moreover, the internal disturbance in the form of model mismatch is inserted in both cases. In case 3, the effect of external disturbance on the system outputs are evaluated. The model of the BMG system is considered as a two-input–two-output transfer function as follows:

$$ \left[\begin{array}{c}{Y}_1(s)\\ {}{Y}_2(s)\end{array}\right]=\left[\begin{array}{cc}{G}_{11}(s)& {G}_{12}(s)\\ {}{G}_{21}(s)& {G}_{22}(s)\end{array}\right]\left[\begin{array}{c}{U}_1(s)\\ {}{U}_2(s)\end{array}\right] $$
(19)

where the particle size and circulating load are the system outputs and the fresh ore feed rate as well as the dilution water flow rate are considered as the inputs, respectively [1]. The transfer functions can be defined as:

$$ {\displaystyle \begin{array}{l}{G}_{11}(s)={g}_{11}(s){e}^{-{\tau}_{11a}s}=\frac{-0.58}{2.5s+1}{e}^{-0.68s}\\ {}{G}_{12}(s)={g}_{12}(s){e}^{-{\tau}_{12a}s}=\frac{4\left(1-0.9938{e}^{-0.47s}\right)}{\left(2s+1\right)\left(6s+1\right)}{e}^{-0.2s}\\ {}\begin{array}{l}{G}_{21}(s)={g}_{21}(s){e}^{-{\tau}_{21a}s}=\frac{2.2}{6s+1}{e}^{-0.6s}\\ {}{G}_{22}(s)={g}_{22}(s){e}^{-{\tau}_{22a}s}=\frac{2.83}{3.5s+1}{e}^{-0.13s}\end{array}\end{array}} $$

The first thing that should be performed in controller design for a multi-input–multi-output system is to select the proper input–output pairs. For the system expressed in Eq. (19), according to the RGA analysis, suitable control loops are u1 − y1 and u2 − y2. Moreover, the Q filter was considered as a low-pass filter as Eq. (20) to ensure that the response of the system has good speed and minimized overshoot:

$$ Q(s)=\frac{1}{\lambda s+1} $$
(20)

For the grinding system, there are some constraints on the inputs and outputs. Table 4 shows the system constraints.

Table 4 Physical constraints in the grinding system [1]
Full size table

4.1 Trajectory Tracking in the Presence of Model Mismatches

For the first simulation, it is assumed that the model of the BMG system operates as follows [1]:

$$ \left[\begin{array}{c}{Y}_1(s)\\ {}{Y}_2(s)\end{array}\right]=\left[\begin{array}{cc}{P}_{11}(s)& {P}_{22}(s)\\ {}{P}_{21}(s)& {P}_{22}(s)\end{array}\right]\left[\begin{array}{c}{U}_1(s)\\ {}{U}_2(s)\end{array}\right] $$
(21)

where:

$$ {\displaystyle \begin{array}{l}{P}_{11}(s)=\frac{-0.4}{3.5s+1}{e}^{-0.5s}\\ {}{P}_{12}(s)=\frac{3.42\left(1-0.994{e}^{-0.47s}\right)}{\left(2s+1\right)\left(s+1\right)}{e}^{-0.13s}\\ {}\begin{array}{l}{P}_{21}(s)=\frac{0.8}{3.2s+1}{e}^{-0.3s}\\ {}{P}_{22}(s)=\frac{2.5}{5.5s+1}{e}^{-0.3s}\end{array}\end{array}} $$

It should be noted that, due to the lack of an accurate model in practical systems, the existence of model mismatch is inevitable in most cases. From the comparison of the system model in Eq. (19) and the real dynamics of the system in Eq. (21), it can be concluded that the system model is not accurate and there is a mismatch between the model and the real system, which can be considered as an internal disturbance.

In this section, the grinding circuit is simulated in a closed-loop form by using the FLST-PID controller based on the IDOB algorithm. Moreover, to evaluate the performance of the proposed controller, a PI controller based on the IDOB algorithm [1] is designed for the system and the results are compared for three cases. Note that the controller is designed for the system model and applied to the actual system dynamics.

4.2 Case 1: Change in Particle Size Set-Point

In the first case, it is assumed that the reference input of particle size changes from 70% to 71% at t = 1200 s.

The response of the system outputs as particle size and circulating load to the performed change is demonstrated in Fig. 11. In this figure, the system response to both controllers is shown. Additionally, the variation in the system inputs as fresh ore feed rate and the dilution water flow rate to these changes is illustrated in Fig. 12. It should be noted that the controllers are designed for the mismatched model.

Fig. 11
figure 11

Outputs response of the ball mill grinding (BMG) system to the set-point change in particle size: a particle size, b circulating load

Full size image
Fig. 12
figure 12

Control signal of the ball mill grinding (BMG) system to the set-point change in particle size: a fresh ore feed rate, b dilution water flow rate

Full size image

In Fig. 11, the reference inputs for the final product size and circulating load are initially set to 70% and 150, respectively, and the outputs reached their set-points without any steady-state error. Variation in the set-point of particle size leads to changes in the system inputs and outputs. As can be comprehended from Fig. 11a, the particle size tracks the reference trajectory without any overshoot or steady-state error for both the PI-IDOB and FLST-PID-IDOB controllers, albeit the proposed controller is faster. The rise and settling times for the system with the FLST-PID-IDOB controller are 284 and 508 s, respectively, which are lower than that with the PI-IDOB controller (573 and 1023 s, respectively). Figure 11b demonstrates that the change in particle size set-point affects only the transient response of the circulation load and has no influence on the steady-state response. This means that decoupling between the inputs and outputs of the grinding circuit multivariable model is performed completely. Similar to the first output, the rise and settling times of the proposed controller for the circulating load are much shorter than for the PI-IDOB controller.

Table 5 compares the performance of the controllers in case 1. Furthermore, Fig. 12 demonstrates that the control signals of fresh ore feed rate and dilution water flow rate for both controllers satisfy the physical constraints on the BMG system.

Table 5 A comparison between the performances of the controllers in case 1
Full size table

4.3 Case 2: Change in Circulating Load Set-Point

In this case, the reference input for the circulating load is set as a step signal with a size of 150 t/h that changed to 155 t/h at t = 1200 s. Similar to case 1, the corresponding changes in system outputs and inputs for both controllers in the presence of model mismatches are illustrated in Figs. 13 and 14, respectively.

Fig. 13
figure 13

Outputs response of the ball mill grinding (BMG) system to the set-point change in circulating load: a particle size, b circulating load

Full size image
Fig. 14
figure 14

The control signal of the ball mill grinding (BMG) system to the set-point change in circulating load: a fresh ore feed rate, b dilution water flow rate

Full size image

Similar to case 1, the final product size and circulating load are initially set at 70% and 150, respectively. At t = 1200 s, the reference of the circulating load is changed to 155. Figure 13a illustrates that the variation on the circulation load set-point has not affected the final value of product size due to the good decoupling between system inputs and outputs. In addition, Fig. 13b demonstrates that the changes in the signal reference are completely tracked by both controllers, albeit the proposed controller has a faster response. The rise and settling times for the system with the FLST-PID-IDOB controller are 138 and 245 s, respectively, which are lower than that with the PI-IDOB controller (379 and 674 s, respectively). It should be noted that the responses given in Fig. 13 are related to real dynamic responses of the system, which are different from the assumed model. This means that the proposed approach can overcome the internal disturbance in the form of model mismatches.

Figure 14 indicates that the control signals for both controllers satisfy the limitation on the system inputs and outputs. A comparison between the performances of the controllers in case 2 is presented in Table 6.

Table 6 A comparison between the performances of the controllers in case 2
Full size table

4.4 Disturbance Rejection

One of the most common problems that occurs in controlling the grinding circuit is the presence of large external disturbance, such as changes in the degree of ore hardness and the amount of ore injected into the system. External disturbances during designing the controllers and tuning their parameters cause many problems and may even lead to process instability. Also, the degree of ore hardness has a huge influence on the final particle size and the amount of circulating load. The dynamics of the disturbance can be modeled as a first-order system with a delay time, which is a common model used to describe industrial systems. For simulation, the transfer function of the process with external disturbance is considered as follows:

$$ \left[\begin{array}{c}{Y}_1(s)\\ {}{Y}_2(S)\end{array}\right]=\left[\begin{array}{cc}{G}_{11}(S)& {G}_{12}(s)\\ {}{G}_{21}(S)& {G}_{22}(S)\end{array}\right]\left[\begin{array}{c}{U}_1(s)\\ {}{U}_2(s)\end{array}\right]+\left[\begin{array}{c}{H}_1(s)\\ {}{H}_2(S)\end{array}\right]{D}_{ex} $$
(22)
$$ {D}_{ex1}(s)={H}_1(s){D}_{ex}(s)=-\frac{0.32{e}^{-0.52s}}{4.8s+1}{D}_{ex}(s) $$
$$ {D}_{ex2}(s)={H}_2(s){D}_{ex}(s)=\frac{1.6{e}^{-0.46s}}{5.3s+1}{D}_{ex}(s) $$

In the above equations, Dex(s) represents the external disturbance. To evaluate the ability of the proposed controller compared to the PI-IDOB controller in disturbance rejection, the BMG system is simulated in the presence of the external disturbance. A disturbance is considered as a 10% increase in time t = 1200 s in the hardness of the injected ore. The closed-loop response of the system outputs and the control signal as the system inputs are demonstrated in Figs. 15 and 16, respectively.

Fig. 15
figure 15

Outputs response of the ball mill grinding (BMG) system to the set-point change in circulating load: a particle size, b circulating load

Full size image
Fig. 16
figure 16

The control signal of the ball mill grinding (BMG) system to the set-point change in circulating load: a fresh ore feed rate, b dilution water flow rate

Full size image

The closed-loop responses of particle size and circulating load in the presence of external disturbance show that both controllers performed well and rejected the effect of changes in the ore hardness. However, the disturbance rejection in the system with the FLST-PID-IDOB controller is performed in a shorter time, especially the settling time. The settling time of this controller for particle size and circulating load are 288 and 772 s, respectively, which are shorter than for the PI-IDOB controller (737.5 and 1114 s, respectively). Additionally, the fresh ore feed rate and dilution water flow rate are completely in the allowed range presented in Table 7, illustrating that the approach selected in this study is applicable to the BMG system.

Table 7 A comparison between the performances of the controllers in the presence of external disturbance
Full size table

5 Conclusion

Since ball mill grinding (BMG) systems have several challenges, such as multi-input–multi-output (MIMO) structure, high interaction, the variation of system parameters in the form of model mismatches, and the existence of time delays and large external disturbances, their control is very difficult. In this paper, the problem of simultaneous controlling of particle size and circulating load by regulating the fresh ore feed rate and the dilution water flow rate has been addressed. The proposed approach of this paper employed a self-tuning PID controller based on fuzzy logic which has the ability to handle the system delays and uncertainties due to its robust and adaptive specifications. Besides, to enhance the controller’s performance in eliminating large disturbances, an improved disturbance observer (DOB) is designed to minimize the influence of disturbance on the output of the system by using a leading compensator. On the other hand, a fuzzy logic self-tuning PID (FLST-PID) controller based on an improved disturbance observer (IDOB) structure is proposed for the ore grinding system with the ability to handle the system problems. Simulation results on the system in the presence of internal and external disturbances demonstrate the better performance of the FLST-PID controller based on IDOB compared to that of the PI-IDOB controller, especially in the transient response.