Keywords

1 Introduction

PID controllers are still widely accepted in process industries for their simple design and easy tuning methodologies [1]. Due to lack of availability of exact process model usually model-free tuning techniques are relatively preferred compared to model-based tuning schemes. Ziegler-Nichols (ZN) setting [2] is one of the most widely accepted model-free tuning guidelines since from its inception. However, during closed-loop control for higher-order processes, ZN tuned PID controller (ZN-PID) is found to provide undesired oscillations during set point change and load varying phases [1]. To reduce process oscillations during set point tracking, set point weighting, and set point filtering [3,4,5] methods are widely used at the cost of increased rise time. But the reported filtering and fixed set point weighting (FSPW) mechanisms fail to offer any improvement during load rejection phases. In FSPW-based PID controller (FSPW-PID), a fixed weighting factor (β = 0.5–0.7) is multiplied to the set value. Variable set point weighting (VSPW) technique is suggested in [6] to restrict process oscillations during set point response without compromising in rise time value.

In VSPW, instead of a fixed weighting factor, three different values are provided as the set point weight depending on the process operating conditions during set point tracking phase. Notably, VSPW still fails to offer any improvement during load variation. The responses of ZN-PID, FSPW-PID (β = 0.6), and VSPW-PID are depicted in Fig. 1 where hardly any improvement is observed for VSPW-PID in comparison with FSPW-PID and ZN-PID during load rejection phase. To achieve an optimal response during set point change and load variation, separate set point weighting factors for proportional and derivative terms are derived in [7] using heuristic algorithms. Toward achieving improved responses during set point change as well as load variation simultaneously, an online dynamic set point weighting (DSPW) technique is reported in [8, 9]. In DSPW, the dynamic set point weighting factor β d is heuristically derived from the instantaneous process states such as error e(k) and change of error Δe(k).

Fig. 1
figure 1

Responses of ZN-PID, FSPW-PID, and VSPW-PID for second-order process

Full size image

To further enhance the overall performance of a PID controller during transient as well as steady-state operating phases; here, we propose a fuzzy rule-based set point weighting mechanism (FRSPW) for conventional PID controller and the resulting controller is named as FRSPW-PID. In the proposed FRSPW, instantaneous value of the weighting factor is obtained from a fuzzy rule base consisting of twenty-five rules only. Here, the rule base is designed based on sliding mode principle. Input variables of the fuzzy rules are considered to be error e(k) and change of error Δe(k), whereas the output is defined as the set point weighting factor β. Hence, the value of set point weighting factor varies depending on the process operating conditions in such a manner that an overall improved process response can be obtained from a conventional PID controller. To substantiate the efficacy of the proposed scheme, performance of FRSPW-PID controller is evaluated on under-damped second-order processes in comparison with variable set point weighting-based PID (VSPW-PID) and dynamic set point weighting-based PID (DSPW-PID) controllers. Designing steps of the proposed FRSPW-PID are discussed in Sect. 2, and its performance evaluation is made in Sect. 3. Considerable overall improvement is obtained during simulation study for the proposed scheme as estimated through a number of performance indices. At the end conclusion is provided in Sect. 4.

2 Controller Design

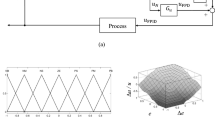
Block schematic of the proposed controller under closed-loop operation is shown in Fig. 2a. Here, the instantaneous value of the set point weighting factor is calculated from a pre-defined fuzzy rule base consisting twenty-five rules as shown in Table 1. This rule base is designed based on sliding mode principle; hence, no prior knowledge about the process is necessary for its designing. Input variables of the fuzzy rules are process error e(k) and change of error Δe(k) which are defined over the common normalized domain −1 to +1 with five triangular membership functions (MFs) as shown in Fig. 2b. The output variable β (weighting factor, normalized) is also denoted by five MFs defined over −1 to +1 as shown in Fig. 2b. All the triangular MFs are identical in shape having 50% overlap with their neighboring MFs. Input scaling factors are denoted as G e  = 1 and GΔe = 20 and the output scaling factor is considered to be G β  = 1 for de-normalization of the weighting factor β N as given by Eqs. (1)–(3). The blocks F and DF of Fig. 2a represent fuzzification and defuzzification modules, respectively. Nature of the weighting surface as depicted in Fig. 2c is found to be quite nonlinear in nature.

Fig. 2
figure 2

a Block diagram of the proposed FRSPW-PID controller. b MFs for input and output variables. c Surface of weighting factor

Full size image
Table 1 Fuzzy rule base for β
Full size table
$$ e_{N} = G_{e} \,e $$
(1)
$$ \Delta e_{N} = G_{\Delta e} \Delta e $$
(2)
$$ \beta = G_{\beta } \,\beta_{N} $$
(3)

Discrete form of fixed set point weighted PID controller at kth sampling instant is given by

$$ u\left( k \right) = k_{p} \left[ {\left\{ {\beta \times \,y_{r} - y\left( k \right)} \right\} + \frac{\Delta t}{{T_{i} }}\sum\limits_{i = 0}^{k} {e\left( i \right)} + T_d\,\,\left\{ {\frac{{e\left( k \right) - e\left( {k - 1} \right)}}{\Delta t}} \right\}} \right] $$
(4)

Here, β represents the fixed weighting factor, y(k) is the process output at kth instant, k p denotes the proportional gain, T i is the integral time, T d is the derivative time, and Δt is the sampling interval.

In the reported dynamic set point mechanism [9], the weighting factor β d is dynamic in nature and it is defined by the Eq. 5.

$$ \beta_{d} \left( k \right) = \left[ {1 + \gamma \times \theta \times \Delta e_{N} \left( k \right)} \right] $$
(5)

In Eq. (5), γ is an adjustable tuning parameter and θ is the normalized dead time of the process, and Δe N (k) is the normalized change of error at kth instant. But in our proposed FRSPW-PID scheme, the weighting factor β is continuously updated at every sample instant by the following relation

$$ \beta \left( k \right) = 0.5 \times (1 + \beta_{N} ) $$
(6)

where the instantaneous value of β N is directly obtained from a fuzzy rule base as defined in Table 1. Here, it is to mention that in contrary to the dynamic set point weighting, process knowledge is not required for our proposed FRSPW-PID in calculating the value of the weighting factor. Moreover, the rule base for obtaining the weighting factor is designed based on sliding mode principle depending on the process error e(k) and change of error Δe(k) which can be calculated by the following relations

$$ e\left( k \right) = y_{r} \left( k \right) - y\left( k \right) $$
(7)
$$ \Delta e\left( k \right) = e\left( k \right) - e\left( {k - 1} \right) . $$
(8)

The resultant weighting factor β is multiplied with the set point toward obtaining the weighted set point for proportional action only. This rule base (Table 1) is so designed which provides suitable weighting factor during both the transient and steady-state operating conditions in such a manner that process oscillations can be restricted within the acceptable limit. Here, it is to note that for designing the fuzzy rule base it doesn’t require any prior knowledge about the concerned process. Moreover, in case of our proposed FRSPW-PID, no additional parameter (γ, θ) is required for computation of the dynamic weighting factor. The overall control strategy for the proposed FRSPW-PID is described as follows-

  • When the output is diverging in nature or in other words the process response is moving away from the set point, both e(k) and Δe(k) are of similar sign, i.e., either negative or positive. During such circumstances, strong proportional action is required to bring the response back to the desired value and to restrict the further divergence of the response. Hence, the weighting factor value is so adjusted that the magnitude of effective error gets increased under such operating conditions.

  • In contrary, when the response converges toward the set point (where the sign of e(k) and Δe(k) is opposite), there is a possibility of larger undershoot or overshoot in subsequent phases. Under such circumstances, the value of the weighting factor is so adjusted that the proportional control action gets reduced to restrict the probable undesired oscillation.

3 Results

Performance of the proposed FRSPW-PID is compared with variable set point weighting-based PID (VSPW-PID) and dynamic set point weighted PID (DSPW-PID) controllers through simulation study for second-order linear and second-order marginally stable processes with dead time. To have a clear comparison among the reported controllers, a number of performance indices—%OS (percentage overshoot), T p (peak time), T r (rise time), T s (settling time), IAE (integral absolute error), and ITAE (integral time absolute error) are evaluated for each case separately. Mamdani-type inferencing is used with centroid method for defuzzification. The general expression of a second-order process with dead time can be given by

$$ G{}_{p}\left( s \right) = \frac{{k\,e^{ - Ls} }}{{as^{2} + bs + c}} $$
(9)

where k is the open-loop process gain and L is the dead time.

3.1 Second-Order Linear Process

A second-order linear process can be realized by considering a = 1, b = 1 and c = 0.2. Transfer function for the second-order linear process with open-loop gain k = 1 and dead time L = 0.4 s is given by

$$ G{}_{p}\left( s \right) = \frac{{\,e^{ - 0.4s} }}{{s^{2} + s + 0.2}} . $$
(10)

Unit step input is applied as set point change and once the process reaches the steady state, a load disturbance is applied. The overall performance indices for all the reported controllers are listed in Table 2a. To verify the robustness of the proposed FRSPW-PID along with VSPW-PID and DSPW-PID, process model parameters are perturbed by a considerable amount (20%). The perturbed model is given by Eq. (11), and corresponding performance indices are depicted in Table 2b. Responses for both the nominal and perturbed models are shown in Fig. 3a, b, respectively.

Table 2 a Performance analysis for nominal model given by Eq. (10). b Performance analysis for perturbed model given by Eq. (11)
Full size table
Fig. 3
figure 3

a Responses of nominal model given by Eq. (10). b Responses for perturbed model given by Eq. (11)

Full size image
$$ G{}_{p}\left( s \right) = \frac{{\,1.2e^{ - 0.4s} }}{{1.2s^{2} + 0.8s + 0.24}} $$
(11)

3.2 Second-Order Marginally Stable Process

A second-order marginally stable process can be realized from Eq. (12) by considering a = 1, b = 1 and c = 0. The open-loop gain is considered to be k = 1 and dead time L = 0.3 s.

$$ G{}_{p}\left( s \right) = \frac{{\,e^{ - 0.3s} }}{{s^{2} + s}} $$
(12)

This particular model as given by Eq. (12) is very important for industrial automation processes as it represents the servo position control system. Due to location of one pole at origin, it provides highly oscillatory responses. Performance of our proposed FRSPW-PID controller is evaluated along with the VSPW-PID and DSPW-PID controllers under both set point change and load variation. Robustness feature of the reported controllers are also verified with considerable perturbation in process parameters as given by Eq. (13). Responses as shown in Fig. 4a, b along with performance indices as listed in Table 3a, b for the nominal and perturbed models clearly substantiate the superiority of the proposed FRSPW-PID in comparison with VSPW-PID and DSPW-PID.

Fig. 4
figure 4

a Responses of nominal model given by Eq. (12). b Responses of perturbed model given by Eq. (13)

Full size image
Table 3 a Performance analysis for nominal model given by Eq. (12). b Performance analysis for perturbed model given by Eq. (13)
Full size table
$$ G{}_{p}\left( s \right) = \frac{{\,1.2e^{ - 0.3s} }}{{1.2s^{2} + 0.8s}} $$
(13)

Based on the simulation study, we can find that our proposed fuzzy rule-based set point weighting mechanism is quite effective in providing the desired set point response with smaller overshoot and faster settling. In addition, during load variation, it is capable to provide early recovery to regain the desired steady-state behavior. The most important feature of this proposed weighting scheme is that it does not require any prior knowledge about the process to be controlled. Hence, this technique can be used for any type of closed-loop control applications toward performance enhancement of conventional PID controllers. Number of rules in the fuzzy rule base may be increased for achieving more smooth and preferred variation of the weighting factor so that closed-loop responses can be further enhanced and all such possibilities are there in the future scope.

4 Conclusion

Fuzzy rule-based set point weighting scheme for PID controller is proposed here. The instantaneous value of the set point weighting factor is provided from a fuzzy rule base depending on the latest process operating conditions in terms of process error and change of error. Enhancement in process response is obtained during both the set point tracking and load rejection phases. The rule base is designed here is based on sliding mode technique without any prior knowledge about the concerned process. Hence, this scheme is quite effective for achieving improved responses for any conventional PID controller employed in closed-loop control applications.