1 Introduction

Nanostructures are increasingly used in the micro/nano-scale and systems such as the biosensor, atomic force microscope, micro-electro-mechanical, and nano-electromechanical systems due to their superior electronic and mechanical properties. In such applications, the effects are experimentally observed in a small scale, these effects are important and must be considered when studying their behavior.

Thin-shell theories are applied successfully basing on continuum mechanics for single-walled and double-walled carbon nanotubes (SWCNTs, DWCNTs) to predict several mechanical properties. For SWCNTs and DWCNTs models, the elastic Donnell shell has been chosen in these references [14, 35,36,37,38,39, 44, 48, 53]. These conventional models of shell based on classical continuous medium theories are not able to describe the effects due to the lack of small scale parameters of the material. In classical theory of local elasticity, the stresses tensor at a structure point is a function of the strain tensor of this point. However, Eringen [10, 12] pointed out that when we examine a small scale structure, the medium can no longer be considered as continuous and the internal characteristic lengths, such as the carbon-carbon bond in the carbon nanotube, must be considered. This motivation is a powerful incentive for Eringen to develop a nonlocal elasticity theory. This theory initiated by Eringen [10], is one of the promising theories that takes into account the size of small scales. The nonlocal elasticity theory implies that the stresses tensor at a point is estimated as a function of the strain tensor in the considered point and strain tensors at all other structure points. In this way, the small scale effects are understood through the use of the governing behavior laws which are based on the nonlocal elasticity theory. The nonlocal effect in the analysis is determinate by a constant appropriate to each material as defined by Eringen [10,11,12], this constant is called the nonlocal parameter as well as denoted by \(e_0\). There are several works in the literature based on the nonlocal continuum theory of Eringen. Kiani [18] studied the axial buckling of a set of SWCNTs aligned vertically in two orthogonal directions. The same researcher Kiani [20] calculated the axial buckling load of the nanosystem using Euler-Bernoulli beam theory, then by implementing Galerkin approach and assumed mode methodology. Hussain et al. [16] indicated that the nonlocal theory play an important role in predicting SWCNT frequencies. The nonlocal Eringen theory is still used by the researchers in recent years [6, 16, 20, 42, 43]. Another group of non-classical theories, which have attracted the researcher’s attention, is the strain gradient and couple stress theories [24,25,26,27, 30,31,32,33].

The static, buckling and vibration behaviors of nanosystems are of great interest and special attention by the applied mechanics community as shown these recent works [9, 21,22,23, 45]. In this context, on the basis of the nonlocal elasticity theory, we propose use the nonlocal Donnell shell theory to study the buckling of DWCNTs subjected to an axial pressure taking into account the effects of internal small length scale and the interactions of Van der Waals between layers. Through this work, a novel approach for the nonlocal critical buckling load of DWCNT is developed.

2 Donnell shell model based on the nonlocal elasticity theory.

In the Donnell shell model [8], the induced stresses are given in the median surface of the shell and the terms of the order \(\frac{1}{n^2}\) are neglected, where n is the circumferential half wavenumber. So in this paper, the assumption \(\frac{1}{n^2}\ll 1\) has been used where the value of n must be greater than 4. On the other hand the thin shell assumption \(\left( \frac{h}{R}\right) ^2\ll 1\) has been used in the derivation, then transverse-shear and rotary-inertia effects have been neglected. In addition, the shear deformation effect is more significant in the low aspect ratio length/radius (\(=\frac{L}{R}\)) of nanotubes. So the other assumption \(\frac{L}{R}\ge 10\) has been used in this paper.

2.1 Equilibrium equations

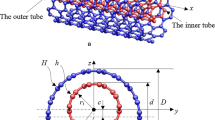
Consider a thin-walled circular cylindrical shell of length L, wall thickness h and a middle surface of radius R with \(h\ll R\) (see Fig. 1). The shell is made of an elastic homogeneous isotopic material of Young modulus E and Poisson ratio \(\nu\).

Fig. 1
figure 1

Thin-walled circular cylindrical shell

Full size image

The middle surface of the shell is referred to cylindrical coordinates x, \(\theta\) and z. The distance from the middle surface is measured by the coordinate z. We note by \(u_x\), \(u_{\theta }\) and \(u_z\) the displacement components in the axial (x), circumferential \((\theta )\) and radial (z) directions respectively. We assume that the shell is subjected to an external pressure \(p= p (x, \theta )\). Using theory of the first shear deformation, the displacements are given by:

$$\begin{aligned} \begin{array}{lll} u_x(x,\theta ,z)=u(x,\theta )-z\frac{\partial w}{\partial x}\\ u_{\theta }(x,\theta ,z)=v(x,\theta )-\frac{z}{R}\frac{\partial w}{\partial \theta }\\ u_{z}(x,\theta ,z)=w(x,\theta ,z) \end{array} \end{aligned}$$
(1)

where u, v and w are the reference surface displacements.

The kinematic relations for normal strain \(\varepsilon _{xx}\) and \(\varepsilon _{\theta \theta }\) and shear strain \(\gamma _{x\theta }\) are expressed by:

$$\begin{aligned} \begin{array}{lll} \varepsilon _{xx}=\frac{\partial u}{\partial x}+\frac{1}{2} \left( \frac{\partial w}{\partial x}\right) ^2\\ \varepsilon _{\theta \theta }=\frac{1}{R}\frac{\partial v}{\partial \theta }+ \frac{w}{R} +\frac{1}{2R^2} \left( \frac{\partial w}{\partial \theta }\right) ^2\\ \gamma _{x\theta }=\frac{\partial v}{\partial x}+ \frac{1}{R}\frac{\partial u}{\partial \theta } +\frac{1}{R} \frac{\partial w}{\partial x}\frac{\partial w}{\partial \theta } \end{array} \end{aligned}$$
(2)

The Donnell nonlinear equilibrium equations of the thin-walled circular cylindrical shell are given by [17]:

$$\begin{aligned} \begin{array}{lll} \frac{\partial N_x}{\partial x}+\frac{1}{R} \left( \frac{\partial N_{x\theta }}{\partial \theta }\right) =0\\ \frac{\partial N_{x\theta }}{\partial x}+\frac{1}{R} \left( \frac{\partial N_{\theta }}{\partial \theta }\right) =0\\ \frac{\partial ^2 M_x}{\partial x^2}+ \frac{2}{R}\frac{\partial ^2 M_{x \theta }}{\partial x \partial \theta } +\frac{1}{R^2} \frac{\partial ^2 M_{\theta }}{\partial \theta ^2}\\ \quad +\frac{N_{\theta }}{R}+N_x \frac{\partial ^2 w}{\partial x^2}+ \frac{2N_{x \theta }}{R}\frac{\partial ^2 w}{\partial x \partial \theta }+\frac{N_{\theta }}{R^2}\frac{\partial ^2 w}{\partial \theta ^2}+p=0 \end{array} \end{aligned}$$
(3)

where \(N_x\) and \(N_{\theta }\) are the normal forces, \(N_{x \theta }\) is the internal shear force, \(M_x\) and \(M_{\theta }\) are the bending moments and \(M_{x \theta }\) is the twisting moment, which are related to internal stress \(\sigma _x\) , \(\sigma _{\theta }\) and \(\tau _{x \theta }\) by the following integrals:

$$\begin{aligned} N_x= & \int ^{h/2}_{-h/2} \sigma _{xx}dz, \quad N_{\theta }=\int ^{h/2}_{-h/2} \sigma _{\theta \theta }dz, \nonumber \\ &\quad N_{x \theta }= \int ^{h/2}_{-h/2} \tau _{x \theta }dz\nonumber \\ M_x= & \int ^{h/2}_{-h/2} z\sigma _{xx}dz, \quad M_{\theta }=\int ^{h/2}_{-h/2} z\sigma _{\theta \theta }dz, \nonumber \\ &\quad M_{x \theta }= \int ^{h/2}_{-h/2} z\tau _{x \theta }dz \end{aligned}$$
(4)

2.2 Nonlocal elasticity theory and Donnell shell theory

To take small scale effects into consideration in the buckling analysis of the Donnell cylindrical shell, we apply the nonlocal elasticity theory introduced by Eringen [10, 12]. This is a semi-empirical theory based on the atomic theory and experimental observations. It assumes that the stress tensor at each point of the continuum body depends on the strain tensor at that point and also the strains at all neighboring points of the body. However, in the macroscopic (local) elasticity theory, the stress at each point depends only on the strain at that point. To express the nonlocal stress at each point x for homogeneous isotropic material, Eringen proposed the following constitutive equation :

$$\begin{aligned} \begin{array}{lll} \sigma ^{nl}_{ij}=\int _{V} \alpha (|x'-x|,\tau ) C_{ijkl} \varepsilon _{kl}(x')dV(x')\\ \end{array} \end{aligned}$$
(5)

where \(\sigma ^{nl}_{ij}\) is the nonlocal stress tensor, \(|x'-x|\) is the Euclidian distance, \(C_{ijkl}\) is the elastic modulus, \(\varepsilon _{kl}\) is the strain tensor, \(\alpha (|x'-x|,\tau )\) is the kernel function having the length dimension and expresses the nonlocal modulus into the constitutive equation, \(\tau =\frac{e_0 a }{\ell }\) with a is an internal characteristic length (carbon-carbon bonds lengths, granular distance... etc.), \(\ell\) is an external characteristic length (rupture length, wavelength... etc.) and \(e_0\) is an appropriate constant depends on the considered material. Consequently, another characteristic length \(e_0\) influences on predictions in nonlocal elasticity theory. It is often difficult to find an explicit expression of the kernel function \(\alpha (|x'-x|,\tau )\) and calculate the triple integral of Eq. (5). In 1983, Eringen [11] has developed more practical differential forms. The kernel function is determined by matching the lattice dynamics with nonlocal elasticity of Eringen and given by the following form:

$$\begin{aligned} \begin{array}{lll} \alpha (|x'-x|,\tau )=\frac{1}{2\pi d^2 \tau ^2}K_0\left( \frac{|x'-x|}{l\tau }, \frac{e_0 a}{l}\right) \end{array} \end{aligned}$$
(6)

where \(K_0\) is the modified Bessel function which represents the integral constitutive relation in an equivalent differential form as follows:

$$\begin{aligned} \begin{array}{lll} (1-(e_0 a)^2\nabla ^2)\sigma ^{nl}_{mn} =C_{mnkl} \varepsilon _{kl} \end{array} \end{aligned}$$
(7)

The nonlocal Hooke’s law for the stress and strain relation is expressed by:

$$\begin{aligned} \begin{array}{lll} \sigma _{xx}-(e_0 a)^2\nabla ^2 \sigma _{xx}=\frac{E}{1-\nu ^2} \varepsilon _{xx}+\frac{\nu E}{1-\nu ^2} \varepsilon _{\theta \theta }\\ \sigma _{\theta \theta }-(e_0 a)^2\nabla ^2 \sigma _{\theta \theta }=\frac{\nu E}{1-\nu ^2} \varepsilon _{xx}+ \frac{E}{1-\nu ^2}\varepsilon _{\theta \theta }\\ \sigma _{x \theta }-(e_0 a)^2\nabla ^2 \sigma _{x \theta }=\frac{E}{1-\nu ^2}\frac{(1-\nu )}{2}\gamma _{x \theta }\\ \end{array} \end{aligned}$$
(8)

From equations (2) and (8), the nonlocal constitutive relations of Donnell shell become:

$$\begin{aligned} \begin{array}{lll} (1-(e_0 a)^2\nabla ^2) N_{x}=C (\varepsilon _{xx}+\nu \varepsilon _{\theta \theta })\\ (1-(e_0 a)^2\nabla ^2) N_{\theta }=C (\varepsilon _{\theta \theta }+\nu \varepsilon _{xx})\\ (1-(e_0 a)^2\nabla ^2) N_{x \theta }=\frac{C}{2}(1-\nu ) \gamma _{x \theta }) \end{array} \end{aligned}$$
(9)

and

$$\begin{aligned} \begin{array}{lll} (1-(e_0 a)^2\nabla ^2) M_{x}=-D \left( \frac{\partial ^2 w}{\partial x^2}+\frac{\nu }{R^2}\frac{\partial ^2 w}{\partial \theta ^2}\right) \\ (1-(e_0 a)^2\nabla ^2) M_{\theta }=-D \left( \nu \frac{\partial ^2 w}{\partial x^2}+\frac{1}{R^2}\frac{\partial ^2 w}{\partial \theta ^2}\right) \\ (1-(e_0 a)^2\nabla ^2) M_{x \theta }=- \frac{D}{R}(1-\nu )\frac{\partial ^2 w}{\partial x \partial \theta }\Bigg ) \end{array} \end{aligned}$$
(10)

where C and D are extensional and bending stiffness rigidities of the shell given by:

$$\begin{aligned} C= \frac{Eh}{1-\nu ^2}, \quad D=\frac{Eh^3}{12(1-\nu ^2)} \end{aligned}$$
(11)

Multiplying the operator \((1-(e_0 a)^2\nabla ^2)\) by the third equation of system (3), we obtain:

$$\begin{aligned} \begin{array}{lll} \frac{\partial ^2 }{\partial x^2}\left[ (1-(e_0 a)^2\nabla ^2) M_x\right] + \frac{2}{R}\frac{\partial ^2}{\partial x \partial \theta }\left[ (1-(e_0 a)^2\nabla ^2) M_{x \theta }\right] \\ \quad +\frac{1}{R^2} \frac{\partial ^2 }{\partial \theta ^2}\left[ (1-(e_0 a)^2\nabla ^2) M_{\theta }\right] +(1-(e_0 a)^2\nabla ^2)\\ \quad \left[ \frac{N_{\theta }}{R}+N_x \frac{\partial ^2 w}{\partial x^2}+ \frac{2N_{x \theta }}{R}\frac{\partial ^2 w}{\partial x \partial \theta }+\frac{N_{\theta }}{R^2}\frac{\partial ^2 w}{\partial \theta ^2}+p\right] =0 \end{array} \end{aligned}$$
(12)

which leads to:

$$\begin{aligned} \begin{array}{lll} k^2\varDelta ^2 w -(1-(e_0 a)^2\nabla ^2) \\ \quad \left[ \rho \frac{N_{\theta } }{Eh}+\frac{1}{Eh}\left( N_x\frac{\partial ^2w}{\partial x^2}+2\frac{N_{xy}}{R}\frac{\partial ^2w}{\partial x \partial \theta }+\frac{N_{\theta }}{R^2}\frac{\partial ^2w}{\partial \theta ^2}\right) +\frac{p}{Eh}\right] =0 \end{array} \end{aligned}$$
(13)

where \(k^2=D/Eh\), \(\rho =1/R\) is the curvature.

To investigate the possible existence of an adjacent equilibrium configurations, we use the adjacent equilibrium criterion [4]. We examine the two adjacent configurations represented by the displacements before and after increments as in the reference [43]. We consider that the indices 0 and b indicate respectively the pre-buckling and post-buckling quantities. According to the shell theory, the membrane forces \(N_{xb}\), \(N_{\theta b}\) and \(N_{x \theta b}\) are connected to the stress function \(\varPhi \,\,\left( N_x=\frac{Eh}{R^2}\frac{\partial ^2\phi }{\partial \theta ^2}, N_{\theta }= Eh\frac{\partial ^2\phi }{\partial x^2}, N_{x \theta }=\frac{Eh}{R}\frac{\partial ^2\phi }{\partial x \partial \theta } \right)\). Neglecting the terms of second order in index b, we obtain the following equation:

$$\begin{aligned} \begin{array}{lll} k^2\varDelta ^2 w_b -(1-(e_0 a)^2\nabla ^2)\\ \quad \left[ \rho \frac{\partial ^2 \varPhi }{\partial x^2}+\frac{1}{Eh}\left( N_{x0}\frac{\partial ^2w_b}{\partial x^2}+2\frac{N_{x \theta 0}}{R}\frac{\partial ^2w_b}{\partial x \partial \theta }+\frac{N_{\theta 0}}{R^2}\frac{\partial ^2w_b}{\partial \theta ^2}\right) +\frac{p_b}{Eh}\right] =0 \end{array} \end{aligned}$$
(14)

The stress function \(\varPhi (x, \theta )\) verifies the following compatibility condition :

$$\begin{aligned} \varDelta ^2 \phi + \rho \frac{\partial ^2 w_b}{\partial x^2}+(e_0 a)^2\left[ 3\rho ^2\frac{\partial ^6 \phi }{\partial x^4 \partial \theta ^2}+3\rho ^4 \frac{\partial ^6 \phi }{\partial x^6}+\rho ^6 \frac{\partial ^6 \phi }{\partial \theta ^6}\right] =0 \end{aligned}$$
(15)

If the shear membrane forces are neglected \(N_{x \theta 0}=0\), the axial compression is \(N_{x0}=P\) and the circumferential membrane force is \(N_{\theta 0}=F\), the system (14)–(15) giving the Donnell equations becomes:

$$\begin{aligned}&k^2\varDelta ^2 w_b -(1-(e_0 a)^2\nabla ^2) \left[ \rho \frac{\partial ^2 \phi }{\partial x^2}\right. \nonumber \\&\qquad \left. +\left( \lambda \frac{\partial ^2w_b}{\partial x^2}+\frac{F}{R^2}\frac{\partial ^2w_b}{\partial \theta ^2}\right) +\frac{p_b}{Eh}\right] =0\nonumber \\&\varDelta ^2 \phi + \rho \frac{\partial ^2 w_b}{\partial x^2}+(e_0 a)^2\left[ 3\rho ^2\frac{\partial ^6 \phi }{\partial x^4 \partial \theta ^2}\right. \nonumber \\&\qquad \left. +3\rho ^4 \frac{\partial ^6 \phi }{\partial x^6}+\rho ^6 \frac{\partial ^6 \phi }{\partial \theta ^6}\right] =0 \end{aligned}$$
(16)

where \(\lambda =\frac{P}{Eh}\) is the load parameter.

Note that when \(e_0=0\), the system of coupled equations (14) reduces to the classical (local) Donnell equilibrium equations in which the effect of small length scale is neglected.

2.3 Discussion on the nonlocal parameter \(e_0\) of the nonlocal theory

The characteristic length \(e_0\), of nonlocal continuum mechanics for modeling carbon nanotubes, identifies the nonlocal effect in the analysis. It is determined by experience or by the intersection of dispersion curves for the planes wave with those of lattice dynamics. Eringen [11] defines \(e_0\) as a constant appropriate to each material and finds \(e0 = 0.39\), for some materials, by a comparison between the results of lattice dynamics and the nonlocal elasticity theory. Zhang et al. [54] estimated the value of the nonlocal parameter, using the curve fitting of the results of nonlocal elasticity theory to those of molecular mechanics simulations, for the critical buckling strain of SWCNTs under axial compression. Sears and Batra [41] compared their molecular mechanics results to these of nonlocal cylindrical shell model based on the Donnell shell theory to show that \(e_0=0.82\). Zhang et al. [55] determined that the values of \(e_0\) varied between 0.546 and 1.043 for different chiral angles using the curve fitting of the molecular dynamics simulation results and those of nonlocal cylindrical shell model based on the Donnell shell theory. Wang and Hu [47] obtained the value of \(e_0\) by comparing of the gradient method with atomic lattice dynamics of a one-dimensional lattice. Figure 2 [51] shows the dispersion of a crystal for the one-dimensional lattice where \(c_0\) is the equivalent sound velocity in the crystal, c is the phase velocity in the lattice and k is the lattice wavenumber.

Fig. 2
figure 2

Dispersion curves of one-dimensional lattice [51]

Full size image

The results of the gradient method are in excellent agreement with the dispersion curves obtained via the Born-Karman model of lattice dynamics particularly at smaller values of ka. There is an other work on the estimated of the parameter \(e_0\) [41, 47, 49, 50, 54, 55]. Different values of the non-local parameter are used in literature. Hussain et al. [16] discussed the nonlocal effect on the vibration of armchair and zigzag SWCNTs with different values of the nonlocal parameter \(e_0 = 0.5\), 1, 1.5 and 2. The same values are used by Amara et al. [3] for the buckling studies of MWCNTs under temperature field. Kiani [18,19,20] showed his results using different small scale parameters \(e_0a\) between 0 and 2nm.

3 Multiple Donnell shells continuum approach

Consider a multi-walled carbon nanotube (MWCNT), consisting of N tubes of radius \(R_j(j=1;2;...;N)\), length L, same thickness h and Young’s modulus E. It subjected to an axial compression P. The walls of adjacent tubes interact through Van der Waals forces as shown in Fig. 3.

Fig. 3
figure 3

Multi-walled carbone nanotube (MWCNT) under axial compression

Full size image

Using the continuum Donnell concentric multi-shells, each tube \(j(j=1,2,.,N)\) is modeled by an elastic homogeneous and isotropic circular cylindrical shell of length L, thickness h, radius \(R_j\), Young’s modulus E and Poisson’s ratio \(\nu\). The considered circular cylindrical shells are coupled by Van der Waals interaction. We denote by \(u_i(x,\theta )\), \(v_i(x,\theta )\) and \(w_i(x,\theta )\), the components of displacement vector with x and \(\theta\) are the axial and circumferential coordinates respectively. According to Sect. 2.2, the transverse displacement \(w_i(x,\theta )\) and the corresponding stress functions \(\varPhi _j(x,\theta )\) are solutions of the following nonlocal Donnell shell equilibrium equation:

$$\begin{aligned} \begin{array}{lll} k^2\varDelta ^2_j w_j -(1-(e_0 a)^2\nabla _j^2) \left[ \lambda \frac{\partial ^2w_j}{\partial x^2}+ \rho _j \frac{\partial ^2\phi _j}{\partial x^2} +\frac{F^{vdw}_j}{Eh}\right] = 0 \\ \varDelta ^2_j \phi _j + \rho _j \frac{\partial ^2w_j}{\partial x^2}+(e_0 a)^2 \left[ 3\rho ^2\frac{\partial ^6 \phi }{\partial x^4 \partial \theta ^2}+3\rho ^4 \frac{\partial ^6 \phi }{\partial x^6}+\rho ^6 \frac{\partial ^6 \phi }{\partial \theta ^6}\right] = 0 \end{array} \end{aligned}$$
(17)

where \(j=1,2,...,N\), \(\rho _j=\frac{1}{R_j}\) is the curvature radius of \(j^{th}\) tube, \(\varDelta _j^2 = \left( \frac{\partial ^2}{\partial x^2} + \rho _j^2\frac{\partial ^2}{\partial \theta ^2}\right) ^2\) is the bi-laplacian operator, \(\phi _j\) is the stress function of \(j^{th}\) tube. The Van der Waals force \(F^{vdw}_j\) is expressed by:

$$\begin{aligned} \begin{array}{lll} F^{vdw}_j= \frac{F_j}{R^2_j} \frac{\partial ^2w_j}{\partial \theta ^2}-p_j \end{array} \end{aligned}$$
(18)

with \(F_j\) are the forces by the length unit, prior buckling, in the circumferential direction of tube j and \(p_j\) is the Van der Waals interaction between the tubes of MWCNT which is written in the form:

$$\begin{aligned} \begin{array}{ll} p_j = \sum _{k=1}^{N}\left( w_j-w_k\right) c_{jk} \end{array} \end{aligned}$$
(19)

with \(c_{jk}\) are the Van der Waals coefficients given by :

$$\begin{aligned} \begin{array}{l} c_{jk} = -\left[ \frac{1001\pi \epsilon \sigma ^{12}}{3a^4}E_{jk}^{13}-\frac{1120\pi \epsilon \sigma ^{6}}{9a^4}E_{jk}^7\right] R_k \end{array} \end{aligned}$$
(20)

and \(E_{jk}^m\) the elliptic integrals expressed as:

$$\begin{aligned} E_{jk}^m=\frac{1}{(R_j+R_k)^m}\int ^\frac{\pi }{2}_{0} \frac{d\theta }{(1-K_{jk}cos^2(\theta ))^{m/2}}R_k \end{aligned}$$
(21)

with a is the length of the C–C bond, \(\epsilon\) is the depth of Lennard–Jones potential, \(\sigma\) is a parameter being determined by the equilibrium distance and \(K_{ii}\) defined by:

$$\begin{aligned} \begin{array}{l} K_{jk}=\frac{4R_jR_k}{(R_j+R_k)^2} \end{array} \end{aligned}$$
(22)

Putting

\(\mu = e_0 a\) and taking into account of Eqs. (18) and (19) can be written as:

$$\begin{aligned}&k^2\varDelta ^2_j w_j -(1-\mu ^2\nabla _j^2) \left[\lambda \frac{\partial ^2w_j}{\partial x^2} + \rho _j \frac{\partial ^2\phi _j}{\partial x^2} \right.\nonumber \\&\left.+ \frac{1}{Eh} (\frac{F_j}{R^2_j} \frac{\partial ^2w_j}{\partial \theta ^2}+\sum _{k=1}^{N}\left( w_j-w_k\right) c_{jk})\right] = 0 \nonumber \\& \varDelta ^2_j \phi _j + \rho _j \frac{\partial ^2w_j}{\partial x^2}+(e_0 a)^2 \left[ 3\rho ^2\frac{\partial ^6 \phi }{\partial x^4 \partial \theta ^2}\right. \nonumber \\&\qquad \left. +3\rho ^4 \frac{\partial ^6 \phi }{\partial x^6}+\rho ^6 \frac{\partial ^6 \phi }{\partial \theta ^6}\right] = 0 \end{aligned}$$
(23)

where \(j=1,2,...,N\).

4 Buckling analysis of double-walled carbon nanotubes (DWCNTs)

4.1 Buckling load \(\lambda\)

The solution of the problem (23) is sought in the following form:

$$\begin{aligned} w_j(x,\theta )= & A_j exp\left(i\frac{m\pi }{L}x\right) cos(n\theta )+cc \nonumber \\&\qquad \qquad j=1,2,3,...,N \nonumber \\ \phi _j(x,\theta )= & a_j exp\left(i\frac{m\pi }{L}x\right) cos(n\theta )+cc \end{aligned}$$
(24)

where m and n are respectively the axial and circumferential half wavenumbers of the \(j^{th}\) tube, \(A_j\) and \(a_j\) are arbitrary complex constants and cc denotes the complex conjugate. As a special case \(N=2\) (DWCNT), the substitution of Eq. (24) in Eq. (23) gives :

$$\begin{aligned} \quad j=1 \left\{ \begin{array}{llll} k^2\left( p^2+q_1^2\right) ^2A_1-\lambda \left[ p^2+\mu ^2 p^2 \left( p^2+q_1^2\right) \right] A_1 \\ \quad +\frac{c_{12}}{Eh}\left[ \left( 1+\mu ^2 \left( p^2+q_1^2\right) \right) A_2-\left( 1+\mu ^2 \left( p^2+q_1^2\right) \right) A_1 \right] \\ \quad -\frac{F_{1}}{Eh}\left[ q_1^2-\mu ^2 q_1^2 \left( p^2+q_1^2\right) \right] A_1 \\ \quad +\rho _1\left[ p^2+\mu ^2p^2 \left( p^2+q_1^2\right) \right] a_1=0\\ \\ \left( p^2+q_1^2\right) a_1+\mu ^2\left[ 3q_1^2 p^4+3q_14 p^2+p^6+q_1^6\right] a_1\\ \quad -p^2A_1=0 \end{array} \right. \end{aligned}$$
(25)

and

$$\begin{aligned} for \quad j=2 \left\{ \begin{array}{llll} k^2\left( p^2+q_2^2\right) ^2A_2-\lambda \left[ p^2+\mu ^2 p^2 \left( p^2+q_2^2\right) \right] A_2\\ \quad +\frac{c_{21}}{Eh}\left[ \left( 1+\mu ^2 \left( p^2+q_2^2\right) \right) A_2-\left( 1+\mu ^2 \left( p^2+q_2^2\right) \right) A_1 \right] \\ \quad -\frac{F_{2}}{Eh}\left[ q_2^2-\mu ^2 q_2^2 \left( p^2+q_2^2\right) \right] A_2 \\ \quad +\rho _2\left[ p^2+\mu ^2p^2 \left( p^2+q_2^2\right) \right] a_2=0\\ \left( p^2+q_2^2\right) a_2+\mu ^2\left[ 3q_2^2 p^4+3q_2^4 p^2+p^6+q_2^6\right] a_2\\ \quad -p^2A_2=0 \end{array} \right. \end{aligned}$$
(26)

where \(p=m\pi /L\) and \(q_j=n/R_j\).

The second equations in systems (25) and (26) lead to:

$$\begin{aligned} \begin{array}{lll} a_1=\frac{p^2 A_1}{\left( p^2+q_1^2\right) ^2+\mu ^2\left( 3q_1^2 p^4+3q_1^4 p^2+p^6+q_1^6\right) }\\ a_2=\frac{p^2 A_2}{\left( p^2+q_2^2\right) ^2+\mu ^2\left( 3q_2^2 p^4+3q_2^4 p^2+p^6+q_2^6\right) } \end{array} \end{aligned}$$
(27)

Inserting (27) in the first equations of the system (25) and (26), we obtain the following system:

$$\begin{aligned}&\left[ \alpha _1-\lambda p^2\left( 1+\mu ^2 p^2\left( 1+\beta _1^2\right) \right) \right] A_1\nonumber \\&\qquad +\frac{c_{12}}{Eh}\left[ 1+\mu ^2 p^2\left( 1+\beta _1^2\right) \right] A_2=0 \nonumber \\&\frac{c_{12}}{Eh}\left[ 1+\mu ^2 p^2\left( 1+\beta _2^2\right) \right] A_1\nonumber \\&\qquad +\left[ \alpha _2-\lambda p^2\left( 1+\mu ^2 p^2\left( 1+\beta _2^2\right) \right) \right] A_2=0 \end{aligned}$$
(28)

where \(\beta _1=q_1/p\) and \(\beta _2=q_2/p\) are the aspect ratios, \(\alpha _1\) and \(\alpha _2\) are expressed by:

$$\begin{aligned} \begin{array}{lll} \alpha _1&=k^2\left( 1+\beta _1^2\right) ^2p^4 +\frac{\rho _1\left( 1+\mu ^2p^2\left( 1+\beta _1^2\right) \right) }{\left( 1+\beta _1^2\right) ^2+\mu ^2p^2\left( 3\beta _1^2+3\beta _1^4+\beta _1^6+1\right) }\\ &\quad -\frac{c_{12}}{Eh}\left( 1+\mu ^2 p^2\left( 1+\beta _1^2\right) \right) -\frac{F_{1}}{Eh}\beta _1^2\left( 1-\mu ^2 p^4\left( 1+\beta _1^2\right) \right) \\ \alpha _2&=k^2\left( 1+\beta _2^2\right) ^2p^4 +\frac{\rho _2\left( 1+\mu ^2p^2\left( 1+\beta _2^2\right) \right) }{\left( 1+\beta _2^2\right) ^2+\mu ^2p^2\left( 3\beta _2^2+3\beta _2^4+\beta _2^6+1\right) }\\ &\quad -\frac{c_{21}}{Eh}\left( 1+\mu ^2 p^2\left( 1+\beta _2^2\right) \right) -\frac{F_{2}}{Eh}\beta _2^2\left( 1-\mu ^2 p^4\left( 1+\beta _2^2\right) \right) \end{array} \end{aligned}$$
(29)

The system (28) has non-trivial solution \(A_1\) and \(A_2\) if its determinant is zero. This requirement is the buckling condition which leads to:

$$\begin{aligned} \left( X_0 p^4\right) \lambda ^2-X\lambda +Y=0 \end{aligned}$$
(30)

where

$$\begin{aligned} X_0= & \left( 1+\mu ^2p^2\left( 1+\beta _1^2\right) \right) \left( 1+\mu ^2p^2\left( 1+\beta _2^2\right) \right) \nonumber \\ X= & p^2\left[ \alpha _1\left( 1+\mu ^2p^2 \left( 1+\beta _2^2\right) \right) \right. \nonumber \\&\quad \left. +\alpha _2\left( 1+\mu ^2p^2\left( 1+\beta _1^2\right) \right) \right] \nonumber \\ Y= & \alpha _1\alpha _2-\frac{c_{12}c_{21}}{(Eh)^2} \left( 1+\mu ^2p^2\left( 1+\beta _1^2\right) \right) \nonumber \\&\quad \times \left( 1+\mu ^2p^2\left( 1+\beta _2^2\right) \right) \end{aligned}$$
(31)

The solution of (30) gives the expression of the buckling load:

$$\begin{aligned} \lambda =\frac{X-\sqrt{X^2-4X_0Yp^4}}{2X_0p^4} \end{aligned}$$
(32)

This root is obtained by taking the negative sign before the square-root. The expression (32) can be written according to m and n (\(\lambda (m,n)\)) and it can also be written according to \(\beta _1\), \(\beta _2\) and p (\(\lambda (\beta _1,\beta _2,p)\)) in the following compact form:

$$\begin{aligned}&\lambda (\beta _1,\beta _2,p)\nonumber \\&\quad =\frac{1}{2p^2\zeta _1\zeta _2} \left( \alpha _1\zeta _2+\alpha _2\zeta _1- \sqrt{ \left( \alpha _1\zeta _2+\alpha _2\zeta _1\right) ^2+Z} \right) \end{aligned}$$
(33)

where

$$\begin{aligned} \begin{array}{lll} \zeta _1=\left( 1+\mu ^2p^2\left( 1+\beta _1^2\right) \right) \\ \zeta _2=\left( 1+\mu ^2p^2\left( 1+\beta _2^2\right) \right) \\ Z=4\zeta _1\zeta _2 \left( \zeta _1\zeta _2\frac{c_{12}c_{21}}{(Eh)^2}-\alpha _1\alpha _2\right) \end{array} \end{aligned}$$
(34)

The minimization of the buckling load (\(\lambda (m,n)\)), by searching numerically the values of m and n, allows to obtain the critical buckling load of the double-walled carbon nanotubes as in [17, 37]. This method is very expensive and does not give a good precision. In the next section, we propose a novel approach for determination of the nonlocal critical buckling load of DWCNTs for a fixed aspect ratio \(\beta _1\) and \(\beta _2\) and with respect to the wave of axial number p. To validate the proposed approach, we compare the results with those obtained by the minimization procedure of the buckling load (\(\lambda (m,n)\)) with respect to the integer numbers m and n.

4.2 Proposed approach for the nonlocal critical buckling load of the DWCNTs

The numerical experiments show that the relative error of the critical buckling load \(\lambda _{cr}(p_{cr})\), using the equation (33), decreases as the axial wave number p increases at the beginning. Continuously increasing p, the relative error of \(\lambda _{cr}\) becomes larger and gives an incorrect result for larger p. By considering these remarks as shown in reference [17] and in order to find \(p_{cr}\) quickly, we propose the following algorithm:

$$\begin{aligned} \begin{array}{lll} d=2\\ S=100\\ \epsilon =0.05\\ \lambda ^{0}_{cr} =0.0001\\ p =p_{prediction}\\ error1 = 4\\ error2 = 3\\ error3= 2\\ error4=1\\ \\ for \, i = 0 : d\\ \quad \quad for j = 1 : S\\ \quad \quad \quad \quad p_j^i=p+j10^{-i}\\ \quad \quad end\\ \\ \quad \quad n=0\\ \quad \quad while \left( min (error3, error4) < min (error1, error2) \right) \\ \quad \quad \quad \quad n = n +1\\ \quad \quad \quad \quad \lambda ^{n}_{cr}=\lambda (p_n^i) \quad (see \, Eq. (33))\\ \quad \quad \quad \quad error(p_n^i)=|\frac{\lambda ^{(n-1)}_{cr}-\lambda ^{n}_{cr}}{\lambda ^{(n-1)}_{cr}}|\\ \quad \quad \quad \quad error1 = error2\\ \quad \quad \quad \quad error2 = error3\\ \quad \quad \quad \quad error3 = error4\\ \quad \quad \quad \quad error4 = error(m_n^i)\\ \quad \quad end \\ \\ \quad \quad if \left( n - 3 > 0 \right) \\ \quad \quad \quad \quad p = p_{n-3}^i + \epsilon \\ \quad \quad else\\ \quad \quad \quad \quad p = p_{1}^i -10^{-i}\\ \quad \quad end\\ \\ end\\ p_{cr} = p\\ \lambda _{cr}=\lambda (p_{cr}) \quad (see \, Eq. (33))\\ \end{array} \end{aligned}$$
(35)

where d denotes the accuracy of \(p_{cr}\) to the mth decimal place, \(\epsilon\) is related to the starting point of the test scope and gets a value between 0 and 1.

5 Numerical analysis for the critical buckling load of DWCNTs

Numerical results are presented in this section for validating the proposed approach of the nonlocal critical buckling load of DWCNTs under axial compression. In these numerical tests, data of double Donnell shells model are given as follows: the inner diameter \(R_1=2\,\mathrm{nm}\), the median inter-shell spacing between carbon of DWCNTs \(\delta R=0.34\), the aspect ratios (length to radius) \(L/R_1=10\), \(h =0.066\,\mathrm{nm}\), \(a=0.142\,\mathrm{nm}\), \(E=5500\,GPa\), \(\upsilon =0.34\), \(c_{12}=\frac{-320 \times 10^{-3}}{0.16a^2} \mathrm{nN}/\mathrm{nm}^3\), \(c_{21}=(R_1/R_2) c_{12}\), \(F_1=0\), \(e_0=0.39\) [11, 15, 52]. The validation process consists in comparing the results of minimizing the buckling load (\(\lambda (m,n)\)) and those of the proposed approach (35) with fixed values of aspect ratios \(\beta _1\) and \(\beta _2\).

The buckling load \(\lambda (m,n)\), for the nonlocal parameter \(e_0=0.39\), are plotted in Fig. 4 versus the half-wave numbers in the axial and circumferential directions (m, n).

Fig. 4
figure 4

Buckling loads \(\lambda\) versus (m, n) for the nonlocal parameter \(e_0=0.39\)

Full size image

To validate the proposed approach of the nonlocal critical buckling load, we consider the values of aspect ratios \(\beta _1=0.72\) and \(\beta _2=0.62\) which are equivalent to the critical values \((m =22, n =5)\) as a shown in Fig. 4. The chosen parameters of the proposed approach are \(d=2\), \(S=100\), \(\epsilon =0.01\), \(p_{prediction}= 0\) and \(\lambda ^0 _{cr}=0.0001\). Using the proposed approach (see Eq. (35)), Fig. 5 represent the first estimate \((i=0)\) of the critical wave number \(p_{cr}\) in axial direction, by plotting the variation of the relative error variation versus the wave number p in axial direction, which gives a value between \(3 \mathrm{nm}^{-1}\) and \(4 \mathrm{nm}^{-1}\).

Fig. 5
figure 5

Relative error variation versus the wave number p in axial direction for the first estimate where \((i=0)\) and \(r=6\)

Full size image

So, in the second estimate \((i=1)\), we are looking for precision in the interval \([3 \mathrm{nm}^{-1}, 4 \mathrm{nm}^{-1}]\) or the accuracy of \(p_{cr}\) to the first decimal place as shown the Fig. 6.

Fig. 6
figure 6

Relative error variation versus the wave number p in axial direction for the second estimate where \((i=1)\) and \(r=6\)

Full size image

In the same way in the interval \([3.3 \mathrm{nm}^{-1}, 3.4 \mathrm{nm}^{-1}]\) as you can see in the Fig. 7, the accuracy of \(p_{cr}\) to the second decimal place gives the critical wave number \(p_{cr}=3.38 nm^{-1}\) which is equivalent to the critical buckling load \(\lambda _{cr}=0.01775\) with the relative error \(10^{-3}\%\). This critical value is equal to the minimum value of the critical buckling load of the curve given by minimizing numerically \(\lambda (m,n)\). We can note that the proposed approach allows to determine the critical load according to aspect ratios with good precision and according to the quality requested by the user. In the following we will present some tests using the proposed approach (see Eq. (35)) to show the influence of various parameters on the critical load \(\lambda _{cr}.\)

Fig. 7
figure 7

Relative error variation versus the wave number p in axial direction for the third estimate where \((i=2)\) and \(r=8\)

Full size image

The critical buckling load of DWCNTs decreases when the nonlocal parameter \(e_0\) increase as shown in the Fig. 8 which shows that we cannot neglect the effect of small scales especially for the great values of \(e_0\). Secondly, these results demonstrate that the approximation given by Ru [37], in which the ratio \((R_2-R_1)/R_1\) is neglected, provides a higher critical buckling load.

Fig. 8
figure 8

Critical buckling load versus the nonlocal parameter \(e_{0}\) for equal and different radii

Full size image

In Fig. 9, we plot the critical buckling load versus the aspect ratio for a fixed force \(F_1=0\) and different nonlocal parameters \(e_0\). It is clear that for \(F_1=0\) and a fixed nonlocal parameter, \(\lambda _{cr}\) increases with increasing values of aspect ratio \(\beta _1\). We can also notice that for \(F_1=0\) and a fixed aspect ratio \(\beta _1\), \(\lambda _{cr}\) decreases with increasing values of nonlocal parameter \(e_0\).

Fig. 9
figure 9

Critical buckling load versus the aspect ratio \(\beta _1\) for a fixed force \(F_1=0\) and different nonlocal parameters \(e_0\)

Full size image

Now we are interested to study the effect of the force \(F_1\) for a fixed nonlocal parameter as shown in Figs. 10 and 11. These graphs show that, for each value of the nonlocal parameter, there is a certain value F of the force \(F_1\) such that for all force \(F_1\) greater than F, the critical buckling load parameter in terms of the aspect ratio presents a maximum and decreases from this aspect ratio corresponding to this maximum. Below this value leads to the increasing of \(\lambda _{cr}\) with increasing the aspect ratio. Analysis of the results shows that the value of F increases with increasing values of the nonlocal parameter \(e_0\).

Fig. 10
figure 10

Critical buckling load versus the aspect ratio \(\beta _1\) for a fixed nonlocal parameter \(e_0=0.39\) and different values of the force \(F_1\)

Full size image
Fig. 11
figure 11

Critical buckling load versus the aspect ratio \(\beta _1\) for a fixed nonlocal parameter \(e_0=0.5\) and different values of the force \(F_1\)

Full size image

In Fig. 12, we draw the critical buckling load of DWCNTs versus the aspect ratio \((R_2-R_1)/R_1\) for some nonlocal parameters values \(e_0=0.39\), \(e_0=0.5\) and \(e_0=0.7\) where the force \(F_1=0\). This figure indicates that the critical buckling load increases with increasing values of the ratio \((R_2-R_1)/R_1\). The same observation remains true whatever the value of the force \(F_1\) as shown in the Fig. 13.

Fig. 12
figure 12

Critical buckling load versus the ratio \((R_2-R_1)/R_1\) for a fixed force \(F_1=0\) and different nonlocal parameters \(e_0=0.39\), \(e_0=0.5\) and \(e_0=0.7\)

Full size image
Fig. 13
figure 13

Critical buckling load versus the ratio \((R_2-R_1)/R_1\) for a fixed nonlocal parameter \(e_0\) and different forces \(F_1=0\), \(F_1=10^{-2}Eh\) and \(F_1=3.10^{-2}Eh\)

Full size image

6 Conclusion

An approach of the nonlocal critical buckling load of double-walled carbon naotube (DWCNTs) under axial compression for fixed values of aspect ratios has been developed. The derivation of the proposed approach is performed using the nonlocal multiple Donnell shells continuum approach without any assumption over tubes radii. This proposed solution approach permits to take into consideration the small scale effects using the nonlocal elasticity theory of Eringen and the median inter-shell spacing which their omission leads to an overestimation of the critical buckling load. We can observe in the numerical applications that the small scale effect becomes very important with increasing the nonlocal parameter \(e_0\) which leads to a lower critical buckling load. On the other hand, this critical buckling load increases with increasing of the aspect ratio \(\beta =\frac{L/m\pi }{R/n}\) (long axial wavelengths/circumferential wavelengths). But there is a certain value F of the force \(F_1\) from which the critical buckling load accept a maximum in terms of the aspect ratio \(\beta\), from the correspond aspect ratio to this maximum the critical buckling load decreases.