1 Introduction

Rotating cylindrical shells are one of the most commonly used geometric shapes and industrial equipment. These shells may be used in gas turbines, aerospace structures, planes and many others systems. In recent years, the use of composites and functionally graded materials (FGMs) has increased in most engineering areas including aerospace, automation, urban construction, marine industries, and many other industries. Free vibration analysis and critical speed of rotary shafts have been widely studied in recent years.

Free vibration analysis of thin rotating laminated cylindrical shell based on Love’s first approximation theory studied by Lam and Loy [1, 2]. Also, they [3] investigated influence of boundary conditions and fiber orientation on the natural frequencies of thin laminated cylindrical shells. The analysis is carried out using Love’s shell theory and solved using Galerkin’s method. The displacement fields employed consist of beam functions models and Fourier functions in the axial and the circumferential direction, respectively. Then, analysis of free vibration of cylindrical shells made of FGMs that composed of stainless steel and nickel studied by Loy et al. [4].

Lee and Choi [5] studied free vibration of circular cylindrical shells with an interior plate, that reacceptance method employed to obtain the vibrational characteristics of a simply supported cylindrical shell with an interior plate. The effects of boundary conditions on the frequencies of free vibration analysis of rotating cylindrical shells with harmonic reproducing kernel particle method carried out by Liew et al. [6]. In the other research Pellicano et al. [7] expressed the non-linear vibration of circular cylindrical shells with simply support condition by using Donnell’s non-linear shallow-shell theory. Free vibration characteristics of thick laminated composite non-circular cylindrical shells with elliptical cross sections using higher order theory analyzed by Ganapathi and Haboussi [8]. Also, shown the behaviors of first-order model in analyzing the non-circular shell is qualitatively same as that of higher-order theory. Then Sofyev [9] investigated the buckling of FGMS cylindrical thin shells composed of ceramic and metal under external pressure load based on Love’s shell theory.

Bhangale and Ganesan [10] expressed analysis of free vibration of simply supported non-homogeneous functionally graded magneto-electro-elastic finite cylindrical shells. Analysis of free vibration of a thin circular cylindrical shell for orthotropic materials based on Flugge’s shell theory have been illustrated by Xuebin [11]. That he solved the equations with using general displacement and new type of polynomial eigenvalue problem. Bahtui and Eslami [12] studied the coupled thermoelastic response of a FGMs circular cylindrical shell. That coupled thermoelastic and the energy equations are simultaneously solved for a FGMs axisymmetric cylindrical shell subjected to thermal shock load.

Analytical solutions for axisymmetric transverse free vibration analyses of cylindrical shell with thickness variation under simply supported and clamped ends conditions in arbitrary power form due to forces acting in the transverse direction has been expressed by Duan and Koh [13]. For analytical solution, he used the Frobenius method for solve the governing differential equations. Also, thermoelastic vibration and buckling characteristics of the functionally graded piezoelectric cylindrical based on the first order shear deformation theory investigated by Sheng and Wang [14]. That, they used a piezoelectric material having gradient change along the thickness of the cylindrical shells. Also, Sofyev [15] presented the dynamic behavior of FGMS cylindrical shells composed of metal and ceramic under axial tension, internal compressive load.

Amabili [16] studied the geometrically nonlinear forced vibrations of laminated circular cylindrical shells by using the Amabili–Reddy higher-order shear deformation theory. The result shown that the Amabili–Reddy and Novozhilov theories give good results for thin laminated shells. On the other hand, for thick laminated shells, the Amabili–Reddy theory should be used in order to have accurate results. The nonlinear vibration of a functionally graded cylindrical shell subjected to axial and transverse mechanical loads using improved Donnell shell theory under simply support conditions presented by Bich and Nguyen [17]. The Galerkin method, the Volmir’s assumption and fourth-order Runge–Kutta method are used for dynamical analysis of shells to give expressions of nonlinear frequency. Also, they shown the effects of pre-loaded axial compression and dimensional ratios on the dynamical behavior of shells.

Strozzi and Pellicano [18] analyzed the nonlinear vibrations of FGMs circular cylindrical shells, that Sanders–Koiter theory is applied to model the nonlinear dynamics of the system in the case of finite amplitude of vibration. Nonlinear vibration problem of simply supported FGMs cylindrical shells with embedded piezoelectric layers studied by Jafari et al. [19]. Sofyev et al. [20] studied the frequencies and critical axial load of sandwich cylindrical shell containing an FGMS core with shear stresses, rotary inertia and subjected to axial compressive load based on Donnell’s shell theory using the shear deformation theory.

Free vibration analysis of a laminated composite beams based on von Karman nonlinear theory and finite strain demonstrated by Ghasemi et al. [21]. Sofiyev [22] investigated the non-linear free vibration of FGMs orthotropic cylindrical shells taking into account the shear stresses based on the shear deformation theory (SDT) and von Karman-type strain displacement relationships. Also, Sofyevet al [23] analyzed the free vibration and stability of axially loaded sandwich FGMS cylindrical shells composed of stainless steel and zirconium oxide without shear stresses and rotary inertia resting Pasternak foundations based on the first order shear deformation theory under simply supported boundary conditions. Then, Sofiyev et al. [24] based on first and higher order shear deformation theory investigated the instability of FGMS orthotropic cylindrical shell. Wang and Wu [25] studied the focuses on performing a free vibration analysis of a functional graded porous cylindrical shell subjected to different sets of immovable boundary conditions. The nonlinear vibration behavior of graphene-reinforced composite (GRC) laminated cylindrical shells in thermal environments investigated by Shen et al. [26].

Ghasemi and Mohandes [27] studied free vibration analysis of rotating fiber–metal laminate (FMLs) thin circular cylindrical shells based on Love’s first approximation shell theory. Also, they [28] investigated free vibration of FMLs thin circular cylindrical shells with different boundary conditions based on Love’s first approximation shell theory and beam modal function model. Then they analyzed [29] the micro and nano FMLs cylindrical shells based on modified couple stress theory; that, the frequencies of the shells calculated for different volume fractions of composite section, lay-ups, material length scale parameters, length to radius ratio, axial and circumferential wave numbers. Free vibration characteristics of the functionally graded graphene reinforced porous nanocomposite cylindrical shell with spinning motion demonstrated by Dong et al. [30]. The nonlinear dynamic behaviors of functionally graded cylindrical shells under combined parametric and external excitations based on the von Kármán nonlinear theory, studied by Sheng and Wang [31].

In this research, the free vibration of rotating circular cylindrical shells composited of FGMs layer with simply support boundary condition are investigated. Using the Love’s first approximation shell theory, and according to Hamilton’s principle, the governing equations for the cylindrical shell extracted. Also, the Navier’s solution is used to solve the equations of the cylindrical shell due to the simply support boundary condition. Then, analysis for length to radius ratio, rotating speed, axial and circumferential wave number are illustrated.

2 Governing equations

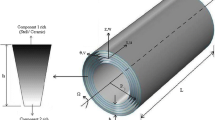
In this section, the fundamental relations for the analysis of the rotating FGMs shell are presented. By Consider the rotating cylindrical shell, which R shell radius, L cylindrical lengths, h shell thickness and \(\varOmega\) is angular speed of rotation. where u, v, w, are axial, circumferential and radial displacements along the x, \(\theta\) and z directions respectively. According to Love’s first shell theory, the axial, circumferential, and shear strain is defined as follows [1],

$$\begin{aligned} \varepsilon_{xx} & = \varepsilon_{x,o} + zk_{x} \\ \varepsilon_{\theta \theta } & = \varepsilon_{\theta ,o} + zk_{\theta } \\ \varepsilon_{x\theta } & = \varepsilon_{x\theta ,o} + zk_{x\theta } \\ \end{aligned}$$
(1)

That z is distance from the shell’s middle surface, and \(\varepsilon_{x,o}\), \(\varepsilon_{x,o}\), \(\varepsilon_{x,o}\) are axial, circumferential and shear strain of the shell’s middle surface, respectively that are expressed as follows [2, 15],

$$\begin{aligned} \varepsilon_{x,o} & = \frac{\partial u}{\partial x} \\ \varepsilon_{\theta ,o} & = \frac{1}{R}\left( {\frac{\partial v}{\partial \theta } + w} \right) \\ \varepsilon_{\theta ,o} & = \frac{\partial v}{\partial x} + \frac{1}{R}\frac{\partial u}{\partial \theta } \\ \end{aligned}$$
(2)

Also \(k_{x}\), \(k_{x}\), \(k_{x}\) are axial, circumferential and shear curvature of the shell’s middle surface, respectively that are expressed as follows [2, 15],

$$\begin{aligned} k_{x} & = - \frac{{\partial^{2} w}}{{\partial x^{2} }} \\ k_{\theta } & = - \frac{1}{{R^{2} }}\left( {\frac{{\partial^{2} w}}{{\partial \theta^{2} }} - \frac{\partial v}{\partial \theta }} \right) \\ k_{x\theta } & = - \frac{2}{R}\left( {\frac{{\partial^{2} w}}{\partial x\partial \theta } - \frac{\partial v}{\partial x}} \right) \\ \end{aligned}$$
(3)

For the FGM cylindrical shells, the stress and strain relations are as follows [4, 9],

$$\left\{ {\begin{array}{*{20}c} {\sigma_{x} } \\ {\sigma_{\theta } } \\ {\sigma_{x\theta } } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 \\ {Q_{12} } & {Q_{22} } & 0 \\ 0 & 0 & {Q_{66} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{\theta } } \\ {\varepsilon_{x\theta } } \\ \end{array} } \right\}$$
(4)

where,

$$\begin{aligned} Q_{11} & = Q_{22} = \frac{E}{{1 - \nu^{2} }} \\ Q_{12} & = \frac{\nu E}{{1 - \nu^{2} }} \\ Q_{66} & = \frac{E}{2(1 + \nu )} \\ \end{aligned}$$
(5)

For the FGMs, the properties of material are defined as follows [4, 20, 23],

$$\begin{aligned} E & = (E_{1} - E_{2} )\left( {\frac{z}{h} + 0.5} \right)^{N} + E_{2} \\ \nu & = (\nu_{1} - \nu_{2} )\left( {\frac{z}{h} + 0.5} \right)^{N} + \nu_{2} \\ \rho & = (\rho_{1} - \rho_{2} )\left( {\frac{z}{h} + 0.5} \right)^{N} + \rho_{2} \\ \end{aligned}$$
(6)

where \(E,\nu ,\rho\) are Young’s modulus Young’s modulus, Poisson’s ratio and mass Density respectively. Also, N is the power-law exponent that \(0 \le N \le \infty\). The Hamilton principle is used to obtain the equilibrium equations, where is expressed [32],

$$\int\limits_{{t_{1} }}^{{t_{2} }} {\left( {\delta U_{e} + \delta U_{h} - \delta T} \right)} dt = 0$$
(7)

where \(U_{e}\) is the strain energy,\(T\) is the kinetic energy of the plate and \(U_{h}\) is the strain energy due to shell rotation. That strain energy is defined [33],

$$U_{e} = \frac{1}{2}\int\limits_{0}^{L} {\int\limits_{0}^{2\pi } {\sigma_{ij} \varepsilon_{ij} Rdxd\theta } }$$
(8)

where strain energy due to shell rotation is expressed [34],

$$\begin{aligned} U_{h} & = \frac{1}{2}\int\limits_{0}^{L} {\int\limits_{0}^{2\pi } {\bar{N}_{\theta } \left\{ {\left( {\frac{1}{R}\frac{\partial u}{\partial \theta }} \right)^{2} + \left[ {\frac{1}{R}\left( {\frac{\partial v}{\partial \theta } + w} \right)} \right]^{2} } \right.} } \\ & \quad \left. { + \left[ {\frac{1}{R}\left( { - \frac{\partial w}{\partial \theta } + v} \right)} \right]^{2} } \right\}Rdxd\theta \\ \end{aligned}$$
(9)

where \(\mathop N\limits^{ - }_{\theta } = \rho h\varOmega^{2} R^{2}\) is centrifugal force that is the result of cylindrical shell rotation. Also, kinetic energy is defined [35],

$$\begin{aligned} T & = \frac{1}{2}\rho h\int\limits_{0}^{L} {\int\limits_{0}^{2\pi } {\bar{V}\bar{V}Rdxd\theta } } \\ \bar{V} & = \mathop u\limits^{ \bullet } i + \mathop v\limits^{ \bullet } j + \mathop w\limits^{ \bullet } k + \left( {\varOmega i \times wk} \right) + \left( {\varOmega i \times vj} \right) \\ \end{aligned}$$
(10)

where i, j, k are vectors along the x, \(\theta\) and z directions, respectively. With substitution of variation of strain energies, and kinetic energy, to Hamilton’s principle, the equations of motion for the cylindrical shell are obtained as [2, 27],

$$\begin{aligned} & \frac{{\partial N_{x} }}{\partial x} + \frac{1}{R}\frac{{\partial N_{x\theta } }}{\partial \theta } + \bar{N}_{\theta } \left( {\frac{1}{{R^{2} }}\frac{{\partial^{2} u}}{{\partial \theta^{2} }} - \frac{1}{R}\frac{\partial w}{\partial x}} \right) - \rho h\frac{{\partial^{2} u}}{{\partial t^{2} }} = 0 \\ & \quad \frac{{\partial N_{x\theta } }}{\partial x} + \frac{1}{R}\frac{{\partial N_{\theta } }}{\partial \theta } + \frac{1}{R}\frac{{\partial M_{x\theta } }}{\partial x} + \frac{1}{{R^{2} }}\frac{{\partial M_{\theta } }}{\partial \theta } + \frac{1}{R}\bar{N}_{\theta } \frac{{\partial^{2} u}}{\partial x\partial \theta } \\ & \quad - \rho h\left( {\frac{{\partial^{2} v}}{{\partial t^{2} }} + 2\varOmega \frac{\partial w}{\partial t} - \varOmega^{2} v} \right) = 0 \\ & \frac{{\partial^{2} M_{x} }}{{\partial x^{2} }} + \frac{2}{R}\frac{{\partial^{2} M_{x\theta } }}{\partial x\partial \theta } - \frac{1}{R}N_{\theta } + \frac{1}{{R^{2} }}\bar{N}_{\theta } \left( {\frac{{\partial^{2} w}}{{\partial \theta^{2} }} - \frac{\partial v}{\partial \theta }} \right) \\ & \quad - \rho h\left( {\frac{{\partial^{2} w}}{{\partial t^{2} }} - 2\varOmega \frac{\partial v}{\partial t} - \varOmega^{2} w} \right) = 0 \\ \end{aligned}$$
(11)

in which the resultant components \(N_{i} ,M_{i}\) are given by,

$$\begin{aligned} \int {\sigma_{i} } dz & = N_{i} ,\left( {i = x,\theta ,x\theta } \right) \\ \int {\sigma_{i} } zdz & = M_{i} ,\left( {i = x,\theta ,x\theta } \right) \\ \end{aligned}$$
(12)

By introducing the Eqs. (1), (4) and (12) in Eq. (11), we have,

$$\begin{aligned} & A_{11} \frac{{\partial^{2} u}}{{\partial x^{2} }} - B_{11} \frac{{\partial^{3} w}}{{\partial x^{3} }} + A_{12} \left( {\frac{1}{R}\frac{{\partial^{2} v}}{\partial x\partial \theta } + \frac{1}{R}\frac{\partial w}{\partial x}} \right) \\ & \quad - B_{12} \left( {\frac{1}{{R^{2} }}\frac{{\partial^{3} w}}{{\partial x\partial \theta^{2} }}} \right.\left. { - \frac{1}{{R^{2} }}\frac{{\partial^{2} v}}{\partial x\partial \theta }} \right) + A_{66} \left( {\frac{1}{R}\frac{{\partial^{2} v}}{\partial x\partial \theta }} \right. \\ & \quad + \left. {\frac{1}{{R^{2} }}\frac{{\partial^{2} u}}{{\partial \theta^{2} }}} \right) - B_{66} \left( {\frac{2}{{R^{2} }}\frac{{\partial^{3} w}}{{\partial x\partial \theta^{2} }}} \right.\left. { - \frac{2}{{R^{2} }}\frac{{\partial^{2} v}}{\partial x\partial \theta }} \right)\mathop + \bar {N}_{\theta } \\ & \quad \left( {\frac{1}{{R^{2} }}\frac{{\partial^{2} u}}{{\partial \theta^{2} }} - \frac{1}{R}\frac{\partial w}{\partial x}} \right) - \rho h\frac{{\partial^{2} u}}{{\partial x^{2} }} = 0 \\ \end{aligned}$$
(13a)
$$\begin{aligned} & A_{12} \frac{1}{R}\frac{{\partial^{2} u}}{\partial x\partial \theta } - B_{12} \frac{1}{{R^{2} }}\frac{{\partial^{3} w}}{{\partial x^{2} \partial \theta }} + A_{22} \left( {\frac{1}{{R^{2} }}\frac{{\partial^{2} v}}{{\partial \theta^{2} }}} \right. \\ & \quad \left. { + \frac{1}{{R^{2} }}\frac{\partial w}{\partial \theta }} \right) - B_{22} \left( {\frac{1}{{R^{3} }}\frac{{\partial^{3} w}}{{\partial \theta^{3} }} + \frac{1}{{R^{3} }}\frac{{\partial^{2} v}}{{\partial \theta^{2} }}} \right) + A_{66} \\ & \quad \left( {\frac{1}{R}\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{1}{R}\frac{{\partial^{2} u}}{\partial x\partial \theta }} \right) - B_{66} \left( {\frac{2}{R}\frac{{\partial^{3} w}}{{\partial x^{2} \partial \theta }} - \frac{2}{R}\frac{{\partial^{2} v}}{{\partial x^{2} }}} \right) \\ & \quad + B_{12} \frac{1}{{R^{2} }}\frac{{\partial^{2} u}}{\partial x\partial \theta } - D_{12} \frac{1}{{R^{2} }}\frac{{\partial^{3} w}}{{\partial x^{2} \partial \theta }} + B_{22} \left( {\frac{1}{{R^{3} }}\frac{{\partial^{2} v}}{{\partial \theta^{2} }}} \right) \\ & \quad \left( { + \frac{1}{{R^{3} }}\frac{\partial w}{\partial \theta }} \right. - D_{22} \left( {\frac{1}{{R^{4} }}\frac{{\partial^{3} w}}{{\partial \theta^{3} }} - \frac{1}{{R^{4} }}\frac{{\partial^{2} v}}{{\partial \theta^{2} }}} \right) + B_{66} \\ & \quad \left( {\frac{2}{R}\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{2}{{R^{2} }}\frac{{\partial^{2} u}}{\partial x\partial \theta }} \right) - D_{66} \left( {\frac{4}{{R^{2} }}\frac{{\partial^{3} w}}{\partial x^{2}\partial \theta } - \frac{4}{{R^{2} }}\frac{{\partial^{2} v}}{{\partial x^{2} }}} \right) \\ & \quad + \frac{1}{R}\bar{N}_{\theta } \frac{{\partial^{2} u}}{\partial x\partial \theta } - \rho h\left( {\frac{{\partial^{2} v}}{{\partial t^{2} }} + 2\varOmega \frac{\partial w}{\partial t} - \varOmega^{2} v} \right) = 0 \\ \end{aligned}$$
(13b)
$$\begin{aligned} & B_{11} \frac{{\partial^{3} u}}{{\partial x^{3} }} - D_{11} \frac{{\partial^{3} w}}{{\partial x^{4} }} + B_{12} \left( {\frac{1}{R}\frac{{\partial^{3} v}}{{\partial x^{2} \partial \theta }} + \frac{1}{R}\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) \\ & \quad - D_{12} \left( {\frac{1}{{R^{2} }}\frac{{\partial^{4} w}}{{\partial x^{2} \partial \theta^{2} }} - \frac{1}{{R^{2} }}\frac{{\partial^{3} v}}{{\partial x^{2} \partial \theta }}} \right)B_{12} \frac{1}{{R^{2} }}\frac{{\partial^{3} u}}{{\partial x\partial \theta^{2} }} \\ & \quad - D_{12} \frac{1}{{R^{2} }}\frac{{\partial^{4} w}}{{\partial x^{2} \partial \theta^{2} }} + B_{22} \left( {\frac{1}{{R^{3} }}\frac{{\partial^{3} v}}{{\partial \theta^{3} }} + \frac{1}{{R^{3} }}\frac{{\partial^{2} w}}{{\partial \theta^{2} }}} \right) \\ & \quad - D_{22} \left( {\frac{1}{{R^{4} }}\frac{{\partial^{4} w}}{{\partial \theta^{4} }} - \frac{1}{{R^{4} }}\frac{{\partial^{3} v}}{{\partial \theta^{3} }}} \right) + B_{66} \left( {\frac{2}{R}\frac{{\partial^{3} v}}{{\partial x^{2} \partial \theta }} + \frac{2}{{R^{2} }}\frac{{\partial^{3} u}}{{\partial x\partial \theta^{2} }}} \right) \\ \end{aligned}$$
$$\begin{aligned} - D_{66} \left( {\frac{4}{{R^{2} }}\frac{{\partial^{4} w}}{{\partial x^{2} \partial \theta^{2} }} - \frac{4}{{R^{2} }}\frac{{\partial^{3} v}}{{\partial x^{2} \partial \theta }}} \right) + A_{12} \frac{1}{R}\frac{\partial u}{\partial x} \hfill \\ - B_{12} \frac{1}{R}\frac{{\partial^{2} w}}{{\partial x^{2} }} + A_{22} \left( {\frac{1}{{R^{2} }}\frac{\partial v}{\partial \theta } + \frac{w}{{R^{2} }}} \right) - B_{22} \hfill \\ \left( {\frac{1}{{R^{3} }}\frac{{\partial^{2} w}}{{\partial \theta^{2} }} + \frac{1}{{R^{3} }}\frac{\partial v}{\partial \theta }} \right) + \frac{1}{{R^{2} }}\mathop {\bar{N}_{\theta }} \left( {\frac{{\partial^{2} w}}{{\partial \theta^{2} }} - \frac{\partial v}{\partial \theta }} \right) \hfill \\ - \rho h\left( {\frac{{\partial^{2} w}}{{\partial t^{2} }} - 2\varOmega \frac{\partial v}{\partial t} - \varOmega^{2} w} \right) = 0 \hfill \\ \end{aligned}$$
(13c)

Coefficients \(A_{ij}\), \(B_{ij}\) and \(D_{ij}\) are defined as follows,

$$\int {\left( {1,z,z^{2} } \right)} Q_{ij} dz = A_{ij} ,B_{ij} ,D_{ij}$$
(14)

3 Analytical solution

In this research, due to the simply support boundary conditions, the Navier’s solution is used to solve the equations. Simply support boundary conditions is expressed as [1, 2],

$$v = w = N_{x} = M_{x} = 0$$
(15)

The Navier’s solution procedure is expressed for simply-supported boundary condition as follows [3, 27],

$$\begin{aligned} u(x,\theta ,t) = U\left( x \right)\cos \left( {\frac{m\pi }{L}x} \right)\cos (n\theta + wt) \hfill \\ v(x,\theta ,t) = V\left( x \right)\sin \left( {\frac{m\pi }{L}x} \right)\sin (n\theta + wt) \hfill \\ w(x,\theta ,t) = W\left( x \right)\sin \left( {\frac{m\pi }{L}x} \right)\cos (n\theta + wt) \hfill \\ \end{aligned}$$
(16)

By introducing the Eq. (16), into Eq. (13), the following relation is obtained,

$$H_{3 \times 3} \left\{ {U,V,W} \right\}^{T} = \left\{ {0,0,0} \right\}^{T}$$
(17)

By equaling the determinant of the H matrix set to zero, the natural frequency of the rotating FGMs cylindrical shell is obtained base on each values of n and m. Also the non-dimensional natural frequency \(\omega^{*} = \omega \sqrt {\rho_{m} R^{2} /E_{m} }\) is used to obtain the results of this research. The \(\rho_{m}\) is mass density of metal, and \(E_{m}\) is Young modulus of metal. Also, the material properties used of the FGMs follows at Table 1 [36].

Table 1 Material properties used for the FGMs
Full size table
Table 2 Comparison of the natural frequency of the FGM cylindrical shell for simply supported boundary conditions (\(m = 1,h/R = 0.002,L/R = 20,\varOmega = 0\))
Full size table

4 Results and discussion

The natural frequency obtained with the method in this study is compared with the results of other investigations and the results are shown in Table 2. Also, material properties considered for to compare the results, are presented in Table 3 [4].

Table 3 Material properties used in the FGM for to compare
Full size table

The FGMs shell for comparison is composed of Nickel on its inner surface and Stainless steel on its outer surface. The comparison demonstrated that has good agreement present method with the result Lam et al. [4].

Table 4 shows the effect of power-law exponent N at different n on the non-dimensional frequency of rotating FGMs (metal outer, ceramic inner) cylindrical shell. That, non-dimensional natural frequency is decreased with increase the volume fraction N. Also, with increase the n, the non-dimensional natural frequency decreased and then increased. In this research, for the all results presented of the diagram, FGMs is considered to be metal on the outer surface and ceramic on the inner surface of the cylinder.

Table 4 Non dimensional natural frequency of the FGMs cylindrical shell with respect to power-law exponent N for different value of n (\(m = 1,h/R = 0.002,L/R = 10,\varOmega = 1\))
Full size table

In Fig. 1, effect of variation of the n on the non-dimensional natural frequency of the rotating FGMs cylindrical shells for different value of rotation is indicated. In this figure, with increase the rotating speed, backward non-dimensional frequency increased and forward non dimensional frequency decreased. Further, with increase of the n from 1 to 3, the backward and forward frequency are reduced and for n = 1 is greater than n = 2, 3.

Fig. 1
figure 1

Effect of variation of the n on the non-dimensional natural frequency for different value of rotation

Full size image

Influence of different value of rotating speed and variation of m on non-dimensional natural frequency of rotating FGMs cylindrical shells is expressed at Fig. 2. The result shown that with increase the rotating speed, forward and backward non-dimensional frequency are increased and decreased, respectively. With increase of the m, difference between backward and forward frequency are reduced. Also, forward and backward non-dimensional frequency are increased with increase of the m.

Fig. 2
figure 2

Effect of variation of the m on the non-dimensional natural frequency for different value of rotation

Full size image

Figure 3 is illustrated the effect of variation of rotation speed on non-dimensional natural frequency for different value of n. Where with increase of the n, forward and backward non-dimensional frequency are decreased and then increased. Also, with increase of the rotating speed, forward and backward non-dimensional frequency are increased. In Fig. 4 influence of different value of rotating speed and variation of m on the non-dimensional natural frequency of rotating FGMs cylindrical shell are studied. It expressed that with increase of the m forward and backward non-dimensional frequency are increased, that with increase of the rotating speed the difference between forward and backward non-dimensional frequency increased.

Fig. 3
figure 3

Effect of variation of rotation on non-dimensional natural frequency for different value of n

Full size image
Fig. 4
figure 4

Effect of variation of rotation on non-dimensional natural frequency for different value of m

Full size image

Figures 5 and 6 shown the influence of variation of m on backward and forward non-dimensional natural frequency for different value of the length to radius ratio (L/R) for \(\varOmega = 10,50\). The result illustrated with increase of the m backward and forward non-dimensional natural frequency increased. Also, backward and forward non-dimensional natural frequency decreased with increase of the length to radius ratio (L/R). That with increase of the rotating speed, the difference between forward and backward non-dimensional frequency increased. Also, in both figures with increase of the length to radius ratio (L/R), in first step, for L/R < 10, the non-dimensional frequency decreased rapidly and then for L/R > 10 mildly declined.

Fig. 5
figure 5

Effect of variation of m on non-dimensional natural frequency for different value of L/R (\(\varOmega = 10\))

Full size image
Fig. 6
figure 6

Effect of variation of m on non-dimensional natural frequency for different value of L/R (\(\varOmega = 50\))

Full size image

Effect of variation of n on the backward and forward non-dimensional natural frequency for different value of the length to radius ratio (L/R) for \(\varOmega = 10,50\) are expressed at Figs. 7 and 8. It is observed that with increase of the L/R, the first step, for L/R < 5 backward and forward non-dimensional natural frequency quickly decreased and then for L/R > 5 slowly decreased. Also, the difference between backward and forward non-dimensional natural frequency with increase of the rotating speed increased. Further with increase of the n, backward and forward non-dimensional natural frequency decreased.

Fig. 7
figure 7

Effect of variation of n on non-dimensional natural frequency for different value of L/R(\(\varOmega = 10\))

Full size image
Fig. 8
figure 8

Effect of variation of n on non-dimensional natural frequency for different value of L/R(\(\varOmega = 50\))

Full size image

5 Conclusions

In the research, free vibration analysis of rotating FGMs cylindrical shells are investigated. The governing equation of motion with Hamilton’s principle method are obtained. Also, Navier’s solution is used for simply supported boundary condition. The result of this study can be expressed as follows:

  1. 1.

    With increasing of the axial wave number n at first step, the forward and backward non-dimensional frequency decreased and then increased.

  2. 2.

    With increase of the L/R ratio, the forward and backward non-dimensional frequency decreased and with increase of the rotating speed difference between forward and backward non-dimensional frequency increased.

  3. 3.

    Also, with increase of the rotating speed, the backward and forward non-dimensional frequency, increased and decreased, respectively.