Introduction

In the past few decades, there has been an increase in the number of people engaging in the analysis of fractional differential equations (FDEs). Classical differential equations in mathematical physics, vibration, engineering, and oscillation are transformed into these by substituting a fractional derivative (FD) of order fulfilling \(1 < \eta \le 2\) for the second-order time derivative. To explain how various materials and processes retain and transmit their unique characteristics, fractional derivatives are a helpful tool.

The analysis of the vibration equation (VE) is both a fascinating and necessary component of the application. Membranes are used to make the many parts that go into cell phones, MP3 players, and other electronic gadgets. Additionally, membranes can be used to study the physics and transmission of waves. In the field of bio-engineering, different kinds of human tissue could be seen as barriers. The natural properties of the VE of an eardrum are used to make the human body tolerant of the conversation component. To make suitable devices to help deaf people, you need to know how membranes work when they vibrate. Inside the ruling equation, the time-fractional derivatives are taken into account. These days, fractional calculus is seen as a helpful tool for figuring out different real-life problems in a way that is both useful and correct. As you can see from the sources, other researchers have done more work in this area [1,2,3,4,5].

Various authors have conducted various types of research on VE. The differential equation was solved by Yildirim et al. [6] using the homotopy perturbation technique (HPM). The TFVE of large membranes was investigated by Mohyud-Din and Yildirim [7] using HPM. The nonlinear vibration model for a pre-stretched membrane was investigated by Sunny et al. [8] using the Adomian decomposition method (ADM). The fractional vibration equation (FVE) was solved by Srivastava et al. [9] utilizing the Laplace decomposition method and the Laplace transform method of q-homotopy analysis. Karunakar et al. [10] solved shifted Chebyshev polynomials based solution of partial differential equations. Analytical approach for traveling wave solution of non-linear fifth-order time-fractional Korteweg–De Vries equation by Sherriffe and Behera [11,12,13]. Singh [14] used Jacobi polynomials to solve the FVE of large membranes.

Most of the authors have taken the variables and parameters involved in the VE as exact (crisp). However, in practice, it can be challenging to determine the parameters due to errors in testing, observations, etc. As a result, the factors and variables must be treated as unknowns. Therefore, uncertainty in differential equations is an essential aspect of practical modeling problems. In this paper, we explore the fuzzy/interval nature of these uncertain relationships. Since solving a fuzzy or interval DE might be challenging, a numerically efficient solution for such a DE is necessary. Chang and Zadeh [15] proposed the concept of a fuzzy derivative, which is often credited to them as the first to do so. Prade and Dubois [16] described and investigated the extension principle from Ref. [15]. Fuzzy DEs (FDEs) and initial value difficulties were the focus of research by Seikkala [17] and Kaleva [18]. Regarding various physical problems associated with differential equations in the presence of uncertainty, Chakraverty et al. [4, 5, 19, 20] have conducted an extensive amount of research.

As a result of the work discussed in this article, the fractional fuzzy vibration equation (FFVE) has been reduced to a parametric form of differential equation, making it possible to apply a new idea known as the double parametric form of fuzzy numbers. After that, a fuzzy/interval solution in double parametric form (DPF) is obtained by solving the corresponding differential equation using ADM. FVE with an uncertain initial condition (IC) has been considered. Uncertainties are expressed in terms of convex normalized triangular fuzzy numbers.

Most of the analyses for the FVE have been noted in literature for the forward case only, which deals with crisp environments and seldom in uncertain environments. Solving the inverse problem related to FVE in an uncertain environment may be interesting. Accordingly, in this work, we have looked for forward as well as inverse problems in a fuzzy-number-based uncertain environment, with the initial condition being a TFN. The novelty of this paper is that it gives an idea of how to figure out unknown parameters by using known displacements of free vibration from numerical results or experiments (if available). In addition to taking less time, this method requires less computing power and higher accuracy. Only a few experts have looked at how to solve fuzzy DE using other methods in the last few years [21,22,23,24]. Tapaswini et al. [25,26,27,28] have explained a few works on uncertain differential equations.

Our work mainly applies ADM to the FVE uncertainty problem,

$$\begin{aligned}{} & {} \frac{\partial ^2 \widetilde{\omega }}{\partial r^{2}} + \frac{1}{r} \frac{\partial \widetilde{\omega }}{\partial r} \nonumber \\{} & {} =\frac{1}{\widetilde{c}^2} \frac{\partial ^\eta \widetilde{\omega } }{\partial t^{\eta }}, \quad r \ge 0, \quad t \ge 0, \quad 1 < \eta \le 2 \end{aligned}$$
(1)

Corresponding fuzzy initial condition (FIC) is considered as

$$\begin{aligned} \widetilde{\omega } (r, 0)= & {} (0.2, 1, 1.8)\varphi (r) \end{aligned}$$
(2)
$$\begin{aligned} \widetilde{\omega }_{t} (r, 0)= & {} \widetilde{c} \zeta (r) \end{aligned}$$
(3)

where \(\varphi (r)\), \(\zeta (r)\) are the functions of the radius of the membrane (r) and, \(\widetilde{c}\) and \(\widetilde{\omega } (r, t)\) are the wave velocity and displacement of free vibration in an uncertain environment.

The structure of the present paper is as follows: “Preliminaries” contains the fundamental concepts of fuzzy theory and the basic definitions of fractional derivatives and integrals. “Double parametric form of FFVE” incorporates the structure of the double parametric form of a fuzzy fractional vibration equation. “Implementing ADM for solving FFVE” implements ADM for solving FFVE. In “Particular cases”, the FICs are given for particular cases. The inverse problem is described in “Inverse Problem”. “Numerical results and discussions” illustrates the numerical results and their discussions. Lastly, the conclusion is drawn in “Conclusion”.

Preliminaries

Definition 1

[29, 30] A fuzzy set \(\widetilde{\omega }\) is defined as the collection of order pairs (h, m(h)), L is the universal set, and h belongs to L, here m(h) as its membership value of \(\omega\) then it can be written as

$$\begin{aligned} \widetilde{\omega } = \left\{ \left( h, m(h)\right) : h \in L, \quad m(h) \in [0, 1] \right\} \end{aligned}$$

Definition 2

Triangular fuzzy number (TFN) [19, 31] The arbitrary TFN is a convex fuzzy set \(\widetilde{\omega } = (\alpha ,\beta ,\gamma )\) is taken into consideration in the real line \({\mathbb {R}}\). The membership function \(\mu _{\widetilde{\omega }}\) of \(\widetilde{\omega }\) is represented as.

$$\begin{aligned} \mu _{\widetilde{\omega } } (x) = {\left\{ \begin{array}{ll} 0, \qquad {x \le \alpha }\\ \frac{x - \alpha }{\beta - \alpha }, \quad {\alpha \le x \le \beta } \\ \frac{\gamma - x}{\gamma - \beta }, \quad {\beta \le x \le \gamma }\\ 0, \qquad {x \ge \gamma } \end{array}\right. } \end{aligned}$$

It satisfies,

  1. 1.

    There exists exactly one \(x_{0}\in \widetilde{\omega }\) such that \(\mu _{\widetilde{\omega } } (x_{0})=1\).

  2. 2.

    \(\mu _{\widetilde{\omega } } (x)\) is piecewise continuous.

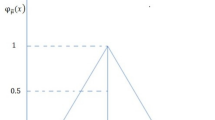
Let us consider a TFN \(\widetilde{\omega } = (\alpha ,\beta ,\gamma )\) as in Fig. 1. By using the \(\sigma\)-cut approach, we may express the TFN \(\widetilde{\omega } = (\alpha ,\beta ,\gamma )\) as an ordered pair of functions, thus \([\underline{\omega }(\sigma ),\overline{\omega }(\sigma )] = [(\beta - \alpha )\sigma + \alpha , -(\gamma - \beta )\sigma + \gamma ]\), where \(\sigma \in [0, 1]\).

Fig. 1
figure 1

Triangular fuzzy number \(\widetilde{\omega }=(\alpha ,\beta ,\gamma )\)

Full size image

Definition 3

[19] Generally, a fuzzy number \(\widetilde{\omega }\) is defined by \(\widetilde{\omega }=[\underline{\omega }(\sigma ),\overline{\omega }(\sigma )]\) in its parametric form, with the required conditions as follows:

  1. (I)

    \(\underline{\omega }(\sigma )\) is an increasing function, bounded and left continuous, between closed intervals 0 to 1.

  2. (II)

    \(\overline{\omega }(\sigma )\) is a decreasing function, bounded, and right continuous, between closed interval 0–1.

  3. (III)

    \(\underline{\omega }(\sigma ) \le \overline{\omega }(\sigma )\), where \(\sigma\) belongs to closed interval 0–1.

Definition 4

Double parametric form of fuzzy number (DPFFN) [19]

Using the single parametric form as discussed in Definition 2, we have \(\widetilde{\omega }=[\underline{\omega }(\sigma ),\overline{\omega }(\sigma )].\)

This may now be expressed in double parametric form as \(\widetilde{\omega } (\sigma , \rho )= \rho (\overline{\omega }(\sigma ) - \underline{\omega }(\sigma )) + \underline{\omega }(\sigma ),\) where \(\sigma\) and \(\rho \in [0, 1].\)

Definition 5

[5, 32] For the fractional integral (FI) of a function \(\omega (t)\), we defined the Riemann–Liouville (RL) type of order \(\eta > 0\). It follows that

$$\begin{aligned} { J^{\eta }\omega (t) }&{=} {\frac{1}{\Gamma (\eta )} \int _{0}^{t}(t-\psi )^{\eta -1} \omega (\psi )d\psi , \quad t>0, \eta \in {\mathbb {R}}^{+} } \end{aligned}$$
(4)
$$\begin{aligned} J^{0}\omega (t)&= \omega (t) \end{aligned}$$
(5)

Definition 6

[5, 32] The fractional derivative of order \(\eta\) and the function \(\omega (t)\) can be represented in the Caputo type as

$$\begin{aligned} ^cD^{\eta }_{t} \omega (t)&= J^{m-\eta }D^m\omega (t) \end{aligned}$$
(6)
$$\begin{aligned}&= \left\{ \frac{1}{\Gamma (m-\eta )} \int _{0}^{t}(t-\psi )^{m-\eta -1}\frac{d^m \omega (\psi )}{dt^{m}}d\psi ,\right. \nonumber \\&\left. \quad m-1< \eta < m\right\} \end{aligned}$$
(7)
$$\begin{aligned}&{ = \frac{d^m\omega (t)}{dt^m}, \quad \eta = m, m \in {\mathbb {N}} } \end{aligned}$$
(8)

Double parametric form of FFVE

First, using the single parametric form, the FFVE is changed into an interval-based fuzzy differential equation. Then, the fuzzy differential equation based on intervals is transformed into a parametric form of FVE with two parameters that can control the uncertainty using the double parametric form. Lastly, ADM is used to solve the fractional differential equation that goes with it to get the desired solution in terms of fuzzy/interval.

Here’s how to rewrite Eq. (1) in a single parametric form:

$$\begin{aligned}{} & {} \left[ \frac{1}{\underline{c}(\sigma )}, \frac{1}{\overline{c}(\sigma )} \right] ^2 \left[ \frac{\partial ^\eta \underline{\omega } (r, t; \sigma ) }{\partial t^{\eta }}, \frac{\partial ^\eta \overline{\omega } (r, t; \sigma ) }{\partial t^{\eta }} \right] \nonumber \\{} & {} \quad = \left[ \frac{\partial ^2 \underline{\omega } (r, t; \sigma )}{\partial r^{2}}, \frac{\partial ^2 \overline{\omega } (r, t; \sigma ) }{\partial r^{2}} \right] \nonumber \\{} & {} \quad +\frac{1}{r} \left[ \frac{\partial \underline{\omega } (r, t; \sigma )}{\partial r}, \frac{\partial \overline{\omega } (r, t; \sigma )}{\partial r} \right] \end{aligned}$$
(9)

with FICs

$$\begin{aligned}{} & {} { \left[ \underline{\omega } (r, 0; \sigma ), \overline{\omega } (r, 0; \sigma ) \right] = \left[ 0.2 + 0.8 \sigma , 1.8 - 0.8 \sigma \right] {\varphi (r)} } \end{aligned}$$
(10)
$$\begin{aligned}{} & {} \left[ \underline{\omega }_{t} (r, 0; \sigma ), \overline{\omega }_{t} (r, 0; \sigma ) \right] \nonumber \\{} & {} \quad = \left[ \underline{c} (\sigma ), \overline{c} (\sigma ) \right] \zeta (r) \end{aligned}$$
(11)

where \(\sigma \in [0, 1]\). The interval form is used in Eqs. (9), (10), and (11). This interval fractional differential equation can be solved directly, although dealing with interval computations may sometimes be a bit challenging. In this case, the writers have used the double parametric form on the aforementioned three equations to get

$$\begin{aligned}{} & {} \left\{ \rho \left( \frac{\partial ^\eta \overline{\omega } (r, t; \sigma ) }{\partial t^{\eta }} - \frac{\partial ^\eta \underline{\omega } (r, t; \sigma ) }{\partial t^{\eta }} \right) + \frac{\partial ^\eta \underline{\omega } (r, t; \sigma ) }{\partial t^{\eta }} \right\} \nonumber \\{} & {} \quad = \left\{ \rho (\overline{c}(\sigma ) - \underline{c}(\sigma )) + \underline{c}(\sigma ) \right\} ^{2} \nonumber \\{} & {} \quad \left( \left\{ \rho \left( \frac{\partial ^{2} \overline{\omega } (r, t; \sigma ) }{\partial r^{2}} - \frac{\partial ^{2} \underline{\omega } (r, t; \sigma ) }{\partial r^{2}} \right) + \frac{\partial ^{2} \underline{\omega } (r, t; \sigma ) }{\partial r^{2}} \right\} \right. \nonumber \\{} & {} \left. \quad + \frac{1}{r} \left\{ \rho \left( \frac{\partial \overline{\omega } (r, t; \sigma ) }{\partial r} - \frac{\partial \underline{\omega } (r, t; \sigma ) }{\partial r} \right) + \frac{\partial \underline{\omega } (r, t; \sigma ) }{\partial r} \right\} \right) \end{aligned}$$
(12)

with FICs

$$\begin{aligned}&\left\{ \rho \left( \overline{\omega } (r, 0 ; \sigma ) - \underline{\omega } (r, 0 ; \sigma ) \right) + \underline{\omega } (r, 0 ; \sigma ) \right\} \nonumber \\&\quad = \left\{ \rho (1.4 - 1.4 \sigma ) + (0.3 +0.7 \sigma ) \right\} \varphi (r) \end{aligned}$$
(13)
$$\begin{aligned}& \left\{ \rho \left( \overline{\omega }_{t} (r, 0 ; \sigma ) - \underline{\omega }_{t} (r, 0 ; \sigma ) \right) +\underline{\omega }_{t} (r, 0 ; \sigma ) \right\} \nonumber \\&\quad = \left\{ \rho \left( \overline{c} (\sigma ) - \underline{c} (\sigma ) \right) + \underline{c} (\sigma ) \right\} \zeta (r) \end{aligned}$$
(14)

Then, let’s define

$$\begin{aligned}&\left\{ \rho \left( \frac{\partial ^\eta \overline{\omega } (r, t ; \sigma ) }{\partial t^{\eta }} - \frac{\partial ^\eta \underline{\omega } (r, t ; \sigma ) }{\partial t^{\eta }} \right) + \frac{\partial ^\eta \underline{\omega } (r, t ; \sigma ) }{\partial t^{\eta }} \right\} \\&\quad = \frac{\partial ^\eta \widetilde{\omega } (r, t ; \sigma , \rho ) }{\partial t^{\eta }} \\&\quad \left\{ \rho \left( \frac{\partial ^{2} \overline{\omega } (r, t ; \sigma ) }{\partial r^{2}} - \frac{\partial ^{2} \underline{\omega } (r, t ; \sigma ) }{\partial r^{2}} \right) + \frac{\partial ^{2} \underline{\omega } (r, t ; \sigma ) }{\partial r^{2}} \right\} \\&= \frac{\partial ^{2} \widetilde{\omega } (r, t ; \sigma , \rho ) }{\partial r^{2}} \\&\quad \left\{ \rho \left( \frac{\partial \overline{\omega } (r, t ; \sigma ) }{\partial r} - \frac{\partial \underline{\omega } (r, t ; \sigma ) }{\partial r} \right) + \frac{\partial \underline{\omega } (r, t ; \sigma ) }{\partial r} \right\} \\&= \frac{\partial \widetilde{\omega } (r, t ; \sigma , \rho ) }{\partial r}\\&\quad \left\{ \rho \left( \overline{\omega } (r, 0 ; \sigma ) - \underline{\omega } (r, 0 ; \sigma ) \right) + \underline{\omega } (r, 0 ; \sigma ) \right\} \\&= \widetilde{\omega } (r, 0 ; \sigma , \rho ) \\&\quad \left\{ \rho \left( \overline{\omega }_{t} (r, 0 ; \sigma ) - \underline{\omega }_{t} (r, 0 ; \sigma ) \right) +\underline{\omega }_{t} (r, 0 ; \sigma ) \right\} \\&= \widetilde{\omega }_{t} (r, 0 ; \sigma , \rho ) \\&\quad \left\{ \rho (\overline{c}(\sigma ) - \underline{c}(\sigma )) + \underline{c}(\sigma ) \right\} \\&= \widetilde{c}(\sigma , \rho ) \end{aligned}$$

Solving Eqs. (12)–(14) using the aforementioned equations yields

$$\begin{aligned} \frac{\partial ^\eta \widetilde{\omega } (r, t ; \sigma , \rho ) }{\partial t^{\eta }} = \widetilde{c} (\sigma , \rho )^{2} \left( \frac{\partial ^{2} \widetilde{\omega } (r, t ; \sigma , \rho ) }{\partial r^{2}} + \frac{1}{r} \frac{\partial \widetilde{\omega } (r, t ; \sigma , \rho ) }{\partial r} \right) \end{aligned}$$
(15)

with FICs

$$\begin{aligned} \widetilde{\omega } (r, 0 ; \sigma , \rho )&= \left\{ \rho (1.4 - 1.4 \sigma ) + (0.3 +0.7 \sigma ) \right\} \varphi (r) \end{aligned}$$
(16)
$$\begin{aligned} \widetilde{\omega }_{t} (r, 0 ; \sigma , \rho )&= \widetilde{c} (\sigma , \rho ) \zeta (r) \end{aligned}$$
(17)

If we solve Eq. (15) using the FICs Eqs. (16)–(17), we can get the solution \(\widetilde{\omega } (r, t; \sigma , \rho )\) for \(\sigma\) and \(\rho\). In order to get the lower and upper solutions in one parametric form, we may use the values \(\rho = 0\) and 1, respectively. The mathematical notations for these are

$$\begin{aligned} \begin{aligned} \widetilde{\omega } (r, t; \sigma , 0)&= \underline{\omega } (r, t; \sigma ) \\ \widetilde{\omega } (r, t; \sigma , 1 )&= \overline{\omega } (r, t; \sigma ) \end{aligned} \end{aligned}$$
(18)

When we change the values of \(\sigma\) and \(\rho\), we may get different uncertain solutions as per the requirement.

Implementing ADM for solving FFVE

The operator form of the FFVE Eq. (1) is expressed as

$$\begin{aligned}{} & {} L_{tt} \widetilde{\omega } (r, t; \sigma , \rho ) = \widetilde{c} (\sigma , \rho )^{2} \frac{\partial ^{2 - \eta } }{\partial t^{2 - \eta }} \nonumber \\{} & {} \quad \left( L_{rr} \widetilde{\omega } (r, t; \sigma , \rho ) + \frac{1}{r} L_{r} \widetilde{\omega } (r, t; \sigma , \rho ) \right) \end{aligned}$$
(19)

where \(L_{tt} = \frac{\partial ^{2} }{\partial t^{2}}, L_{rr} = \frac{\partial ^{2} }{\partial r^{2}}\)    and \(L_{r} = \frac{\partial }{\partial r}\)

Applying the \(L^{-1} _{tt}\) both sides of the above equations we have

$$\begin{aligned}{} & {} \widetilde{\omega } (r, t; \sigma , \rho ) = \sigma _{t} + \widetilde{c} (\sigma , \rho )^{2} L^{-1} _{tt} \left( \frac{\partial ^{2 - \eta } }{\partial t^{2 - \eta }} \left( L_{rr} \widetilde{\omega } (r, t; \sigma , \rho ) \right. \right. \nonumber \\{} & {} \left. \left. \quad + \frac{1}{r} L_{r} \widetilde{\omega } (r, t; \sigma , \rho ) \right) \right) \end{aligned}$$
(20)

The solution \(\widetilde{\omega } (r,t: \sigma , \rho )\) is given by Adomian’s method [33, 34] as a series,

$$\begin{aligned} \widetilde{\omega } (r, t; \sigma , \rho ) = \sum _{n=0}^{\infty } \widetilde{\omega }_{n} (r, t; \sigma , \rho ) \end{aligned}$$
(21)

in which the elements of \(\widetilde{\omega }_{0}, \widetilde{\omega }_{1}, \widetilde{\omega }_{2},...\) are usually found by

$$\begin{aligned} \begin{aligned}&\widetilde{\omega }_{0} (r, t: \sigma , \rho ) \\&= \widetilde{\omega } (r, 0: \sigma , \rho ) + t \widetilde{\omega _t} (r, 0: \sigma , \rho )\\&\quad \widetilde{\omega }_{1} (r, t: \sigma , \rho ) \\&= \widetilde{c} (\sigma , \rho )^{2} L^{-1} _{tt} \\&\quad \left( \frac{\partial ^{2 - \eta } }{\partial t^{2 - \eta }} \left( L_{rr} \widetilde{\omega }_{0} (r, t; \sigma , \rho ) + \frac{1}{r} L_{r} \widetilde{\omega }_{0} (r, t; \sigma , \rho ) \right) \right) \\&\quad \widetilde{\omega }_{2} (r, t: \sigma , \rho )\\&= \widetilde{c} (\sigma , \rho )^{2} L^{-1} _{tt} \\&\quad \left( \frac{\partial ^{2 - \eta } }{\partial t^{2 - \eta }} \left( L_{rr} \widetilde{\omega }_{1} (r, t; \sigma , \rho ) + \frac{1}{r} L_{r} \widetilde{\omega }_{1} (r, t; \sigma , \rho ) \right) \right) \\&\quad ...\\&\quad \widetilde{\omega }_{k} (r, t: \sigma , \rho ) \\&= \widetilde{c} (\sigma , \rho )^{2} L^{-1} _{tt} \\&\quad \left( \frac{\partial ^{2 - \eta } }{\partial t^{2 - \eta }} \left( L_{rr} \widetilde{\omega }_{k - 1} (r, t; \sigma , \rho ) + \frac{1}{r} L_{r} \widetilde{\omega }_{k - 1} (r, t; \sigma , \rho ) \right) \right) \end{aligned} \end{aligned}$$
(22)

The final kth term series solution is

$$\begin{aligned}&\widetilde{\omega } (r, t; \sigma , \rho ) = \widetilde{\omega }_{0} (r, t: \sigma , \rho ) + \widetilde{\omega }_{1} (r, t: \sigma , \rho ) \nonumber \\&\quad + \widetilde{\omega }_{2} (r, t: \sigma , \rho ) + \cdots +\widetilde{\omega }_{k - 1} (r, t: \sigma , \rho ). \end{aligned}$$
(23)

Particular cases

This paper uses the single parametric form of FIC and wave velocity as

$$\begin{aligned} \widetilde{\omega } (r, 0; \sigma ) = \left[ 0.2 + 0.8 \sigma , 1.8 - 0.8 \sigma \right] \varphi (r), \quad \widetilde{\omega }_{t} (r, 0; \sigma ) = \left[ 5.2 + 0.8 \sigma , 6.8 - 0.8 \sigma \right] \zeta (r) \end{aligned}$$

and \(\widetilde{c} (\sigma ) = \left[ 5.2 + 0.8 \sigma , 6.8 - 0.8 \sigma \right]\). A few specific cases are considered by looking at different values of \(\varphi (r)\) and \(\zeta (r)\), which may be found in reference [6].

Case 1: When \(\varphi (r) = r^2\) and \(\zeta (r) = r,\) the corresponding Eqs. (1)–(3) are

$$\begin{aligned}&\frac{\partial ^\eta \widetilde{\omega } }{\partial t^{\eta }} \\&= \left[ 5.2 + 0.8 \sigma , 6.8 - 0.8 \sigma \right] ^{2} \left( \frac{\partial ^{2} \widetilde{\omega } }{\partial r^{2}} + \frac{1}{r} \frac{\partial \widetilde{\omega } }{\partial r} \right) \\&\quad \widetilde{\omega } (r, 0; \sigma ) \\&= \left[ 0.2 + 0.8 \sigma , 1.8 - 0.8 \sigma \right] \varphi (r) \\&\quad \widetilde{\omega }_{t} (r, 0; \sigma ) \\&= \left[ 5.2 + 0.8 \sigma , 6.8 - 0.8 \sigma \right] \zeta (r) \end{aligned}$$

These three equations can be written in the following double-parametric form:

$$\begin{aligned}&\frac{\partial ^\eta \widetilde{\omega } (r, t ; \sigma , \rho ) }{\partial t^{\eta }} \nonumber \\&\quad = \left[ \rho (1.6 - 1.6 \sigma ) + ( 5.2 +0.8 \sigma )\right] ^{2} \nonumber \\&\qquad \left( \frac{\partial ^{2} \widetilde{\omega } (r, t ; \sigma , \rho ) }{\partial r^{2}}\right. \nonumber \\&\qquad \left. + \frac{1}{r} \frac{\partial \widetilde{\omega } (r, t ; \sigma , \rho ) }{\partial r} \right) \end{aligned}$$
(24)
$$\begin{aligned}&\qquad \widetilde{\omega } (r, 0 ; \sigma , \rho ) = \left\{ \rho (1.6 - 1.6 \sigma ) + (0.2 +0.8 \sigma ) \right\} r \end{aligned}$$
(25)
$$\begin{aligned}&\qquad \widetilde{\omega }_{t} (r, 0 ; \sigma , \rho ) = \left\{ \rho (1.6 - 1.6 \sigma ) + (5.2 +0.8 \sigma ) \right\} \end{aligned}$$
(26)

Putting Eqs. (24)–(26) into Eq. (22), we get

$$\begin{aligned} \begin{aligned}&\widetilde{\omega }_{0} (r, t ; \sigma , \rho ) \\&= \left( \rho (1.6 - 1.6 \sigma ) + ( 5.2 +0.8 \delta ) \right) r t \\&\quad + \left( \rho (1.6 - 1.6 \sigma ) + ( 0.2 +0.8 \sigma ) \right) r^2 \\&\quad \widetilde{\omega }_{1} (r, t ; \sigma , \rho ) \\&= 4 \left( \rho (1.6 - 1.6 \sigma ) + (0.2 +0.8 \sigma ) \right) \\&\quad \left( \rho (1.6 - 1.6 \sigma ) + (5.2 +0.8 \sigma ) \right) ^2 \frac{t^{\eta }}{\Gamma (\eta +1) } \\&\quad + \frac{1}{r} \left( \rho (1.6 - 1.6 \sigma ) + (5.2 +0.8 \sigma ) \right) ^3 \frac{t^{\eta + 1}}{\Gamma (\eta +2) } \\&\quad \widetilde{\omega }_{2} (r, t ; \sigma , \rho ) \\&= \frac{\left( \rho (1.6 - 1.6 \sigma ) + (5.2 +0.8 \sigma ) \right) ^5}{r^3} \\&\quad \frac{t^{2\eta + 1}}{\Gamma (2\eta +2) } \\&\quad \widetilde{\omega }_{3} (r, t ; \sigma , \rho ) \\&= \frac{9 \left( \rho (1.6 - 1.6 \sigma ) + (5.2 +0.8 \sigma ) \right) ^7}{r^5} \\&\quad \frac{t^{3\eta + 1}}{\Gamma (3\eta +2) } \\&\quad \widetilde{\omega }_{4} (r, t ; \sigma , \rho ) \\&= \frac{225 \left( \rho (1.6 - 1.6 \sigma ) + (5.2 +0.8 \sigma ) \right) ^9}{r^7} \\&\quad \frac{t^{4\eta + 1}}{\Gamma (4\eta +2) } \end{aligned} \end{aligned}$$
(27)

and so on.

The obtained 5th term series solution is

$$\begin{aligned}{} & {} \widetilde{\omega } (r, t; \sigma , \rho ) = \widetilde{\omega }_{0} (r, t: \sigma , \rho ) + \widetilde{\omega }_{1} (r, t: \sigma , \rho ) \nonumber \\{} & {} \quad +\widetilde{\omega }_{2} (r, t: \sigma , \rho ) +\widetilde{\omega }_{3} (r, t: \sigma , \rho ) + \widetilde{\omega }_{4} (r, t: \sigma , \rho ) +... \end{aligned}$$
(28)

The final series solution is

$$\begin{aligned} \begin{aligned}&\widetilde{\omega } (r, t ; \sigma , \rho ) = \left( \rho (1.6 - 1.6 \sigma ) + ( 5.2 +0.8 \delta ) \right) r t \\&\quad + \left( \rho (1.6 - 1.6 \sigma ) + ( 0.2 +0.8 \sigma ) \right) r^2 \\&\quad + 4 \left( \rho (1.6 - 1.6 \sigma ) + (0.2 +0.8 \sigma ) \right) \\&\quad \left( \rho (1.6 - 1.6 \sigma ) + (5.2 +0.8 \sigma ) \right) ^2 \frac{t^{\eta }}{\Gamma (\eta +1) } \\&\quad + \frac{1}{r} \left( \rho (1.6 - 1.6 \sigma ) + (5.2 +0.8 \sigma ) \right) ^3 \\&\quad \frac{t^{\eta + 1}}{\Gamma (\eta +2) } + \frac{\left( \rho (1.6 - 1.6 \sigma ) + (5.2 +0.8 \sigma ) \right) ^5}{r^3} \\&\quad \frac{t^{2\eta + 1}}{\Gamma (2\eta +2) } \\&\quad + \frac{9 \left( \rho (1.6 - 1.6 \sigma ) + (5.2 +0.8 \sigma ) \right) ^7}{r^5}\\&\quad \frac{t^{3\eta + 1}}{\Gamma (3\eta +2) } + \frac{225 \left( \rho (1.6 - 1.6 \sigma ) + (5.2 +0.8 \sigma ) \right) ^9}{r^7} \\&\frac{t^{4\eta + 1}}{\Gamma (4\eta +2) } + \cdots \end{aligned} \end{aligned}$$
(29)

By putting \(\rho = 0\) and \(\rho = 1\) into Eq. (29), we get lower and upper fuzzy solutions as follows,

$$\begin{aligned} \begin{aligned}&\widetilde{\omega } (r, t ; \sigma , 0) = (0.2 + 0.8 \sigma ) r^2 \\&\quad + (5.2 + 0.8 \sigma ) r t + 4 (0.2 + 0.8 \sigma ) (5.2 + 0.8 \sigma )^2 \frac{t^{\eta }}{\Gamma (\eta + 1) } \\&\quad + \frac{1}{r} (5.2 + 0.8 \sigma )^3 \frac{t^{\eta + 1}}{\Gamma (\eta + 2) } + \frac{1}{r^3} (5.2 + 0.8 \sigma )^5 \frac{t^{2\eta + 1}}{\Gamma (2\eta + 2) } \\&\quad +\frac{9}{r^5} (5.2 + 0.8 \sigma )^7 \frac{t^{3\eta + 1}}{\Gamma (3\eta + 2) }\\&\quad + \frac{225}{r^7} (5.2 + 0.8 \sigma )^9 \frac{t^{4\eta + 1}}{\Gamma (4\eta + 2) } + \cdots \end{aligned} \end{aligned}$$
(30)

and

$$\begin{aligned} \begin{aligned}&\widetilde{\omega } (r, t ; \sigma , 1) = (1.8 - 0.8 \sigma ) r^2 + (6.8 - 0.8 \sigma ) r t \\&\quad + 4 (1.8 - 0.8 \sigma ) (6.8 - 0.8 \sigma )^2 \frac{t^{\eta }}{\Gamma (\eta + 1) } \\&\quad + \frac{1}{r} (6.8 - 0.8 \sigma )^3 \frac{t^{\eta + 1}}{\Gamma (\eta + 2) } \\&\quad + \frac{1}{r^3} (6.8 - 0.8 \sigma )^5 \frac{t^{2\eta + 1}}{\Gamma (2\eta + 2) } \\&\quad +\frac{9}{r^5} (6.8 - 0.8 \sigma )^7 \frac{t^{3\eta + 1}}{\Gamma (3\eta + 2) }\\&+ \frac{225}{r^7} (6.8 - 0.8 \sigma )^9 \frac{t^{4\eta + 1}}{\Gamma (4\eta + 2) } + \cdots \end{aligned} \end{aligned}$$
(31)

In particular, it is seen that the solution obtained by the present method at \(\sigma = 1\) and \(c = 6\) is the same as that obtained by using the value of \(\eta = 2\), Yildirim et al. [6]. The series mentioned above will converge if and only if the values of \(\mid \frac{t}{r} \mid \le 1\).

Case 2: Here we consider \(\varphi (r) = r\) and \(\zeta (r) = 1\). In a similar way as above, we get the solution as

$$\begin{aligned} \begin{aligned}&\widetilde{\omega } (r, t ; \sigma , \rho ) = \left( \rho (1.6 - 1.6 \sigma ) + ( 5.2 +0.8 \delta ) \right) t \\&\quad + \left( \rho (1.6 - 1.6 \sigma ) + ( 0.2 +0.8 \sigma ) \right) r \\&\quad + \left( \rho (1.6 - 1.6 \sigma ) + (0.2 +0.8 \sigma ) \right) \left( \rho (1.6 - 1.6 \sigma ) \right. \\&\quad \left. + (5.2 +0.8 \sigma ) \right) ^2 \frac{t^{\eta }}{r \Gamma (\eta +1) } \\&\quad + \left( \rho (1.6 - 1.6 \sigma ) + (0.2 +0.8 \sigma ) \right) \left( \rho (1.6 - 1.6 \sigma ) \right. \\&\left. \quad + (5.2 +0.8 \sigma ) \right) ^4 \frac{t^{2 \eta }}{r^3 \Gamma (2 \eta +1) }\\&\quad + 9 \left( \rho (1.6 - 1.6 \sigma ) + (0.2 +0.8 \sigma ) \right) \left( \rho (1.6 - 1.6 \sigma ) \right. \\&\left. \quad + (5.2 +0.8 \sigma ) \right) ^6 \frac{t^{3 \eta }}{r^5 \Gamma (3 \eta +1) } \\&\quad + 225 \left( \rho (1.6 - 1.6 \sigma ) + (0.2 +0.8 \sigma ) \right) \left( \rho (1.6 - 1.6 \sigma ) \right. \\&\left. \quad + (5.2 +0.8 \sigma ) \right) ^8 \frac{t^{4 \eta }}{r^7 \Gamma (4 \eta +1) } + \cdots \end{aligned} \end{aligned}$$
(32)

By plugging \(\rho = 0\) and \(\rho = 1\) into Eq. (32), we get the lower and upper bounds of the fuzzy solution as

$$\begin{aligned} \begin{aligned}&\widetilde{\omega } (r, t ; \sigma , 0) = (0.2 + 0.8 \sigma ) r + (5.2 + 0.8 \sigma ) t \\&\quad + (0.2 + 0.8 \sigma ) (5.2 + 0.8 \sigma )^2 \frac{t^{\eta }}{r \Gamma (\eta + 1) } \\&\quad + (0.2 + 0.8 \sigma ) (5.2 + 0.8 \sigma )^4 \frac{t^{2 \eta }}{r^3 \Gamma (2 \eta + 1) } \\&\quad + 9 (0.2 + 0.8 \sigma ) (5.2 + 0.8 \sigma )^6 \frac{t^{3 \eta }}{r^5 \Gamma (3 \eta + 1) } \\&\quad + 225 (0.2 + 0.8 \sigma ) (5.2 + 0.8 \sigma )^8 \frac{t^{4 \eta }}{r^7 \Gamma (4 \eta + 1) } + \cdots \end{aligned} \end{aligned}$$
(33)

and

$$\begin{aligned} \begin{aligned}&\widetilde{\omega } (r, t ; \sigma , 1) = (1.8 - 0.8 \sigma ) r + (6.8 - 0.8 \sigma ) t \\&\quad + (1.8 - 0.8 \sigma ) (6.8 - 0.8 \sigma )^2 \frac{t^{\eta }}{r \Gamma (\eta + 1) } \\&\quad + (1.8 - 0.8 \sigma ) (6.8 - 0.8 \sigma )^4 \frac{t^{2 \eta }}{r^3 \Gamma (2 \eta + 1) } \\&\quad + 9 (1.8 - 0.8 \sigma ) (6.8 - 0.8 \sigma )^6 \frac{t^{3 \eta }}{r^5 \Gamma (3 \eta + 1) } \\&\quad + 225 (1.8 - 0.8 \sigma ) (6.8 - 0.8 \sigma )^8 \frac{t^{4 \eta }}{r^7 \Gamma (4 \eta + 1) } + \cdots \end{aligned} \end{aligned}$$
(34)

The crisp result of Yildirim et al. [6] at \(\eta = 2\) matches the obtained result for \(c = 6\) and \(\sigma = 1\).

Case 3: Let us take now, \(\varphi (r) = \sqrt{r}\) and \(\zeta (r) = \frac{1}{\sqrt{r}}\), and then in double parametric form, the solution can be expressed as

$$\begin{aligned} \begin{aligned}&\widetilde{\omega } (r, t ; \sigma , \rho ) = \left( \rho (1.6 - 1.6 \sigma ) + ( 0.2 +0.8 \sigma ) \right) \sqrt{r} \\&\quad + \left( \rho (1.6 - 1.6 \sigma ) + ( 5.2 +0.8 \sigma ) \right) \frac{t}{\sqrt{r}} \\&\quad + \left( \rho (1.6 - 1.6 \sigma ) + ( 0.2 +0.8 \sigma ) \right) \\&\quad \left( \rho (1.6 - 1.6 \sigma ) + ( 5.2 +0.8 \sigma ) \right) ^{2} \\&\quad \frac{1}{4 r^{\frac{3}{2}}} \frac{t^{\eta }}{\Gamma (\eta + 1) } \\&\quad + \left( \rho (1.6 - 1.6 \sigma ) + ( 5.2 +0.8 \sigma ) \right) ^{3}\\&\quad \frac{1}{4 r^{\frac{5}{2}}} \frac{t^{\eta + 1}}{\Gamma (\eta + 2) } \\&\quad + \left( \rho (1.6 - 1.6 \sigma ) + ( 0.2 +0.8 \sigma ) \right) \\&\quad \left( \rho (1.6 - 1.6 \sigma ) + ( 5.2 +0.8 \sigma ) \right) ^{4} \\&\quad \frac{9}{16 r^{\frac{7}{2}}} \frac{t^{2 \eta }}{\Gamma (2 \eta + 1) } \\&\quad + \left( \rho (1.6 - 1.6 \sigma ) + ( 5.2 +0.8 \sigma ) \right) ^{5} \\&\quad \frac{25}{16 r^{\frac{9}{2}}} \frac{t^{2\eta + 1}}{\Gamma (2\eta + 2) } \\&\quad + \left( \rho (1.6 - 1.6 \sigma ) + ( 0.2 +0.8 \sigma ) \right) \\&\quad \left( \rho (1.6 - 1.6 \sigma ) + ( 5.2 +0.8 \sigma ) \right) ^{6} \\&\quad \frac{441}{64 r^{\frac{11}{2}}} \frac{t^{3\eta }}{\Gamma (3\eta + 1) } \\&\quad + \left( \rho (1.6 - 1.6 \sigma ) + ( 5.2 +0.8 \sigma ) \right) ^{7} \\&\quad \frac{2025}{64 r^{\frac{13}{2}}} \frac{t^{3\eta + 1}}{\Gamma (3\eta + 2) }\\&\quad +\left( \rho (1.6 - 1.6 \sigma ) + ( 0.2 +0.8 \sigma ) \right) \\&\quad \left( \rho (1.6 - 1.6 \sigma ) + ( 5.2 +0.8 \sigma ) \right) ^{8} \\&\quad \frac{53361}{256 r^{\frac{15}{2}}} \frac{t^{4\eta }}{\Gamma (4\eta + 1) } \\&\quad + \left( \rho (1.6 - 1.6 \sigma ) + ( 5.2 +0.8 \sigma ) \right) ^{9} \\&\quad \frac{342225}{256 r^{\frac{17}{2}}} \frac{t^{4\eta + 1}}{\Gamma (4\eta + 2) } + \cdots \end{aligned} \end{aligned}$$
(35)

The lower and upper fuzzy solution of the present case is obtained as

$$\begin{aligned} \begin{aligned}&\widetilde{\omega } (r, t ; \sigma , 0) = ( 5.2 +0.8 \sigma ) \frac{t}{\sqrt{r}} \\&\qquad + ( 0.2 +0.8 \sigma ) \sqrt{r} \\&\qquad + ( 0.2 +0.8 \sigma ) ( 5.2 +0.8 \sigma )^{2} \frac{1}{4 r^{\frac{3}{2}} } \frac{t^{\eta }}{\Gamma (\eta + 1) } \\&\qquad + ( 5.2 +0.8 \sigma )^{3} \frac{1}{4 r^{\frac{5}{2}} } \frac{t^{\eta + 1}}{\Gamma (\eta + 2) } \\&\qquad + ( 0.2 +0.8 \sigma ) ( 5.2 +0.8 \sigma )^{4} \frac{9}{16 r^{\frac{7}{2}} } \frac{t^{2\eta }}{\Gamma (2\eta + 1) } \\&\qquad + ( 5.2 +0.8 \sigma )^{5} \frac{25}{16 r^{\frac{9}{2}} } \frac{t^{2\eta +1}}{\Gamma (2\eta + 2) } \\&\qquad + ( 0.2 +0.8 \sigma ) ( 5.2 +0.8 \sigma )^{6} \frac{441}{64 r^{\frac{11}{2}} } \frac{t^{3\eta }}{\Gamma (3\eta + 1) } \\&\qquad + ( 5.2 +0.8 \sigma )^{7} \frac{2025}{64 r^{\frac{13}{2}} } \frac{t^{3\eta +1}}{\Gamma (3\eta + 2) } \\&\qquad + ( 0.2 +0.8 \sigma ) ( 5.2 +0.8 \sigma )^{8} \frac{53361}{256 r^{\frac{15}{2}} } \frac{t^{4\eta }}{\Gamma (4\eta + 1) } \\&\qquad + ( 5.2 +0.8 \sigma )^{9} \frac{342225}{256 r^{\frac{17}{2}} } \frac{t^{4\eta +1}}{\Gamma (4\eta + 2) } + \cdots \end{aligned} \end{aligned}$$
(36)

and

$$\begin{aligned} \begin{aligned}&\widetilde{\omega } (r, t ; \sigma , 1) = ( 6.8 - 0.8 \sigma ) \frac{t}{\sqrt{r}} \\&\quad + ( 1.8 - 0.8 \sigma ) \sqrt{r} + ( 1.8 - 0.8 \sigma ) ( 6.8 - 0.8 \sigma )^{2} \\&\quad \frac{1}{4 r^{\frac{3}{2}} } \frac{t^{\eta }}{\Gamma (\eta + 1) } \\&\quad + ( 6.8 - 0.8 \sigma )^{3} \frac{1}{4 r^{\frac{5}{2}} } \frac{t^{\eta + 1}}{\Gamma (\eta + 2) } \\&\quad + ( 1.8 - 0.8 \sigma ) ( 6.8 - 0.8 \sigma )^{4} \frac{9}{16 r^{\frac{7}{2}} } \frac{t^{2\eta }}{\Gamma (2\eta + 1) } \\&\quad + ( 6.8 - 0.8 \sigma )^{5} \frac{25}{16 r^{\frac{9}{2}} } \frac{t^{2\eta +1}}{\Gamma (2\eta + 2) } \\&\quad + ( 1.8 - 0.8 \sigma ) ( 6.8 - 0.8 \sigma )^{6} \frac{441}{64 r^{\frac{11}{2}} } \frac{t^{3\eta }}{\Gamma (3\eta + 1) } \\&\quad + ( 6.8 - 0.8 \sigma )^{7} \frac{2025}{64 r^{\frac{13}{2}} } \frac{t^{3\eta +1}}{\Gamma (3\eta + 2) } \\&\quad + ( 1.8 - 0.8 \sigma ) ( 6.8 - 0.8 \sigma )^{8} \frac{53361}{256 r^{\frac{15}{2}} } \frac{t^{4\eta }}{\Gamma (4\eta + 1) } \\&\quad + ( 6.8 - 0.8 \sigma )^{9} \frac{342225}{256 r^{\frac{17}{2}} } \frac{t^{4\eta +1}}{\Gamma (4\eta + 2) } + \cdots \end{aligned} \end{aligned}$$
(37)

respectively.

Case 4: We assume \(\varphi (r) = r^2\) and \(\zeta (r) = 1\), then we obtain the solution as

$$\begin{aligned} \begin{aligned}&\widetilde{\omega } (r, t ; \sigma , \rho ) = \left( \rho (1.6 - 1.6 \sigma ) + ( 5.2 +0.8 \delta ) \right) t \\&\quad + \left( \rho (1.6 - 1.6 \sigma ) + ( 0.2 +0.8 \sigma ) \right) r^2 \\&\quad + 4 \left( \rho (1.6 - 1.6 \sigma ) + (0.2 +0.8 \sigma ) \right) \\&\quad \left( \rho (1.6 - 1.6 \sigma ) + (5.2 +0.8 \sigma ) \right) ^2 \frac{t^{\eta }}{\Gamma (\eta +1) } \\ \end{aligned} \end{aligned}$$
(38)

In this case, the lower and upper solutions are as follows:

$$\begin{aligned} \begin{aligned}&\widetilde{\omega } (r, t ; \sigma , 0) = (0.2 + 0.8 \sigma ) r^2 \\&\quad + (5.2 + 0.8 \sigma ) t + 4 (0.2 + 0.8 \sigma ) (5.2 + 0.8 \sigma )^2 \\&\quad \frac{t^{\eta }}{\Gamma (\eta + 1) } \\ \end{aligned} \end{aligned}$$
(39)

and

$$\begin{aligned} \begin{aligned}&\widetilde{\omega } (r, t ; \sigma , 1) = (1.8 - 0.8 \sigma ) r^2 \\&\quad + (6.8 - 0.8 \sigma ) t + 4 (1.8 - 0.8 \sigma ) (6.8 - 0.8 \sigma )^2 \\&\quad \frac{t^{\eta }}{\Gamma (\eta + 1) } \\ \end{aligned} \end{aligned}$$
(40)

Case 5: Let us consider \(\varphi (r) = r^{2}\) and \(\zeta (r) = r^{2}\), then we have

$$\begin{aligned} \begin{aligned}&\widetilde{\omega } (r, t ; \sigma , \rho ) \\&= \left( \rho (1.6 - 1.6 \sigma ) + ( 5.2 +0.8 \delta ) \right) r^{2} t \\&\quad + \left( \rho (1.6 - 1.6 \sigma ) + ( 0.2 +0.8 \sigma ) \right) r^2 \\&\quad + 4 \left( \rho (1.6 - 1.6 \sigma ) + (0.2 +0.8 \sigma ) \right) \\&\quad \left( \rho (1.6 - 1.6 \sigma ) + (5.2 +0.8 \sigma ) \right) ^2 \frac{t^{\eta }}{\Gamma (\eta +1) } \\&\quad + 4 \left( \rho (1.6 - 1.6 \sigma ) + (5.2 +0.8 \sigma ) \right) ^{3} \\&\quad \frac{t^{\eta + 1}}{\Gamma (\eta + 2) } \end{aligned} \end{aligned}$$
(41)

Solution sets for the lower and upper bounds are

$$\begin{aligned} \begin{aligned}&\widetilde{\omega } (r, t ; \sigma , 0) = (0.2 + 0.8 \sigma ) r^2 + (5.2 + 0.8 \sigma ) r^{2} t \\&\quad + 4 (0.2 + 0.8 \sigma ) (5.2 + 0.8 \sigma )^2 \frac{t^{\eta }}{\Gamma (\eta + 1) } \\&\quad + 4 (5.2 + 0.8 \sigma )^3 \frac{t^{\eta + 1}}{\Gamma (\eta + 2) } \end{aligned} \end{aligned}$$
(42)

and

$$\begin{aligned} \begin{aligned}&\widetilde{\omega } (r, t ; \sigma , 1) = (1.8 - 0.8 \sigma ) r^2 + (6.8 - 0.8 \sigma ) r^{2} t \\&\quad + 4 (1.8 - 0.8 \sigma ) (6.8 - 0.8 \sigma )^2 \frac{t^{\eta }}{\Gamma (\eta + 1) } \\&\quad + 4 (6.8 - 0.8 \sigma )^3 \frac{t^{\eta + 1}}{\Gamma (\eta + 2) } \end{aligned} \end{aligned}$$
(43)

Inverse Problem

In order to look at the inverse case, let us suppose that we know the wave displacement \(\widetilde{\omega }\) from the numerical or experiment procedure and the given fuzzy displacement is \(\widetilde{\omega } = [\omega _l, \omega _c, \omega _u]\) for particular \(\varphi\) and \(\zeta\) values. The unknown wave velocity \(\widetilde{c}\) is required to obtain. It is possible to create a discrete, double-parametric form of the provided fuzzy displacement as

$$\begin{aligned}{} & {} \widetilde{\omega } = [ \omega _l, \omega _c, \omega _u ] \nonumber \\{} & {} \quad = \rho (\omega _u - \omega _l) (1 - \sigma ) + \omega _l \nonumber \\{} & {} \qquad + (\omega _c - \omega _l), \quad \sigma , \rho \in [0, 1] \end{aligned}$$
(44)

where \(\omega _l\) = fuzzy lower displacement, \(\omega _c\) = fuzzy center displacement, \(\omega _u\) = fuzzy upper displacement. The TFN’s fuzziness, \(\widetilde{\omega } = [ \omega _l, \omega _c, \omega _u ]\), is determined by the values of \(\sigma\) and \(\rho\).

It is possible to obtain a nonlinear algebraic equation in terms of \(\widetilde{\omega } (\sigma , \rho )\) by inserting Eq. (44) into Eq. (28). Therefore, the algebraic equation for obtaining the wave velocity in double parametric form can be solved using any efficient numerical approach. Once again, the desired results can be attained by converting the double parametric form of the wave velocity acquired to TFN. In this case, the desired wave velocity was determined using an approximation based on five terms of fuzzy displacement. Substituting Eq. (44) into Eq. (23) and solving the resulting equation yields the kth-term approximation for wave velocity. This procedure may be repeated for every case.

Numerical results and discussions

Firstly, we will discuss the forward problem of approximate solutions for FFVE of large membranes using ADM. The validity of the present study is shown by comparing the solutions found with those found in the work of Yildirim et al. [6]. The calculated results are shown graphically in Figs. 2, 3, and 4. We found the numerical solutions to Eqs. (30), (31), (33), (34), (36), (37), (39), (40), (42), and (43) by limiting the infinite series to the first five terms. The series ends after the second term in cases 4 and 5. Particular cases 1–5 illustrate the lower and upper bounds of fuzzy solutions to the problem outlined in the title by varying t from 0 to 2 while maintaining the membrane radius constant at \(r = 25\). Subsequently, Fig. 2a–e illustrate interval solutions for various scenarios, where \(\sigma\)-cut is any of 0.2, 0.4, 0.6, 0.8, and 1, time t 0–8, and r equals 25. The interval solutions are all located on either side of the exact result \((\sigma = 1)\), as illustrated in Fig. 3a–e. Similarly, Fig. 4a–e represent the interval solutions for various r values at time \(t = 1\). For all cases, it is important to observe that the present results at \(\sigma = 1\) coincide precisely with the solution proposed by Yildirim et al. [6]. Tables 1, 2, 3 and 4 show that when \(\sigma = 1\), the results obtained match the solution of Yildirim et al. [6], with the upper and lower limits being the same for each of the five cases. The left and right boundaries of the unknown displacement expand with time for various values of \(\sigma\) and r, as presented in Fig. 3a–e. Additionally, for cases 1–3, as shown in Fig. 4a–c for various values of \(\sigma\) and t, the fuzzy displacement decreases initially and then rises as r increases. The depiction of the behaviour as r increases may be seen in Fig. 4d and e, corresponding to cases 4 and 5, respectively.

Fig. 2
figure 2

All cases of fuzzy displacement of membranes at \(\eta = 1.5\) and \(r = 25\), red = lower solution, green = upper solution

Full size image
Fig. 3
figure 3

All cases of interval solutions for fuzzy displacement at \(\eta = 1.5\) and \(r = 25\)

Full size image
Fig. 4
figure 4

All cases of interval solutions for fuzzy displacement at \(\eta = 1.5\) and \(t = 1\)

Full size image
Table 1 Fuzzy and crisp solutions at \(\eta = 2\) and \(r = 25\) (for case 1)
Full size table
Table 2 Fuzzy and crisp solutions at \(\eta = 2\) and \(r = 25\) (for case 2)
Full size table
Table 3 Fuzzy and crisp solutions at \(\eta = 2\) and \(r = 25\) (for case 3)
Full size table
Table 4 Fuzzy and crisp solutions at \(\eta = 2\) and \(r = 25\) (for cases 4 and 5)
Full size table

In the inverse case, we have to calculate fuzzy velocity. For these, known parameters are \(\widetilde{\omega }(t), \varphi\) and \(\zeta\) to use in different cases, that is, what are five possible cases used in forward cases that we are also operating in the inverse case, which are named cases 6–10. Here, the Fuzzy displacement \(\widetilde{\omega }(t)\) is known for the particular values \(r = 25\) and \(\eta = 2\), respectively. The required fuzzy velocity for the given fuzzy displacement has been computed using the procedure discussed in “Inverse Problem”. That information is shown in Tables 5, 6, 7 and 8. To find the velocity for \(\widetilde{\omega }(0.2), r = 25\), and \(\eta = 2\), look at the first row of Table 5. The second row shows the same thing for \(\widetilde{\omega } (0.4), r = 25,\) and \(\eta = 2,\) and so on. From the last column of Table 5, it may be observed that every row of the table converges to the same fuzzy velocity \(\widetilde{\omega } = [5.2 + 0.8 \sigma , \quad 6.8- 0.8 \sigma ]\); if \(\sigma = 0\), we get a lower solution as 5.2 and upper solution as 6.8 if \(\sigma = 1\) then we get the center solution as 6. So, our targeted fuzzy velocity is \(\widetilde{\omega } = [5.2, 6, 6.8]\). We also observed the needed fuzzy velocity in Tables 5, 6, 7 and 8. We got a result that is very close to the targeted inverse solution for fuzzy velocity, which can be seen in Fig. 5. This is the required TFN for case 6 at \(t = 0.2, t = 0.4, t = 0.6, t = 0.8\), and \(t = 1\). We also get cases 7–10 in the same way.

Table 5 Fuzzy velocity at \(\eta = 2\) and \(r = 25\) (case 6)
Full size table
Table 6 Fuzzy velocity at \(\eta = 2\) and \(r = 25\) (case 7)
Full size table
Table 7 Fuzzy velocity at \(\eta = 2\) and \(r = 25\) (case 8)
Full size table
Table 8 Fuzzy velocity at \(\eta = 2\) and \(r = 25\) (cases 9 and 10)
Full size table
Fig. 5
figure 5

Fuzzy velocity for case 6

Full size image

Conclusion

In this paper, the forward and inverse problems of the time-fractional vibration equation of large membranes in an uncertain environment have been successfully solved by the Adomian decomposition method. In this approach, the double parametric form of a fuzzy number has been implemented successfully. This approach is simple because it takes FFVE and turns it into a crisp form with two parameters that control the uncertainty. When the results are compared with Yildirim et al. [6] in every forward case, they are in perfect agreement. As the number of terms in the approximate series solution by ADM goes up, it has also been seen that the fuzzy displacement grows closer together. Five-term approximations have been utilized to converge the obtained results. Furthermore, along with the known \(\varphi\) and \(\zeta\), the converged fuzzy displacement has been used to investigate the inverse case of velocity determination. Also presented in tabular format is convergence for the inverse problem. The observed fuzzy velocity is sufficiently close to the target value. This concept could determine the unknown parameter if experimental results are known.