Introduction

Using ambient energy to generate electricity has increasingly become an important form of green energy [1,2,3]. Vibration is widespread in nature amongst various types of environmental energy forms [4, 5]. Therefore, vibration-based energy harvesting is widely studied at present [6, 7]. It can be used to power low-energy devices such as biomedical engineering [8], environmental or industrial monitoring [9, 10] and military applications [11] where periodic battery replacement is difficult.

According to the different conversion mechanisms, the vibration energy harvesting technologies can mainly be divided into three types: electromagnetic [12, 13], electrostatic [14], and piezoelectric [15, 16]. Among the three types, piezoelectric vibration energy harvesting technology utilized the piezoelectric effect of piezoelectric materials to convert the ambient vibration into electricity output [17, 18]. Compared with the other vibration energy conversion mechanisms, piezoelectric energy harvesting has many advantages such as anti-electromagnetic interference, high efficiency and easy integration [19]. They can be widely used in micro power electronic devices such as microelectromechanical systems [20, 21] and wireless network nodes [22,23,24].

The common structure of piezoelectric energy harvesters is the cantilever beam [25, 26]. It is more suitable for low frequency and small excitation. However, the linear properties of the material are confined to a very restricted frequency range, which makes it challenging to match the ambient excitation to achieve resonance [27, 28]. For this reason, researchers have proposed different improved structures based on cantilever beam. For instance, nonlinear energy harvesters with magnetic coupling can exhibit bi-stable [29,30,31] or multi-stable [32,33,34] state, which can broaden the frequency band and improve the harvesting efficiency. Pereira et al. [35] analyzed a bi-stable energy harvester (BEH), and discussed the response under three excitation conditions (pure harmonic, pure random and combination of harmonic and random excitation). Jiang et al. [36] designed a magnetic coupling bi-stable piezoelectric energy harvester which consists of a main beam and a parasitic beam, it shows broadband characteristics by controlling the magnets spacing. Wang et al. [37] added a fixed magnet to present a tri-stable state, resulting in a wider frequency band than bi-stable energy harvesters. Lai et al. [38] proposed a multi-stable piezomagnetic elastic energy harvester array, increasing the harvesting efficiency and extending the working bandwidth to a lower frequency. Introducing nonlinearity and multi-stable through structure change has improved the harvesting efficiency at different levels. However, it is crucial to note that high strain is only generated at the root of the cantilever beam while the strain far away from the root is small. Consequently, this reduces the energy harvesting efficiency of the whole beam.

In order to make the other parts of the cantilever beam also generate large strain, researchers have made a series of improvements. Zhou et al. [39] considered four types of stoppers including one-side fixed stopper, two-side fixed stopper, one-side followed stopper, and two-side followed stopper. The experiment results show that the two sides followed stopper type can greatly improve the bandwidth compared to the other types, and the soft material stoppers can make the resonance area wider and the output voltage higher. Wang et al. [40] studied a new type of mechanical-magnetic energy harvester. The mechanical part is a cantilever beam with elastic stoppers installed on both sides. The analysis shows that it can harvest lower frequency vibration and achieve higher harvesting efficiency. On this basis, Wang et al. [41] proposed a broadband piezoelectric energy harvester, which consists of a cantilever beam and two symmetric constraints. The kinetic equations are established by fitting the experimental results. This structure not only improves the harvesting efficiency under low excitation, but also extends the operating band to lower frequency. According to the similar model, Silva et al. [42] used parameter identification to establish the kinetic equations. In the above works, researchers used experimental or parameter identification modeling methods. The analytical expression of the restoring force of the cantilever beam was not obtained. The present work has limitations and cannot reveal the dynamic evolution law of the harvester more systematically, so it is not conducive to the parameter design of the harvester.

In the past few years, researchers have studied the nonlinear behaviour [43, 44] and modelling methods [45, 46] of beam structures. Besides, the dynamic characteristics and modelling of the constrained cantilever beam are studied. Sarkar et al. [47] studied the natural frequency of a cantilever beam with any number of constraint springs. Dumont et al. [48] established a mathematical model for the dynamics of a cantilever beam between two rigid stoppers, and compared different algorithms for simulating the vibration of the beam. Ding et al. [49] investigated the response of any point on the beam with lateral constraints, and established the kinetic equations by using Lagrange equation and Euler–Bernoulli beam theory. Farokhi et al. [50] proposed a cantilever beam equipped with two stoppers at a certain distance from the root of the cantilever beam. The two stoppers, simplified as springs with large stiffness coefficients, move harmoniously with the beam. Kinetic equations based on Euler–Bernoulli beam theory and Hamilton’s principle are derived. Li et al. [51] put the cantilever beam in a constraint similar to the zipper, and found that the new model can obtain a higher output voltage.

Therefore, there are still the following issues with the current piezoelectric cantilever beam energy harvesters: (a) large strain is only generated at the root of the beam, not resulting in high harvesting efficiency; (b) collision structures will cause damage to beams and piezoelectric patches, affecting the life of the energy harvester; (c) the mathematical analytical model of EHSC is not obtained, and the appropriate physical parameters and excitation parameters cannot be selected accordingly to make EHSC have high harvesting efficiency. It is of considerable scientific and engineering significance to propose and analyze non-collision, easy-to-assemble, and multi-stable energy harvesters for low-frequency and low-intensity excitation harvesting.

In this paper, a cantilever piezoelectric vibration energy harvester with symmetric surface constraints is proposed and analyzed. The surface constraints strengthen the nonlinear stiffness of the harvester system, which is beneficial to broaden the frequency band. The surface constraints can also make the beam to generate large strain even far away from the beam root, which is beneficial to improve the harvesting efficiency. Meanwhile, the contact between the surface constraint and the beam will not cause collision damage. The system forms a bi-stable state under the action of magnetic force, thus broadening the application scenarios and improving adaptability for the harvesters. Based on the obtained mathematical analytical model, selecting appropriate physical and excitation parameters can ensure high harvesting efficiency of EHSC. The structure of this paper is as follows: Sect. 2 establishes the nonlinear kinetic equations of the system. Section 3 carries out the static bifurcation analysis to obtain part of the highest efficiency parameters by evaluating the effects of main parameters on the equilibrium points spacing, potential well depth. Section 4 numerically analyzes some key parameters including magnets spacing and external excitation parameters to increase harvesting efficiency. Section 5 compares the power generation of EHSC and BEH. Section 6 experimentally validates the theoretical results of the harvester. Conclusions are drawn in the last section.

Modeling

Assumptions

To build the mathematical model of the EHSC, the following assumptions are made:

  1. 1.

    Through the reasonable placement of EHSC, the gravity is orthogonal to the restoring force and inertia force, so the gravity can be ignored.

  2. 2.

    The shear deformation of the beam is ignored since the beam thickness is very small relative to its length.

  3. 3.

    Influence of the bonding layer between the MFC and the elastic beam is neglected.

  4. 4.

    The material of the piezoelectric beam is assumed to be linear elastic. All of the other components are rigid.

  5. 5.

    The elastic beam and piezoelectric material are homogeneous.

  6. 6.

    The magnetic field is uniformly distributed in the space.

Model Structure

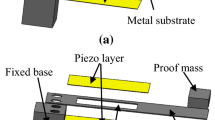
EHSC is shown in Fig. 1. It is composed of a cantilever beam with low stiffness and two symmetrical constraints with given geometry. The piezoelectric patch (model: m2807 P2, Smart Material Corp) is attached to a large area near the root of the beam, while a pair of magnets provide magnetoelastic force for the beam. The magnetic repulsion at the tip of the beam can make EHSC have two stable equilibrium points in static state (bi-stable state), which may generate large strain of beam during vibration. At the same time, due to the effect of the surface constraints, the piezoelectric patch attached to the larger area of the beam root can maintain large strain, thus generate more electric charges. To reduce the natural frequency of the cantilever beam, copper metal blocks are attached to the tip magnet. The external excitation is the lateral motion acting on the beam root. Figure 1 is a top view of the real model placement. The gravity is orthogonal to beam surface without impact on system dynamics. So the influence of gravity is ignored in this work. When the beam is strained, the MFC attached to the beam will generate output voltage and realize the conversion from mechanical to electrical energy.

Fig. 1
figure 1

a EHSC schematic diagram; b top and right view of the pure beam

Full size image

With the external excitation, the cantilever beam will gradually attach to the constraint, while the stiffness is gradually increases. For the cantilever beam without constraints, only in the area near the root has a large deformation [52], and the deformation away from the root is small. Therefore, the MFC cannot be attached within a large range and cannot generate more electricity. After applying constraints, as external excitation changes, the portion near the root of the beam attaches to the constraints. Due to the small stiffness of the beam design, a large portion will fit with the constraint surface. This allows the part far from the root of the beam have significant deformation (related with the shape of the constraints). Besides, the symmetrical constraints make the beam have symmetrical stable equilibrium points. Therefore, it is convenient to generate significant motion across the symmetric equilibrium points. If the surface constraints are asymmetric, the beam is likely to move only across one stable equilibrium point closer to the static equilibrium. This is not conducive to generating large motion across two stable equilibrium points. In summary, symmetrical surface constraints enable large strain even far from the root.

The shape of the fixed constraints can be expressed as follows [41]

$$S(x) = d_{{\text{g}}} \left( {\frac{x}{{l_{{\text{s}}} }}} \right)^{n} ,$$
(1)

where dg is the height of the constraint; ls is the length of the constraint. n is a natural number larger than 2 to ensure that the curvature of the constraint at the root is 0. In this paper, n = 3.

Since the bending stiffness of the beam is low and the tip is attached with blocks, EHSC can be simplified as a single degree of freedom system with equivalent quality meq, as shown in Fig. 2. The equivalent quality meq can be represented [53] as meq = βM (mc + me) + mA + 2mT, in which βM means Rayleigh–Ritz approximation constant, mc, me, mA, mT are the quality of cantilever beam, piezoelectric patch, magnet A and the blocks, respectively. It can be seen that, the equivalent quality is subjected to nonlinear magnetic force Fv, electromechanical coupling force Fp, nonlinear restoring force Fk, and damping force Fc in the opposite direction. In order to establish the kinetic equations, it is first necessary to calculate the forces acting on the equivalent quality, especially the nonlinear restoring force Fk and the nonlinear magnetic force Fv.

Fig. 2
figure 2

a EHSC model with lumped parameter; b image of force diagram

Full size image

Nonlinear Restoring Force

The nonlinear restoring force of the beam can be expressed by the relationship between the lateral force acting on the beam tip and the lateral displacement of the tip, as shown in Fig. 3. In the coordinate system O1x1y1, the free tip of the beam produces lateral displacement y1 under the action of the lateral force Fk. The material of the beam is assumed to be linear elastic. The length of the beam O1A is divided into two parts with M as the demarcation point. O1M is completely fitted with the surface constraints, and MA can be regarded as a smaller cantilever beam.

Fig. 3
figure 3

Deformation of cantilever beam under lateral force Fk at the free end

Full size image

According to the mechanics of materials [52], the differential form of the deflection curve of MA can be written as

$${\text{EI}}y^{\prime\prime}_{1} = F_{{\text{k}}} (l_{{\text{c}}} - x_{1} ) \, (x_{M} \le x_{1} \le l_{{\text{c}}} ),$$
(2)

where lc is the length of cantilever beam, x1 is the abscissa of any point N on the beam, xM is the abscissa of the demarcation point M. EI is the equivalent bending stiffness of the piezoelectric beam, which can be expressed [53] as

$${\text{EI}} = {\text{EI}}_{{\text{c}}} \frac{{l_{x} }}{{l_{{\text{c}}} }} + EI_{{{\text{ce}}}} \frac{{l_{{\text{e}}} }}{{l_{{\text{c}}} }} + {\text{EI}}_{{\text{c}}} \frac{{l_{{\text{c}}} - l_{x} - l_{{\text{e}}} }}{{l_{{\text{c}}} }},$$

where, \({\text{EI}}_{{\text{c}}} = \frac{{E_{{\text{c}}} w_{{\text{c}}} h_{{\text{c}}}^{3} }}{12}\), \({\text{EI}}_{{{\text{ce}}}} = \frac{1}{3}E_{{\text{c}}} w_{{\text{c}}} (yy_{1}^{3} - yy_{0}^{3} ) + \frac{1}{3}E_{{\text{e}}} w_{{\text{e}}} (yy_{2}^{3} - yy_{1}^{3} )\), \(yy = \frac{{E_{{\text{e}}} w_{{\text{e}}} h_{{\text{e}}}^{2} + E_{{\text{c}}} w_{{\text{c}}} h_{{\text{c}}}^{2} + 2E_{{\text{e}}} w_{{\text{e}}} h_{{\text{e}}} h_{{\text{c}}} }}{{2(E_{{\text{e}}} w_{{\text{e}}} h_{{\text{e}}} + E_{{\text{c}}} w_{{\text{c}}} h_{{\text{c}}} )}}\), \(yy_{0} = - yy\), \(yy_{1} = h_{{\text{c}}} - yy\), \(yy_{2} = (h_{{\text{c}}} + h_{{\text{e}}} ) - yy\), lx is shown in Fig. 1b, le is the length of piezoelectric patch, Ec, Ee are the elastic modulus of cantilever beam and piezoelectric patch, respectively, wc, we are the width of cantilever beam and piezoelectric patch, respectively, hc, he are the thickness of cantilever beam and piezoelectric patch, respectively.

Integrating Eq. (2) and using the boundary conditions at point M to determine the integral constant, let x1 = lc, we obtain that

$$y_{1} = F_{{\text{k}}} \cdot \frac{{(l_{{\text{c}}} - x_{M} )^{3} }}{{3{\text{EI}}}} + S^{\prime}(x_{M} ) \cdot (l_{{\text{c}}} - x_{M} ) + S(x_{M} ).$$
(3)

We can see in Fig. 4 that the displacement y1 is composed of three parts: yI is the vertical coordinate of M, yI = S(xM); yII is calculated by the slope of the tangent line of M, yII = Sʹ(xM)(lc − xM); yIII is the deflection of cantilever beam MA with M as the fixed end, yIII\(= \frac{{F_{{\text{k}}} \cdot (l_{{\text{c}}} - x_{{\text{M}}} )^{3} }}{{3{\text{EI}}}}\).

Fig.4
figure 4

Geometry diagram of beam tip displacement decomposition

Full size image

Differentiate Eq. (3) with respect to xM, according to the relationship between the force on the tip of the cantilever beam and the lateral displacement, it can be obtained that

$$F_{k} = \frac{{S^{\prime\prime}(x_{M} )EI}}{{l_{c} - x_{M} }}$$
(4)

Substitute Eq. (4) into Eq. (3) and consider Eq. (1), one can get

$$y_{1} = \left[ {\frac{{72d_{g}^{3} (EI)^{2} }}{{l_{s}^{6} F_{k}^{2} }} + \frac{{18d_{g}^{2} EI}}{{l_{s}^{3} F_{k} }} + d_{g} } \right] \cdot \left(\frac{{F_{k} l_{c} l_{s}^{2} }}{{6d_{g} EI + F_{k} l_{s}^{3} }}\right)^{3}$$
(5)

Equation (5) gives the relationship between the tip displacement and restoring force of the beam. To build the kinetic model of the system, it is necessary to obtain the analytical expression of the restoring force expressed by the beam tip displacement. For this reason, Fk is expanded as Taylor series of y1 and retained to the third order. The approximate expression of Fk can be obtained by substituting Taylor series of Fk into Eq. (5). Owing to the model is symmetry about x1-axis, it should have the relationship of Fk (y1) = − Fk (− y1). So

$$F_{{\text{k}}} = \frac{{3{\text{EI}}}}{{l_{{\text{c}}}^{3} }}y_{1} + \frac{{9{\text{EI}}l_{{\text{s}}}^{3} }}{{4d_{{\text{g}}} l_{{\text{c}}}^{6} }}y_{1} \left| {y_{1} } \right| + \frac{{15{\text{EI}}l_{{\text{s}}}^{6} }}{{8d_{{\text{g}}}^{2} l_{{\text{c}}}^{9} }}y_{1}^{3} .$$
(6)

From Eq. (6), the approximate analytical expression of the restoring force can be further analyzed. The first term reflects the linear characteristics of the unconstrained cantilever beam, while the latter two terms reflect the nonlinear characteristics of the constrained cantilever beam. The stiffness of the beam is related with the length ls and height dg of the constraint. When the length ls increases, the bending stiffness of the beam increases and changes rapidly; when the height dg decreases, the stiffness of the beam also increases.

Selecting the beam parameters shown in "List of Symbols" and calculating Eqs. (5) and (6) respectively, the results are shown in Fig. 5. When the displacement of the cantilever beam tip is below 0.008 m, the approximate analytical expression can accurately describe the force–displacement relationship at the beam tip. Thereafter, as the restoring force increases, the error of the approximate analytical expression increases; when the tip displacement does not exceed 0.016 m, the error can still be kept within 6%.

Fig. 5
figure 5

Approximate and precise solutions of the relationship between the restoring force and displacement at the beam tip

Full size image

The results indicate that, when the ratio of beam tip displacement to beam length is within 16% (usually motion is in this range), the error of the approximate analytical expression is less than 15%. Therefore, the approximate solution can accurately describe the stiffness characteristics of the beam in this range.

Nonlinear Magnetic Force

The nonlinear magnetic force can greatly affect the dynamic performance of the energy harvester. In the previous works [40], the magnetic force of EHSC is established by experimental data fitting, which seems to be not suitable for structural optimization. In this section, we use the magnetizing current method [54] to deduce the analytical expression of the magnetic force. Moreover, the rotation angle of magnet is also considered in order to improve the accuracy of the formula. Figure 6 is a structural diagram of the piezoelectric energy harvester in an applied magnetic field.

Fig. 6
figure 6

Structure diagram of piezoelectric energy harvester in applied magnetic field

Full size image

The force Fv of the magnetic field on the magnetically conductive material along the i-axis direction is [55]

$$F_{{\text{v}}} = \iint\limits_{S} {{\mathbf{K}}_{{\mathbf{m}}} } \times \mu_{0} {\mathbf{H}}_{{\mathbf{j}}} {\text{d}}s_{{\text{A}}} = \left\{ \begin{gathered} - \iint\limits_{{S_{{\text{A}}} }} {M_{{\text{A}}} \times \mu_{0} H_{{{\mathbf{j}}1}} {\text{d}}s_{{\text{A}}} {\hat{\mathbf{i}}} \, ({\text{Top surface}})} \hfill \\ \iint\limits_{{S_{{\text{A}}} }} {M_{{\text{A}}} \times \mu_{0} H_{{{\mathbf{j}}2}} {\text{d}}s_{{\text{A}}} {\hat{\mathbf{i}}}{\text{ (Bottom surface)}}} \hfill \\ \end{gathered} \right.,$$
(7)

where, Km = M × n is the density of surface magnetization current; n is the surface normal vector; μ0 is the permeability of vacuum; Hj is the strength of the magnetic field; sA is the area of the upper and lower surfaces of magnet A; Hj1 and Hj2 respectively present the strength of the magnetic field along the j-axis direction at the centre of the top and bottom surfaces of the magnet A; MA is the magnetization of magnet A. Assuming that the magnetic field is uniformly distributed in the area, the magnetic force Fv can be given by

$$F_{{\text{v}}} = \mu_{0} M_{{\text{A}}} s_{{\text{A}}} (H_{{{\mathbf{j}}2}} - H_{{{\mathbf{j}}1}} ).$$
(8)

With the centre of magnet B as the coordinate origin, the magnetic field strength along the j-axis generated at the coordinates (i, j, k) of any point in space is [56]

$$H_{j} (i,j,k) = \frac{{M_{{\text{B}}} }}{4\pi }\left[ {\arctan \left( {\frac{{i_{p} k_{p} }}{{j\sqrt {i_{p}^{2} + k_{p}^{2} + j^{2} } }}} \right) + \arctan \left( {\frac{{i_{n} k_{n} }}{{j\sqrt {i_{n}^{2} + k_{n}^{2} + j^{2} } }}} \right) - \arctan \left( {\frac{{i_{n} k_{p} }}{{j\sqrt {i_{n}^{2} + k_{p}^{2} + j^{2} } }}} \right) - \arctan \left( {\frac{{i_{p} k_{n} }}{{j\sqrt {i_{p}^{2} + k_{n}^{2} + j^{2} } }}} \right)} \right],$$
(9)

where, MB is the of magnet B, \(i_{p} = i + \frac{{h_{{\text{B}}} }}{2}\), \(i_{n} = i - \frac{{h_{{\text{B}}} }}{2}\), \(k_{p} = k + \frac{{w_{{\text{B}}} }}{2}\), \(k_{n} = k - \frac{{w_{{\text{B}}} }}{2}\), hB, wB are the thickness and width of magnet B, respectively.

When magnet A is subjected to lateral force, the bending beam will generate a rotation angle α at the beam tip. As shown in Fig. 7, O1A0 is the initial state when the beam is without bending; MA1 is the tangent of the surface constraint at point M; O1A is the state where the beam tip is subjected to a force. The rotation angle can be divided into two parts: the angle of the beam tip corresponding to the beam from A0 to A1 is α1; the increased angle of the beam tip corresponding to the beam from A1 to A is α2.

Fig. 7
figure 7

Geometry diagram of beam tip displacement decomposition

Full size image

Combining Eqs. (1), (3), (4), the relationship between the displacement y1 of beam tip and the abscissa xM of the beam–constraint demarcation point M can be obtained as follow,

$$y_{1} = \frac{{d_{{\text{g}}} l_{{\text{c}}} }}{{l_{{\text{s}}}^{3} }}x_{M} (2l_{{\text{c}}} - x_{M} ).$$
(10)

Since the condition y1 = 0, xM = 0 must be satisfied, xM can be solved by Eq. (10),

$$x_{M} = l_{{\text{c}}} - l_{{\text{c}}} \sqrt {1 - \frac{{l_{{\text{s}}}^{3} y_{1} }}{{d_{{\text{g}}} l_{{\text{c}}}^{3} }}} \approx l_{{\text{c}}} - l_{{\text{c}}} \left( {1 - \frac{1}{2}\frac{{l_{{\text{s}}}^{3} y_{1} }}{{d_{{\text{g}}} l_{{\text{c}}}^{3} }}} \right) = \frac{{l_{{\text{s}}}^{3} }}{{2d_{{\text{g}}} l_{{\text{c}}}^{2} }}y_{1} .$$
(11)

MA1 is the tangent of the constraint at point M, α1 is the angle of the tangent. Since the angle of the tangent line is small, α1 can be regarded as a small quantity, yields

$$\tan \alpha_{1} = S^{\prime}(x_{M} ) = \frac{{3d_{{\text{g}}} }}{{l_{{\text{s}}}^{3} }}x_{M}^{2} \approx \alpha_{1} ,$$
(12)

α2 can be approximated as the cantilever beam MA moving from the MA1 position to the MA position. Therefore, based on the properties of the cantilever beam, α2 can be represented as

$$\alpha_{2} = \frac{{3y_{12} }}{{2(l_{{\text{c}}} - x_{M} )}},$$
(13)

where y12 is the lateral displacement of the beam tip from A1 to A, as shown in Fig. 7. In addition, the geometric meaning of y11 in Fig. 7 gives

$$y_{11} = S(x_{M} ) + S^{\prime}(x_{M} ) \cdot (l_{{\text{c}}} - x_{M} ) = \frac{{d_{{\text{g}}} }}{{l_{{\text{s}}}^{3} }}x_{M}^{2} (3l_{{\text{c}}} - 2x_{M} ).$$
(14)

Then, from Eq. (10) and Eq. (14), it follows that

$$y_{12} = y_{1} - y_{11} = \frac{{2d_{{\text{g}}} }}{{l_{{\text{s}}}^{3} }}x_{M} (l_{{\text{c}}} - x_{M} )^{2} .$$
(15)

The relationship between the rotation angle and displacement of magnet A can be obtained as follow

$$\alpha = \frac{3}{{2l_{{\text{c}}}^{2} }}y_{1} .$$
(16)

Therefore, for the EHSC system, the rotation angle and displacement of the beam tip are related with the beam length lc.

The displacement of magnet A in the j-direction is very small, and it has little effect on the total potential energy of the system, so it can be ignored. When the cantilever beam is in a horizontal position, the centre coordinate of magnet A is (0, d, 0), d = e + lA/2 + lB/2 is the distance between the centres of the two magnets, e is the magnets interval, as shown in Fig. 6. When magnet A vibrates, considering the coordinates at the centre of the top and bottom surfaces of magnet A, the force between the magnets along the vertical direction is

$$F_{{\text{v}}} = \mu_{0} M_{{\text{A}}} S_{{\text{A}}} \left[ {H_{{{\mathbf{j}}2}} \left( {y_{1} - \frac{{h_{{\text{A}}} }}{2}\cos \alpha ,d - \frac{{h_{{\text{A}}} }}{2}\sin \alpha ,0} \right) - H_{{{\mathbf{j}}1}} \left( {y_{1} + \frac{{h_{{\text{A}}} }}{2}\cos \alpha ,d + \frac{{h_{{\text{A}}} }}{2}\sin \alpha ,0} \right)} \right],$$
(17)

where α is obtained from Eq. (16). Therefore, Fv is related to the size, properties, spacing of magnets and the beam tip displacement.

When α = 0 and α ≠ 0, the images are drawn according to Eq. (17), as shown in Fig. 8. We can see that the angle of magnet A has a great influence on the magnetic force. Therefore, when using the magnetizing current method to calculate the magnetic force, it is necessary to consider the angle of the tip magnet.

Fig. 8
figure 8

Comparison of magnetic force with or without considering the magnet rotation angle

Full size image

Taylor expansion of Eq. (17) at y1 = 0 gives the magnetic force between the two magnets in the vertical direction

$$F_{{\text{v}}} = \frac{{\mu_{0} M_{{\text{A}}} M_{{\text{B}}} S_{{\text{A}}} w_{{\text{B}}} }}{{2l_{{\text{c}}}^{2} \pi (4d^{2} + w_{{\text{B}}}^{2} )}}\left[(A_{1} + A_{2} )y_{1} + \frac{1}{{1536d^{6} l_{{\text{c}}}^{4} }}(B_{1} + B_{2} + B_{3} )y_{1}^{3}\right ] + {\rm O}(y_{1}^{5} ).$$
(18)

The coefficients are detailed in Appendix 1.

Kinetic Equations

In addition to the restoring force Fk and the magnetic force Fv, the equivalent quality at the beam tip is also affected by the electromechanical coupling force caused by the piezoelectric patch [57]. Neglecting the influence of the bonding layer between the MFC and the elastic beam, the MFC moves with the deformation of the beam. In such an electromechanical coupling structure, the piezoelectric constitutive equations are [58]

$$S_{1} = s_{11}^{E} T_{1} + d_{31} E_{3} ,$$
(19)
$$D_{3} = s_{11}^{E} d_{31} T_{1} + \varepsilon_{33}^{T} E_{3} ,$$
(20)

where, S1 is the strain of piezoelectric patch, \(s_{11}^{E}\) is the compliance coefficient of piezoelectric materials under constant electric field, T1 is the stress of piezoelectric patch, E3 is the electric field intensity, D3 is the electric displacement, \(\varepsilon_{33}^{T}\) is the dielectric coefficient under constant stress.

When the strain is 0, Eq. (19) can be rewritten as

$$T_{1} = - \frac{{d_{31} V(t)}}{{s_{11}^{E} h_{{\text{e}}} }},$$
(21)

where V(t) the voltage, V(t) = E3he.

According to the calculation formula of normal stress in bending, one has

$$T_{1} = \frac{1}{{l_{{\text{e}}} }}\int_{0}^{{l_{{\text{e}}} }} {\frac{{F_{{\text{p}}} (l_{{\text{c}}} - x)(h_{e} + l_{c} )}}{2J}} {\text{d}}x = \frac{{F_{{\text{p}}} (2l_{{\text{c}}} - l_{{\text{e}}} )(h_{{\text{e}}} + l_{{\text{c}}} )}}{4J},$$
(22)

where J is the moment of inertia of the beam cross-section to the neutral axis.

Combining Eq. (21) with Eq. (22), further calculations lead to

$$- \frac{{d_{31} V(t)}}{{s_{11}^{E} h_{{\text{e}}} }} = \frac{{F_{{\text{p}}} (2l_{{\text{c}}} - l_{{\text{e}}} )(h_{{\text{e}}} + h_{{\text{c}}} )}}{4J}.$$
(23)

Considering E3 = 0, the relation between y1(t) and the current i is obtained from Eq. (20).

$$D_{3} = d_{31} T_{1} = d_{31} E_{{\text{e}}} S_{1} = \frac{{3E_{{\text{e}}} d_{31} (2l_{{\text{c}}} - l_{{\text{e}}} )(h_{{\text{e}}} + h_{{\text{c}}} )}}{{4l_{{\text{c}}}^{3} }}y_{1} (t).$$
(24)

So

$$i = 2w_{{\text{e}}} l_{{\text{e}}} \dot{D}_{3} = \kappa_{{\text{c}}} \dot{y}_{1} (t),$$
(25)

where \(\kappa_{{\text{c}}} = \frac{{3E_{{\text{e}}} w_{{\text{e}}} l_{{\text{e}}} d_{31} (2l_{{\text{c}}} - l_{{\text{e}}} )(h_{{\text{e}}} + h_{{\text{c}}} )}}{{2l_{{\text{c}}}^{3} }}\). The electromechanical coupling force is obtained by Eq. (23),

$$F_{{\text{p}}} = - \kappa_{{\text{c}}} V(t).$$
(26)

Hence, Fp is related with the size of beam, piezoelectric patch, and the beam tip displacement.

By now, the restoring force Fk, magnetic force Fv and electromechanical coupling force Fp, have been derived. So we can establish the kinetic equations of the system. Considering the damping force Fc, as shown in Fig. 2, and assuming electromechanical piezoelectric coupling is linear, the mechanical and electrical equations of the energy harvester system can be obtained according to Newton's law and Kirchhoff's law as follows

$$\left\{ \begin{gathered} \ddot{y}_{1} (t) + \zeta \dot{y}_{1} (t) + ay_{1} (t){ + }by_{1} (t)\left| {y_{1} (t)} \right| + cy_{1}^{3} (t) - \gamma V(t) = - P(t) \hfill \\ \dot{V}(t) + \mu V(t) + \vartheta \dot{y}_{1} (t) = 0 \hfill \\ \end{gathered} \right.,$$
(27)

where, \(\zeta = \frac{{c_{{{\text{eq}}}} }}{{m_{{{\text{eq}}}} }}\), ceq is damping coefficient, \(a = \frac{{3{\text{EI}}}}{{m_{{{\text{eq}}}} l_{{\text{c}}}^{3} }} - \frac{{\mu_{0} M_{{\text{A}}} M_{{\text{B}}} s_{{\text{A}}} w_{{\text{B}}} }}{{2l_{{\text{c}}}^{2} \pi (4d^{2} + w_{{\text{B}}}^{2} )m_{{{\text{eq}}}} }}(A_{1} + A_{2} )\), d is the distance between the centres of magnet A and B, \(b = \frac{{9{\text{EI}}l_{s}^{3} }}{{4m_{{{\text{eq}}}} d_{{\text{g}}} l_{{\text{c}}}^{6} }}\),\(c = \frac{{15{\text{EI}}l_{s}^{6} }}{{8m_{{{\text{eq}}}} d_{{\text{g}}} l_{{\text{c}}}^{9} }} - \frac{{\mu_{0} M_{{\text{A}}} M_{{\text{B}}} S_{{\text{A}}} w_{{\text{B}}} }}{{3072d^{6} l_{{\text{c}}}^{6} \pi (4d^{2} + w_{{\text{B}}}^{2} )m_{{{\text{eq}}}} }}(B_{1} + B_{2} + B_{3} )\), \(\gamma = \frac{{\kappa_{{\text{c}}} }}{{m_{{{\text{eq}}}} }}\), \(P(t) = p\cos (2\pi \Omega t)\), p is the excitation acceleration, Ω is the excitation frequency,\(\mu = \frac{1}{{C_{{\text{p}}} R_{{\text{L}}} }}\), Cp is the equivalent capacitance, RL is the load resistance, \(\vartheta = \frac{{\kappa_{{\text{c}}} }}{{C_{{\text{p}}} }}\).

Static Analysis

The static bifurcation characteristics of EHSC can be obtained by analyzing the equilibrium points and stability of the autonomous system Eq. (27), so as to further study the dynamic response of the system. Let \(Y_{1} = y_{1} (t)\), \(Y_{2} = \dot{y}_{1} (t)\), \(Y_{3} = V(t)\). Then the autonomous system corresponding to Eq. (27) can be written as first-order differential equations

$$\left[ \begin{gathered} \dot{Y}_{1} \hfill \\ \dot{Y}_{2} \hfill \\ \dot{Y}_{3} \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} {Y_{2} } \\ { - \zeta Y_{2} - aY_{1} - bY_{1} \left| {Y_{1} } \right| - cY_{1}^{3} + \gamma Y_{3} } \\ { - \mu Y_{3} - \vartheta Y_{2} } \\ \end{array} } \right].$$
(28)

According to the Routh-Hurwitz theorem, there is a stable zero equilibrium point when \(a > \frac{{b^{2} }}{4c}\); there are two stable non-zero equilibrium points and one unstable zero equilibrium point when \(a < \frac{{b^{2} }}{4c}\). Therefore, it is a pitchfork bifurcation point. The equilibrium points spacing of the system is \(\frac{{ - b + \sqrt {b^{2} - 4ac} }}{c}\); the potential well depth is \(\frac{{(b - \sqrt {b^{2} - 4ac} )^{2} ( - b^{2} + 6ac + b\sqrt {b^{2} - 4ac} )}}{{96c^{3} }}\).

According to the principle of piezoelectric power generation, energy harvesters achieve higher harvesting efficiency when they can achieve greater amplitude at lower excitation. For adapting smaller excitation, the potential well depth of the system should be as shallow as possible; for increasing the amplitude of the beam, the system should exhibit bi-stability and the equilibrium points spacing should be as large as possible. Based on the above analysis, the beam length, beam width and magnet spacing are key parameters according to the expressions of equilibrium points spacing and potential well depth. Besides, these three parameters are easy to change in the experiment. Therefore, we focused on the analysis of these three parameters.

Figure 9 shows the relationships among the beam length, beam width, the magnets spacing, the equilibrium points spacing, and the potential well depth, respectively. Figure 9a, b shows that the equilibrium points spacing and potential well depth increase with the increase of beam length, but the potential well depth tends to a fixed value (about 0.10 m) when the beam length is about 0.25 m. Figure 9c, d show that the equilibrium points spacing and the potential well depth decrease with the increase of beam width. Because there is no extreme value point in this case, only can selecting an appropriate value according to other parameters. Figure 9e, f show that, when the magnets spacing e is about 0.02 m, the balance point spacing has a maximum value of 0.028 m, while the potential well depth decreases with the increase of e. The curves in the figures provides a basis for the parameter design. Because the system is usually expected to have larger equilibrium points spacing and a smaller potential well depth, it is beneficial to meet these two conditions with an appropriate large beam length and an appropriate small beam width. Especially note the extreme point in Fig. 9e, in which there is an "optimal" e to maximize the equilibrium points spacing, so the result provides a guidance for selecting value of e. Combined with Fig. 9f, e should be selected at the "optimal" value or slightly larger than that.

Fig. 9
figure 9

Relationship between the main parameters of the system and the equilibrium points spacing or potential well depth

Full size image

The diagram of potential energy function can further reveal the properties of system equilibrium points. Figures 10 and 11 show that, when e decreases, the potential well is deeper and less likely to produce large vibration. Meanwhile, when e decreases, the equilibrium points spacing decreases, the amplitude also decreases. In Fig. 11, lc will affect the steady-state number of the system. In order to harvest more energy, the system should be bi-stable. As the length lc of the beam increases, it required more energy to cross the potential barrier; on the other hand, it will obtain a larger amplitude. Therefore, it is necessary to analyze further to obtain a suitable parameter domain. However, potential well has no relation to length ls and height dg of the constraints.

Fig. 10
figure 10

Variation of potential energy with magnets spacing e, where lc = 0.1 m, ls = 0.12 m, dg = 0.018 m

Full size image
Fig. 11
figure 11

Variation of the potential energy with the length of the parametric beam lc, where ls = 0.12 m, e = 0.013 m, dg = 0.018 m

Full size image

Figure 12 shows the static bifurcation diagrams. The solid and dash lines represent the stable and unstable solutions, respectively. In Fig. 12a, the saddle-node bifurcation occurs when lc = 0.078 m, and then the amplitude of the system increases with the increase of lc; when lc is about 0.25 m, the trend of amplitude increase slows down. In Fig. 12b, wc has almost no effect on the amplitude, and the system remains in a bi-stable state within this range. In Fig. 12c, as e increases, the amplitude of the system increases first and then decreases, the amplitude reaches the maximum when e is about 0.02 m, and the system remains in a bi-stable state within this range. Figures 8, 9, 10, 11, 12 can confirm each other.

Fig.12
figure 12

Static bifurcation diagrams

Full size image

According to the results of the static analysis, the most efficiency EHSC system should have the following parameters configuration: (1) system should be bi-stable state; (2) the potential well should not be too deep. The shallower the potential well is, the easier the oscillator jump between potential wells, resulting in a large inter-well oscillation; (3) choose the suitable larger e to get the higher harvesting efficiency; (4) a "optimal" solution for magnets spacing can maximizes the equilibrium points spacing, choose this value or a slightly larger can obtain a larger displacement of the beam tip.

In summary, by analyzing and selecting the parameter domain that makes the system have larger equilibrium points spacing and smaller potential well depth, the system has good harvesting efficiency. Considering the application occasions, the size of EHSC should not be too large. Therefore, preliminarily select lc = 0.15 m, wc = 0.015 m, e = 0.02 m in the following work.

Numerical Simulation

According to the static analysis in Sect. 3, part of physical parameters of EHSC can be determined, such as the size of the beam. However, the amplitude and frequency of the excitation are the key conditions for the system to achieve large vibration. In addition, the magnets spacing has a great influence on the equilibriums of the system under dynamic conditions, so it is discussed in this section. The basic physical parameters of the system are determined by the subsequent experiments, as shown in “List of Symbols”. This paper only uses numerical analysis to optimize.

Effect of Excitation Amplitude

Referring to the results in Fig. 9e, we choose e = 0.02 m. Figure 13 shows the bifurcation diagram when Ω = 2.5 Hz, 5 Hz, 7.5 Hz and 10 Hz, respectively. The excitation amplitude is used as the bifurcation parameter to compare the bifurcation plots at different excitation frequencies.

Fig. 13
figure 13

Bifurcation diagrams with excitation amplitude as bifurcation parameter at different excitation frequencies

Full size image

Take Fig. 13b as an example to analyze the influence of different excitation amplitudes on vibration in detail. In area ①: when the excitation amplitude is small, the system does not have enough energy to cross the potential barrier, so it move around one equilibrium point in a small range. With the increase of the excitation amplitude, the system has enough energy to cross the barrier and make stable large-amplitude periodic vibration between two equilibrium points, as in Fig. 12a. Then the system makes small vibration in area ②, as shown in Fig. 14b. Chaos occurs in the system in region ③, as shown in Fig. 14c. Large-amplitude periodic vibration occurs in region ④. The period doubling bifurcation occurs in region ⑤, resulting in large Period-2 motion, as shown in Fig. 14d. Chaos appears in region ⑥. In region ⑦, the system performs large Period-3 motion, as shown in Fig. 14e. When p = 1.28 g, the system performs large Period-9 motion, as shown in Fig. 14f. In area ⑧, the system first performs large Period-5 motion, as shown in Fig. 14g, and then performs large Period-9 motion, as shown in Fig. 14h. Chaos appears in region ⑨.

Fig. 14
figure 14

Phase diagram of the system in different states when 5 Hz excitation frequency

Full size image

As shown in Fig. 15, the higher the frequency is, the lower the excitation amplitude is required to generate large vibration. Apparently, when the excitation amplitude p > 0.4 g, large vibration will occur in the system.

Fig. 15
figure 15

The higher excitation frequency, the lower excitation amplitude required to generate large periodic vibration

Full size image

Effect of Excitation Frequency

Figure 16 shows the bifurcation diagrams of the system changing with excitation frequency when p = 1 g, 1.2 g.

Fig. 16
figure 16

Bifurcation diagrams with excitation frequency as the bifurcation parameter for different excitation amplitudes

Full size image

When p = 1 g. In region ①, the system performs small periodic vibration. In region ②, the system performs small periodic vibration. With Ω = 3.5 Hz, the system performs large Period-5 motion, as shown in Fig. 17a. In region ③, the system performs large Period-3 motion, as shown in Fig. 17b. Chaos appears in region ④. Small periodic vibration appears in region ⑤ with Ω = 5–5.6 Hz; Ω = 5.8–7.3 Hz for large scale periodic vibration. In region ⑥, Ω = 7.4–10.5 Hz is for large scale periodic vibration, and Ω = 10.5–17.8 Hz is for small scale periodic vibration. With Ω = 18 Hz, the system appears large Period-3 motion, as shown in Fig. 17c. In region ⑦, the system performs small periodic vibration.

Fig. 17
figure 17

Phase diagram of the system at different states when the excitation amplitude is 1 g

Full size image

When p = 1.2 g. The system makes small periodic vibration in region ①. The system performs large Period-2 motion in region ②. Small periodic vibration occurs in region ③. Chaos occurs in region ④. Large periodic vibration occurs in region ⑤. Chaos occur in region ⑥. Large periodic vibration occurs in region ⑦. Chaos occurs in region ⑧. Large Period-3 motion is performed in the region ⑨. Chaos occurs in region ⑩. Large periodic vibration occurs in region ⑪. Large periodic vibration occurs in region ⑫ with Ω = 7–11 Hz, while small periodic vibration occurs with Ω = 12–20 Hz.

The above analysis shows that, when p = 1 g, large vibration occurs when excitation frequency is 0–20 Hz. When the excitation amplitude is p = 1 g, the excitation amplitude can occur in the range of 1.6–12 Hz. Also, the higher the excitation amplitude, the lower the frequency is needed to produce large vibration. As the excitation amplitude increases, the excitation frequency band for generating large vibration becomes wider.

Effect of Magnets Spacing

Figure 18 shows the bifurcation diagrams of the system response with the change of magnets spacing e when Ω = 2 Hz and p = 1 g, Ω = 5 Hz and p = 1.2 g, Ω = 14 Hz and p = 1 g, Ω = 14 Hz and p = 1.2 g, respectively.

Fig. 18
figure 18

Bifurcation diagrams of the system with e for different excitation frequencies and excitation amplitudes

Full size image

As shown in Fig. 18a, when Ω = 5 Hz and p = 1 g, in region ① and region ② the system performs small periodic vibration, chaos in region ③, large periodic vibration in region ④. When e = 0.0223 m, large Period-2 motion is performed. In region ⑤, the system continues to perform large periodic vibration.

As shown in Fig. 18b, when Ω = 5 Hz and p = 1.2 g, the system performs small periodic vibration in region ① and region ②, large Period-3 motion occurs in region ③, chaos occurs in region ④, large periodic vibration occurs in region⑤.

As shown in Fig. 18c, when Ω = 14 Hz and p = 1.2 g, the system performs small periodic vibration in region ①, large periodic vibration in region②, chaos in region ③, small periodic vibration in region ④. In region ⑤, large Period-3 motion occurs before e = 0.0255 m, as shown in Fig. 19a. Small Period-2 motion occurs when e = 0.0255–0.0265 m, as shown in Fig. 19b. In region ⑥, the system performs small periodic vibration when e = 0.027–0.035 m, while the system performs large periodic vibration when e = 0.035 ~ 0.038 m. Large periodic vibration occurs in region ⑦.

Fig. 19
figure 19

The phase diagrams of the system under different states when Ω = 14 Hz and p = 1 g

Full size image

As shown in Fig. 18d, when Ω = 14 Hz and p = 1.2 g, the system performs small periodic vibration in region ①, large periodic vibration in region②, chaos in region ③, small periodic vibration in region ④. In region ⑤, large Period-9 motion occurs when e = 0.0238–0.0245 m, as shown in Fig. 20a. Large Period-3 motion occurs when e = 0.0245–0.0264 m, as shown in Fig. 20b. The system then briefly enters small Period-2 motion when e = 0.0265 m, as shown in Fig. 20c, small periodic vibration occurs in region ⑥, large periodic vibration occurs in region ⑦.

Fig. 20
figure 20

The phase diagrams of the system under different states when Ω = 14 Hz and p = 1.2 g

Full size image

From the above analysis, when Ω = 5 Hz and p = 1 g, the system performs large vibration with e = 0.0205–0.05 m. When Ω = 5 Hz and p = 1.2 g, the system performs large vibration with e = 0.0205–0.05 m. When Ω = 14 Hz and p = 1 g, the system performs large vibration with e = 0.008–0.016 m, e = 0.024–0.0255 m and e = 0.035–0.05 m. Also, under the same excitation amplitude, with excitation frequency increases, large vibration can occur in the area which has smaller e. As shown in the bifurcation diagrams, under the same excitation frequency with excitation amplitudes increase, large vibration can occur in the area which has smaller e. Which means, the spacing where system can generate the large vibration become larger. As e decreases, the energy required to cross the barrier becomes larger. Therefore, both of increasing the excitation amplitude or excitation frequency can cause the system to make large vibration.

Energy Harvesting Performance

In order to evaluate the performance of the energy harvester proposed in this paper, this section compares the constrained harvester EHSC with the traditional bi-stable harvester BEH without constraints. The traditional bi-stable harvester BEH is composed of a cantilever beam and a pair of magnets. The bi-stable state is formed by repulsive force generated between the tip magnet and fixed magnet.

The basic principle of piezoelectric power generation is to use the piezoelectric effect of piezoelectric materials to generate stress and strain in the piezoelectric patch of the device under external excitation, leading to the flow of internal charges and the formation of output voltage [17, 59]. The output power is usually used to describe the power generation of the energy harvester [60]. The amplitude, bandwidth and output voltage of the system are positively correlated with the output power. The following research is taken from these perspectives. When the potential well depth of the system is shallower, the inter-well motion can be achieved more easily. Based on the principle of piezoelectric power generation, the greater the strain, the more energy harvested. As shown in Fig. 21, EHSC has shallower potential wells than BEH in the vibration range under the same other parameters. EHSC is easier to jump between potential wells than the oscillator in the traditional BEH, resulting in the occurrence of large amplitude oscillation, which makes EHSC show more potential in the energy harvesting of low intensity vibration.

Fig. 21
figure 21

Compared with EHSC and BEH potential energy function

Full size image

Due to the action of nonlinear force (magnetic force) or nonlinear structure (fixed constraints), the frequency response curve will deflect, so that the system maintain a large amplitude in a wider frequency band, thus achieve the goal of expanding the working frequency band [61]. Figure 22 shows the displacement and voltage responses of EHSC and traditional BEH under the excitation of sweep sinusoidal function, with the acceleration amplitudes of 0.5 g and 0.8 g respectively. Obviously, EHSC has a wider frequency bandwidth than BEH. When the acceleration amplitude of the excitation is 0.5 g, as shown in Fig. 22a, the EHSC can perform large inter-well vibration in the frequency range of 7.9–17.7 Hz, which in turn results in high voltage output. On the contrary, BEH only generate large amplitude vibration in the range of 10.6–12 Hz under the same excitation. When the excitation acceleration amplitude rises to 0.8 g, as shown in Fig. 22b, BEH can enter a large inter-well vibration in the frequency range of 9.4–13.4 Hz. At this time, the large vibration bandwidth of EHSC are 3.0–5.14 Hz and 7.2–27.7 Hz, which is 7 times higher than that of BEH, and EHSC can excite large vibration at low excitation frequency. Therefore, EHSC has higher harvesting efficiency than traditional BEH.

Fig. 22
figure 22

The simulated responses of tip displacement and output voltage under up-sweep excitation for a 0.5 g, b 0.8 g

Full size image

The larger the amplitude of the system, the greater the strain produced by MFC, and thus the output voltage and output power will increase, improving the energy harvesting efficiency. Figure 23 shows the instantaneous power response of EHSC and BEH when 105 Ω impedance under simple harmonic excitation with acceleration amplitude of 0.8 g and frequency of 19 Hz. By calculating the output power of the harvester at different stages, the energy harvesting efficiency at corresponding stages can be obtained. By calculating the average power of EHSC and BEH within 99–100 s, the average power of EHSC is 3.80 mW while BEH is 3.09 mW. EHSC has 23.0% higher energy harvesting power compared to the conventional BEH.

Fig. 23
figure 23

EHSC and BEH when 105 Ω load under simple harmonic excitation with excitation frequency of 19 Hz and acceleration amplitude of 0.8 g a output voltage; b output power

Full size image

Experimental Verification

Experimental Setup

The overall design of the experimental system and the EHSC prototype are shown in Fig. 24. The experimental system consists of the following experimental devices and instruments: harvester prototype, signal generator, power amplifier, shaker, accelerometer (model: aepe, sensitivity: 10.16 mV/g), laser displacement sensor (model: IL100, Keyence), resistance box, digital oscilloscope (model: DSOX1204G, Keysight), signal analyzer (model: 3039, Brüel & Kjær), etc. Piezoelectric material MFC (model: m2807 P2, Smart Material Corp) is attached to beryllium bronze beam by epoxy glue (model: DP460, 3 M). Also, in order to reduce the natural frequency of the system, two beryllium bronze blocks are attached on both sides of the tip magnet. In order to reduce the influence of the weight of the oscillator on the position of the stable equilibrium points, the prototype is placed as shown in Fig. 24b. The shaker provides horizontal vibration excitation for the experimental prototype, which is bolted to the excitation table.

Fig. 24
figure 24

a Overall experiment setup; b prototype experiment model

Full size image

Experimental Results and Discussion

The experimental prototype is set when 105 Ω load resistance, and the excitation frequency is 5–20 Hz (in steps of 1 Hz). We adjust the gain of power amplifier to keep the amplitude of excitation acceleration at 0.5 g and 1 g. The experiment responses are compared with the numerical simulation results, as shown in Fig. 25.

Fig. 25
figure 25

Numerical and experimental responses under 0.5 g and 1 g sinusoidal excitation

Full size image

It can be seen from Fig. 25 that the experimental frequency bandwidth and amplitude are roughly the same as the predicted theoretical results. The differences in the frequency bands may be due to prototype assembly errors.

In order to further verify the correctness of the theoretical results, the corresponding fixed frequency experiment is taken on the basis of the sweep frequency experiment. The comparison between the experimental and the theoretical results is shown in Fig. 26. Due to some unavoidable external influences, such as the influence of adhesive when the piezoelectric patch is attached to the beam and air resistance, the vibration is slightly different from the prediction, but the overall fit is pretty well. Therefore, the experimental results verify the correctness of the theoretical conclusions.

Fig. 26
figure 26

Numerical and experimental responses under constant frequency excitation

Full size image

Conclusions

In order to improve cantilever piezoelectric energy harvesting efficiency, this paper deals with the modelling and dynamic design of a cantilever-based energy harvester with surface constraints (EHSC). EHSC is composed of a low stiffness cantilever beam and two symmetrical constraints with a given geometry, while a pair of magnets provide magnetoelastic force for the beam. The constraints can also make the beam to generate large strain far from the root. Based on the principle of piezoelectric power generation, it can improve the harvesting efficiency greatly. Besides, the magnetic force makes the system bi-stable and broaden the working bandwidth. Through static and dynamic analysis, the parameter domain that makes EHSC achieve high efficiency is determined. A test rig is built to valid experimentally. The main conclusions obtained are as follows:

  1. 1.

    The approximate analytical expression of the nonlinear restoring force of EHSC is obtained. Under the same other conditions, the constraint length ls is positively related to the bending stiffness of the beam, and changes rapidly; the height dg of the constraint is negatively related to the stiffness of the beam. The analytical expression can accurately describe the nonlinear stiffness characteristics of the constrained cantilever beam within the actual working range, and can be directly used for nonlinear dynamic modelling. Considering the rotation angle of the beam tip magnet, a more accurate magnetic force model using the magnetization current method is obtained. The analytical kinetic equations of EHSC facilitate subsequent parameter analysis.

  2. 2.

    Through static bifurcation analysis and dynamic bifurcation analysis, it is found that the system can present rich nonlinear vibration patterns, such as multi-period motion, period-doubling bifurcation, chaos, etc. The EHSC parameter design method is used for selecting the appropriate physical parameters (such as magnets spacing) and excitation parameters to make the EHSC have high harvesting efficiency. The EHSC is easier to jump across potential wells while achieving large motions, which allows the device to perform output high power in low-intensity environments. The results can provide guidance for design and optimization of constrained piezoelectric energy harvesters.

  3. 3.

    Compared with BEH without constraints, EHSC can broaden the bandwidth by about 7 times, and can generate higher voltage output at low frequency. When compared with traditional BEH, the energy harvesting power of EHSC increases by 23.0%. EHSC is a non-collision, easy-to-assemble, and multi-stable energy harvester for low-frequency and low-intensity excitation harvesting. EHSC has a unique configuration, excellent efficiency, the possibility of practical application and academic research value.