Introduction

Capturing the effects of mechanical characteristics of a porous functionally graded material (FGM) is a challenging yet highly intriguing topic. Functionally graded (FG) materials are constructed in two phases [1,2,3], metal and ceramic are often chosen as the base materials. They are formed by gradually changing the proportion at each phase in the thickness direction of the material. FG materials first came into picture during the 1980s. It was invented by a Japanese scientist to form a thermal barrier for a thrust chamber in an aerospace project [4] where the outside temperature was 1500 K and inside was 300 K. The thickness of the FGM was 10 mm and it was made of copper (Cu) as the metal and the ceramic was \({\mathrm{TiB}}_{2}\). During the construction phase of these materials other than the considered materials, there is an inherent anomaly in the structure. This is due to the presence of voids formed during the construction phase. In material modeling, this characteristically vary the performance of the structure [5,6,7,8,9]. The formation of voids in a FGM induces the property of porosity in the structure. Porosity may be formed in two categories, viz., even porosity and uneven porosity. Even porosity in an FG material is formed when the pores/voids are synchronized and evenly distributed throughout the material. Similarly, uneven porosity is caused due to uneven distribution of voids/pores in the structure. In this paper, we are considering even porosity distribution for an FGM plate. Free vibration or natural frequency analysis of a material is a concerned topic for the researchers. Free vibration refers to a type of force in which an object or a component of it is permitted to vibrate at its natural frequency without any support from an external medium. Liu et al. [10] analyzed the fundamental frequencies for in-plane inhomogeneity in the material of an FGM plate. To analyze the free vibration of an FGM plate, a semi-analytical plate formulation based on isogeometric analysis and scaled boundary element approach is conducted. It is revealed that the stiffness of FGM plates is significantly influenced by the power index and width-to-thickness ratio [11]. Similarly, the natural frequencies of a sigmoid functionally graded material plate placed on the Winkler–Pasternak elastic foundation has been calculated using the dynamic stiffness method [12]. Although a lot of work is done and is still going on the deterministic area to evaluate the free vibration of FG materials, it is equally important to dive deep in probabilistic region to gather the information due to uncertainty in the material characteristics (Fig. 1).

Fig. 1
figure 1

Structure of the analysis performed on porous functionally graded material

Full size image

In this light, Monte Carlo simulation (MCS) plays an important role to identify the the degree of uncertainty in the system. Ravi et al. [13] explored the uncertainty in the material parameters and found the stochastic natural frequencies of a FGM plate by incorporating MCS-based approach. MCS-based approach is employed to evaluate the responses in various domains and provides effective results to quantify the uncertainty in the system [14,15,16,17,18,19,20,21,22]. Although the efficiency of MCS-based approach is high, it also has some drawbacks. MCS-based approach is a time-consuming process. This limitation can be mitigated by applying machine learning (ML) models. ML utilizes the pattern of the input–output data’s by analyzing the stochastic system and provides architecture to frame a model which can replicate the MCS-based model. ML is extensively utilized in various domains to predict the responses efficiently with negligible errors. In this light, Vaishali et al. [3] explored the support vector machine (SVM) ML model to evaluate the natural frequencies of different FG shell structures in conjunction to MCS. Similarly, Kritesh et al. [23] utilized a hybrid ML model combining polynomial chaos expansion and Kriging ML model. The output quantity of interest is to predict the dependency of fracture toughness and cohesive energy in the input parameters via molecular dynamics simulations of graphene. Ravi et al. [21] utilized Radial Basis function (RBF) ML model in conjunction with MCS to predict the natural frequencies of a skewed sandwich plate. A novel isogeometric approach is utilized to predict the damage assessment of FGM plate incorporating an improved artificial neural network model [24]. Based on the thorough literature study, it is found that a comparative analysis of the ML models in porous FGM plate is not carried out. The novelty of the present analysis is to compare the ML models that can predict the free vibration of a porous FGM plate. On this regard, five ML models viz., radial basis function (RBF), linear regression (LR), Gaussian progression regression (GPR), artificial neural network (ANN), and support vector machine (SVM) are considered based on the model fitment analysis.

Theoretical Formulation

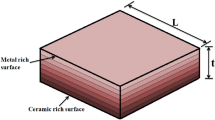
The geometry of a porous FG plate and porosity distributions are depicted in Fig. 2. Consider a porous square FGM plate with length L, width b, and thickness t. The porosity distributions occur in both x and y directions. There are two varieties of porosity distributions such as even and uneven as defined by Wang and Zu [25]. We used porous FGM plate in this investigation, which is composed of stainless steel (SUS304) as the metal and silicon nitride as the ceramic material. The top surface (z = t/2) of plate is considered as ceramic rich and it varies continuously to the bottom surface (z =  − t/2) of plate, which is metal rich, by following the power law index. In this study, the porous plate is considered in which the porosities are spreading within the plate cross-section due to defects generated during manufacturing. To obtain the material properties at different sections of the even porous FG material, power law is employed [30]. It is expressed as,

$$q(t) = q_{m} + (q_{c} - q_{m} )\left[ {\frac{z}{t} + \frac{1}{2}} \right]^{p} - (q_{c} + q_{m} )\frac{\alpha }{2}$$
(1)

where α represents porosity index, qm is material property of metal, qc is the material property of ceramic, t represents the thickness of plate, and p is the power law index. Similar to Eq. (1), material properties of even porous FGM plate can be determined as following:

$$E\left(t\right)={E}_{m}+ \left[{E}_{c}-{E}_{m}\right]{\left[\left(\frac{2z+t}{2t}\right)\right]}^{p}-[{E}_{c}+{E}_{m}]\frac{\alpha }{2}$$
(2)
$$G\left(t\right)={G}_{m}+ \left[{G}_{c}-{G}_{m}\right]{\left[\left(\frac{2z+t}{2t}\right)\right]}^{p}-[{G}_{c}+{G}_{m}]\frac{\alpha }{2}$$
(3)
$$\rho \left(t\right)={\rho }_{m}+ \left[{\rho }_{c}-{\rho }_{m}\right]{\left[\left(\frac{2z+t}{2t}\right)\right]}^{p}-[{\rho }_{c}+{\rho }_{m}]\frac{\alpha }{2}$$
(4)
$$\upmu \left(t\right)={\upmu }_{m}+ \left[{\upmu }_{c}-{\upmu }_{m}\right]{\left[\left(\frac{2z+t}{2t}\right)\right]}^{p}-[{\upmu }_{c}+{\upmu }_{m}]\frac{\alpha }{2}$$
(5)

where E, G, μ, and ρ represent Young’s modulus, shear modulus, Poisson’s ratio, and mass density of FGM plate, respectively. Considering uneven distribution of porosity, the material properties in Eqs. (2–5) can be replaced by

Fig. 2
figure 2

a Isometric view of a porous FGM plate b even and uneven porosity of FGM plate

Full size image
$$E\left(t\right)={E}_{m}+ \left[{E}_{c}-{E}_{m}\right]{\left[\left(\frac{2z+t}{2t}\right)\right]}^{p}-\frac{\alpha }{2}[{E}_{c}+{E}_{m}] [1-\frac{2z}{t}]$$
(6)
$$G\left(t\right)={G}_{m}+ \left[{G}_{c}-{G}_{m}\right]{\left[\left(\frac{2z+t}{2t}\right)\right]}^{p}-\frac{\alpha }{2}[{G}_{c}+{G}_{m}][1-\frac{2z}{t}]$$
(7)
$$\rho \left(t\right)={\rho }_{m}+ \left[{\rho }_{c}-{\rho }_{m}\right]{\left[\left(\frac{2z+t}{2t}\right)\right]}^{p}-\frac{\alpha }{2}[{\rho }_{c}+{\rho }_{m}][1-\frac{2z}{t}]$$
(8)
$$\mu \left(t\right)={\mu }_{m}+ \left[{\mu }_{c}-{\mu }_{m}\right]{\left[\left(\frac{2z+t}{2t}\right)\right]}^{p}-\frac{\alpha }{2}[{\mu }_{c}+{\mu }_{m}][1-\frac{2z}{t}]$$
(9)

Also, the material properties depend on the operating temperature, which can be comprehended by the Touloukian model [26] as

$$q = q_{0} + q_{ - 1} T^{ - 1} + 1 + q_{1} T + q_{2} T^{2} + q_{3} T^{3}$$
(10)

where \(q_{0}\), \(q_{ - 1}\), \(q_{1}\), \(q_{2}\), \(q_{3}\) are the temperature-dependent coefficients, and T represents the temperature in Kelvin.

Governing Equations

For an orthogonal co-ordinate system, considered (x, y) as the mid-plane of the reference plane as shown in Fig. 1. According to the FSDT, Eqs. (11), (12), and (13) are utilized to depict the displacement field relations in the three axis of the system

$$a\left( {x,y,z} \right) = a_{0} \left( {x,y} \right) - za\left( {x,y} \right)_{{}}^{{}} {\mathcal{R}}_{x} \left( {x,y} \right)$$
(11)
$$b\left( {x,y,z} \right) = b_{0} \left( {x,y} \right) - zb\left( {x,y} \right)_{{}}^{{}} {\mathcal{R}}_{y} \left( {x,y} \right)$$
(12)
$$c\left( {x,y,z} \right) = c\left( {x,y} \right) = c_{0} \left( {x,y} \right)$$
(13)

where the displacements in x, y, and z directions are represented by a, b, and c, respectively, and the displacements at mid-plane are represented by \(a_{0}\), \(b_{0}\), and \(c_{0}\), respectively. The rotation in the direction of x and y is represented by \({\mathcal{R}}_{x}\) and \({\mathcal{R}}_{y}\). The dynamic equilibrium equation excluding damping is expressed as

$$\left[m\left(\varpi \right)\right]\left\{\ddot{x}\right\}+\left[k\left(\varpi \right)\right]\left\{x\right\}=\{f\}$$
(14)

where{\(\ddot{x}\)}is a global acceleration vector,\(\left\{ x \right\}\) represents the global displacement vector,\(\left[ {m\left( \varpi \right)} \right]\) represents the random global mass matrix, \(\left[ {k\left( \varpi \right)} \right]\) is the random stiffness matrix, and \(\left\{ f \right\}\) is an externally applied force vector. For the free vibration problem, there will be no external force; hence, Eq. (14) is depicted as,

$$\left[m\left(\varpi \right)\right]\left\{\ddot{x}\right\}+\left[k\left(\varpi \right)\right]\left\{x\right\}=0$$
(15)

The static and dynamic components are considered for the present analysis. From Eq. (15), [{x} = {xs} + {xp}, where {xp} is a time reliant perturbation about {xs}, and {xs} is the static displaced position]. The equation of motion is stated as

$$\left[ {m\left( \varpi \right)} \right]\left\{ {\ddot{x}_{p} } \right\} + \left\{ {\left[ {k\left( \varpi \right)} \right] + [k_{p} ]\left( \varpi \right)} \right\}\left\{ {x_{p} + x_{s} } \right\} = 0$$
(16)

For natural frequency analysis, the equation of motion is stated as

$$\left[ {m\left( \varpi \right)} \right]\left\{ {\ddot{x}_{p} } \right\} + \left\{ {\left[ {k\left( \varpi \right)} \right] + [k_{p} ]\left( \varpi \right)} \right\}\left\{ {x_{p} } \right\} = 0$$
(17)

In Eq. (17), the displacement {xp} depends upon time and space. In natural frequency analysis, the time and space coordinates of displacement space and time coordinated are stated as

$$\left\{ {x_{p} } \right\} = A^{\prime}e^{i\omega t} \{ \theta \}$$
(18)
$$\left\{ {\ddot{x}_{p} } \right\} = - A^{\prime}\omega^{2} e^{i\omega t} \{ \theta \}$$
(19)

where i = 1,2,3,….,n

Substituting the values from Eqs. (18) and (19), the modified equation of motion is

$$A^{\prime}e^{i\omega t} ( - \omega^{2} [m]\{ \theta \} + ([k] + [k_{\sigma } ])\left\{ \theta \right\}) = 0$$
(20)

As \({\rm A}^{\prime}e^{i\omega t} \ne 0\)

$$\omega^{2} [m]\{ \theta \} = ([k] + [k_{\sigma } ])\left\{ \theta \right\}$$
(21)

here \(\omega\)(natural frequency) is the output quantity of interest for the present analysis. Now, Eq. (21) is further transformed utilizing QR iteration algorithm as

$$\left[ A \right]\left\{ \theta \right\} = \lambda \left\{ \theta \right\}$$
(22)
$$\left[ A \right] = \left( {\left[ k \right] + \left[ {k_{\sigma } } \right]} \right)^{ - 1} \left[ m \right]$$
$${\text{and}}\;\lambda = 1/\omega^{2}$$
(23)

Finite Element (FE) Formulation

The FE formulation of the porous FGM cantilever plate is designed considering a quadratic element with eight nodal structures as depicted in Fig. 3. There are three translational and two rotational degrees of freedom in the nodal points. The interpolation polynomial function for the present model is expressed as

$$a(\xi ,\eta ) = F_{0} + F_{1} \xi + F_{2} \eta + F_{3} \xi^{2} + F_{4} \xi \eta + F_{5} \eta^{2} + F_{6} \xi^{2} \eta + F_{7} \xi \eta^{2}$$
(24)

where \(F_{0} ,F_{1} ,.........F_{7}\) are the degrees of freedom.

Fig. 3
figure 3

Matrix, elemental, and nodal level co-ordinate system constructed by finite element method

Full size image

In FE formulation, the shape functions (Sj) are the function of local natural coordinates of the element (1, v). Here η = − 1 for nodes 1, 4, 8; η =  + 1 for nodes 2, 3, 6; and ζ = − 1 for nodes 1, 2, 5; and ζ =  + 1 for nodes 3, 4, 7 as shown in Fig. 3. The shape functions \(S_{i}\) can be depicted as:

$$\begin{gathered} S_{i} = 0.25\left( {1 + \xi \xi_{i} } \right)\left( {1 + \eta \eta_{i} } \right)\left( {\xi \xi_{i} + \eta \eta_{i} - 1} \right)\quad \cdots i = 1,2,3,4 \hfill \\ S_{i} = 0.5\left( {1 + \eta \eta_{i} } \right)\left( {1 - \xi^{2} } \right)\quad \cdots i = 5,7 \hfill \\ S_{i} = 0.5\left( {1 + \xi \xi_{i} } \right)\left( {1 - \eta^{2} } \right)\quad \cdots i = 6,8 \hfill \\ \end{gathered}$$
(25)

The shape functions accuracy is evaluated by

$$\sum\limits_{i = 1}^{8} {S_{i} {\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} 1,\quad \sum\limits_{i = 1}^{8} {\frac{{\partial S_{i} }}{\partial \xi }} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} {\kern 1pt} 0\quad {\text{and}}\quad \sum\limits_{i = 1}^{8} {\frac{{\partial S_{i} }}{\partial \eta }} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} {\kern 1pt} 0}$$
(26)

The bending formulation for the coordinates (x, y) is stated as

$$x = \sum\limits_{i = 1}^{8} {S_{i} {\kern 1pt} {\kern 1pt} x_{i} } \quad {\text{and}}\quad y = \sum\limits_{i = 1}^{8} {S_{i} {\kern 1pt} {\kern 1pt} y_{i} }$$
(27)

The displacement at any nodes can be expressed as

$$a = \sum\limits_{i = 1}^{8} {S_{i} {\kern 1pt} {\kern 1pt} a_{i} ,\quad b = \sum\limits_{i = 1}^{8} {S_{i} {\kern 1pt} {\kern 1pt} b_{i} } ,} \quad c = \sum\limits_{i = 1}^{8} {S_{i} {\kern 1pt} {\kern 1pt} c_{i} } ,\quad \varphi_{x} = \sum\limits_{i = 1}^{8} {S_{i} {\kern 1pt} {\kern 1pt} \varphi_{xi} } ,\quad \varphi_{y} = \sum\limits_{i = 1}^{8} {S_{i} {\kern 1pt} {\kern 1pt} \varphi_{yi} }$$
(28)

where

$$\left[ \begin{gathered} N_{i,x} \hfill \\ N_{i,y} \hfill \\ \end{gathered} \right] = [J]^{ - 1} {\kern 1pt} {\kern 1pt} \left[ \begin{gathered} N_{i,\xi } \hfill \\ N_{i,\eta } \hfill \\ \end{gathered} \right]\quad {\text{and}}\quad \left[ J \right] = \left[ {\begin{array}{*{20}c} {X_{\zeta } } & {Y_{\zeta } } \\ {X_{\eta } } & {Y_{\eta } } \\ \end{array} } \right]$$
(29)

MCS-Based Random Free Vibration Analysis

In the present study, uncertain material properties, structural, and environmental parameters such as thickness, temperature, porosity index are taken as input parameters, and first three natural frequencies are considered as responses. The individual and combined variation in material properties and other parameters are considered as follows:

1. The impact of individual variations in material properties:

  1. (a)

    Young’s modulus:\(I_{1}^{v} (\omega ) = \Psi [{\rm E}_{z} (\omega )]\)

  2. (b)

    Shear modulus:\(I_{2}^{v} (\omega ) = \Psi [G_{z} (\omega )]\)

  3. (c)

    Material density:\(I_{3}^{v} (\omega ) = \Psi [\rho_{z} (\omega )]\)

  4. (d)

    Poisson’s ratio:\(I_{4}^{v} (\omega ) = \Psi [\mu_{z} (\omega )]\)

2. The impact of combined variations in material properties:

$$C_{o}^{{{\text{combined}}}} = \Psi [\{ {\rm E}_{z} (\omega )\} ,\{ G_{z} (\omega )\} ,\{ \rho_{z} (\omega )\} ,\{ \mu_{z} (\omega )\} ]$$
(30)

where\(\upomega\) represents the randomness in parameters, and ψ is a symbolic operator of the MCS. In the FGM plate, the constitute materials distributed cross the thickness (t) and randomness is introduced in the material properties with certain limits to capture the randomness caused due to unavoidable reasons. The randomness in material mainly occurs during the manufacturing of the FGM plates. The random input variables follow the uniform distribution (as shown in Fig. 4) with bound limits of \(\pm\) P % with respect to deterministic value of material properties. In the random analysis, the degree of randomness is considered as 10%. In this analysis, a random natural frequency analysis of porous FGM plates is carried out by coupling the FE code with Monte Carlo simulation as shown in Fig. 4. In general, for porous FGM, the output of free vibration analysis is not available as an explicit function of the input parameters. The random analysis of complex porous FGM plates can only be carried out numerically by the finite element method coupled with MCS considering 10,000 number of iterations.

Fig. 4
figure 4

Flowchart for stochastic analysis of the porous functionally graded material

Full size image

Machine Learning (ML) Models

ML models are generally utilized to predict the response of a particular analysis based on the interaction between the input and output parameters. The models are categorized mainly into two categories, supervised and unsupervised ML models [28]. A function that converts an input to an output is learned under supervision using sample input–output pairs. Unlike supervised learning, unsupervised learning is used to draw inferences and find patterns from input data without references to labeled outcomes [29]. The present analysis involves supervised learning of the ML models from a finite element analysis to obtain the free vibration of a porous FGM plate. The details of the utilized ML models are mentioned in the Supplementary file (1–5).

Results and Discussion

A thorough description of the observations derived from the stochastic FE-based dynamic analysis of the FG cantilever plates is portrayed in this section. We first validated the results of the FE technique using the published literature before carrying out the stochastic analysis. In this regard, at room temperature (T = 300 K), the dynamic response (natural frequency) of a rectangular FGM plate made of structural steel (SUS304) and silicon nitride (Si3N4) with dimensions of 0.2 m × 0.2 m × 0.025 m (L × b × t) and 0.28 Poisson's ratio is recorded. Silicon nitride is a very effective ceramic with great thermal shock and impact resistance. It possesses better combinations of creep and oxidation resistance, outperforming the high temperature capabilities of most metals. Structural steel (SUS304) has an excellent corrosion resistance to numerous chemical corrodents and industrial atmospheres. It is also a heat resistance grade. The combination of these two materials is utilized to evaluate the fundamental natural frequency of the designed FG material. The validation results are summarized in Table 1, which shows that the chosen FE approach has some promise for providing reliable results. We continued to do the FE analysis for the FGM taken into consideration in the current investigation because we had adequate confidence in the chosen FE approach. The FGM cantilever plate that was the subject of the current investigation is made of metal aluminium and ceramic zirconia. Table 2 lists the specific material characteristics of the FGM ingredients. Unless otherwise specified, the thickness (t) of a plate is assumed to be 2 mm, while the dimensions (l, w) are assumed to be 1 m.

Table 1 Comparison of frequency parameter for a stationary SUS304/Si3N4 FGM plate
Full size table
Table 2 Material properties of constitutes for the FGM plate at 300 K [31]
Full size table

In the current investigation, the FGM constructions are specified with two types of porosity (even and uneven) with a porosity index (α) of 0.1 unless otherwise stated (see Fig. 1b). The stochastic analysis is carried out considering 10,000 samples (N) to conduct the MCS-based analysis. The results of the first three natural frequencies from MCS provide as the benchmark for the succeeding machine learning model analysis. A comparative analysis is carried out for the machine learning models in the form of mean error analysis, standard deviation error analysis, and first three natural frequency distribution in the form of probability density function analysis. Five machine learning models are considered for the present analysis based on the performance of each model.

The ML models considered are radial basis function (RBF), linear regression (LR), Gaussian progression regression (GPR), artificial neural network (ANN), and support vector machine (SVM). The mean error analysis is portrayed in Fig. 5 for the first three natural frequencies. The mean error analysis is conducted to check the applicability of the ML models for different sample sizes.

Fig. 5
figure 5

Mean error distribution of the porous FGM plate for a first natural frequency (FNF) b second natural frequency (SNF) c third natural frequency (TNF)

Full size image

The relation of the mean error is established by comparing the mean data of each sample sizes with the mean results of MCS. In this case, four different sample sizes (256, 512, 1024, and 2048) are considered for the study. The error is calculated as \(\left[|\frac{\mathrm{Direct MCS result}-\mathrm{ML based result}}{\mathrm{Direct MCS result}}|\times 100\right]\). The error plots are presented in three-dimensional histogram form. The mean and standard deviation percentage errors are calculated by comparing the stochastic data of machine learning models with the MCS model for each failure theory's first-ply failure data. It is found that as the sample sizes are increased from smaller number to higher, the mean error is reduced. It can be noticed from Fig. 5a–c that for the first, second, and third natural frequencies, N = 2048 provides a minimal mean error. Thus, it is safe and efficient to proceed with this sample size for further study. The standard deviation error analysis is also conducted to check the applicability of the ML models for different sample sizes. By contrasting the standard deviation data from each sample size with the MCS results, the relationship between the standard deviation error and sample size is established. Like the mean error analysis, four different sample sizes (256, 512, 1024 and 2048) are considered for the study. It is found that the standard deviation error is reduced as the sample size is increased. It can be noticed from Fig. 6a–c that for the first, second, and third natural frequencies, N = 2048 provides a minimal standard deviation error. Thus, it is safe and efficient to proceed with this sample size for further study. It is also to be noticed that from the mean and standard deviation error analysis, the sample sizes can be increased further but as it is well established that the ML models are able to predict the output efficiently (less than 1% error in all cases). Also, it is computationally time consuming and inefficient to increase the sample sizes. The probability density function is plotted for the five machine learning models viz., radial basis function (RBF), linear regression (LR), Gaussian progression regression (GPR), artificial neural network (ANN), and support vector machine (SVM) in Fig. 7. The PDF plots for the ML models are plotted in curved lines. For the authentication of the prediction by the ML models for each fundamental natural frequencies, the MCS data are plotted in dotted curved lines along with the ML models. From Fig. 7, a clear inference can be drawn that the ML models perform efficiently to predict the first three fundamental natural frequencies. The peak point of the bell-shaped curve represents the mean data for the fundamental natural frequency. The deviation from the mean value on both sides of the curve represents the standard deviation due to the stochastic effect on the input material properties. Normal distribution of data is chosen for plotting the PDF for machine learning models and MCS-based model. The MCS plot and ML model plot for each model display a good agreement in the PDF plot.

Fig. 6
figure 6

Standard deviation error distribution of the porous FGM plate for a first natural frequency b second natural frequency, c third natural frequency

Full size image
Fig. 7
figure 7

Probability distribution function (PDF) plots of the porous FGM plate for a first natural frequency,, b second natural frequency, c third natural frequency for respective ML models

Full size image

The scatter plot depiction is utilized to display the relation for the actual response of the original finite element model in conjunction with the machine learning-based model's predicted response. The response observed in Fig. 8 displays a high positive correlation between the true and predicted response. From error analysis, it can be confirmed that the machine learning models converge efficiently with the MCS-based model for sample size 2048. The predicted response of the model is plotted for sample size (Ns = 2048). This sample size is found to be displaying the most negligible error for all the machine learning models. This indicates that the machine learning-based model can replace the time-consuming conventional finite element model concerning 161 material input parameters for subsequent analyses. It leads to a significant reduction in time without compromising the accuracy of the model. Figure 8 displays the scatter plot for first three fundamental natural frequencies. The six machine learning models (RBF, LR, GPR, ANN, and SVM) are depicted in scatter plots. The scattering of data is observed comparatively less in all the machine learning models except for a few cases like FNF prediction through SVM and ANN, SNF prediction through ANN. This is due to the presence of noise in the prediction of ML models. From Fig. 8, it can be predicted that among all, the machine learning model performs efficiently, due to less mean and standard deviation error. It is also observed that the scattering of data is least in the case of GPR, LR, and RBF.

Fig. 8
figure 8

Scatter plots of the porous FGM plate for first three natural frequencies and their respective ML models

Full size image

Conclusion

The present paper presents a comparison of different ML models and their prediction capability for first three fundamental natural frequencies in a porous FGM plate. The FGM plate is designed of stainless steel (SUS304) as the first material and silicon nitride (Si3N4), a ceramic as the second material with dimensions of 0.2 m × 0.2 m × 0.025 m (L × b × t). Elastic and shear moduli (along and across the direction of the fibers), Poisson’s ratio, mass density, and thickness are among the input factors whose variability is taken into account. To examine the stochastic natural frequency, 10% combined stochasticity is provided on the input parameters. The output quantity of interest is first evaluated by Monte Carlo simulation. Since, this method is a time-consuming process, machine learning models are utilized to mitigate the issue. The effectiveness of the machine learning models viz., radial basis function, linear regression, Gaussian progression regression, artificial neural network, and support vector machining is compared in a brief examination. The results are presented in the form of mean error analysis, standard deviation error analysis, probability density function plot, and scatter plots. The comparison analysis of the ML models is predicted in the form of first three fundamental natural frequencies. It is found that the predictive output of ANN in the form of scatter plot depicts the presence of noise in the datasets for all the three responses. SVM model also depicted the presence of scattering of datasets for first natural frequency. The other three ML model’s prediction is found to be satisfactory of the present stochastic model. The machine learning models performed efficiently in the probability density function plot when compared with the Monte Carlo simulation model.

The results presented in the paper will help the designers in building an efficient and robust model for various other porous FGM structures in future due to the uncertainty in the system.