Introduction

Beam string steel structure system is currently the main structural form of long-span spatial structures, which has been applied widely in sports venues, exhibition center, airport, train station, shopping malls and other infrastructures. Moreover, it can also be used in the bridge structure. In the aforementioned structure, the wire rope participates in the overall stress of the structural system as a tensile component, and the tension state of the steel cable can directly indicate the internal force distribution of the structure. In the service state, the identification of cable force can be used as the reference for the status of structural health and the performance of members. Therefore, the identification of cable forces is of great significance for the safety of string structures.

Existing identification methods for cable force have hydraulic pressure gauge measuring method, pressure sensor measuring method, measuring the elongation of cable, magnetic flux method, and the frequency method. The first four methods get tensile force of the cable through the measurement of the tension or the deformation, and the frequency method indicates the relationship between the frequency and tensile force through the dynamic characteristics of the cable. The frequency method is still the most practical and convenient method at this stage [1, 10, 13]. By picking up the dynamic response signal acting on the cable under the forced excitation and identifying the frequency of the cable, the corresponding cable force can then be obtained using the formula between the frequency and the cable force [5,6,7, 11, 12]. The engineering practice indicates that when the ratio of cable single-span lengths to cable diameter is larger than 100 and the diameter of the cable is less than 44 mm, the relationship between the force and the frequency of the cable is relatively simple, then the cable force obtained from the frequency method would have higher accuracy. There are two major considerations for the extension of the frequency method to the multi-span cable. First, the aspect ratio of cables is usually less than 100 and the cable diameter is greater than 44 mm in practical engineering. The application of this short and thick cable accounts for more than 80% of tensioned string structures; therefore, it has a broad application background. Second, existing well-developed frequency methods mainly focus on the single-span cable [2, 4, 8, 9], and the dynamic response characteristics of the beam string structure with multi-span cables are complicated due to the complex strut constraints and the bending stiffness of that short and thick cable [3, 14, 17]. Similar advances have been made recently in the study of the dynamic characteristics of the cable [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39].The relationship between the characteristic frequency and cable force cannot be expressed by simple analytic function, and the theoretical results still lag behind the engineering practice at the current stage. A series of new advances have also been made on the dynamic characteristics of damped and series springs along circular or elliptic paths under resonant frequency excitation. For example, Amer et al. obtained the analytical solutions of bifurcated diagram and time-history diagram using series approximation method on the motion characteristics of elemental points along circular paths under internal resonant frequency excitation 40, and then the analytical solutions of three series simple pendulums were obtained [45]. Similarly, the vibration characteristics of a single spring pendulum with linear damping in an elliptical path under the action of approximate resonance excitation were studied, and the resonant response was obtained, respectively. The time-history characteristics of the stable and unstable regions were analyzed [41,42,43,44] In addition, an analytical solution is obtained for the time-history response along the elliptic path under the frequency excitation of the double pendulum resonance [46, 47]. In terms of the structural working state detection theory, Zhou et al. developed a simulation evaluation method for detecting the damage generation from expansion of steel structures under composite fatigue loads [48]. On the aspect of structural vibration signal processing, there is also some new progress based on vibration signal SHM method [49]. As for the study of vibration isolation effect by using flexible plate support as flexible boundary condition, the results of Hao et al. show that the nonlinear hopping phenomenon can be eliminated in the low-frequency range and the frequency detuning can be avoided at the same time [50]. Some dynamics about structures have made some progress [51,52,53,54,55,56,57].

Therefore, it is necessary to study the characteristic frequency and cable force of beam string structure with the multi-span cable.

The test results indicate that the characteristic natural vibration frequency of the cable of tension-string structure is related to the tensile force of the cable, the bending stiffness of the cable, the bending stiffness of the constraints at both ends, and the compressive stiffness. The sag of the cable is affected by its linear density, bending stiffness, and the tensile force. Moreover, the compressive stiffness and rotational stiffness at the ends determine the pattern of the cable and restrict the deformation of the cable at both ends. The relationship between natural vibration frequency and tension of cable considering the bending stiffness of the constraint at both ends has received much attention from the literature. However, the rigid struts of the cable and the vertical stiffness of the constraints at both ends has not been reasonably considered, and most string structures are composed of the multi-span cable which has multiple struts. Therefore, it is necessary to consider the influence of the constraint stiffness of the struts and the rotational stiffness and the vertical stiffness of the constraint at both ends, which is essential to accurately establish the nonlinear relationship between the low-order/multi-order characteristic frequencies and the tensile force of the cable as well as all the constraint stiffness at the boundary. First, based on the single-span tensioning string structure, the relationship between tension, rotational stiffness, vertical stiffness and the low-order frequency is established with the consideration of rotational stiffness and vertical stiffness at constraints of both ends. Second, to extend the relationship among tensile force, restraint stiffness, and the low frequency of the single-span cable to the multi-span string structure, the rotation of the strut and the constraint effect of vertical stiffness on the cable have also been considered to develop the nonlinear formulation of the multi-span string structure. When the value of low-order frequency is measured, the corresponding tensile force and the constraint stiffness can then be obtained through the above relationships.

The research on the relationship between the tensile force and the frequency of the single cable is summarized as follows.

  1. (1)

    Tensioning string theory [58].

    $$T = 4ml^{2} \left( {\frac{{f_{n} }}{n}} \right)^{2} .$$
    (1)

In the above formula, T is the tension of the cable, m is the line mass of the cable, l is the length of the single-span cable, n is the order of the corresponding nth order frequency, and fn is the natural frequency of the corresponding nth order.

  1. (2)

    Simply supported beam theory [59]

    $$T = 4ml^{2} \left( {\frac{{f_{n} }}{n}} \right)^{2} - {{n^{2} \pi^{2} EI} \mathord{\left/ {\vphantom {{n^{2} \pi^{2} EI} {l^{2} }}} \right. \kern-0pt} {l^{2} }}.$$
    (2)
  2. (3)

    Japanese Zui H theory [60]

    $$\begin{array}{*{20}c} {T = \frac{4\omega }{g}\left( {f_{1} l} \right)^{2} \left[ {1 - 2.2\frac{C}{{f_{1} }} - 0.55\left( {\frac{C}{{f_{1} }}} \right)^{2} } \right]} & {\left( {17 \le \xi } \right)} \\ \end{array} ,$$
    (3)
    $$\begin{array}{*{20}c} {T = \frac{4\omega }{g}\left( {f_{1} l} \right)^{2} \left[ {0.865 - 11.6\left( {\frac{C}{{f_{1} }}} \right)^{2} } \right]} & {\left( {6 \le \xi \le 17} \right)} \\ \end{array} ,$$
    (4)
    $$\begin{array}{*{20}c} {T = \frac{4\omega }{g}\left( {f_{1} l} \right)^{2} \left[ {0.828 - 10.5\left( {\frac{C}{{f_{1} }}} \right)^{2} } \right]} & {\left( {0 \le \xi \le 6} \right)} \\ \end{array} .$$
    (5)

It is obvious that the greater the strength of the cable, the greater the corresponding bending stiffness, so a dimensionless parameter ξ reflecting the bending stiffness can be defined, and different ξ can be used to obtain the above three formulas.

$$\xi = l\sqrt {\frac{{T_{0} }}{EI}} .$$
(6)

In the above formula, T0 is the corresponding initial tension of the cable, E is the elastic modulus of the cable, and I is the resistance moment of the cable section.

  1. (4)

    Shao Xudong energy method theory [62]

    $$\begin{array}{*{20}c} {T = 4ml^{2} f_{0}^{2} - {{\pi^{2} EI} \mathord{\left/ {\vphantom {{\pi^{2} EI} {l^{2} }}} \right. \kern-0pt} {l^{2} }}} & {\eta \ge 70} \\ \end{array} ,$$
    (7)
    $$\begin{array}{*{20}c} {T = \left( {3.3 + 0.01\eta } \right)ml^{2} f_{0}^{2} - \left( {42 - 0.46\eta } \right){{EI} \mathord{\left/ {\vphantom {{EI} {l^{2} }}} \right. \kern-0pt} {l^{2} }}} & {\eta \le 70} \\ \end{array} .$$
    (8)
  2. (5)

    Ren Weixin energy method theory [61]

    $$\begin{array}{*{20}c} {T = 3.432ml^{2} f_{0}^{2} - 45.191{{EI} \mathord{\left/ {\vphantom {{EI} {l^{2} }}} \right. \kern-0pt} {l^{2} }}} & {\left( {0 \le \xi \le 18} \right)} \\ \end{array} ,$$
    (9)
    $$\begin{array}{*{20}c} {T = m\left( {2lf - \frac{2.363}{l}\sqrt{\frac{EI}{m}} } \right)^{2} } & {\left( {18 \le \xi \le 210} \right)} \\ \end{array} ,$$
    (10)
    $$\begin{array}{*{20}c} {T = 4ml^{2} f_{0}^{2} } & {\left( {210 \le \xi } \right)} \\ \end{array} .$$
    (11)
  3. (6)

    Chen Huai fixed beam theory [63]

    $$\begin{array}{*{20}c} {T = 4ml^{2} f_{1}^{2} \left[ {0.8232 - 10.437\left( {\frac{C}{{f_{1} }}} \right)^{2} } \right]} & {\left( {0 \le \xi \le 9} \right)} \\ \end{array} ,$$
    (12)
    $$\begin{array}{*{20}c} {T = 4ml^{2} f_{1}^{2} \left[ {0.8881 - 12.7931\left( {\frac{C}{{f_{1} }}} \right)^{2} } \right]} & {\left( {9 \le \xi \le 20} \right)} \\ \end{array} ,$$
    (13)
    $$\begin{array}{*{20}c} {T = ml^{2} f_{1}^{2} \left[ {1 + \sqrt {1 - 4.314\left( {\frac{C}{{f_{1} }}} \right)} } \right]^{2} } & {\left( {20 \le \xi } \right)} \\ \end{array} .$$
    (14)

Wherein, the parameter C in the above equation can be expressed in the following form, which is obviously also a process parameter to express the bending stiffness of the line.

$$C = \sqrt {\frac{EI}{{ml^{4} }}} .$$
(15)

In formula (14), it is obvious that when ξ is large enough, the corresponding linear bending stiffness is small enough and the corresponding C value is small enough, and the ratio to first-order natural vibration frequency is usually small, ensuring that the calculated value under the root sign is greater than zero.

  1. (7)

    Ma Hongxu test calibration method theory [64]

    $$T = 0.0264f_{i}^{2} + 0.0002f - 0.0018.$$
    (16)

In the above formulas, fi represents the characteristic frequency of the i order, and T represents the tension value of the corresponding anchor cable. The aforementioned methods can directly derive the relationship between the frequency and tension of the single cable based on some kind of constraints. However, the constraint conditions are the results under the ideal condition. At present, the method to reasonably consider the boundary constraint of strut is less from the literature. Based on the fact that the constraint of strut on the single cable is a state between the fixed and the hinged constraints, the constraints of struts are decomposed into the vertical tension and compression stiffness and the bending stiffness considering the rotation, the formulation of single-span cable under general constraints can then be derived. The second step is to connect the above single-span cables in series to obtain the vibration equation of multi-span cables that have multiple struts.

The aforementioned methods can directly derive the relationship between the frequency and tension of the single cable based on some kind of constraints. However, the constraint conditions are the results under the ideal condition. At present, in a variety of practical cable structural engineering, especially in bridge structural engineering, the supporting member that plays a supporting role provides the corresponding supporting stiffness and vertical constraints for the cable. However, in the existing literature, there is almost no mention of the above which can reflect the constraint effect of the strut between the cable, and what was mentioned in the past may be simplified as rigid support conditions. But this is not in line with the pole has a certain stiffness of the actual situation. The cable force model proposed in this paper is based on the general constraint conditions at both ends of the cable. The two ends are considered as double spring constraints that can consider rotational stiffness and a certain compressive stiffness at the same time. Meanwhile, to reasonably consider the vertical constraint effect of the strut on the cable, the strut is also considered as double spring constraints with a certain compressive stiffness and bending stiffness. The frequency vibration equations of the cable model with n-span strut are derived under the general constraints. The undetermined parameters containing 2n + 2 unknown stiffness and 1 unknown cable force can be obtained by using the multi-frequency fitting method. The optimization algorithm model can be used for calculation, the optimization objective function is established, and the iterative function is used for iterative solution. Finally, the constraint spring stiffness of 2n + 2 and the tension value of the cable are obtained.

Vibration Equation of Single-Span Cable Under General Constraints

Basic Assumptions

For the analytical solution of the single-span cable, some basic assumptions are required. The basic assumptions of this problem are summarized as follows:

  1. (1)

    Assuming the problem as a plane problem, and the vibration and the mode shape of single or multi-span cables are within the vertical plane;

  2. (2)

    Single or multi-span cables and struts can be simplified as the ideal elastic material, which conform to Hooke’s law;

  3. (3)

    Friction occurs between the seven strands of the steel wire in the cable due to the tension. It is assumed that the seven strands of steel wire are uniformly stressed without stress difference;

  4. (4)

    As the cable is also affected by the gravity, the cable will form a pattern similar to the catenary shape with certain sag under the condition of zero tension, portion of the cable will correspond to higher characteristic frequency as the sag directly improves the bending stiffness of the cable. The value of the cable force will be overestimated if the effect of sag is not taken into account. However, when slenderness ratio is relatively large, the aforementioned effect is minor which can be ignored;

  5. (5)

    It is assumed that the relationship between the characteristic frequency and the tension of the cable remains constant within the range of normal temperature, which represents that the effect of the temperature fluctuation within the normal range is negligible;

  6. (6)

    The inclination of the cable has no effect on the relationship between the characteristic frequency and the tension of the cable, which indicates that the placement of cable in the form of horizontal or inclined has negligible influence on the relationship.

Mechanical Model

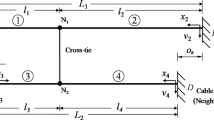
For the vibration analysis of the single cable under general constraints, the stress model of single cable unit AB has been depicted in Fig. 1. In the vibration process, the vibration amplitudes of the force P at both ends of the cable are the moment amplitudes MA and MB, and the shear amplitudes QA and QB, respectively. The vibration amplitudes of the displacement δ at both ends of the cable are the amplitude of the angular displacement φA and φB, and the amplitude of the vertical displacement YA and YB, respectively.

Fig. 1
figure 1

Vibration model of single-span cable under general constraints

Full size image

The general solution of the vibration equation of the single cable can be given by:

$$Y\left( x \right) = C_{1} ch\beta x + C_{2} sh\beta x + C_{3} \cos \gamma x + C_{4} \sin \gamma x,$$
(17)

where C1, C2, C3, and C4 are undetermined constants.

$$\gamma = \sqrt {\left( {\lambda^{4} + \frac{{\alpha^{4} }}{4}} \right)^{0.5} + \frac{{\alpha^{2} }}{2}} ,$$
(18)
$$\beta = \sqrt {\left( {\lambda^{4} + \frac{{\alpha^{4} }}{4}} \right)^{0.5} - \frac{{\alpha^{2} }}{2}} ,$$
(19)
$$\begin{array}{*{20}c} {\alpha^{2} = \frac{N}{EI}} & {\lambda^{4} = \frac{{\omega^{2} m}}{EI}} \\ \end{array} .$$
(20)

The expression of the boundary conditions can be established according to Fig. 1.

Regarding the general boundary conditions, the vibration frequency of the bending moment and the shear force at one end is ω, and the vibration amplitude is M0, Q0; the vibration cycle of the rotation and the deflection is ω, and the amplitude is φ0, Y0.

$$\begin{array}{*{20}c} {Y\left( 0 \right) = Y_{0} } & {Y^{\prime}\left( 0 \right) = \varphi_{0} } & { - EIY^{\prime\prime}\left( 0 \right) = M_{0} } & { - EIY^{\prime\prime\prime}\left( 0 \right) = Q_{0} } \\ \end{array} .$$
(21)

It is stipulated that the downward deflection is positive, the clockwise inclination is positive, the tension on the lower side of the bending moment is positive, and the clockwise shear is positive.

Considering the general solutions and boundary conditions of the vibration equations simultaneously, the following equations can be obtained:

$$\left\{ \begin{aligned} Y_{0} & = C_{1} + C_{3} \\ \varphi_{0} & = C_{2} \beta + C_{4} \gamma \\ - \frac{{M_{0} }}{EI} & = C_{1} \beta^{{2}} - C_{3} \gamma^{{2}} \\ - \frac{{Q_{0} }}{EI} & = C_{2} \beta^{3} - C_{4} \gamma^{3} \\ \end{aligned} \right..$$
(22)

By solving these equations simultaneously, the undetermined coefficients can be obtained.

$$\left\{ {\begin{array}{*{20}c} {C_{1} = \frac{{Y_{0} \gamma^{{2}} - \frac{{M_{0} }}{EI}}}{{\beta^{{2}} + \gamma^{{2}} }}} \\ {C_{2} = \frac{{\varphi_{0} \gamma^{{2}} - \frac{{Q_{0} }}{EI}}}{{\beta \gamma^{{2}} + \beta^{3} }}} \\ {C_{3} = \frac{{Y_{0} \beta^{{2}} + \frac{{M_{0} }}{EI}}}{{\beta^{{2}} + \gamma^{{2}} }}} \\ {C_{4} = \frac{{\varphi_{0} \beta^{{2}} + \frac{{Q_{0} }}{EI}}}{{\beta^{2} \gamma + \gamma^{3} }}} \\ \end{array} } \right..$$
(23)

Then, substituting these coefficients back to the equation of the general solution, the equation for the deflection, rotation, and the shear force can be established directly:

$$\begin{aligned} Y\left( x \right) & = \frac{{\gamma^{2} ch\beta x + \beta^{2} \cos \gamma x}}{{\gamma^{2} + \beta^{2} }}Y_{0} + \frac{{\gamma^{3} sh\beta x + \beta^{3} \sin \gamma x}}{{\gamma \beta \left( {\gamma^{2} + \beta^{2} } \right)}}\varphi_{0} \\ & + \frac{\cos \gamma x - ch\beta x}{{\gamma^{2} + \beta^{2} }}\frac{{M_{0} }}{EI} + \frac{\beta \sin \gamma x - \gamma sh\beta x}{{\gamma \beta \left( {\gamma^{2} + \beta^{2} } \right)}}\frac{{Q_{0} }}{EI}, \\ \end{aligned}$$
(24)
$$\begin{aligned} \varphi \left( x \right) & = \frac{{\beta \gamma^{2} sh\beta x - \gamma \beta^{2} \sin \gamma x}}{{\gamma^{2} + \beta^{2} }}Y_{0} + \frac{{\gamma^{2} ch\beta x + \beta^{2} \cos \gamma x}}{{\left( {\gamma^{2} + \beta^{2} } \right)}}\varphi_{0} \\ & - \frac{\beta sh\beta x + \gamma \sin \gamma x}{{\gamma^{2} + \beta^{2} }}\frac{{M_{0} }}{EI} + \frac{\cos \gamma x - ch\beta x}{{\left( {\gamma^{2} + \beta^{2} } \right)}}\frac{{Q_{0} }}{EI}, \\ \end{aligned}$$
(25)
$$M\left( x \right) = - EI\left( {\frac{{\beta^{2} \gamma^{2} ch\beta x - \gamma^{2} \beta^{2} \cos \gamma x}}{{\gamma^{2} + \beta^{2} }}Y_{0} + \frac{{\beta \gamma^{2} sh\beta x - \gamma \beta^{2} \sin \gamma x}}{{\left( {\gamma^{2} + \beta^{2} } \right)}}\varphi_{0} - \frac{{\gamma^{2} \cos \gamma x + \beta^{2} ch\beta x}}{{\gamma^{2} + \beta^{2} }}\frac{{M_{0} }}{EI} - \frac{\gamma \sin \gamma x + \beta sh\beta x}{{\left( {\gamma^{2} + \beta^{2} } \right)}}\frac{{Q_{0} }}{EI}} \right),$$
(26)
$$Q\left( x \right) = - EI\left( {\frac{{\beta^{2} \gamma^{2} \left( {\beta sh\beta x + \gamma \sin \gamma x} \right)}}{{\gamma^{2} + \beta^{2} }}Y_{0} + \frac{{\beta^{2} \gamma^{2} \left( {ch\beta x - \cos \gamma x} \right)}}{{\left( {\gamma^{2} + \beta^{2} } \right)}}\varphi_{0} + \frac{{\gamma^{3} \sin \gamma x - \beta^{3} sh\beta x}}{{\gamma^{2} + \beta^{2} }}\frac{{M_{0} }}{EI} - \frac{{\gamma^{2} \cos \gamma x + \beta^{2} ch\beta x}}{{\left( {\gamma^{2} + \beta^{2} } \right)}}\frac{{Q_{0} }}{EI}} \right).$$
(27)

For the single-span cable, the relationship between the reaction force and the displacement at the end of the cable also needs to be considered. For single-span cable AB with the length of L, the corresponding deflection, rotation, bending moment, and shear force at point B can be given by the following.

$$\begin{aligned} Y_{B} & = \frac{{\gamma^{2} ch\beta l + \beta^{2} \cos \gamma l}}{{\gamma^{2} + \beta^{2} }}Y_{A} + \frac{{\gamma^{3} sh\beta l + \beta^{3} \sin \gamma l}}{{\gamma \beta \left( {\gamma^{2} + \beta^{2} } \right)}}\varphi_{A} \\ & + \frac{\cos \gamma l - ch\beta l}{{\gamma^{2} + \beta^{2} }}\frac{{M_{A} }}{EI} + \frac{\beta \sin \gamma l - \gamma sh\beta l}{{\gamma \beta \left( {\gamma^{2} + \beta^{2} } \right)}}\frac{{Q_{A} }}{EI}, \\ \end{aligned}$$
(28)
$$\begin{aligned} \varphi_{B} & = \frac{{\beta \gamma^{2} sh\beta l - \gamma \beta^{2} \sin \gamma l}}{{\gamma^{2} + \beta^{2} }}Y_{A} + \frac{{\gamma^{2} ch\beta l + \beta^{2} \cos \gamma l}}{{\left( {\gamma^{2} + \beta^{2} } \right)}}\varphi_{A} \\ & - \frac{\beta sh\beta l + \gamma \sin \gamma l}{{\gamma^{2} + \beta^{2} }}\frac{{M_{A} }}{EI} + \frac{\cos \gamma l - ch\beta l}{{\left( {\gamma^{2} + \beta^{2} } \right)}}\frac{{Q_{A} }}{EI}, \\ \end{aligned}$$
(29)
$$M_{B} = - EI\left( {\frac{{\beta^{2} \gamma^{2} ch\beta l - \gamma^{2} \beta^{2} \cos \gamma l}}{{\gamma^{2} + \beta^{2} }}Y_{A} + \frac{{\beta \gamma^{2} sh\beta l - \gamma \beta^{2} \sin \gamma l}}{{\left( {\gamma^{2} + \beta^{2} } \right)}}\varphi_{A} - \frac{{\gamma^{2} \cos \gamma l + \beta^{2} ch\beta l}}{{\gamma^{2} + \beta^{2} }}\frac{{M_{A} }}{EI} - \frac{\gamma \sin \gamma l + \beta sh\beta l}{{\left( {\gamma^{2} + \beta^{2} } \right)}}\frac{{Q_{A} }}{EI}} \right),$$
(30)
$$Q_{B} = - EI\left( {\frac{{\beta^{2} \gamma^{2} \left( {\beta sh\beta l + \gamma \sin \gamma l} \right)}}{{\gamma^{2} + \beta^{2} }}Y_{A} + \frac{{\beta^{2} \gamma^{2} \left( {ch\beta l - \cos \gamma l} \right)}}{{\left( {\gamma^{2} + \beta^{2} } \right)}}\varphi_{A} + \frac{{\gamma^{3} \sin \gamma l - \beta^{3} sh\beta l}}{{\gamma^{2} + \beta^{2} }}\frac{{M_{A} }}{EI} - \frac{{\gamma^{2} \cos \gamma l + \beta^{2} ch\beta l}}{{\left( {\gamma^{2} + \beta^{2} } \right)}}\frac{{Q_{A} }}{EI}} \right).$$
(31)

By solving the first two equations simultaneously, MA and QA can be solved; then, substituting MA and QA into the last two equations, MB and QB can also be obtained as following:

$$\left\{ \begin{aligned} M_{A} & = i\left( {D\varphi_{A} + E\varphi_{B} + F\frac{{Y_{A} }}{l} - G\frac{{Y_{B} }}{l}} \right) \\ M_{B} & = i\left( {E\varphi_{A} + D\varphi_{B} + G\frac{{Y_{A} }}{l} - F\frac{{Y_{B} }}{l}} \right) \\ Q_{A} & = - \frac{i}{l}\left( {H\varphi_{A} + G\varphi_{B} + K\frac{{Y_{A} }}{l} - R\frac{{Y_{B} }}{l}} \right) \\ Q_{B} & = - \frac{i}{l}\left( {G\varphi_{A} + H\varphi_{B} + R\frac{{Y_{A} }}{l} - K\frac{{Y_{B} }}{l}} \right) \\ \end{aligned} \right..$$
(32)

The capital letter in the above equation can then be expressed by the following formulas sequentially:

$$\Pi = 2\beta *\gamma *\left( {1 - \cos \gamma * ch\beta *} \right) + \left( {\beta *^{2} - \gamma *^{2} } \right)sh\beta *\sin \gamma * ,$$
(33)
$$D = \frac{1}{\Pi }\left( {\beta *^{2} + \gamma *^{2} } \right)\left( {\beta *\sin \gamma * ch\beta * - \gamma *\cos \gamma * sh\beta *} \right),$$
(34)
$$E = \frac{1}{\Pi }\left( {\beta *^{2} + \gamma *^{2} } \right)\left( {\gamma *sh\beta * - \beta *\sin \gamma * } \right),$$
(35)
$$F = \frac{1}{\Pi }\beta *\gamma *\left[ {2\beta *\gamma * \sin \gamma * sh\beta * - \left( {\beta *^{2} - \gamma *^{2} } \right)\left( {1 - \cos \gamma * ch\beta *} \right)} \right],$$
(36)
$$G = \frac{1}{\Pi }\beta *\gamma *\left( {\beta *^{2} + \gamma *^{2} } \right)\left( {ch\beta * - \cos \gamma * } \right),$$
(37)
$$F = \frac{1}{\Pi }\beta *\gamma *\left[ {2\beta *\gamma * \sin \gamma * sh\beta * - \left( {\beta *^{2} - \gamma *^{2} } \right)\left( {1 - \cos \gamma * ch\beta *} \right)} \right],$$
(38)
$$H = \frac{1}{\Pi }\left[ {\beta *\gamma * \left( {\beta *^{2} - \gamma *^{2} } \right)\left( {1 - \cos \gamma * ch\beta *} \right) + \sin \gamma * sh\beta *\left( {\beta *^{4} + \gamma *^{4} } \right)} \right],$$
(39)
$$K = \frac{1}{\Pi }\beta *\gamma * \left( {\beta *^{2} + \gamma *^{2} } \right)\left( {\gamma *ch\beta *\sin \gamma * + \beta *sh\beta *\cos \gamma * } \right),$$
(40)
$$R = \frac{1}{\Pi }\beta *\gamma * \left( {\beta *^{2} + \gamma *^{2} } \right)\left( {\gamma *\sin \gamma * + \beta *sh\beta *} \right),$$
(41)
$$i = \frac{EI}{l},$$
(42)

where i represents the linear stiffness of single-span cable.

$$\beta * = \beta l,\,\,\gamma * = \gamma l.$$
(43)

When π not equals zero, the characteristic equation of the single-span vibration can be expressed by the above equation; when π equals 0, the condition switches to the fixed connection at both ends, the characteristic equation of single-span vibration can then be expressed in a general form as the following:

$$\left\{ {\begin{array}{*{20}c} {K_{11} \Delta_{1} + K_{12} \Delta_{2} + K_{13} \Delta_{3} + K_{14} \Delta_{4} = P_{1} } \\ {K_{21} \Delta_{1} + K_{22} \Delta_{2} + K_{23} \Delta_{3} + K_{24} \Delta_{4} = P_{2} } \\ {K_{31} \Delta_{1} + K_{32} \Delta_{2} + K_{33} \Delta_{3} + K_{34} \Delta_{4} = P_{3} } \\ {K_{41} \Delta_{1} + K_{42} \Delta_{2} + K_{43} \Delta_{3} + K_{44} \Delta_{4} = P_{4} } \\ \end{array} } \right..$$
(44)

The displacements in the above equations are:

$$\begin{array}{*{20}c} {\Delta_{1} = \varphi_{A} } & {\Delta_{2} = \varphi_{B} } & {\Delta_{3} = Y_{A} } & {\Delta_{4} = Y_{B} } \\ \end{array} .$$
(45)

Moreover, the stiffness coefficients in the above equations are:

$$\begin{array}{*{20}c} {K_{11} = K_{22} = iD} & {K_{21} = K_{12} = iE} \\ \end{array} ,$$
(46)
$$\begin{array}{*{20}c} {K_{13} = - K_{24} = \frac{i}{l}F} & {K_{14} = - K_{23} = K_{32} = K_{41} = - \frac{i}{l}G} \\ \end{array} ,$$
(47)
$$\begin{array}{*{20}c} {K_{31} = K_{42} = - \frac{i}{l}H} & {K_{33} = - K_{44} = - \frac{i}{{l^{2} }}K} \\ \end{array} ,$$
(48)
$$K_{34} = - K_{43} = \frac{i}{{l^{2} }}R.$$
(49)

Vibration Equations Under Two Typical Boundary Conditions

  1. (1)

    Hinged at both ends

The model with both hinged boundary is shown in Fig.2. The following characteristic equation can be obtained when both ends of the cable are hinged:

$$\begin{array}{*{20}c} {M_{A} = 0} & {M_{B} = 0} & {Y_{A} = 0} & {Y_{B} = } \\ \end{array} 0.$$
(50)

Substituting this characteristic equation into the stiffness equations in the previous section, the following equation can be developed;

$$\left\{ {\begin{array}{*{20}c} {D\varphi_{A} + E\varphi_{B} = 0} \\ {E\varphi_{A} + D\varphi_{B} = 0} \\ \end{array} } \right..$$
(51)

Its characteristic equations are:

$$D^{{2}} - E^{2} = 0,$$
(52)
$$\begin{gathered} \frac{1}{{\Pi^{2} }}\left( {\beta *^{2} + \gamma *^{2} } \right)^{2} \left( {\beta *ch\beta *\sin \gamma * - \gamma *sh\beta *\cos \gamma * } \right)^{2} \hfill \\ - \frac{1}{{\Pi^{2} }}\left( {\beta *^{2} + \gamma *^{2} } \right)^{2} \left( {\gamma * sh\beta * - \beta *\sin \gamma * } \right)^{2} = 0. \hfill \\ \end{gathered}$$
(53)

Arranging the above equations leads to the following:

$$\frac{1}{\Pi }\left( {\beta *^{2} + \gamma *^{2} } \right)^{2} \sin \gamma * sh\beta * = 0,$$
(54)

where

$$\left( {\beta *^{2} + \gamma *^{2} } \right)^{2} sh\beta * \ne 0,$$
(55)
$$\sin \gamma * = 0.$$
(56)
  1. (2)

    Fixed at both ends

The model with two fixed boundary had been shown in Fig.3. The boundary conditions of the single-span cable with two fixed ends can be described as:

$$\begin{array}{*{20}c} {\varphi_{A} = 0} & {M_{B} = 0} & {Y_{A} = 0} & {Y_{B} = } \\ \end{array} 0.$$
(57)

Substituting the boundary condition into the stiffness equation, the following equation can be developed:

$$D\,\, = \,\,0,$$
(58)
$$\left\{ {\begin{array}{*{20}c} {\frac{1}{\Pi }\left( {\beta *^{2} + \gamma *^{2} } \right)\left( {\beta *ch\beta *\sin \gamma * - \gamma *sh\beta *\cos \gamma * } \right) = 0} \\ {\Pi \ne 0,\,\,\beta *^{2} + \gamma *^{2} \ne 0} \\ {\beta *ch\beta *\sin \gamma * - \gamma *sh\beta *\cos \gamma * = 0} \\ \end{array} } \right..$$
(59)

Vibration Equation of Single-Span Cable Under Arbitrary Elastic Boundary Conditions

The model with arbitrary elastic constraints had been shown in Fig.4. Under arbitrary elastic constraints, the vibration equation of the cable can be described as:

$$\left\{ {\begin{array}{*{20}c} {\left( {K_{11} + k_{1} } \right)\Delta_{1} + K_{12} \Delta_{2} + K_{13} \Delta_{3} + K_{14} \Delta_{4} = 0} \\ {K_{21} \Delta_{1} + \left( {K_{22} + k_{2} } \right)\Delta_{2} + K_{23} \Delta_{3} + K_{24} \Delta_{4} = 0_{2} } \\ {K_{31} \Delta_{1} + K_{32} \Delta_{2} + \left( {K_{33} + k_{3} } \right)\Delta_{3} + K_{34} \Delta_{4} = 0} \\ {K_{41} \Delta_{1} + K_{42} \Delta_{2} + K_{43} \Delta_{3} + \left( {K_{44} + k_{4} } \right)\Delta_{4} = 0} \\ \end{array} } \right..$$
(60)

The frequency equation can be given by:

$$\left| {\begin{array}{*{20}c} {\left( {K_{11} + k_{1} } \right)} & {K_{12} } & {K_{13} } & {K_{14} } \\ {K_{21} } & {\left( {K_{22} + k_{2} } \right)} & {K_{23} } & {K_{24} } \\ {K_{31} } & {K_{32} } & {\left( {K_{33} + k_{3} } \right)} & {K_{34} } \\ {K_{41} } & {K_{42} } & {K_{43} } & {\left( {K_{44} + k_{4} } \right)} \\ \end{array} } \right| = 0.$$
(61)

It can be seen clearly that the above equation contains five unknowns, which are the cable force T, and four stiffness, K1, K2, K3, and K4.

The above equation can be simplified as:

$$f\left( {EI,l,m,\omega_{n} ,T,k_{1} ,k_{2} ,k_{3} ,k_{4} } \right) = 0.$$
(62)

According to the above nonlinear equation, these five unknown parameters can be determined by setting the 5th order frequency ω1–ω5. Then, the following nonlinear equation composed of five equations can be developed, and the five unknown parameters can be determined by solving this equation.

$$\left\{ {\begin{array}{*{20}c} {f\left( {EI,l,m,\omega_{1} ,T,k_{1} ,k_{2} ,k_{3} ,k_{4} } \right) = 0} \\ {f\left( {EI,l,m,\omega_{2} ,T,k_{1} ,k_{2} ,k_{3} ,k_{4} } \right) = 0} \\ {f\left( {EI,l,m,\omega_{3} ,T,k_{1} ,k_{2} ,k_{3} ,k_{4} } \right) = 0} \\ {f\left( {EI,l,m,\omega_{4} ,T,k_{1} ,k_{2} ,k_{3} ,k_{4} } \right) = 0} \\ {f\left( {EI,l,m,\omega_{5} ,T,k_{1} ,k_{2} ,k_{3} ,k_{4} } \right) = 0} \\ \end{array} } \right..$$
(63)

For the error analysis of cable force, the identification of cable force distortion caused by the dislocation of the frequency order can be conducted for the above equations. It is relatively easy to identify as the difference between the real cable force and the cable force induced by the distortion is relatively large. Taking simply supported single cable as the illustration, the formulation of single cable tensile force can be described as the following:

$$T = 4mf_{n}^{2} \left( \frac{l}{n} \right)^{2} - \frac{{\pi^{2} EI}}{{\left( \frac{l}{n} \right)^{2} }}.$$
(64)

When the real frequency is the n-order frequency but identified mistakenly as the k-order frequency, the error in the cable force under this condition is:

$$\Delta T_{mk} = T_{n} - T_{k} = 4mf_{n}^{2} \left[ {\left( \frac{l}{n} \right)^{2} - \left( \frac{l}{k} \right)^{2} } \right] - \left( {\frac{{n^{2} - k^{2} }}{{l^{2} }}} \right)\pi^{2} EI,$$
(65)
$$\Delta T_{mk} = \frac{{\left( {k^{2} - n^{2} } \right)}}{{k^{2} }}\left( {\frac{{4mf_{n}^{2} l^{2} }}{{n^{2} }} + \frac{{k^{2} \pi^{2} EI}}{{l^{2} }}} \right).$$
(66)

The value of the relative error is:

$$\frac{{\Delta T_{mk} }}{{T_{mk} }} = \frac{{\left( {1 - \frac{{n^{2} }}{{k^{2} }}} \right)\left( {\frac{{4mf_{n}^{2} l^{2} }}{{n^{2} }} + \frac{{k^{2} \pi^{2} EI}}{{l^{2} }}} \right)}}{{\left( {\frac{{4mf_{n}^{2} l^{2} }}{{n^{2} }} - \frac{{n^{2} \pi^{2} EI}}{{l^{2} }}} \right)}}.$$
(67)

When the frequency order is low, for the adjacent frequency order (k = n–1), the calculated cable force under this condition is 1 time greater than the real cable force. When the frequency order is high, the value of the relative error can be determined if the effect of the difference in stiffness of the cable is ignored.

As illustrated in Table 1, the estimations of the cable force error for the first 20 frequencies are summarized. When the real frequency is mistaken judged as a frequency of one order less, the ratio of the interpolation between the calculated cable force and real cable force to the real cable force was greater than 2.

Table 1 Estimation of cable force error induced by mistaken identification of the frequency
Full size table

Vibration Equation of Multi-Span Cable with Multiple Braces

Multi-span cables can be developed by connecting the single-span cables in series. A number of struts with certain rotational stiffness and vertical stiffness are (Figs. 2, 3, 4, 5) placed between two ends of the multi-span cables. These struts further constrain the freedom of the cable in the vertical plane, and the vibration equation of the multi-span cables can be established as:

$$\left\{ {\begin{array}{*{20}c} {\left( {Z_{11} + k_{1} } \right)\Delta_{1} + Z_{12} \Delta_{2} + Z_{13} \Delta_{3} \cdots + Z_{1n} \Delta_{n} = 0} \\ {Z_{21} \Delta_{1} + \left( {Z_{22} + k_{2} } \right)\Delta_{2} + Z_{23} \Delta_{3} \cdots + Z_{2n} \Delta_{n} = 0} \\ {Z_{31} \Delta_{1} + Z_{32} \Delta_{2} + \left( {Z_{33} + k_{3} } \right)\Delta_{3} \cdots + Z_{3n} \Delta_{n} = 0} \\ \cdots \\ {Z_{n1} \Delta_{1} + Z_{n2} \Delta_{2} + Z_{n3} \Delta_{3} \cdots + \left( {Z_{nn} + k_{n} } \right)\Delta_{n} = 0} \\ \end{array} } \right..$$
(68)
Fig. 2
figure 2

Vibration model of single-span cable with two hinged ends

Full size image
Fig. 3
figure 3

Vibration model of single-span cable fixed at both ends

Full size image
Fig. 4
figure 4

Vibration model of single-span cable under arbitrary elastic constraints

Full size image
Fig. 5
figure 5

Vibration model of multi-span cable under arbitrary elastic constraints

Full size image

The non-zero elements of the stiffness coefficients in the above equations are:

$$Z_{11} = K_{11}^{\left( 1 \right)} ,$$
(69)
$$\left\{ \begin{aligned} Z_{12} & = K_{12}^{\left( 1 \right)} ,Z_{21} = K_{21}^{\left( 1 \right)} ,Z_{22} = K_{22}^{\left( 1 \right)} + K_{11}^{\left( 2 \right)} \\ Z_{23} & = K_{12}^{\left( 2 \right)} ,Z_{32} = K_{21}^{\left( 2 \right)} ,Z_{22} = K_{22}^{\left( 2 \right)} + K_{11}^{\left( 3 \right)} \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \cdots \\ Z_{{\left( {n - 1} \right)n}} & = K_{12}^{{\left( {n - 1} \right)}} ,Z_{{n\left( {n - 1} \right)}} = K_{21}^{{\left( {n - 1} \right)}} ,Z_{nn} = K_{22}^{{\left( {n - 1} \right)}} \\ \end{aligned} \right..$$
(70)

The corresponding characteristic equation of the frequency can be expressed as:

$$\left| {\begin{array}{*{20}c} {\left( {Z_{11} + k_{1} } \right)} & {Z_{12} } & \cdots & 0 \\ {Z_{21} } & {\left( {Z_{22} + k_{2} } \right)} & \cdots & 0 \\ \cdots & \cdots & \cdots & 0 \\ 0 & 0 & \cdots & {\left( {Z_{nn} + k_{n} } \right)} \\ \end{array} } \right| = 0.$$
(71)

The above determinant can be described in the form of equation with multiple unknowns as following:

$$\begin{array}{*{20}c} {f\left( {T,k_{1} ,k_{2} , \cdots ,k_{n} } \right) = 0} & {\left( {i = 1,2,3 \cdots } \right)} \\ \end{array} .$$
(72)

According to above formulations, if the bending stiffness of multi-span cables (EI), the compressive stiffness of struts (EA), linear density of cables (m), and cable length of each span (L) are known, the cable forces and n constraint stiffness coefficients (K1, K2… Kn) can be determined by measuring the frequency of overall cable structure at n + 1th order.

According to the calculation model of multi-span cable, the following nonlinear equations about cable force and natural frequency can be established. For a cable with strut with m span and n unknown constraint stiffness, the following frequency characteristic equations can be established.

$$\left\{ {\begin{array}{*{20}c} {f_{1} \left( {EI,m,\omega_{1} ,l_{1} ,l_{2} ,...,l_{m} ,T,k_{1} ,k_{2} ,...,k_{n} } \right) = 0} \\ {f_{2} \left( {EI,m,\omega_{2} ,l_{1} ,l_{2} ,...,l_{m} ,T,k_{1} ,k_{2} ,...,k_{n} } \right) = 0} \\ {...} \\ {f_{n + 1} \left( {EI,m,\omega_{n + 1} ,l_{1} ,l_{2} ,...,l_{m} ,T,k_{1} ,k_{2} ,...,k_{n} } \right) = 0} \\ \end{array} } \right..$$
(73)

For the identification of characteristic parameters of multi-span cables, the unknown constraint stiffness and tension force can be obtained by using multi-order frequencies as known quantities. As long as the number of unknown stiffness and unknown tension is equal to the measured frequency number n + 1, the above equations can theoretically be obtained to obtain the corresponding unknown stiffness and tension values. For the problem of multi-span cable force identification, the cable force and the corresponding constraint stiffness of the cable can be obtained by using the vibration model of the multi-span cable and the multi-frequency fitting technology.

Based on the optimization method, multi-frequency fitting algorithm is used to obtain the constraint stiffness of multi-span cable forces and the principle process of cable force value algorithm is shown as follows.

  1. (1)

    Establish the physical vibration model of multi-span cable

For a m span cable with a strut and n unknown constraint stiffness, the characteristic equation is established as follows.

$$f_{i} \left( {EI,m,\omega_{i} ,l_{1} ,l_{2} ,...,l_{m} ,T,k_{1} ,k_{2} ,...,k_{n} } \right) = 0(i = 1,2,...n + 1),$$
(74)

where the cable stiffness is EI, the line density is m, and the cable lengths of each section are l1,l2… lm parameter is known, cable force T and n constraint stiffness have n + 1 parameters to be determined.

  1. (2)

    Multi-span cable model natural vibration frequency testing and cable force stiffness optimization identification model

n + 1 natural vibration frequency ωi can be obtained through measurement test, and then n + 1 values about cable force T and constraint stiffness k1, k2… kn is a system of equations with unknown quantity. The optimization algorithm model is designed to establish the optimization objective function.

$$f_{obj} = \min \left\{ {\sum {\left| {f_{i} \left( {EI,m,\omega_{i} ,l_{1} ,l_{2} ,...,l_{m} ,T,k_{1} ,k_{2} ,...,k_{n} } \right)} \right|} } \right\}.$$
(75)
  1. (3)

    Calculation and recognition of cable force

The initial cable force parameters were selected, n + 1 unknown parameters were calculated by regression on the optimization objective function, and the optimized cable force values and n constraint stiffness were obtained, and the corresponding boundary constraint stiffness was identified.

  1. (4)

    Verify the correctness of the calculated cable force value

The implementation flow chart of the multi-frequency fitting method is shown in Fig. 6.

Fig. 6
figure 6

Multi-frequency fitting implementation flow chart

Full size image

Theory Validation

  1. a)

    Verification of cable force and vibration stiffness of single-span cable

Assuming there is a single-span cable with unknown constraint stiffness, the linear density is 252.72 kg/m, the length of the cable (L) is 10 m, the bending stiffness of the cable is 1.02 × 107 Nm2, and the force exerted on the cable is 680.4 kN. The finite element method is adopted to determine its 1st to 6th order of the frequency, which are 4.09, 13.65, 29.46, 51.56, 79.98, and 114.7 Hz, respectively, and the bending stiffness at both ends is determined as K1 = 7.16 × 104 Nm2, and K2 = 2.5 × 104 Nm2. According to the model depicted in Fig. 7, the optimization method based on the objective function is used to calculate the cable force, and the results obtained from the analytical solution are then compared with the numerical results obtained from the finite element method. The comparison indicates a good consistency between the results from the optimization formulation and the finite element method (Table 2).

Fig. 7
figure 7

Tensile force test of single cable when the end-restraint stiffness unknown

Full size image
Table 2 Comparison of cable force between FEM and analytical method
Full size table

The error in the cable force between the optimization method presented in this study and the finite element method is 0.2%, which indicates that the optimization method is capable for the calculation of single-span cable force, and the results can also meet the accuracy requirements.

  1. b)

    Verification of cable force and vibration stiffness of multiple-span cable

Considering the vibration model of a double-span cable which has fixed end-constraints and the struts: the length of the cable is 2L, the bending stiffness is EI, the prestressed tension is N, the ends of the cable is fixed, and the connection between the bracing rod and the cable is hinged, as illustrated in Fig. 8. Assuming that the rotation at the strut is δ and zero at the ends of the cable, then substituting the boundary conditions into the frequency characteristic equation of the multi-span cable and the internal force equation of the boundary:

$$2D\Delta = 0.$$
(71)
Fig. 8
figure 8

Tensile force test of double-span cable when ends constraint stiffness unknown

Full size image

As δ not equals 0, the following equation can then be derived:

$$D = \frac{1}{\Pi }\left( {\beta *^{2} + \gamma *^{2} } \right)\left( {\beta *\sin \gamma * ch\beta * - \gamma *\cos \gamma * sh\beta *} \right) = 0,$$
(72)

where

$$\frac{1}{\Pi }\left( {\beta *^{2} + \gamma *^{2} } \right) \ne 0.$$
(73)

Subsequently, the following equation can be developed:

$$\beta *\sin \gamma * ch\beta * - \gamma *\cos \gamma * sh\beta * = 0.$$
(74)

The above equation is identical with the natural vibration characteristic equation of the cable which is fixed at one end and hinged at the other end, so the effectiveness of the vibration equation of the multi-span cable is validated.

Conclusion

The theoretical analysis and measured results indicate that under the external dynamic impact, the vibration characteristics of the cable load are extremely complex, and the spectral characteristics are not only affected by the constraint stiffness at both ends, but also by the prestressed tension on the cable. Through the analysis of the natural vibration frequency, the constraint stiffness, and tension of cable, the following conclusions can be deduced:

  1. (1)

    Based on the reasonable assumptions, the vibration characteristics of the cable subjected to a certain prestressed tension are analyzed, and the relationship between the tension force and the natural vibration frequency of the cable under various end constraint stiffness is established. Using the above natural vibration characteristic equation, the constraint stiffness of the end and the tensile force of the cable can be simply solved when the multi-order natural vibration frequency is known.

  2. (2)

    To establish the natural vibration frequency equation of the multi-span cable with multiple struts, the vibration equation of the multi-span cable under the impact load is developed. The multi-order natural vibration frequency is adopted to determine the constraint stiffness of the ends and the struts, including rotational stiffness and compressive stiffness. The corresponding nonlinear equation to the vibration equation of the multi-span cable presented in this study can be solved by multi-order frequency optimization algorithm, then the corresponding constraint stiffness and tension can be obtained.

  3. (3)

    The force of the single-span cable solved by the iteration on the nonlinear equation related to the characteristic frequency, the constraint stiffness, and the tension presented in this study is basically consistent with the numerical results of the cable force from the finite element method. The characteristic frequency equation of the multi-span cable degraded to the characteristic frequency equation of the standard double-span cable with a fixed end by assuming the boundary condition of the multi-span cable, the effectiveness and the applicability of the nonlinear equation of the multi-span cable characteristic frequency can be validated further.

  4. (4)

    The vibration modes of single-span cable are analyzed by finite element simulation, and its formation is analyzed. Based on the analysis of the first six orders of formation, the corresponding first six orders of natural vibration frequency can be obtained. By comparing the analytical method in this paper with the finite element method, it can be seen that the parameters of cable force and constraint stiffness obtained by the analytical method in this paper with the finite element method are basically the same. This further verifies the analytical method proposed in this paper to obtain the cable force by using the multi-frequency fitting method.

Discussion

Since the materials assumed in this paper are elastic materials, the nonlinear problems of materials are not involved. Just because the vibration frequency equations obtained are nonlinear equations, the relationship between cable force, natural vibration frequency and corresponding constraint stiffness, including the elastic constraint stiffness of both ends and the strut, is typical nonlinear. Therefore, it can be called the exploration of nonlinear constraint stiffness calculation method. The premise is that the cable is a pure elastic tensioned member. On the one hand, it can be effectively simplified when establishing the vibration frequency equation of the cable, so as to avoid dealing with the hardening or softening problems in plastic mechanics. On the other hand, in practical engineering practice, most of the cable is in the elastic working state, not to reach the elastic ultimate stress state. On the other hand, Since the boundary conditions constituting both ends of the cable are set as a combination of complete spring and compressive spring, the struts are also set in the same way for the support of the cable. Since the cable is in a state of tension under load, the cable has a certain interface, so it has a certain degree of flexural stiffness EI, and the vertical action of loads such as dead weight on the cable will produce sag effect. The sag effect will increase the cable force, and the large displacement phenomenon of the structure will be formed under the action of working load. In addition, the constraint of both ends and the constraint reaction of the supporting rod on the cable make the cable in a geometric nonlinear state. Therefore, the vibration frequency equation obtained from the cable deflection has typical nonlinear characteristics. So the proposed method by authors to solve the calculation for nonlinear stiffness of boundary and cable force is demonstrated effectively.