Introduction

Rolling bearings are widely used in mechanical equipment such as aero engines and aero gas turbines [1,2,3,4]. Due to excitation by strong nonlinear sources such as oil film forces, many nonlinear problems can occur in the rolling bearing system. Moreover, wear, cracks, and other damage often occur due to the harsh working environment, resulting in more prominent nonlinear problems. As mechanical equipment is developing towards high power, light structure, high speed, etc., many abnormal vibrations of rolling bearings can no longer be well explained by linear theory [5,6,7]. Therefore, it is necessary to study the complex dynamic behavior of rolling bearings via nonlinear theory and methods.

As a result, the nonlinear dynamic characteristics of faulty rolling bearings have attracted academic attention. Satoru et al. [8] first investigated the nonlinear behavior of bearings through computer technology. He studied the periodic and chaotic motion behavior of 6306 ball bearings, which opened a new direction for accurately analyzing the complex dynamic equations of bearings. Mevel and Guyader [9] studied the mechanism of 6306 ball bearings into chaotic behavior. Changing the parameters indicated two different chaotic paths: the subharmonic path and the quasi-periodic motion. A mechanical model of a motor rotor supported by ball bearings is established by Tiwari et al. [10], considering radial clearance. The results show that the appearance of periodic, subharmonic, and chaotic behavior depends on radial internal clearance. Zhang et al. [11] established a dynamic equation of rolling bearings considering local damage and bearing force. He analyzed the nonlinear dynamic characteristics of the bearing through time–frequency domain parameters such as spectrum, mean square value, and peak kurtosis. Gu et al. [12] established a rolling bearing model considering the waviness of the inner or outer raceway and other factors. They studied the influence of the waviness on the nonlinear dynamic characteristics by employing bifurcation diagrams, power spectrum diagrams, and Poincare diagrams. Lin et al. [13] realized the rapid calculation of a bearing system’s complex nonlinear dynamic equations through dynamic grid technology to obtain the orbit characteristics of the shaft centerline. Liu et al. [14] developed a nonlinear dynamic model of a motor car axle box bearing with one defect on the outer raceway. They described the bifurcation and chaos characteristics of the system through nonlinear methods such as bifurcation diagrams and phase diagrams. Li et al. [15, 16] studied the chaotic characteristics of bearing system by employing recursive diagrams, the CLY method, power spectrums, least squares support vector machine, and Lyapunov exponent spectrums. Yao et al. [17] transformed the bearing equation by coordinates to establish dimensionless equations and solved the equations to obtain the nonlinear characteristics. Luo et al. [18] developed a bearing dynamic similarity model by integral similarity method. They simulated the 6208 bearings according to the similarity relationship-β, which led to the displacement bifurcation diagrams and velocity bifurcation diagrams. Kappaganthu and Nataraj [19] proposed a nonlinear dynamic model of a rotor-bearing system and studied the bifurcation and chaotic response caused by bearing clearance. Gao et al. [20] presented a force model for inter-shaft bearing with a local defect on the outer or inner raceway. They investigated the nonlinear dynamic characteristics of the bearing affected by the defect. Sharma et al. [21,22,23] formulated a mathematical model of a rotor-bearing system considering the combined effects of the parametric excitation, such as nonlinear stiffness, varying compliance, and Hertz contact force. The qualitative and quantitative evaluation of the nonlinearity of the rotor-bearing system is performed via Poincare maps and Higuchi's fractal dimensions. Zhang et al. [24, 25] investigated the hysteretic characteristics of the varying compliance principal resonance in a ball bearing and a rigid-rotor ball bearing system with Hertzian contact and radial internal bearing clearance. To reveal the effects of pocket diameter, small diameter, and large diameter of cage on the dynamic behaviors of the bearing system, Deng et al. [26] proposes a nonlinear dynamic model of angular contact ball bearings with elastohydrodynamic lubrication and cage whirl motion.

In industrial practice, mechanical equipment is usually only overhauled or replaced after it has been damaged to a certain extent, taking into account costs and other related factors. Under such a background, cracks, pits, spalling, and other rolling bearing defects often co-occur or in succession, resulting in defect clusters or multiple defects. As a result, the nonlinear problem of rolling bearings becomes more prominent. However, only the case of rolling bearings with one defect has been considered in the literature mentioned above.

Zhao et al. [27, 28] investigated the effects of defect size, defect location, and defect number on the dynamic behavior of rolling bearings with the help of phase trajectories, shaft center orbits, and frequency spectrums. However, the study was performed based on a transient model. In the transient model, the displacement deviation caused by the collision of the defects to rolling elements is considered to change instantaneously, and the magnitude of the deviation is equal to the defect depth. The deviation should change gradually, and its magnitude should depend on the defect width.

To cope with the main problems in the current research, a novel model of rolling bearings with one defect is proposed considering the asymptotic change of the displacement deviation. The change rule and the specific calculation method of the deviation are explored. Then, the asymptotic model is extended to apply to the case of multiple defects, and an asymptotic model for rolling bearings with multiple defects on the outer raceway is proposed. Finite element models and experiments validate the proposed model. The effects of defect location and number on the dynamic behavior of rolling bearings are investigated with the help of phase orbits and shaft center orbits.

The rest of the sections can be divided into four parts. In Sect. 2, the asymptotic model of rolling bearings with multiple defects on the outer raceway is developed. In Sect. 3, the correctness of the proposed model is verified. In Sect. 4, the effects of defect number, defect distribution, and defect width on the nonlinear dynamic behavior of the bearing are investigated. In the final section, some valuable conclusions are drawn.

Theoretical Model

Model for Rolling Bearings with One Defect

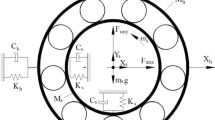
The discussed model is a rolling bearing with one inner raceway, one outer raceway, rolling elements, and unit resonators. The schematic of the model is depicted in Fig. 1 [29, 30]. The following hypotheses should be made to establish the dynamics equations of the model.

  1. (1)

    The outer raceway is fixed on the frame [31], and the inner raceway rotates at a constant speed.

  2. (2)

    The rolling elements are arranged equidistantly in the raceway for pure rolling.

  3. (3)

    The flaky spalling extends in the axial direction and runs through the entire outer raceway.

Fig. 1
figure 1

Schematic diagram of rolling bearings model

Full size image

In the figure, K is the equivalent coefficient of stiffness and c is the equivalent damping coefficient [32]. For a normal bearing without defect, the contact deformation δj of the jth rolling element can be calculated by

$$\delta_{j} = x\cos \theta_{j} + y\sin \theta_{j} ,$$
(1)
$$\theta_{j} = \omega_{c} t + \frac{{2{\uppi }(j - 1)}}{Z} + \theta_{1} ,$$
(2)
$$\omega_{c} = \frac{1}{2}\left[ {\omega_{i} \left( {1 - \frac{{D_{b} }}{{D_{m} }}\cos \alpha } \right)} \right],$$
(3)

where θj represents the azimuth angle of the jth rolling element, ωc represents the angular acceleration of the cage, Z represents the number of rolling elements, θ1 represents the azimuth angle of the 1st rolling element, ωi represents the rotational speed of the inner raceway, Db represents the diameter of rolling elements, Dm represents the pitch diameter, and α represents the contact angle [33].

Due to the influence of the displacement deviation λ and the eccentric e, the total contact deformation can be calculated by

$$\delta_{j} = x\cos \theta_{j} + y\sin \theta_{j} - \beta_{j} \lambda - e,$$
(4)
$$\beta_{j} = \left\{ \begin{gathered} 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \theta_{s} - \frac{{\Delta\Phi _{s} }}{2} < \theta_{j} < {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \theta_{s} + \frac{{\Delta\Phi _{s} }}{2} \hfill \\ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{others}} \hfill \\ \end{gathered} \right.,$$
(5)

where βj is a switch function, θs represents the azimuth angle of the defect, and ΔΦs represents the span angle of the defect. Since the outer raceway is fixed, the azimuth angle θs of the defect remains unchanged. The switch function indicates that the displacement deviation exists if the rolling elements roll into the defect span [34]. Otherwise, the displacement deviation no longer exists. The span angle ΔΦs of the defect can be calculated by

$$\Delta \Phi_{s} = 2\arcsin \frac{{b_{c} }}{{R_{o} }} \approx \frac{{{2}b_{c} }}{{R_{o} }},$$
(6)

where bc represents half the defect width, and Ro represents the radius of the outer raceway.

The current deviation release model is an ideal model. As soon as the rolling element enters the defect area, it immediately releases all deformation and regains contact deformation at the moment of departure. The actual process of deformation release and reacquisition is gradual. As the rolling element enters and leaves the defect area, the released deformation is zero. As the rolling element approaches the lowest point, the deformation becomes progressively larger. Since the rolling element rolls asymptotically in the defect span, the displacement deviation should gradually change and can be written as

$$\lambda = \lambda_{\max } - R_{o} * [1 - \cos (\theta_{s} - \theta_{j} )],$$
(7)

where λmax represents the maximum deviation when the rolling element contacts the defect. Figure 2 shows the contact, wherein d' represents the defect depth, and Cdr and Cdo represent the deviation of the rolling element and the outer raceway, respectively. From Fig. 2, the maximum deviation λmax should be written as

$$\lambda_{\max } = C_{{{\text{dr}}}} - C_{{{\text{do}}}} ,$$
(8)
$$C_{{{\text{dr}}}} = \frac{{D_{b} }}{2} - \sqrt {\left( {\frac{{D_{b} }}{2}} \right)^{2} - b_{c}^{2} } ,$$
(9)
$$C_{{{\text{do}}}} = R_{o} - \sqrt {(R_{o} )^{2} - b_{c}^{2} } .$$
(10)
Fig. 2
figure 2

The contact between a rolling element and a defect

Full size image

According to Hertz’s theory, the spring load Qj produced by the point contact between the jth rolling element and raceways can be written as

$$Q_{j} = K \times \delta_{j}^{3/2} ,$$
(11)
$$K = 1/[(1/K_{o} )^{2/3} + (1/K_{i} )^{2/3} ]^{3/2} ,$$
(12)

where K represents the total load–deflection constant, and Ko and Ki represent the contact stiffness of the outer and inner raceway, respectively. For ball bearings, the stiffness can be calculated by

$$K_{o} (K_{i} ) = 2.15 \times 10^{5} \times (\Sigma \rho )^{ - 1/2} (n_{\delta } )^{3/2} ,$$
(13)

where Σρ is the sum of contact principal curvature and nδ is a coefficient related to the difference function [35].

The total spring load is obtained by adding all the spring loads and projecting on the X-axis and Y-axis, i.e.,

$$\left\{ \begin{gathered} Q_{x} = \sum\limits_{j = 1}^{Z} {(Q_{j} \cdot \cos \theta_{j} )} \hfill \\ Q_{y} = \sum\limits_{j = 1}^{Z} {(Q_{j} \cdot \sin \theta_{j} )} \hfill \\ \end{gathered} \right..$$
(14)

The dynamics equations of rolling bearings with one defect on the outer raceway are written as

$$\left\{ \begin{gathered} mx^{\prime\prime} + cx^{\prime} + Q_{x} = F_{r} + F_{e} \cos \omega_{i} t \hfill \\ my^{\prime\prime} + cy^{\prime} + Q_{y} = F_{e} \sin \omega_{i} t - mg \hfill \\ \end{gathered} \right.,$$
(15)

where m is the mass of rolling bearings, Fe is the eccentric load, and Fr is the external load.

Model for Rolling Bearings with Multiple Defects

In industrial practice, multiple defects can coexist in rolling bearings. Under certain conditions, defects may even uniformly distribute. For example, due to current corrosion, multiple defects arrange at equal intervals on the inner or outer raceway of rolling bearings [36]. Figure 3 shows a schematic diagram of the asymptotic model of rolling bearings with multiple defects on the outer raceway.

Fig. 3
figure 3

Asymptotic model of rolling bearings with multiple defects on the outer raceway

Full size image

Due to the influence of multiple defects, the deformation of one rolling element is affected by the collision of itself with defects and the collision of other rolling elements with defects. Since one rolling element collides with only one defect at the same time, the deformation of the jth rolling element can be rewritten as

$$\delta_{j} = x\cos \theta_{j} + y\sin \theta_{j} - e - \sum\limits_{k = 1}^{N} {\beta_{jk} \lambda_{jk} } ,$$
(16)

where N is the number of defects, βjk is the judgment function for determining whether the jth rolling element has entered the span of the kth defect, and λjk is the deformation deviation caused by the collision of the jth rolling element to the kth defect. The judgment function can be rewritten as

$$\beta_{jk} = \left\{ \begin{gathered} 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \theta_{sk} - \frac{{\Delta\Phi _{sk} }}{2} < \theta_{j} < {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \theta_{sk} + \frac{{\Delta\Phi _{sk} }}{2} \hfill \\ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{others}} \hfill \\ \end{gathered} \right.,$$
(17)
$$\Delta \Phi_{sk} = 2\arcsin \frac{{b_{ck} }}{{R_{i} }} \approx \frac{{{2}b_{ck} }}{{R_{i} }},$$
(18)

where θsk represents the azimuth angle of the kth defect, ΔΦs represents the span angle of the kth defect, and bck represents the width of the kth defect. Since the outer raceway is fixed, θsk remains unchanged. The span angle is calculated from the geometrical parameters of the defect and rolling bearing. Therefore, the span angle is also determined once the defect is determined.

The rolling element should roll asymptotically in the defect span, i.e., the deviation should gradually change. Therefore, the deviation can be written as

$$\lambda_{jk} = \lambda_{\max k} - R_{i} * [1 - \cos (\theta_{sk} - \theta_{j} )],$$
(19)

where λmaxk represents the maximum deviation affected by the collision of all rolling elements to the kth defect.

Validation of Rolling Bearing Asymptotic Model

In this section, we will verify the accuracy of the proposed model. NSK 6205 bearing with two defects or three defects on the outer raceway is employed. The main dimensional parameters of the bearing and simulation conditions are summarized in Table 1 [37]. The width of both defects is 0.2 mm, and the height is 0.1 mm. The characteristic frequency fo of the rolling element passing through the defects is given in Table 2. According to the conclusion from Ref. [36], when the interval of two defects is equal to half of the interval of two rolling elements, the odd harmonic of the characteristic frequency disappears. Only the even harmonic components are present. It can be seen from the fact that the employed bearing has nine rolling elements. The interval between the two rolling elements is 360° /9 = 40°. Therefore, the interval angle between the two defects is set here to 20° and that between the three defects is set to 13.33°.

Table 1 Parameters of the NSK 6205 bearing and the simulation parameters
Full size table
Table 2 Characteristic frequency of rolling element passing through defects on the outer raceway
Full size table

Figures 4 and 5 show the simulation results of the asymptotic model.

Fig. 4
figure 4

Time–frequency response of the asymptotic model of rolling bearings with two defects on the outer raceway. a Time domain response of horizontal acceleration. b Frequency spectrum of horizontal acceleration. c Time domain response of vertical acceleration. d Frequency spectrum of vertical acceleration

Full size image
Fig. 5
figure 5

Time–frequency response of the asymptotic model of rolling bearings with three defects on the outer raceway. a Time domain response of horizontal acceleration. b Frequency spectrum of horizontal acceleration. c Time domain response of vertical acceleration. d Frequency spectrum of vertical acceleration

Full size image

From Fig. 4, 2fo is visible when the interval angle between the two defects is 20°. In addition, fo and 3fo can be found. This result is consistent with the conclusion in Ref. [36]. Comparing the time domain response in Figs. 4 and 5 shows that the shock peaks appear faster and faster as the number of defects increases. Reflected in the frequency spectrogram, only 3fo can be detected in Fig. 5.

Verification by Finite Element Models

First, the geometric model of the NSK 6205 bearing is constructed in SOLIDWORKS based on dimensional parameters. Two or three defects are set on the outer raceway, which are the same as those set in the simulation. Then, the geometric model is imported into ANSYS WORKBENCH to generate the finite element model shown in Fig. 6.

Fig. 6
figure 6

Finite element model of rolling bearings with two defects on the outer raceway

Full size image

Modulus of elasticity of 206 GPa, and a Poisson's ratio of 0.3. The cages are made of brass with a density of 8920 kg/m3, an elastic modulus of 100 GPa, and a Next, the model needs to be set up. The inner raceway, outer raceway, and rolling elements are made of bearing steel with a density of 7850 kg/m3, a Poisson's ratio of 0.36. The model is meshed by the automatic partitioning method in WORKBENCH with a mesh size of 3 mm. Due to the small size of the defects, the mesh at the defect location is encrypted to 0.1 mm. Depending on the installation and operating conditions of the bearing, some movements of the components need to be restrained. The translation and rotation of the outer raceway in the X, Y, and Z directions are constrained, and the translation of the inner raceway along the shaft is limited. Finally, the finite element model is solved, and the results are shown in Fig. 7 and 8.

Fig. 7
figure 7

Time–frequency response of the finite element model of rolling bearings with two defects on the outer raceway. a Time domain response of horizontal acceleration. b Frequency spectrum of horizontal acceleration. c Time domain response of vertical acceleration. d Frequency spectrum of vertical acceleration

Full size image
Fig. 8
figure 8

Time–frequency response of the finite element model of rolling bearings with three defects on the outer raceway. a Time domain response of horizontal acceleration. b Frequency spectrum of horizontal acceleration. c Time domain response of vertical acceleration. d Frequency spectrum of vertical acceleration

Full size image

In Fig. 7, 2fo is the primary frequency, similar to the asymptotic model results. However, fo and 3fo are drowned out by the noise. In Fig. 8, only 3fo can be detected. In addition, the amplitudes of both the time domain and frequency domain responses are different from those in Fig. 4, especially the frequency domain response. The possible reason is that the contact force and contact deformation are calculated based on Hertz contact in the simulation. However, Hertz contact is proposed based on some assumptions [38].

Verified by Experiments

To verify the above dynamics model, experiments of rolling bearings with multiple defects on the outer raceway are conducted on the test bed shown in Fig. 9.

Fig. 9
figure 9

Setup of rolling bearings test bed

Full size image

The test bed consists of a variable frequency motor, a two-stage gear booster, a shaft, a faulty bearing, and a loader. In the experiments, the same NSK 6205 bearing was used. Two defects or three defects were machined on the outer raceway by EDM wire cut. The width of the defects is 0.2 mm, and the depth is 0.1 mm. The interval between the two defects was set at 20°. Figure 10 shows the experimental bearing with two defects on the outer raceway. During the experiment, the shaft speed is set to 1800 r/min. The vibration data in the X and Y directions are recorded by SENTHER 510A-50 acceleration sensors and input to the LMS acquisition instrument. The sampling frequency is 12800 Hz. The results of the experiments are shown in Figs. 11 and 12.

Fig. 10
figure 10

Experimental bearing with two defects on the outer raceway

Full size image
Fig. 11
figure 11

Time–frequency response of the experiments of rolling bearings with two defects on the outer raceway. a Time domain response of horizontal acceleration. b Frequency spectrum of horizontal acceleration. c Time domain response of vertical acceleration. d Frequency spectrum of vertical acceleration

Full size image
Fig. 12
figure 12

Time–frequency response of the experiments of rolling bearings with three defects on the outer raceway. a Time domain response of horizontal acceleration. b Frequency spectrum of horizontal acceleration. c Time domain response of vertical acceleration. d Frequency spectrum of vertical acceleration

Full size image

From Fig. 11, it can be found that 2fo is clearly visible. Only 3fo can be detected in Fig. 5. It is worth noting that the experiment results contain more noise components, while the results of the asymptotic model contain mainly the characteristic frequency and its multiple frequencies. The reason is that external factors, such as the vibration of the test bed, are not considered when solving the asymptotic model of rolling bearings. In addition, since the experiments use piezoelectric sensors, the amplitude unit of the experimental response is voltage, which is not consistent with the acceleration of the simulated response.

After comparison, it can be concluded that the results of the asymptotic model agree with those of experiments and the finite element model. Therefore, the proposed model for rolling bearings with multiple defects on the outer raceway is correct and can be used to study the nonlinear characteristics of rolling bearings with multiple defects.

Results and Discussions

In this section, we will focus on the effect of multiple defects on the nonlinear characteristics of rolling bearings. In the following study, the parameters are set according to Table 1.

Influence of the Defect Number

The number of defects appearing on the outer raceway surface is not certain in the actual operation of rolling bearings. Therefore, it is necessary to explore the effects of the defect number so as to provide theoretical support for diagnosing rolling bearing defects.

Here, it is assumed that multiple defects are distributed between two adjacent rolling elements. Moreover, the lowest point in the vertical direction is assumed to be 0°, and the defects are evenly distributed at 10° intervals from the lowest point. Each defect has a width of 0.2 mm, and a height of 0.1 mm. Figures 13, 14, 15, 16, 17 and 18 show the phase trajectory and shaft center orbit of rolling bearings with different numbers of defects.

Fig. 13
figure 13

Rolling bearings without defects. a Phase trajectory in horizontal direction. b Phase trajectory in vertical direction. c Shaft center orbit

Full size image
Fig. 14
figure 14

Rolling bearings with one defect on the outer raceway. a Phase trajectory in horizontal direction. b Phase trajectory in vertical direction. c Shaft center orbit

Full size image
Fig. 15
figure 15

Rolling bearings with two defects on the outer raceway. a Phase trajectory in horizontal direction. b Phase trajectory in vertical direction. c Shaft center orbit

Full size image
Fig. 16
figure 16

Rolling bearings with three defects on the outer raceway. a Phase trajectory in horizontal direction. b Phase trajectory in vertical direction. c Shaft center orbit

Full size image
Fig. 17
figure 17

Rolling bearings with four defects on the outer raceway. a Phase trajectory in horizontal direction. b Phase trajectory in vertical direction. c Shaft center orbit

Full size image
Fig. 18
figure 18

Rolling bearings with five defects on the outer raceway. a Phase trajectory in horizontal direction. b Phase trajectory in vertical direction. c Shaft center orbit

Full size image

Figure 13 shows the phase trajectory and shaft center orbit of rolling bearings without defects. From Fig. 13, it can be seen that the phase trajectory and shaft center orbit show a regular elliptical shape, which also reflects the fact that there is no defect in the rolling bearing.

Figure 14 shows the phase trajectory and shaft center orbit of rolling bearings with one defect on the outer raceway. Compared with Fig. 13, the magnitudes of displacement and velocity response in both horizontal and vertical directions increase substantially. At the same time, the phase trajectory and shaft center orbit become more complex. The horizontal velocity climbs sharply at a certain moment due to the influence of the defect. However, this phenomenon was not clearly visible in the vertical direction. The probable reason is that the defect is set at the lowest point in the vertical direction. Since the vertical acceleration is the smallest at this lowest point, the increase in velocity response caused by the defect is minor.

Figures 15, 16, 17 and 18 show the phase trajectory and shaft center orbit of rolling bearings with different numbers of defects on the outer raceway, respectively. Compared to the case of rolling bearings with one defect on the outer raceway, the trajectories shown in Figs. 15, 16, 17 and 18 contain more track lines, which are very chaotic. As the defect number increases, the number of abrupt changes in the horizontal velocity increases significantly and matches the number of defects. Since not all defects are arranged at the lowest point in the vertical direction, there is also a significant abrupt change in the vertical velocity. However, there is still one defect located at the lowest point, such that the number of abrupt changes in the vertical phase trajectory is one less than the defect number. When five defects are evenly distributed on the raceway at 10°, the interval between the first and last defects is equal to that of the rolling element, which means that there will be two rolling elements in contact with the defects at the same time. Therefore, such a situation can be considered as having four defects distributed on the outer raceway, thus explaining why the number of abrupt changes shown in Fig. 18 is less than expected. Moreover, the superposition of the collision effects caused by simultaneous contact increases the amplitudes of displacement and velocity in the horizontal and vertical directions.

Figure 19 shows the frequency waterfall for rolling bearings with different numbers of defects on the outer raceway. From Fig. 19, it can be observed that the frequency at the maximum amplitude increases exponentially as the defect number increases. From the previous analysis, it is clear that the distribution of five defects on the outer raceway can be considered as the case of four defects. However, when five defects are distributed on the outer raceway, the frequency at the maximum amplitude is not 4fo but fo. It is noted that the amplitude of fo is more significant compared to the case where only one defect is distributed on the outer raceway. The reason for the above phenomenon is the superposition of the collision effects.

Fig. 19
figure 19

Frequency waterfall of rolling bearings with different numbers of defects

Full size image

Influence of the Defect Distribution

In addition to the defect number, the distribution of multiple defects also specifically influences the nonlinear characteristics of rolling bearings. In a practical rolling bearing, multiple defects appearing on the raceway may be uniformly or randomly distributed. Different distributions induce different dynamic behaviors and vibrations. Therefore, the effect of the distribution of multiple defects on the nonlinear dynamics of rolling bearings needs to be investigated. This section simulates a rolling bearing with two defects on the outer raceway to analyze the effects of different defect distributions. Each defect has a width of 0.2 mm and a height of 0.1 mm.

Different Distribution Modes

From the discussion in the previous section, the lowest point in the vertical direction was 0°, and the defects are evenly distributed at 10° intervals from the lowest point. This distribution mode resulted in all defects being distributed on the same side of the lowest point. Next, we will focus on the influence of different distribution modes on the nonlinear dynamic characteristics of rolling bearings. Here, the two defects are set at 30° and are distributed at different angles on both sides of 0°.

Figures 20, 21, 22 and 23 show the phase trajectory and shaft center orbit of rolling bearings under different distribution modes. With the gradual transition of defects from ipsilateral distribution to symmetrical distribution on both sides, the phase trajectory and shaft center orbit in the horizontal direction hardly change. While the number of abrupt changes in the vertical velocity gradually transitions from only one to two. Next, we will investigate the process by which the defects continue to transition. According to the conclusion from Figs. 20, 21, 22 and 23, only the phase trajectory in the vertical direction is shown here.

Fig. 20
figure 20

Two defects are distributed at (0°, 30°). a Phase trajectory in horizontal direction. b Phase trajectory in vertical direction. c Shaft center orbit

Full size image
Fig. 21
figure 21

Two defects are distributed at (− 5°, 25°). a Phase trajectory in horizontal direction. b Phase trajectory in vertical direction. c Shaft center orbit

Full size image
Fig. 22
figure 22

Two defects are distributed at (− 10°, 20°). a Phase trajectory in horizontal direction. b Phase trajectory in vertical direction. c Shaft center orbit

Full size image
Fig. 23
figure 23

Two defects are distributed at (− 15°, 15°). a Phase trajectory in horizontal direction. b Phase trajectory in vertical direction. c Shaft center orbit

Full size image

Observing Fig. 24, the number of abrupt changes in the vertical velocity gradually changes from two to only one, which is the opposite of the change process in Figs. 20, 21, 22 and 23. The disappearing abrupt change is precisely the one that already existed in Fig. 20b, not the new one in Fig. 23b. This result also confirms the conclusion that the abrupt changes at the lowest point are not noticeable.

Fig. 24
figure 24

Phase trajectory of rolling bearings in the vertical direction when the defect distribution changes further. a (− 20°, 10°). b (− 25°, 5°). c (− 30°, 0°)

Full size image

Different Distribution Intervals

In addition to the distribution mode of the defects, the distribution interval of multiple defects can also have a certain impact on the nonlinear dynamic characteristics of rolling bearings. In this section, we will investigate the influence of the defect distribution interval. The two defects of the outer raceway of rolling bearings are arranged at intervals of 10°, 20°, 30°, 40°, 90°, and 180°, respectively. Theoretically, the cases where the interval exceeds 40° all correspond to one case where the interval is less than 40°. Figures 25, 26, 27, 28, 29 and 30 show the phase trajectories and shaft center orbits of rolling bearings with different defect distribution intervals.

Fig. 25
figure 25

The interval of two defects is 10°. a Phase trajectory in horizontal direction. b Phase trajectory in vertical direction. c Shaft center orbit

Full size image
Fig. 26
figure 26

The interval of two defects is 20°. a Phase trajectory in horizontal direction. b Phase trajectory in vertical direction. c Shaft center orbit

Full size image
Fig. 27
figure 27

The interval of two defects is 30°. a Phase trajectory in horizontal direction b Phase trajectory in vertical direction. c Shaft center orbit

Full size image
Fig. 28
figure 28

The interval of two defects is 40°. a Phase trajectory in horizontal direction. b Phase trajectory in vertical direction. c Shaft center orbit

Full size image
Fig. 29
figure 29

The interval of two defects is 90°. a Phase trajectory in horizontal direction. b Phase trajectory in vertical direction. c Shaft center orbit

Full size image
Fig. 30
figure 30

The interval of two defects is 180°. a Phase trajectory in horizontal direction. b Phase trajectory in vertical direction. c Shaft center orbit

Full size image

Figure 25 shows the phase trajectory and shaft center orbit of rolling bearings when the interval of the two defects is 10°. In Fig. 25a, two distinct velocity abrupt processes can be seen, and only one can be seen in Fig. 25b. This is consistent with the conclusion obtained in the previous section. However, the degree of abrupt change in the vertical velocity is not apparent. The possible reason for this phenomenon is similar to that for which only one abrupt change can be seen in the vertical velocity. Since both defects are close to the lowest point in the vertical direction, the degree of abrupt change in the vertical velocity is not obvious.

Figure 26 shows the phase trajectory and shaft center orbit of rolling bearings when the interval of the two defects is 20°. Compared with the trajectory in Fig. 25, the two trajectory lines triggered by the defects have almost no overlap in Fig. 26, and their amplitudes are relatively small. The reason for this phenomenon is that the increase in the defect interval allows enough time for the trajectories to return to normal. It is also due to the increase of the defect interval that the degree of abrupt change in the vertical velocity enhances, and the distance between two abrupt changes in the horizontal velocity increases.

Figure 27 shows the phase trajectory and shaft center orbit of rolling bearings when the interval of two defects is 30°. Theoretically, the results in this case should be approximately the same as those when the interval of two defects is 10°. Comparing Fig. 27 with Fig. 25, it can be found that the trajectories in the two figures are basically the same. What makes the difference is that the distance between the two abrupt changes in the horizontal velocity increases due to the increase of the defect interval, and the abrupt change in the vertical velocity is obvious.

Figure 28 shows the phase trajectory and shaft center orbit of rolling bearings when the interval of two defects is 40°. At this time, the interval between the two defects is exactly equal to that of two adjacent rolling elements. In other words, there will be two rolling elements in contact with the two defects at the same time. This case should be similar to the case where there is only one defect, as evidenced by the fact that there is only one abrupt change in the horizontal velocity in Fig. 28a. Also, the amplitude increases compared to Fig. 10, which is caused by the interaction of the two defects.

Figure 29 shows the phase trajectory and shaft center orbit of rolling bearings when the interval of the two defects is 90°. Theoretically, the result of this case should be the same as that of the case when the interval is 10°. However, the trajectories in Fig. 29 differ greatly from those in Fig. 25. The amplitude of the vertical velocity in Fig. 29 is significantly larger. In addition, there is only one abrupt change in the horizontal velocity, which is inconsistent with the fact of two defects. The reason for this phenomenon may be similar to the reason why the vertical velocity has only one abrupt change. That is, the defect is set at the end of the horizontal direction.

Figure 30 shows the phase trajectory and shaft center orbit of rolling bearings when the interval of two defects is 180°. Theoretically, the result of this case should be the same as that when the interval is 20°. However, comparing Fig. 30 with Fig. 26, it can be found that the trajectories in the two figures differ greatly. The amplitude of the phase trajectory in Fig. 30 is significantly larger. In addition, the vertical velocity has no obvious abrupt change, which is inconsistent with the fact of two defects. This phenomenon may be caused by that the defects are set at two extremes of the vertical direction.

Figure 31 shows the frequency waterfall of rolling bearings with different defect distributions. From Fig. 31, it can be noticed that the spectrum contains mainly fo and its high multiples. When the interval of two defects is 10°, 30°, 40°, and 90°, fo is the main component. When the interval is 20° and 180°, 2fo is the main component.

Fig. 31
figure 31

Frequency waterfall of rolling bearings with different defect distributions

Full size image

Influence of Defect Width

During actual manufacture and service, the dimensions of the defects appearing on the raceways may be random. This section investigates the influence of the defect width on the nonlinear dynamics of rolling bearings. Two defects with the same width and a height of 0.1 mm are arranged on the outer raceway of rolling bearings at an interval of 20°. Figures 32, 33, 34, 35 and 36 show the phase trajectories and shaft center orbits of rolling bearings with defects of different widths.

Fig. 32
figure 32

The defect width is 0.1 mm. a Phase trajectory in horizontal direction. b Phase trajectory in vertical direction. c Shaft center orbit

Full size image
Fig. 33
figure 33

The defect width is 0.2 mm. a Phase trajectory in horizontal direction. b Phase trajectory in vertical direction. c Shaft center orbit

Full size image
Fig. 34
figure 34

The defect width is 0.3 mm. a Phase trajectory in horizontal direction. b Phase trajectory in vertical direction. c Shaft center orbit

Full size image
Fig. 35
figure 35

The defect width is 0.4 mm. a Phase trajectory in horizontal direction. b Phase trajectory in vertical direction. c Shaft center orbit

Full size image
Fig. 36
figure 36

The defect width is 0.5 mm. a Phase trajectory in horizontal direction. B Phase trajectory in vertical direction. c Shaft center orbit

Full size image

Comparing Figs. 32, 33, 34, 35 and 36, it can be found that the shape of the phase trajectory in both horizontal and vertical directions is almost unchanged. The amplitude of the phase trajectory increases dramatically with the aggravation of the defect width. It illustrates that the change of the defect width intensifies the vibration of the rolling bearing and thus reduces the accuracy of the bearing operation.

Figure 37 shows the frequency waterfall diagram of rolling bearings with different width defects on the outer raceway. From Fig. 37, it can be observed that the frequency spectrum mainly contains fo and its high multiples. Since the outer raceway has two defects, the main frequency component is 2fo. As the width increases, the amplitude of the primary frequency component gradually increases.

Fig. 37
figure 37

Frequency waterfall of rolling bearings with different width defects on the outer raceway

Full size image

Conclusions

In this paper, an asymptotic model of rolling bearings with multiple defects on the outer raceway was established, and the influence of raceway defects on the nonlinear dynamic behavior was explored. With the help of phase trajectories, shaft center orbits, and frequency waterfall diagrams, the influence of defect number, defect distribution, and defect width on the nonlinear dynamic behavior of the bearing was investigated. The following conclusions were drawn.

  • (1) Defects complicate the motion of rolling bearing systems. The horizontal velocity climbs sharply at a certain moment due to the influence of defects.

  • (2) As the defect number increases, the number of abrupt changes in the horizontal velocity increases significantly, which matches the defect number. The frequency at the maximum amplitude also increases exponentially.

  • (3) Due to the increase of the defect interval, the abrupt change in the vertical velocity enhances, and the distance between two abrupt changes increases. When multiple defects are unevenly distributed within the interval of two adjacent rolling elements, the main component of frequency is the characteristic frequency of the rolling element passing through defects on the outer raceway. When multiple defects are evenly distributed, the multiplier of characteristics frequency is the main component.

  • (4) As the defect width intensifies, the shape of the phase trajectory in both horizontal and vertical directions remains almost unchanged, but the amplitude increases substantially. The amplitude of the multifrequency component also gradually increases.

In this paper, the effect of clearance on the bearing stiffness was not considered in the analysis and will be included in subsequent studies.